与晶体的压电效应不同,孔隙介质动电效应与界面双电层、孔隙的连通性/渗透性密切相关(Pride,1994;胡恒山等,2003;金鼎等,2010). 因此,利用动电效应进行地层参数的评估也成为目前地下油气勘探的一个新方向(严洪瑞等,1999;Zhu et al.,1999,崔志文,2004;Dupuis and Butler,2006;Haines et al.,2007;高永新和胡恒山,2009;王军等,2010;Revil and Jardani,2010;关威等,2011;Jouniaux and Ishido,2012),如动电效应测井,该方法希望利用井中声波诱导的动电转换信号来分析被测地层特性(胡恒山和王克协,1999,2000;Zhu and Toksöz,2003;Guan et al.,2013a,2013b;门百永等,2013;Li et al.,2014,王军等,2015,2016). 动电测井中动电转换信号的强弱、电场特性及其与地层参数的关系取决于两个因素:一是声波信号的强度和基本特性;二是声场和电场的耦合特性. 由于动电效应激发的电场对声场本身的影响极小,那么在声场特性已知的前提下(如需要可依据声波测井理论获得),流体饱和孔隙介质的动电耦合特性决定了动电场的幅度和特性. 虽然已有描述动电耦合特性的参数以及计算公式(Pride,1994;Glover et al.,2012),但是这些公式本身是在一定的假设条件下得出来的,而且公式中包含着必须通过实验才能确定的参数. 比如,目前被大家广泛认可的动电耦合系数(Pride,1994),其定义表达式中含有一个物理量(zeta电势),必须通过实验来确定(Perrier and Froiderond,2003;王军等,2011;Wang et al.,2015). 因此,通过实验测量的方式研究动电耦合特性是必不可少的.
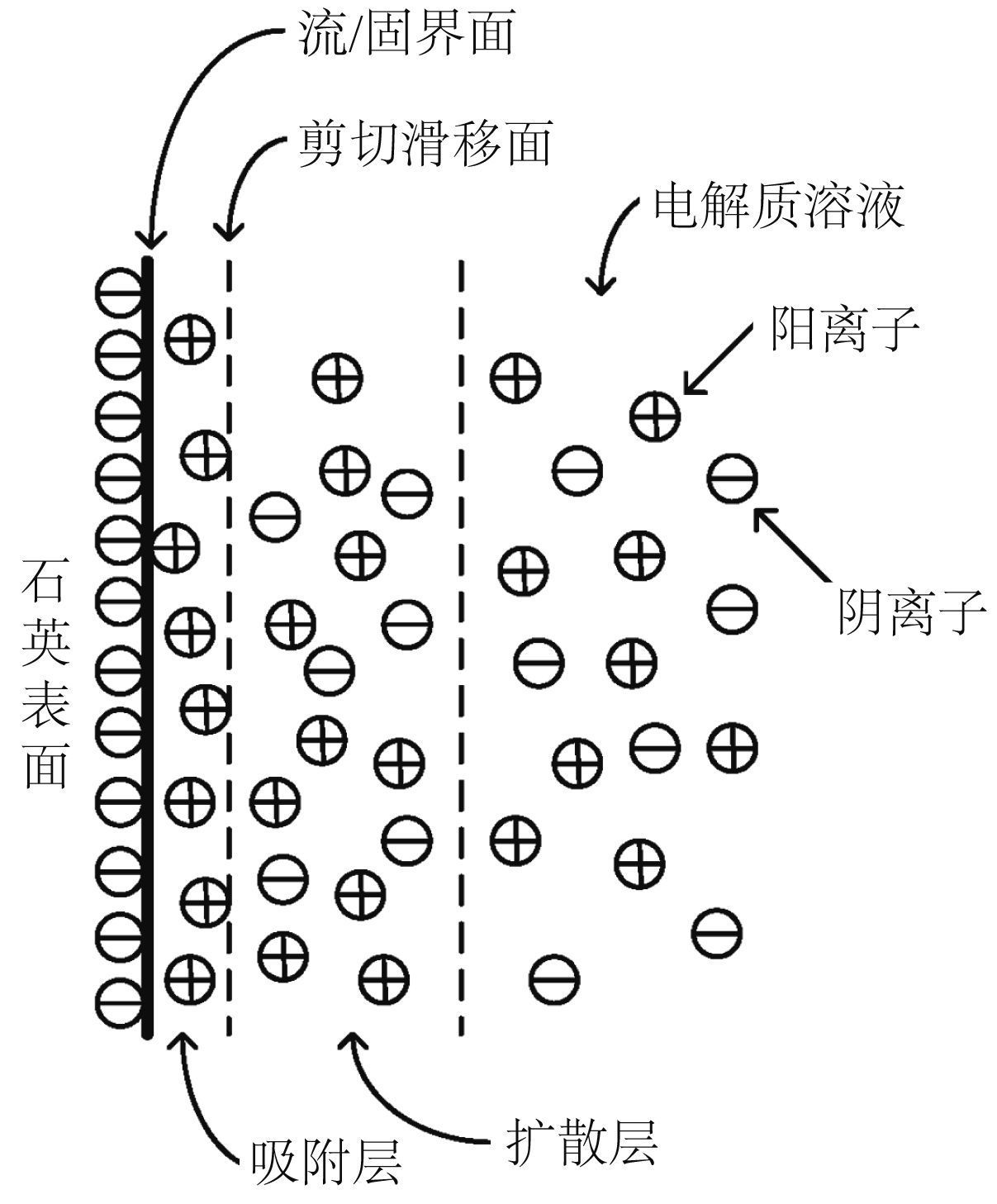
双电层是激发动电现象的前提,常见于岩石的固体-流体界面(Morgan et al.,1989),如图 1所示的含水石英砂岩界面双电层,石英表面会吸附溶液中的阴离子,使溶液中出现净剩阳离子,从而构成吸附层和扩散层,这两层一起称为双电层结构. 吸附层很薄,只有纳米量级的厚度(Ishido and Mizutani,1981;Jackson and Leinov,2012);而扩散层的厚度与孔隙流体的离子浓度有关,一般远大于吸附层. 吸附层和扩散层由剪切滑移面分开,一般认为吸附层中离子是不易流动的,扩散层离子可在电场力作用下移动,也可伴随流体运动而移动(Pride,1994). 井下声波之所以引起电场,就是因为动电效应引起双电层中净剩离子和固相骨架之间发生相对运动,形成流动电流(streaming current),进而使孔道两端出现电势差,即所谓的“流动电势”(streaming potential). 单位压强梯度下的流动电势被称为流动电势系数(Pengra et al.,1999),其量纲为[V/Pa],该系数反映了流体饱和孔隙介质的动电耦合能力(Jouniaux and Pozzi,1995;Zhu and Toksöz,2013).
考虑到动电测井记录到的电信号即为流动电势,且目前很难在实验室或现场进行大量动电测井测量,因此针对小岩样的流动电势实验是研究动电特性的较好途径(Revil et al.,1999),它能够更好地分析不同状态下动电场与声场信号的相关性和差异性,包括不同浓度、温度、饱和度、渗透率等,从而可研究这些参数对流动电势(流动电势系数) 的影响,探讨利用动电测井可对哪些地层参数进行有效探测. 本文则通过多块参数不同岩样的流动电势实验,分析了岩石动电耦合特性随溶液浓度、岩样渗透率和泥质含量的变化规律,为动电测井的可行性提供实验基础.
|
图 1 双电层模型示意图 Fig. 1 Schematic diagram of double-layer electric model |
岩石流动电势的实验测量源于电化学领域熟知的毛细管动电现象(Ishido and Mizutani,1981),描述毛细管中流动电势的著名公式(Helmholtz-Smoluchovski,缩写为HS) 为
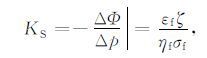
|
(1) |
式中流动电势系数 KS 是测量到的流动电势 ΔΦ 与流体压强差 Δp 的比值, KS 与孔隙流体介电常数 εf、黏度ηf 和电导率 σf 以及双电层zeta电势(ζ) 有关. 由于目前无法直接测量zeta电势,不能证明毛细管HS公式可适用于孔隙介质. 但人们提出有效zeta电势的思想,将HS公式应用于包括地下岩石在内的孔隙介质. 对于孔隙岩石而言,式(1) 中的电导率σf应包括自由流体电导率和表面电导率. 后者与固-液界面附近的表面电导以及岩石的微观结构(如孔隙度、胶结指数和粒径等) 有关,以至于HS被改写为
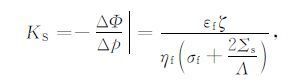
|
(2) |
式中的 Σs 为表面电导率, Λ 为反映孔隙微观结构的特征尺寸(有效半径). 对于黏土含量高或矿化度低的岩石,表面电导的影响较大(王军等,2011).
上述HS公式在薄双电层假设条件下,被认为是合理的. 薄双电层假设是指:双电层中的扩散层厚度远小于孔隙半径,净剩电荷集中在固-液界面附近,扩散层中的净剩电荷密度呈Maxwell-Boltzmann分布,随远离界面距离的增大而减小. 与之相反的厚双电层假设是指:双电层厚度大于孔隙半径,净剩电荷均匀分布在整个孔隙空间,净剩电荷密度为常数. Revil和Mahardika(2013)给出了厚双电层假设时的流动电势系数表达式:
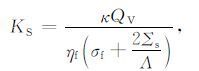
|
(3) |
式中的 κ 为渗透率, QV 为孔隙流体流动引起的净剩电荷密度. Jackson和Leinov(2012)的研究表明:大部分的天然岩石满足薄双电层假设.
上述公式是基于毛细管流动电势理论获得,Li等(1995)和Pengra等(1999)从Pride动电耦合方程组出发,结合实验测量原理,给出流动电势系数的另一种关系式:
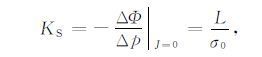
|
(4) |

|
(5) |
其中 J 为电流, L 为动电耦合系数, φ 为孔隙度, α∞ 为岩样弯曲度, σ0 为岩样在压强差为零时的电导率.(4) 式假设岩石样品在颗粒尺度上是均匀的,而且加载信号的波长要远大于样品的长度,这样当 J=0 时,系统达到平衡,通过测量岩样两端的电势差 ΔΦ 和作用于岩样两端的流体压强差 Δp 便可获得岩样的流动电势系数 KS. 进而可获得动电耦合系数L. 此外,通过(4) 式可以看出, KS与L 成正比关系,因此,流动电势系数与动电耦合系数具有相似的物理意义,能够反映孔隙介质的动电耦合特性.
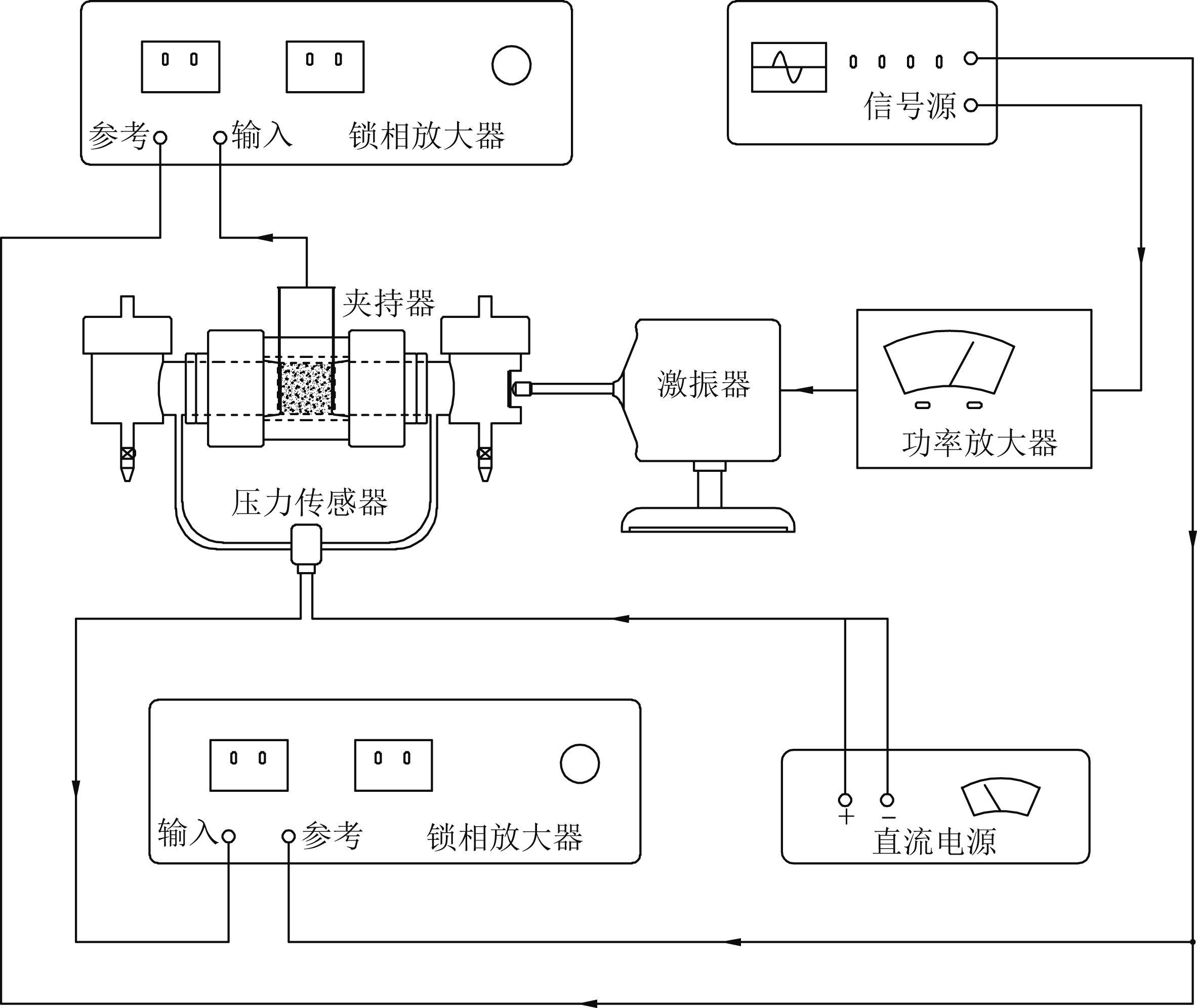
2.2 实验原理及测量系统本文按照Li等(1995)实验原理设计流动电势实验. 图 2是实验测量系统流程图,图 3为岩心夹 持器和激振器实物. 实验中激振杆提供周期的振动信号,通过振动膜将压力传递给水平管道中的液体,并在岩样两端形成压力差,从而激发动电现象发生,产生流动电流和流动电势. 当系统平衡后,利用Ag/AgCl电极测量流动电流和流动电势;利用差压传感器(Honeywell 26PC) 测量岩样两端的压差,然后利用锁相放大器将压力差信号和流动电势(流动电流) 信号检测出来. 实验时保持信号源和功率放大器的输出不变,利用锁相放大器测量差压传感器的输出信号,同时,选择另一台锁相放大器的电流档或电压档分别测量电流和电压,这样就能得到相同压差条件下的流动电流和流动电势,进而得到流动电流系数和流动电势系数. 由于实验装置及测量方法与王军等(2010,2011) 相同,本文不再详细描述实验测量流程,将主要针对测量结果进行实验分析.
|
图 2 流动电势实验测量系统原理图 Fig. 2 Diagram showing principle of streaming potential measurement system |

|
图 3 岩心夹持器和激振器实物图 Fig. 3 Core holder and vibrator for streaming potential measurement |
表 1给出本文所用岩石样品的物性参数,岩石样品是从同一口井中获取,深度在地下2390~2550 m之间,表中参数由中石油测井技术中心提供. 岩石样品的形状为圆柱体,端面直径2.54 cm,长度约2 cm. 岩样在使用前进行了洗油和洗盐处理,并进行加压饱和. 本文在不同浓度的NaCl饱和溶液中进行了流动电势实验,其浓度分别为0.02 mol/L、0.05 mol/L、0.1 mol/L、0.2 mol/L、0.4 mol/L和0.6 mol/L. 实验室温度约为25 ℃±0.5 ℃,饱和溶液pH值为6.4±0.3.
|
|
表 1 岩样物性参数 Table 1 Parameters of physical properties of rock samples |
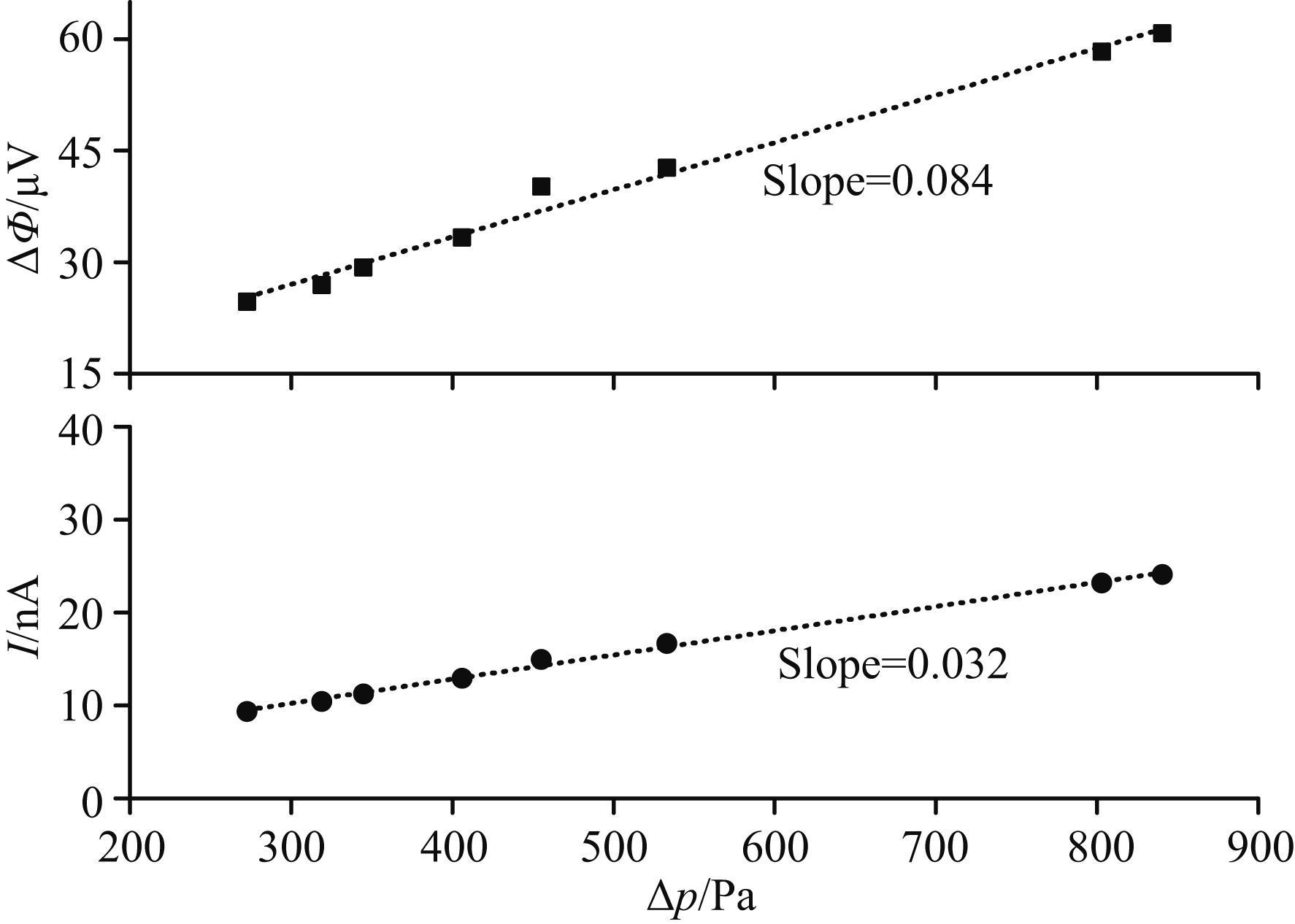
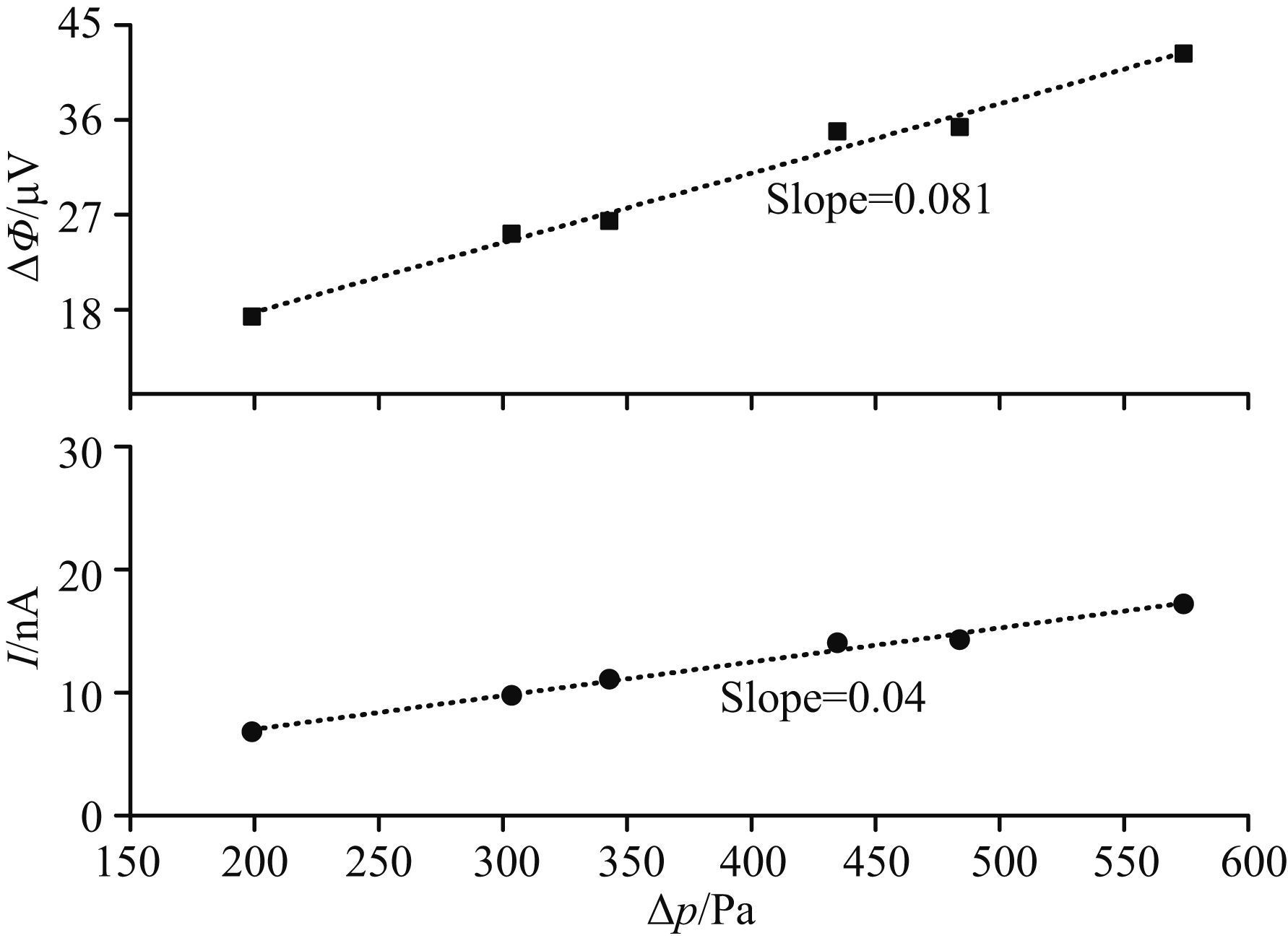
图 4和图 5分别是岩样D1和D2在激发频率 为7 Hz时的测量数据. 实验使用NaCl饱和溶液的浓度为0.02 mol/L,图中给出了岩样D1和D2的流动电势(ΔΦ) 和流动电流(I) 随外界压力差变化的规律. 由两图可以看出,流动电势和流动电流与外界激励形成的压力差成正比关系,即随着压力差增大,流动电流和流动电势均增大. 但这种线性关系在压力差很大的情况下(Δp>100 kPa) 就不再成立,Morgan等(1989)实验结果表明,当压力差从10 kPa增大到300 kPa时,流动电势系数减小1/4~1/2. 这是因为压力差过大,破坏了原有的孔道结构,甚至将部分孔道压裂,甚至坍塌堵塞了孔道,从而对动电效应产生严重影响. 因此,本文中最大压强差为几千帕,以保证岩样内部结构不被破坏. 依据流动电势系数KS和流动电流系数KSC的定义(KS=ΔΦ/Δp,KSC=I/Δp) 可知,ΔΦ-Δp和I-Δp曲线的斜率即为KS和KSC,如图 4中岩样D1的KS=84 nV/Pa,KSC=32 pA/Pa. 因此,采用在同一频率点,施加不同压力驱动的方法,可得该频率下的流动电势系数和流动电流系数,然后在其他频率点重复应用此方法便可获得整个频率范围内KS和KSC,进而可分析动电耦合系数的频率响应特性.
|
图 4 岩样D1的流动电势和流动电流与压强差关系 Fig. 4 Streaming potentials and currents of sample D1 versus applied pressure differences |
|
图 5 岩样D2的流动电势和流动电流与压强差关系 Fig. 5 Streaming potentials and currents of sample D2 versus applied pressure differences |
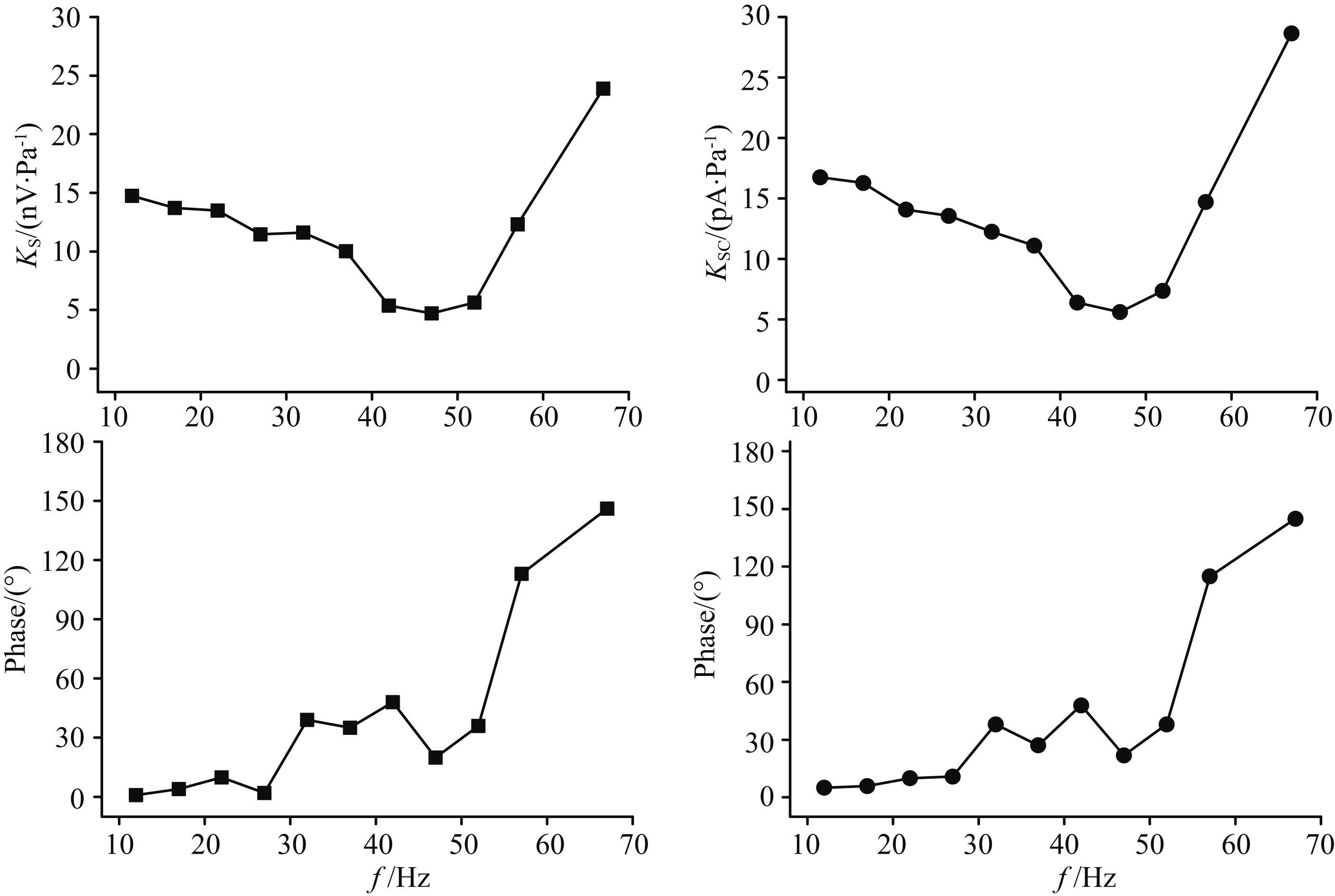
图 6为一块代表性岩样(D3) 的KS和KSC随频率变化的响应曲线,样品的饱和浓度为0.1 mol/L. 由图 6看出,岩样的KS和KSC具有相似的频率响应关系,这是因为两者之比为岩样电阻,它在实验测量频率下(低于100 Hz) 是几乎不变的. 在10~70 Hz频率范围内KS和KSC的幅度均出现一个凹点,而且凹点频率附近KS和KSC的相位急剧减小. Pengra等(1999)实验结果中也出现类似现象,并指出是传感器的响应造成. 但我们选用不同的差压传感器(Honeywell 26PC、Omega PX26(Pengra et al.,1999) 和PX163),对同一样品进行重复测量,发现凹点并没有发生变化. 而实验的原始数据(图 7) 表明:在凹点频率附近测量到的压力差突然变大,但此时流动电势并没有同步的增大,从而使得此频率KS和KSC计算结果变小,该结果与图 4和图 5中实验规律相悖. 此外,Pride(1994)推导动电耦合系数的表达式时,还模拟了耦合系数的频率响应,其结果表明:在低频范围内(低于1000 Hz),动电耦合系数不随频率的变化而改变,且数值近似为直流情况下的动电耦合系数. 因此,我们猜测凹点现象可能是由动电测量系统的机械部分引起.
|
图 6 岩样D3的流动电势系数和流动电流系数随频率变化关系 Fig. 6 Frequency responses of streaming potential and streaming current coefficients of sample D3 |
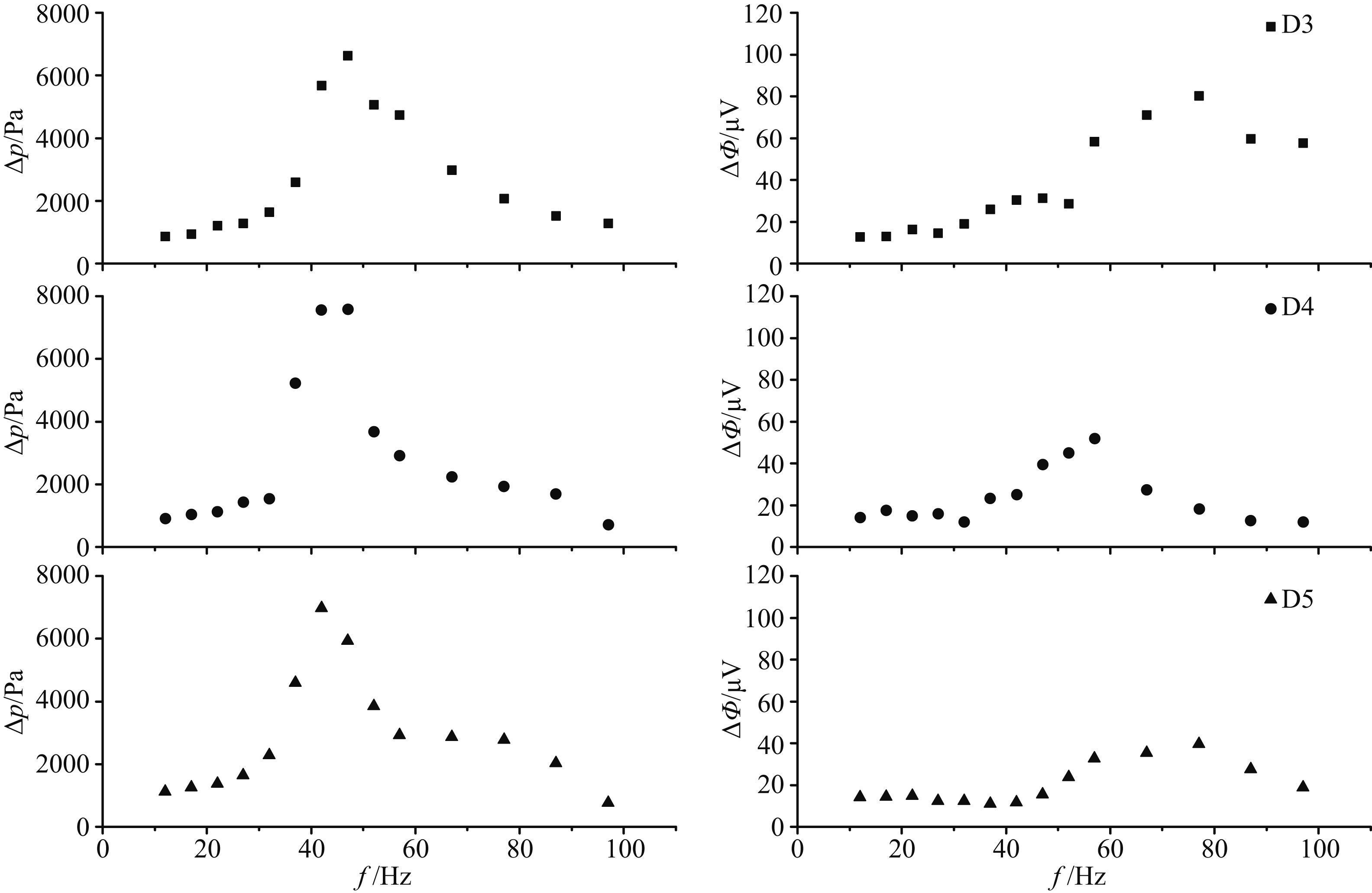
另外,分析实验数据发现:针对不同岩样实验,测量到的压力差峰值所对应的频率均为42 Hz,如图 7中所示的三块岩样D3、D4、D5,若凹点现象是岩样自身特性的话,这有些不合情理,因为3块岩样自身的参数是不同的(见表 1),所以这种情况说明凹点现象并非岩样本身的频率响应特性,而是由其他因素引起的,与岩样参数无关.在实验进行中我们还发现,在凹点频率附近测量时夹持器的震动非常剧烈,并伴随“嗡嗡”声. 综上分析得出:凹点频率可能是夹持器的固有频率,故在此频率附近测量时引起夹持器共振,导致测量的压力差不再是引起流动电势现象的真实值,而是一个共振压力差,从而出现凹点现象. 为了验证这一结果,我们重新制作了一个更重一些的夹持器,发现凹点对应频率变低. 虽然凹点频率变低不利于实验测量,但说明我们的分析是正确的,这为改进流动电势实验装置设计提供了思路.
|
图 7 岩样D3、D4和D5的流动电势和压力差随频率变化结果 Fig. 7 Measured streaming potentials and pressure differences of three samples(D3,D4,D5)with different frequencies |
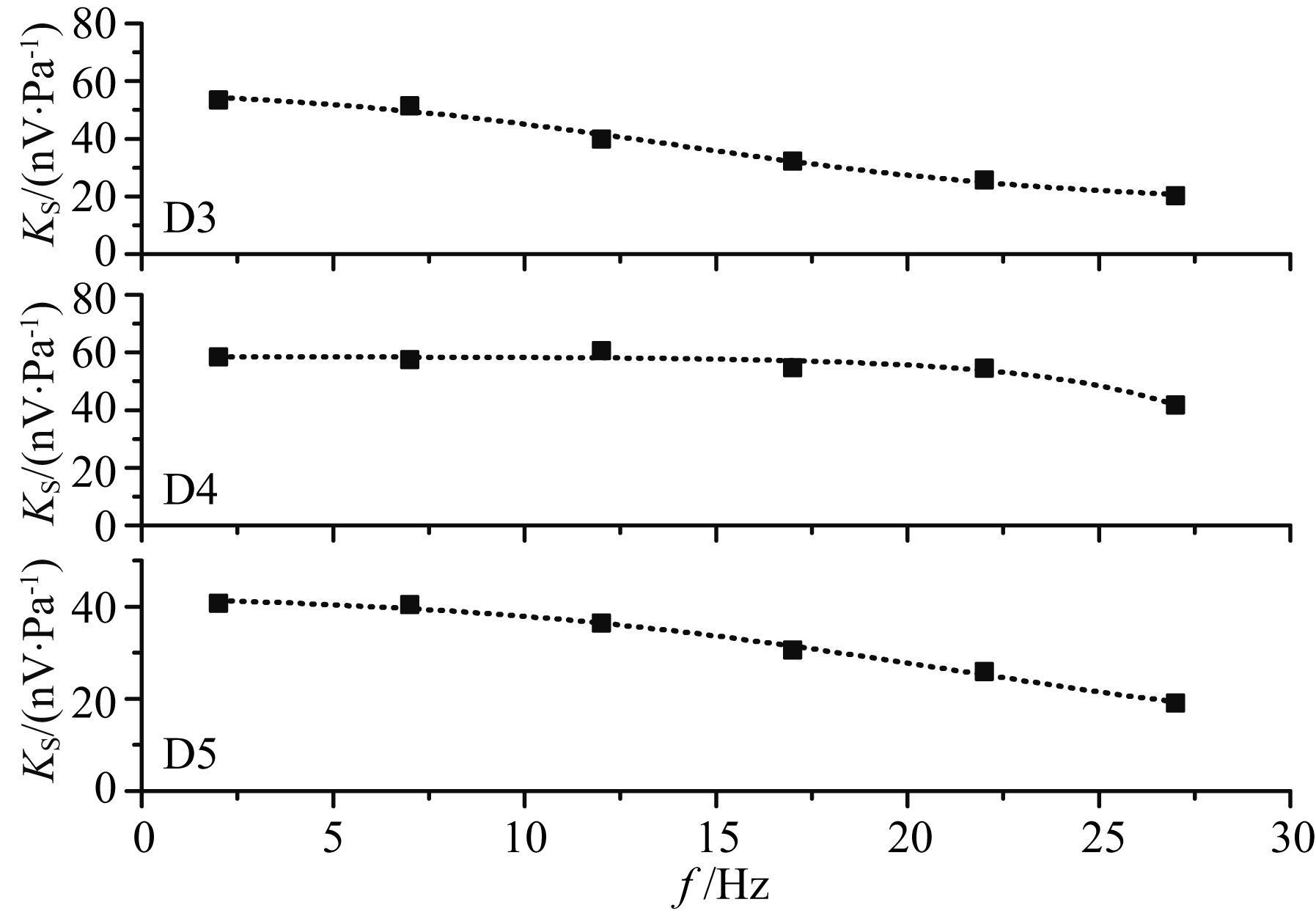
但重要的是,凹点现象不会影响KS和KSC在低频极限情况下的结果,通过图 7可以看出,当频率低于27 Hz后,流动电势还是趋于稳定的. 因此,我们在饱和浓度为0.02 mol/L情况下,对上述岩样进行了重复测量,获得了较理想的实验结果(见图 8). 而且利用KS和KSC计算了岩样的动电渗透率,并将实验结果与气渗透率进行对比. 结果表明,实验获得的动电渗透率与气渗透率具有很好的相关性(王军等,2010). 这说明本文实验数据是有效的,而且在较低浓度下实验数据的有效性增强(见图 8). 我们在3.2节进一步分析饱和溶液浓度对流动电势系数的影响. 此外,针对地震过程中的动电效应而言,由于地震波的频率通常为几赫兹,甚至更低. 因此,我们的实验结果还对地震波引起动电现象的研究有参考价值.
|
图 8 岩样在0.02 mol/L饱和溶液中的流动电势系数 中文注解 Fig. 8 Measured streaming potential coefficients in saturated solution with 0.02 mol/L concentration 英文注解 |
|
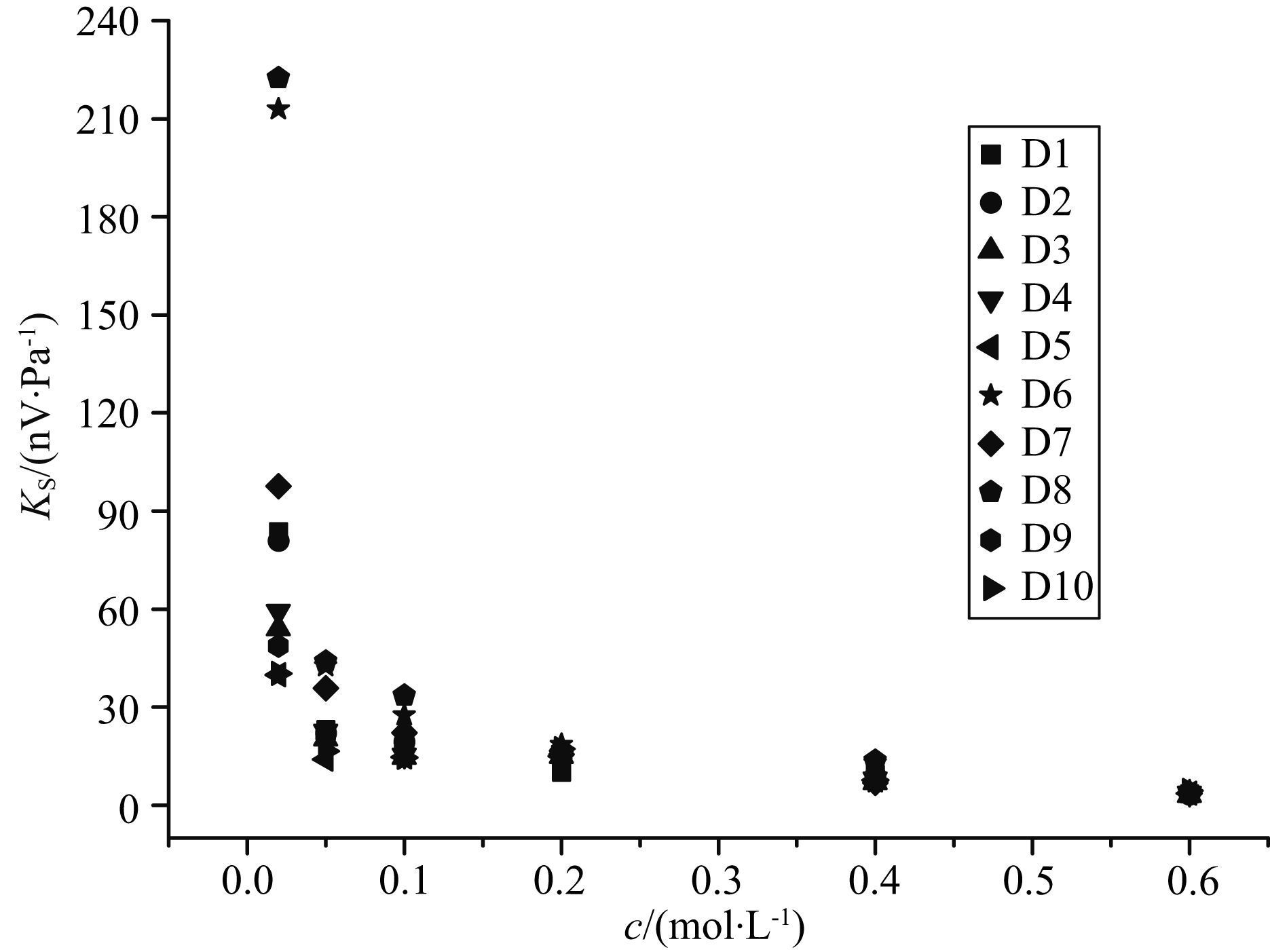
图 9 岩样流动电势系数与溶液浓度的关系 Fig. 9 Streaming potential coefficients of rock samples versus solution concentrations |
|
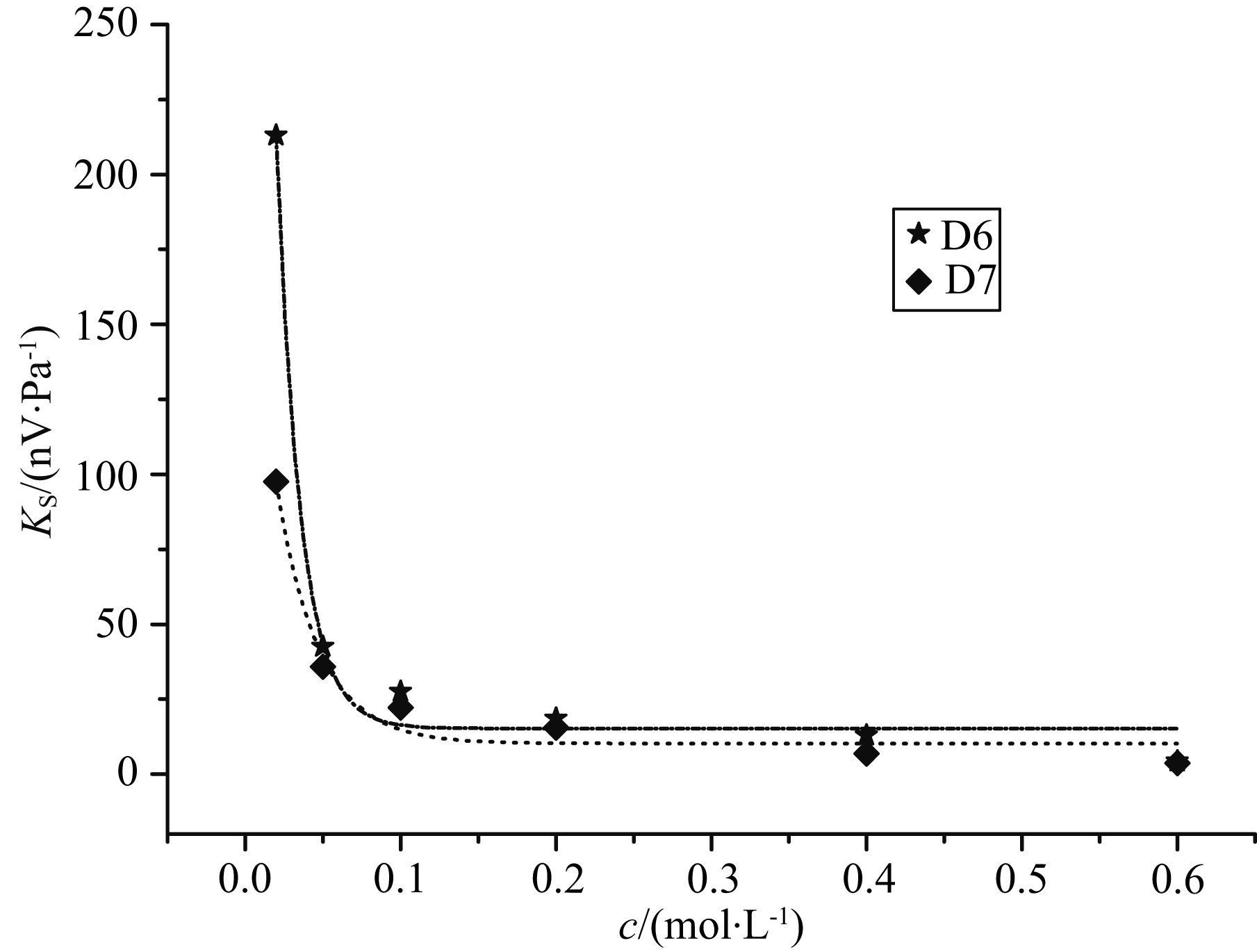
图 10 岩样D6和D7的流动电势系数与溶液浓度的关系 Fig. 10 Streaming potential coefficients of samples D6 and D7 versus solution concentrations |
饱和溶液浓度是影响动电现象的重要因素之一,因此,我们在不同饱和浓度下进行了岩样的流动电势实验. 由于流动电流系数和流动电势系数具有相似的变化规律,下文仅针对流动电势系数进行分析. 图 9给出了10块岩样在6种饱和浓度下的实验结果,为了更清晰地分析样品流动电势系数(KS) 随浓度变化的规律,我们另外绘出其中两块样品KS随溶液浓度变化的结果,见图 10. 上述结果表明:KS随饱和溶液浓度的降低而增大,呈指数规律变化,特别是在较低浓度溶液中,KS增大幅度较大. 这说明流动电势效应在低浓度溶液中更强. 从本文结果中还可得出,随着溶液浓度的增大,不同岩样KS之间的差距在缩小,当溶液浓度为0.6 mol/L时,10块岩样的KS值几乎相等,约为3.5 nV/Pa,见图 9. 这一现象表明:在高浓度溶液饱和情况下,流动电势实验获得的数据将较难区分不同岩样的动电特性,因为所有样品的KS都非常接近,这样依据前文公式(2)、公式(5) 计算出的zeta电势和动电耦合系数,也必将十分接近. 因此,在高浓度情况下,利用流动电势的幅度很难对不同岩样的动电特性进行区分,进而使得利用动电信号进行地层评价的有效性降低.
但上述结果还表明了动电效应的另一个特性,即在高浓度溶液饱和情况下,流动电势现象(动电现象) 并没有消失,只是这种耦合能力非常微弱(KS约为3.5 nV/Pa). Jaafar等(2009)在更高浓度范围内进行了流动电势实验,当浓度在0.4~5.5 mol/L变化时,流动电势系数从2.8 nV/Pa减小到0.12 nV/Pa,变化量不足3 nV/Pa. 其结果表明当饱和溶液浓度高于0.4 mol/L时,KS随浓度增大而减小的程度非常缓慢,而且即使在接近海水(浓度约为7 mol/L) 饱和情况下,动电转换依然存在(Perrier and Froiderond,2003). 因此,若不利用动电信号的幅度对地层参数进行直接评价,而只考虑动电信号的到时信息来间接评价地层参数,在高浓度溶液饱和情况下,进行动电勘探也是有价值的,如利用动电测井的时域波形来提取地层波速(Zhu et al.,1999;王军等,2015,2016),因为该技术只需要动电转换波的到时信息便可获得被测地层的纵横波速度,进而评价地层的力学特性. 而且目前声波测井换能器在井中激发声压信号可达到70 kPa(门百永等,2013),依据该声压幅度进行动电测井时,可得到的流动电势为8 μV量级(KS=0.12 nV/Pa),考虑现有检测设备的性能,该量级的电信号是可测量的,因此,在进行动电测井时需要考虑被测地层的矿化度,以有效利用动电测井数据进行地层参数评价. 低矿化度地层中,动电测井信号的幅度及到时信息均有效,而高矿化度地层中,只有动电信号的到时信息是可靠的.
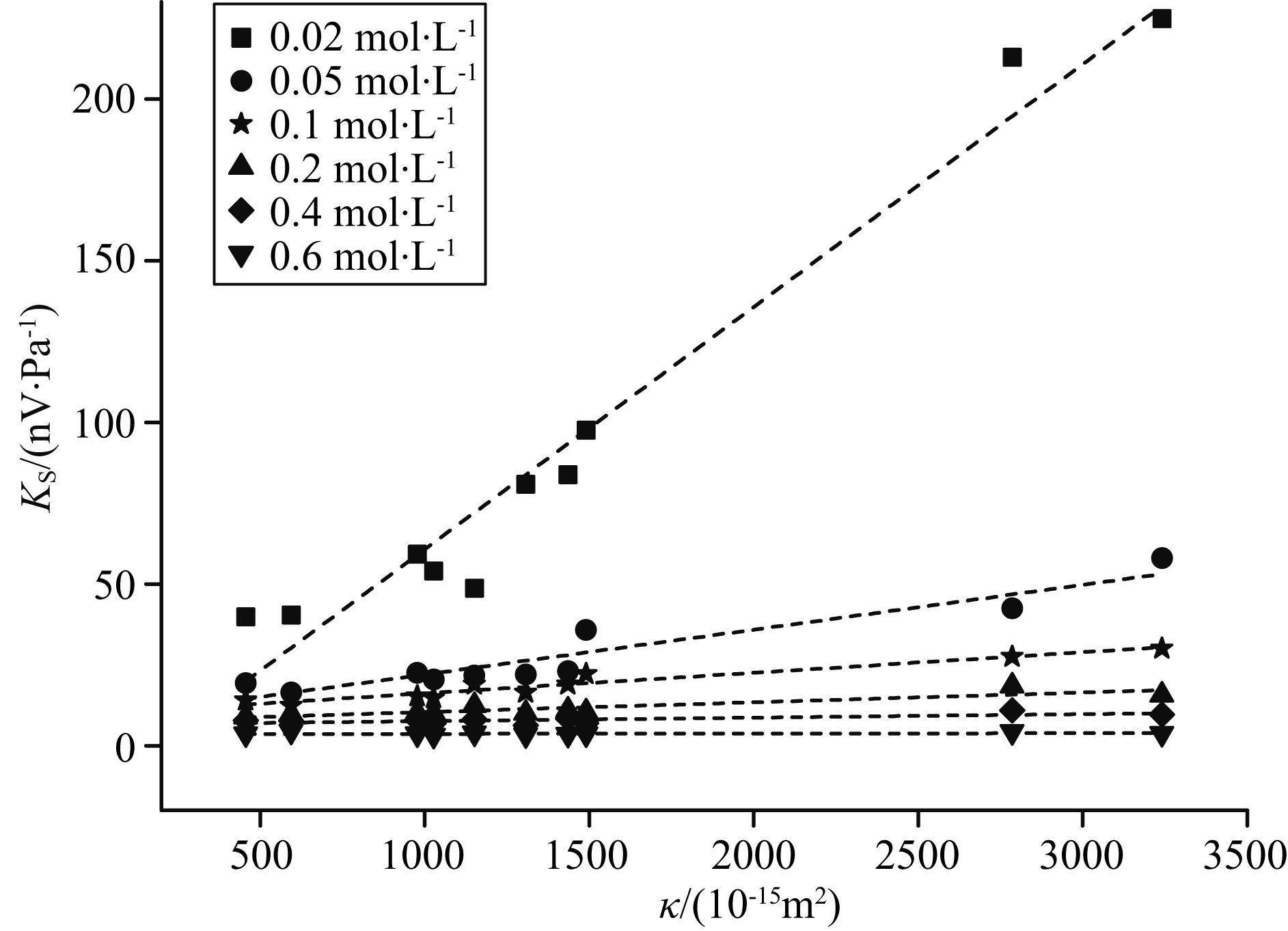
3.3 渗透率对流动电势系数的影响图 11和图 12给出了10块样品在不同浓度饱和溶液中,渗透率与流动电势系数的关系,由图 11看出,当溶液浓度为0.02 mol/L时,流动电势系数与渗透率成明显的正比关系. 此现象与我们的预期一致,因为动电效应的本质是孔道内流动的液流和电流之间的耦合作用,渗透率则反映着孔道内部流体的流通性. 因此,渗透率越高,流体的流通性越强,进而激发的动电效应越强. 而且结合公式(4) 和公式(5) 可知,流动电势系数与弯曲度成反比,而通常情况下,弯曲度是与渗透率成反比的,因此,流动电势系数与渗透率成正比是合理的.
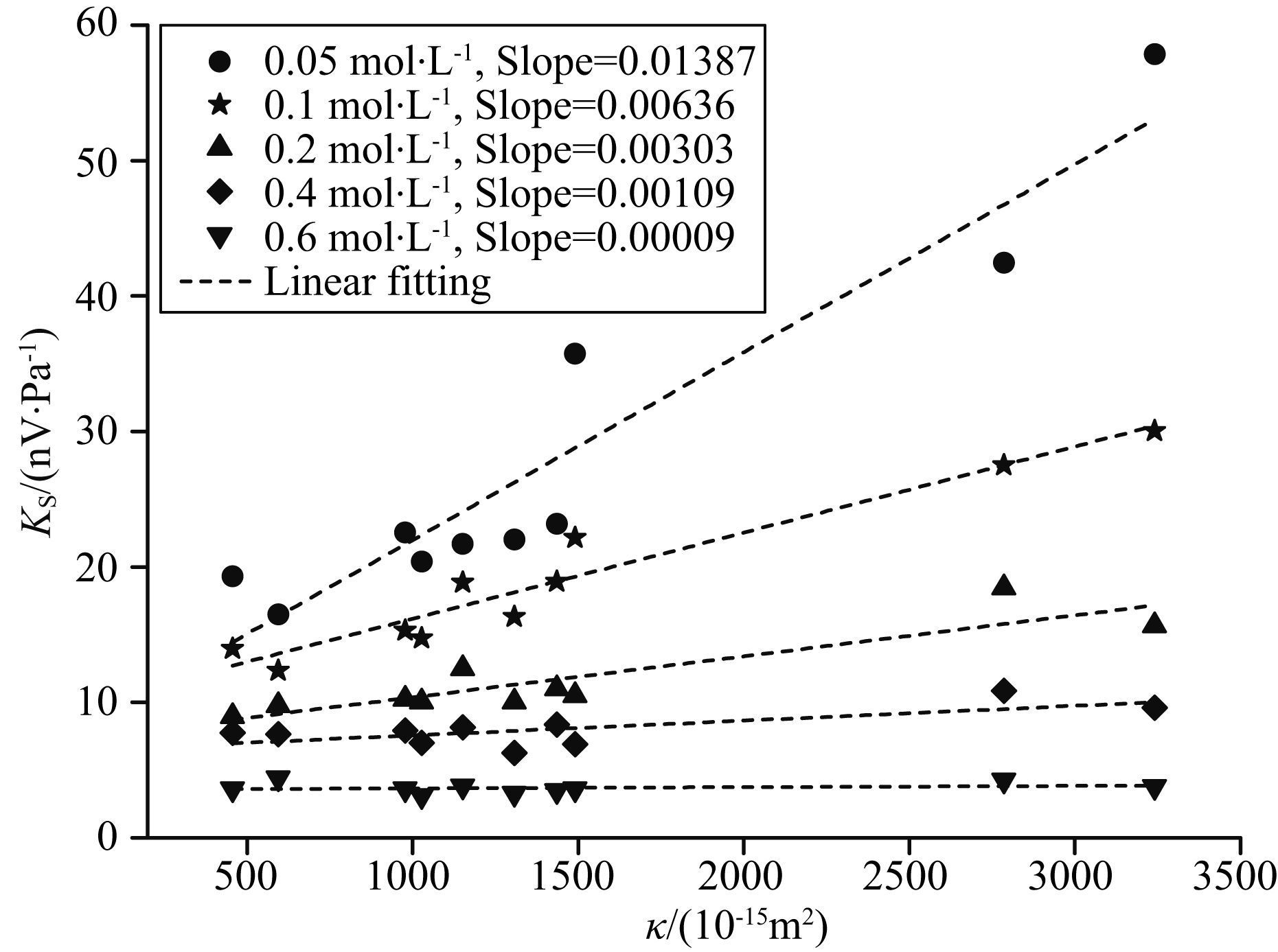
但随着溶液浓度增大,虽然流动电势系数依然随渗透率增大而增大,但流动电势系数对渗透率的敏感度呈现变弱的趋势,见图 12,图中数据是除了0.02 mol/L之外的5种浓度溶液饱和下的实验数据. 图中结果表明:拟合线的斜率由0.05 mol/L时的0.01387减小到0.6 mol/L时的0.00009,缩小近1/140,特别在0.4 mol/L和0.6 mol/L浓度溶液饱和情况下,流动电势系数几乎不受渗透率的影响. 该结果说明在高浓度情况下,流动电势(系数) 的幅度无法区分不同岩样渗透率的差别,这是本文的一个重要发现,该结果给出了利用动电效应评价地层渗透率的适应条件.
|
图 11 岩样流动电势系数与渗透率的关系 Fig. 11 Streaming potential coefficient versus permeability |
|
图 12 岩样流动电势系数随渗透率的变化关系 Fig. 12 Streaming potential coefficient versus variation of permeability |
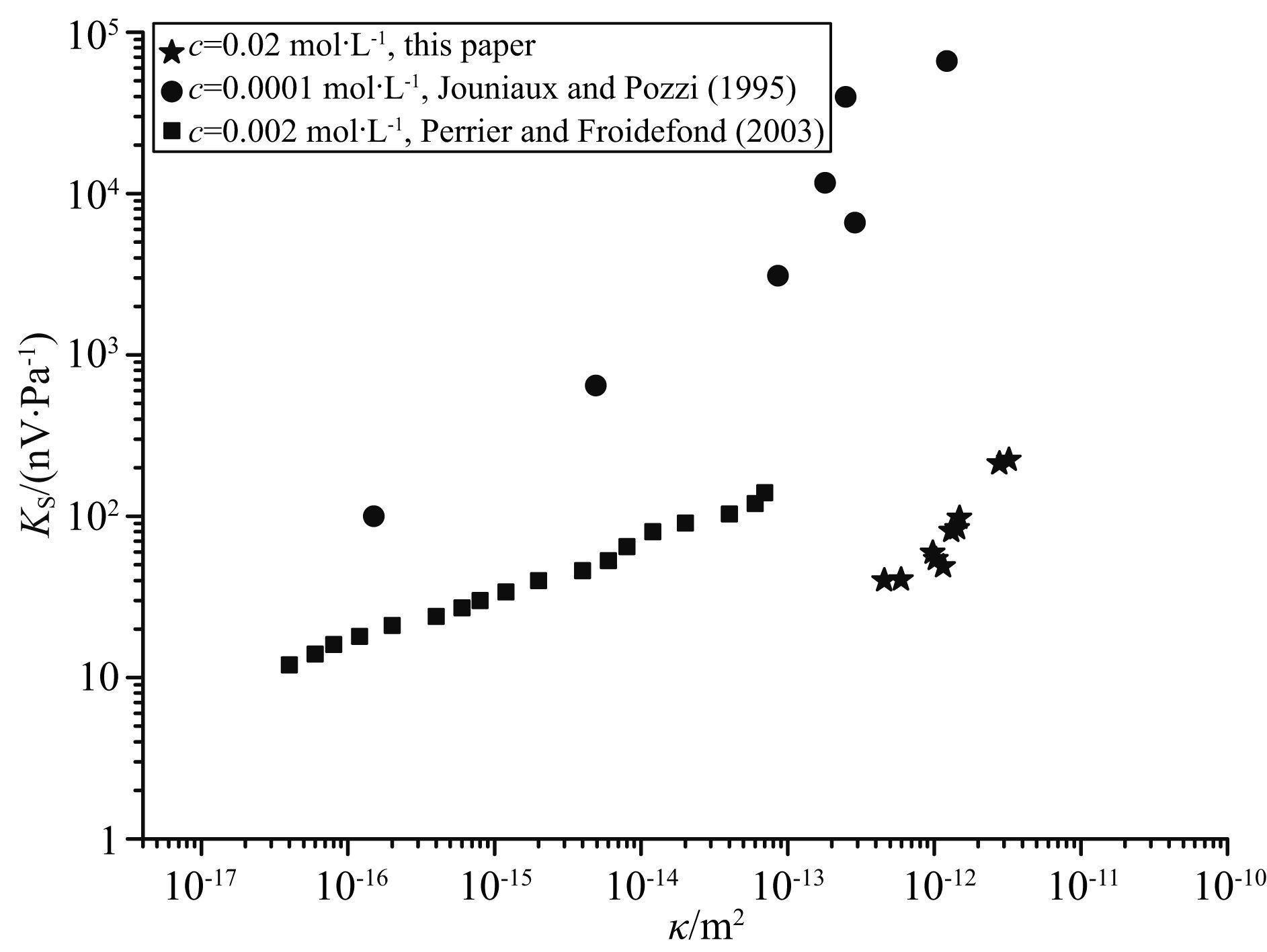
此外,由于目前被大家广泛认可的Pride动电理论(Pride,1994) 推导过程中,将渗透率看作一个独立的参数引入到动电耦合方程组,从而无法从理论上说明动电耦合系数与介质渗透率之间的关系,这使得人们对于实验结果中两者之间的正比关系存在疑虑. 虽然公式(3) 表明流动电势系数与渗透率的正比关系,但该公式是在厚双电层条件下获得的,与本文中岩样的薄双电层结构不相符,而且人们对其推导过程和参数的引入有较大争议,因此,我们未用公式(3) 来对比分析本文实验结果. 但是,我们在分析前人流动电势实验数据时发现:在较低浓度溶液中,流动电势系数也随渗透率的增大而增大(图 13),这与本文在低浓度溶液饱和情况下的结果一致. 因此,
|
图 13 岩样流动电势系数结果比较 Fig. 13 Comparison of streaming potential coefficients of rock samples from different sources |
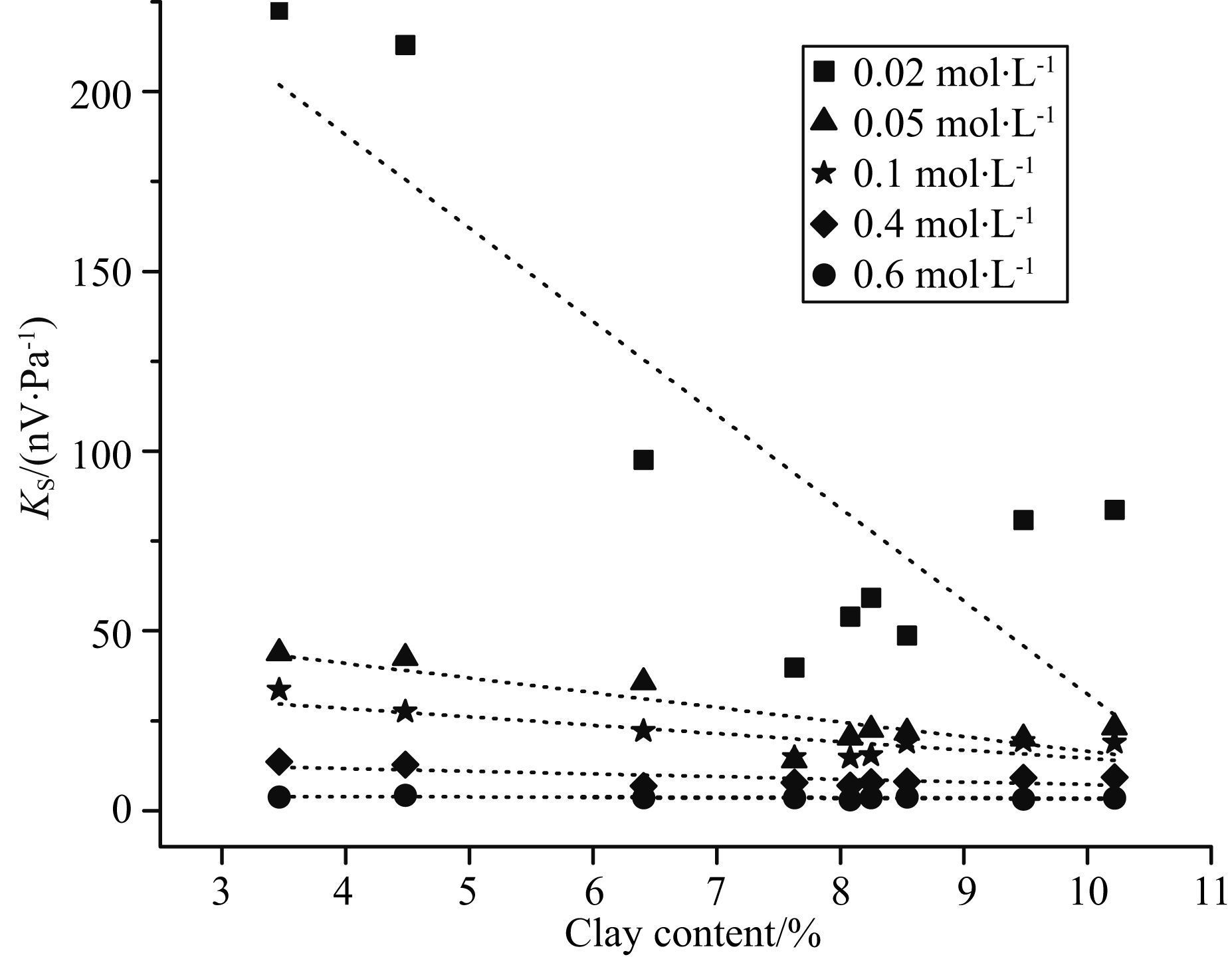
|
图 14 岩样流动电势系数与泥质含量的关系 Fig. 14 Streaming potential coefficient versus clay content |
结合前人实验数据及本文实验结果,我们认为:流动电势系数(动电耦合系数) 对渗透率的敏感性由饱和溶液的浓度决定. 在其他参数不变的情况下,当饱和溶液浓度较低时,流动电势系数与渗透率呈明显的正比关系,随介质渗透率的增大而增强. 但在高浓度溶液饱和情况下,流动电势系数几乎与渗透率变化无关. 而且本文实验用岩样的孔隙度非常接近,可以排除孔隙度对流动电势系数的影响,所以本文结论对于动电测井评价地层渗透率有较大参考意义.
3.4 泥质含量对流动电势系数的影响图 14给出了流动电势系数与泥质含量的关系,由以上的分析可知,只有在较低浓度饱和情况下,岩样自身参数特性的差别才能通过流动电势系数的幅度直接反映出来,对泥质含量的评价也不例外. 图 14中在0.02 mol/L饱和情况下,随着泥质含量的增大,流动电势系数呈现出减小的趋势. 其他浓度溶液中,流动电势系数与泥质含量几乎无关. 泥质含量影响流动电势系数的原因在于,随着时间的推移,饱和砂岩中的泥质会膨胀,导致岩样内部的几何结构发生变化,如孔道变窄,甚至被堵塞. 而流动电势现象是由于流动的液流带动双电层中净剩离子的定向移动形成,流通孔道减小必然会降低净剩离子的传输能力,从而使动-电耦合转换减弱,流动电势系数也随之减小. 另外,泥质含量还对表面电导有很大贡献(Revil et al.,1999),由式(2) 可知,流动电势系数随着表面电导的增大而减小,而表面电导随浓度降低而增大(王军等,2011),因此,在低浓度溶液饱和情况下,流动电势系数受泥质含量的影响较大,且与泥质含量成反比关系.不过,由于本文实验用岩样的数量有限,上述反比关系的线性度不够好,有待进一步的实验分析.
4 结论本文通过10块岩样在6种不同浓度下的动电效应(流动电势) 实验,分析了岩样流动电势系数与固/液相参数(饱和溶液浓度、岩样渗透率、泥质含量) 之间的关系,得到如下主要结论:
(1) 低频流动电势系数频响曲线中的凹点现象是由岩样夹持器与激振器的共振引起,并非孔隙介质的动电特性. 通过改变夹持器的质量可调节凹点对应频率,进而改善流动电势实验数据的有效性.
(2) 不同饱和浓度下的流动电势实验表明:流动电势系数KS随溶液浓度增大而减小. 这说明在低浓度地层中进行动电测井的效果最佳. 但是当溶液浓度达到0.4 mol/L之后,KS随溶液浓度增大而减小的程度非常缓慢,即使在很高浓度情况下,动电效应依然存在(KS约为1 nV/Pa量级),因此,依据现有测井设备的性能(井中声压可达70 kPa),测量井中动电转换信号(微伏量级或更高) 是可行的.
(3) 针对不同渗透率和泥质含量的流动电势实验表明:流动电势系数对这两地层参数的敏感性由饱和溶液浓度决定,在低浓度溶液饱和情况下,流动电势系数与渗透率成正比,与泥质含量成反比;在高浓度溶液饱和情况下,流动电势系数几乎与它们无关. 因此,进行动电测井时,在低矿化度地层中,可利用动电信号(流动电势) 的幅度对渗透率进行直接评价. 而高矿化度地层中则可利用动电测井信号的时间信息进行间接评价,如依据动电测井的时域波形可获得地层的纵、横波速度,进而可评价被测地层的渗透率.
| CuiZ W. 2004. Theoretical and numerical study of modified Biot's models, acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources[Ph. D. thesis] (in Chinese). Changchun:Jilin University. | |
| Dupuis J C, Butler K E. 2006. Vertical seismoelectric profiling in a borehole penetrating glaciofluvial sediments. Geophys. Res. Lett , 33 (16) : L16301. DOI:10.1029/2006GL026385 | |
| Gao Y X, Hu H S. 2009. Numerical simulation and analysis of seismoelectromagnetic wave fields excited by a point source in layered porous media. Chinese J. Geophys. (in Chinese) , 52 (8) : 2093-2104. | |
| Glover P W J, Walker E, Jackson M D. 2012. Streaming-potential coefficient of reservoir rock:A theoretical model. Geophysics , 77 (2) : D17-D43. DOI:10.1190/geo2011-0364.1 | |
| Guan W, Hu H S, Tang T Z, et al. 2011. The ratio of the acoustoelectric field to the acoustic pressure in the borehole and its dependence on permeability. Chinese J. Geophys. (in Chinese) , 54 (6) : 1660-1671. DOI:10.3969/j.issn.0001-5733.2011.06.026 | |
| Guan W, Hu H S, Zheng X B. 2013a. Theoretical simulation of the multipole seismoelectric logging while drilling. Geophys. J. Int. , 195 (2) : 1239-1250. DOI:10.1093/gji/ggt294 | |
| Guan W, Hu H S, Wang Z. 2013b. Permeability inversion from low-frequency seismoelectric logs in fluid-saturated porous formations. Geophysical Prospecting , 61 (1) : 120-133. DOI:10.1111/gpr.2013.61.issue-1 | |
| Haines S S, Pride S R, Klemperer S L, et al. 2007. Seismoelectric imaging of shallow targets. Geophysics , 72 (2) : G9-G20. DOI:10.1190/1.2428267 | |
| Hu H S, Wang K X. 1999. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation:theory (I). Well Logging Technology (in Chinese) , 23 (6) : 427-432. | |
| Hu H S, Wang K X. 2000. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation:numerical simulation of acoustically induced fields (Ⅱ). Well Logging Technology (in Chinese) , 24 (1) : 3-13. | |
| Hu H S, Liu J Q, Wang H B, et al. 2003. Simulation of acousto-electric well logging based on simplified pride equations. Chinese J. Geophys. (in Chinese) , 46 (2) : 259-264. | |
| Ishido T, Mizutani H. 1981. Experimental and theoretical basis of electrokinetic phenomena in rock-water systems and its applications to geophysics. J. Geophys. Res. , 86 (B3) : 1763-1775. DOI:10.1029/JB086iB03p01763 | |
| Jaafar M Z, Vinogradov J, Jackson M D. 2009. Measurement of streaming potential coupling coefficient in sandstones saturatedwith high salinity NaCl brine. Geophys. Res. Lett. , 36 (21) : L21306. DOI:10.1029/2009GL040549 | |
| Jackson M D, Leinov E. 2012. On the validity of the "Thin" and "Thick" double-layer assumptions when calculating streaming currents in porous media. International Journal of Geophysics, Article ID 897807, doi:10.1155/2012/897807. | |
| Jin D, Sun B D, Hu H S, et al. 2010. Electrokinetic logging:state of the art and future challenges. Well Logging Technology (in Chinese) , 34 (4) : 309-313. | |
| Jouniaux L, Pozzi J P. 1995. Streaming potential and permeability of saturated sandstones under triaxial stress:consequences for electrotelluric anomalies prior to earthquakes. J. Geophys. Res. , 100 (B6) : 10197-10209. DOI:10.1029/95JB00069 | |
| Jouniaux L, Ishido T. 2012. Electrokinetics in earth sciences:a tutorial. International Journal of Geophysics, Article ID 286107, doi:10.1155/2012/286107 | |
| Li F B, Ju X D, Qiao W X, et al. 2014. Research and experimental testing of a new kind electrokinetic logging tool. Applied Geophysics , 11 (4) : 364-373. DOI:10.1007/s11770-014-0466-9 | |
| Li S X, Pengra D B, Wong P Z. 1995. Onsager's reciprocal relation and the hydraulic permeability of porous media. Physical Review E , 51 (6) : 5748-5751. DOI:10.1103/PhysRevE.51.5748 | |
| Men B Y, Ju X D, Qiao W X, et al. 2013. Electronic system design for electrokinetic logging sonde. Well Logging Technology (in Chinese) , 37 (4) : 406-410. | |
| Morgan F D, Williams E R, Madden T R. 1989. Streaming potential properties of Westerly granite with applications. J. Geophys. Res.:Solid Earth , 94 (B9) : 12449-12461. DOI:10.1029/JB094iB09p12449 | |
| Pengra D B, Li S X, Wong P Z. 1999. Determination of rock properties by low-frequency AC electrokinetics. J. Geophys. Res. , 104 (B12) : 29485-29508. DOI:10.1029/1999JB900277 | |
| Perrier F, Froiderond T. 2003. Electrical conductivity and streaming potential coefficient in a moderately alkaline lava series. Earth and Planetary Science Letters , 210 (1-2) : 351-363. DOI:10.1016/S0012-821X(03)00105-5 | |
| Pride S R. 1994. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B , 50 (21) : 15678-15696. DOI:10.1103/PhysRevB.50.15678 | |
| Revil A, Pezard P A, Glover P W J. 1999. Streaming potential in porous media:1. Theory of the zeta potential. J. Geophys. Res. , 104 (B9) : 20021-20031. DOI:10.1029/1999JB900089 | |
| Revil A, Jardani A. 2010. Seismoelectric response of heavy oil reservoirs:theory and numerical modelling. Geophys. J. Int. , 180 (2) : 781-797. DOI:10.1111/gji.2010.180.issue-2 | |
| Revil A, Mahardika H. 2013. Coupled hydromechanical and electromagnetic disturbances in unsaturated porous materials. Water Resources Research , 49 (2) : 744-766. DOI:10.1002/wrcr.20092 | |
| Wang J, Hu H S, Xu X R, et al. 2010. Experimental measurement study on rock permeability based on the electrokinetic effect. Chinese J. Geophys. (in Chinese) , 53 (8) : 1953-1960. DOI:10.3969/j.issn.0001-5733.2010.08.021 | |
| Wang J, Hu H S, Yang G, et al. 2011. Experimental measurements on streaming current and zeta-potential of core samples under the excitation of low-frequency sinusoidal pressure. Chinese J. Geophys. (in Chinese) , 54 (8) : 2169-2176. DOI:10.3969/j.issn.0001-5733.2011.08.025 | |
| Wang J, Hu H S, Guan W, et al. 2015. Electrokinetic experimental study on saturated rock samples:zeta potential and surface conductance. Geophys. J. Int. , 201 (2) : 869-877. DOI:10.1093/gji/ggv013 | |
| Wang J, Li H, Hu H S, et al. 2015. Electrokinetic experimental studies in borehole model 1:the evaluation of rock permeability. Chinese J. Geophys. (in Chinese) , 58 (10) : 3855-3863. DOI:10.6038/cjg20151035 | |
| Wang J, Guan W, Hu H S, et al. 2016. Electrokinetic experimental studies in borehole model 2:localized and radiated seismoelectric field. Chinese J. Geophys. (in Chinese) , 59 (1) : 381-390. DOI:10.6038/cjg20160132 | |
| Yan H R, Liu H, Li Y M, et al. 1999. Daqing oilfield experiment of seismo-electric exploration. Chinese J. Geophys. (in Chinese) , 42 (2) : 257-267. | |
| Zhu Z Y, Haartsen M W, Toksöz M N. 1999. Experimental studies of electrokinetic conversions in fluid-saturated borehole models. Geophysics , 64 (5) : 1349-1356. DOI:10.1190/1.1444639 | |
| Zhu Z Y, Toksöz M N. 2003. Crosshole seismoelectric measurements in borehole models with fractures. Geophysics , 68 (5) : 1519-1524. DOI:10.1190/1.1620625 | |
| Zhu Z Y, Toksöz M N. 2013. Experimental measurements of the streaming potential and seismoelectric conversion in Berea sandstone. Geophysical Prospecting , 61 (3) : 688-700. DOI:10.1111/gpr.2013.61.issue-3 | |
| 崔志文. 2004. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士论文]. 长春:吉林大学. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=0&CurRec=1&recid=&FileName=2004100268.nh&DbName=CDFD9908&DbCode=CDFD&pr= | |
| 高永新, 胡恒山. 2009. 水平分层孔隙介质中点源激发的震电波场数值模拟及分析. 地球物理学报 , 52 (8) : 2093–2104. | |
| 关威, 胡恒山, 汤天知, 等. 2011. 声电效应测井电声比及其与地层渗透率的关系. 地球物理学报 , 54 (6) : 1660–1671. DOI:10.3969/j.issn.0001-5733.2011.06.026 | |
| 胡恒山, 王克协. 1999. 井孔周围轴对称声电耦合波:理论(I). 测井技术 , 23 (6) : 427–432. | |
| 胡恒山, 王克协. 2000. 井孔周围轴对称声电耦合波:声电效应测井数值模拟(Ⅱ). 测井技术 , 24 (1) : 3–13. | |
| 胡恒山, 刘家琦, 王洪滨, 等. 2003. 基于简化的Pride理论模拟声电效应测井响应. 地球物理学报 , 46 (2) : 259–264. | |
| 金鼎, 孙宝佃, 胡恒山, 等. 2010. 动电效应测井研究现状和展望. 测井技术 , 34 (4) : 309–313. | |
| 门百永, 鞠晓东, 乔文孝, 等. 2013. 动电效应测井探测器电子系统设计. 测井技术 , 37 (4) : 406–410. | |
| 王军, 胡恒山, 徐小蓉, 等. 2010. 基于动电效应的岩芯渗透率实验测量. 地球物理学报 , 53 (8) : 1953–1960. DOI:10.3969/j.issn.0001-5733.2010.08.021 | |
| 王军, 胡恒山, 杨光, 等. 2011. 低频交变压差作用下岩心流动电流和zeta电势实验测量. 地球物理学报 , 54 (8) : 2169–2176. DOI:10.3969/j.issn.0001-5733.2011.08.025 | |
| 王军, 李惠, 胡恒山, 等. 2015. 动电测井实验研究Ⅰ:渗透率的评价. 地球物理学报 , 58 (10) : 3855–3863. DOI:10.6038/cjg20151035 | |
| 王军, 关威, 胡恒山, 等. 2016. 动电测井实验研究Ⅱ:伴随动电场和界面动电场. 地球物理学报 , 59 (1) : 381–390. DOI:10.6038/cjg20160132 | |
| 严洪瑞, 刘洪, 李幼铭, 等. 1999. 震电勘探方法在大庆油田的实验研究. 地球物理学报 , 42 (2) : 257–267. | |
 2016, Vol. 59
2016, Vol. 59


