近年来,电缆声波远探测技术获得了长足的进展(Li et al.,2002; 车小花和乔文孝,2004; 楚泽涵等,2005; Tang et al.,2007; 陶果等,2008; 唐晓明和魏周拓,2012a).Schlumberger(1998)、大港油田研制的单极远探测仪器和中海油田服务公司研制的偶极远探测仪器在井外地质构造探测方面取得了较好的应用效果(柴细元等,2009; 张承森等,2011; 唐晓明和魏周拓,2012b; 庄春喜等,2014).但随着随钻测井的作业和地质导向需求的日益增多,需要发展随钻声波的远探测探边技术,为钻井过程实时地提供井周围地质构造的成像结果,指导钻进的最佳方向,提高钻井施工的精确度和钻进效率.
目前,人们对随钻远探测技术已经开展了研究工作.Tang等(2007)利用实际的单极随钻声波数据得到了井旁地层界面的成像图,指出了随钻地质导向的可行性和潜在的应用价值.陈雪莲和魏周拓(2012)采用三维有限差分方法研究了单极声源在随钻反射成像方面的应用,通过对井周八个方位上接收的信号做矢量计算,得到了来自井旁地层界面的反射纵波.上述研究主要集中在随钻单极远探测方面,声源采用的激发频率较高,对井周地质体的探测深度有限.相比之下,随钻偶极远探测技术继承了偶极声源激发频率低,井外探测深度大的优点,能够较早地确定井孔周围地质体的位置,为钻头钻进方向的预判赢取更多的时间.
随钻偶极远探测声场受井中声源的辐射,声场在地层中的反射,以及井对入射波的响应等多种因素影响(Tang and Patterson,2009),其中,声源的辐射与井孔对入射波的接收满足互易原理,二者对弹性波的响应特征相同(Tang et al.,2014),因此,研究声源的辐射特征对随钻偶极远探测测井具有重要的意义.为此,本文从声源的辐射特性出发,重点讨论不同频率下随钻偶极声源激发的沿井传播的导波能流和辐射波能流,考察声源辐射效率随频率的变化规律,优选出随钻偶极声源的激发频段,最终利用一种快速地计算方法模拟了随钻偶极远探测数据,并给出了该模拟数据的成像处理结果.
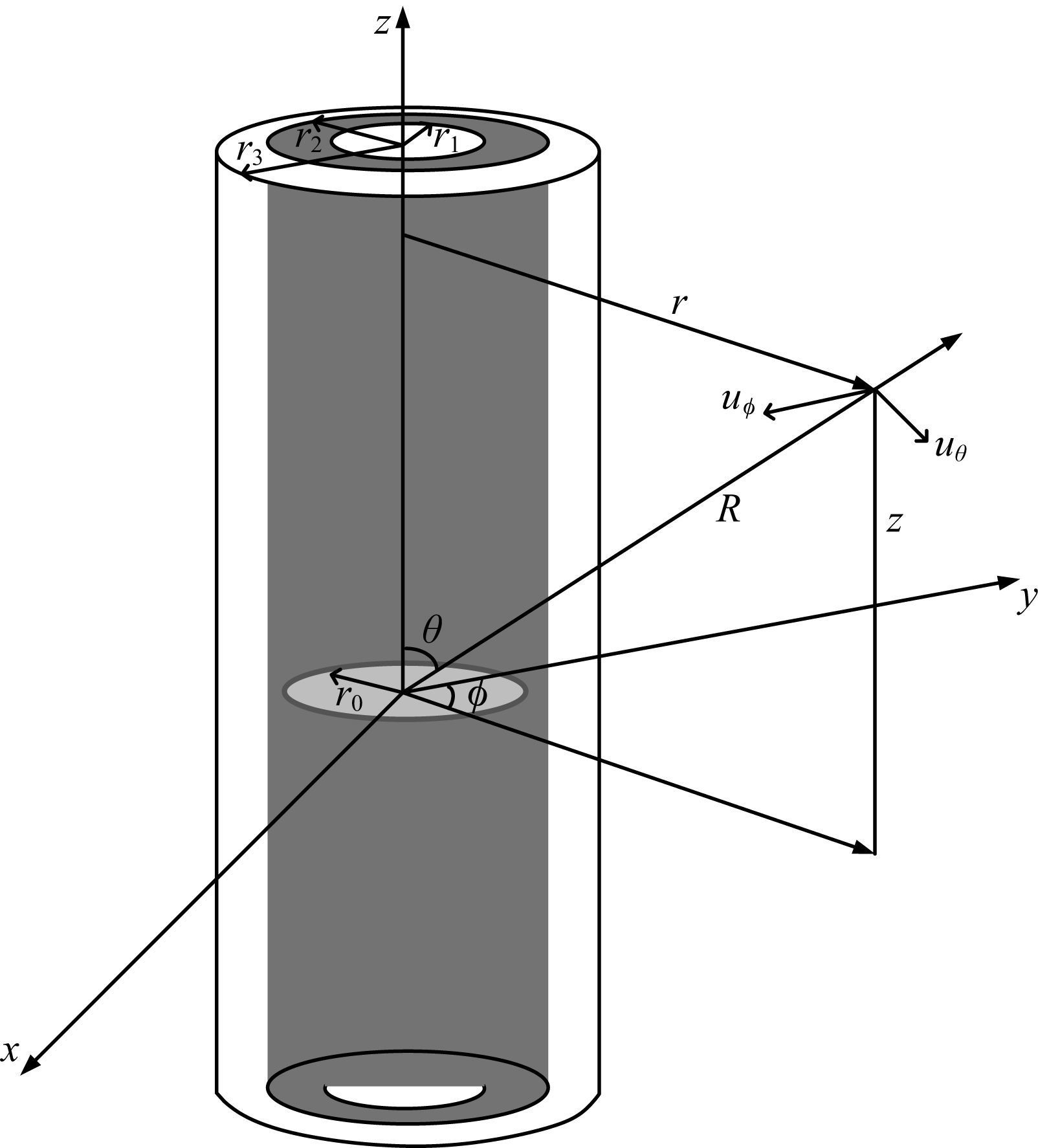
2 基本理论在研究声源的辐射问题中,Winbow(1991)引入了“辐射效率”的概念,其具体的定义为声源向井外的辐射波能流与沿井轴传播的导波能流之比,它体现了声源的辐射性能.为了考察随钻偶极声源的辐射效率,本文推导了声源激发的沿井传播的导波能流和井外辐射波能流的计算公式,推导过程采用的描述井中声源激发声场的坐标系如图 1所示.环状声源以坐标原点为中心置于钻铤外侧,声源半径r0等于钻铤外半径r2; r1和r3分别表示了钻铤内半径和井孔半径;R为声源到场点的辐射距离,r和z分别是辐射场点的径向和轴向距离;θ是声源到场点的辐射方向与z轴正方向之间的夹角,φ为辐射方向与z轴所在竖直平面的方位与y轴正方向之间的夹角.
|
图 1 采用直角坐标系研究随钻条件下偶极声源激发的充液井孔内外声场 Fig. 1 A rectangular coordinate system used to analyze the wavefield of a LWD dipole source inside and outside a borehole |
随钻测井下,介质空间在径向上被划分为钻铤内泥浆、钻铤、钻铤外泥浆环和井外无限大地层等四部分,其中,钻铤内泥浆与钻铤、泥浆环与地层等固-液界面处的边条件要求径向位移和径向应力连续,切向应力为零;而对于钻铤与泥浆环界面而言,由于声源的存在,边界处的径向位移边条件还需要考虑声源产生的位移,由此激发出介质空间中的弹性波场.声源的具体加载过程见附录B.由上述三个界面处的边界条件,可以得到一个含有十二个未知系数的矩阵方程(唐晓明和郑传汉,2004)
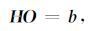
|
(1) |
式中,H为12×12的矩阵, b=[0,0,0,0,urs,0,0,0,0,0,0,0]T,O=[Afin,Aco,Bco,Cco,Dco,Eco,Fco,Afout,Bfout,Bfm,Dfm,Ffm]T,urs为声源产生的径向位移,其表达式见附录(B3) 式;向量O中上标为in和out的字母分别表示了钻铤内、外泥浆液中纵横波的振幅系数,下标为co和fm的字母分别表示了钻铤和无限大地层中纵横波的振幅系数.
2.2 沿井传播的导波的能流密度和能流在图 1所示的随钻测井模型中,偶极声源激发的沿井传播的导波能流密度包括钻铤内泥浆、钻铤、钻铤外泥浆环和无限大地层等四部分的贡献,分别用 Efin、Esco、Efout和Esfm 表示. Esco 在所关心的声源工作频域( <10 kHz) 内由最低阶钻铤波构成,而 Esfm 包括了地层一阶和二阶两种模式波的贡献.对于偶极导波而言,尽管导波能流密度的计算包括了波在轴向、径向和环向三个方向上的应力和速度分量,但其能流的方向仅为井轴z的方向.随钻偶极导波沿井轴z方向传播的能流密度的表达式如下:
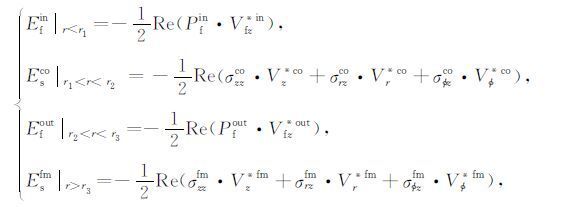
|
(2) |
式中, Pfin、Pfout和Vfz*in、Vfz*out 分别为钻铤内外泥浆压力和轴向质点振动速度的复共轭; σzzco、σrzco、σφzco和σzzfm、σrzfm、σφzfm 分别为钻铤与地层的轴向正应力、径向和环向切应力; Vz*co、Vr*co、Vφ*co和Vz*fm、Vr*fm、Vφ*fm 分别为钻铤与地层中轴向、径向和环向质点振动速度的复共轭.上述各物理量的表达式见附录A,式中声场在井内、外的振幅系数可以通过矩阵方程(1) 得到,在求解过程中所用波数 k 须是导波的波数,由以下的频散方程决定(唐晓明和郑传汉,2004):
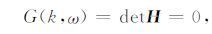
|
(3) |
其中, detH 为(1) 式系数矩阵的行列式.
附录A中的应力和速度是波数 k 域中的表达式,将它们沿波数的实轴积分后得到频域内的响应谱.对于井中导波而言,该积分值等于(3) 式确定的导波极点留数的贡献.以 Pfin(ω,k) 为例,利用留数定理得到它的频域响应函数:
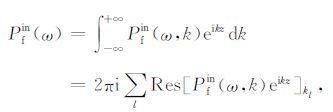
|
(4) |
其中,Res表示 Pfin(ω,k)eikz 在第l个极点 kl 处的留数.最后,将应力和速度的频域响应函数代入(2) 式便可得到导波在钻铤、钻铤内外泥浆和地层中的能流密度,将它们在与井轴垂直的井筒-地层截面上积分,得到导波沿井轴传播的能流:
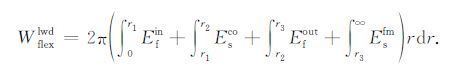
|
(5) |
与随钻测井相比,电缆测井下介质空间在径向上只有井内流体和井外无限大地层两部分,偶极声源激发的沿井传播的导波只有最低阶地层弯曲波的贡献,此时,电缆偶极导波沿井轴z方向传播的能流密度和能流可以表示为:
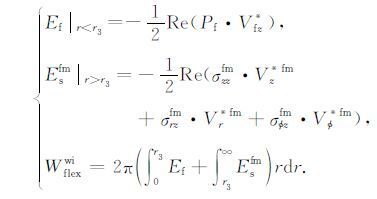
|
(6) |
其中, Pf和Vfz* 分别为泥浆压力和轴向质点振动速度的复共轭,具体表达式见附录A.此时,应力和速度分量在频域内响应谱的求取过程仍按照式(3)—(5) 所示的步骤.
2.3 地层中辐射横波的能流密度和能流对于偶极远探测而言,SH和SV反射横波是进行井旁地质构造成像的基础,因此,本文只考虑了这两种弹性波.无限大地层中SH和SV横波位移的远场渐近解在频率域内的表达式为(Tang et al.,2014):
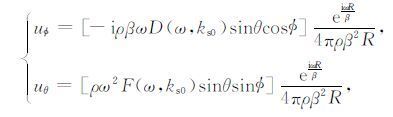
|
(7) |
其中, ks0=ωcosθβ,ρ 为地层密度, β 为地层横波速度.(7) 式中方括号里的表达式分别定义了SH和SV横波的远场辐射指向性(Tang et al.,2014):
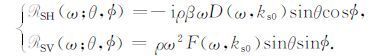
|
(8) |
在已知位移分量 uφ和uθ 的基础上,将二者乘以 iω 因子得到 φ和θ 方向上质点的振动速度 vφ和vθ; 另外,把它们代入到球坐标系下位移-应变关系式(程昌钧和朱媛媛,2005),再利用胡克定律得到 φ和θ 方向上的地层应力 σRφ和σRθ 的表达式:

|
(9) |
与沿井传播的导波的情况不同,声源辐射到井外地层中的弹性波以球面波的形式向外传播.半径为R的球面上一面元上的能流密度表达式为:
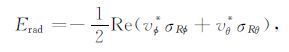
|
(10) |
式中, vφ*σRφ和vθ*σRθ 分别表示了SH和SV横波的能流密度, vφ*和vθ* 分别为 vφ和vθ 的复共轭.将上述求取的应力和速度代入(10) 式,便可得到地层中辐射波的能流密度 Erad, 再将该能流密度在以声源为中心,半径为R的球面上进行积分可以得到辐射波的能流:

|
(11) |
(7) 到(9) 式中辐射声场的振幅系数 D(ω,ks0) 和F(ω,ks0) 同样由(1) 式决定,所不同的是在计算SH和SV横波辐射时,式中的波数 k 要用 ks0 来替换.此时,计算得到的应力和速度分量已是频率的响应函数,无需再对波数 k 做积分.
2.4 远探测声场的快速计算方法偶极远探测声场的模拟是一个复杂的理论问题,以往采用三维有限差分方法,但该方法计算速度较慢,只能有效地模拟井中特定深度点处的远探测声场,不适用于井段声场模拟.为了研究过井或井旁地质构造在井段上产生的远探测声场,Tang等(2014)提出了一种快速模拟偶极远探测声场的计算方法.该方法中,井中发射和接收的SH或SV横波远探测声场的频域表达形式如下:
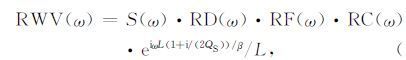
|
(12) |
其中, S(ω) 为声源频谱,L为弹性波从声源到反射体,再从反射体到接收器的总传播距离,RF为波在地层反射体处的反射系数,RD和RC分别为声场的辐射和接收因子,根据声源辐射与井孔接收之间的互易性,RC=RD,由(8) 式给出.
3 数值计算结果及分析表 1给出了本文计算随钻偶极导波能流、辐射波能流和横波远场辐射指向性时采用的泥浆、钻铤和地层的弹性参数,其中地层1和2分别表示常见的砂岩和灰岩地层.
|
|
表 1 模型参数 Table 1 Model parameters |
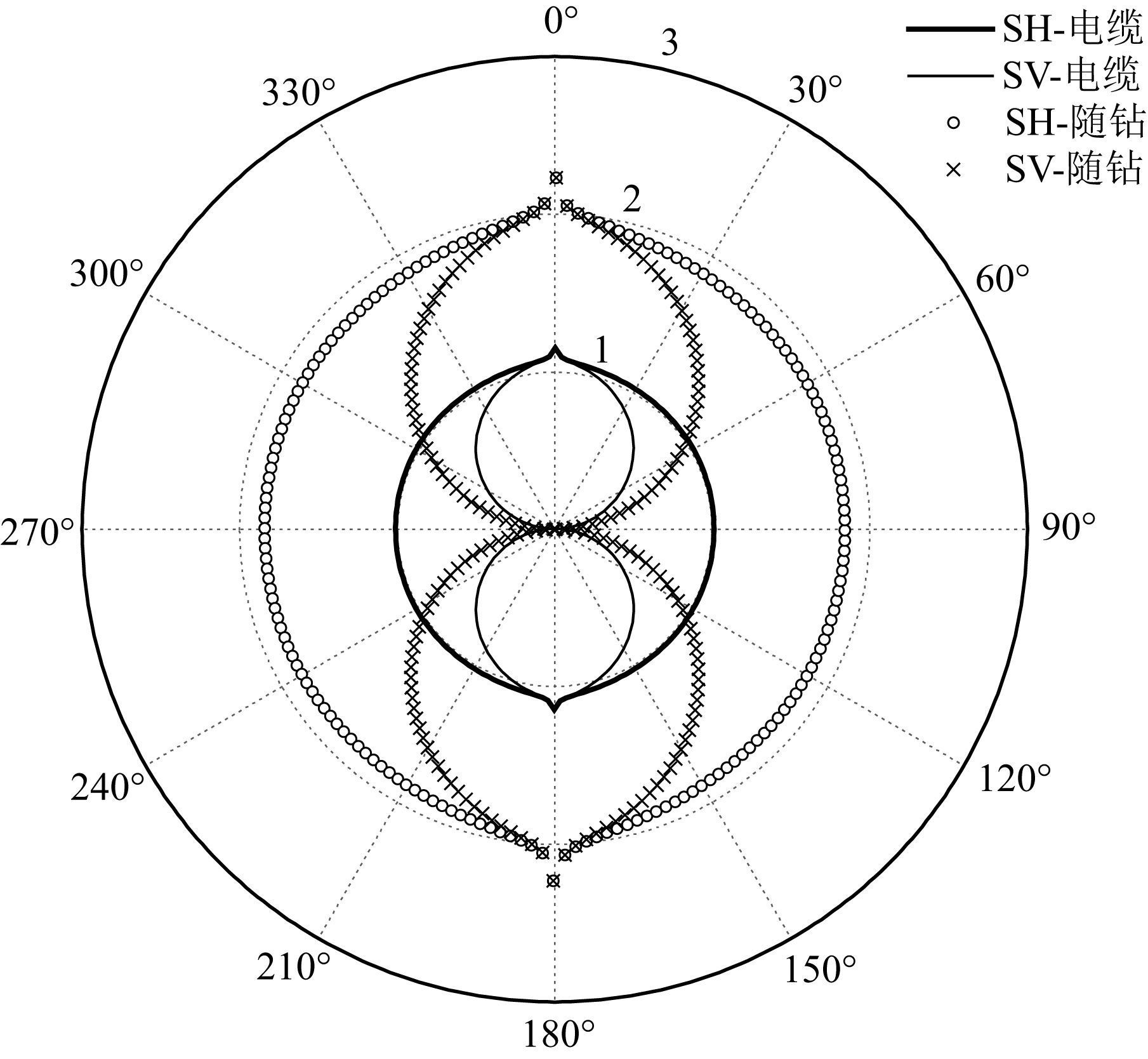
图 2和图 3分别给出了声源频率为500 Hz和4000 Hz时电缆(曲线) 和随钻(标识符) 测井下偶极声源激发的SH与SV横波的辐射指向性.其中,径向刻度表示了单位强度的声源辐射到地层中的弹性波的相对幅度值,环向刻度表示声源到场点的辐射
|
图 2 砂岩地层中,声源频率为500 Hz时随钻和电缆偶极声源辐射的SH与SV横波指向性对比结果 Fig. 2 SH- and SV-wave radiation patterns of wireline and LWD dipole source in sandstone formation. Source frequency is 500 Hz |
|
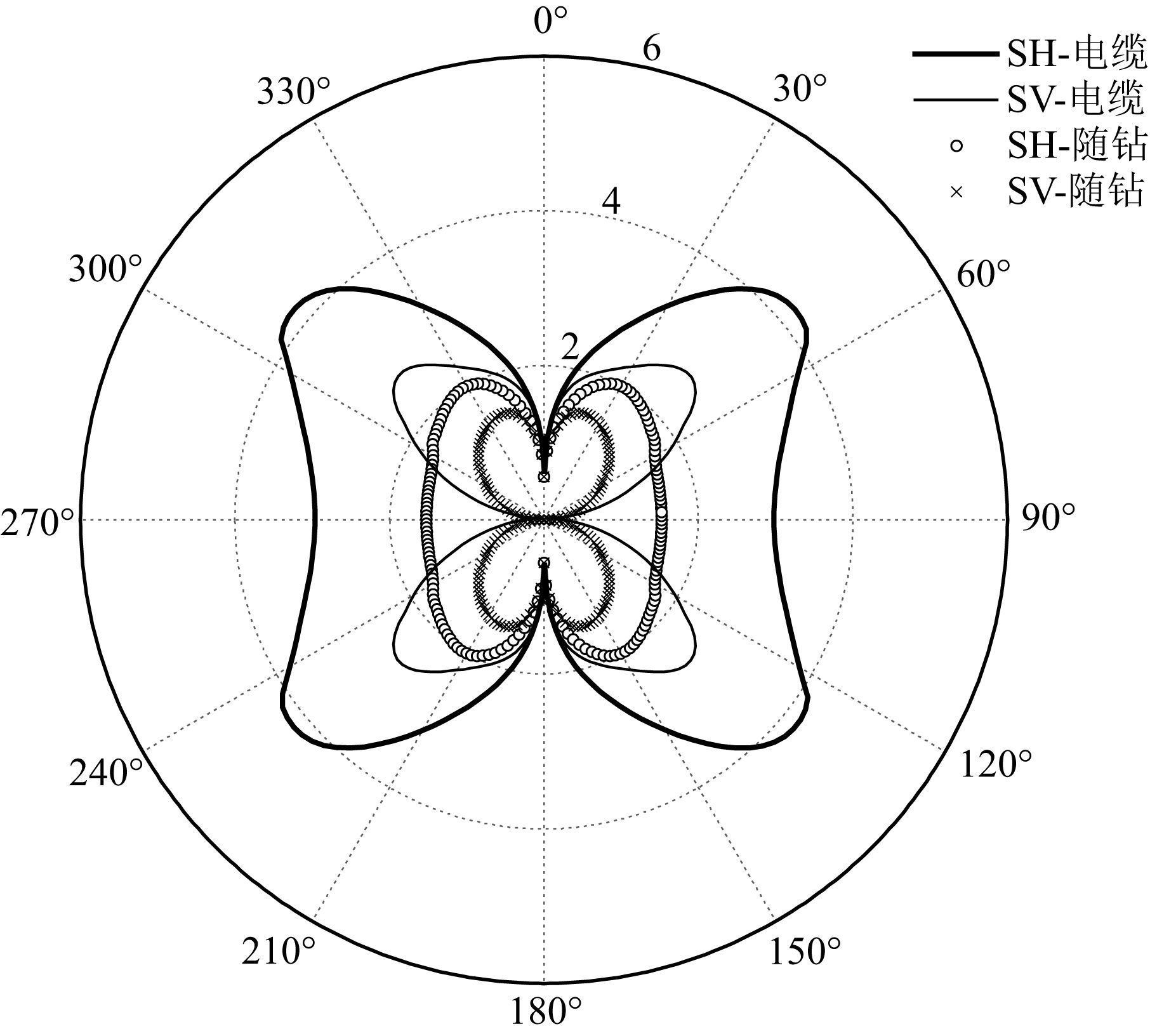
图 3 砂岩地层中,声源频率为4000 Hz时随钻和电缆偶极声源辐射的SH与SV横波指向性对比结果 Fig. 3 SH- and SV-wave radiation patterns of wireline and LWD dipole source in sandstone formation. Source frequency is 4000 Hz |
方向与井轴在竖直平面内的夹角.本文只考虑了yoz平面内SH横波和xoz平面内SV横波的指向性,在这两个平面之外的SH和SV的辐射指向性则分别以 cosφ和sinφ 的形式呈规律性的变化,如式(8) 所示.从图中可以看出,钻铤的存在对井外辐射声场有明显影响,频率较低时,钻铤使得偶极声源产生的SH和SV横波的指向因子大于电缆偶极的情况(见图 2),但随着频率的增加,两者发生反转(见图 3),这说明随钻和电缆偶极声源的优势激发频段有所不同.与电缆偶极横波的辐射规律类似,随钻情况下的SV横波的指向因子恒小于SH横波,且在水平方向上存在零点,表明了SH横波较SV横波对井外不同倾角的反射体具有更好的辐射覆盖性,在随钻偶极远探测测井中SH横波仍然占据了主导地位.
3.2 激发频率对声源辐射效率的影响砂岩地层中随钻和电缆偶极声源激发的导波的频散曲线如图 4所示.其中,实线表示了随钻测井下一阶地层模式波,它在整个频段内都存在,其速度随着频率增加逐渐增大,最终趋于井液界面的Scholte波速度(唐晓明和郑传汉,2004).点线表示了随钻情况下二阶地层模式波,与一阶地层模式波不同的是它存在截止频率,其速度在截止频率附近与地层横波速度相同,在截止频率之上大于一阶地层模式波的速度.虚线表示了钻铤模式波,它的截止频率高于二阶地层模式波,速度较一阶和二阶地层模式波都大.圆圈表示了电缆偶极声源激发的弯曲波,其截止频率介于钻铤模式波和二阶地层模式波之间,速度在截止频率和高频处分别与二阶和一阶地层模式波的速度相近.
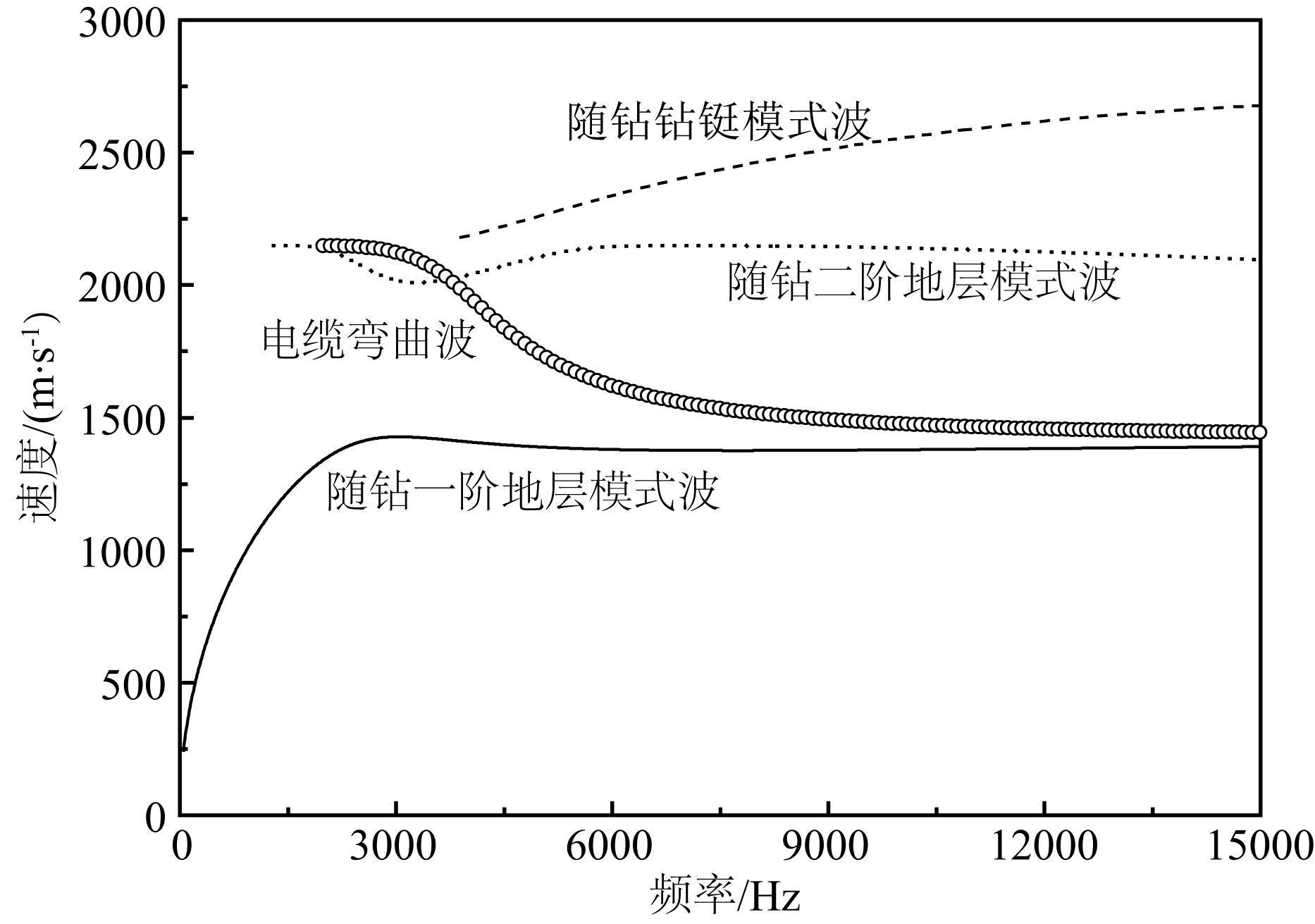
|
图 4 砂岩地层中,随钻和电缆偶极声源激发的井中导波的频散曲线 Fig. 4 Dispersion curves of wireline and LWD dipole waves guided along a borehole in sandstone formation |
已知导波波数k后,采用式(5) 和(6) 计算了随钻与电缆偶极声源激发的沿井传播的导波能流,由图 5给出.其中,纵坐标表示利用单位声源功率归一后的能流大小.从图中可以看出,电缆偶极声源激发的弯曲波能流随着频率增加先增大,在4.5 kHz附近达到最大值之后逐渐减小,整个频段仅存在一个峰值.与电缆的情况相比,随钻条件下,由于钻铤波和一、二阶地层模式波的存在,导波能流相对较为复杂.频率在4 kHz以下,导波能流只包括一阶和二阶地层模式波的贡献,而能流在4 kHz出现的断点对应着钻铤波的出现,此后,能流随频率的增加逐渐减小.另外,频率低于1 kHz时,沿井传播的导波能流随着频率的降低急剧增大,说明了钻铤的存在对声源激发的沿井传播的导波声场影响较大.
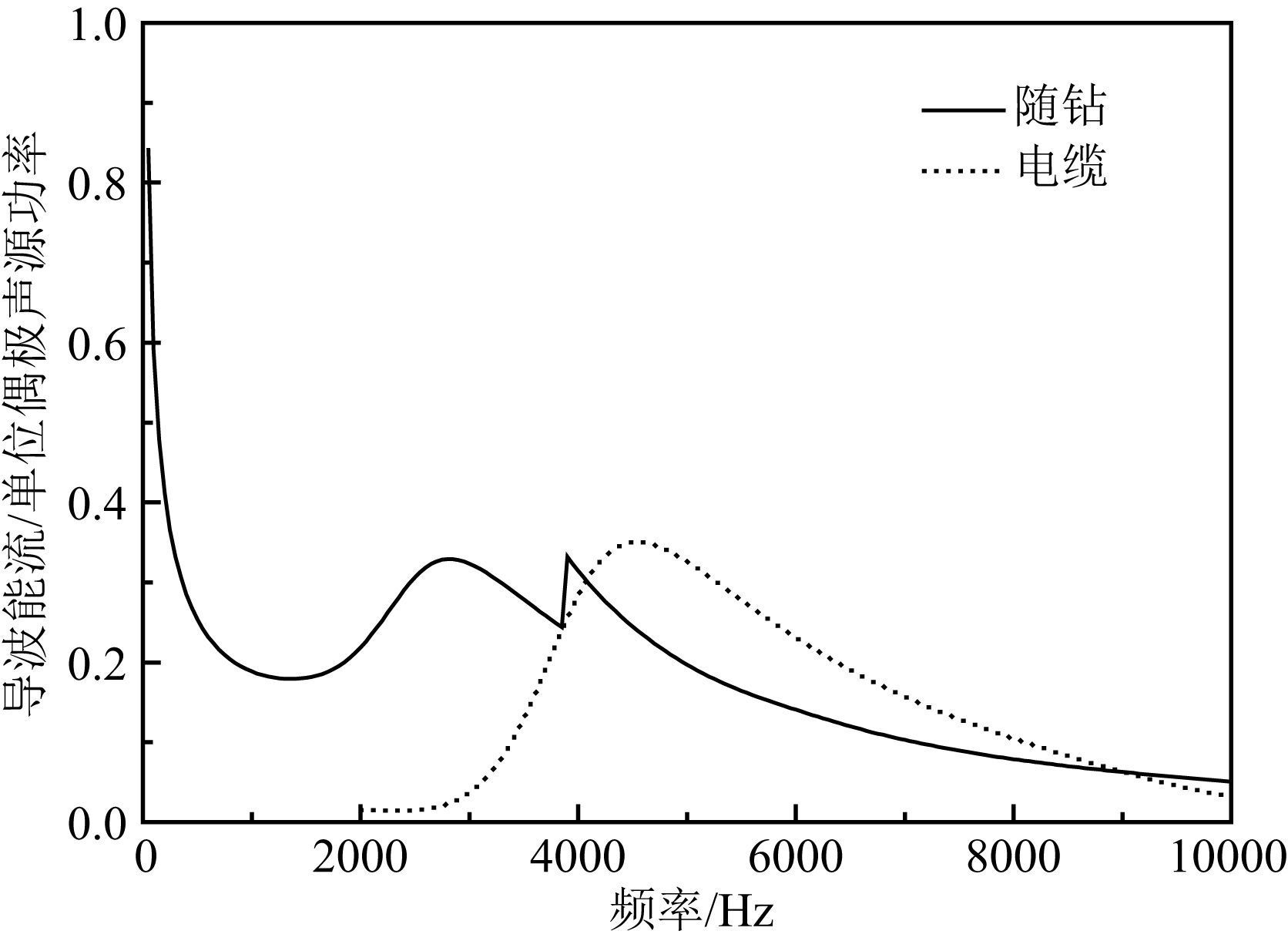
|
图 5 砂岩地层中,随钻和电缆偶极声源激发的沿井传播的导波能流 Fig. 5 Energy flux of wireline and LWD dipole waves guided along the borehole in sandstone formation |
对于随钻和电缆偶极声源产生的SH和SV横波的辐射能流,由式(11) 计算得到,结果见图 6所示.图中随钻和电缆横波辐射能流随频率的变化规律相似,都随着频率的增加先增大达到最大值之后逐渐减小,但二者的不同之处在于:电缆偶极横波辐射能流达到最大值对应的极值频率在3.5 kHz附近,而随钻测井下极值频率较电缆的情况有所降低,为2.5 kHz左右,且横波辐射能流的最大值也变小,因而会出现低频时随钻测井中声源辐射到地层中的横波能量大于电缆测井,高频时恰恰相反的情况,这与图 2和图 3所示的随钻与电缆之间的横波辐射指向因子的大小关系一致.另外,声源辐射到地层中的SV横波的能流远小于SH横波,进一步表明了SH横波在偶极远探测测井中的主导地位.
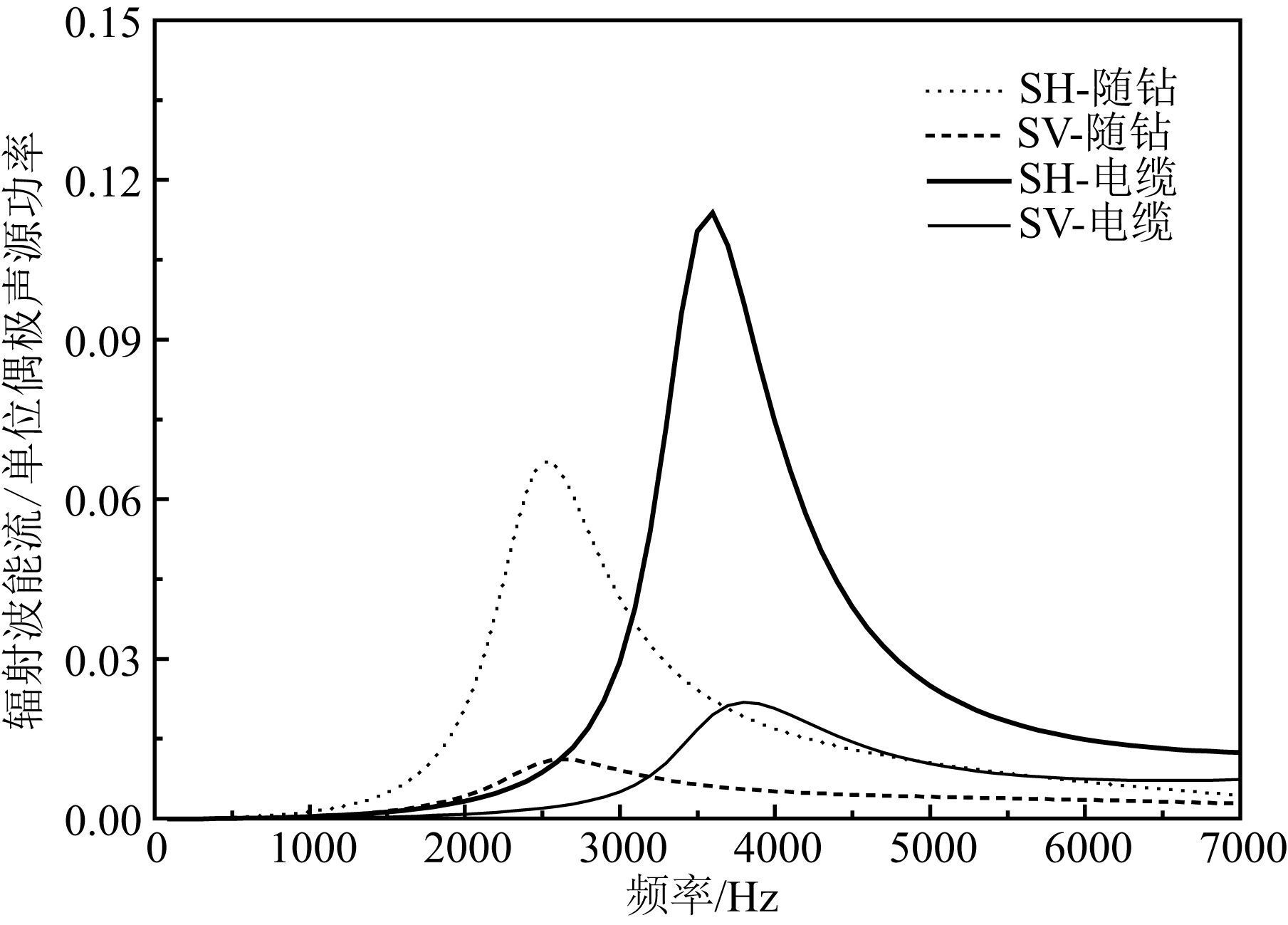
|
图 6 砂岩地层中,随钻和电缆偶极声源辐射到地层中的SH和SV横波能流 Fig. 6 SH- and SV-wave energy flux radiated by wireline and LWD dipole sources in sandstone formation |
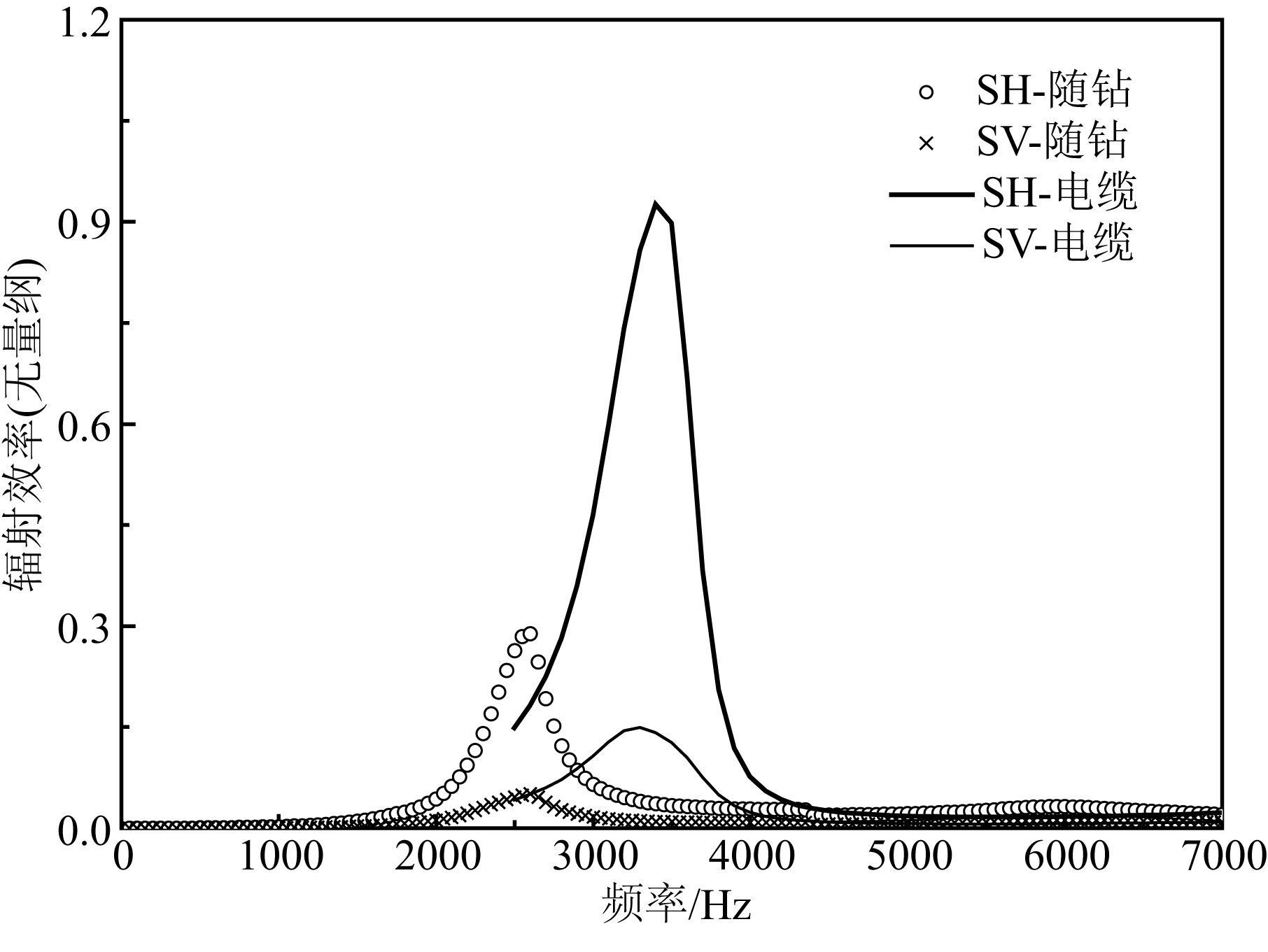
砂岩地层中随钻(标识符) 和电缆(曲线) 偶极SH与SV横波的辐射效率由图 7给出,其中,随钻偶极SH和SV横波的辐射效率随着频率的增加先增大,在2.5 kHz左右达到最大值后又逐渐减小,辐射效率在4 kHz处的间断是由钻铤波的出现所致.与随钻的情况相比,电缆偶极SH和SV横波的辐射效率随频率的变化趋势相似,但不同之处在于电缆测井下SH横波的最大辐射效率大于随钻测井的情况,为随钻SH横波辐射效率的三到四倍.另外,电缆测井下横波最大辐射效率对应的极值频率在3.5 kHz附近,较随钻测井的情况有所升高.结合图 6所示的不同频率下声源辐射到地层中的横波能流可知,随钻远探测测井中声源频率设为2.5 kHz左右对探测井旁地质构造较为有利.

|
图 7 砂岩地层中,随钻和电缆偶极SH和SV横波辐射效率随频率的变化规律 Fig. 7 SH- and SV-wave radiation efficiency of wireline and LWD dipole sources and its variation with frequency in sandstone formation |
为了考察不同岩性对声源辐射效率的影响,本文又计算了灰岩地层下随钻和电缆偶极SH与SV横波的辐射效率,如图 8所示.与图 7砂岩地层的情况相比,灰岩地层中声源辐射效率所跨频段变窄,SH和SV横波的最大辐射效率略有升高,但在这两种地层中声源辐射效率随激发频率的变化规律大体相似.
|
图 8 灰岩地层中,随钻和电缆偶极SH和SV横波辐射效率随频率的变化规律 Fig. 8 SH- and SV-wave radiation efficiency of wireline and LWD dipole sources and its variation with frequency in limestone formation |
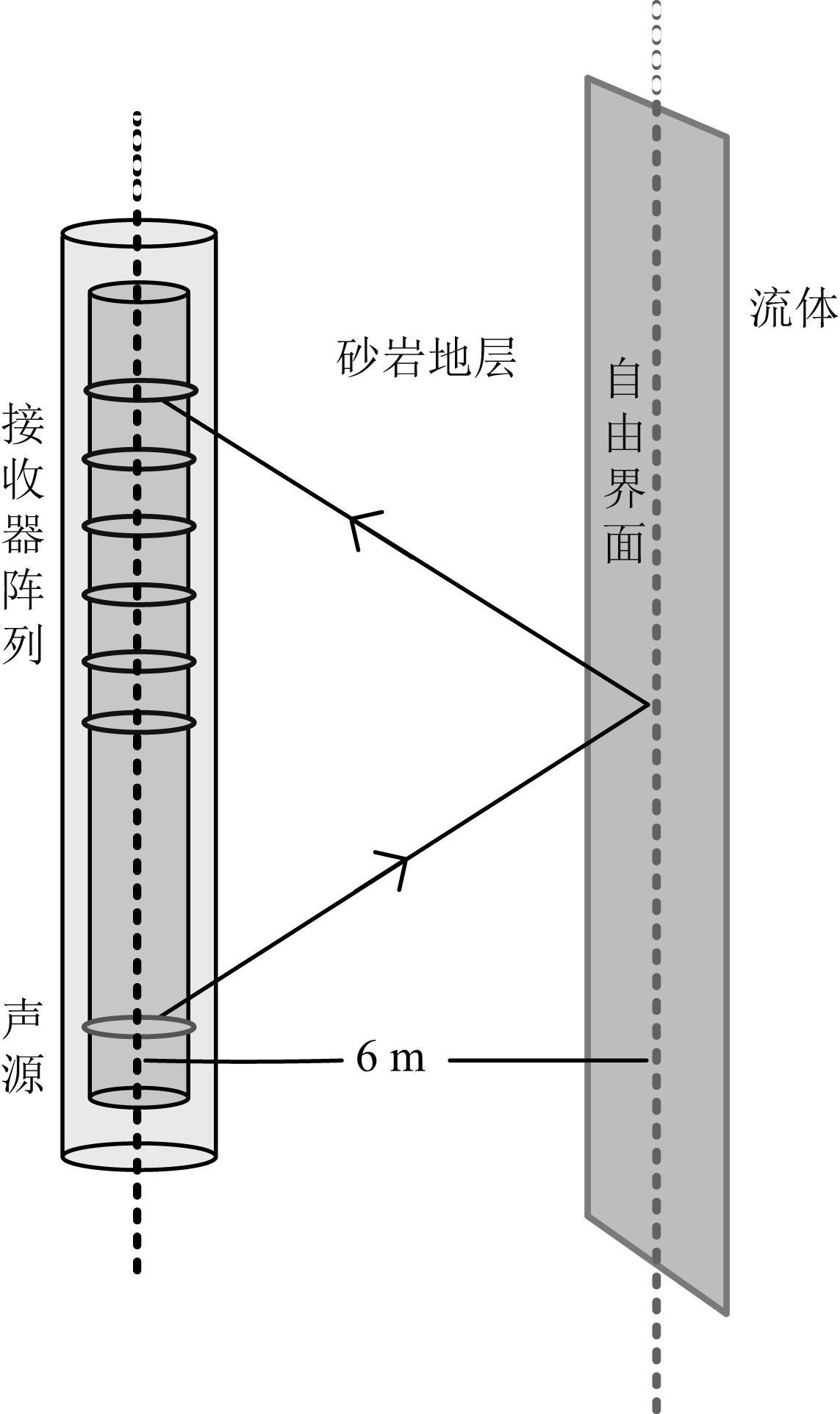
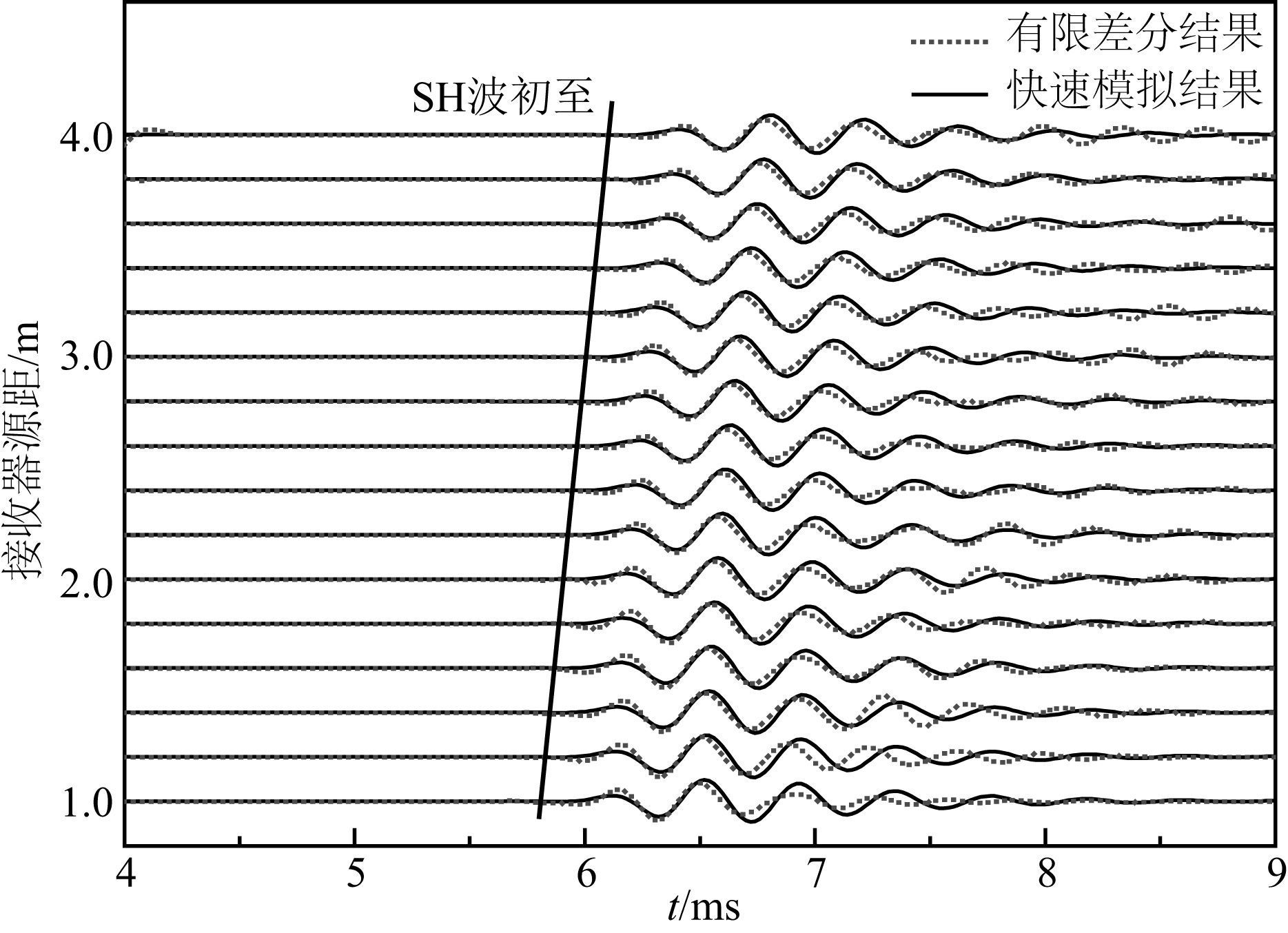
为了验证本文理论分析的正确性和随钻偶极远探测的可行性,以SH反射横波为例,对图 9所示的反射体模型用本文方法(由式(12)) 进行了随钻远探测测井的数值模拟,并将模拟结果与三维有限差分的精确模拟结果进行比较,如图 10所示.为了简单起见,本文设定的反射体模型为一距井轴6 m与井平行的自由界面,左侧为砂岩地层,右侧为流体,界面的法线方向与声源的偏振方向相互正交,接收器沿钻铤表面从距声源1 m到4 m每隔0.2 m放置一个,共计16个.计算采用了Kelly声源,中心频率为2.5 kHz.差分方法是全波模拟方法,其结果包括了钻井弯曲波和后续的反射波,而快速模拟方法只计算了全波中的反射波部分.为了使对比结果更加清晰,图 10中仅显示了4~9 ms时间段内的反射波波形.由图可知,两种方法的模拟结果吻合较好,表明了本文方法的正确性和有效性.然而,这两种方法的计算效率差别巨大,利用三维有限差分模拟上述结果需要耗费数小时,而快速计算方法耗时仅数十秒,这为模拟井段横波远探测数据提供了一种快速有效的方法.
|
图 9 井旁自由界面反射体模型 Fig. 9 Free interface reflection model outside a borehole |
|
图 10 分别利用有限差分方法和快速模拟方法计算的SH反射波的结果对比 Fig. 10 Comparison of SH reflection data calculated using finite difference and the fast simulated method |
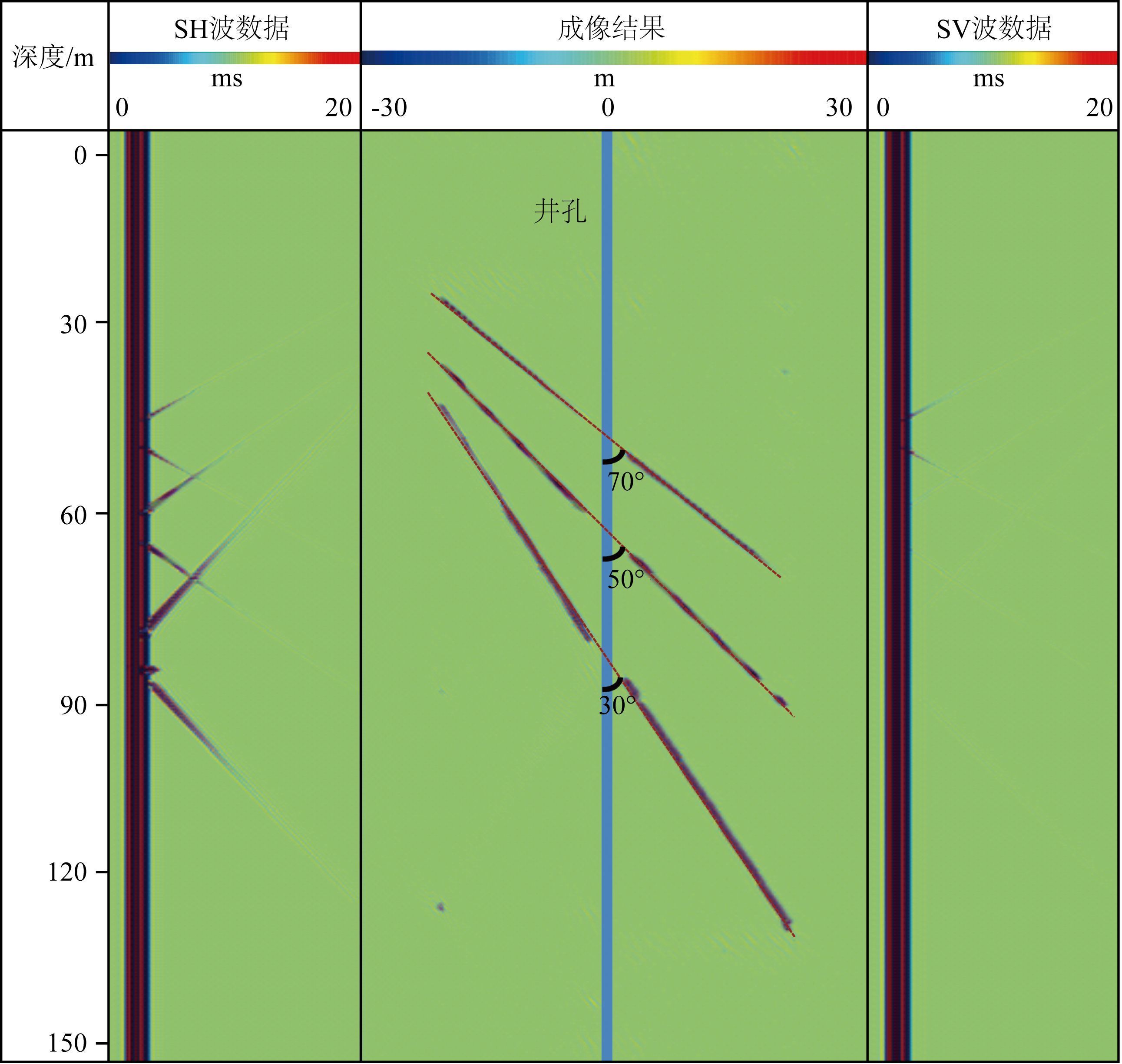
图 11是利用快速计算方法模拟的井段深度为150 m的随钻偶极远探测声场,其中,左边和右边分别为第一个接收器上SH和SV横波远探测数据的变密度图,图的颜色反映了波幅的强弱;中间为计算所采用的三个过井反射界面模型(图中虚线所示),自上而下与井轴的交角分别为70°、50°和30°,界面左侧为砂岩地层,右侧为灰岩地层,地层参数详见表 1.从图中可以看出,首先到达接收器的是钻井弯曲波,其幅度远大于来自过井地层界面的反射波幅度.根据SH和SV波的辐射特性(参见图 2和图 3) 以
|
图 11 对过井多反射界面模型模拟的随钻偶极SH和SV横波远探测数据及由该数据处理得到的反射界面的成像结果 Fig. 11 Multiple reflective interface model and calculated LWD dipole SH and SV full waves in borehole. Processing the data gives the reflector images in middle figure |
及前者相对于后者的良好覆盖性,SH反射横波的幅度明显大于SV反射横波的幅度.这一结果与电缆情况相似,说明SH横波是偶极远探测测井的重要基础.对模拟的随钻偶极SH和SV横波远探测数据进行成像处理,结果见图 11中间所示的变密度图.由图可知,地层反射界面与模型中界面位置完全吻合,界面与井的交角越小,成像的径向深度越深.该结果从理论上表明了随钻条件下进行偶极远探测测井是可行的.
5 结论通过对随钻与电缆偶极声源激发的导波能流、辐射波能流、辐射效率以及随钻偶极横波远探测井段数据模拟分析,得到以下几点认识:
(1) 与电缆声波测井相比,随钻偶极声源的优势激发频率有所降低,对于所选取的钻铤和钻井尺寸,其辐射的优势频率约在2.5 kHz左右,这一结果为随钻偶极远探测测井声源频率的优选提供了理论依据;
(2) 受钻铤的影响,随钻偶极SH横波的最大辐射效率由电缆的0.9降低为0.3左右,两者之间相差三到四倍;
(3) 利用快速计算方法模拟的远探测井段数据的成像结果表明了偶极横波远探测技术在随钻声波测井下的可行性.
附录A圆柱坐标系中,偶极子声场位移势函数在频率-波数域内可以表示为(唐晓明和郑传汉,2004):
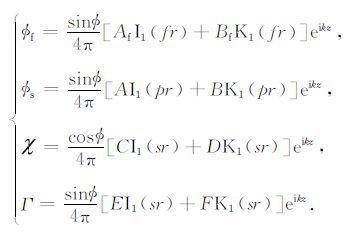
|
(A1) |
其中, φf 表示流体纵波位移势函数; φs、和Γ 分别表示固体介质中纵波、SH横波和SV横波位移势函数; k和f 分别为流体内纵波的轴向与径向波数; p和s 分别为纵横波径向波数;振幅系数 Af、A、C和E 与第一类变型贝塞尔函数 In 有关,描述了从外向内传播的声波,振幅系数 Bf、B、D和F 与第二类变型贝塞尔函数 Kn 有关,表示从内向外传播的声波.
把势函数 φf 代入关系式 Pf=ρfω2φf和Vfz=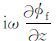
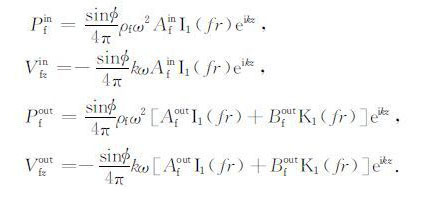
|
(A2) |
式中, Ainf、Afout和Bfout 分别为钻铤内外泥浆中弹性波的振幅系数; ρf 为流体密度; ω 为圆频率.
把势函数 φs、和Γ 代入固体介质中势函数-位移的关系式(唐晓明和郑传汉,2004),得到钻铤中弹性波的径向、环向与轴向位移分量:
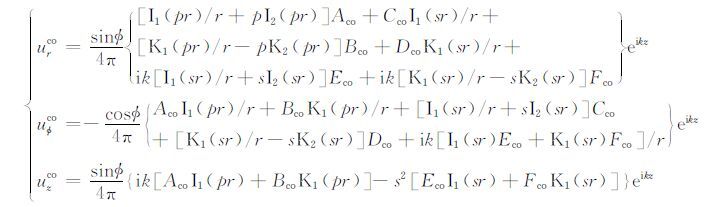
|
(A3) |
其中, Aco、Bco、Cco、Dco、Eco和Fco 分别为钻铤中纵横波的振幅系数.将(A3) 式中各位移分量乘以 iω 因子可得到径向、环向与轴向质点速度 Vrco、Vφco和Vzco. 再将上述三个方向上的位移分量代入到应变-位移关系式,利用胡克定律得到应力分量:
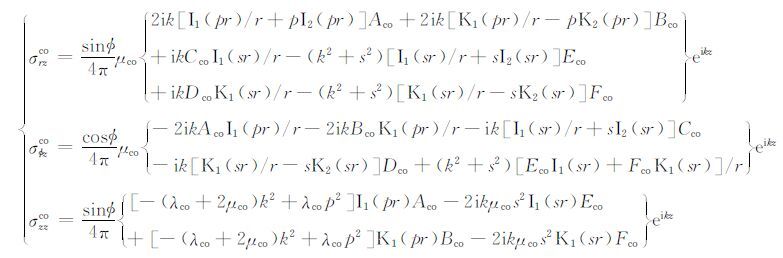
|
(A4) |
式中, λco和μco 分别为钻铤的拉梅常数和剪切模量.
井壁周围地层中径向、环向与轴向的质点速度和应力与钻铤的情况类似,但相对简便,按照与求解钻铤中质点速度和应力相同的方法推导了地层中上述三个方向上速度和应力的分量如下:
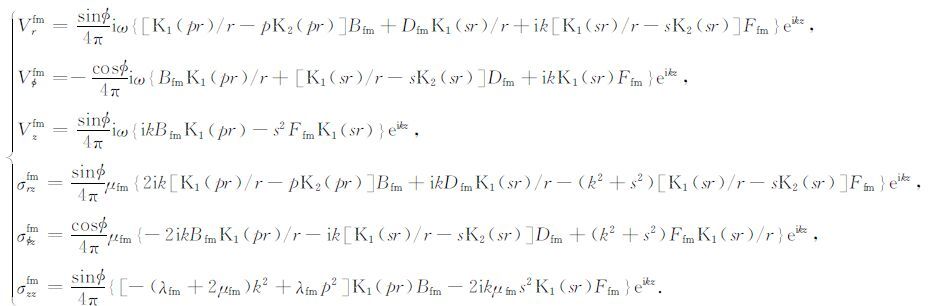
|
(A5) |
其中, Bfm、Dfm和Ffm 分别为无限大地层中纵横波的振幅系数; λfm和μfm 分别为地层的拉梅常数和剪切模量.
附录B随钻测井仪器采用的环状偶极声源可以表述为沿钻铤外半径r2(或r0) 的圆周上分布着的一系列子点源,这些子点源的强度随方位按 sin(φ0-ψ) 变化, φ0 是子点源在圆周上相对于某一参考方位 ψ (可取 ψ=0°) 的方位角.偶极子点声源产生的位移势函数的数学表达式为:
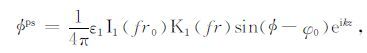
|
(B1) |
其中, φ 是辐射场点相对于子点源方位 φ0 的方位角; ε1=2 为权重系数.
将方程(B1) 的右边乘上 sin(φ0-ψ) 并沿圆周积分,即将圆周上所有子点源的贡献叠加,得到环状偶极声源在井内流体中产生的位移势:
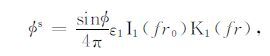
|
(B2) |
把位移势 φs 代入关系式 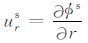
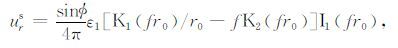
|
(B3) |
类似于电缆的情况(Tang et al.,2014),为了使文中(8) 式所示的随钻偶极辐射指向因子为无量纲的组合,需将位移 urs 乘以因子 1/(ρfω2r0).
最后,按照如下方式将声源位移加载在钻铤外表面处的边界条件上:
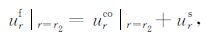
|
(B4) |
式中, urf和urco 分别为边界处流体和钻铤的径向位移.由此边条件,再加上钻铤内径和井壁处的边条件,便可导出(1) 式中的矩阵方程.
| Chai X Y, Zhang W R, Wang G Q, et al. 2009. Application of remote exploration acoustic reflection imaging logging technique in fractured reservoir. Well Logging Technology (in Chinese) , 33 (6) : 539-543. | |
| Che X H, Qiao W X. 2004. Acoustic field in formation generated by linear phased array transmitters in fluid-filled boreholes. Chinese J. Geophys. (in Chinese) , 47 (4) : 731-736. | |
| Chen X L, Wei Z T. 2012. Numerical simulation of monopole acoustic reflection imaging logging in the logging-while-drilling condition. Acta Petrolei Sinica (in Chinese) , 33 (5) : 835-840. | |
| Cheng C J, Zhu Y Y. Elasticity (in Chinese). (in Chinese) Shanghai: Shanghai University Press., 2005 . | |
| Chu Z H, Xu L T, Yin Q W, et al. 2005. Progress of lab study on remote exploration acoustic reflection logging methods. Well Logging Technology (in Chinese) , 29 (2) : 98-101. | |
| Li Y, Zhou R, Tang X, et al. 2002. Single-well imaging with acoustic reflection survey at Mounds, Oklahoma, USA.//64th EAGE Conference & Exhibition. Florence, Italy, 141. | |
| Schlumberger Geoquest. 1998. Geoframe BARS user' guide. Version 1.0. Kanagawa:Schlumberger K. K. , 1 . | |
| Tang X M, Zheng C H. Quantitative Borehole Acoustic Methods (in Chinese). (in Chinese) Beijing: Petroleum Industry Press, 2004 . | |
| Tang X M, Glassman H, Patterson D. 2007. Single-well acoustic imaging in anisotropic formations.//SEG/San Antonio Annual Meeting, 109-113. | |
| Tang X M, Patterson D J. 2009. Single-well S-wave imaging using multicomponent dipole acoustic-log data. Geophysics , 74 (6) : WCA211-WCA223. DOI:10.1190/1.3227150 | |
| Tang X M, Wei Z T. 2012a. Significant progress of acoustic logging technology:remote acoustic reflection imaging of a dipole acoustic system. Applied Acoustics (in Chinese) , 31 (1) : 10-17. | |
| Tang X M, Wei Z T. 2012b. Single-well acoustic reflection imaging using far-field radiation characteristics of a borehole dipole source. Chinese J. Geophys. (in Chinese) , 55 (8) : 2798-2807. DOI:10.6038/j.issn.0001-5733.2012.08.031 | |
| Tang X M, Cao J J, Wei Z T. 2014. Shear-wave radiation, reception, and reciprocity of a borehole dipole source:with application to modeling of shear-wave reflection survey. Geophysics , 79 (2) : T43-T50. DOI:10.1190/geo2013-0096.1 | |
| Tao G, He F J, Wang B, et al. 2008. The study on 3D wave field simulation for acoustic reflection imaging logging in formation. Science in China, Series D:Earth Sciences (in Chinese) , 38 : 166-173. | |
| Winbow G A. 1991. Seismic sources in open and cased boreholes. Geophysics , 56 (7) : 1040-1050. DOI:10.1190/1.1443112 | |
| Zhang C S, Xiao C W, Liu X L, et al. 2011. Application of remote detection acoustic reflection logging to fractured-vuggy carbonate reservoir evaluation. Xinjiang Petroleum Geology (in Chinese) , 32 (3) : 325-328. | |
| Zhuang C X, Yan F, Sun Z F, et al. 2014. Data processing and applications of dipole shear-wave imaging logging. Well Logging Technology (in Chinese) , 38 (3) : 330-336. | |
| 柴细元, 张文瑞, 王贵清, 等. 2009. 远探测声波反射波成像测井技术在裂缝性储层评价中的应用. 测井技术 , 33 (6) : 539–543. | |
| 车小花, 乔文孝. 2004. 充液井孔中的相控线阵声波辐射器在地层中产生的声场. 地球物理学报 , 47 (4) : 731–736. | |
| 陈雪莲, 魏周拓. 2012. 随钻单极子声反射测井数值模拟. 石油学报 , 33 (5) : 835–840. | |
| 程昌钧, 朱媛媛. 弹性力学. 上海: 上海大学出版社, 2005 . | |
| 楚泽涵, 徐凌堂, 尹庆文, 等. 2005. 远探测反射波声波测井方法实验研究进展. 测井技术 , 29 (2) : 98–101. | |
| 唐晓明, 郑传汉. 定量测井声学. 北京: 石油工业出版社, 2004 . | |
| 唐晓明, 魏周拓. 2012a. 声波测井技术的重要进展——偶极横波远探测测井. 应用声学 , 31 (1) : 10–17. | |
| 唐晓明, 魏周拓. 2012b. 利用井中偶极声源远场辐射特性的远探测测井. 地球物理学报 , 55 (8) : 2798–2807. DOI:10.6038/j.issn.0001-5733.2012.08.031 | |
| 陶果, 何峰江, 王兵, 等. 2008. 声反射成像测井在地层中的三维波场模拟方法研究. 中国科学D辑:地球科学 , 38 (增刊1) : 166–173. | |
| 张承森, 肖承文, 刘兴礼, 等. 2011. 远探测声波测井在缝洞型碳酸盐岩储集层评价中的应用. 新疆石油地质 , 32 (3) : 325–328. | |
| 庄春喜, 燕菲, 孙志峰, 等. 2014. 偶极横波远探测测井数据处理及应用. 测井技术 , 38 (3) : 330–336. | |
 2016, Vol. 59
2016, Vol. 59


