2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 西安交通大学电子与信息工程学院, 西安 710049;
4. 中海油研究总院, 北京 100027
2. Institute of Geology and Geophysics, The Chinese Academy of Sciences, Beijing 100029, China;
3. School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
4. Research Center of CNOOC, Beijing 100027, China
随着油气勘探从构造油气藏向地层-岩性等隐蔽油气藏的转移,对断层、裂缝以及地质体边缘等不连续性结构的刻画有着更加重要的意义.由于目前三维地震勘探的大规模应用以及高密度地震数据采集逐步进入工业生产,三维叠后数据量巨大,利用人工提取断层等不连续结构不仅工作量巨大,而且受主观因素的影响造成结果的不确定性.
相干体技术是近些年来发展起来的一项强大的地震属性解释技术,可大大缩短三维地震数据的解释周期(苑书金,2007)、确定断层的空间分布以及目的层的岩性变化、判断数据采集以及处理的质量(Chopra and Marfurt,2007).Bahorich等人于1995年提出了基于归一化道互相关的相干体算法(第一代相干体算法),虽然该项技术在计算标准道相干性时只用了三道地震数据,但实际应用效果立刻在业界引起了巨大的反响(Bahorich and Farmer,1995; Bahorich et al.,1995).陆文凯等人将第一代相干体算法进行发展,提出基于超道技术和高阶统计量的相干体算法(Lu et al.,2005).Marfurt等人于1998年提出基于相似度量的相干体算法(第二代相干体算法),该算法利用分析窗内平均道的能量与所有道能量的比值来度量相干性(Marfurt et al.,1998).该方法提高了相干体的信噪比,但增加了计算量,同时降低了空间分辨率.Gersztenkorn与Marfurt于1999年将第一代相干体算法推广到任意J道(Gersztenkorn and Marfurt,1996,1999; Marfurt et al.,1999),提出基于特征结构的相干体算法(第三代相干体算法).第三代相干体算法运算量实际应用效果好,抗噪性能强,分辨率高,但是其运算复杂程度高,计算耗时,限制了其在工业界的大规模应用.多位学者采用各种加速方法来提高第三代相干体算法的计算速度,取得了明显的加速效果(孙夕平和杜世通,2000; 叶增炉和何建军,2006; Wang et al.,2012).Marfurt与Kirlin将第三代相干体算法与雷达信号处理中的空间谱估计技术相结合,提出了基于MUSIC的相干体算法(Marfurt and Kirlin,2000; 宋建国等,2005).Cohen和Coifman于2002年提出局部结构熵算法(Cohen and Coifman,2002),从而来度量地震数据体中的不连续性结构,大大提高了计算效率.Randen等人提出基于梯度结构张量技术来估计地震数据的纹理属性(Randen et al.,2000; Chopra and Marfurt,2007; 张军华等,2007).以此为基础,多位学者提出基于梯度结构张量的相干算法(Randen et al.,2000; Bakker,2003).单一的相干属性有时不能满足解释人员的需要,因此也有诸多许多学者提出将相干体技术与瞬时属性联合应用提高地质目标体的分辨率(王西文等,2002a,2002b; 张军华等,2004; Zhou et al.,2007; 苑书金,2007; 周艳辉和高静怀,2007).
自从法国女工程师Morlet在处理地震资料时首次提出小波变换的思想以后(Antoine et al.,2004),一维小波变换在地震信号处理及解释领域取得了相当多成功的应用(Chopra and Marfurt,2007).1987年,Murenzi在与Grossmann以及Daubichies等人讨论以后,在其博士论文中首次提出两维连续小波变换并对其进行了详细的讨论(Murenzi,1990).随后,高维连续小波变换在轮廓检测(张长江等,2006)、字符识别(Antoine et al.,1995a; Murenzi et al.,1999)、目标辨识(Antoine et al.,1995b)、医学图像处理(Choi et al.,2001)、模式识别(Antoine et al.,1999)、天体图像处理及目标识别(Antoine et al.,2002)、探地雷达信号处理(陈文超等,2000,2003)等各个领域均取得了成功应用.在高维连续小波变换中,对母小波的操作有平移、伸缩和旋转,这三种操作由平移因子、尺度以及角度所控制.常用的二维Morlet小波具有较好的方向选择性,因此被广泛采用.由于高维连续小波变换的结果为四维的,数据量巨大且不易显示,Murenzi初步探讨了二维连续小波变换系数的快速实现算法(Murenzi et al.,1997).
二维连续小波变换在地震信号处理中也取得了许多应用,例如:面波去除(刘财等,2003; 李媛媛等,2004; 张华等,2007)、噪声衰减(高振山等,1998; 杨立强等,2005)、提高分辨率(吴爱弟和牟永光,1997)等.Mallat等人提出利用一维小波变换系数模的极大值来检测信号的奇异性(Mallat and Hwang,1992).以Mallat等人提出的方法为基础,Li Chun-Feng等人提出利用基于一维小波变换的Holder指数奇异性属性刻画地层边界等(Li and Liner,2008).Ouillon与Sornette等人首次将二维连续小波变换用于分析断层等奇异性结构,提出利用各向异性小波变换结果的最优系数来检测各个尺度断层的走向(Ouillon et al.,1995,1996).他们采用二维各向异性Mexcian Hat小波作为母小波,在给定的分辨率下保留模最大的小波系数,这样被保留下的小尺度系数能够反映较小断层的结构和走向,大尺度系数能够反映更大区域内断层的结构和走向.随后,Darrozes与Gaillot等人将上述方法进行改进,利用归一化最优各向异性小波系数来检测多尺度的断层结构,并采用玫瑰方向图来判断各个分辨率下的目标区域的断层走向(Darrozes et al.,1997; Gaillot et al.,1997,1999).但上述分析方法采用的均为Mexican小波,方向选择性较差.Bouchereau首次利用二维Morlet小波作为母小波,将两维连续小波变换用于勘探地震资料的断层检测.她采用二维Morlet小波这种具有方向选择性的小波作为母小波,并与自适应滤波技术相结合,对断层面检测进行了研究初探(Bouchereau,1997).
本文直接以三维连续小波变换为基础检测地震资料的不连续性,安排如下:首先介绍高维连续小波变换的基本理论及快速实现方法,然后给出基于高维连续小波变换的地震资料不连续性检测方法及实现流程,接着将本文所提出的方法用于合成信号及实际资料处理,最后给出结论及展望.
2 高维连续小波变换的基本理论及快速实现 2.1 二维连续小波变换假设ψ(x)是二维母小波,对母小波的基本操作有三种:平移、伸缩以及旋转.经过这三种操作的小波为
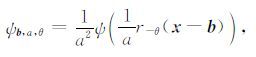
|
(1) |
其中, x=(x,y)T 为二维变量,平移由平移因子 b(b=(bx,by)T) 控制,伸缩由尺度因子a控制,旋转由旋转因子(即角度)θ控制,r-θ()表示对变量逆时针旋转角度θ.对二维母小波的三种操作示意如图 1所示.
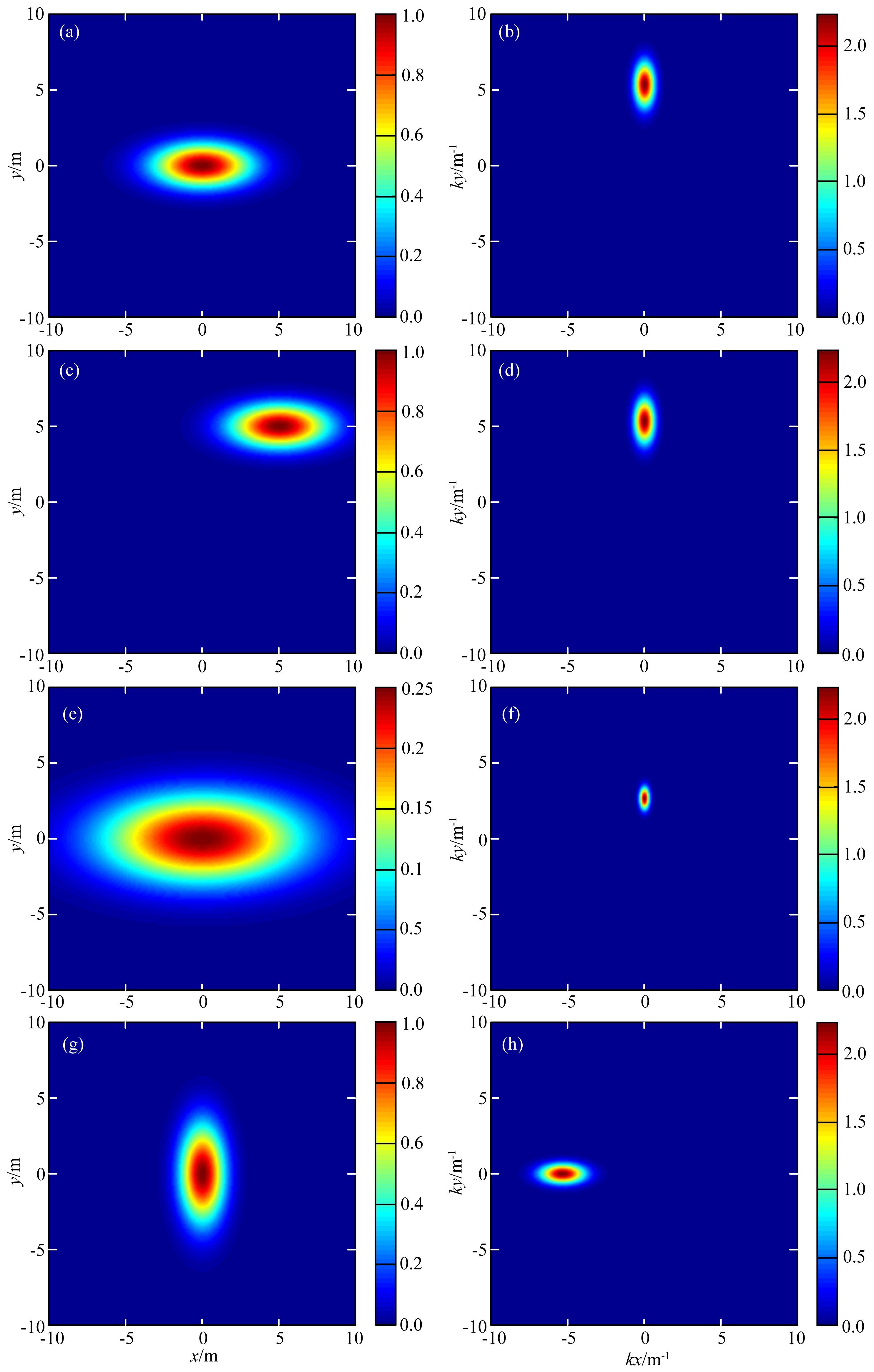
|
图 1 对母小波的各种操作 (a)空间域母小波的包络;(b)二维傅里叶域母小波的模值;(c)空间域经过平移的小波包络;(d)二维傅里叶域经过平移母小波的模值;(e)空间域经过伸缩的小波包络;(f)二维傅里叶域经过伸缩母小波的模值;(g)空间域经过旋转的小波包络;(h)二维傅里叶域经过旋转母小波的模值. Fig. 1 Sketches showing operations on mother wavelets (a)Envelop of mother wavelet(in space domain);(b)Modulus of mother wavelet(in 2D Fourier transform domain);(c)Envelop of shifted wavelet(in space domain);(d)(b)Modulus of shifted wavelet(in 2D Fourier transform domain);(e)Envelop of dilated wavelet(in space domain);(f)Modulus of dilated wavelet(in 2D Fourier transform domain);(e)Envelop of rotated wavelet(in space domain);(f)Modulus of rotated wavelet(in 2D Fourier transform domain). |
设 f(x) 是二维信号,则 f(x) 的二维连续小波变换(Two-Dimensional Continuous Wavelet Transform,2DCWT)定义为
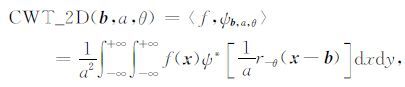
|
(2) |
如果一个母小波的傅里叶变换 ψ^(k) 在二维傅里叶域被包含在一个以原点为顶点的凸锥内,就称这个母小波是方向性小波.常用的方向性小波有二维Morlet小波、二维Cauchy小波等.二维Morlet是一种典型的方向性小波,其空间域及二维傅里叶变换域的表达式为

|
(3) |
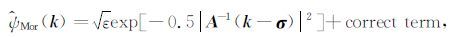
|
(4) |
其中,参数 σ 为调制波矢量, A=diag[ε-0.5,1](ε≥1) 为2×2的各向异性矩阵,控制着小波函数的支撑域形状(ε=1时为圆形,ε >1时为椭圆形).式(3)和式(4)中的第二项是由于要强制满足母小波容许性条件 ψ^(0)=0 所产生的修正项.对于调制波矢量σ的模值大于5.33时,这个修正项就可以忽略不计,则其空间域及二维傅里叶变换域的表达式就简化为
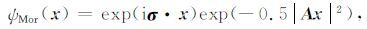
|
(5) |
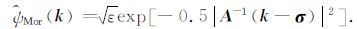
|
(6) |
通常情况下,取参数 σ=(0,σy)T 后,式(5)和式(6)简化为
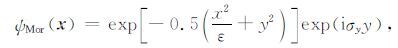
|
(7) |
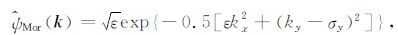
|
(8) |
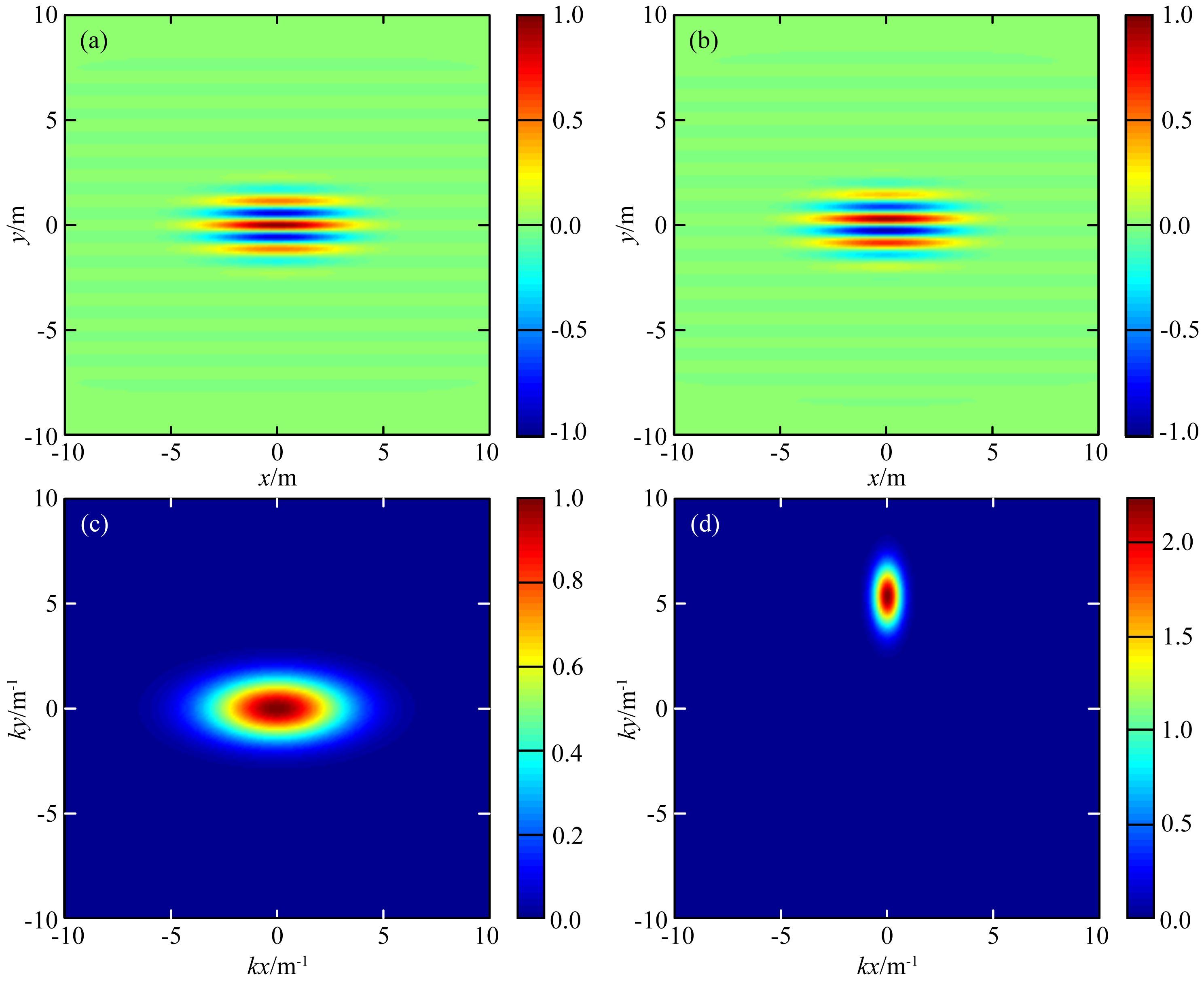
选取ε=5,采用参数σ=(0,5.33)T时二维Morlet小波的实部、虚部、包络及二维傅里叶振幅谱如图 2所示.
|
图 2 ε=5,σ=(0,5.33)T时二维Morlet小波 (a)实部;(b)虚部;(c)包络;(b)振幅谱. Fig. 2 2D Morlet with ε=5 and σ=(0,5.33)T (a)Real-part;(b)Imaginary-part;(c)Envelop;(d)Amplitude spectrum. |
当所采用的母小波为不具有方向选择性时,例如二维Mexican Hat小波,旋转操作不起作用,这时二维信号f(x)的2DCWT退化为
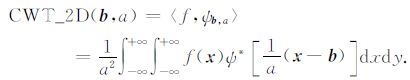
|
(9) |
2DCWT的系数共有四个参数,也就是变换的结果是四维的,那么系数无法直接显示.为了解决这些问题,固定2DCWT系数中的两个参数,这样就只有两个参数变化,可以得到2DCWT系数的二维切片,便于显示.二维切片共有6种,最为常用且意义比较明确的有空间位置切片以及尺度-角度切片:
(a)空间位置切片:固定尺度和旋转角度,变化空间位置.利用空间位置切片可以分析某类特征在整个二维平面的分布情况.空间位置切片在诸如图像处理、湍流分析、断层检测等各个方面取得了成功的应用.
(b)尺度角度切片:固定空间位置,变化尺度和旋转角度.利用尺度-角度切片,可以观察固定空间位置的所有尺度和角度下的2DCWT系数,在分析小波函数的尺度特性以及角度分辨率方面有着重要的作用.采用如下一个合成信号(带有衰减的二维复合平面波),公式为
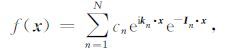
|
(10) |
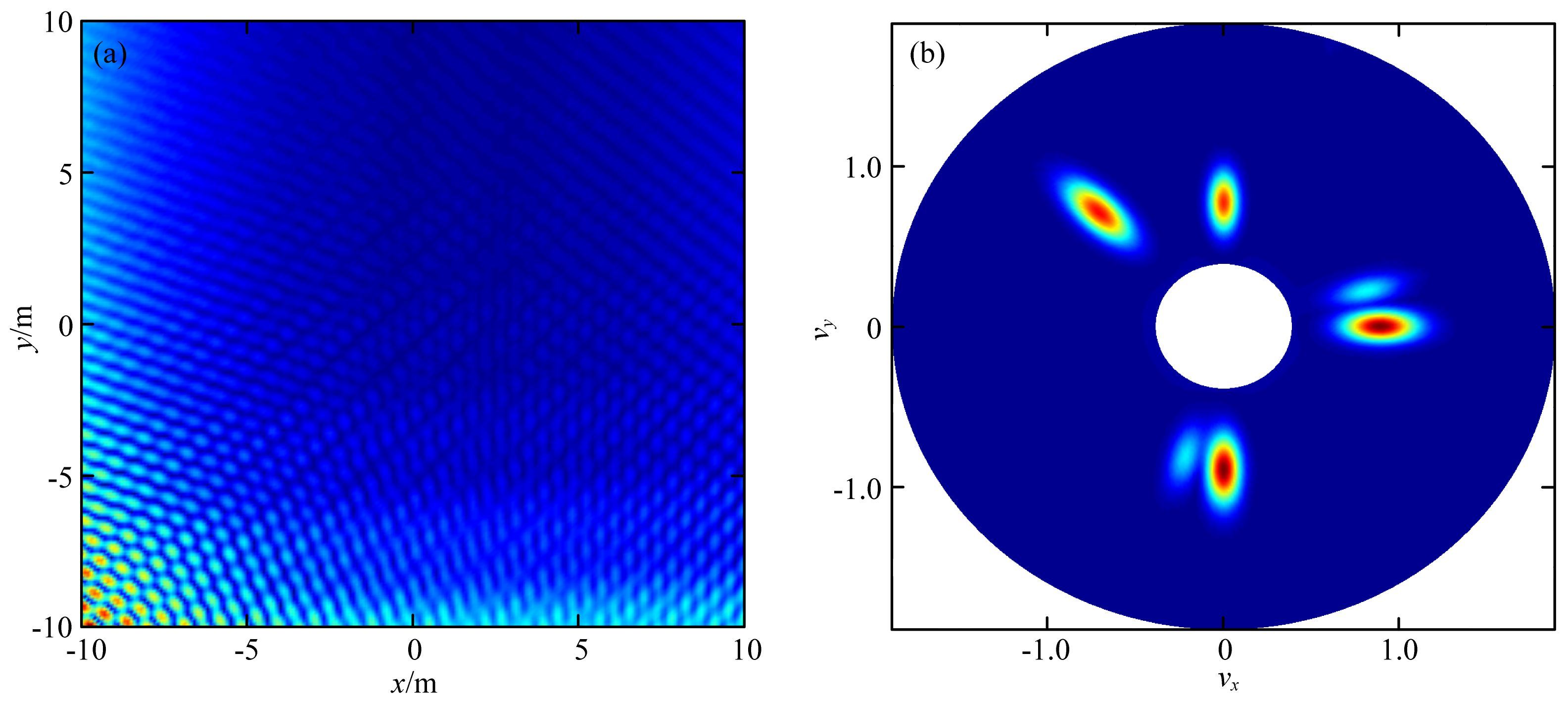
其中 cn 表示第n个平面波的振幅,kn表示第n个平面波的传播方向及频率,In表示衰减方向及衰减因子.该二维信号包络如图 3a所示,原点处的2DCWT系数尺度角度切片如图 3b所示,其中 vx=cos(θ)/a,vy=sin(θ)/a, 可以在此切片上清晰的看出该二维信号在原点附近有六个平面波分量(对应于六个峰值).
|
图 3 二维合成信号及其尺度角度切片 (a)含有六个平面波的合成信号(振幅);(b)原点处的尺度角度切片. Fig. 3 2D synthetic signals and scale-angle slices of 2DCWT coefficients (a)Synthetic signal which contains six plane waves;(b)One of 2DCWT coefficients scale-angle slices at origin. |
由2DCWT的定义(如式(2)所示),计算一个2DCWT系数需要一个二重积分,对于离散情况而言,需要一个二维累加求和.上面已经提到,2DCWT的结果是四维的,因此,直接利用式(2)计算复杂度很高.在波数域式(2)可简写为
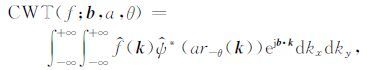
|
(11) |
f^(k)是f(x)的二维傅里叶变换, ψ^(k)是ψ(x)的二维傅里叶变换.如果固定尺度和角度,上式可以利用逆二维傅里叶变换实现,即:
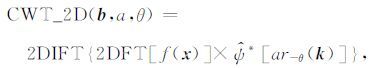
|
(12) |
其中2DFT和2DIFT2分别表示二维傅里叶变换和逆二维傅里叶变换.由于二维傅里叶变换有快速算法的支持,因此,利用上式可以快速计算2DCWT系数的空间位置切片.2DCWT系数空间位置切片的快速实现流程图见图 4所示.由于有快速傅里叶变换的支持,计算一个2DCWT系数空间位置切片的运算复杂度由O(N4)降低为O(N2logN).

|
图 4 2DCWT系数空间位置切片的快速实现流程 Fig. 4 Flow chart of fast realization of 2DCWT coefficients(position slice) |
目前工业界内使用的成果地震数据多为三维的,因此三维变换更适合处理三维地震资料,所以有必要将二维连续小波变换推广到三维.一维连续小波变换推广到二维连续小波变换时,平移因子由一维变成二维向量,并且增加了一个旋转因子.将二维连续小波变换推广到三维时,对母小波的操作仍是三种:平移、伸缩及旋转,但是平移因子为三维向量,旋转操作里包含两个变量,即沿倾角方向的旋转以及沿方位角的旋转.设f(x)为三维信号,ψ(x)为三维母小波,则的三维连续小波变换(Three-Dimensional Continuous Wavelet Transform,3DCWT)定义为
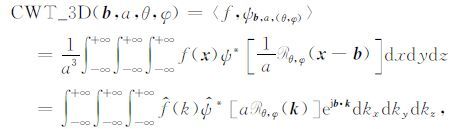
|
(13) |
其中 x=(x,y,z)T 为三维向量, b(b=(bx,by,bz)T)、a、(θ,φ) 分别表示对小波的平移、尺度和旋转因子; Rθ,φ 表示对向量沿倾角方向旋转θ,沿方位角方向旋转φ;f^(k)是f(x)的三维傅里叶变换,ψ^(k)是ψ(x)的三维傅里叶变换.
常用的三维小波有三维Mexican-hat小波、三维Morlet小波以及三维Cauchy小波.三维Mexican-hat小波不具有方向选择性,因此我们只介绍具有方向选择性的三维Morlet小波.三维Morlet小波的空间域及三维傅里叶域表达式为
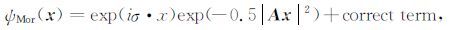
|
(14) |
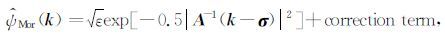
|
(15) |
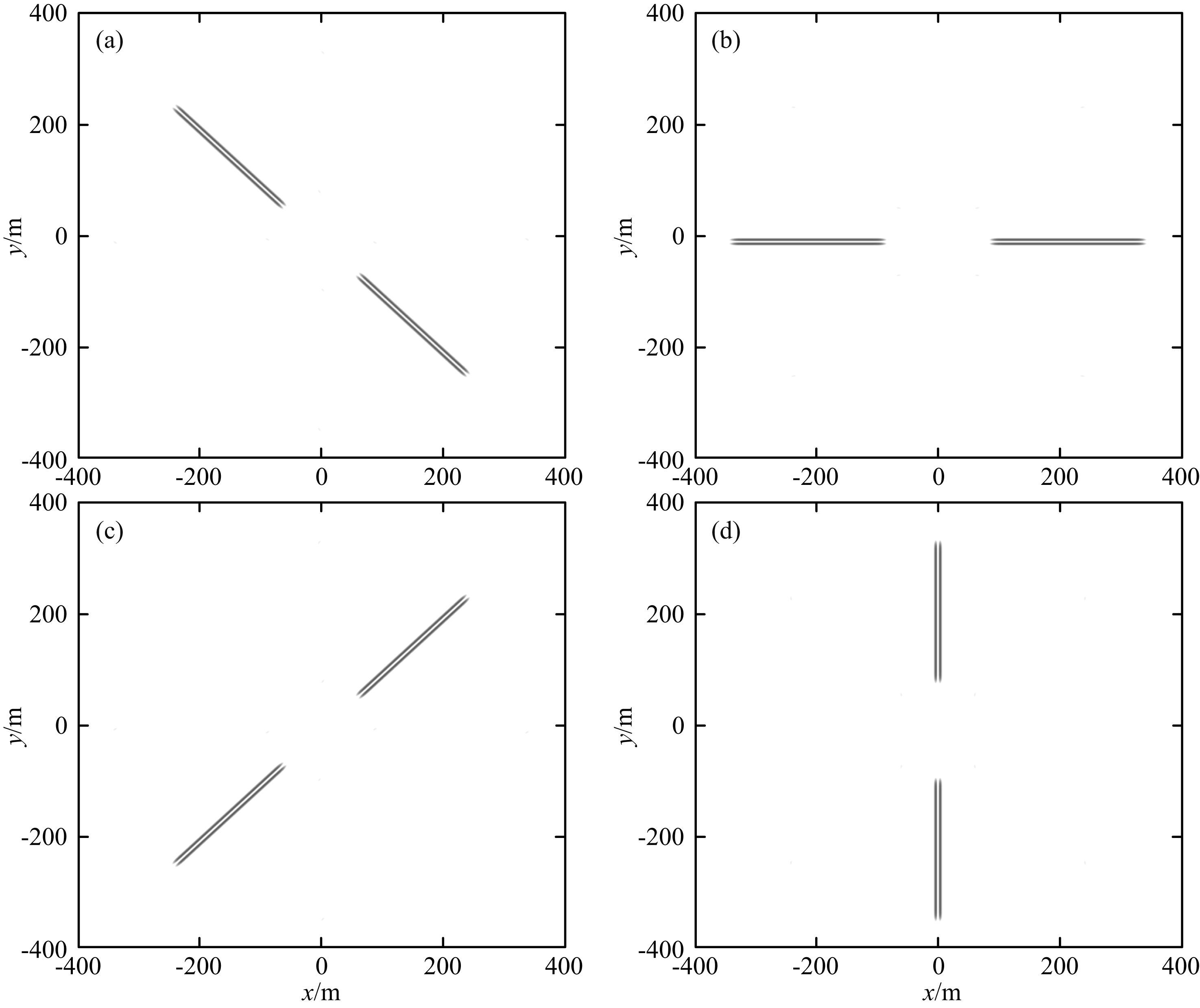
其中,参数σ为调制波矢量, A=diag[εx-0.5,εy-0.5,1](εx≥1,εy≥1) 为3×3的各向异性矩阵.式(14)和式(15)中的第二项是由强制满足容许性条件ψ^(0)=0所产生的修正项.对于调制波矢量σ的模值大于5.33时,这个修正项就可以忽略不计.
由于3DCWT的系数为六维,也存在两维连续小波变换的问题.与两维连续小波变换相同,也有两种常用系数“切片”:空间位置“切片”(a、θ及φ固定)以及尺度方向“切片”(b固定).空间位置“切片”可以通过类似于图 4的流程利用FFT技术快速实现,如图 5所示.

|
图 5 3DCWT系数空间位置切片的快速实现流程 Fig. 5 Flow chart of fast realization of 3 DCWT coefficients(position slice) |
一维连续小波变换及其模极大值已被广泛地用于一维信号的奇性检测,其小尺度系数模能够精确地定位奇性位置(Mallat,2008).目前业内使用的地震资料均为二维/三维,直接利用一维连续小波变换不能充分利用道与道之间的相关性来检测地震资料的横向不连续性,因此有必要采用高维变换来检测地震资料的横向不连续性.
3.1 高维连续小波变换角度分辨率分析不具有方向选择性高维Mexican-Hat小波不能区分地震资料的横向不连续性和纵向不连续性.具有一定方向选择性的二维张量积小波变换具有三个方向,但所具有的三个方向的方向选择性较差,这样会使倾斜方向的不连续性在水平细节分量、垂直细节分量上均有体现.合成信号如图 6a所示,包含有垂直、水平及倾斜三个方向的不连续性.二维张量积小波变换最小尺度的水平、垂直以及倾斜分量分别如图 6b、图 6c以及图 6d所示,倾斜方向的不连续性不但在倾斜分量上(图 6d)有所体现,在水平分量及垂直分量上也有所体现.因此,在实际应用中二维张量积小波变换仅能区分水平和垂直两个方向的不连续性,不能区分介于垂直和水平方向之间的倾斜方向不连续性,这对检测地震资料横向不连续性是远远不够的.
|
图 6 合成测试信号的二维张量积小波分解结果 (a)合成的测试信号;(b)二维张量积小波变换-水平分量;(c)二维张量积小波变换-垂直分量;(d)二维张量积小波变换-倾斜分量. Fig. 6 2D wavelet decomposition of synthetic signal (a)Synthetic test signal;(b)Coefficients of 2D tensor-product wavelet transform(in horizontal direction);(c)Coefficients of 2D tensor-product wavelet transform(in vertical direction);(d)Coefficients of 2D tensor-product wavelet transform(in oblique direction). |
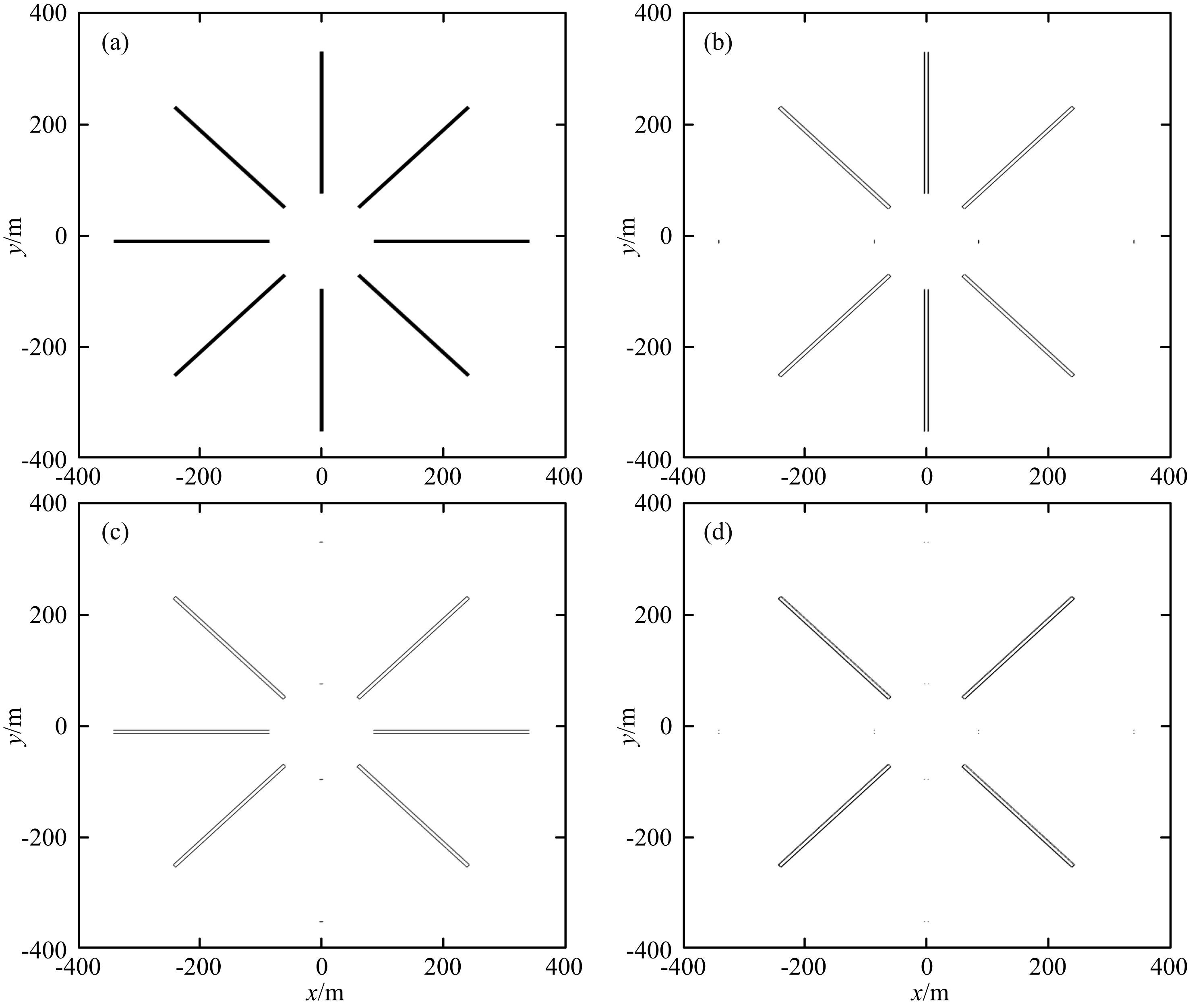
采用具有方向选择性的二维Morlet小波作为母小波,对合成信号(图 6a)做2DCWT,小尺度下-45°、0°、45°、90°的2DCWT系数如图 7a、图 7b、图 7c以及 图 7d所示,倾斜方向的不连续性只出现在图 7a及图 7c中,并不影响其他方向变换的结果.因此,相比于二维张量积小波变换,2DCWT(采用具有方向选择性的母小波,例如二维Morlet小波)具有很好的方向选择性,更适合检测指定方向的不连续性.由于常用的叠后地震数据为三维的,因此,本节采用具有方向选择性的三维Morlet小波作为母小波,利用小尺度3DCWT系数的模极大值来刻画三维地震资料的横向不连续性.
|
图 7 合成测试信号的2DCWT结果(小尺度) (a)-45°;(b)0°;(c)45°度;(d)90°. Fig. 7 2DCWT coefficients of synthetic signal(small scale) (a)-45 degree;(b)0 degree;(c)45 degree;(d)90 degree. |
一维连续小波变换的小尺度系数模极大值来可被用来定位/度量信号中的不连续性(Mallat,2008).在小尺度下,小波具有很好的时间分辨率,因此在度量不连续性时均在小尺度下进行.一维连续小波变换中对母小波的操作为平移和伸缩,在三维连续小波变换中,对母小波的操作增加了旋转操作(包含倾角和方位角),另外平移因子变为一个高维矢量.因此,在利用三维连续小波变换度量地震资料不连续性时,固定在小尺度下,需要对倾角及方位角进行扫描以得到小尺度系数模极大值来度量/定位地震资料的不连续性,公式为
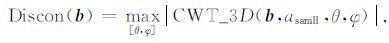
|
(16) |
由于断层等不连续性结构表现为空间方向上的不连续性,因此在角度扫描时可以限制角度搜索范围.
3.3 实现流程采用小波系数模极大值来度量地震资料的不连续性时,由于各处振幅不相同,因此会造成强振幅区域不连续度量较强,而弱振幅区域不连续性度量较弱.因此我们利用瞬时相位数据体作为三维连续小波变换的输入,来检测三维地震资料的不连续性.将利用高维连续小波变换检测地震资料横向不连续性的步骤总结如下:
步骤1:记这个三维地震数据体为f(x,y,t).为简单起见,用向量x表示三维地震数据体中某点的坐标(即 x=(x,y,t)T), 那么三维地震数据体可简单记为f(x),其中,x,y表示位置坐标,t表示时间轴.对该三维地震数据体进行保边缘滤波(王伟等,2012;Zhang Bo,2016)等预处理.
步骤2:对三维地震数据体f(x)每道进行Hilbert变换,得到复地震道F(x),并在此基础上提取瞬时相位得到三维瞬时相位数据体Phase(x),进而获得三维相位余弦数据体PhC为
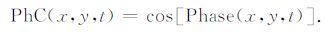
|
(17) |
步骤3:由于现有的计算机内存有限,加之计算过程中需要大量的内存,因此采用分块的办法减少对内存的依赖性.将步骤2生成的三维相位余弦数据体进行分为N个子块,每个子块记为PhC_Block(n,x),分块时,子块各个方向上的点数尽量选择2的整数次幂,有利于使用FFT来减少计算量.
步骤4:分别对每个三维相位余弦数据体子块PhC_Block(n,x)进行三维连续小波变换得到其三维连续小波变换系数 CWT_3D(n,x,asmall,θ,φ) 为
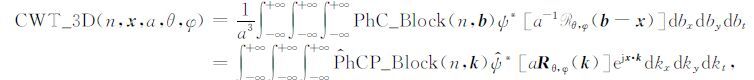
|
(18) |
其中 P^hC_block(n,k)是PhC_block(n,x) 的
三维傅里叶变换, ψ^(k)是ψ(x) 的三维
傅里叶变换,b表示临时变量;尺度a选为最小尺度(可由采样间隔确定).
上述三维连续小波变换可以通过图 5所示的流程快速实现.
步骤5:利用每个三维相位余弦数据体子块的三维连续小波变换系数 CWT_3D(n,x,asmall,θ,φ) 来进行三维地震资料的不连续性检测.利用小尺度三维连续小波变换系数模来确定地震资料不连续性的方向及度量不连续性,公式为
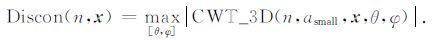
|
(19) |
步骤6:将生成的各个分块不连续性数据体Discon(n,x)进行拼接并输出,得到整个地震资料的不连续性数据体,完成检测.
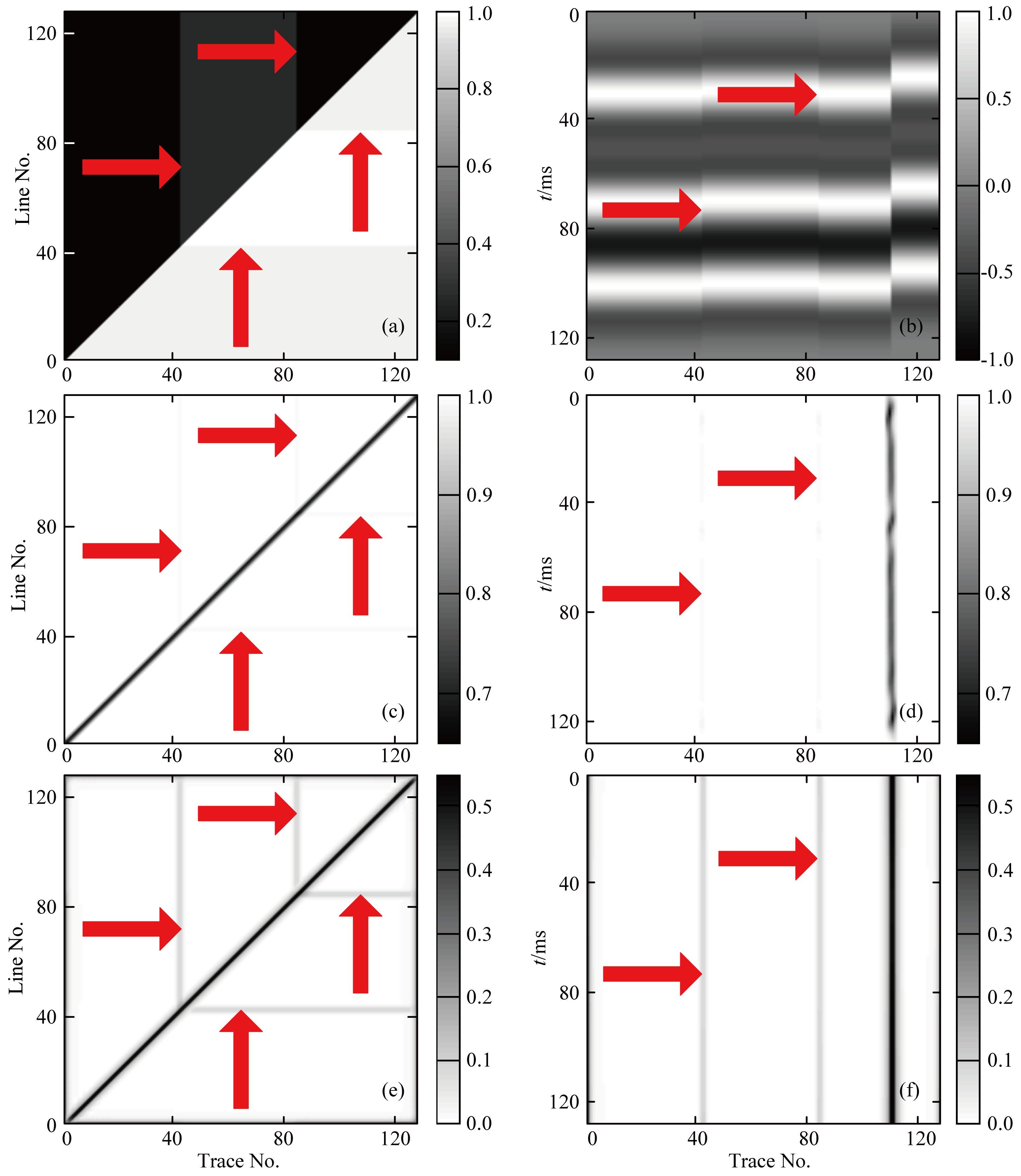
4 模型及实际资料处理首先对一个三维合成地震数据进行测试.该三维模型含有三个水平反射界面,另外在对角线方向有一较大断层,水平方向和垂直方向各有两个较弱断层,采用褶积模型产生三维合成数据.图 8a是合成三维信号的时间切片,红色箭头所指分别为水平及垂直方向的两个弱断层,图 8c为相干体(第三代相干体算法)的时间切片(时间与图 8a对应),图 8e为采用本方法检测不连续性结果的时间切片(时间与图 8a对应).图 8b是合成三维信号的一条测线,能够看出有三个水平反射波,红色箭头所指为两个较弱断层,图 8d为相干体的一条测线(测线号与图 8b对应),图 8f为采用本方法检测不连续性结果的一条测线(测线号与图 8b对应).上述两组对比结果表明,相比较于相干体的结果,采用本文提出的方法,不但能够刻画明显的不连续性,也能够刻画弱连续性.
|
图 8 合成三维地震信号横向不连续性检测结果 (a)合成三维信号的某时间切片;(b)合成三维信号的某测线;(c)相干体的对应时间切片;(d)相干体的对应测线;(e)本文方法结果的对应时间切片;(f)本文方法结果的对应测线. Fig. 8 Discontinuity detecting results of synthetic 3D seismic data (a)A time slice of synthetic 3D signal;(b)A line of synthetic 3D signal;(c)Detecting result of coherence algorithm(corresponding to(a));(d)Detecting result of coherence algorithm(corresponding to(b));(e)Detecting result of proposed method(corresponding to(a));(f)The detecting result of proposed method(corresponding to(b)). |
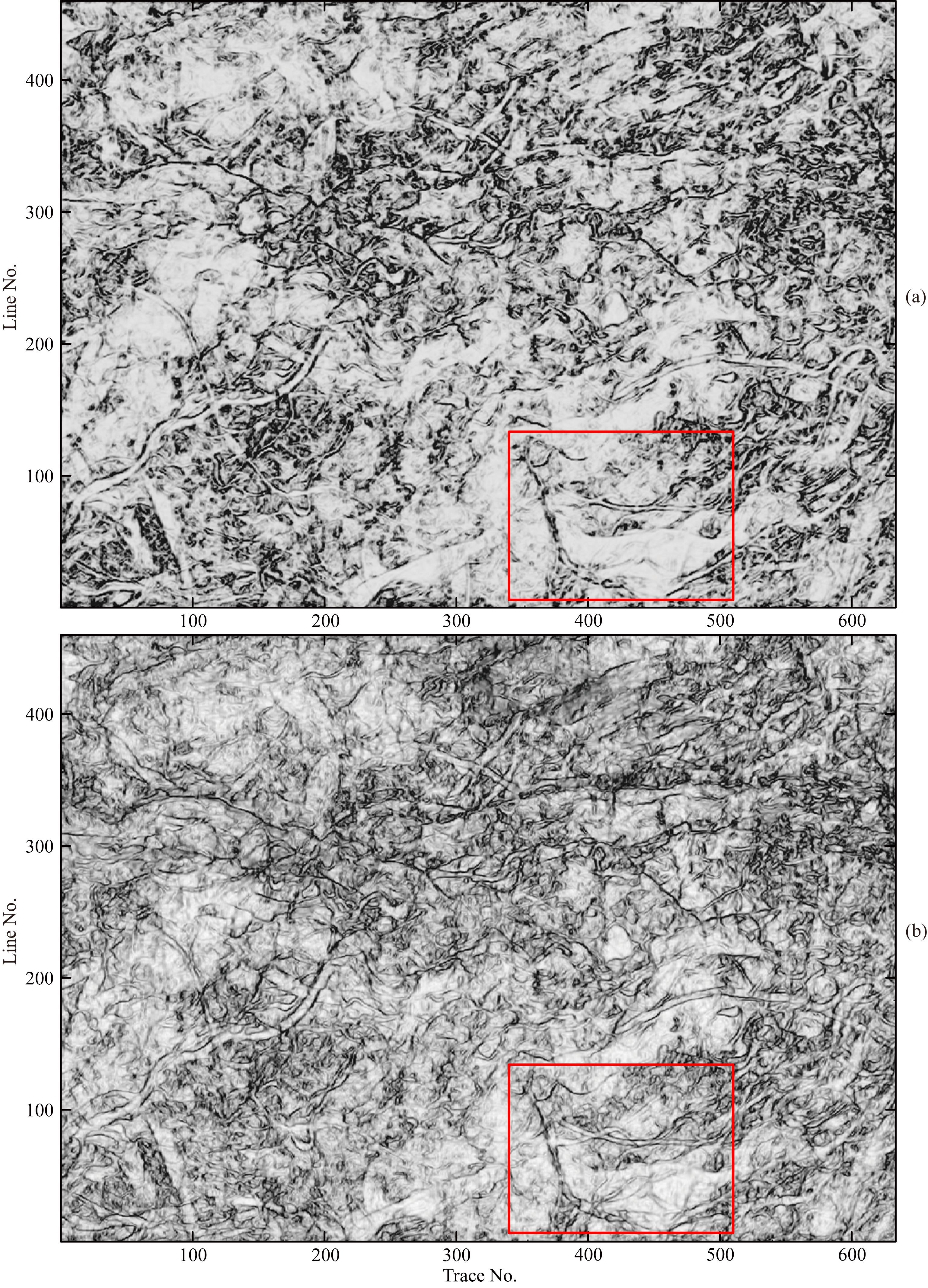
然后我们将本文提出的基于高维连续小波变换的地震资料横向不连续性检测方法用于某油田的一块三维海上实际地震资料.采用商业软件得到的相干体结果时间切片1如图 9a所示,而采用本文方法结果的时间切片如图 9b所示.本文方法刻画断层更为清晰,另外弱不连续性结构检测能力强于商业软件,如红色方框区域内的小河道及弱不连续性结构.在另一个时间切片2上,本文方法结果如图 10b所示,相比于上商业软件结果(如图 10a所示),本文方法能够清晰的刻画东北区域的断层(蓝色椭圆内)以及北部的细小河道(红色椭圆内).
|
图 9 实际三维地震资料不连续性检测结果时间切片1 (a)商业软件;(b)本文方法. Fig. 9 One slice of discontinuity detecting results of real field-data (a)Commercial software.(b)Proposed method in this study. |

|
图 10 实际三维地震资料不连续性检测结果时间切片2 (a)商业软件;(b)本文方法. Fig. 10 Another slice of discontinuities detecting results of real field-data (a)Commercial software;(b)Proposed method. |
本文在介绍了高维连续小波变换基本理论的基础上,提出了基于高维连续小波变换的地震资料不连续性检测方法.该方法以瞬时相位数据体为基础数据,并利用小尺度高维连续小波变换系数模值来度量不连续性.合成及实际地震资料的处理结果表明:相比较于常用商业软件,本文所提方法的结果对细微不连续性结构的检测能力更强.
| Antoine J P, Demanet L, Hochedez J F, et al. 2002. Application of the 2-D wavelet transform to astrophysical images. Physicalia Mag. , 24 (1) : 93-116. | |
| Antoine J P, Murenzi R, Vandergheynst P. 1999. Directional wavelets revisited:Cauchy wavelets and symmetry detection in patterns. Applied and Computational Harmonic Analysis , 6 (3) : 314-345. DOI:10.1006/acha.1998.0255 | |
| Antoine J P, Murenzi R, Vandergheynst P, et al. Two-Dimensional Wavelets and Their Relatives. Cambridge: Cambridge University Press, 2004 . | |
| Antoine J P, Vandergheynst P, Bouyoucef K, et al. 1995a. Alternative representations of an image via the 2D wavelet transform:Application to character recognition.//Proceedings of the SPIE 2488, Visual Information Processing IV. Orlando, FL, United States:SPIE. | |
| Antoine J P, Vandergheynst P, Bouyoucef K, et al. 1995b. Target detection and recognition using two-dimensional isotropic and anisotropic wavelets.//Proceedings of the SPIE 2485, Automatic Object Recognition V. Orlando, FL, United States:SPIE. | |
| Bahorich M, Farmer S. 1995. 3-D seismic discontinuity for faults and stratigraphic features:The coherence cube. The Leading Edge , 14 (10) : 1053-1058. DOI:10.1190/1.1437077 | |
| Bahorich M S, Lopez J, Haskell N L, et al. 1995. Stratigraphic and structural interpretation with 3-D coherence.//SEG Technical Program Expanded Abstracts. SEG, 97-100. | |
| Bakker P. 2003. Image structure analysis for seismic interpretation[Ph. D]. Dutch:Technische Universiteit Delft. | |
| Bouchereau E B. 1997. Analyse d'images par transformées en ondelettes[Ph. D]. Français:Université Joseph Fourier-Grenoble I. | |
| Chen W C, Shi Z S, Wang W B, et al. 2000. Suppressing the direct wave noise in GPR data using the 2-D continue directional wavelets. Chinese Journal of Radio Science (in Chinese) , 15 (3) : 352-357. | |
| Chen W C, Wang W B, Zhao R C. 2003. Ground penetrating radar (GPR) wavelet constructing and application to high resolution processing of GPR data. Coal Geology & Exploration (in Chinese) , 31 (5) : 46-48. | |
| Choi Y, Koo J Y, Lee N Y. 2001. Image reconstruction using the wavelet transform for positron emission tomography. IEEE Transactions on Medical Imaging , 20 (11) : 1188-1193. DOI:10.1109/42.963822 | |
| Chopra S, Marfurt K J. 2007. Seismic Attributes for Prospect Identification and Reservoir Characterization. Tulsa:Society of Exploration Geophysicists and European Association of Geoscientists and Engineers. | |
| Cohen I, Coifman R R. 2002. Local discontinuity measures for 3-D seismic data. Geophysics , 67 (6) : 1933-1945. DOI:10.1190/1.1527094 | |
| Darrozes J, Gaillot P, De Saint-Blanquat M, et al. 1997. Software for multi-scale image analysis:The normalized optimized anisotropic wavelet coefficient method. Computers & Geosciences , 23 (8) : 889-895. | |
| Gaillot P, Darrozes J, Bouchez J L. 1999. Wavelet transform:a future of rock fabric analysis?. Journal of Structural Geology , 21 (11) : 1615-1621. DOI:10.1016/S0191-8141(99)00073-5 | |
| Gaillot P, Darrozes J, de Saint Blanquat M, et al. 1997. The normalised optimised anisotropic wavelet coefficient (NOAWC) method:An image processing tool for multi-scale analysis of rock fabric. Geophysical Research Letters , 24 (14) : 1819-1822. DOI:10.1029/97GL01601 | |
| Gao Z S, Li Q X, Liu C, et al. 1998. Application of 2D wavelet transform in coherent noise estimation. Journal of Changchun University of Science and Technology (in Chinese) , 28 (4) : 433-437. | |
| Gersztenkorn A, Marfurt K J. 1996. Eigenstructure based coherence computations.//1996 SEG Annual Meeting. Denver, Colorado:SEG, 328-331. | |
| Gersztenkorn A, Marfurt K J. 1999. Eigenstructure-based coherence computationsas an aid to 3-D structural and stratigraphic mapping. Geophysics , 64 (5) : 1468-1479. DOI:10.1190/1.1444651 | |
| Li C F, Liner C. 2008. Wavelet-based detection of singularities in acoustic impedances from surface seismic reflection data. Geophysics , 73 (1) . | |
| Liu C, Wang D, Yang B J, et al. 2003. Apply of 2-D wavelet transforms in surface wave eliminations of seismic exploration. Progress in Geophysics (in Chinese) , 18 (4) : 711-714. | |
| Li Y Y, Li Q C, Ding L B, et al. 2004. The iterative ground-roll suppressing method based on 2D wavelet transform. The 20th Annual Meeting of Chinese Geophysical Society, Xi'an, Chinese Geophysical Society. | |
| Lu W K, Li Y D, Zhang S W, et al. 2005. Higher-order-statistics and supertrace-based coherence-estimation algorithm. Geophysics , 70 (3) : P13-P18. DOI:10.1190/1.1925746 | |
| Mallat S. A Wavelet Tour of Signal Processing:The Sparse Way. New York: Academic Press, 2008 . | |
| Mallat S, Hwang W L. 1992. Singularity detection and processing with wavelets. IEEE Transactions on Information Theory , 38 (2) : 617-643. DOI:10.1109/18.119727 | |
| Marfurt K J, Kirlin R L. 2000. 3-D broad-band estimates of reflector dip and amplitude. Geophysics , 65 (1) : 304-320. DOI:10.1190/1.1444721 | |
| Marfurt K J, Kirlin R L, Farmer S L, et al. 1998. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics , 63 (4) : 1150-1165. DOI:10.1190/1.1444415 | |
| Marfurt K J, Sudhaker V, Gersztenkorn A, et al. 1999. Coherency calculations in the presence of structural dip. Geophysics , 64 (1) : 104-111. DOI:10.1190/1.1444508 | |
| Murenzi R. 1990. Ondelettes multidimensionnelles et applications à l'analyse d'images[Ph. D]. Belgique:Louvain-la-Neuve, Université Catholique de Louvain. | |
| Murenzi R, Kaplan L, Antoine J P, et al. 1997. Computational complexity of the continuous wavelet transform in two dimensions.//Proc. Army Research Laboratory Symp. on Sensors and Electron Devices, College Park. | |
| Murenzi R, Zhai W P, Namuduri K R, et al. 1999. Scale-angle CWT features:Application in object recognition.//Proc. SPIE 3813, Wavelet Applications in Signal and Image Processing VⅡ. Denver, CO, USA:SPIE, 16-27. | |
| Ouillon G, Castaing C, Sornette D. 1996. Hierarchical geometry of faulting. Journal of Geophysical Research-Solid Earth , 101 (B3) : 5477-5487. DOI:10.1029/95JB02242 | |
| Ouillon G, Sornette D, Castaing C. 1995. Organisation of joints and faults from 1 cm to 100 km scales revealed by optimized anisotropic wavelet coefficient methodand multifractal analysis. Nonlinear Processes in Geophysics , 2 : 158-177. DOI:10.5194/npg-2-158-1995 | |
| Randen T, Monsen E, Signer C, et al. 2000. Three-dimensional texture attributes for seismic data analysis.//SEG Technical Program Expanded Abstracts. SEG, 668-671. | |
| Song J G, Wang H K, Mu X. 2005. Research and implementation of cohere algorithm based on DOA. Progress in Geophysics (in Chinese) , 25 (5) : 1662-1669. | |
| Sun X P, Du S T. 2000. An application of power algorithm in the seismic attribute analysis. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 22 (4) : 316-321. | |
| Wang W, Gao J H, Chen W C, et al. 2012. Random seismic noise suppression via structure-adaptive median filter. Chinese J. Geophys. (in Chinese) , 55 (5) : 1732-1741. | |
| Wang X K, Gao J H, Chen W C, et al. 2012. An efficient implementation of eigenstructure-based coherence algorithm using recursion strategies and the power method. Journal of Applied Geophysics , 82 : 11-18. DOI:10.1016/j.jappgeo.2012.03.009 | |
| Wang X W, Du M J, Liu J Y, et al. 2002a. Computation of seismic coherence cube based on wavelet transform and its application. Geophysical Prospecting for Petroleum (in Chinese) , 41 (3) : 334-338. | |
| Wang X W, Yang K Q, Zhou L H, et al. 2002b. Methods of calculating coherence cube on the basis of wavelet transform. Chinese J. Geophys. (in Chinese) , 45 (6) : 847-852. | |
| Wu A D, Mou Y G. 1997. The use of 2D wavelet transform in imporving the resolution of seismic data. Geophysical Prospecting for Petroleum (in Chinese) , 36 (1) : 36-42. | |
| Yang L Q, Song H B, Hao T Y, et al. 2005. Method of 2-D wavelet transform in attenuating random noise. Geophysical Prospecting for Petroleum (in Chinese) , 44 (1) : 4-6. | |
| Ye Z L, He J J. 2006. The improvement of the coherency cube technique and its application. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 28 (2) : 121-123. | |
| Yuan S J. 2007. A review of seismic coherence techniques. Progress in Exploration Geophysics (in Chinese) , 30 (1) : 7-15. | |
| Zhang C J, Wang X D, Zhang H R, et al. 2006. Algorithm for image edge detection based on two-dimension continuous wavelet transform. Opto-Electronic Engineering (in Chinese) , 33 (4) : 93-96. | |
| Zhang H, Pan D M, Zhang X Y. 2007. Application of 2-D wavelet transformation in eliminating surface wave interference. Geophysical Prospecting for Petroleum(in Chinese) , 46 (2) : 147-150. | |
| Zhang J H, Dong M, Zhou Z X, et al. 2007. The coherence method based on GST and its application. Natural Gas Industry (in Chinese) , 27 (S1) : 381-383. | |
| Zhang J H, Wang Y Y, Zhao Y, et al. 2004. Detection of coherent data volume by wavelet multi resolution and application. Oil Geophysical Prospecting (in Chinese) , 39 (1) : 33-36. | |
| Zhou Y H, Gao J H. 2007. Application of local structural entropy measure on the detection of discontinuity of seismic data. Coal Geology & Exploration (in Chinese) , 35 (1) : 71-73. | |
| Zhou Y H, Gao J H, Chen W C. 2007. Local structural entropy based on frequency-division instantaneous phase for enhancing seismic discontinuities.//SEG Technical Program Expanded Abstracts. SEG, 846-850. | |
| Zhang B, Lin T F, Guo S G, et al. 2016. Noise suppression of time-migrated gathers using prestack structure-oriented filtering. Interpretation , 4 (2) . | |
| 陈文超, 师振盛, 汪文秉, 等. 2000. 小波变换在去除探地雷达信号直达波的应用. 电波科学学报 , 15 (3) : 352–357. | |
| 陈文超, 汪文秉, 赵荣椿. 2003. 探地雷达小波的构造及在提高雷达信号分辨率中的应用. 煤田地质与勘探 , 31 (5) : 46–48. | |
| 高振山, 李勤学, 刘财, 等. 1998. 二维小波变换在消除相干噪声中的应用. 长春科技大学学报 , 28 (4) : 433–437. | |
| 李媛媛, 李庆春, 丁梁波等. 2004. 二维小波变换迭代法去除地震面波.//中国地球物理学会第二十届年会. 西安:中国地球物理学会. | |
| 刘财, 王典, 杨宝俊, 等. 2003. 二维小波变换在地震勘探面波消除中的应用. 地球物理学进展 , 18 (4) : 711–714. | |
| 宋建国, 王海昆, 穆星. 2005. 基于DOA的相干算法研究与应用. 地球物理学进展 , 25 (5) : 1662–1669. | |
| 孙夕平, 杜世通. 2000. 乘幂法在地震属性分析中的应用. 物探化探计算技术 , 22 (4) : 316–321. | |
| 王伟, 高静怀, 陈文超, 等. 2012. 基于结构自适应中值滤波器的随机噪声衰减方法. 地球物理学报 , 55 (5) : 1732–1741. | |
| 王西文, 苏明军, 刘军迎, 等. 2002a. 基于小波变换的地震相干体算法及其应用. 石油物探 , 41 (3) : 334–338. | |
| 王西文, 杨孔庆, 周立宏, 等. 2002b. 基于小波变换的地震相干体算法研究. 地球物理学报 , 45 (6) : 847–852. | |
| 吴爱弟, 牟永光. 1997. 二维小波变换在提高地震资料分辨率中的应用. 石油物探 , 36 (1) : 36–42. | |
| 杨立强, 宋海斌, 郝天珧, 等. 2005. 基于二维小波变换的随机噪声压制方法研究. 石油物探 , 44 (1) : 4–6. | |
| 叶增炉, 何建军. 2006. 地震相干体算法的改进及应用. 物探化探计算技术 , 28 (2) : 121–123. | |
| 苑书金. 2007. 地震相干体技术的研究综述. 勘探地球物理进展 , 30 (1) : 7–15. | |
| 张长江, 汪晓东, 张浩然, 等. 2006. 图像边缘检测的二维连续小波 变换法. 光电工程 , 33 (4) : 93–96. | |
| 张华, 潘冬明, 张兴岩. 2007. 二维小波变换在去除面波干扰中的应用. 石油物探 , 46 (2) : 147–150. | |
| 张军华, 王月英, 赵勇, 等. 2004. 小波多分辨率相干数据体的提取及应用. 石油地球物理勘探 , 39 (1) : 33–36. | |
| 张军华, 董猛, 周振晓, 等. 2007. 基于GST的相干体方法研究及应用. 天然气工业 , 27 (S1) : 381–383. | |
| 周艳辉, 高静怀. 2007. 局部结构熵算法在地震数据不连续性检测中的应用. 煤田地质与勘探 , 35 (1) : 71–73. | |
 2016, Vol. 59
2016, Vol. 59


