2. 中国石油大学(北京)海洋石油勘探国家工程实验室, 北京 102249;
3. 华北水利水电大学资源与环境学院, 郑州 450045;
4. Bureau of Economic Geology, John A. and Katherine G. Jackson School of Geosciences, The University of Texas at Austin, University Station, Box X, Austin, TX 78713-8924, USA
2. National Engineering Laboratory for Offshore Oil Exploration, China University of Petroleum, Beijing 102249, China;
3. School of Resources and Environment, North China University of Water Resources and Electric Power, Zhengzhou 450045, China;
4. Bureau of Economic Geology, John A. and Katherine G. Jackson School of Geosciences, The University of Texas at Austin, University Station, Box X, Austin, TX 78713-8924, USA
在地震成像早期,偏移主要是为了得到地下地质体的构造信息.现在获取地下介质真反射系数已经引起了地震勘探界的广泛关注,这就要求在偏移延拓和成像中对影响成像振幅的因素做校正处理(Zhang et al.,2002).然而,固有的吸收因子在常规偏移方法中经常被忽略.因为深层高频损失,地震波穿过覆盖层时,介质的空间变化引起地震振幅衰减,子波相位畸变,成像分辨率降低,使得异常区(比如气层)振幅衰减,频带变窄,造成深层识别和解释的困难,也影响了准确预测储层的能力.因此,需要补偿因为这类衰减引起的吸收效应.
在叠后Q偏移方面,Wang和Guo(2004)提出了偏移加反Q滤波算法,并给出了稳定的偏移算子,但这种算子只适用于一维模型.Wang(2008)将一维模型推广到二维,提出了适用于速度和Q值随空间变化的Q偏移算法.在叠前Q偏移方面,Traynin等(2008)利用Kirchhoff 叠前深度Q偏移对气藏下方的区域进行振幅和频带恢复;Xie等(2009)发展了叠前Kirchhoff Q偏移,利用射线追踪计算沿射线的吸收效应,并在偏移中对每一个频带进行补偿,但这些方法都是基于Kirchhoff.由于射线理论的缺陷(比如在焦散区、阴影区失效),该方法不能处理复杂的地质体.为解决这一问题,Xie等(2010)将Kirchhoff叠前深度Q偏移拓展到高斯束.Xiao等(2014)进一步提出共偏移距激光束算法,通过限制束的发散,使其传播类似激光,实现叠前激光束Q偏移.对波动方程Q偏移,Mittet(2007)提出了补偿振幅衰减和校正相位的策略,并且证明在Q有10%误差的情况下,Q补偿的偏移依然能得到较好的成像效果,相较于未补偿的剖面,分辨率明显提高.Zhang和Wapenaar(2002)通过限制延拓步数和最大偏移角,提出了条件稳定的延拓算子,但是该方法只能实现地下介质有限倾角和深度的成像.Valenciano等(2011)利用傅里叶有限差分法进行波场延拓,在衰减介质中引入一种新的波动方程偏移方法.通过改进的标量方程,Deng和McMechan(2007)提出时间域Q补偿的弹性逆时偏移,然而,该方法只补偿振幅衰减,而忽略了相位校正.基于吸收系数和频率满足近似线性关系的假设,Zhang等(2010)推导了常Q模型的波动方程,在叠前逆时偏移中补偿地震数据的衰减效应,Suh等(2012)将该方法拓展到各向异性介质.Fletcher等(2012)通过两次波传播来估算沿传播路径的衰减走时,利用该走时对常规的震源和检波点波场进行滤波,在偏移前补偿Q的影响.基于标准的线性固体模型假设,Bai等(2013)推导了时空域的黏滞波动方程,方程中包含伪微分算子项来模拟黏滞性,与Zhang等(2010)相比,此方法更容易实现.Yan和Liu(2013)采用优化的时空域高阶有限差分实现黏滞波动方程的叠前逆时偏移,该方程具有高的差分精度.Zhu等(2014)分析了逆时偏移中Q对震源波场和检波点波场的影响,在黏滞波动方程波场延拓中对影响振幅和相位的算子进行解耦,实现Q逆时偏移.李振春等(2014)提出了黏滞波动方程的最小二乘逆时偏移,与未补偿的结果相比,能得到更准确的反射界面及更均衡的振幅值,然而该方法所需计算量较大.
多分量地震勘探能得到PP波和PS波数据,与单纯的PP波相比,PS数据携带了目标区域不同的信息,能提供更多的物性参数,有效改进地震勘探的准确性.比如在PP波信号弱的区域,PS波可以增强照明.联合PP波和PS波的多分量成像技术能够更准确地反映地下特征.然而,常规的地震数据处理只考虑记录的P波分量,而忽略了转换PS波.因此,为了充分利用多分量信息,需要更有效的多分量偏移技术.
在多分量偏移方面,基于弹性波的Kirchhoff偏移方法最先被提出(Kuo and Dai,1984;Wapenaar et al.,1990;Hokstad,2000;Du and Hou,2008).这些方法的关键是计算PP波和PS波的走时,以此求和计算成像振幅.为了克服Kirchhoff成像的弱点,一些学者提出了弹性单程波动方程偏移(Fisk and McCartor,1991;Wu,1994;Xie and Wu,2005).由于是双程波的近似,单程波偏移方法受到成像角度、波的传播路径问题的限制,影响成像精度.因此,近年来利用双程波动方程的多分量逆时偏移方法成为热点.多分量的逆时偏移方法有两类:弹性波偏移和标量偏移(Hou and Marfurt,2002).弹性波偏移是直接输入多分量地震数据,利用弹性波动方程构建矢量波场(Chang and McMechan,1994;Yan and Sava,2008;Du et al.,2012,2014).此外,也有些研究者通过把波场分离成PP波和PS波,提出了多分量地震数据的标量偏移方法(Wang and Nemeth,1997;Jin et al.,1998;Sun and McMechan,2001;Hou and Marfurt,2002;Sun et al.,2004,2006;Han et al.,2013).
以上的方法中,射线类偏移具有高的效率和灵活性,但是不能处理复杂的地质体.波动方程逆时偏移更精确,但是计算量大.Popov等(2007,2008,2010)结合高斯束的高效灵活性和波动方程逆时偏移的高精度,提出了高斯束逆时偏移,即以Kirchhoff积分为基础,利用高斯束的叠加积分计算格林函数的逆时偏移算法.由于高斯束的叠加积分是严格按照数学理论推导的,因此避免了多值走时和不精确的振幅计算,另外可通过控制成像条件的时间窗来消除续至波,更适合基于目标的成像.与Hill(2001)提出的高斯束叠前深度偏移方法相比,高斯束逆时偏移不做局部倾斜叠加和最速下降近似,在理论上要优于前者.
目前对于高斯束偏移方法的研究主要集中于纵波,对多分量地震记录的研究较少(Li and Mao,2015).另外,高斯束逆时偏移作为一种新的偏移方法,对转换波成像及吸收衰减补偿的效果尚不清楚.因此,本文在前人研究基础上提出了基于吸收衰减补偿的多分量高斯束逆时偏移,首先把波场分解为PP波和PS波(李志远等,2013),然后分别基于声波方程的标量方法偏移,目的是提供一个新的有效的多分量数据成像技术,同时补偿地震记录的吸收衰减.文中首先给出声波高斯束逆时偏移中的正向和反向延拓波场表达式,将声波反向延拓波场格林函数拓展到弹性波,得到P波和S波的反向延拓波场,再将其与正向延拓波场互相关,推导波场分离后的PP波和PS波共炮域高斯束叠前逆时偏移表达式.在此基础上引入与Q有关的补偿算子,实现基于吸收衰减补偿的多分量高斯束叠前逆时偏移.最后用数值算例证明了本文方法的有效性和优越性.
2 多分量高斯束逆时偏移Popov等(2010)首先提出了高斯束逆时偏移的计算方法,并给出详细的思路和推导过程.这里,我们只讨论关键步骤.考虑标量声波方程,波场 U(x,t) 满足:
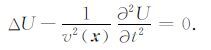
|
(1) |
其中, x=(x,z) 是空间内一点,Δ是拉普拉斯算子, v(x) 是波传播速度.
2.1 正向和反向延拓波场的构建由地面点源 xs 产生的正向延拓波场 U(D)(x,t;xs), 是如下方程的解:
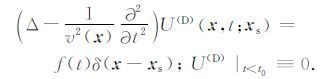
|
(2) |
式中 f(t) 是初始波(震源子波 f(t)|t0=0). 利用高斯束计算格林函数,则正向延拓波场可以表示为:
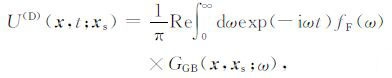
|
(3) |
其中, fF(ω) 是初始子波的傅里叶变换, GGB(x,xs;ω) 是高斯束表示的格林函数的渐近式.
对于反传波场,地下成像区域内一点 x0 的格林函数 G(x,t;x0,t0) 满足:
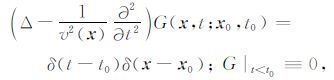
|
(4) |
其中 t0 是瞬时时刻,满足 0≤t0≤T. 利用Kirchhoff积分,得到 x0 点反传波场 U(x0,t0) 的表达式:

|
(5) |
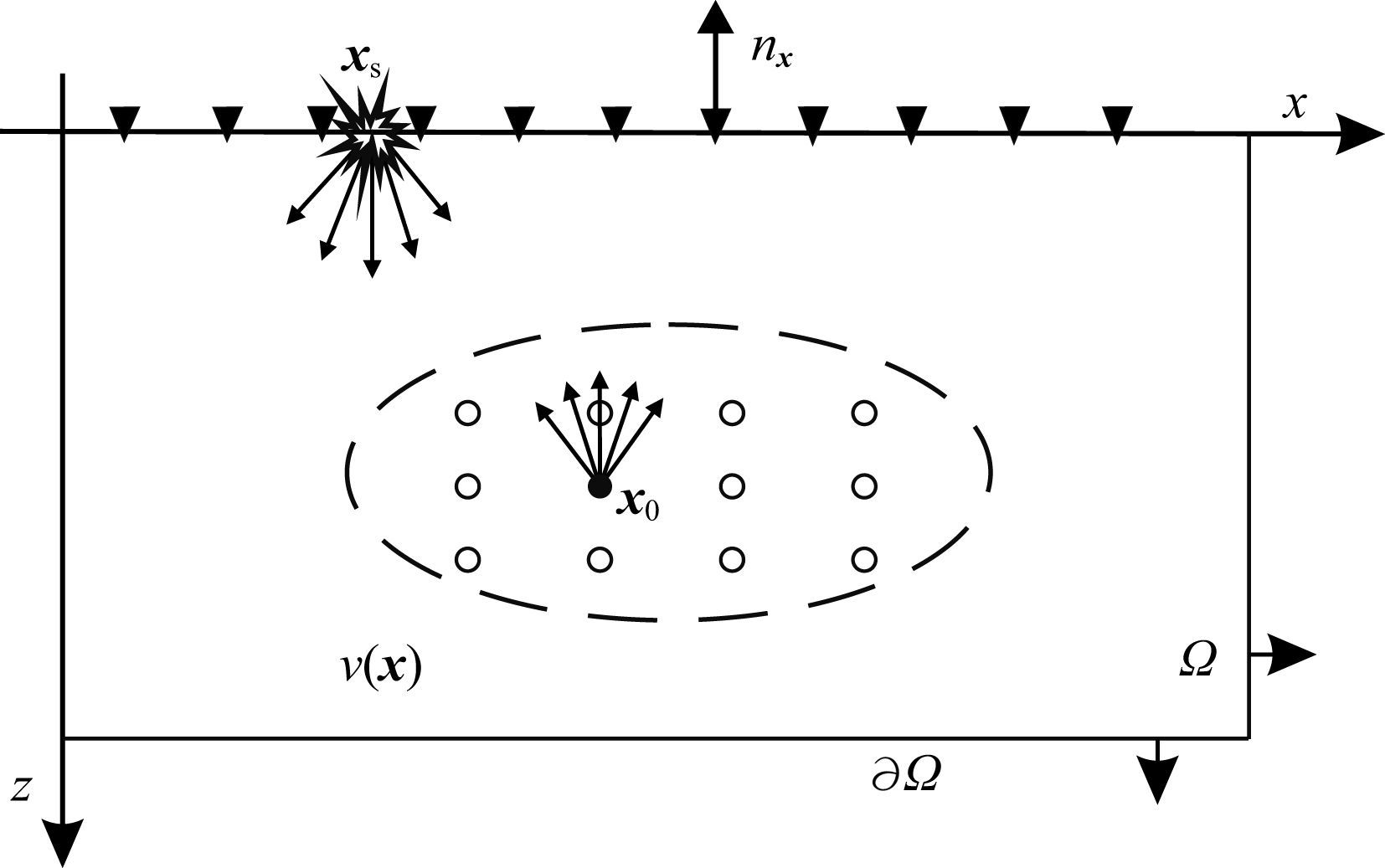
式中:∂Ω 是闭合空间 Ω 的边界, U(0)(x,t) 是地震记录,∂/∂nx 是沿 Ω 外法线方向的导数,如图 1所示.
|
图 1 偏移域 Ω 的参数化 xs和x0 分别表示震源和地下成像区域(虚线内)任一点, v(x) 是速度, nx是Ω 在记录表面的外法向导数, Ω 的边界向外延伸至无穷. Fig. 1 Parametrization of the migration domain Ω xs and x0 are positions of the source and a point in the migration domain(refer to the dashed range),respectively, v(x) is the velocity,and nx is the external normal to domain Ω on the recording surface.The boundary of Ω is extended outward to infinite. |
此外,假设地球的水平面为边界 ∂Ω 的一部分,则∂Ω 的两侧对波场的贡献可以忽略.格林函数满足Kirchhoff近似中的边界条件 G|z=0=0, 则偏移域内一点 x0 的反向延拓波场为:
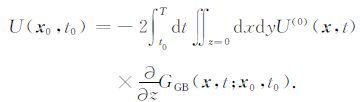
|
(6) |
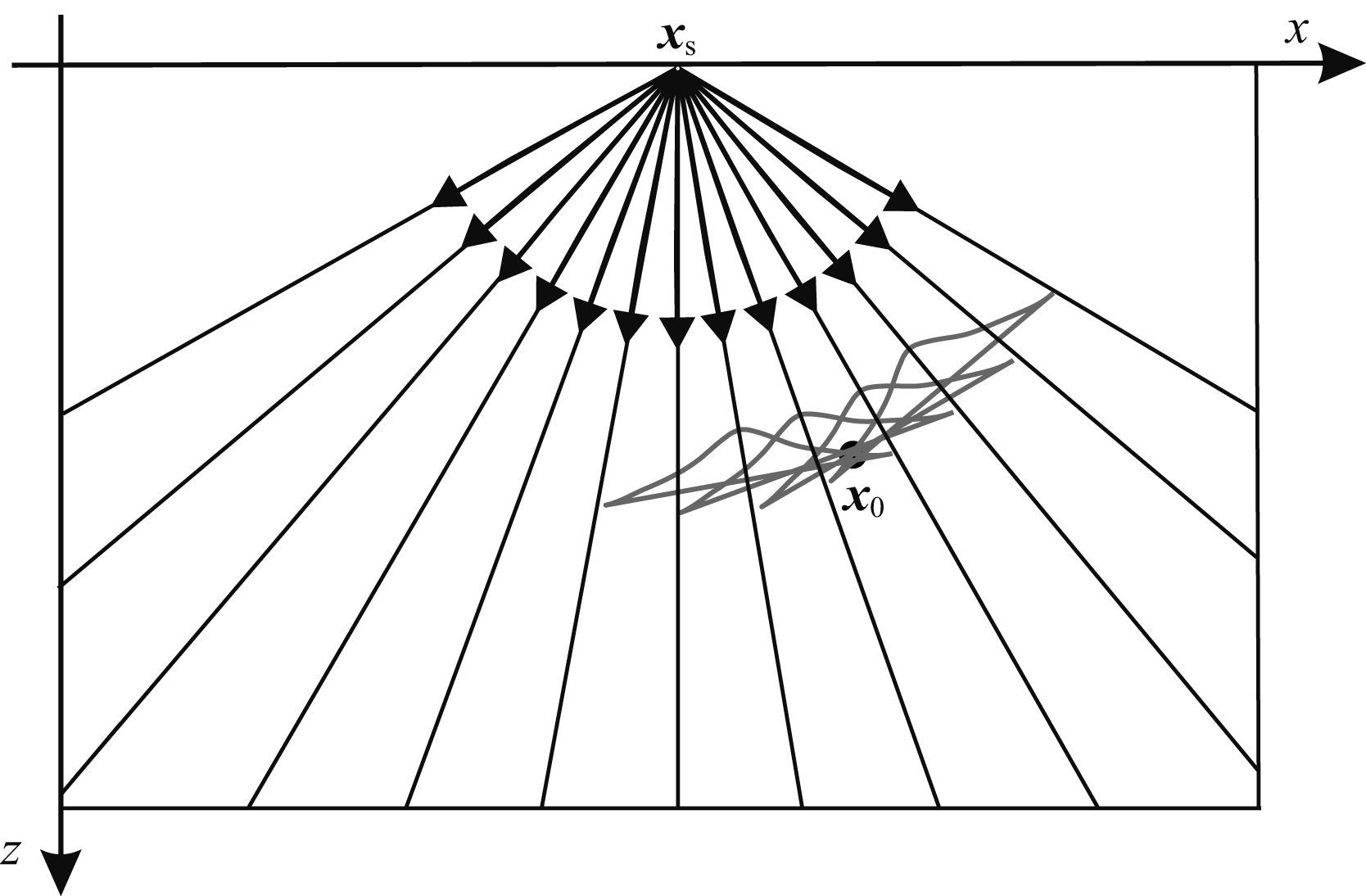
高斯束逆时偏移中最重要的步骤是构建高斯束表示的格林函数渐近式.格林函数 GGB(x,xs,ω) 是通过一系列由源点出射的,具有不同出射角的高斯束叠加积分表示的,如图 2.
|
图 2 高斯束表示的格林函数 Fig. 2 Sketch of Green function in terms of Gaussian beams |
对于正向延拓波场,从源点 xs 处以不同的角度出射中心射线束,每条中心束附近波场值用高斯束方法求取,地下介质中一点 x 的波场值由与其临近的多条高斯束叠加而得,格林函数 GGB(x,xs,ω) 的表达式为(Hill,2001,Gray and Bleistein,2009):
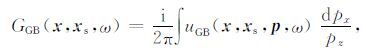
|
(7) |
其中, uGB(x,xs,p,ω) 为高斯束方法求取的波场位移:
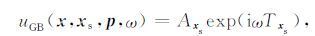
|
(8) |
式中, px和pz 分别表示射线参数的水平分量和垂直分量, ω 是频率, A 为振幅, T 是复值走时.
反向延拓波场的格林函数为:
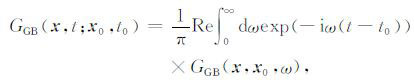
|
(9) |
其中,
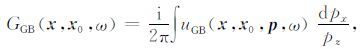
|
(10) |
式中, x0和x 分别为偏移域内任一点和地下介质中计算点的位置.
对于P波,有

|
(11) |
对于S波,有
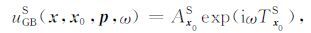
|
(12) |
所以,对成像区域内一点 x0, PP波和PS波的走时分别为:
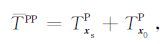
|
(13) |
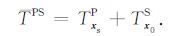
|
(14) |
式(8)和式(11)、(12)中高斯束的复值振幅 A 和走时 T 分别表示为(Hill,1990,2001):

|
(15) |

|
(16) |
式中, s 是射线路径, τ(s) 是沿着射线的走时. p(s)和q(s) 是动力学射线追踪方程组的复值解(erveny,2007),它们决定了高斯束的能量分布. n 表示沿射线法线方向的距离.射线追踪过程(Popov et al.,2010)见附录A.
2.3 成像条件对原始地震记录进行波场分离后,采用适用于PP波和PS波的高斯束方法对其进行偏移.本文应用互相关成像条件,则PP波和PS波高斯束逆时偏移公式为:
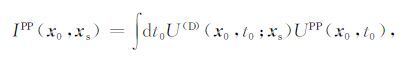
|
(17) |
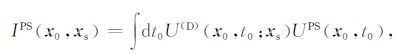
|
(18) |
其中, U(D)(x0,t0;xs)和U(x0,t0) 的表达式见方程(3)和(6).
对PP波成像,震源和地下一点的复值走时 TPxs和TTPx0用P波速度计算;而对PS波,复值走时 TPxs和TPx0 则分别用P波速度和S波速度计算.与PP波相比,PS波地震记录有极性反转问题,对PS波直接偏移会严重影响偏移结果.因此,基于PS波的极性特征,在高斯束叠前逆时偏移时须给以校正(毕丽飞等,2015).
3 衰减介质多分量高斯束逆时偏移为了得到衰减补偿的多分量高斯束逆时偏移表达式,本小节首先给出衰减补偿原理,然后分析高斯束在衰减介质中传播的精度.
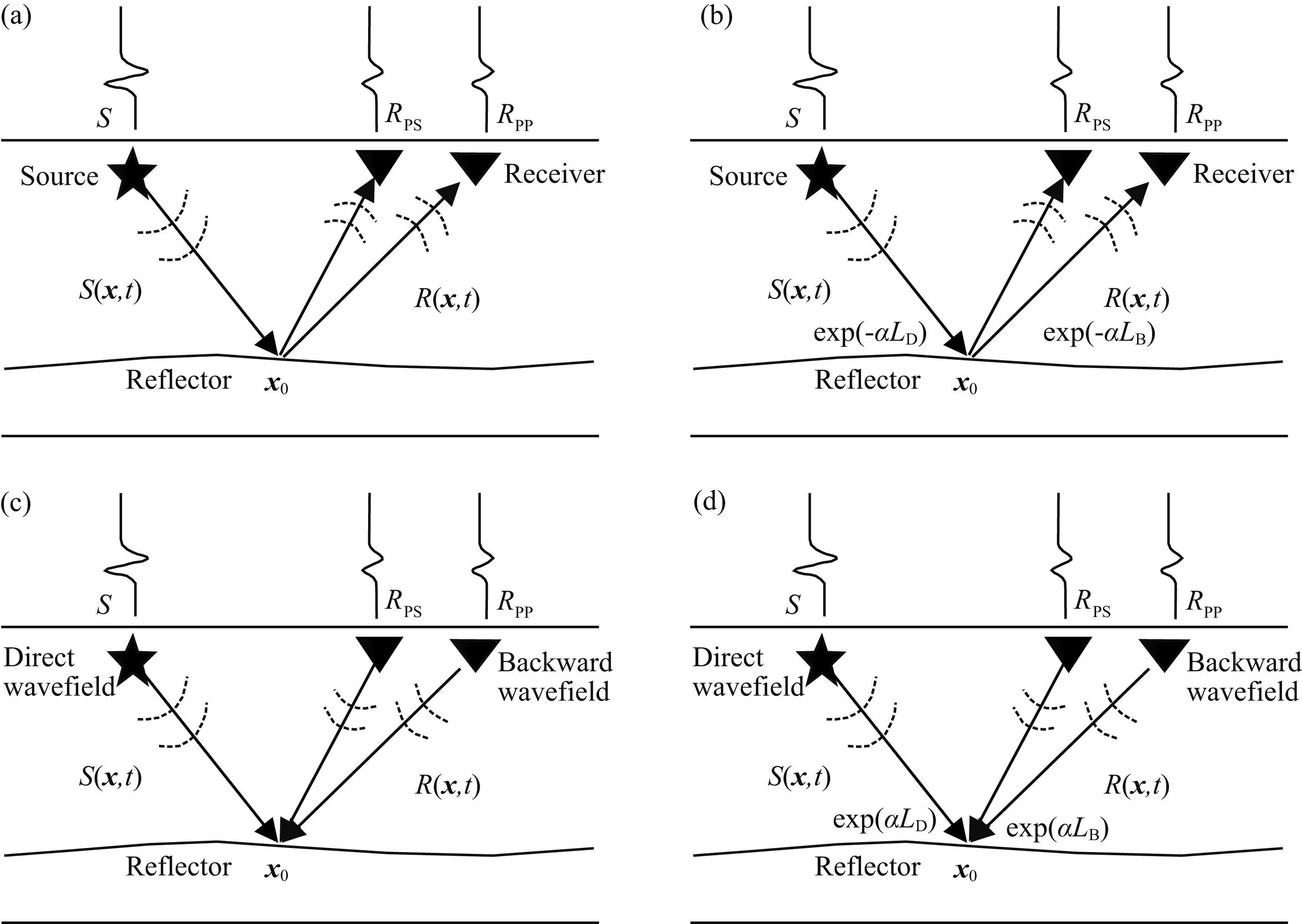
3.1 衰减和补偿原理图 3为衰减与无衰减介质中多分量正演和偏移示意图,其中S是震源位置, RPP和RPS 是PP波和PS波地震记录.图 3a和3c表示无衰减介质正演与偏移,图 3b和3d表示衰减介质正演与偏移. S(x,t)和R(x,t) 分别为参考震源波场和检波点波场(即无衰减介质中的波场).波在衰减介质中传播如图 3b所示,从震源到反射点,再到检波点,沿整个路径的累积衰减量为 exp(-αLB)exp(-αLD),其中LB和LD 分别为反传波场和震源波场的传播距离, α
|
图 3 无衰减介质与衰减介质正演和偏移示意图.(a)、(c)为无衰减介质正演和偏移;(b)、(d)为衰减介质正演和偏移 Fig. 3 Schematic of forward modeling(a)and migration extrapolation(c)in a non-attenuation medium, and forward modeling(b)and migration extrapolation(d)in an attenuating medium |
是衰减系数.地面接收到的衰减记录为 R⌒(x,t)=R(x,t)exp(-αLB)exp(-αLD).
为了实现对波场的完全补偿,偏移过程中的校正量应该为 exp(αLB)exp(αLD). 然而在互相关成像中,传播距离为 LB 的检波点补偿算子为 exp(αLB) (检波点到反射点),补偿后的检波点波场为 RC(x,t)=R⌒(x,t)exp(αLB). 因此,还需要同时补偿震源波场.沿射线路径,传播距离为 LD 的震源补偿算子为 exp(αLD) (震源到反射点),补偿后的震源波场为 SC(x,t)=S(x,t)exp(αLD), 如图 3d所示.这样补偿后的互相关成像剖面才能达到与参考偏移剖面相当的效果.
3.2 高斯束在衰减介质中的传播精度波在黏弹性介质中传播可认为是复速度的波在弹性介质中传播,复速度的实部分别是弹性介质中的速度 vP和vS, 品质因子Q代表衰减. QP和QS 分别是纵横波的品质因子,如果衰减小 (1/Q1), 则复速度为(Keers et al.,2001):
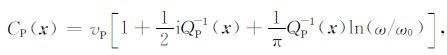
|
(19) |

|
(20) |
式中 ω0 是参考频率,Q不依赖于频率,速度的虚部引起沿着射线路径的指数振幅衰减,速度的实部包含频散项,确保波动方程解的因果性.
考虑衰减(补偿)的PP波和PS波的复值走时分别为:
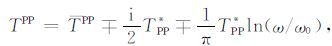
|
(21) |
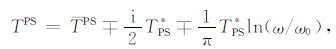
|
(22) |
其中,
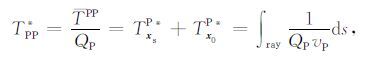
|
(23) |

|
(24) |
式中, s 表示PP波传播路径, s1和s2 表示PS波传播路径.公式(21)、(22)中,与 T* 有关项的符号:负号表示衰减,正号表示补偿.用补偿的 TPP和TPS 表达式替换(13),(14)中 PP和PS, 再将得到的格林函数代入叠前逆时偏移公式,即可得到衰减补偿的PP波和PS波高斯束逆时偏移公式.
由于本文是基于波场分离后的标量方程计算,因此,下面以声波和黏声介质为例,分析高斯束在衰减和无衰减情况下的波场传播精度.
我们设计了一个均匀介质模型,速度为2000 m·s-1,模型大小为201×201,dx=dz=10 m,震源使用主频为20 Hz的雷克子波,位于(1000 m,1000 m)处.分别用高斯束积分和频率域波动方程来模拟无衰减介质和衰减介质中地震波的传播,并与解析解对比,分析两者的精度.
基于Futterman(1962)的理论,利用Valenciano等(2011)推导的频率域波动方程:
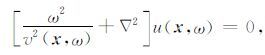
|
(25) |
其中,复速度
该式求解采用频率域有限差分法(Jo et al.,1996).
解析解的表达式为(Abramowitz and Stegun 1965):
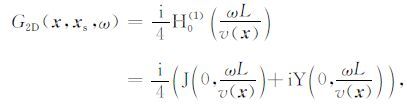
|
(27) |
其中, L 为地下一点 x 到震源 xs 的距离, H0(1)是零阶第一类Hankel函数,J和Y分别表示第一类和第二类Bessel函数.
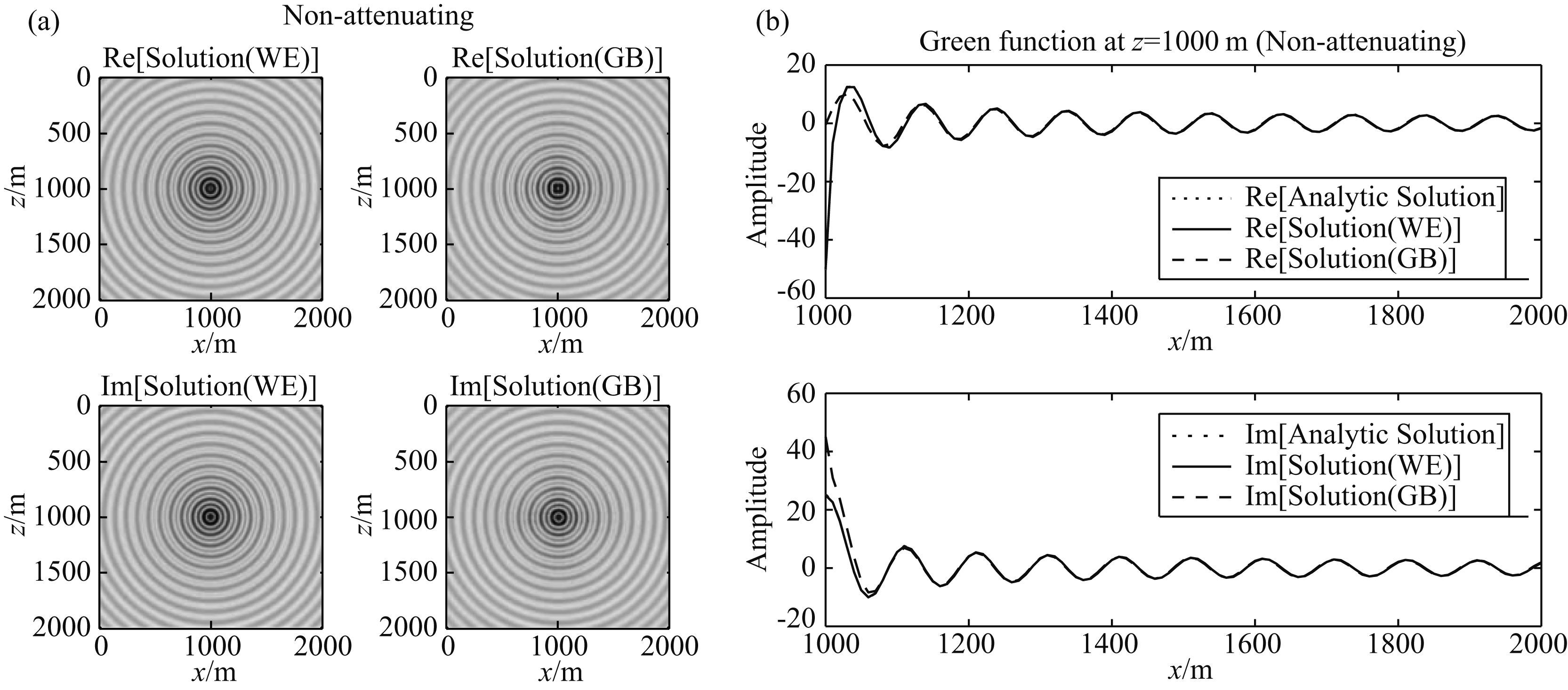
在无衰减均匀介质中,分别用高斯束积分和频率域声波方程合成格林函数,并将其与解析的格林函数进行比较(如图 4).图 4a左是用频率域有限差分法求解得到的格林函数(WE),频率为20 Hz(下同);图 4a右是用高斯束求解得到的格林函数(GB).图中可以看出:无论实部还是虚部,两个波场形态基本一致.图 4b是从图 4a的单频波场中,抽出的深度z=1000 m处的值与解析格林函数的对比.曲线图表明:当传播距离大于100 m时,图 4a中单频波场的实部、虚部均与解析解的实部、虚部吻合较好(震源附近的振幅差异是因为射线理论是一种高频近似方法,属于远场近似,震源是射线理论的奇异点).这进一步证明了高斯束和频率域波动方程求解的准确性,也说明高斯束积分所计算的格林函数很好地近似了解析的格林函数.
|
图 4 无衰减介质中,高斯束积分和波动方程计算的格林函数(a)及其与解析格林函数的精度对比(b) Fig. 4 Green function solved by wave equation and Gaussian beam in non-attenuation medium(a) and comparison to analytical Green function(b) |
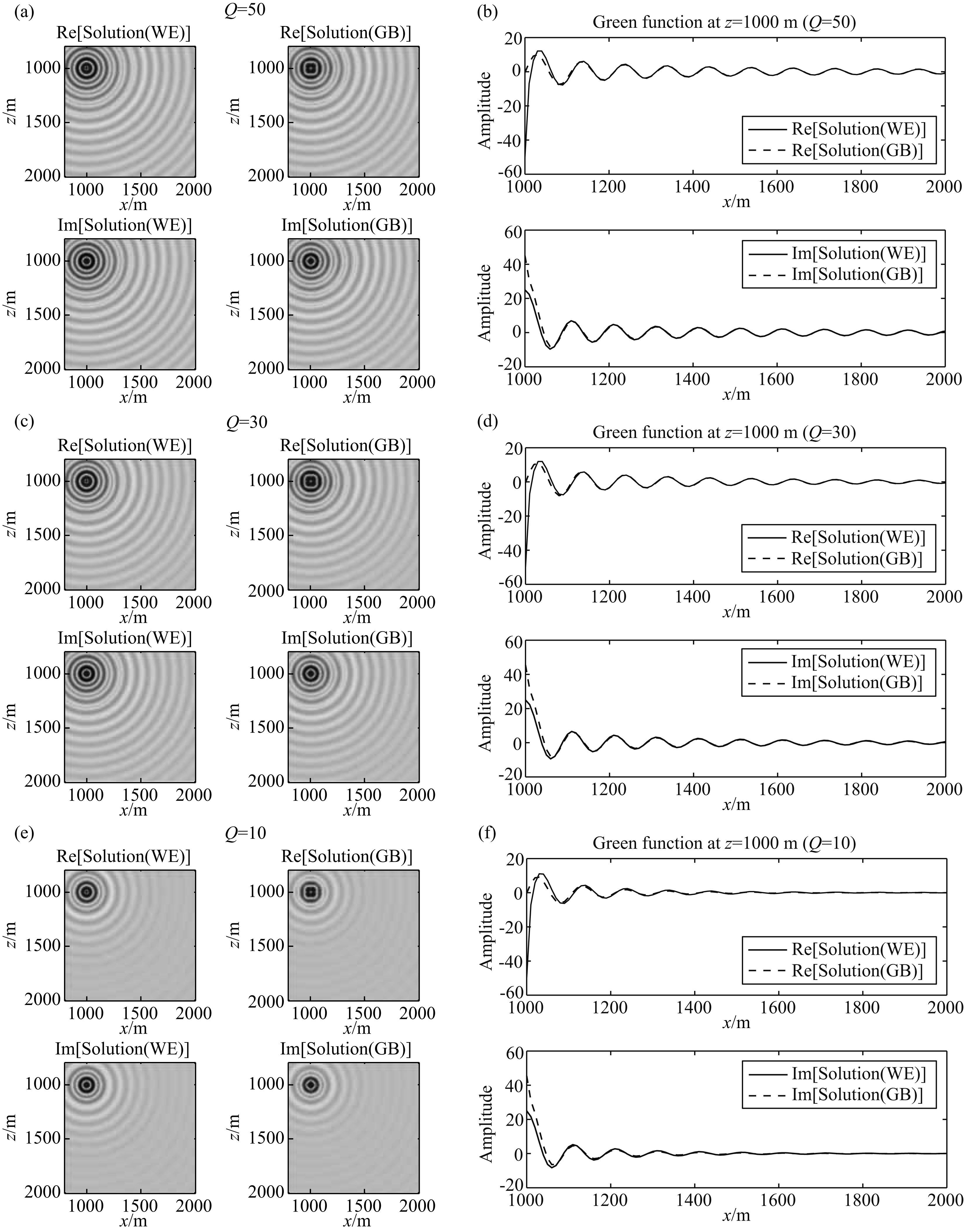
图 5是在衰减的均匀介质中,Q=50,30,10时,分别用高斯束积分和频率域黏声波方程合成的格林函数,以及它们的精度比较(为了更好地对比格林函数的细节,选取局部放大图).图 5a,5c,5e分别为两种方法求得的单频波场;图 5b,5d,5f分别是抽取的z=1000 m处的值所做的精度对比.从两者实部和虚部的对比可以看出,这两种方法模拟得到的实部和虚部的振幅和相位均吻合较好,由此也验证了高斯束表示的格林函数能较好地描述波在黏声介质中的传播.
|
图 5 衰减介质中,高斯束积分和波动方程计算的格林函数及其精度对比(局部放大图) (a,b)Q=50;(c,d)Q=30;(e,f)Q=10. Fig. 5 Green function solved by wave equation and Gaussian beam and accuracy comparison in attenuation medium(partial enlargement) |
为验证基于吸收衰减补偿的多分量高斯束叠前逆时偏移方法的有效性,本文设计了两个试验.
4.1 两层模型模型大小为3000 m×3000 m,如图 6所示.震源采用雷克子波,其频率为20 Hz.震源坐标为(1500 m,0 m),共设计了301个检波点,分别布置在地表 0 m到3000 m处,道间距为10 m,接收记录长度为2.0 s,时间采样间隔是0.001 s.

|
图 6 两层模型 Fig. 6 Two-layer model |
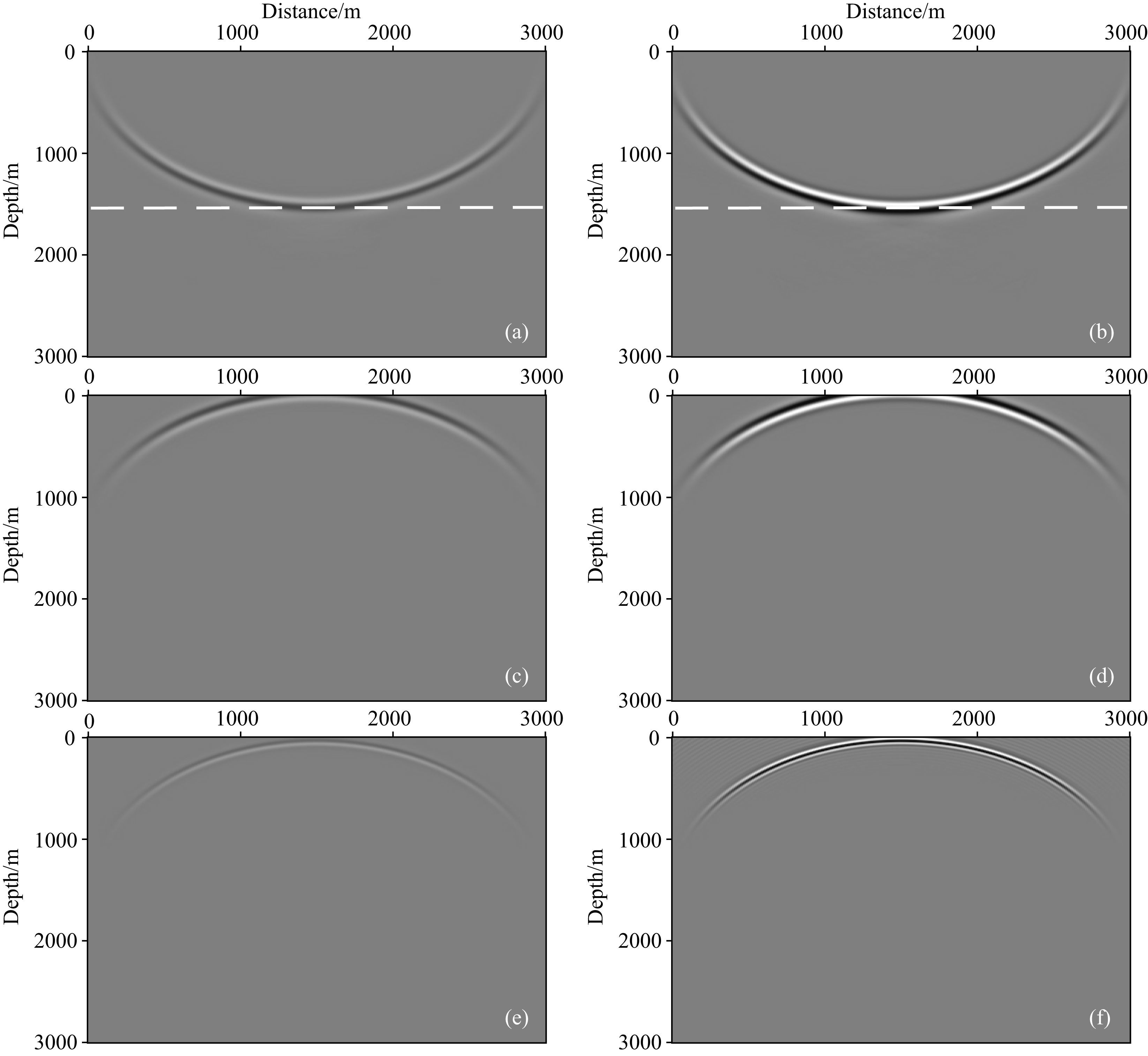
为了更直观地反映补偿过程,以地下一点(1500 m,1500 m)处的成像为例,分别输出PP波与PS波震源和反传波场的原始波场快照以及补偿后的波场快照,如图 7所示.其中图 7a和7b为参考和补偿后的震源波场,图 7c和7d为参考和补偿后地下一点 x0 的PP波波场.由图可以看出补偿后的震源波场振幅加强,物理意义如图 3d所示,用于补偿与 exp(-αLD) 有关的吸收.同样, x0 点的波场用以补偿与 exp(-αLB) 有关的吸收,补偿后的 x0 点波场与地震记录相关,实现逆时偏移中波场的反传过程.由于震源和反传波场都得到了补偿,因而相关之后 x0 点的成像值,振幅恢复,相位得到校正.对地下所有点成像之后的PP波单炮偏移结果如图 8所示.相似地,图 7e和7f为参考和补偿后地下一点 x0 的PS波波场,对地下所有点成像之后的PS波单炮偏移剖面见图 9.
|
图 7 波到达界面之后某一时刻的原始波场快照和补偿后的波场快照 震源波场:(a)参考,(b)补偿后;地下一点(1500 m,1500 m)的PP波波场:(c)参考,(d)补偿后;PS波波场:(e)参考,(f)补偿后. Fig. 7 Snapshots of reference wavefield and compensated wavefield at the time when waves arrives at the interface Source wavefield: (a)Reference;(b)Compensated. PP-wavefield:(c)Reference;(d)Compensated; PS-wavefield:(e)Reference;(f)Compensated at the point x0 (1500 m,1500 m)in the subsurface |

|
图 8 PP波单炮偏移 (a)参考;(b)未补偿;(c)补偿后. Fig. 8 PP-wave migration results of single shot (a)Reference;(b)Not compensated;(c)Compensated. |
|
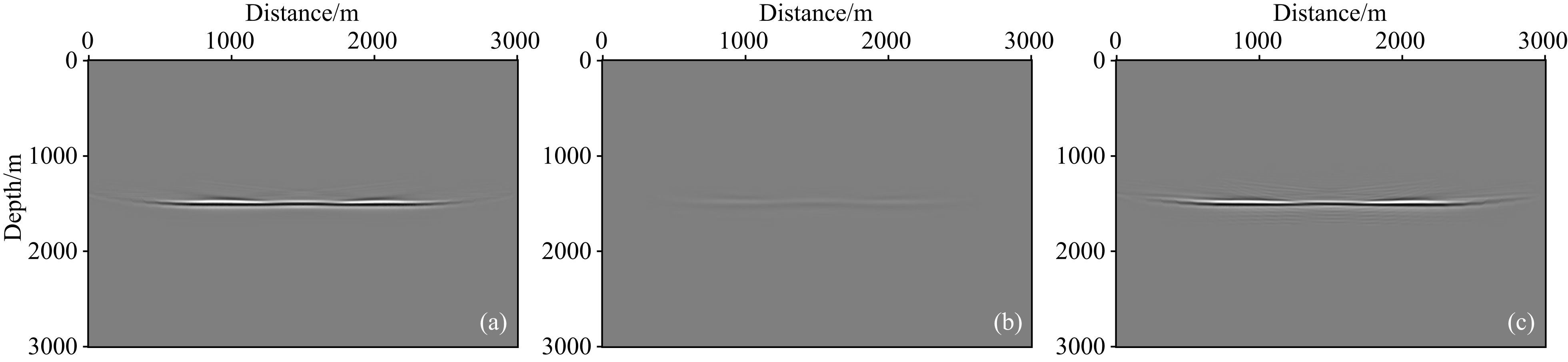
图 9 PS波单炮偏移 (a)参考;(b)未补偿;(c)补偿后. Fig. 9 PS-wave migrated results of single shot (a)Reference;(b)Not compensated;(c)Compensated. |
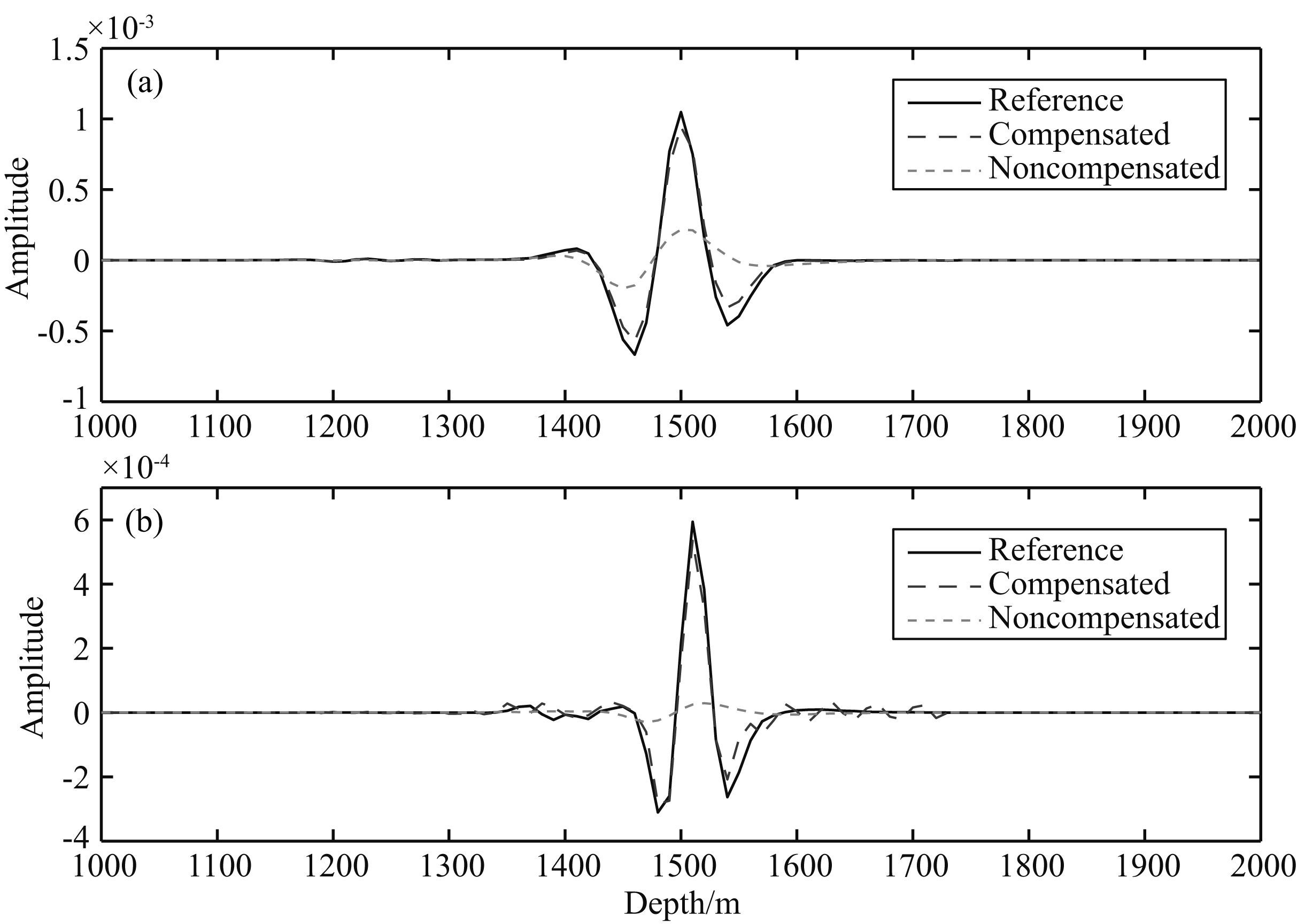
图 8和图 9分别是三种情况下(参考,未补偿,补偿后)的PP波和PS波单炮偏移剖面.从图中可以看出,基于吸收衰减补偿的高斯束叠前逆时偏移考虑了地层的吸收效应,在偏移过程中对地震记录的衰减能量进行了补偿,补偿后的偏移剖面更接近理想的偏移剖面.图 10是从图 8和图 9中抽取的单道波形.通过对比发现,本文方法有效地补偿了地下介质对地震波的吸收.图 11为图 8和图 9对应的振幅谱和功率谱,从频谱对比可以看到,补偿后的剖面能量得到恢复,尤其是中高频能量成分得到了加强.
|
图 10 从图 8和图 9中抽出的单道波形 (a)PP波;(b)PS波. Fig. 10 Comparison of single-trace waveforms extracted from Figs. 8 and 9 (a)PP-waves;(b)PS-waves. |

|
图 11 图 8和图 9对应的振幅谱和功率谱 (a)和(c)为PP波;(b)和(d)为PS波. Fig. 11 Amplitude spectra and power spectra of Figs. 8 and 9 (a)and(c)PP waves;(b)and(d)PS waves. |
在第二个例子中,我们考虑实际的衰减模型.图 12是速度模型和相应的Q模型(BP模型的一部分).模型的顶部偏中是由于气云的存在导致的低速和高衰减区.横波速度和Q值由纵波速度与Q值按比例得到, vP/vS=1.73,QP/QS=1.2, 模型网格数为398×161,网格大小是10 m×10 m.

|
图 12 气云模型 (a)速度模型;(b)Q模型. Fig. 12 Gas chimney model (a)Velocity model;(b)Q model. |
我们采用弹性和黏弹性方程模拟地震记录(Zhu and Carcione,2014),共40炮,震源采用主频为15 Hz的雷克子波,炮间距为100 m,每一炮都是全地表等距(10 m)接收.接收记录长度为3 s,时间采样间隔为0.001 s.
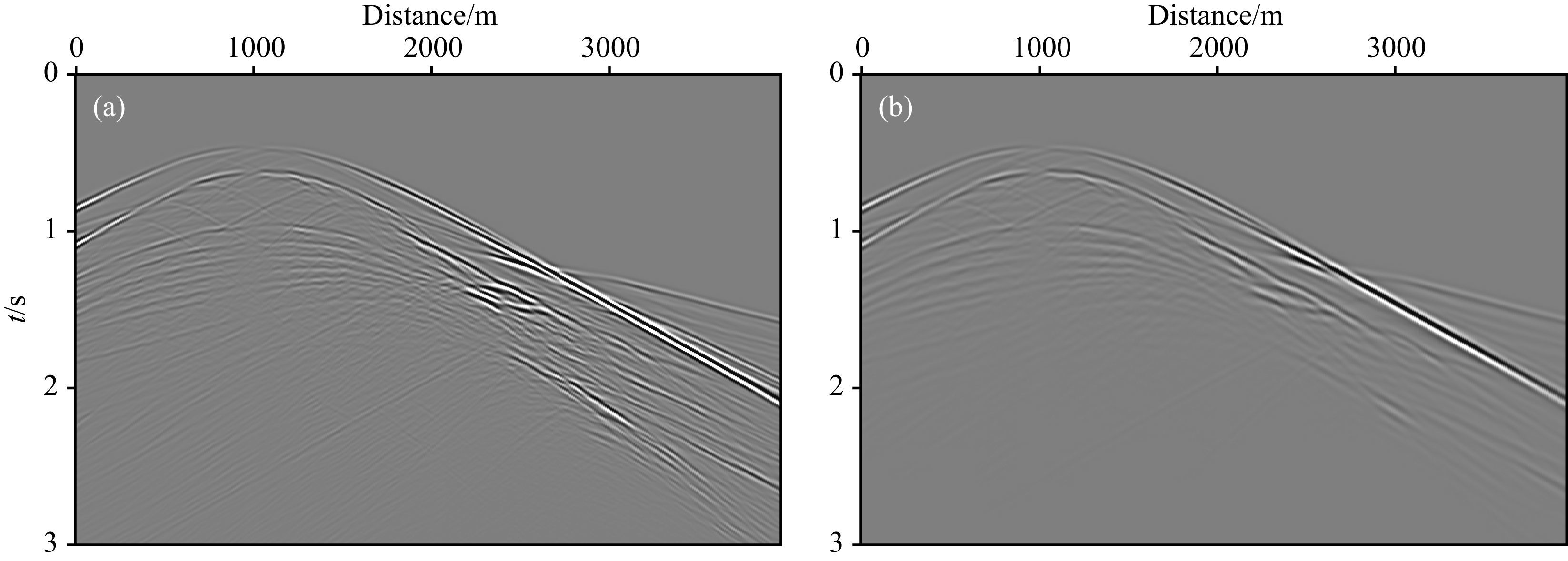
取其中一炮的记录,如图 13和图 14所示,炮点位于1000 m处.从图中可以看出,不管是x分量还是z分量,黏弹性记录中,反射波的同相轴能量均相对较弱,且同相轴的波形要宽,介质的黏滞性对地震波能量的吸收和衰减作用明显.因为经过高衰减区的反射消失了,所以黏弹性记录更干净.
|
图 13 x分量:(a)弹性;(b)黏弹性 Fig. 13 x-component:(a)Elastic;(b)Viscoelastic |

|
图 14 z分量:(a)弹性;(b)黏弹性 Fig. 14 z-component:(a)Elastic;(b)Viscoelastic |
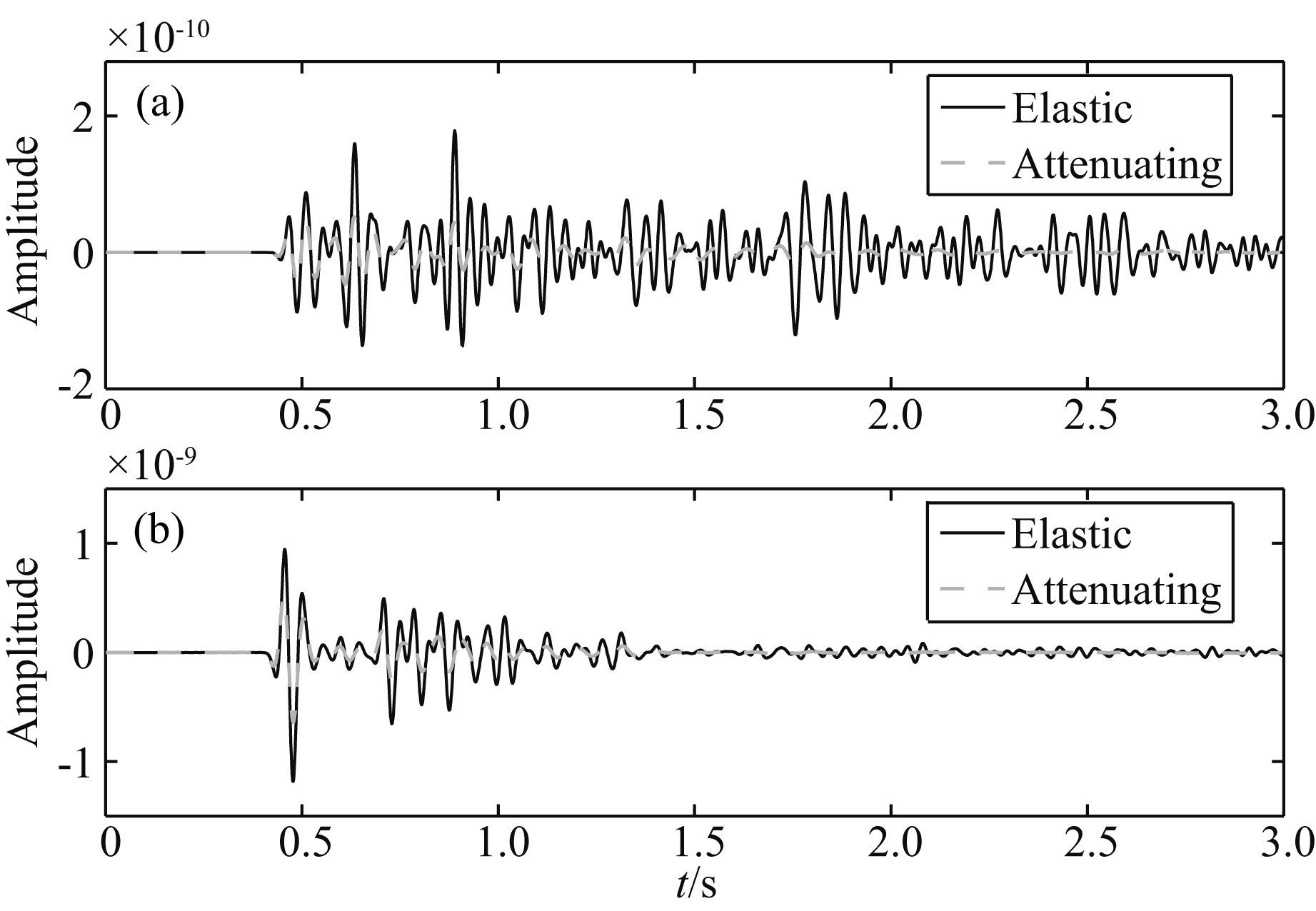
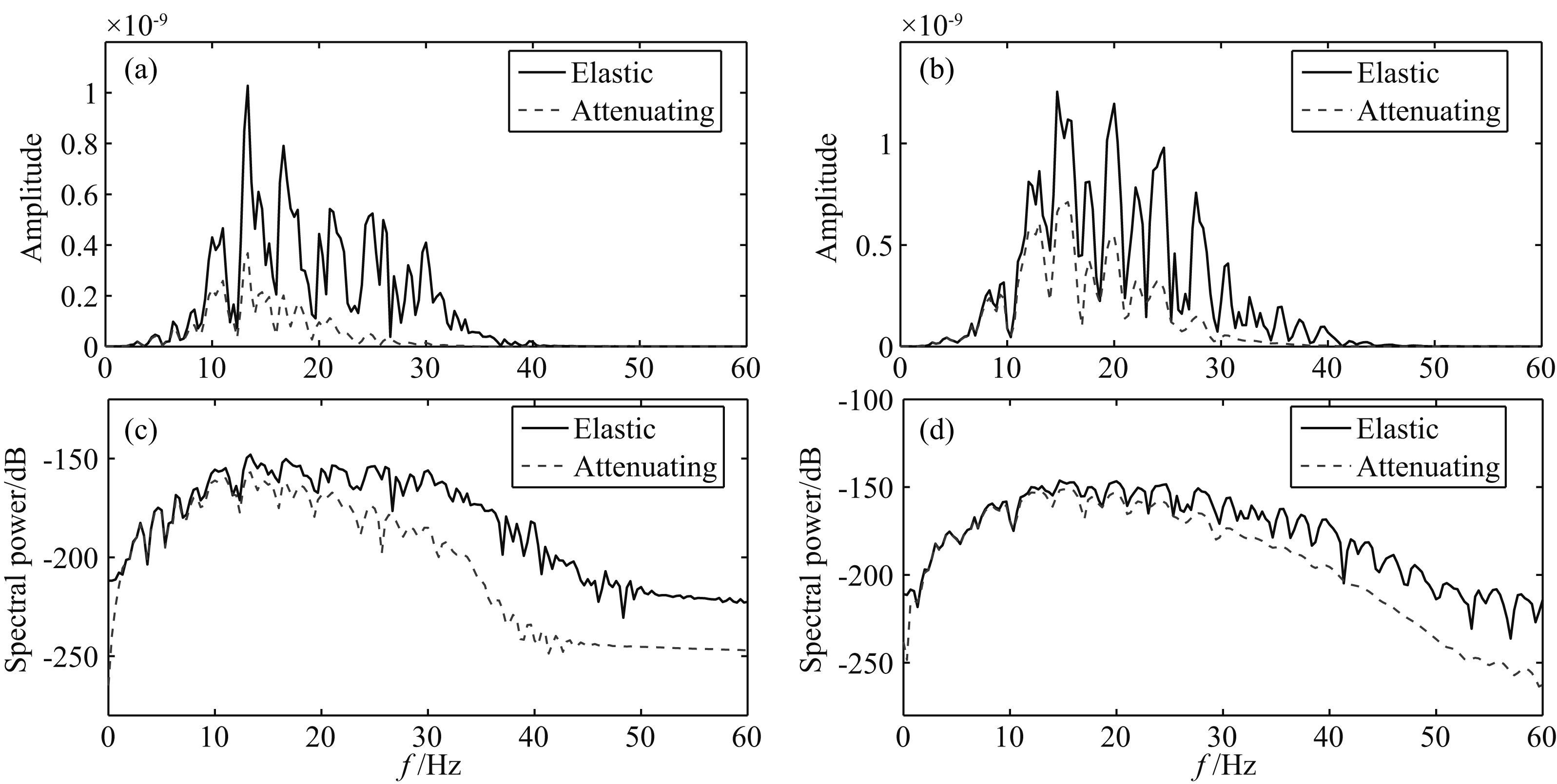
图 15是从图 13和图 14中抽出的第101道(横向距离1000 m)的波形对比,从图中也可以看出,介质的黏滞性对地震波的衰减作用明显.图 16是图 13和图 14对应的振幅谱和功率谱.
|
图 15 从图 13和图 14中抽取的第101道波形(横向距离1000 m) (a)x分量;(b)z分量. Fig. 15 Comparison of 101st-trace wave forms extracted from Figs. 13 and 14(at distance of 1000 m) (a)x-component;(b)z-component. |
|
图 16 图 13、14对应的振幅谱和功率谱 (a)和(c)分别为x分量;(b)和(d)为z分量. Fig. 16 Amplitude spectra and power spectra of Figs. 13 and 14 (a)and(c)x component;(b)and(d)z component. |
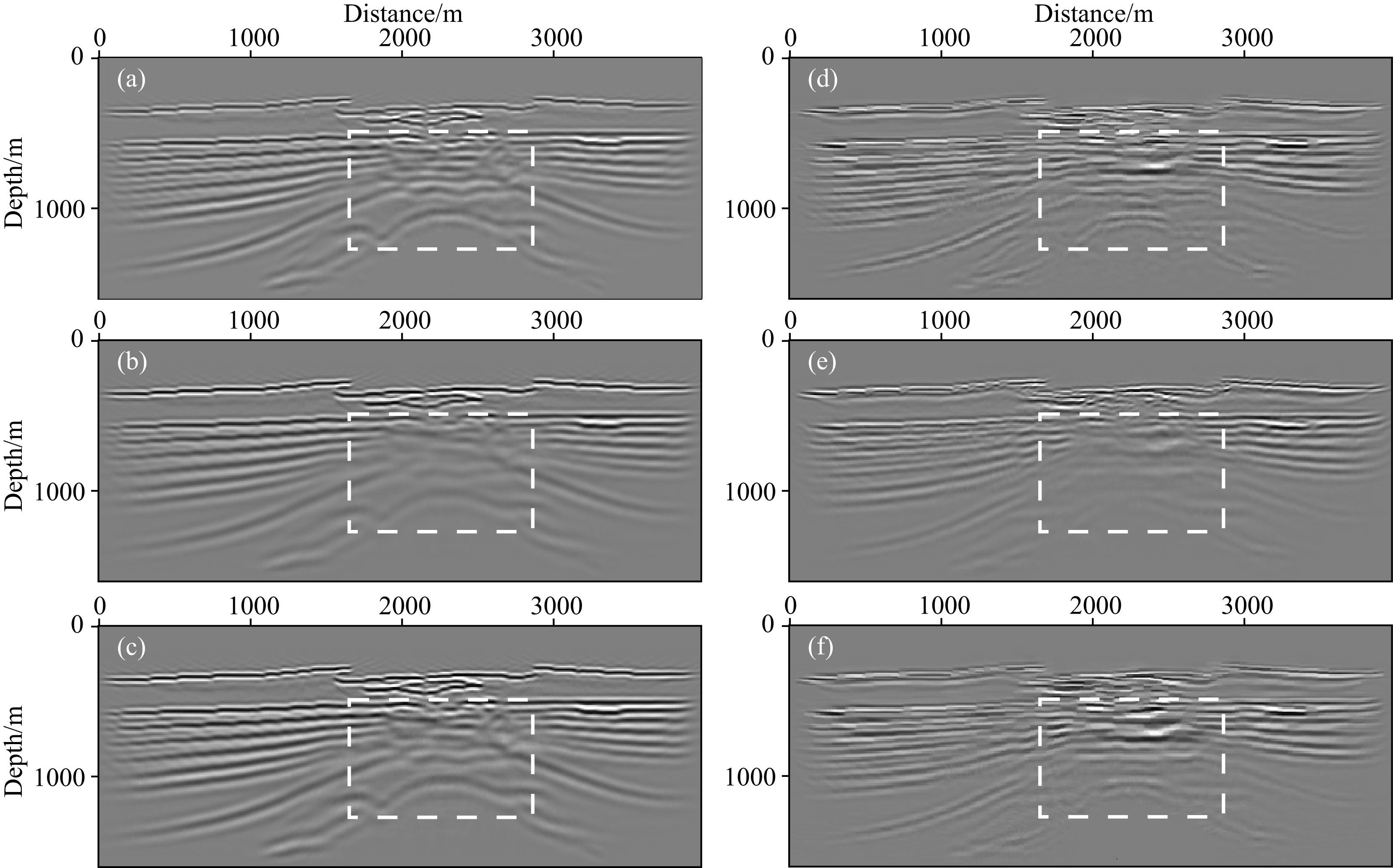
图 17为PP波和PS波40炮的偏移结果,其中图 17a、17b、17c分别为PP波参考、未补偿和补偿后的偏移剖面;图 17d、17e、17f分别为PS波参考、未补偿和补偿后的偏移剖面.从图中可以看出,无论是纵波还是转换波,新方法均对地震记录的衰减能量进行了补偿,对相位进行了校正,补偿后的能量均强于没补偿的偏移剖面,尤其在深部,并且补偿后的同相轴更连续.
|
图 17 PP波和PS波偏移剖面 PP波:(a)参考;(b)未补偿;(c)补偿后; PS波:(d)参考;(e)未补偿;(f)补偿后. Fig. 17 PP-wave and PS-wave migration results PP waves:(a)Reference;(b)Not compensated;(c)Compensated; PS waves:(d)Reference;(e)Not compensated;(f)Compensated. |
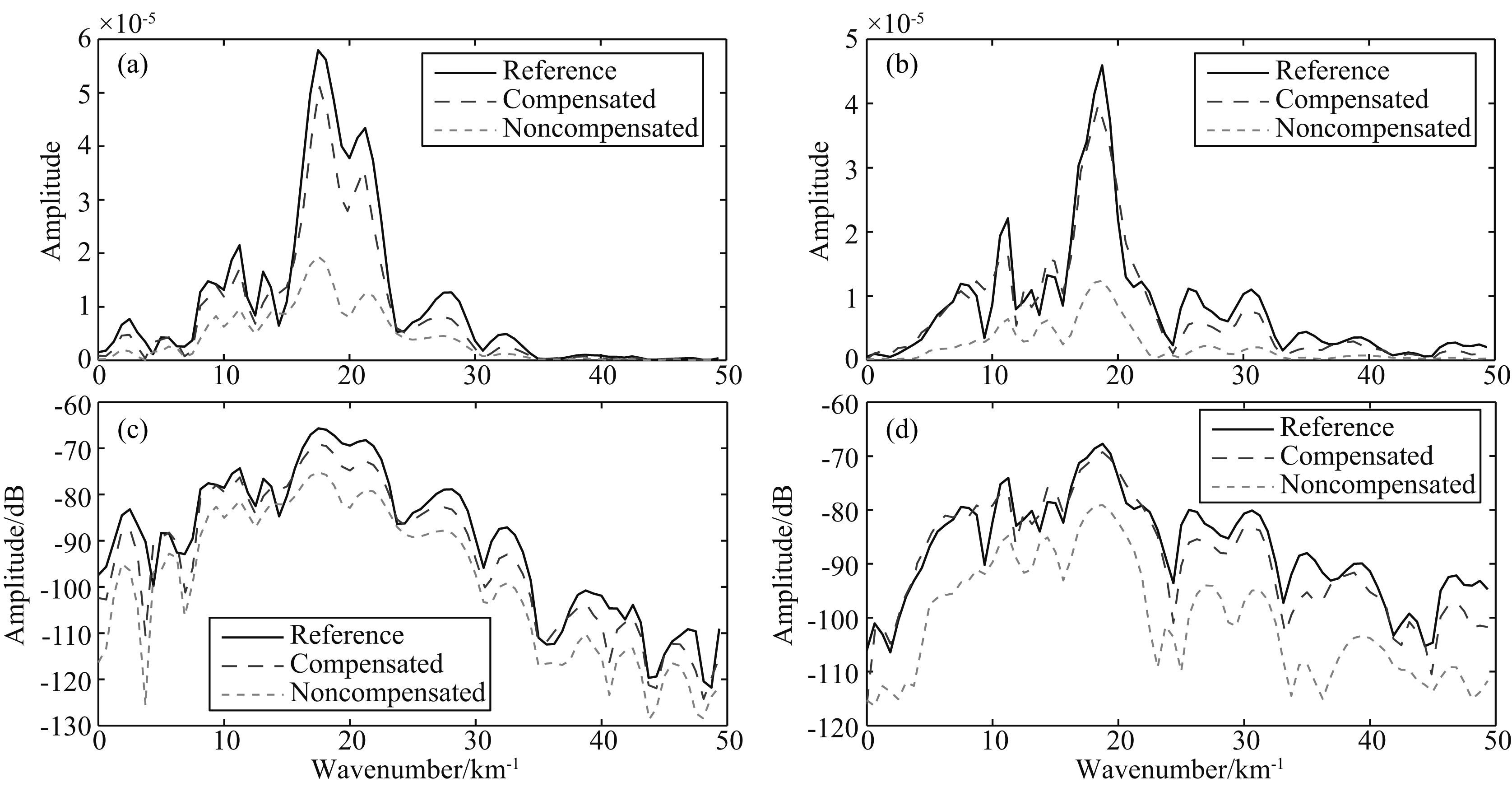
图 18为图 17对应的振幅谱和功率谱,从频谱对比可以看到,频率成分(尤其是中高频)能量得到了加强,即相对未补偿的偏移剖面,补偿后的剖面分辨率更高.
|
图 18 图 17对应的振幅谱和功率谱 PP波:(a)振幅谱;(c)功率谱; PS波:(b)振幅谱;(d)功率谱. Fig. 18 Amplitude spectra and power spectra of Fig. 17 PP waves:(a)Amplitude spectra;(c)Power spectra; PS waves:(b)Amplitude spectra;(d)Power spectra. |
本文提出的基于吸收衰减补偿的多分量高斯束叠前逆时偏移可以有效补偿衰减对多分量成像结果的影响.基于衰减补偿的多分量高斯束逆时偏移是一种优秀的偏移算法,因为它不仅具有常规射线类Q偏移方法高效的优点,而且具有接近于波动方程逆时Q偏移的成像精度.数值实验中,对PP波和PS波的准确成像表明了新方法能有效地补偿多分量地震数据的衰减效应,提高分辨率,改进成像效果,尤其对于强吸收区域.本文是在波场分离之后分别对PP和PS波做标量偏移,处理过程中没有考虑波传播的矢量特征.因此,为了得到更好的转换波成像结果,作者下一步将研究基于矢量波场延拓的黏弹性高斯束逆时偏移方法.
附录A 射线追踪高斯束是波动方程沿中心射线的高频近似解,解的过程包括运动学射线追踪(计算射线路径和走时)和动力学射线追踪(计算中心射线周围的能量值).
对于光滑的二维速度模型(P波或S波),运动学射线追踪公式为:
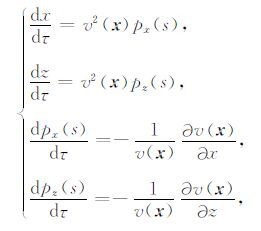
|
(A1) |
式中,初始条件 x(0)=x0,z(0)=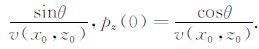
动力学射线追踪可以表示为:
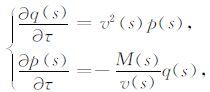
|
(A2) |
其中, M(s) 是关于速度场二阶导数的一个2×2矩阵的行列式展开:
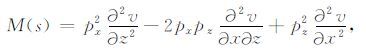
|
(A3) |
式中, p(s)和q(s) 是复值动力学参数,它们决定了高斯束的波前曲率和束宽.
致谢感谢朱铁源博士提供气云速度和Q值模型;第一作者感谢国家留学基金委在联合培养期间给予的资助.感谢两位审稿专家提出的宝贵修改意见和本文编辑细致而负责的工作,从而使得论文更加完善.
| Abramowitz M,Stegun I A.1965. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover New York. | |
| Bai J Y, Chen G Q, Yingst D, et al. 2013. Attenuation compensation in viscoacoustic reverse time migration.//83rd Annual International Meeting, SEG, Expanded Abstracts, 3825-3830. | |
| Bi L F, Qin N, Yang X D, et al. 2015. Gauss beam reverse time migration method for elastic multiple wave. Geophysical Prospecting for Petroleum (in Chinese) , 54 (1) : 64-70. | |
| ČervenyV. 2007. A note on dynamic ray tracing in ray-centered coordinates in anisotropic inhomogeneous media. Studia Geophysica Et Geodaetica , 51 (3) : 411–422. | |
| Chang W F, McMechan G A. 1994. 3-D elastic prestack reverse-time depth migration. Geophysics , 59 (4) : 597-609. DOI:10.1190/1.1443620 | |
| Deng F, McMechan G A. 2007. True-amplitude prestack depth migration. Geophysics , 72 (3) : S155-S166. DOI:10.1190/1.2714334 | |
| Du Q Z, Hou B. 2008. Elastic Kirchhoff migration of vectorial wave-fields. Applied Geophysics , 5 (4) : 284-293. DOI:10.1007/s11770-008-0045-z | |
| Du Q Z, Zhu Y T, Ba J. 2012. Polarity reversal correction for elastic reverse time migration. Geophysics , 77 (2) : S31-S41. DOI:10.1190/geo2011-0348.1 | |
| Du Q Z, Gong X F, Zhang M Q, et al. 2014. 3D PS-wave imaging with elastic reverse-time migration. Geophysics , 79 (5) : S173-S184. DOI:10.1190/geo2013-0253.1 | |
| Fisk M D, McCartor G D. 1991. The phase screen method for vector elastic waves. Journal of Geophysical Research:Solid Earth (1978-2012) , 96 (B4) : 5985-6010. DOI:10.1029/91JB00201 | |
| Fletcher R P, Nichols D, Cavalca M. 2012. Wavepath-consistent effective Q estimation for Q-compensated reverse-time migration.//74th EAGE Conference and Exhibition, Extended Abstracts. A020. | |
| Futterman W I. 1962. Dispersive body waves. Journal of Geophysical Research , 67 (13) : 5279-5291. DOI:10.1029/JZ067i013p05279 | |
| Gray S H, Bleistein N. 2009. True-amplitude Gaussian-beam migration. Geophysics , 74 (2) : S11-S23. DOI:10.1190/1.3052116 | |
| Han J G, Wang Y, Lu J. 2013. Multi-component Gaussian beam prestack depth migration. Journal of Geophysics and Engineering , 10 (5) : 055008. DOI:10.1088/1742-2132/10/5/055008 | |
| Hill N R. 1990. Gaussian beam migration. Geophysics , 55 (11) : 1416-1428. DOI:10.1190/1.1442788 | |
| Hill N R. 2001. Prestack Gaussian-beam depth migration. Geophysics , 66 (4) : 1240-1250. DOI:10.1190/1.1487071 | |
| Hokstad K. 2000. Multicomponent Kirchhoff migration. Geophysics , 65 (3) : 861-873. DOI:10.1190/1.1444783 | |
| Hou A, Marfurt K J. 2002. Multicomponent prestack depth migration by scalar wavefield extrapolation. Geophysics , 67 (6) : 1886-1894. DOI:10.1190/1.1527088 | |
| Jin S W, Wu R S, Xie X B, et al. 1998. Wave equation-based decomposition and imaging for multicomponent seismic data. Journal of Seismic Exploration , 7 (2) : 145-158. | |
| Jo C H, Shin C, Suh J H. 1996. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics , 61 (2) : 529-537. DOI:10.1190/1.1443979 | |
| Keers H, Vasco D W, Johnson L R. 2001. Viscoacoustic crosswell imaging using asymptotic waveforms. Geophysics , 66 (3) : 861-870. DOI:10.1190/1.1444975 | |
| Kuo J T, Dai T F. 1984. Kirchhoff elastic wave migration for the case of noncoincident source and receiver. Geophysics , 49 (8) : 1223-1238. DOI:10.1190/1.1441751 | |
| Li X L, Mao W J. 2015. Multicomponent Gaussian beam migration in elastic medium.//77th EAGE Conference and Exhibition, Extended Abstracts. | |
| Li Z C, Guo Z B, Tian K. 2014. Least-squares reverse time migration in visco-acoustic medium. Chinese J. Geophys. (in Chinese) , 57 (1) : 214-228. DOI:10.6038/cjg20140118 | |
| Li Z Y, Liang G H, Gu B L. 2013. Improved method of separating P-and S-waves using divergence and curl. Chinese J. Geophys. (in Chinese) , 56 (6) : 2012-2022. DOI:10.6038/cjg20130622 | |
| Mittet R. 2007. A simple design procedure for depth extrapolation operators that compensate for absorption and dispersion. Geophysics , 72 (2) : S105-S112. DOI:10.1190/1.2431637 | |
| Popov M M, Semtchenok N M, Popov P M, et al. 2007. Reverse time migration with Gaussian beams and its application to a few synthetic data sets.//76th EAGE Conference and Exhibition, Extended Abstracts, 2165-2169. | |
| Popov M M, Semtchenok N M, Popov P M, et al. 2008. Reverse time migration with Gaussian beams and velocity analysis applications.//70th EAGE Conference and Exhibition, Extended Abstracts, F048 | |
| Popov M M, Semtchenok N M, Popov P M, et al. 2010. Depth migration by the Gaussian beam summation method. Geophysics , 75 (2) : S81-S93. DOI:10.1190/1.3361651 | |
| Suh S, Yoon K, Cai J, et al. 2012. Compensating visco-acoustic effects in anisotropic reverse-time migration. //82nd Annual International Meeting, SEG, Expanded Abstracts , 1 . | |
| Sun R, McMechan G A. 2001. Scalar reverse-time depth migration of prestack elastic seismic data. Geophysics , 66 (5) : 1519-1527. DOI:10.1190/1.1487098 | |
| Sun R, McMechan G A, Hsiao H H, et al. 2004. Separating P-and S-waves in prestack 3D elastic seismograms using divergence and curl. Geophysics , 69 (1) : 286-297. DOI:10.1190/1.1649396 | |
| Sun R, McMechan G A, Lee C S, et al. 2006. Prestack scalar reverse-time depth migration of 3D elastic seismic data. Geophysics , 71 (5) : S199-S207. DOI:10.1190/1.2227519 | |
| Traynin P, Liu J, Reilly J M. 2008. Amplitude and bandwidth recovery beneath gas zones using Kirchhoff prestack depth Q-migration.//78th Annual International Meeting, SEG, Expanded Abstracts, 2412-2416. | |
| Valenciano A A, Chemingui N, Whitmore D, et al. 2011. Wave equation migration with attenuation and anisotropy compensation.//81st Annual International Meeting, SEG, Expanded Abstracts, 232-236. | |
| Wang Y, Nemeth T. 1997. Multi-component separation of PP and SS by a least-squares migration method:Synthetic and field data tests.//67th Annual International Meeting, SEG, Expanded Abstracts, 1222-1225. | |
| Wang Y H, Guo J. 2004. Seismic migration with inverse Q filtering. Geophysical Research Letters , 31 (21) : L21608. | |
| Wang Y H. 2008. Inverse-Q filtered migration. Geophysics , 73 (1) : S1-S6. DOI:10.1190/1.2806924 | |
| Wapenaar C P A, Herrmann P, Verschuur D J, et al. 1990. Decomposition of multicomponent seismic data into primary P-and S-wave responses. Geophysical Prospecting , 38 (6) : 633-661. DOI:10.1111/gpr.1990.38.issue-6 | |
| Wu R S. 1994. Wide-angle elastic wave one-way propagation in heterogeneous media and an elastic wave complex-screen method. Journal of Geophysical Research:Solid Earth (1978-2012) , 99 (B1) : 751-766. DOI:10.1029/93JB02518 | |
| Xiao X, Hao F, Egger C, et al. 2014. Final laser-beam Q-migration.//84th Annual International Meeting, SEG, Expanded Abstracts, 3872-3876. | |
| Xie X B, Wu R S. 2005. Multicomponent prestack depth migration using the elastic screen method. Geophysics , 70 (1) : S30-S37. DOI:10.1190/1.1852787 | |
| Xie Y, Xin K F, Sun J, et al. 2009. 3D prestack depth migration with compensation for frequency dependent absorption and dispersion.//79th Annual International Meeting, SEG, Expanded Abstracts, 2919-2923. | |
| Xie Y, Notfors C, Sun J, et al. 2010. 3D prestack beam migration with compensation for frequency dependent absorption and dispersion.//72nd EAGE Conference and Exhibition, Extended Abstracts. | |
| Yan H Y, Liu Y. 2013. Visco-acoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method. Geophysical Prospecting , 61 (5) : 941-954. DOI:10.1111/gpr.2013.61.issue-5 | |
| Yan J, Sava P. 2008. Isotropic angle-domain elastic reverse-time migration. Geophysics , 73 (6) : S229-S239. DOI:10.1190/1.2981241 | |
| Zhang J F, Wapenaar K. 2002. Wavefield extrapolation and prestack depth migration in anelastic inhomogeneous media. Geophysical Prospecting , 50 (6) : 629-643. DOI:10.1046/j.1365-2478.2002.00342.x | |
| Zhang Y, Karazincir M, Notfors C, et al. 2002. Amplitude preserving v(z) pre-stack Kirchhoff migration, demigration and modeling.//64th EAGE Conference and Exhibition, Extended Abstracts, B011. | |
| Zhang Y, Zhang P, Zhang H Z. 2010. Compensating for visco-acoustic effects in reverse-time migration.//80th Annual International Meeting, SEG, Expanded Abstracts, 3160-3164. | |
| Zhu T Y, Harris J M, Biondi B. 2014. Q-compensated reverse-time migration. Geophysics , 79 (3) : S77-S87. DOI:10.1190/geo2013-0344.1 | |
| Zhu T, Carcione J M. 2014. Theory and modelling of constant-Q P-and S-waves using fractional spatial derivatives. Geophysical Journal International , 196 (3) : 1787-1795. DOI:10.1093/gji/ggt483 | |
| 毕丽飞, 秦宁, 杨晓东, 等. 2015. 弹性多波高斯束逆时偏移方法. 石油物探 , 54 (1) : 64–70. | |
| 李振春, 郭振波, 田坤. 2014. 黏声介质最小平方逆时偏移. 地球物理学报 , 57 (1) : 214–228. DOI:10.6038/cjg20140118 | |
| 李志远, 梁光河, 谷丙洛. 2013. 基于散度和旋度纵横波分离方法的改进. 地球物理学报 , 56 (6) : 2012–2022. DOI:10.6038/cjg20130622 | |
 2016, Vol. 59
2016, Vol. 59

