2. 中国石油塔里木油田分公司勘探开发研究院, 新疆 库尔勒 841000
2. Research Institute of Exploration and Development, Tarim Oilfield Company, Petro China, Korla Xinjiang 841000, China
速度是描述地下介质构造和储层特性的重要物性参数,准确的速度模型对于偏移至关重要.目前常用的速度建模方法主要包括叠加速度分析、偏移速度分析和层析成像等(符力耘等,2013).而随着勘探目标的日益复杂及对成像精度要求越来越高,传统的速度建模方法已经难以满足地震资料处理与解释的需求,而全波形反演(Full\|waveform inversion,FWI)可以有效地弥补其不足.全波形反演综合利用叠前地震波场的运动学和动力学信息,通过不断匹配模拟记录与实测资料来更新速度模型,最终获取可以准确描述地下介质速度分布的深度域速度场模型,具有较高的反演精度,开始越来越多被关注并应用在实际资料中.全波形反演利用地震记录中的全部有效信息,通过局部寻优来进行初始模型的迭代,逐步逼近真实模型,因此本质上是一个极度“病态”的非线性优化问题.地震波场模拟精度、计算效率和地震资料低频成分的保留情况是影响全波形反演方法实际资料应用的重要因素.
20世纪80年代,Tarantola(1984) 首先提出了基于广义最小二乘的时间域全波形反演思想,通过对正演波场和实测记录偏差的最小化约束来更新速度模型.此后国内外研究学者分别从正演和反演两个方向对其进行了发展.在正演模拟方面,Virieux(1984) 将二阶交错网格有限差分方法运用于地震波场模拟;之后,Levander(1988) 将该方法推广至四阶.现在高阶交错网格有限差分法广泛应用于全波形反演中,此外还有伪谱法(Danecek and Seriani,2008)、有限元法(Marfurt,1984)等数值模拟方法.在反演方面,考虑时间域全波形反演可以对数据进行灵活处理,Bunks等(1995) 提出了时间域的多尺度反演方法,通过将问题分解成不同的频率尺度,降低其非线性程度;为了进一步提高计算效率,Pratt和Goulty(1991) 将Tarantola的理论从时间域发展到了频率域,开启了频率域全波形反演的研究热潮;Sirgue和Pratt(2004) 提出基于频率迭代的多尺度全波形反演方法并且给出了反演频率的选择标准.频率域波形反演直接在频率域进行求解,容易实现从低频到高频的多尺度反演,仅需要几个离散的频率便可以完成速度模型的重建,但Operto等(2007) 指出,当处理三维较大模型时,由于三维频率域正演对内存的超大需求,使得三维频率域波形反演有较大的局限性.国内的一些学者(胡光辉等,2013;董烈乾等,2011;王薇等,2013;魏哲枫等,2014;曹书红和陈景波,2014;刘玉柱等,2014;杨勤勇等,2014)针对全波形反演理论研究同样取得了一些成果.
与理论研究相比,全波形反演的实际应用起步较晚,主要原因是全波形反演方法本身的一些局限以及对数据的要求过高.Gauthier等(1986) 和Mora(1987) 于20世纪80年代率先实现了二维地震资料的全波形反演,证明了全波形反演的高精度建模的潜力,但同时也指出全波形反演的“病态”性使其在地震资料缺少低频情况下很难成功;20世纪90年代,全波形反演主要被用于井间地震数据,利用宽角透射波信息重建速度模型(Pratt and Goulty,1991;Song et al.,1995);Sirgue等(2010) 率先对挪威北海油田OBC数据实现了三维全波形反演,对该地区浅层气云和周边充气的断裂构造进行了精细刻画,极大地鼓舞了全波形反演的研究热潮,之后全波形反演在海上地震资料的应用越来越多(Prieux et al.,2010;Ratcliffe et al.,2011;Takougang and Calvert,2011;韩淼,2014).相比海上地震资料全波形反演的应用,陆地资料由于缺少足够多的低频成分和初始模型的限制,使得陆上全波形反演方法的实现较难.2012年,壳牌公司和东方物探合作实现了二维陆上资料的全波形反演,其数据采集基于低频大偏移距的特殊观测系统,但在实际地震采集中很难推广,因此不具有普遍性,但至少验证了陆地全波形反演应用的可行性(Plessix et al.,2012).
塔里木盆地哈拉哈塘地区碳酸盐岩储层普遍埋藏深(超过5500 m)、非均质性强,目的层上覆地层发育厚度不均、速度不同的多期火成岩高速层,该火成岩对速度建模带来极大挑战,火成岩速度的准确与否直接影响缝洞型储层偏移成像位置的准度.常规基于沿层层析和网格层析建模技术刻画火成岩速度精度不高,难以消除由于火成岩速度不准确引起的成像假象.因此,针对该区地质条件,地震资料噪音类型、近地表、能量不均衡等问题,建立了面向全波形反演的叠前保幅去噪、静校正等预处理技术流程,提出了适合该区的全波形反演速度建场技术流程.实际资料全波形反演结果证实了基于波形反演的速度建模方法相比常规层析成像速度建场精度更具优势,其精细刻画了火成岩的构造形态和速度分布,有效改善了火成岩下伏地层的成像精度.
2 陆上资料全波形反演应用挑战及对策全波形反演理论上很完美,但它对数据质量、初始速度模型、正演子波等是有理论假设的.目前,FWI反演很难收敛到正确的结果上,其核心问题在于误差泛函存在非常多的局部极值点,因此需要很好的初始模型来降低误差泛函的非线性.
与海上资料相比,陆上地震资料应用波形反演的主要挑战在于:
(1) 要求宽方位、大偏移距的观测系统.常规陆上三维多为滚动采集,纵横比和偏移距较小,这在很大程度上限制了全波场信息的有效获取;(2) 近地表结构和地下构造的双重复杂导致信噪比低,简单的正演模拟难以描述实际资料中的复杂波;同时地震子波空间不一致性加重了地震波场与反演参数之间的非线性;(3) 缺失低频.海上资料一般最低有效频带为3或者3.5 Hz,常规陆上地震资料的频带有效范围在6 Hz以上,因此,没有低频数据与初始模型的很好耦合,容易陷入局部极小解;(4) 数据预处理难度大.全波形反演要运用地震波的走时信息和动力学信息,在数据预处理时,既要消除噪声干扰又不能破坏波的动力学特征;(5) 陆上炸药震源稳定性较差,随机干扰严重,地面检波器与地面的耦合性远远不如水上检波器与海水的一致性耦合;同时,陆上近地表介质极其复杂,许多不确定因素导致炮、检点分布不规则或者有空洞,炮、检点的高程、坐标不准等误差在构建误差函数时累积,影响其收敛.
在深入分析FWI理论及其陆上资料应用挑战后,提出了实现陆上波形反演实用化的针对性对策.
(1) 优选尽量满足其基本假设的地震数据.
本文研究的YM工区位于塔北隆起南斜坡带,地面海拔在900~1100 m,地形较为平坦,近地表简单;震源子波空间一致性好;低频信息较丰富、低频信息低至3 Hz;纵向最大炮检距为6375 m、最大非纵距4775 m、方位较宽(横纵比达到0.) 最大炮检距为7965;本区二叠系除了发育多期火成岩外,地下构造简单,相对于目的层埋深超过6000 m,偏移距偏小.
(2) 设计保真的数据预处理流程.
陆上资料普遍存在面波、散射面波、环境干扰等,能量高、多在低频段,常规去噪技术往往不同程度地伤害低频有效信号,设计保持动力学和运动学特征的数据预处理流程是关键.
(3) 建立高精度的初始速度模型.
由于该区偏移距偏小,地质体的照明度不足,导致全局收敛慢,需要建立高精度的初始速度模型减少迭代次数和避免局部最优解.
通常陆上资料近地表速度低且变化剧烈,炮、检点的位置和高程也可能不准,现有方法难以描述速度的高频变化,处理中采用静校正的高频分量来消除近地表速度高频,近地表速度的中、长波长分量放在速度建模中解决;在该区采用基于层析成像的速度建模方法建立的初始速度模型,已经基本满足该区的叠前深度偏移成像对速度精度要求.
随着陆上地震采集技术水平的不断提高,全波场、宽频带等观测手段的实现以及保真预处理技术的发展,陆上全波形反演的应用将逐步走向实用化.
3 时间域全波形反演原理及流程实现全波形反演方法的基本原理是通过给定一个初始模型,利用正演模拟得到其传播波场,将正演波场与实测波场进行对比分析,通过不断修正模型使得二者误差达到可允许范围,从而得到反演结果.该方法主要包括三部分(韩淼,2014):首先,基于已知的初始速度模型,通过波动方程正演模拟获得理论地震波场;其次,基于理论地震波场与观测地震波场之间的波场残差,构建目标函数,并将残差逆时传播得到反向波场,并通过正向波场和反向波场计算模型参数梯度;最后,选择一种优化算法对该反问题进行求解.全波形反演方法可以分为时间域全波形反演和频率域全波形反演.为更好适应三维,本文采用时间域全波形反演方法,为了增加问题求解的稳定性降低其非线性程度,保证求解不会陷入局部收敛应用中采取多尺度反演(Bunks et al.,1995).
3.1 时间域全波形反演基本原理时间域正演通过在时间方向的迭代来求各个时间的波场值,内存需求相对较小,能够更好地适应三维问题.
时间域的三维声波方程可表示为(Vigh et al.,2011)
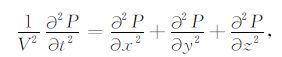
|
(1) |
方程中P(x,y,z,t)是地震波场,V(x,y,z)是速度项.假设P(xr,yr,zr,t)是xr处记录的地震波场,构建如下所示目标函数:
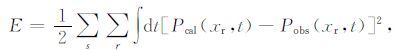
|
(2) |
公式中Pobs是野外观测到的地震数据,Pcal是通过声波波动方程正演的记录.全波形反演通过寻找目标函数E的极小值,使得满足目标函数极小值的速度即为最终的反演速度.
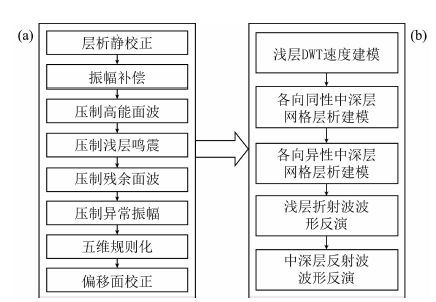
3.2 波形反演速度建模实现流程陆上资料的全波形反演应用主要受限于子波空变、信噪比低、低频信息缺失、数据不规则、低频数据与初始模型的耦合.针对FWI在陆上资料应用受限原因及哈拉哈塘地震资料特点,提出地震保幅预处理流程和实现FWI速度建模流程,流程如图 1所示.
|
图 1 保幅预处理流程(a)与实现FWI速度建模流程(b) Fig. 1 Fidelity preprocessing strategy(a)and FWI velocity modeling strategy(b) |
YM地区地表高程变化不大,北部为农田、中部为浮土、南部为小沙,低降速带厚度变化不大,静校正难度不大;工区内疏松的近地表低降速带对地震波吸收衰减严重,导致深层有效波能量弱、主频较低;主要干扰波为强能量的面波、折射波及异常干扰;奥陶系缝洞型碳酸盐岩是主要目的层,埋藏深、非均质强,因此噪声衰减、恢复弱信号和保护低频信号是资料预处理的关键技术.
4.1 保幅去噪技术针对该区噪音类型,本文首先采用面波模拟方法(Strobbia et al.,2009)去除高能量频散面波;然后利用稳健的地表一致性反褶积(Tnaer and Koehler,1981)压制浅层多次折射波;再利用曲波变换(董烈乾等,2011)去除剩余面波;最后进行异常振幅消除处理,预处理流程见图 1a所示.
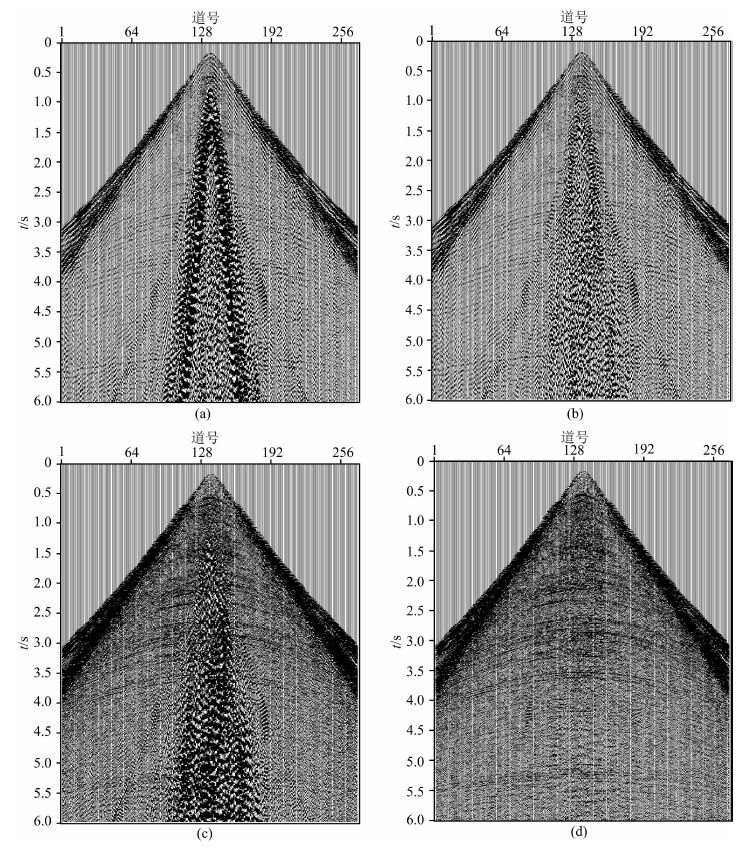
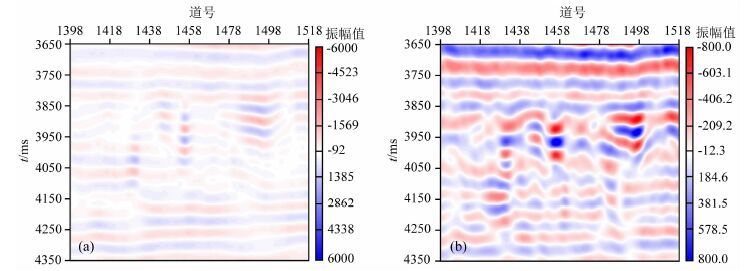
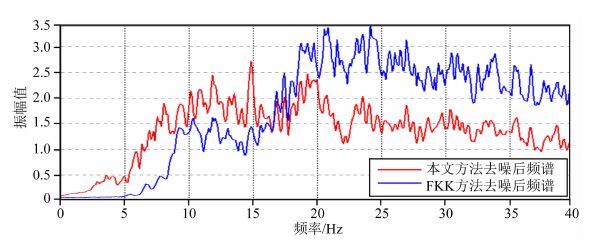
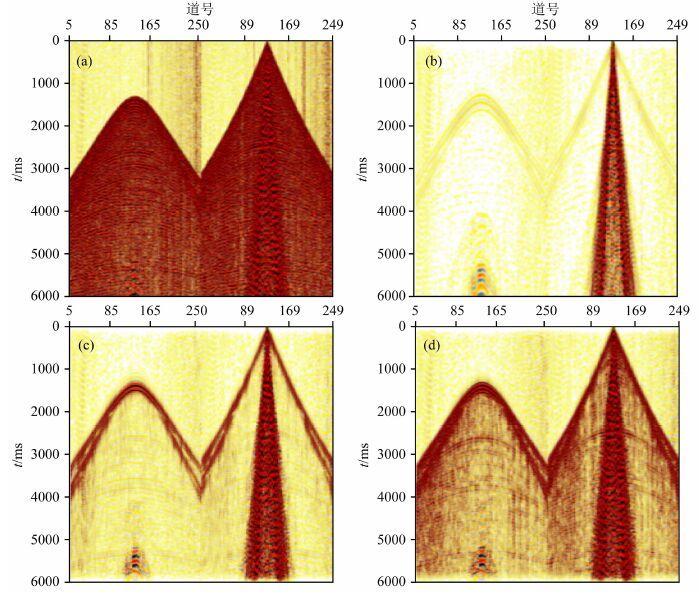
图 2a为静校正后单炮数据,图 2b为面波模拟法压制模拟的基阶、一阶和二阶面波噪声后的结果.衰减剩余更高阶面波和频散面波之前,先对数据压制浅层多次折射波,如图 2c为浅层多次折射波压制后的炮集.图 2d为曲波变换法衰减剩余面波之后的炮集,可以看出高阶面波和频散面波衰减效果好,大大提高了资料信噪比.图 3、图 4为本文方法与常规三维FKK方法去噪后低频信号(0~10 Hz)和频谱图对比,可以看出本文方法可以保留更多的有效低频信息,更有利于后续叠前反演、流体检测、波形反演等技术应用.
|
图 2 噪声压制效果图 (a)静校正后单炮;(b)面波模拟法去除噪声后单炮;(c)压制浅层多次折射后单炮;(d)压制剩余面波后单炮. Fig. 2 (a) Data with field static correction;(b)Noise reduction with surface wave modeling method;(c)Data after surface consistent deconvolution;(d)Residual surface wave reduction |
|
图 3 常规FKK去噪(a)与本文方法去噪(b)PSTM低频部分对比(0~10 Hz) Fig. 3 Low\|frequency component(0~10 Hz)of seismic data after FKK denoising(a)and our method(b) |
|
图 4 常规三维FKK去噪(蓝)与本文方法去噪后(红)频谱对比 Fig. 4 Spectrum of seismic data after FKK denoising(blue)and our method(right) |
YM地区地表简单,高程变化不大、地表障碍极少,不存在严重的数据不规则或较大面积的空洞,仅存在人为施工误差造成原始地震资料的炮点、检波点分布不规则或坏道造成部分数据缺失,给后续正演模拟与实际地震资料匹配带来一定困难.本文采用基于OMP(正交匹配追踪)算法的五维数据规则化技术(Hollander et al.,2012)极大地提高了重建质量,解决了正演模拟与实际资料的匹配问题.
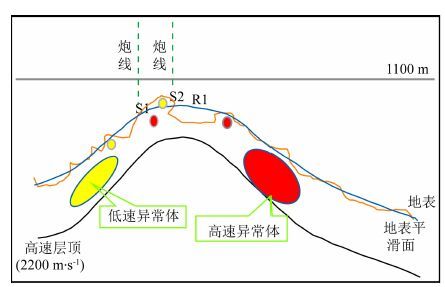
前期静校正处理已经对地表高程变化和低降速带异常时差进行了校正,这对地震波场时间信息的破坏非常大,此时以CMP面或者固定基准面作为偏移的基准面,往往不能正确求取近地表速度,甚至误差很大.理论上讲,应选取真实地表面,但是现有资料无法实现,目前最现实的情况是选取平滑地表作为偏移的基准面,把数据从CMP面校正到近地表平滑面,同时数据中仅仅保留地表平滑面附近因高程变化和存在微小异常体产生的高频静校正时差,而去掉因低降速带异常体引起的中长波长静校正,此部分的速度异常在深度偏移浅层速度建模中考虑,这是陆上地震资料预处理的关键环节之一.
|
图 5 近地表及炮、检点布设示意图 Fig. 5 Diagram of near\|surface and seismic geometry |
全波形反演理论体系完美,但它对数据限制和应用瓶颈很多.陆上资料的全波形反演应用主要受限于子波空变、信噪比低、低频观测数据和满足全波形反演要求的初始速度模型,其中低频数据与初始模型的耦合是全波形反演在实际资料应用中遇到的最大瓶颈.
YM工区地表条件相对简单,子波空间一致性较好,信噪比较高,野外采集没有低截处理;在0~3 Hz低频端地震信号中折射波的能量较强,以折射波信号为主,反射信号能量弱,在在0~5 Hz低频端地震信号中反射波能量强,信号低频较丰富(如图 6所示).上述数据预处理最大程度地保护了数据低频成分,使该区地震资料满足波形反演基本要求.
在实际资料处理中,高精度正演模拟和全波形反演的计算量非常大,所以尽可能通过建立高精度的初始速度模型,减少迭代次数,增加求解的稳定性,提高收敛速度,从而减少计算量.
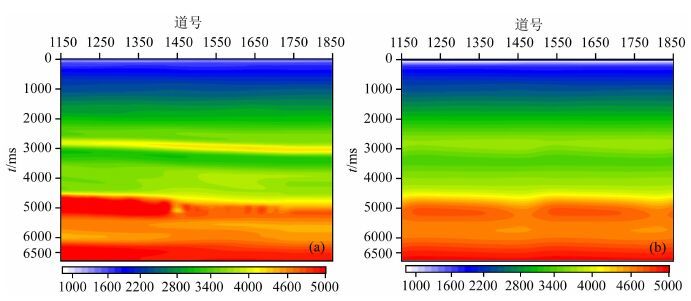
5.1 初始速度模型的建立初始速度模型的建立主要利用走时层析成像技术,具体流程如图 1b.先采用回转波层析成像技术建立浅层速度模型;然后利用反射波层析成像建立中深层各向同性速度模型;再利用井数据标定各向异性参数,建立中深层各向异性速度模型(如图 7a所示);最后,对该各向异性速度模型做平滑处理,去掉速度高频成分的背景速度作为波形反演的最终初始速度模型(如图 7b所示).
初始速度模型建立以后,采用时间域分层多尺度全波形反演精细建模流程,主要分为以下两步:(1) 浅层折射波FWI,(2) 中深层反射波FWI.最后利用叠前深度偏移对地下构造进行偏移成像.
|
图 6 原始数据低频滤波结果对比分析 (a)原始单炮记录;(b)0~3 Hz低通滤波后单炮记录;(c)0~5 Hz低通滤波后单炮记录;(d)0~7 Hz低通滤波后单炮记录. Fig. 6 Low frequency pass filter of raw shot data (a)Raw shot record;(b)Low pass filter of 0~3 Hz;(c)Low pass filter of 0~5 Hz;(d)Low pass filter of 0~7 Hz. |
|
图 7 层析成像建立的各向异性速度模型(a)与FWI初始速度模型(b) Fig. 7 Anisotropy velocity model generated by tomography(a)and initial velocity of FWI(b) |
波形反演成功与否,与波形反演的很多技术细节密切相关.结合本工区实际资料情况,具体技术细节如下:
① 地震正演子波,指导原则是尽可能接近实际资料地震子波.本文从实际地震资料获得,主要考虑地震资料有效频带范围; ② 地震数据匹配过程中的规则化.由于YM工区野外近地表条件简单,资料信噪比也高,五维数据规则化技术已很成熟,数据规则化难度不大,在数据预处理阶段,采用正交匹配追踪的五维数据规则化技术完成规则化; ③ 计算效率/迭代次数问题,波形反演由于包含波动方程地震正演计算,计算量非常大.提高计算效率主要通过两方面:一是提高初始速度模型的精度;二是采用GPU/CPU联合运算.迭代次数主要根据对反演结果的质控和反演效果来决定,否则容易陷入局部极小值; ④ 局部寻优策略选用共轭梯度法.
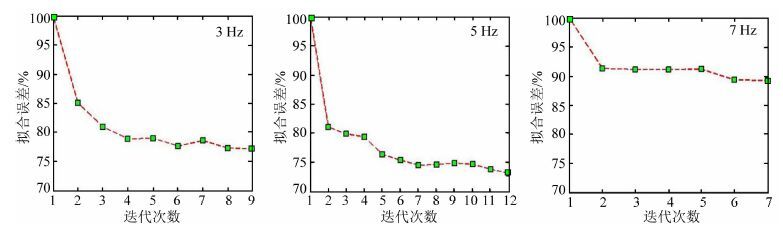
5.3 浅层折射波波形反演浅层速度模型的反演精度是影响地下地质结构成像效果的主要因素之一.本文利用折射波,由低频到高频反演4000 m以内较低频的浅层速度,由于该区地震信号中折射波的能量较强,较丰富的低频折射波有利于反演浅层速度信息.该方法只拾取初至后一段时间的波形信息反演,降低了全波形反演的非线性.为了进一步提高反演稳定性和收敛效果,采用时间域多尺度全波形反演算法,反演主频依次为3 Hz(0~6 Hz),5 Hz(0~10 Hz),7 Hz(0~14 Hz). 全波形反演前后折射波信号的匹配情况如图 8所示,图中箭头左侧为实际数据、右侧为正演模拟记录,可以看出初始速度模型的匹配精度已经很高,这也验证了我们初始模型的有效性,此外,模型更新后正演模拟记录与实际数据更加匹配,说明了浅层速度模型经FWI更新后更加精准;每个频段经10次左右迭代后,误差目标函数趋于收敛(如图 9所示).

|
图 8 FWI前(a)、后(b)不同主频折射波匹配情况(箭头左侧为实际数据,右侧为正演模拟记录) Fig. 8 Comparison of real refraction waves and modeling refraction waves before(a)and after (b) FWI (data left of arrow represents real waves,data right of arrow represents modeling waves) |
|
图 9 不同主频折射波FWI误差目标函数(左为主频3 Hz、中为主频5 Hz、右为主频7 Hz) Fig. 9 Misfit of FWI with refraction waves of different domain frequency(left:3 Hz,middle:5 Hz,right:7 Hz) |
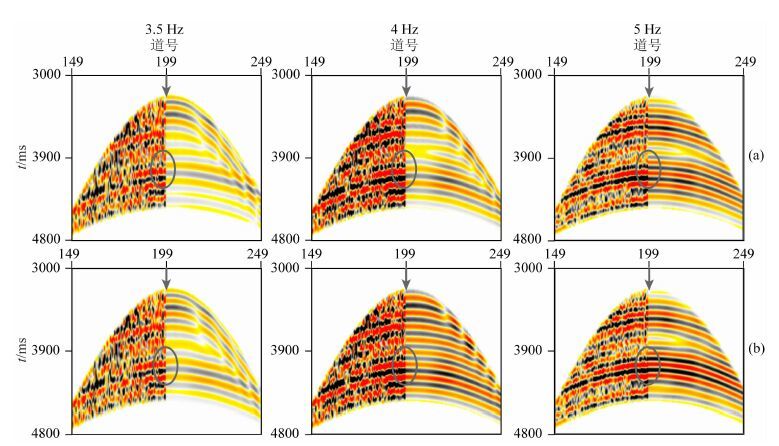
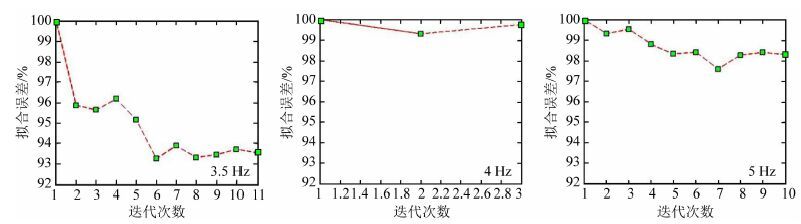
针对中深层丰富的反射信号,采用折射波FWI的最终结果作为反射波FWI的初始模型,同样进行时间域多尺度反演,利用主频依次为3.5 Hz(0~7 Hz)、4 Hz(0~10 Hz)、5 Hz(0~12 Hz),反演较高频的速度信息.全波形反演前后反射波信号的匹配情况如图 10所示,图中箭头左侧为实际数据、右侧为正演记录,同样可以看到模型更新后正演模拟记录与实际数据匹配更好,说明经FWI更新后,中深层速度模型更加精准;除了主频为4 Hz,其余两个主频经10次左右迭代后,误差目标函数趋于收敛(如图 11所示).
|
图 10 FWI前(a)、后(b)不同频段反射波匹配情况(箭头左侧为实际数据,右侧为正演模拟记录) Fig. 10 Comparison of real reflection waves and modeling reflection waves before (a) and after (b) FWI (data left of arrow represents real waves,data right of arrow represents modeling waves) |
|
图 11 不同频段反射波FWI误差目标函数(左为主频3.5 Hz、中为主频4 Hz、右为主频5 Hz) Fig. 11 Misfit of FWI with reflection waves of different domain frequency(left:3.5 Hz,middle:4 Hz,right:5 Hz) |
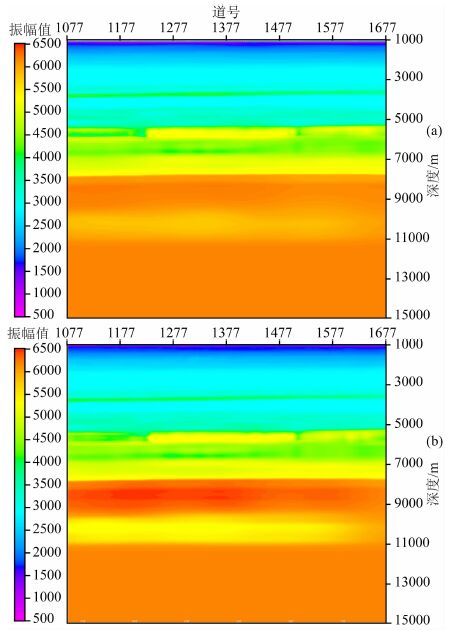
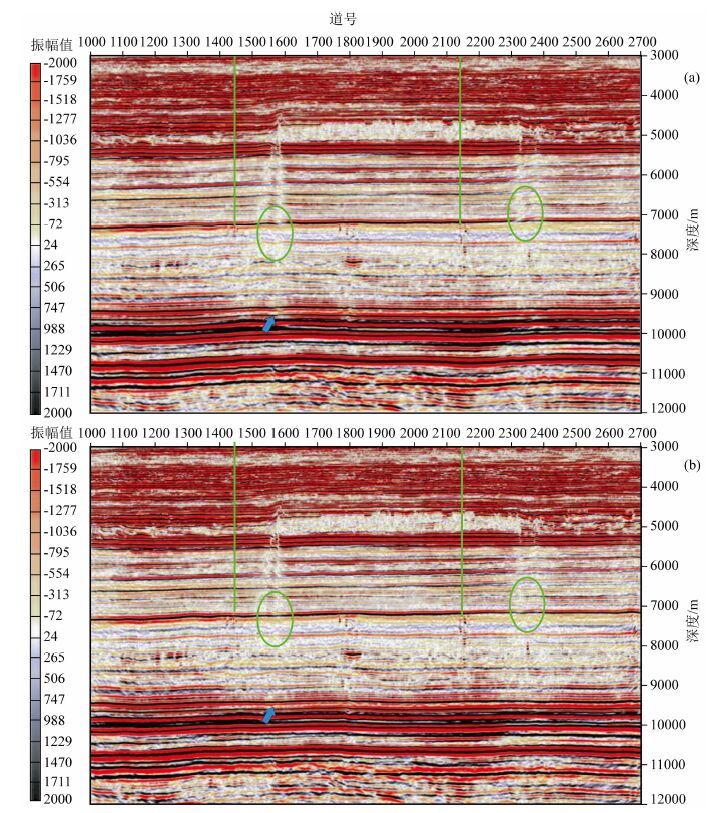
经过反射波FWI以后得到的速度模型即为全波形反演的最终速度模型.图 12为过某测线层析成像和全波形反演得到的速度模型对比图,采用克希霍夫叠前深度偏移进行偏移成像处理,结果如图 13和图 14所示.可以看出:基于FWI精细速度模型的叠前深度偏移有效改善了火成岩以下目的层的成像,消除了由于速度不准造成的火成岩边缘及以下断层和破碎带(图 13椭圆所示)的构造假象以及奥陶系以下假低幅度隆起构造(图 13箭头所示),同时对于深层缝洞型碳酸盐岩储层的成像也更加清晰(如图 14所示).
|
图 12 层析成像速度模型(a)和波形反演速度模型(b)对比 Fig. 12 Comparison of tomography result (a) and FWI result (b) |
|
图 13 不同速度模型的PSDM成像对比 FWI result(b) Fig. 13 PSDM results with tomography velocity(a)and FWI velocity(b) |

|
图 14 不同速度模型的PSDM 7600 m深度切片对比 (a)层析成像速度PSDM深度切片;(b)波形反演速度的PSDM深度切片. Fig. 14 Depth slice(7600 m)of PSDM results with tomography velocity(a)and FWI velocity(b) |
塔里木盆地YM地区二叠系大规模发育火成岩,岩性空间变化大、厚度变化也大.奥陶系目的层埋藏深,上覆地层速度的精度严重影响偏移成像的效果,不同岩性的火成岩速度差异大、厚度空间变化大,火成岩空间分布范围和速度精度描述不准会严重影响低幅构造的落实和缝洞型碳酸盐岩储层空间成像位置.
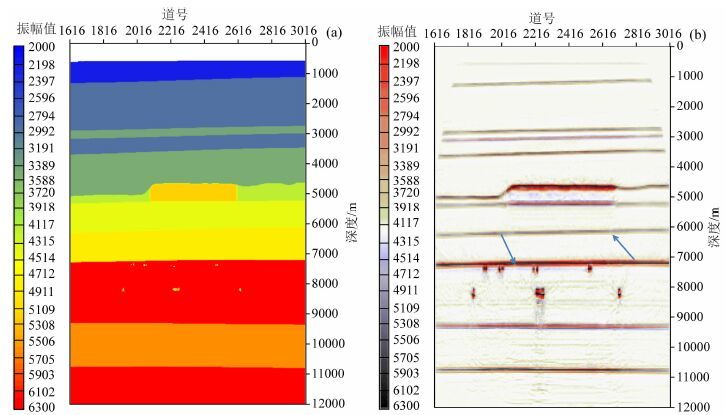
为了验证图 13、图 14成像结果的可靠性和进一步从地球物理角度证明,选择横跨火成岩的一条测线,根据初步地质解释成果、层析成像结果及测井资料,构建简化2.5维的速度模型,如图 15a所示.采用25Hz雷克子波进行有限差分正演模拟,然后对正演结果进行克希霍夫叠前深度偏移,偏移结果如图 15b所示,可以看到箭头所示处没有断层.
|
图 15 简化的速度模型(a)及对应的叠前深度偏移结果(b) Fig. 15 Simplified velocity model(a)and PSDM result with this velocity(b) |
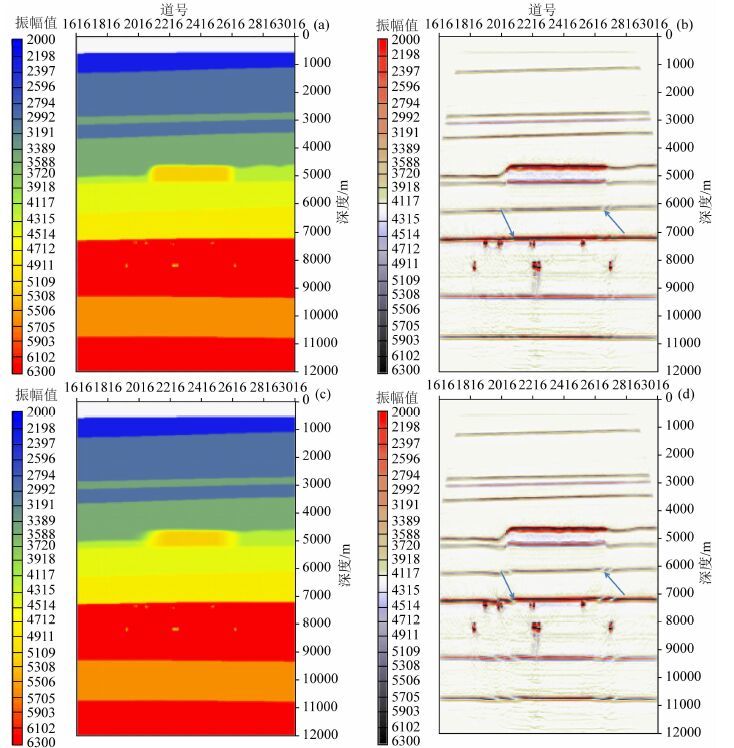
为了展示火成岩的空间边界和速度精度对偏移成像结果的影响,分别对火成岩速度区域进行1000 m 局部平滑(图 16a)和3000 m局部平滑(图 16c),采用平滑的速度模型分别对正演模拟的数据进行叠前深度偏移处理,对应的成像结果如图 16b和16d所示.可以看出,当火成岩空间边界和速度刻画不准时,容易导致火成岩边缘以下对应位置出现“假断层”(如箭头所示),因此精细刻画火成岩的空间边界和速度对火成岩周缘及下伏地层的成像至关重要,火成岩刻画不准也会导致深部的缝洞型储层成像误差,同时证明了本文中全波形反演得到的速度模型的合理性和高精度,实际钻井也已证实该结果.
|
图 16 平滑速度模型及其对应的PSDM剖面 (a)将火成岩区域进行1000 m平滑后的速度模型;(b)1000 m平滑速度模型对应的PSDM剖面;(c)将火成岩区域进行3000 m平滑后的速度模型;(d)3000 m平滑速度模型对应的PSDM剖面. Fig. 16 Smooth velocity model and PSDM results (a)Velocity model with 1000 m local smoothing at volcano rock area;(b)PSDM result with velocity as shown in Fig. 16a;(c)Velocity model with 3000 m local smoothing at volcano rock area;(d)PSDM result with velocity as shown in Fig. 16c. |
全波形反演是一种理论完美,高精度的速度建模技术,初始速度模型的精度和足够低频的观测地震数据是影响波形反演效果的两个关键因素.本文针对塔里木盆地YM工区缝洞型储层成像和地震资料特点,从影响波形反演关键因素角度出发,探索实现了面向缝洞型储层的波形反演技术流程,并得到如下结论:
(1) 初始速度模型的精度是全波形反演成功与否的最大挑战,浅层采用回折波层析成像、中深层采用反射波层析成像技术联合建立各向异性速度模型精度高;
(2) 陆上资料低频信息不足是全波形反演的瓶颈之一,与常规FKK方法相比,基于面波模拟和曲波变换联合去噪技术能够较好地保护低频信息和波的动力学特征,满足全波形反演对数据的要求;
(3) 实现陆上资料波形反演的关键是建立合理流程,在建立较高精度初始速度模型的基础上,采用折射波波形反演速度低频信息,再用反射波反演速度高频信息的波形反演速度迭代流程是一种行之有效的方法;
(4) 虽然目前大部分常规陆上地震采集的数据不能完全满足经典全波形反演的要求,但随着采集新技术的应用和处理技术的发展,尤其是波形反演在塔里木盆地YM地区的成功应用,有望为陆上资料波形反演的工业化发展起到一定的推动和借鉴作用.
| Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion. Geophysics , 60(5): 1457–1473. | |
| Cao S H, Chen J B. 2014. Studies on complex frequencies in frequency domain full waveform inversion. Chinese Journal of Geophysics (in Chinese) , 57(7): 2302–2313. doi: 10.6038/cjg20140724. | |
| Danecek P, Seriani G. 2008. An efficient parallel Chebyshev pseudo-spectral method for large scale 3D seismic forward modelling.//70th EAGE Conference & Exhibition. SPE, EAGE. | |
| Dong L Q, Li Z C, Wang D Y, et al. 2011. Ground-roll suppression based on the second generation Curvelet transform. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 46(6): 897–904. | |
| Fu L Y, Xiao Y J, Sun J W, et al. 2013. Seismic imaging studies of complex high and steep structures in Kuqa depression. Chinese Journal of Geophysics (in Chinese) , 56(6): 1985–2001. doi: 10.6038/cjg20130620. | |
| Gauthier O, Virieux J, Tarantola A. 1986. Two-dimensional nonlinear inversion of seismic waveform: numerical results. Geophysics , 51(7): 1387–1403. | |
| Han M. 2014. Methods and application of full waveform inversion for abyssal seismic data[Ph. D. thesis] (in Chinese). Changchun: Jilin University. | |
| Hollander Y, Kosloff D, Koren Z, et al. 2012. Seismic data interpolation by orthogonal matching pursuit.//74th EAGE Conference & Exhibition. SPE, EAGE. | |
| Hu G H, Jia C M, Xia H R, et al. 2013. Implementation and validation of 3D acoustic full waveform inversion. Geophysical Prospecting for Petroleum (in Chinese) (in Chinese) , 52(4): 417–425. | |
| Levander A R. 1988. Fourth-order finite-difference P-SV seismogram. Geophysics , 53(11): 1425–1436. | |
| Liu Y Z, Xie C, Yang J Z. 2014. Gaussian beam first-arrival waveform inversion based on Born wavepath. Chinese Journal of Geophysics (in Chinese) , 57(9): 2900–2909. doi: 10.6038/cjg20140915. | |
| Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics , 49(5): 533–549. | |
| Mora P. 1987. Nonlinear two-dimensional elastic inversion of multi-offset seismic data. Geophysics , 52(9): 1211–1228. | |
| Operto S, Virieux J, Amestoy P, et al. 2007. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver: a feasibility study. Geophysics , 72(5): SM195–SM211. | |
| Plessix R é, Baeten G, de Maag J, et al. 2012. Full waveform inversion and distance separated simultaneous sweeping: a study with a land seismic data set. Geophysical Prospecting , 60(4): 733–747. | |
| Pratt R G, Goulty N R. 1991. Combining wave-equation imaging with traveltime tomography to form high-resolution images from crosshole data. Geophysics , 56(2): 208–224. | |
| Prieux V, Operto S, Brossier R, et al. 2010. Application of 2D acoustic frequency-domain full-waveform inversion to OBC wide-aperture data from the Valhall field.//SEG Technical Program Expanded Abstracts, Denver, Colorado: SEG, 920-924. | |
| Ratcliffe A, Win C, Vinje V, et al. 2011. Full waveform inversion: a North Sea OBS case study.//Proceedings of the 81st Annual International Meeting. SEG, 2384-2388. | |
| Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies. Geophysics , 69(1): 231–248. | |
| Sirgue L, Barkved O I, Dellinger J, et al. 2010. Full waveform inversion: the next leap forward in imaging at Valhall. First Break , 28(4): 65–70. | |
| Song Z M, Williamson P R, Pratt R G. 1995. Frequency-domain acoustic-wave modeling and inversion of crosshole data: Part II-Inversion method, synthetic experiments and real-data results. Geophysics , 60(3): 796–809. | |
| Strobbia C L, Laake A, Vermeer P L, et al. 2009. Surface waves-use them then lose them.//71th EAGE Conference & Exhibition. Amsterdam, The Newtherlands. | |
| Takougang E M T, Calvert A J. 2011. Application of waveform tomography to marine seismic reflection data from the Queen Charlotte Basin of western Canada. Geophysics , 76(2): B55–B70. | |
| Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics , 49(8): 1259–1266. | |
| Tnaer M T, Koehler F. 1981. Surface consistent corrections. Geophysics , 46(1): 12–22. | |
| Vigh D, Kapoor J, Li H Y. 2011. Full-waveform inversion application in different geological settings.//SEG Technical Program Expanded Abstracts. SEG, 2374-2378. | |
| Virieux J. 1984. SH-wave propagation in heterogeneous media, velocity-stress finite-difference method. Geophysics , 49(11): 1933–1942. | |
| Wang W, Han B, Tang J P. 2013. Regularization method with sparsity constraints for seismic waveform inversion. Chinese Journal of Geophysics (in Chinese) , 56(1): 289–297. doi: 10.6038/cjg20130130. | |
| Wei Z F, Gao H W, Zhang J F. 2014. Time-domain full waveform inversion based on an irregular-grid acoustic modeling method. Chinese Journal of Geophysics (in Chinese) , 57(2): 586–594. doi: 10.6038/cjg20140222. | |
| Wu R S. 2003. Wave propagation, scattering and imaging using dual-domain one-way and one-return propagators. Pure and Applied Geophysics , 160(3-4): 509–539. | |
| Yang Q Y, Hu G H, Wang L X. 2014. Research status and development trend of full waveform inversion. Geophysical Prospecting for Petroleum (in Chinese) (in Chinese) , 53(1): 77–83. | |
| 曹书红, 陈景波. 2014. 频率域全波形反演中关于复频率的研究. 地球物理学报 , 57(7): 2302–2313. | |
| 董烈乾, 李振春, 王德营, 等. 2011. 第二代Curvelet变换压制面波方法. 石油地球物理勘探 , 46(6): 897–904. | |
| 符力耘, 肖又军, 孙伟家, 等. 2013. 库车坳陷复杂高陡构造地震成像研究. 地球物理学报 , 56(6): 1985–2001. | |
| 韩淼. 2014. 深水区地震全波形反演策略与应用[博士论文]. 长春: 吉林大学. | |
| 胡光辉, 贾春梅, 夏洪瑞, 等. 2013. 三维声波全波形反演的实现与验证. 石油物探 , 52(4): 417–425. | |
| 刘玉柱, 谢春, 杨积忠. 2014. 基于Born波路径的高斯束初至波波形反演. 地球物理学报 , 57(9): 2900–2909. | |
| 王薇, 韩波, 唐锦萍. 2013. 地震波形反演的稀疏约束正则化方法. 地球物理学报 , 56(1): 289–297. | |
| 魏哲枫, 高红伟, 张剑锋. 2014. 基于非规则网格声波正演的时间域全波形反演. 地球物理学报 , 57(2): 586–594. | |
| 杨勤勇, 胡光辉, 王立歆. 2014. 全波形反演研究现状及发展趋势. 石油物探 , 53(1): 77–83. | |
 2016, Vol. 59
2016, Vol. 59

