2. 中国地质调查局发展研究中心, 北京 100037;
3. 国土资源部矿产勘查技术指导中心, 北京 100037;
4. 国家海洋局 第二海洋研究所, 杭州 310012;
5. 国家海洋局 海底科学重点实验室, 杭州 310012
2. Center of Development and Research, China Geological Surveys, Beijing 100037, China;
3. Technical Guidance Center for Mineral Exploration, Ministry of Land and Resources, Beijing 100037, China;
4. Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China;
5. Key Laboratory of Submarine Geoscience, State Oceanic Administration, Hangzhou 310012, China
边界识别在地球物理位场数据解释中占有重要位置,通过研究地质体的横向不均匀性,位场数据的边界识别作为一种数据处理手段在金属矿勘探、能源勘探以及区域构造研究中都可以发挥重要作用.目前,有许多方法基于位场数据的水平导数和垂直导数来识别地质体的边界特征.总水平导数THD 的最大值对应地质体的边界(Cordell,1979; Cordell and Grauch,1985).Nabighian(1984) 和Roest等(1992) 证明了解析信号的最大振幅可以直接描绘密度和磁性体的边界.Hsu等(1996) 提出加强解析信号方法进行到高阶导数以增加传统解析信号方法的分辨能力.Cooper和Cowan(2004) 使用不同阶的垂向导数能有效地增强地球物理异常的细节.这些方法的一个主要缺点是不能同时显示强的和弱的异常振幅信息.
近几年,不同的均衡滤波方法得到广泛发展,以便能均衡不同振幅大小的异常体的边界信号强度.Miller和Singh(1994) 使用垂向导数与总水平导数的比来进行边界检测,叫做TDR,其表达式为
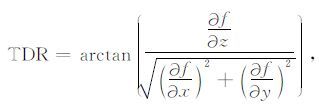
|
(1) |
是第一个均衡滤波器,能均衡不同振幅强度的异常信息.后来众多学者在此基础上发展了Theta图、水平倾斜角TDX和倾斜角的总水平导数等方法(Wijns et al.,2005; Cooper and Cowan,2006; Verduzco et al.,2004).然而,当测量的异常值中同时包含正异常和负异常时,这些方法除了能识别出地质体的边界外,还将产生一些额外的错误的边界结果.针对这一情况,一些学者对其进行改进,大多数都是通过在归一化因子中引入一个正的常数p来去除额外的错误的边界信息(Cooper,2013; Li et al.,2014; Yuan et al.,2014; 袁园等,2015).然而,在常参数p的引入过程中,通常是解释者通过实际经验给定,存在一定的人为主导因素.参数p越大,能更好地去除额外的错误的边界信息,但是会降低真实边界信息的分辨率;参数p越小,去除误差边界信息的能力降低.因此,这种方法在实际数据处理中并不实用.
本文针对位场数据中同时存在正异常和负异常的情况利用解析信号振幅和解析信号振幅的垂向一阶导数的倾斜角方法进行地质体的边界检测,有效地克服了之前传统方法的缺点,称其为加强解析信号倾斜角.
2 加强解析信号倾斜角本文通过解析信号振幅及解析信号振幅的垂向一阶导数定义的倾斜角来进行位场数据的边界识别,其表达式为
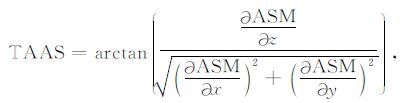
|
(2) |
其中ASM为解析信号振幅,

|
(3) |
f为测量的位场数据.
为了提高边界结果的分辨率,利用解析信号振幅的垂向一阶导数定义边界识别器,
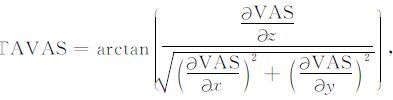
|
(4) |
其中,VAS为解析信号振幅ASM的垂向一阶导数,
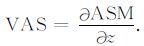
|
(5) |
然而,Florio等(2006) 指出位场数据的解析信号振幅为非调和函数.解析信号振幅垂向一阶导数的直接表达式结果与通过频率域垂向导数算子计算得到的结果之间存在很大差别.为了更好地识别地质体的边界,利用垂向导数算子在频率域中对解析信号AS进行滤波处理,突出其高频成分.因此,文中的垂向导数计算都是通过频率域垂向导数算子计算得到.在TAVAS表达式中,需要计算VAS的垂向一阶导数,等效于计算解析信号振幅ASM的垂向二阶导数.
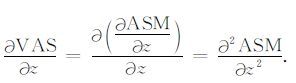
|
(6) |
因此,我们利用(6) 式来代替(4) 式中垂向导数的计算.
TAAS和TAVAS表达式中在x和y方向上水平导数通过中心差分法计算得到.对于任意一个量位场f,解析信号振幅ASM和VAS,其在x方向上的导数为
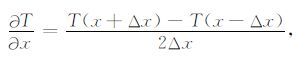
|
(7) |
这里T包括f,ASM和VAS.同理,其在y方向上的导数为

|
(8) |
该具体方法实现通过MATLAB内置函数gradient.m计算得到.
本文方法的具体实现主要分为三步:
(1) 对测得的位场数据在x,y和z三个方向求导,利用(3) 式求得该位场数据的解析信号振幅ASM;
(2) 对求得的解析信号振幅ASM在x,y和z三个方向求导,利用(2) 式求得边界识别器TAAS;
(3) 解析信号振幅ASM的垂直导数VAS进行x,y和z三个方向求导,利用(4) 式求得边界识别器TAVAS.
为了验证本文提出方法的可行性,我们选用五种常用边界识别方法进行对比分析,分别是解析信号振幅ASM、THD、TDR、Theta图和TDX.
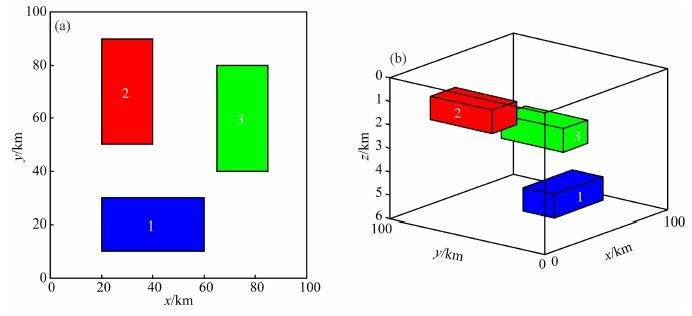
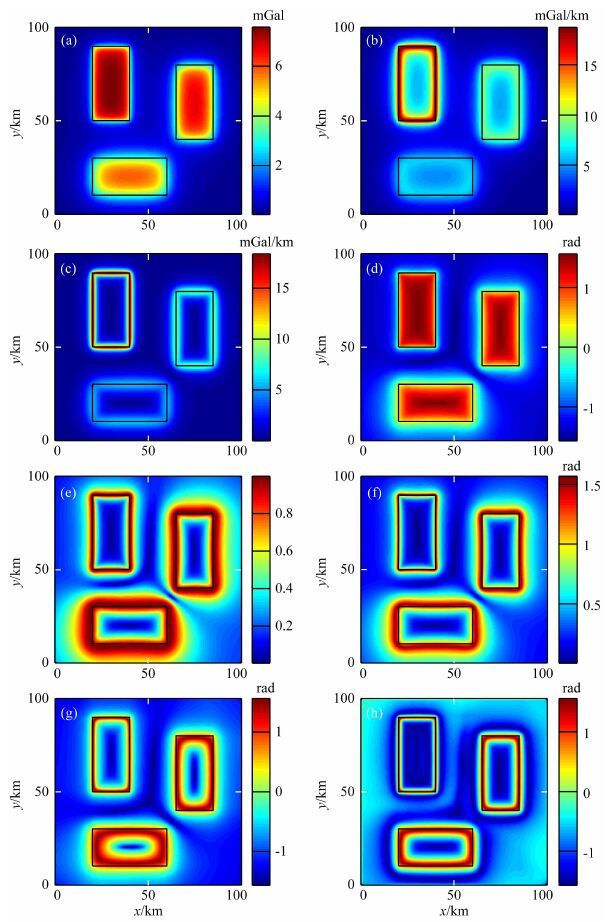
3 模型试验建立一个包含三个埋深不同、大小完全相同的棱柱体产生的重力异常模型,埋藏深度分别为4 km(棱柱体) 1 km(棱柱体) 2.5 km(棱柱体) 所有棱柱体的厚度都为1 km,剩余密度为0.2×103 kg·m-3.图 1为合成模型的平面图和3D图.图 2a为合成的重力异常.图 2b—2h分别为不同边界识别方法ASM、THD、TDR、Theta图、TDX、TAAS和TAVAS的边界检测结果.可以看出,解析信号振幅ASM不能同时描绘浅部和深部的地质体的边界,浅部地质体的边界识别结果振幅较大,深部地质体的边界识别结果振幅较弱.因此,解析信号振幅不能很清晰地描绘深部异常体的边界.总水平导数THD相对于解析信号振幅ASM识别出来的边界结果分辨率高,同样对于深部异常体的边界结 果振幅较弱.然而,方法TDR、Theta图、TDX、TAAS和TAVAS都能有效地均衡不同埋藏深度地质体边界的振幅强度,能同时描绘浅部和深部的边界信息.通过与TDR、Theta图和TDX比较可以看出,TAAS和TAVAS得到的边界结果更加准确,特别是针对深部的地质体.而且,TAAS和TAVAS识别出来的边界结果相对于Theta图和TDX分辨率更高.
|
图 1 (a)模型的平面图;(b)模型的3D图 Fig. 1 (a)Plan view of the model;(b)3D view of the model |
|
图 2 (a)模型一的合成重力异常;(b)ASM边界结果;(c)THD图边界结果;(d)TDR边界结果;(e)Theta图边界结果;(f)TDX边界结果;(g)TAAS边界结果;(h)TAVAS边界结果 Fig. 2 (a)Synthetic gravity anomaly of model 1;(b)ASM of the data;(c)THD of the data;(d)TDR of the data; (e)Theta of the data;(f)TDX of the data;(g)TAAS of the data;(h)TAVAS of the data |
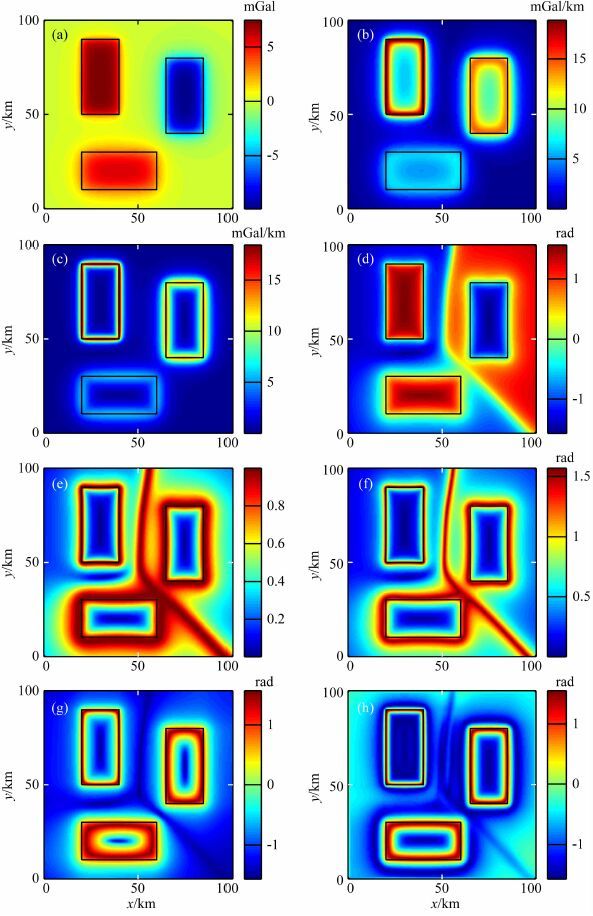
为了验证方法的有效性,本文建立一个更加复杂的地质体模型,其中同时包含正的重力异常和负的重力异常.这里,建立的新模型与上述模型一样,只是棱柱体3的剩余密度为-0.3×103 kg·m-3.图 3a为模型二的合成重力异常.图 3b—3h分别为不同边界识别方法ASM、THD、TDR、Theta图、TDX、TAAS和TAVAS的边界检测结果.可以看出,当重力异常中同时包含正异常和负异常时,传统的边界识别方法TDR、Theta图和TDX将会产生一些额外的错误的边界信息.同样,解析信号振幅ASM和总水平导数THD识别出来深部异常的边界振幅值较小.然而,本文提出的新方法TAAS和TAVAS不仅能清晰地、准确地提取地质体边界信息,而且不产生任何额外的错误的边界信息.并且,TAAS和TAVAS识别的边界有更高的分辨率,特别是TAVAS.
|
图 3 (a)模型二的合成重力异常;(b)ASM边界结果;(c)THD图边界结果;(d)TDR边界结果;(e)Theta图边界结果;(f)TDX边界结果;(g)TAAS边界结果;(h)TAVAS边界结果 Fig. 3 (a)Synthetic gravity anomaly of model 2;(b)ASM of the data;(c)THD of the data;(d)TDR of the data; (e)Theta of the data;(f)TDX of the data;(g)TAAS of the data;(h)TAVAS of the data |
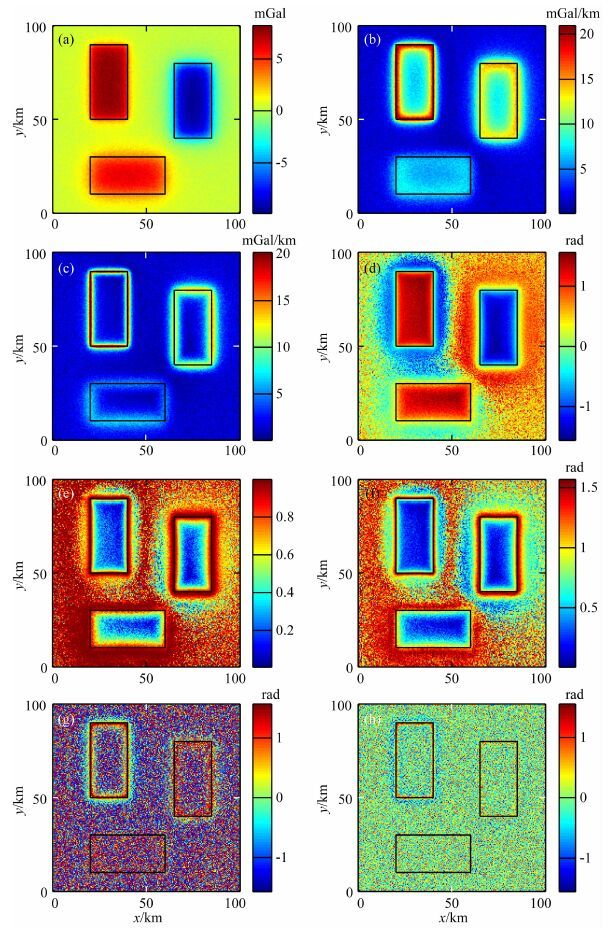
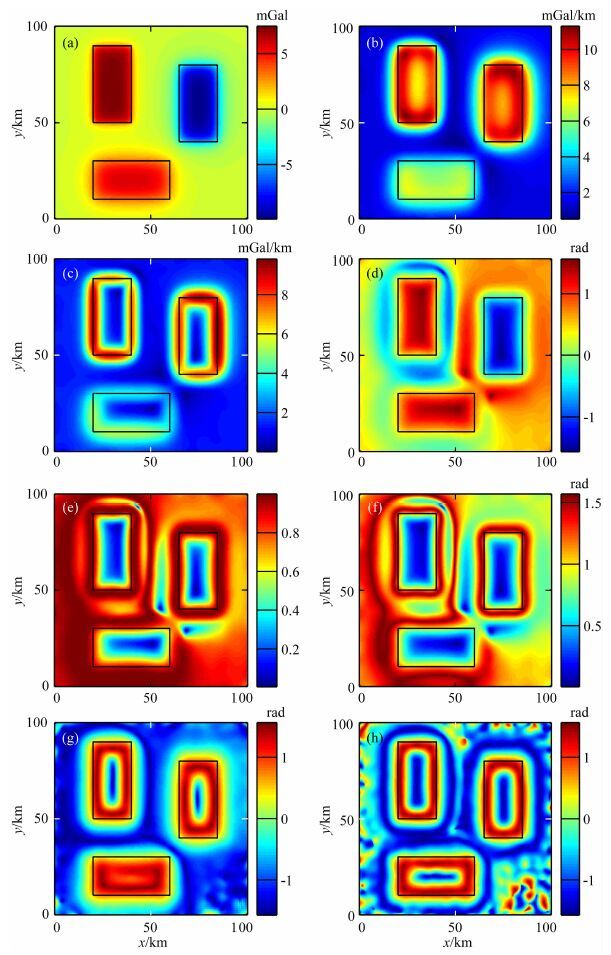
为了进一步验证方法对噪声的抗干扰能力,本文对模型二的合成重力异常数据增加其最大振幅异常的10%的高斯随机白噪声,见图 4a.图 4b—4h分别为 ASM、THD、TDR、Theta图、TDX、TAAS和TAVAS的边界检测结果.通过与图 3相比可以看出,传统的方法ASM和THD受噪声影响较小.方法TDR、Theta图和TDX仍然能清楚地识别出地质体边界.然而,本文提出的新方法TAAS和TAVAS受噪声影响较大,只能识别出浅层地质体的边界.造成这一影响的主要原因是因为它们是以重力异常的二阶和三阶导数来定义的.高阶导数将放大噪声的影响.因此,当测量数据含有大量噪声时,在应用本文提出的新方法之前必须先对测量数据进行滤波处理.设计一个截止波长为300 m的高斯低通滤波对噪声数据进行滤波处理,结果见图 5a.图 5b—5h分别为 ASM、THD、TDR、Theta图、TDX、TAAS和TAVAS 对滤波后数据的边界检测结果.通过比较,传统方法的分辨率都有所降低,特别是传统的均衡滤波器TDR、Theta图和TDX引入了大量的错误边界信息.但是,本文提出的方法都能较准确地识别出地质体的真实边界,而且不引入额外的错误边界信息.
|
图 4 (a)模型二的合成重力异常添加10%高斯噪声;(b)噪声数据的ASM边界结果;(c)噪声数据的THD图边界结果;(d)噪声数据的TDR边界结果;(e)噪声数据的Theta图边界结果;(f)噪声数据的TDX边界结果;(g)噪声数据的TAAS边界结果;(h)噪声数据的TAVAS边界结果 Fig. 4 (a)Synthetic gravity anomaly of model 2 corrupted with 10% Gaussian noise;(b)ASM of the noisy data;(c)THD of the noisy data;(d)TDR of the noisy data;(e)Theta of the noisy data;(f)TDX of the noisy data; (g)TAAS of the noisy data;(h)TAVAS of the noisy data |
|
图 5 (a)噪声数据滤波后的重力异常;(b)滤波后ASM边界结果;(c)滤波后THD图边界结果;(d)滤波后TDR边界结果;(e)滤波后Theta图边界结果;(f)滤波后TDX边界结果;(g)滤波后TAAS边界结果;(h)滤波后TAVAS边界结果 Fig. 5 (a)Filtered gravity anomaly data;(b)ASM of the filtered data;(c)THD of the filtered data;(d)TDR of the filtered data;(e)Theta of the filtered data;(f)TDX of the filtered data;(g)TAAS of the filtered data;(h)TAVAS of the filtered data |
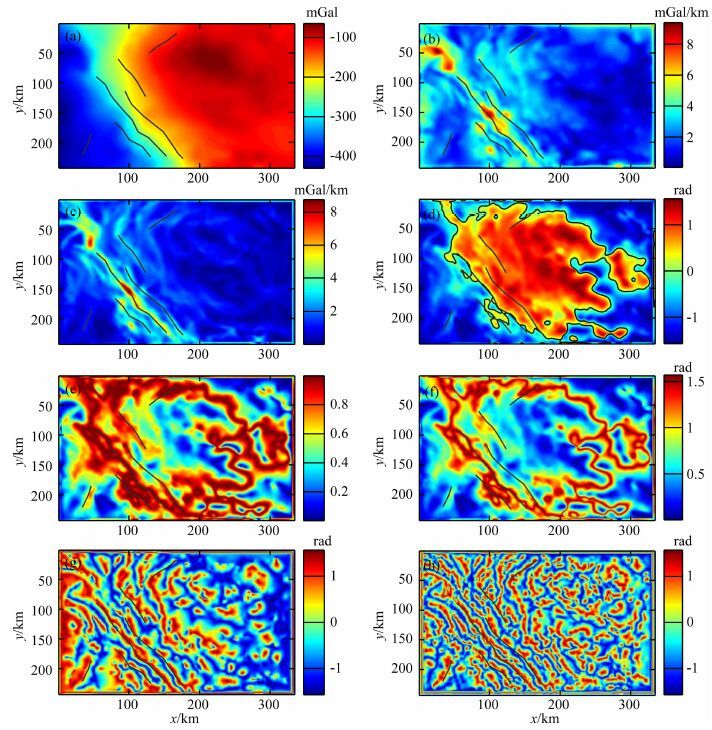
为了测试本文方法在实际资料中的应用效果,对四川盆地的重力异常数据进行处理,图 6a为测量的四川地区重力异常,重力数据采自国家测绘总局编绘的1 ∶ 100万布格重力异常图,并用黑色线在图中标识出已知断裂的水平位置(马国庆等,2012;Yuan and Yu,2015).利用上述方法对重力数据进行处理,来得到该地区的线性构造和地层之间的界线,结果见图 6b—6h.
|
图 6 (a)四川盆地测量的重力异常数据;(b)ASM边界结果;(c)THD图边界结果;(d)TDR边界结果;(e)Theta图边界结果;(f)TDX边界结果;(g)TAAS边界结果;(h)TAVAS边界结果 Fig. 6 (a)Measured gravity anomalies in Sichuan basin,China;(b)ASM of the data;(c)THD of the data; (d)TDR of the data;(e)Theta of the data;(f)TDX of the data;(g)TAAS of the data;(h)TAVAS of the data |
ASM和THD方法对于一些已知断裂的识别能力较差,仅能给出部分已知大断裂的位置,且不是十分清楚,见图 6b—6c.传统方法TDR、Theta图和TDX相对ASM和THD识别能力强,但是也仅能识别出大部分的已知断裂信息,见图 6d—6f.本文提出的新方法TAAS和TAVAS(图 6g—6h)都能很好地识别出所有已知的断裂信息,能较准确地描绘断裂的位置及走势,和与已知断裂一致,且能得到更多的未知的细节信息.
5 结论本文联合解析信号振幅和倾斜角定义了两种新的边界识别滤波器TAAS和TAVAS.该方法中位场数据高阶导数项的引入增加了对测量数据中噪声项的灵敏度.因此,在实际情况下需要事先对数据进行滤波处理.通过模型试验证明了本文方法具有更高的分辨率,且识别出来的边界结果更加准确.当同时包含正、负异常时,本文提出的方法能很好地避免产生错误的边界信息,而传统的均衡滤波方法Theta图和TDX将产生额外的错误的边界信息.通过模型试验和实际数据,证明了本文提出的方法相对于传统的ASM、THD、TDR、Theta图和TDX方法有着更高的分辨率,能更加准确和清晰地给出地质体的边界,而且能给出更多的细节信息,有利于发现小的构造信息.
| Cooper G R J, Cowan D R. 2004. Filtering using variable order vertical derivatives. Computers & Geosciences , 30(5): 455–459. | |
| Cooper G R J, Cowan D R. 2006. Enhancing potential field data using filters based on the local phase. Computers & Geosciences , 32(10): 1585–1591. | |
| Cooper G R J. 2013. Reply to a discussion about the "Hyperbolic tilt angle method" by Zhou et al. Computers & Geosciences , 52: 496–497. | |
| Cordell L. 1979. Gravimetric expression of graben faulting in Santa Fe Country and the Espanola Basin, New Mexico.// New Mexico Geological Society, Guidebook, 30th Field Conference, 59-64. | |
| Cordell L, Grauch V J S. 1985. Mapping basement magnetization zones from aeromagnetic data in the San Juan basin, New Mexico. // Hinzc W J ed. The Utility of Regional Gravity and Magnetic Anomaly Maps. Society of Exploration Geophysics, 181-197. | |
| Florio G, Fedi M, Pasteka R. 2006. On the application of Euler deconvolution to the analytic signal. Geophysics , 71(6). | |
| Hsu S H, Sibuet J C, Shyu C T. 1996. High-resolution detection of geologic boundaries from potential-field anomalies: An enhanced analytic signal technique. Geophysics , 61(2): 373–386. | |
| Li L L, Huang D N, Han L G, et al. 2014. Optimised edge detection filters in the interpretation of potential field data. Exploration Geophysics , 45(3): 171–176. | |
| Ma G Q, Huang D N, Yu P, et al. 2012. Application of improved balancing filters to edge identification of potential field data. Chinese J. Geophys. (in Chinese) , 55(12): 4288–4295. doi: 10.6038/j.issn.0001-5733.2012.12.040. | |
| Miller H G, Singh V. 1994. Potential field tilt—a new concept for location of potential field sources. Journal of Applied Geophysics , 32(2-3): 213–217. | |
| Nabighian M N. 1984. Toward a three-dimensional automatic interpretation of potential field data via generalized Hilbert transforms: Fundamental relations. Geophysics , 49(6): 780–786. | |
| Roest W R, Verhoef J, Pilkington M. 1992. Magnetic interpretation using the 3-D analytic signal. Geophysics , 57(1): 116–125. | |
| Verduzco B, Fairhead J D, Green C M, et al. 2004. New insights into magnetic derivatives for structural mapping. The Leading Edge , 23(2): 116–119. | |
| Wijns C, Perez C, Kowalczyk P. 2005. Theta map: Edge detection in magnetic data. Geophysics , 70(4): L39–L43. | |
| Yuan Y, Huang D N, Yu Q L, et al. 2014. Edge detection of potential field data with improved structure tensor methods. Journal of Applied Geophysics , 108: 35–42. | |
| Yuan Y, Yu Q L. 2015. Edge detection in potential-field gradient tensor data by use of improved horizontal analytical signal methods. Pure and Applied Geophysics , 172(2): 461–472. | |
| Yuan Y, Huang D N, Yu Q L. 2015. Using enhanced directional total horizontal derivatives to detect the edges of potential-field full tensor data. Chinese J. Geophys. (in Chinese) , 58(7): 2556–2565. doi: 10.6038/cjg20150730. | |
| 马国庆, 黄大年, 于平, 等. 2012. 改进的均衡滤波器在位场数据边界识别中的应用. 地球物理学报 , 55(12): 4288–4295. | |
| 袁园, 黄大年, 余青露. 2015. 利用加强水平方向总水平导数对位场全张量数据进行边界识别. 地球物理学报 , 58(7): 2556–2565. | |
 2016, Vol. 59
2016, Vol. 59


