2. 西安交通大学计算地球物理科学系, 西安 710049;
3. 海洋石油勘探国家工程实验室, 西安 710049;
4. 北京数学与信息交叉科学协同创新中心油气勘探与开发平台, 西安 710049
2. Department of computational geophysical science, Xi'an Jiaotong University, Xi'an 710049, China;
3. National engineering laboratory for offshore oil exploration, Xi'an 710049, China;
4. Beijing Center for Mathematics and Information Interdisciplinary Science, Xi'an 710049, China
地震波在传播过程中如果穿过含流体地层,会引起地震波的衰减.因此提取地震资料的衰减属性可以指示地层的含流体特性,这对于直接寻找油气藏有着重要的意义.
在20世纪70—90年代,针对衰减属性的研究工作主要集中于对品质因子Q的定量计算.Q值除了能够指示地层含流体特性外,也可以对地震记录进行有效的反Q滤波补偿(Wang,2008),进而改善地震剖面分辨率.谱比法是常用的Q值定量估计方法之一(Bath,1974),但该方法估计的效果受窗长度的影响很大.此外,受噪声、波干涉等其它因素的影响,准确估算Q值的难度很大.地震波在地层传播时高、低频分量存在衰减差异,在地层含流体时该现象更为明显.因此,Castagna等人提出了在时频域(Mallat and Zhang,1993)定性估算地震波的衰减属性.实际应用效果表明,该方法对地层的含气性有良好的指示作用(Sun et al.,2002; Castagna et al.,2003).在利用时频分析对薄储层含气性进行预测时,时间-频率分辨率至关重要.为此,陈文超等人在小波域利用改进的最佳匹配子波(MBMSW)分析地震波高、低频之间衰减差异(高静怀等,2006;陈文超和高静怀,2007),所得到的衰减特性参数具有较高的时间分辨率及良好的抗噪性能;陈学华等利用S变换(Stockwell et al.,1996;高静怀等,2003)探测与油气有关的低频阴影(陈学华等,2009),有效地刻画了油气储层的岩性边界和空间展布,减小了油气储层检测的多解性;Wang Xiaokai等利用自适应最优核时频表示(AOKTFR)定性描述地震衰减 特性(Jones and Baraniuk,1995;Wang et al.,2013),同时提高了时间及频率分辨率.以上研究均是基于叠后地震资料,在实际地震处理中取得明显的应用效果.
然而,在地震记录的叠加过程中,由地层吸收引起的叠前记录波形变化在受到叠加平均效应后会大幅减弱,进而影响储层衰减参数的预测精度.叠前地震记录是地震信号最原始的记录,包含偏移距、旅行时等丰富信息.为了提高储层预测的精度,一些研究者们选择叠前记录进行分析处理.Zhang Changjun和Ulrych以叠前共中心点道集(CMP)为数据基础,提出了利用峰值频率定量估计Q值的方法(Zhang and Ulrych,2002),该方法的有效性在模型及实际地震资料分析中均得到了验证.由于该研究中假设地震源信号为Ricker子波且利用信号的瞬时频率估算Q值,其应用范围及方法的稳定性均受到了限制.赵静和高静怀等利用小波域包络峰值处瞬时频率法结合层位信息估计Q值(赵静等,2013),研究表明该方法计算精度较高,但方法的准确性依赖于理论子波参数的匹配.李君君和王志章等通过拟合质心频率-传播时间的斜率估算Q值(李君君等,2015),该方法在近地表Q值估算中取得较好的应用效果,但还未能应用于更为复杂的地面地震资料.
在实际叠前资料处理中,受资料低信噪比的影响,定量估计Q值的精度与稳定性受到了很大的限制.因此本文聚焦于在小波域对叠前地震数据的衰减属性进行定性描述,利用地震数据的高、低频分量之间的幅度衰减差异来估计地震衰减:在每个共反射点(CRP)道集中,利用连续小波变换提取高、低频分量的幅度曲线,并利用高、低频幅度曲线所围成的面积刻画地震衰减(即累加道集中每一道信号的衰减),以此反映地层的吸收特性.
2 小波域叠前地震资料衰减参数定性估计 2.1 连续小波变换概述一个地震信号f(t)的连续小波变换可表示为:
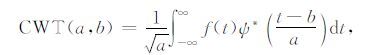
|
(1) |
式中,a为尺度因子,b为时移因子,ψ(t)为母小波函数,ψ(t)的傅里叶变换表示为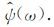
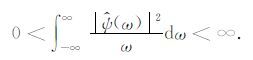
|
(2) |
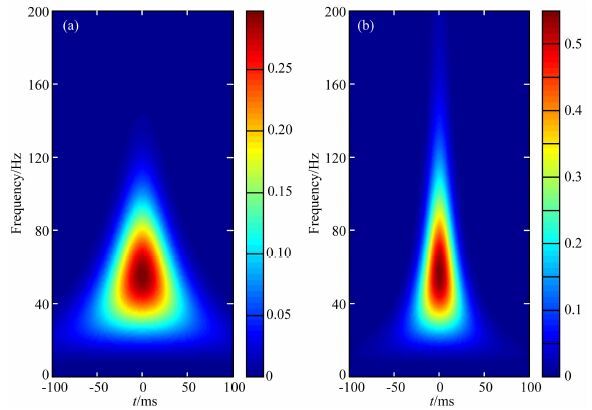
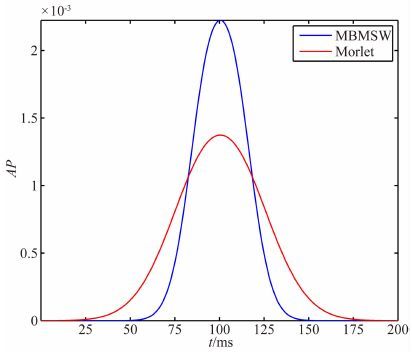
连续小波变换中仅要求母小波满足容许条件,因此实际应用中可以根据具体要求选择小波函数.改进的最佳匹配子波(MBMSW)能够很好地分析振幅快变信号,具有较高的时间分辨率,对于薄储层是一种较好的时频分析工具(高静怀等,2006;陈文超和高静怀,2007).因此,本文选择MBMSW小波作为母小波函数.图 1a与图 1b给出的分别是以Morlet小波及MBMSW小波为母小波对主频为45 Hz的Ricker子波作连续小波变换后的时-频分布图(已经将尺度转换为频率).可以看出采用MBMSW作为母小波所得到的时-频图的时间分辨率明显优于采用Morlet小波作为母小波所得到的时-频分布图.
|
图 1 利用连续小波变换得到的Ricker子波(主频45 Hz)的时频分布图 (a)采用Morlet小波作为母小波;(b)采用MBMSW小波作为母小波. Fig. 1 Using continuous wavelet transform to obtain time-frequency distribution of Ricker wavelet(dominant frequency 45 Hz) (a)Adopting Morlet as mother wavelet;(b)Adopting MBMSW as mother wavelet. |
由于地震波在地层中传播时存在衰减与频散效应,因此地震波的幅度与相位都会发生相应的变化.传播相同距离后,地震波的高频分量比低频分量衰减的更快;另外地震波的高、低频分量的衰减差异会随着储层品质因子Q的减小而增大(Aki and Richards,1980).因而,可以利用地震波的高、低频分量的衰减差异估计地层吸收特性.
|
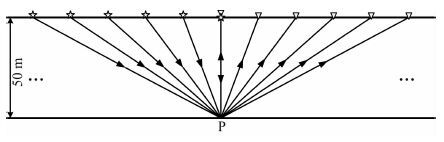
图 2 合成CRP道集的地层模型(五角星对应炮点位置,倒三角对应接收点的位置) Fig. 2 The model for generating CRP gather(star represents the position of shot,and the inverse triangular represents the corresponding receiver). |
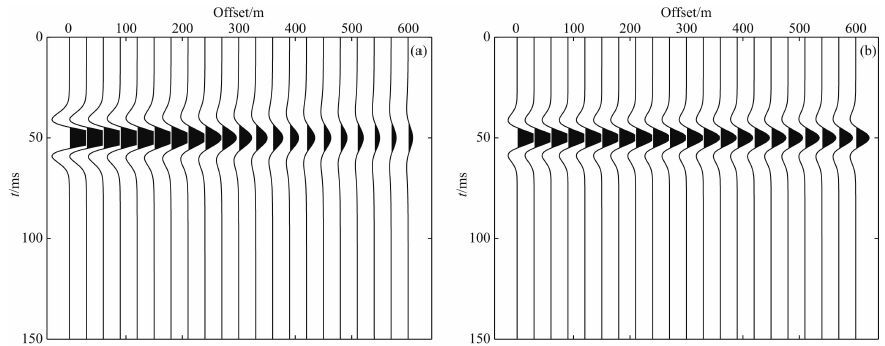
图 2为模拟地层的单层模型,其中层厚为50 m,层速度为2000 m·s-1.利用文献(Zhang and Ulrych,2002)中的方法合成CRP道集(平层模型中CRP道集与CMP道集相同),相邻检波器间隔与相邻炮间隔均为30 m,源信号为主频45 Hz的Ricker子波.Q值分别为30和200时的模拟结果如图 3a与图 3b所示.利用该模型合成数据时忽略几何扩散以及相位等因素的影响且仅考虑一次反射波,则第n个检波器接收到的信号(第n道信号)振幅谱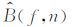
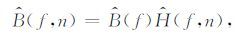
|
(3) |
式中,n=1,2,…,N,N是CRP道集中的总道数,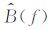
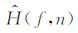
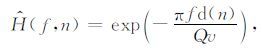
|
(4) |
式中:Q表示品质因子,v是地层速度,d(n)是第n个激发点到第n个检波器的传播距离.如果用l表示检波器间距,h表示层厚,则d(n)可表示为
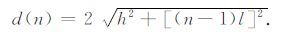
|
(5) |
观察图 3中的两个CRP道集,可以看出信号的能量衰减随着偏移距的增加而增加.另外,由于波在传播过程中高频分量衰减比低频分量衰减的快,随着偏移距的增大,导致信号主频向低频方向移动,在时间轴上表现为子波展宽.比较图 3a与图 3b可以看出,信号衰减以及子波展宽现象在低Q值的CRP道集(图 3a)中尤为明显.这也表明,在低Q值CRP道集中高低频之间的衰减差异大于高Q值CRP道集中的高低频分量之间的衰减差异.因此通过估算高低频分量之间的衰减差异可以定性地指示出地层Q值变化.为了便于分析CRP道集中来自同一反射层的反射波随偏移距的变化,后续分析均采用时差校正处理后CRP道集(如图 4a和图 4b所示).
以上研究表明,对地层吸收特性的定性估计依赖于对CRP道集中信号高、低频分量衰减差异的估算. 在选择高频fH和低频fL时,使得两者满足条件
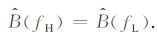
|
(6) |
将图 4所示CRP道集中第n道信号的高、低频分量的振幅分别定义为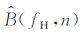
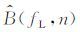
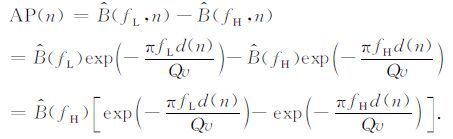
|
(7) |
从公式(7) 可以看出,衰减参数AP(n)值不仅与Q值有关,还与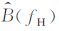
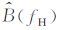
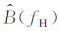
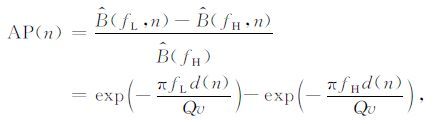
|
(8) |
此时,所求AP(n)除地层传播速度外,只与Q值及传播距离有关.
由于CRP道集中有N道信号,可以估计出N 个衰减参数.将道集中N个衰减参数进行累加作为这个CRP点的衰减参数,记为AP,表达式为
|
图 3 不同Q值下合成的CRP道集 (a)Q=30;(b)Q=200. Fig. 3 Synthetic CRP gathers with different Q factors |
|
图 4 不同Q值下的合成CRP道集经过时差校正后的结果 (a)Q=30;(b)Q=200. Fig. 4 CRP gathers with different Q factors(after time correction) |
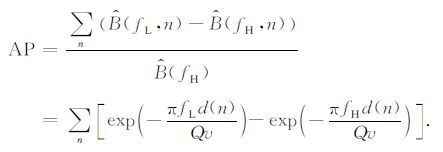
|
(9) |
衰减参数AP的估算,考虑了地震信号的衰减随传播距离影响,同时,对于实际信号,降低了异常道及随机噪声的影响,增强了方法的稳定性.由于采用了多道平均的方法来提高抗噪性能,上式中的AP与Q并没有简单明确的直接对应关系,但可用来定性刻画地层吸收作用.
在CRP道集中,远偏移距地震道在高吸收区域的传播路程大于近偏移距在高吸收区域的传播路程,因此远偏移距地震道上的高低频差异与近偏移距相比较大.然而,与吸收较弱的区域相比,吸收较强的地层区域无论在近偏移距还是远偏移距地震道上高低频差异均比较明显.在实际处理中假设地层的吸收效应在横向变化缓慢,另外本文的主要目标并不是严格估计地层Q值,而是定量估计地层的吸收.在如上基础上,对一定偏移距范围内的高低频进行平均,高低频之间的差值能够定性反映地层吸收的相对强弱.
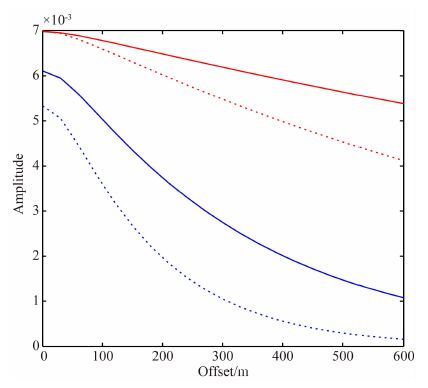
图 5所示为图 4中两个CRP道集对应的高、低频分量的幅度曲线.可以看出,高频幅度曲线比低频幅度曲线衰减更快;随着偏移距的增加,高、低频幅度曲线之间的差异逐渐增大.公式(9) 中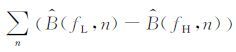
|
图 5 Q值为30和200的CRP道集的高频幅度曲线与低频幅度曲线.红色实线与红色虚线表示Q值为200的CRP道集的低频幅度曲线与高频幅度曲线,蓝色实线与蓝色虚线表示Q 值为30的CRP道集的低频幅度曲线与高频幅度曲线 Fig. 5 High-frequency and low-frequency amplitude curves of CRP gathers with Q=30 and Q=200. Red solid line and red dotted line indicate low- frequency amplitude curve and high-frequency amplitude curve in CRP gather with Q=200,and blue solid line and blue dotted line indicate low-frequency amplitude curve and high-frequency amplitude curve in CRP gather with Q=30. |
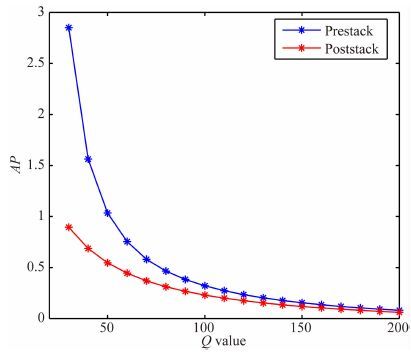
单层模型中其它参数不变,取多组Q值对该叠前道集进行实验,按照公式(9) 求得衰减参数AP,如图 6蓝色星号“*”所示.从图中可看出衰减参数AP值随着Q增大而减小.所以本文定义的衰减参数AP可以指示Q值的变化.图 6中红色星号“*”为利用叠后地震记录估计衰减参数估计结果(叠后数据高低频之差),通过比较可以发现,叠前道集所获得的衰减参数AP随着Q值变化范围更大,这表明在实际地震资料处理中,利用叠前地震数据进行衰减估计可以获得更高的精度.
|
图 6 叠前道集与叠后数据对应不同Q值的衰减参数曲线 Fig. 6 Attenuation parameter curves of synthetic CRPs and stacked data with different Q-factors |
上节利用单层模型合成数据检验了在CRP道集中进行地震衰减定性估计的有效性.考虑到实际叠前地震资料的复杂性(存在有多个反射子波)及时变特性,利用傅里叶变换无法获得信号的时间局部化特性,因此必须选择合适的时频分析工具来获得时频分布以提取高、低频分量.本文利用连续小波变换为时频分析工具并以前文提到MBMSW作为母小波,对地震信号进行分析以获得时频分布.
对于一个实际CRP道集s(t,n),利用前文所述的连续小波变换((1) 式)可以得到其时间尺度分布为
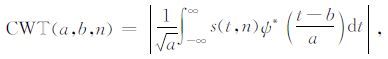
|
(10) |
式中:n表示CRP道集中的道号.由于b为时移因子,与时间具有相同的单位和相同的含义.因此为了描述简单,用变量t表示b,则s(t,n)的时间尺度分布为SW(a,t,n).利用尺度与频率的对应关系(高静怀等,2006),将尺度a变换为频率坐标,即得到时间频率分布为

|
(11) |
σ0为MBMSW的调制频率(单位:弧度/秒).从SW(f,t,n)中提取高频分量SW(fH,t,n)与低频分量SW(fL,t,n),并将小波变换引入到衰减参数定性估计公式(9) 中,得
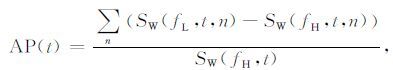
|
(11) |
式中:SW(fH,t)为小波域震源信号的高频分量幅度.在实际地震资料处理中用CRP道集中N道信号高频分量幅度的平均代替源信号的高频分量幅度以提高估计的稳定性,则可得到
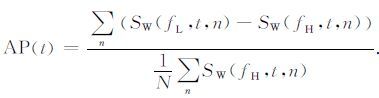
|
(13) |
利用公式(13), 逐CRP道集进行计算,可以得到对应数据的衰减参数AP的剖面.该剖面横轴为CRP号,纵轴为时间,剖面中的亮点区域(大AP值)反映地震波的强衰减区域,可以用来指示地层的吸收异常区(低Q值),进一步可用来指示储层的含油气性.另外,我们对图 2模型生成的合成数据(Q=) 用不同的小波来进行处理(Morlet小波与MBMSW小波)以分析不同小波的时间分辨率.利用Morlet小波和MBMSW小波对合成数据做衰减参数估计,获得实验结果如图 7所示.从图中可以看出MBMSW 小波处理结果的时间分辨率明显高于Morlet小波处理结果,且具有较高的AP值.
|
图 7 不同小波估计的衰减参数分辨率比较(Morlet小波和MBWSW小波) Fig. 7 Comparison of time-resolution of different wavelets |
需要注意的是,在实际资料处理中,地震道集经过动校正之后在远偏移距会产生明显的拉伸现象,影响本文方法对衰减参数的估计.因此,在对实际叠前地震资料处理时,应切除道集中拉伸畸变较为严重的部分,这样可以有效减少动校正的影响且改善衰减参数估计结果.另外,实际叠前数据受噪声等因素影响,信号的幅度变化剧烈,不易直接估算幅度的高、低频差异.所以,在实际数据分析中,可对高、低频幅度曲线进行平滑处理.
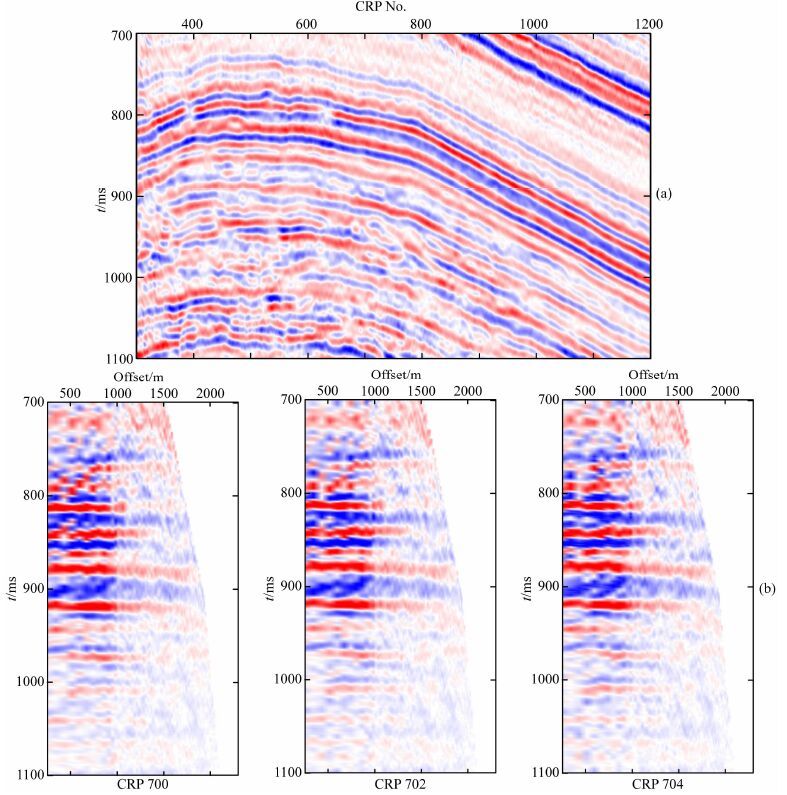
3 实际资料算例图 8a为某油田一条叠后测线,该测线共901个CRP道集,整个叠前数据共87911道信号.有两口探井经过(Well 1与Well ) 测线,分别位于CRP700与CRP800附近,其中Well 1在储层附近获得工业气流,而Well2在储层附近未见工业气流.图 8b为图 8a中第700、702及704个CRP道集(已经过时差校正),可以看出相较于叠后剖面叠前记录显示出更丰富的信息.
|
图 8 实际地震记录(a)叠后地震剖面;(b)叠前地震剖面(CRP道集). Fig. 8 Real seismic records (a)Stacked seismic section;(b)Pre-stack seismic section(CRP gathers). |
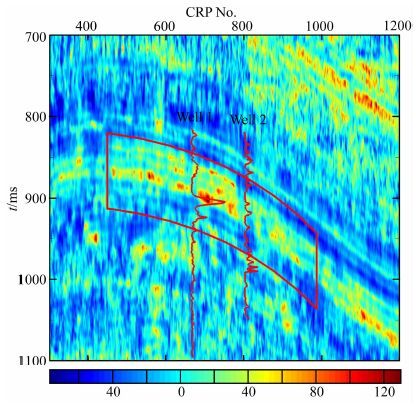
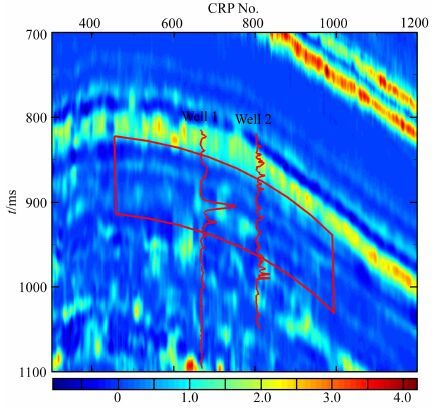
将本文中衰减参数估计方法应用于该叠前数据,得到衰减参数剖面,如图 9所示.图中亮点区域(红色点)为强衰减区域,说明该处吸收异常,表明该段储层含气.图中红色框中指示了储层位置,两条红色曲线分别为Well 1与Well 2的电阻率曲线.可以看出Well1的电阻率曲线高值区域与衰减参数剖面亮点区域位置吻合,而Well2的电阻率曲线没有明显高值,这也同样与衰减参数剖面吻合.
|
图 9 衰减参数(AP)剖面以及Well 1与Well 2的电阻率曲线 Fig. 9 Estimated attenuation parameter(AP)section and resistivity curves of Well 1 and Well 2 |
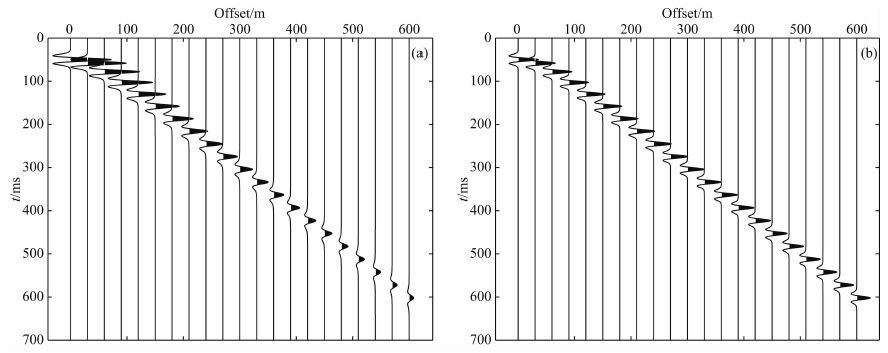
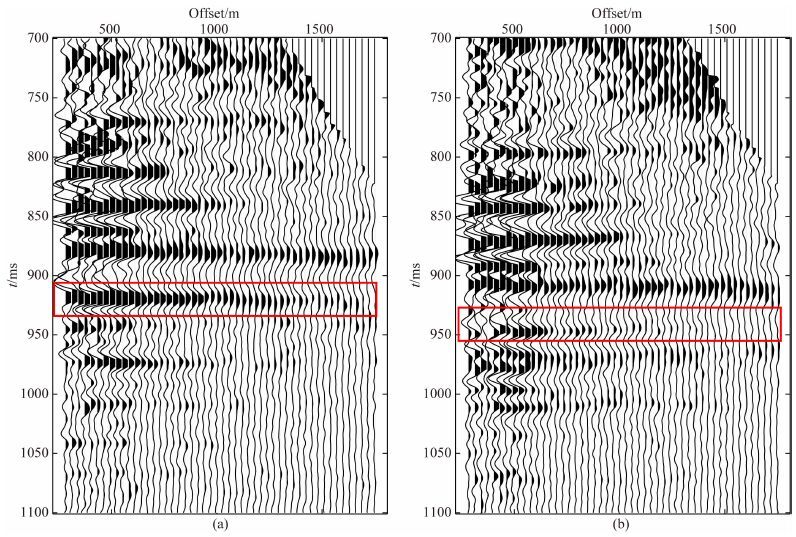
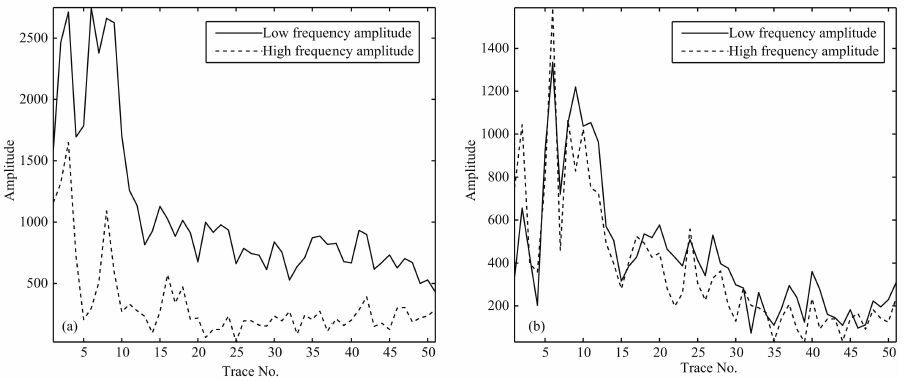
分别分析Well 1与Well 2对应的CRP700与CRP800叠前道集,分别如图 10a与10b所示.图中红色框为储层对应的时间,可以看出,随偏移距的增加,CRP700中信号比CRP800中衰减更明显.对两个CRP道集进行小波分析,提取出相应的高频幅度曲线与低频幅度曲线,如图 11a与11b所示.CRP700 中高低频幅度曲线之间的差异更大,这与该位置获得工业气流非常一致.
|
图 10 叠前地震道集 (a)CRP700;(b)CRP800. Fig. 10 Pre-stacked gathers |
|
图 11 CRP道集高频幅度曲线与低频幅度曲线 (a)CRP 700;(b)CRP 800. Fig. 11 Amplitude curves of high-frequency and low frequency |
我们将本文方法与常用的基于叠后资料衰减估计方法进行了对比.图 12给出了基于AOKTFR的叠后衰减特性剖面(Wang et al.,2013).此方法在储层高含气区域也显示相对高值,但与本文方法结果(图 9)相比,高含气区域异常变化不明显.另外,图 12中箭头所示位置的明显异常区域对应于叠后数据的高振幅区域,与地层衰减无关.本文方法包括了高频分量幅度归一化,因此能够有效地减弱了信号幅度对衰减参数的影响.
|
图 12 基于叠后资料衰减估计方法得到的衰减参数剖面 Fig. 12 Attenuation section obtained by attenuation estimating method for stacked data |
本文提出的基于叠前地震数据的衰减属性定性估计方法是有效的.通过典型的合成数据及实际地震资料分析可以看出,本文方法定义的衰减参数AP用于定性分析地层吸收特性效果良好.相比于以往的基于叠后地震数据衰减参数估计方法,本文方法通过累加CRP道集中每道信号的衰减作为一个CRP点的衰减.由于本文方法考虑了地震信号衰减随波传播距离的变化,因此提高了预测精度和信噪比.另外,通过采用平均高频分量幅度归一化的方法,有效地降低了信号幅值对吸收参数估计精度的影响.
致谢感谢审稿专家和编辑部的大力支持.
| Aki K, Richards P G. 1980. Quantitative Seismology. San Francisco: W. H. Freeman and Company. | |
| Bath M. 1974. Spectral Analysis in Geophysics: Developments in Solid Earth Geophysics. Amsterdam: Elsevier. | |
| Castagna J P, Sun S J, Siegfried R W. 2003. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons. The Leading Edge , 22(2): 120–127. | |
| Ch en, W C, Gao J H. 2007. Characteristic analysis of seismic attenuation using MBMSW wavelets. Chinese J. Geophys. (in Chinese) (in Chinese) , 50(3): 837–843. | |
| Chen X H, He Z H, Huang D J, et al. 2009. Low frequency shadow detection of gas reservoirs in time-frequency domain. Chinese J. Geophys. (in Chinese) (in Chinese) , 52(1): 215–221. | |
| Gao J H, Chen W C, Li Y M, et al. 2003. Generalized S transform and seismic response analysis of thin interbeds. Chinese J. Geophys. (in Chinese) (in Chinese) , 46(4): 526–532. | |
| Gao J H, Wan T, Chen W C, et al. 2006. Three parameter wavelet and its applications to seismic data processing. Chinese J. Geophys. (in Chinese) (in Chinese) , 49(6): 1802–1812. | |
| Jones D L, Baraniuk R G. 1995. An adaptive optimal-kernel time-frequency representation. IEEE Transactions on Signal Processing , 43(10): 2361–2371. | |
| Li J J, Wang Z Z, Zhang Z H, et al. 2015. Quality factor Qestimation based on linear fitting of centroid frequency curve. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 50(2): 254–259. | |
| Mallat S G, Zhang Z F. 1993. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing , 41(12): 3397–3415. | |
| Stockwell R G, Mansinha L, Lowe R P. 1996. Localization of the complex spectrum: the S transform. IEEE Transactions on Signal Processing , 44(4): 998–1001. | |
| Sun S J, Castagna J P, Seigfried R W. 2002. Examples of wavelet transform time-frequency analysis in direct hydrocarbon detection. // 2002 SEG Annual Meeting. Salt Lake City, Utah: SEG, 457-460. | |
| Wang X K, Gao J H, Chen W C, et al. 2013. Seismic attenuation qualitative characterizing method based on adaptive optimal-kernel time-frequency representation. Journal of Applied Geophysics , 89: 125–133. | |
| Wang Y H. 2008. Inverse-Q filtered migration. Geophysics , 73(1). | |
| Zhang C J, Ulrych T J. 2002. Estimation of quality factors from CMP records. Geophysics , 67(5): 1542–1547. | |
| Zhao J, Gao J H, Wang D X, et al. 2013. Estimation of quality factor Q from pre-stack CMP records. Chinese J. Geophys. (in Chinese) , 56(7): 2413–2428. doi: 10.6038/cjg20130727. | |
| 陈文超, 高静怀. 2007. 基于改进的最佳匹配地震子波的地震资料衰减特性分析. 地球物理学报 , 50(3): 837–843. | |
| 陈学华, 贺振华, 黄德济, 等. 2009. 时频域油气储层低频阴影检测. 地球物理学报 , 51(1): 215–221. | |
| 高静怀, 陈文超, 李幼铭, 等. 2003. 广义S变换与薄互层地震响应分析. 地球物理学报 , 46(4): 526–532. | |
| 高静怀, 万涛, 陈文超, 等. 2006. 三参数小波及其在地震资料分析中的应用. 地球物理学报 , 49(6): 1802–1812. | |
| 李君君, 王志章, 张枝焕, 等. 2015. 质心频率线性拟合法估算品质因子Q. 石油地球物理勘探 , 50(2): 254–259. | |
| 赵静, 高静怀, 王大兴, 等. 2013. 利用叠前CMP资料估计介质品质因子. 地球物理学报 , 56(7): 2413–2428. | |
 2016, Vol. 59
2016, Vol. 59


