地球物理学报  2016, Vol. 59 Issue (7): 2641-2649   PDF    
引用本文
石秀林, 孙建国, 孙辉 等. 2016. 基于delta波包叠加的时间域深度偏移. 地球物理学报, 59(7): 2641-2649, doi: 10.6038/cjg20160727.  
SHI X L, SUN J G, SUN H, et al. 2016. The time-domain depth migration by the summation of delta packets. Chinese J. Geophys. (in Chinese), 59(7): 2641-2649, doi: 10.6038/cjg20160727.  
基于delta波包叠加的时间域深度偏移
石秀林 , 孙建国 , 孙辉 , 刘明忱 , 刘志强     
吉林大学地球探测科学与技术学院, 长春 130026
收稿日期 2015-10-10, 2016-03-09 收修定稿
基金项目: 国家自然科学基金(41274120),国家科技专项(Sinoprobe 09-01),国家自然科学基金(41404085,41504084)资助.
作者简介: 石秀林,男,1985年生,吉林大学地球探测与信息技术专业在读博士,主要从事地震偏移成像研究.E-mail:xiulinshi@126.com
通讯作者: 孙建国,男,1956年生,博士,教授,主要从事波动理论与成像技术、地震资料处理方法与解释技术等方面的教学和研究工作.E-mail:sun_jg@jlu.edu.cn
摘要: delta波包可由高斯波束经傅里叶逆变换得到,是高斯波束在时空域的表达.它最早出现在合成理论地震图的研究中,本文将其应用于偏移领域.通过delta波包叠加表达时间域格林函数,可将高斯波束偏移由频率域转换到时间域,再结合Rayleigh积分和激励时间成像条件,本文给出了基于delta波包叠加的深度偏移算法.该偏移算法可在时间域直接计算,但因包含褶积运算,成像时将耗费大量的计算时间.针对这一问题,本文提出了将褶积简化为乘积的近似公式.近似后的偏移算法,不仅保留了高斯波束偏移的优点,而且计算效率得到显著提升.文中通过两个数值算例验证了上述结论.
关键词: delta波包      高斯波束      褶积运算      数值近似      时间域深度偏移     
The time-domain depth migration by the summation of delta packets
SHI Xiu-Lin, SUN Jian-Guo, SUN Hui, LIU Ming-Chen, LIU Zhi-Qiang     
GeoExploration of Science and Technology, Jilin University, Changchun 130026, China
Abstract: Delta packets may serve as building blocks of a wavefield in space-time domain, just as Gaussian beams do in space-frequency domain. This paper will present a depth migration using the summation of delta packets and develop an approximate method that can speed up the convolution between the data and the delta packet. By definition, a delta packet is the inverse Fourier transformation of Gaussian beam under consideration. Thus, the Green's function in the space-time domain can be asymptotically expressed as an integral superposition of delta packets. In the Rayleigh integral, the choice of Green's function determines the migration method. Choosing a Green's function of the delta packet summation form will lead to a new depth migration in space-time domain. The space-time formulation contains a convolution with respect to time between the filtered seismogram and the delta packet, which makes the new depth migration very time-consuming. Here the convolution integration is rewritten in terms of Taylor expansion, and is further reduced to product formula. In the approximate expression of convolution, the time-shifted seismogram only uses multiplication by the term Aattenuation, so that the computational cost is much lower than before approximation. The term Aattenuation indicates attenuation degree of amplitudes, and depends on ratio of parameter Δt (the half width of the integration interval) and imaginary part of the complex travel time. When the value of Δt takes no more than several time sampling intervals, such as Δt=0.005 s, there will be a satisfactory approximation. Numerical tests using the Marmousi and the Sigsbee2A models show that the migration quality for the approximated method is comparable to the one with the exact method. However, the computation time can reduce by about 75%. The depth migration using the summation of delta packets can be recognized as a flexible and effective migration technique. And it is also easily extended to 3-D depth migration and suitable for different kinds of acquisition geometries..
Key words: Delta packet      Gaussian beam      Convolution      Numerical approximation      Time-domain depth migration     
1 引言

20世纪60年代，高斯波束出现在激光物理学的谐振腔研究中(Kogelnik，1965).80年代初，Popov(1982)和Červený等(1982)相继将其引入到勘探地震学，提出了研究地震波传播的高斯波束求和法.高斯波束求和法的基本思路是将高斯波束作为波场分解的元波，经介质传播后，通过叠加求和进行波场重构.该方法的主要优点是在射线管理论的基础上，考虑了能量在垂直于射线管方向的传播，有效解决了经典射线理论中焦散区的振幅计算问题.正因为这个优点，高斯波束求和法在勘探地震学得到了广泛的关注与研究.

20世纪90年代，Hill(1990)将高斯波束应用于偏移成像，提出了基于倾斜叠加的高斯波束偏移方法.该偏移方法通过τ-p变换将波场分解为沿不同方向传播的平面波，经高斯波束传播后，在目标区域叠加成像.Hill的高斯波束偏移算法不仅计算效率高，并且具有可处理多走时，计算焦散区振幅等优点.近些年来，许多勘探地震学者对其进行了研究和改进(Hill，2001; Nowack et al.，2003; Albertin et al.，2004; Gray，2005; Gray and Bleistein，2009; 岳玉波，2011). 但我们同时注意到，若利用高斯波束表达点源波场的格林函数，则无需τ-p变换，就可进行偏移计算.基于此种思路，Popov等(2010)提出了另一种严格遵守Kirchhoff型积分理论的高斯波束偏移算法.它不用进行Hill(2001)和Gray(2005)等人提出的最陡下降近似，理论上要优于Hill的算法，但缺点是耗费更多的计算时间(孙建国，2012).

由于高斯波束是波动方程的时谐解，所以高斯波束的偏移算法主要基于频率域，时间域的研究相对较少.根据 Červený(1983)的推导，当权函数和复振幅与频率无关时，高斯波束经傅里叶逆变换，在时空域存在解析表达式，Červený称其为delta波包.delta波包最早出现在合成理论地震图的研究中(Červený，1983)，本文将其应用于偏移领域，给出了基于delta波包叠加的深度偏移算法：利用delta波包将地震数据分解为局部波场，利用Kirchhoff绕射理论反向延拓至目标点后进行成像.

基于delta波包的偏移算法可在时间域直接计算，并保留了高斯波束偏移的诸多优点，如可计算多走时、计算焦散区振幅等，但因包含褶积运算，成像时将耗费大量的计算时间.针对这一问题，本文根据褶积算子性质，通过泰勒函数展开，将褶积运算简化为乘积运算.理论上，虚部越小，误差越小，近似公式越准确.相反，虚部越大，误差越大.但当虚部变大时，由于delta波包的振幅衰减明显，误差对于叠加结果的影响变小.所以在叠加充分区域，可近似认为成像结果是准确的.在叠加不充分区域，近似误差可能影响成像结果.近似偏移算法，几乎不需褶积运算(仅需对地震记录的时间导数进行一次Hilbert变换)，计算时间仅为近似前的0.2～0.25倍，计算效率得到了显著提升.本文最后通过Marmousi和Sigsbee2a 两个数值算例验证了新偏移算法的成像效果.

2 基本原理 2.1 延拓波场

假设S代表地表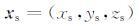，为震源， xg=(xg，yg，zg)为地表检波器的位置，U(xg，t; xs)为检 波器 xg接受到由震源 xs引起的地震反射波场. x′=(x′，y′，z′) 为地下成像点.根据第一种Rayleigh积分，成像点 x 处的延拓波场U(x，x′;t)满足表达式(Born and Wolf，1999；孙建国，2012)

(1)

其中，G(x，x′;t)为检波器 xg到成像点 x′的时间域格林函数.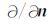代表沿地表外法线方向求导.角标*表示复数共轭.

在高斯波束求和方法中，需要先计算频率域格林函数，再经傅里叶逆变换得时间域格林函数.其中频率域格林函数GGB(x，x′;ω)满足表达式

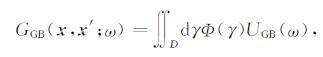
(2)

其中，γ=(γ1，γ2)为射线坐标，通常可以取球坐标系或笛卡尔坐标系，区域D为射线坐标的积分范围.UGB(ω)为单条高斯波束的波场表达式.Φ(γ)为权函数，满足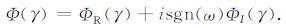

当地表S水平，利用高频渐近方法，忽略掉高阶项，导数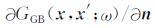可近似为(Popov et al.，2010)

(3)

其中，vg为检波器 xg处的地表速度，θg为检波器 xg处射线出射方向与z坐标轴正方向的夹角.

将公式(3)代入(1)，可得

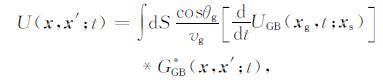
(4)

上式为高斯波束方法计算延拓波场U(x，x′;t)的基本表达式.

2.2 delta波包

与高斯波束求和方法不同，本文在计算时间域 格林函数GGB(x，x′;t)时，采用先对单条高斯波束 进行傅里叶逆变换，再在时间域叠加求和的顺序.

Červený(1983)将高斯波束的傅里叶逆变换称为delta波包(delta packet)，简称DP.它与高斯波束互为傅立叶变换对.

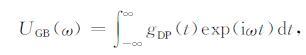
(5a)

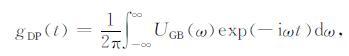
(5b)

其中，gDP(t)为delta波包.

用delta波包叠加表示的时间域格林函数GDP(x，x′;t)为

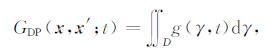
(6)

其中，g(γ，t)满足表达式

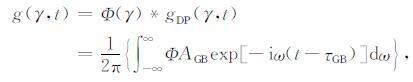
(7)

公式(7)表明利用高斯波束理论中的权函数Φ(γ)、振幅AGB和走时τGB，可计算时间域g(γ，t).为了以后推导方便，去掉角标，使用振幅 A和走时τ表示.这里振幅A和走时τ为复数，满足运动学和动力学射线追踪方程.

将时间域格林函数GDP(x，x′;t)表达式(6)代入延拓波场U(x，x′;t)表达式(4)，可得

(8)

(8)式为delta波包方法计算延拓波场U(x，x′;t)的公式，其中g*(γ，t)满足关系式

(9)

2.3 成像公式

使用激励时间成像条件，当t=0时，成像条件为

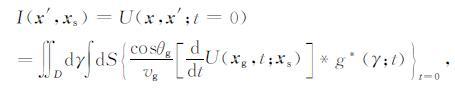
(10)

其中，g*(γ，t)满足关系式(9)，并且

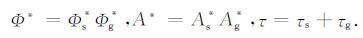
(11)

这里，Φs、As和τs分别代表由震源 xs到成像点 x′的权函数、振幅和走时；Φg、Ag和τg分别代表由检波点 xg到成像点 x′的权函数、振幅和走时.

3 波包解析式

通过之前的推导可知，利用公式(9)—(11)可进行时间域深度偏移.但从数值计算角度考虑，仍存在两个问题：一是delta波包表达式(9)仍需积分计算；二是成像公式(10)中褶积过程会耗费大量计算时间.

二维情况下，权函数 Φ 与频率ω无关.同时，假设振幅 A 也与频率ω无关，则g*(γ，t)在时间域存在解析式(Červený，1983)

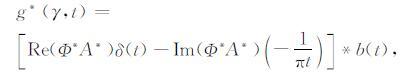
(12)

其中

(13)

这里，函数b(t)为高斯波束中包含复走时τ=τR+iτI项的傅里叶逆变换.需要注意的是，当权函数 Φ 或振幅 A 与频率ω有关时，若权函数 Φ 或振幅 A 的时间域解析式存在，仍可以写成类似公式(13)的形式，但这并不属于本文的研究范围，本文将只讨论权函数 Φ 或振幅 A 与频率ω无关的情况.

本文将b(t)称为褶积算子，褶积算子的性质取决于复走时τ.由于复走时实部τR和虚部τI对算子的影响并不相同，为了便于研究，将b(t)进一步分解为两个子算子，满足b(t)=b1(t)*b2(t)，其中

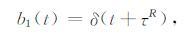
(14a)

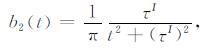
(14b)

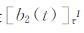
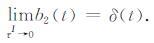
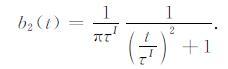
分解后的褶积算子b1(t)只包含τR项，b2(t)只包含τI项.b1(t)的作用就是时移，delta波包的τR对应于经典射线理论中的走时，表示delta波包传播至该点的时间.b2(t)决定了delta波包振幅的衰减程度.由于δ(t)是的弱极限(张元林，2003)，所以当τI→0时，当τI≠0时，对公式(15b)的分子分母同时除以(τI)2，得

(15)

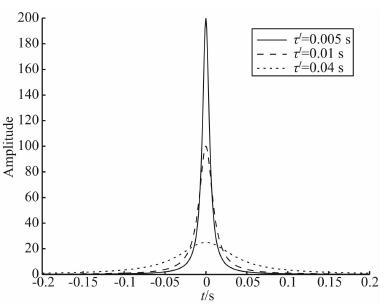
图 1给出了不同τI下褶积算子b2(t)随时间t的变化曲线.结合公式(15)可知，b2(t)为偶函数，峰值为1/πτI.τI越小，峰值越大，能量也越集中于零点附近；τI越大，峰值越小，能量越发散.

图 1 不同τI时褶积算子b2(t) Fig. 1 The amplitude of operator b2(t) with different τI

将 g*(γ，t)的解析式(12)代入延拓波场U(x，x′;t)表达式(8)，可得

(16)

其中

(17)

这里

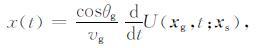
(18a)

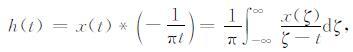
(18b)

h(t)为x(t)的Hilbert变换.公式(16)—(18b)可在时间域直接计算延拓波场U(x，x′;t)，无需傅里叶变换.

4 数值近似

虽然利用公式(16)—(18b)可在时间域直接进行深度偏移，但公式中存在的褶积运算f(t)*b(t)会耗费大量的计算时间.从提升计算效率的角度考虑，本节将根据算子b2(t)的性质，对褶积运算进行数值近似.

4.1 数值积分近似

将子算子(14a)和(14b)代入公式(16)得

(19)

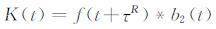
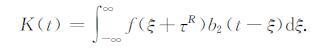
设，将其改写成关于变量ξ的积分形式为

(20)

根据算子b2(t)的性质，b2(t－ξ)关于ξ=t偶对称.所以，假设积分区间为，其中Δt>0，并且当τI→0时，Δt→0.再假设f(ξ+τR)在积分区间 t－Δt，t+Δt 内具有二阶连续导数，在ξ=t处进行一阶泰勒展开，有

(21)

其中，η介于ξ与t之间.所以K(t)可近似为

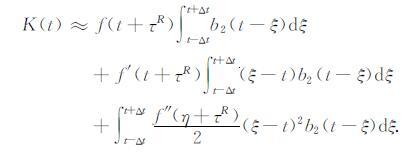
(22)

仔细观察上式，K(t)被写成三项相加求和的形式.因为(ξ－t)在ξ=t处为奇函数，b2(t－ξ)在ξ=t处为偶函数，当τI≠0时，在积分范围[t－Δt，t+Δt]内，第二项的积分值为零.则K(t)可近似为第一项，当τI≠0时，得

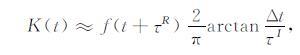
(23)

截断误差由第三项决定，有

(24)

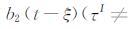
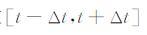
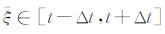
这里，使用了第一积分中值定理(《数学手册》编写组，1979)，若和)在 内有界可积，且b2(t－ξ)在[t－Δt，t+Δt]不变号，则存在，使得公式(24)成立.其中， η=η(ξ)，且η介于ξ与t之间.

4.2 参数取值

通过上节的推导，K(t)被近似为

(25)

其中

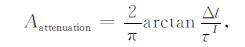
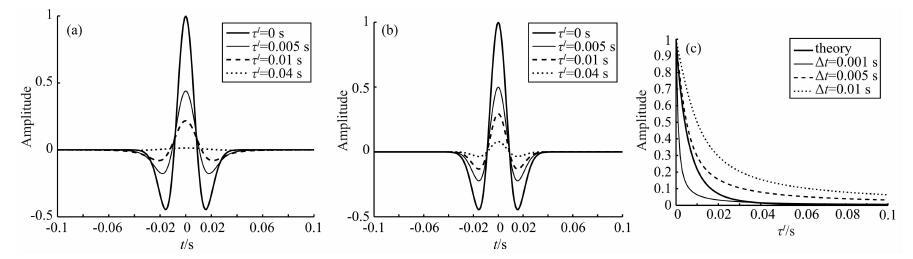
(26)

这里，振幅衰减程度由衰减项A衰决定.A衰为Δt和τI的比值，并且A衰∈[0，1].设β=Δt/τI，β越小，A衰越小，振幅衰减越明显.相反，β越大，A衰趋近于1.

理论上，积分区间[t－Δt，t+Δt]越小，f(t+τR)的一阶泰勒展开越准确，所以本文建议Δt只取几个时间采样间隔.此时，当τI较小时，因为b2(t)能量聚焦于零点附近，所以近似公式(25)仍保有较高精度；当τI较大时，b2(t)的能量发散，近似公式误差变大，但由于delta波包振幅快速衰减，其对叠加结果的影响却变小.综上所述，当Δt只取几个时间采样间隔时，既满足数值近似的精度要求，也满足偏移的需要.

关于Δt的取值，本文还建议最好能保证衰减项A衰与实际振幅衰减程度相近.这里以Ricker子波 为例(如图 2)，褶积计算的K(t)为理论值(见图 2a)，近似公式(25)计算的K(t)为近似值(见图 2b)，图 2c给出了K(t)峰值振幅随τI变化曲线.由图 2c可以看出，随着τI的增大，峰值振幅逐渐变小.Δt越大，振幅衰减越慢；Δt越小，振幅衰减越迅速.当Δt=0.005 s时，K(t)幅值衰减程度与理论值相近.此时，K(t)近似值(图 2b)与褶积值(图 2a)的形态也是一致的.

图 2 (a)K(t)的理论值(不同τI);(b)K(t)的近似值(不同τI)，Δt取0.005 s;(c)K(t)峰值随τI变化曲线(不同Δt) Fig. 2 (a)The theoretical values of K(t) with different τI;(b)The approximate values of K(t) with different τI，Δt=0.005 s;(c)The peak amplitudes of K(t) varies with τI under different Δt
4.3 近似成像公式

将公式(25)、(26)和(17)代入公式(19)，延拓波场U(x，x′;t)满足表达式

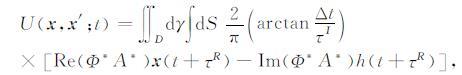
(27)

所以，成像条件I(x′，xs)可重新整理为

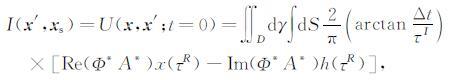
(28)

其中

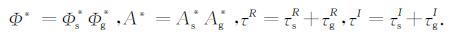
(29)

这里，x(t)和h(t)分别满足公式(18a)和(18b).利用成像条件(28)和(29)可直接在时间域进行深度偏移.近似后的成像条件几乎不需褶积运算(仅需对x(t)进行Hilbert变换得到h(t)，单道地震记录只需计算一次)，计算效率得到很大的提升.

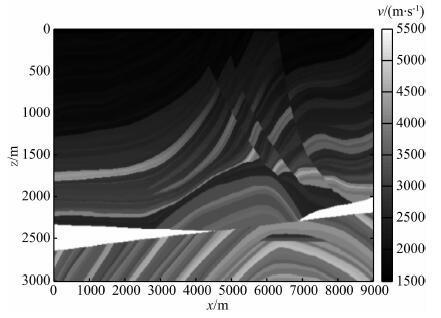
5 数值算例

本节将展示两个数值算例.第一个为Marmousi模型，图 3为速度模型，横向网格节点数为737，网格间距12.5 m；纵向网格节点数为750，网格间隔4 m.使用的地震记录共240炮，第一炮位置在 x=3000 m处，每炮207道，道间距和炮间距均为25 m，中间放炮，两边接收，炮点位置与第104道接收位置相同.每道时间采样点为750个，采样间隔4 ms.

图 3 Marmousi速度模型 Fig. 3 Stratigraphic interval velocity model for Marmousi dataset

图 4为单炮的时间域偏移结果(Δt=0.005 s)，图 4a、4c为包含褶积运算的偏移结果，图 4b、4d为使用近似公式的偏移结果.通过对比可以看出，两种算法的偏移结果基本一致，但在细节处，前者的信噪比要高于后者，图像更为清晰些.

图 4 (a)第100炮褶积运算的偏移结果(x=5475 m)；(b)第100炮近似公式的偏移结果(x=5475 m)；(c)第150炮褶积运算的偏移结果(x=6725 m)；(d)第150炮近似公式的偏移结果(x=6725 m) Fig. 4 (a)The No.100 migrated shot record obtained by using the the exact method(x=5475 m)；(b)The No.100 migrated shot record obtained by using the approximated method(x=5475 m)；(c)The No.150 migrated shot record obtained by using the the exact method(x=6725 m)；(d)The No.150 migrated shot record obtained by using the approximated method(x=6725 m)

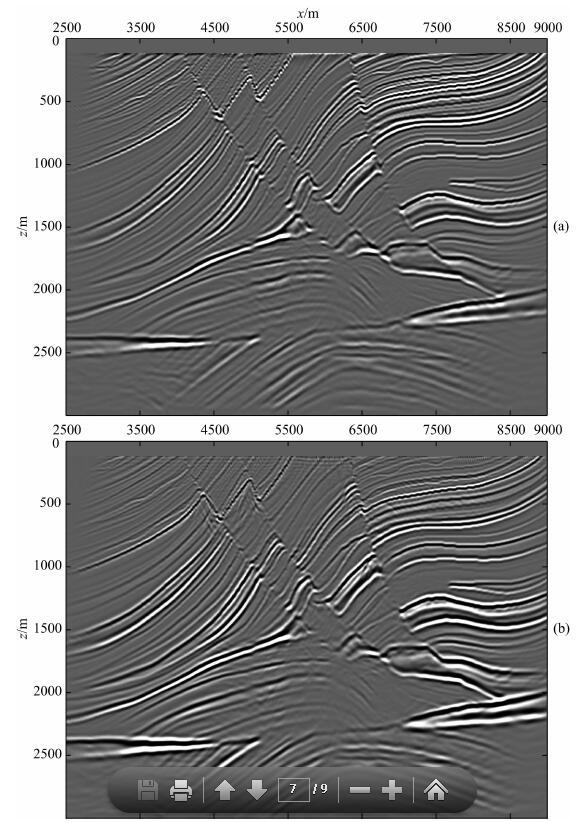
图 5为叠加后的偏移剖面(Δt=0.005 s).可以看出，两种方法偏移结果一致，三个断层与两个背斜构造清晰可见，较浅背斜右侧翼，因为倾角过大，边界模糊.较深背斜中的小储层构造清晰可见.之前单炮记录(近似公式，图 4b、4d)中的噪声，经叠加后被有效压制.表 1给出了两种方法的计算效率(CPU耗时)对比，在使用MPI进行多线程计算条件下，使 用近似公式的计算时间约为近似前的0.2～0.25倍，计算效率得到了明显提升.

图 5 (a)褶积运算的叠加剖面；(b)近似公式的叠加剖面 Fig. 5 (a)Stacked image obtained by using the exact method；(b)Stacked image obtained by using the approximated method
表 1 两种算法的计算效率(CPU耗时)对比(单位：min) Table 1 Efficiency(CPU time)comparison of different algorithms(Unit: min)

第二个算例为Sigsbee2A模型.图 6为速度模 型.横向网格节点数为2133，网格间隔为11.43 m，纵向网格节点数为1201，网格间隔为7.62 m.地震记录共500炮，最大道数为348道，炮间距和道间距均为22.86 m.

图 6 Sigsbee2A速度模型 Fig. 6 Stratigraphic interval velocity model for Sigsbee2A dataset

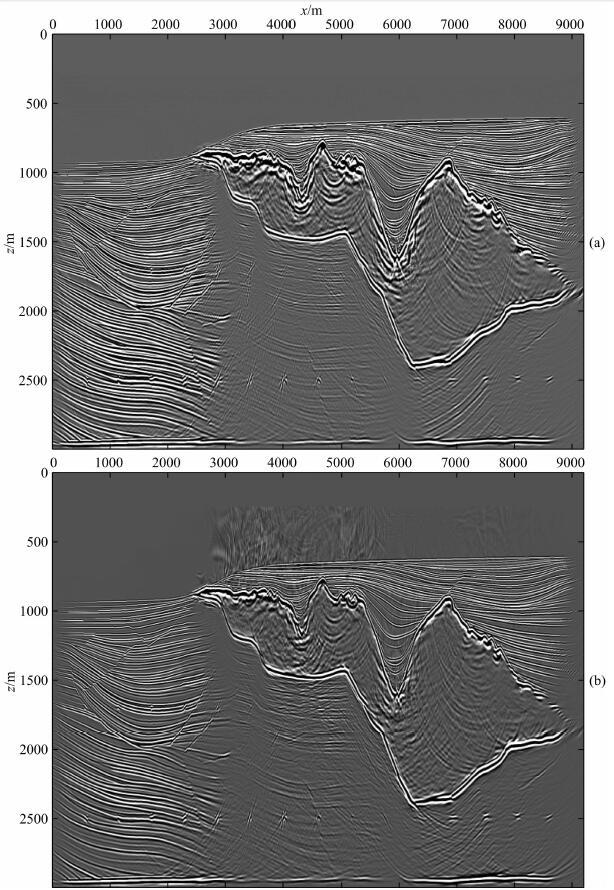
图 7为给出了两种算法的叠加剖面(Δt=0.005 s). 通过对比可以看出，两种方法对盐丘的陡倾边界以 及盐体下断层构造与绕射体进行了较好的成像，但盐体左翼及右翼最深处的下方构造，近似后的成像质量相比近似前，信噪比要低，干扰更大一点，这是由于盐下区域照明不足，delta波包叠加不充分，噪声没有得到有效压制.最后给出两种方法的计算效率(CPU耗时)对比，在使用MPI进行多线程计算 的条件下，近似前的偏移时间为119小时15分，近 似后的偏移时间为25小时13分.

图 7 (a)褶积运算的叠加剖面；(b)近似公式的叠加剖面 Fig. 7 7(a)Stacked image obtained by using the exact method；(b)Stacked image obtained by using the approximated method
6 结论

本文将delta波包应用到偏移领域，给出了基于delta波包叠加的深度偏移算法，并根据褶积算子的性质，进一步将褶积运算简化为乘积形式.在近似公式中，衰减项A衰由Δt和τI的比值β所决定，本文建议Δt的取值为几个时间采样间隔，并最好保证A衰与 实际振幅衰减程度相近.最后，通过Marmousi和Sigsbee2A两个数值实例验证了本文提出的基于delta波包叠加的深度偏移算法，保留了高斯波束偏 移的优点，对复杂介质具有良好的成像能力，并且近似算法的偏移结果与近似前基本一致，但计算时间约为近似前的0.2～0.25倍，计算效率得到显著提升.该偏移算法适用于多种反射地震采集方式(如共炮，共炮检距等)，易于进行面向目标成像，可拓展到3维地震数据偏移，在勘探地震学领域有着广泛的应用前 景.同时，该算法仍存在诸多有待解决的问题，如Δt 的影响，盐下区域成像改善等，需要进一步研究与讨论.

参考文献
Albertin U, Yingst D, Kitchenside P, et al. 2004. True-amplitude beam migration. //74th Annual International Meeting, SEG. Expanded Abstracts, 398-401.
Born M, Wolf E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Cambirdge: Cambridge University Press, 1999 .
Červený V, Popov M M, Pšeník I. 1982. Computation of wave fields in inhomogeneous media—Gaussian beam approach. Geophysical Journal International , 70(1): 109–128.
Červený V. 1983. Synthetic body wave seismograms for laterally varying layered structures by the Gaussian beam method. Geophysical Journal International , 73(2): 389–426.
Compile Group of Mathmatics Handbook. Mathmatics handbook(in Chinese). (in Chinese) Beijing: People's Education Press, 1979 .
Gray S H. 2005. Gaussian beam migration of common-shot records. Geophysics , 70(4): S71–S77.
Gray S H, Bleistein N. 2009. True-amplitude Gaussian-beam migration. Geophysics , 74(2): S11–S23.
Hill N R. 1990. Gaussian beam migration. Geophysics , 55(11): 1416–1428.
Hill N R. 2001. Prestack Gaussian-beam depth migration. Geophysics , 66(4): 1240–1250.
Kogelnik H. 1965. On the propagation of Gaussian beams of light through lenslike media including those with a loss or gain variation. Applied Optics , 4(12): 1562–1569.
Nowack R L, Sen M K, Stoffa P L. 2003. Gaussian beam migration for sparse common-shot and common-receiver data. //73th Annual International Meeting, SEG. Expanded Abstracts, 1114-1117.
Popov M M. 1982. A new method of computation of wave fields using Gaussian beams. Wave Motion , 4(1): 85–97.
Popov M M, Semtchenok N M, Popov P M, et al. 2010. Depth migration by the Gaussian beam summation method. Geophysics , 75(2): S81–S93.
Sun J G. 2012. The history, the state of the art and the future trend of the research of Kirchhoff-type migration theory: a comparison with optical diffraction theory, some new results and new understanding, and some problems to be solved. Journal of Jilin University (Earth Science Edition) (in Chinese) (in Chinese) , 42(5): 1521–1552.
Yue Y B. Study on Gaussian beam migration methods in complex medium [Ph. D. thesis] (in Chinese).. (in Chinese) Qingdao: China University of Petroleum(East China), 2011 .
Zhang Y L. Engineering Mathmatics: Integral Transformation (in Chinese). (in Chinese) Beijing: Higher Education Press, 2003 .
《数学手册》编写组. 数学手册. 北京: 人民教育出版社, 1979 .
孙建国. 2012. Kirchhoff型偏移理论的研究历史、研究现状与发展趋势展望——与光学绕射理论的类比、若干新结果、新认识以及若干有待于解决的问题. 吉林大学学报: 地球科学版 , 42(5): 1521–1552.
岳玉波. 2011. 复杂介质高斯束偏移成像方法研究[博士论文]. 青岛: 中国石油大学(华东).
张元林. 工程数学·积分变换. 北京: 高等教育出版社, 2003 .