2. 中国科学院大学, 北京 100039
2. University of Chinese Academy of Sciences, Beijing 100049, China
大地电磁测深(MT)是一种探测地球深部电性结构的有效方法,它通过在地球表面同步观测天然电、磁场分量,并在频率域根据各分量之间的线性关系获得多种响应函数,如阻抗张量(视电阻率/相位)、倾子等,进而通过反演手段寻找能够满足观测数据并符合物理规律的电阻率模型(Simpson and Bahr,2005).然而,实际观测的MT数据极易受到电流型畸变(Galvanic distortion)的干扰.若不对该畸变进行妥善处理而贸然开展反演,将难以获得真实的地电模型,甚至因此导致错误的解释(Jiracek,1990; 晋光文和孔祥儒,2006).
过去数十年间,国内外同行针对如何消除或压制电流型畸变已开展了大量的理论分析和技术实践,提出了诸多解决方案,其中被广泛使用的是阻抗张量分解方法(Swift,1967; Bahr,1988; Groom and Bailey,1989,1991; Groom and Bahr,1992; McNeice and Jones,2001).这类方法通常假设区域结构可简化为一、二维结构,进而根据阻抗张量/畸变张量的数学/物理特征将畸变从阻抗张量中分解出来,获得基本不受畸变干扰的正常阻抗张量.然而,在实际运用中,这类方法受到两方面的严重制约:首先是其仅适用于较简单区域结构情况(一、二维),其次是其仅能求解部分畸变参数,而对于另外一部分关键的畸变参数(如静位移因子)则无法求取.静态位移效应会造成观测视电阻率曲线发生整体性偏移,一般可采用曲线平移校正、标志层校正、空间滤波、辅助瞬变电磁或大极距直流电测深等方法予以应对(Jones,1988; Pellerin and Hohmann,1990; Sternberg et al.,1988).这些方法在特定环境下具有一定效果,但是均存在不足.比如,很难找到一个普遍适用准则来进行曲线平移,而标志层校正只适用于盆地等特定的地质构造环境,其他空间滤波、瞬变电磁或大极距直流电测深等均需要增加额外的观测.为此,DeGroot-Hedlin(1995)创造性地将静位移和构造走向参数同时引入到二维OCCAM反演中,与电阻率模型一并求解以消除其干扰,取得了较好的效果.
近年来MT三维正反演技术发展迅速,逐渐开始被用于一些实际资料解释中(Zhang et al.,2015;Xiao et al.,2015).在三维区域结构下,电流型畸变对MT观测数据所造成的影响更加复杂和严重,上述现有的张量分解或静校正方法都不再适用,因此发展一套能够配合MT三维反演的畸变消除技术很有必要.已有一些学者对此开展了研究,如Utada和Munekane(2000)利用水平电场与垂直磁场的空间导数关系压制三维区域结构下的电流型畸变干扰.Garcia和Jones(2002)在GB分解的基础上(Groom and Bailey,1989),假设相邻测点遭受不同的畸变影响但反映相同的区域电性结构,利用牛顿法求解三维区域结构中的畸变参数.Bibby等(2005)利用不受电流型畸变影响的相位张量获得地下维度信息,进而采用低维度(一,二维)数据求解畸变参数.Patro等(2013)直接三维反演了相位张量数据,有效压制了畸变干扰,然而由于相位张量数据中不包含幅值信息导致初始电阻率模型的选取对反演结果影响很大.Sasaki和Meju(2006)参考DeGroot-Hedlin(1995)的思路,试图将静位移参数与三维电阻率结果同时反演.然而,在三维区域结构中,由于阻抗张量各分量的模值和相位均受到畸变干扰,仅仅采用静位移参数来描述电流畸变是不够的(Jones,2011).针对这一缺陷,Avdeeva等(2015)将完整的电流型畸变参数引入到三维反演中,采用拟牛顿法将其与电阻率参数同步反演,取得了较好的效果.
本文首先给出了三维区域结构下电流型畸变作用于区域阻抗张量的数学表达形式,并依据大量实测数据分析了电流畸变各参数的大致分布特征.根据上述信息,建立了新的目标函数,进一步采用非线性共轭梯度算法同时反演了三维电阻率结构和电流型畸变参数.三维理论模型测试表明,该算法可以有效压制电流型畸变的影响,获得更接近真实的电阻率模型.
2 电流型畸变 2.1 电流型畸变的物理涵义电流型畸变是由近地表小尺度非均匀体电性界面处的电荷积累所产生的散射场与区域结构所产生的正常场矢量叠加所造成的(Berdichevsky and Dmitriev,1976).假设三维区域背景的电导率分布为σ0(r),而近地表分布着多个局部三维散射体,其中第k个散射体的电导率为σk(r),它与区域电导率的差异为δσk(r)=σk(r)-σ0(r).Chave和Smith(1994)推导了第k个散射体内外任意位置r处的电场E(r)的积分方程解为
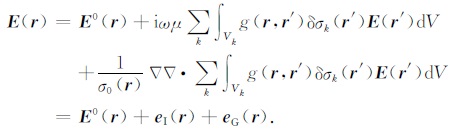
|
(1) |
式中r′为该散射体内任意点的空间位置,E(r′)为r′处的电场矢量,Vk是第k个散射体的体积,g(r,r′)为标量全空间格林函数,积分对近地表所有局部散射体所占据的区域进行.右侧第一项E0(r)通常被称为正常场或区域场,是由我们感兴趣的区域结构所产生的电场.右侧剩余的两项分别为近地表局部非均匀体产生的感应型畸变电场eI(r)和电流型畸变电场eG(r).这两个畸变场的强度取决于近地表局部异常体的体积、形状及其与区域电导率的差异情况.采用波恩近似,可将(1)式积分内的近地表散射体内部的电场E(r′)替换为区域电场E0(r),得到观测电场E(r)与区域电场E0(r)之间的关系:
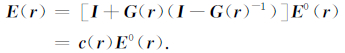
|
(2) |
上式中G(r)为格林并矢张量函数.对于常规大地电磁的观测频段(尤其在低频段),感应型畸变迅速减小,通常忽略不计.因此,畸变张量c(r)一般可以简化为一个与频率无关的二阶实数张量.对于磁场,一般认为在低频段局部电荷积累对观测磁场B(r)的影响一般较小(Chave and Smith,1994),不予考虑.将(2)式代入阻抗张量的一般表达式,可以得到观测阻抗张量D(r)与区域阻抗张量Z(r)二者的关系式如下:
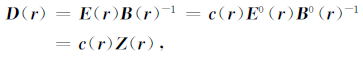
|
(3) |
上式中D(r)和Z(r)均为二阶复数张量,随频率而变化.当观测数据不受电流型畸变影响时,c(r)退化为单位矩阵I(晋光文和孔祥儒,2006).
2.2 三维区域结构中的电流型畸变当区域电性结构是三维时,区域阻抗张量Z的对角、非对角分量均不为零,将(3)式展开有
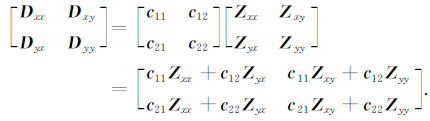
|
(4) |
很明显,观测阻抗张量D各分量的幅值和相位均受到了畸变张量c的影响.上式中包含畸变张量c中4个和区域阻抗张量Z中8个(实、虚部各4个)共12个待求解参数,在不作假设的情况下,无法根据观测阻抗张量D中8个(实、虚部各4个)已知量建立的方程组直接求解这个非线性的欠定问题.
2.3 电流型畸变参数的分布特征2.1节中已证实MT数据受到的电流型畸变通常只与观测位置附近的浅层环境相关,因此具有很强的随机性. Degroot-Hedlin(1995)在将静位移因子引入到二维反演中时,采用了对数域内所有测点所受静态位移之和为零作为约束,测试结果表明当测点间距较小且数量较多时,这种约束是大致合理的. Sasaki和Meju(2006)依据不同地质环境中采集的MT和瞬变电磁(TEM)数据分析了静态位移参数的分布特点,认为其大体呈高斯分布,在高度风化或沉积低阻盖层地区表现为负静态位移(视电阻率曲线下移),而在火山岩分布地区表现为正静态位移(视电阻率曲线上移).Avdeev等(2015)根据经验假设电流型畸变张量的对角分量大体以1为中心呈对称分布,非对角分量大体以0为中心呈对称分布.需要指出的是,上述假设均缺乏充分的实测数据的证实.
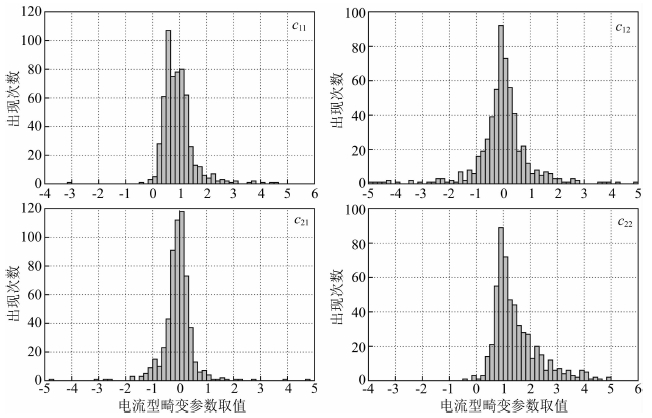
基于美国台阵项目USARRAY(www.usarray.org)所采集的587个测点的高质量MT数据,我们采用相位张量分解方法(Caldwell et al.,2004; Bibby et al.,2005)估算了所有测点遭受的畸变情况,统计结果如图 1所示.这些观测数据覆盖范围广,地质构造环境丰富,具有较好的代表性.分析结果表明,畸变张量的非对角分量(c12,c21)取值以0为中心呈大致对称;对角分量(c11,c22)取值主要集中在1的附近,但在1的右侧具有较长的尾部,在1的左侧出现的次数迅速下降.
|
图 1 USARRAY实测数据所受的电流型畸变参数值分布 非对角分量(c12,c21)取值以0为中心呈近对称分布;对角分量(c11,c22)在1附近集中出现, 但在1的右侧具有更长的尾部 Fig. 1 Histograms of the galvanic distortion parameters of the USARRAY MT data The value of off-diagonal elements symmetrically distributed around zero, while the diagonal elements are concentrated around one but have a longer tail on the right side. |
与其他地球物理反演问题一样,能够拟合一组MT观测数据的电阻率模型和电流型畸变参数都不是唯一的,因此需要根据这两类参数各自的特征在反演过程中进行有效的约束.基于常规MT反演的目标函数,我们重新定义了一个考虑电流型畸变的目标函数:
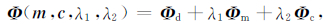
|
(5) |
右侧第一项Φd为观测数据拟合项,其具体形式为

|
(6) |
式中dobs为观测阻抗张量,f(m)为预测电阻率模型m正演计算得到的阻抗张量响应,dpred=cf(m)为受到预测电流型畸变c影响的阻抗张量响应,Wd-1为由观测数据误差构成的协方差加权矩阵(通常为一个对角矩阵).
右侧第二项Φm为电阻率模型约束项,定义为
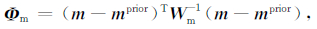
|
(7) |
式中m与mprior分别为预测和先验电阻率模型,在反演开始前需要为m设置一个初始状态,称为初始电阻率模型m0;Wm-1为电阻率模型的协方差矩阵,通常称为粗糙度矩阵,对反演的电阻率模型起到光滑作用;λ1为该项的正则化因子.若无可靠先验信息,一般设置mprior为均匀半空间.
右侧第三项Φc为电流型畸变参数约束项,c与cprior分别为预测和先验畸变参数,在反演开始前同样需要为c设置一个初始状态,即初始畸变参数c0;λ2为该项的正则化因子.从统计学的观点来看,对于大致满足高斯分布的数据采用L2范数解比较合理(王家映,1998).上文2.3节分析已表明畸变张量的对角、非对角分量大致分别以1和0呈近似对称高斯分布,因此我们采用了预测和先验畸变参数二者之差的L2范数这种约束形式,即

|
(8) |
在没有精确的先验信息情况下,同样可根据畸变张量的分布特征将cprior设为单位矩阵I.
3.2 非线性共轭梯度反演算法共轭梯度法(CG)最早由Stiefel(1951)和Hestenes(1951)分别独立提出,Hestenes和Stiefel(1952)给出了用CG方法求解正定系数矩阵的线性方程组的详细过程.经过Fletcher和Reeves(1964)发展后,CG被用于解决非线性最优化问题.Mackie和Madden(1993)首先在三维MT反演中采用了CG方法.Rodi和Mackie(2001)发展了非线性共轭梯度法(NLCG),并将其成功用于MT二维反演中.由于无需直接计算和存储雅克比矩阵且收敛速度较快,NLCG很快得到了广泛应用.Newman和Alumbaugh(2000,注:该工作实际在Rodi和Mackie(2001)之后)首先把NLCG方法用于三维MT反演中,有效降低了三维反演的计算成本.
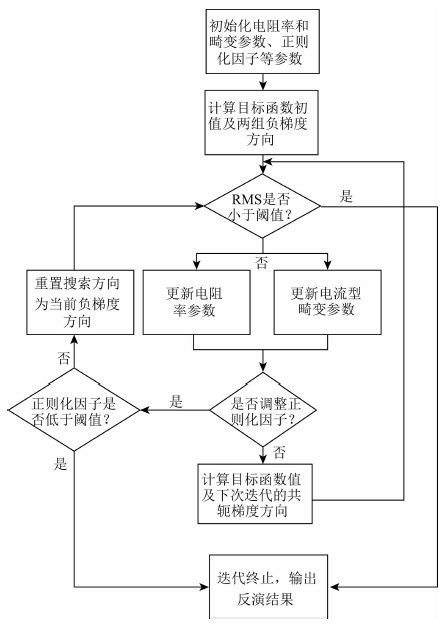
本文算法以目标函数(5)式关于电阻率模型m和电流型畸变参数c的负梯度方向分别作为二组参数的初始搜索方向,之后在每一次迭代中以当前的两组Polak-Ribiere共轭梯度方向作为搜索前进方向(Polak and Ribière,1969).在每一次迭代中,通过三次多项式插值确定两组最优搜索步长,按照两组搜索方向和步长更新两组参数,并通过Armijo条件判断当前迭代中目标函数的下降是否充分,若不充分则需要调整正则化因子,重新计算目标函数值并将搜索方向置为当前的负梯度方向,重新开始迭代直至收敛.算法的详细步骤见图 2.
|
图 2 自适应压制电流型畸变的三维MT反演算法流程图 Fig. 2 Diagram of the 3D MT inversion algorithm with adaptive galvanic distortion suppression |
两组共轭梯度方向的计算是上述算法的一个关键点.将(6)—(8)式代入(5)式可得到目标函数的完整表达形式,将其对电阻率模型m及畸变参数c分别求偏导,可以得到当前的两组梯度方向:
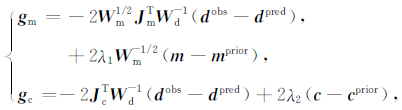
|
(9) |
式中Jm为受到电流型畸变c影响的预测阻抗张量dpred关于电阻率模型m的敏感度矩阵(雅克比矩阵),表达式如下
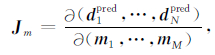
|
(10) |
式中N=Nsite×Nfreq为数据总量(Nsite为测点数,Nfreq为频点数),M为电阻率模型m的电阻率参数总量.对于第i个测点的第j个频点而言,
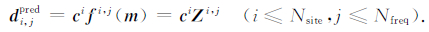
|
(11) |
注意第i个测点所受电流型畸变ci与频率无关,同等作用于该测点的所有频点.由于引起电流型畸变的浅层异常体的规模远小于MT信号波长,MT数据的横、纵向分辨率不足以分辨这些异常体,因此一般认为电阻率模型m与电流型畸变c无关,可得
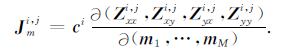
|
(12) |
与常规的NLCG方法相比,本算法计算Jm仅需要将各测点的预测畸变参数与常规的敏感度矩阵相乘即可.对于如何高效计算和存储常规的敏感度矩阵,前人已开展了大量有意义的工作(Mackie and Madden,1993; Farquharson and Oldenburg,1996; 胡祖志等,2006; Egbert and Kelbert,2012).本文采用了Egbert和Kelbert(2012)给出的电磁反演问题中敏感度矩阵的一般表达形式,为了缩小计算量和存储的规模,将敏感度矩阵分解为多个单元分别予以求解.
(9)式中的Jc是电流型畸变的敏感度矩阵,同样对于第i个测点的第j个频点而言,有
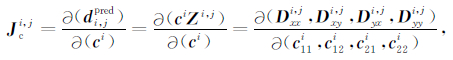
|
(13) |
将(4)式中D各分量的表达式代入上式,并逐项求偏导,即可得单一测点单一频点的Jci,j表达式如下:
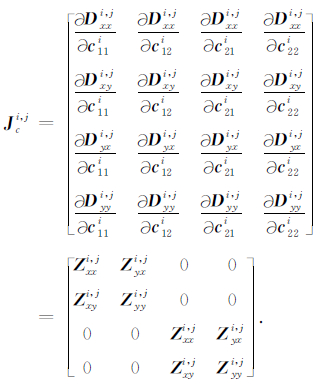
|
(14) |
很明显Jci,j与畸变参数ci本身无关,而只与未受畸变影响的预测阻抗张量Zi,j相关.进一步推广至所有测点和频点,即可求得完整的Jc.
3.3 自适应双正则化因子策略正则化反演的一个难点是如何确定合理的正则化因子.(5)式中的λ1若取值过大将会对模型约束过于严厉,难以拟合观测数据,而取值过小又容易过度拟合,导致模型的稳定性欠佳.本文在引入电流型畸变参数约束项的同时引入了一个新的正则化因子λ2,在反演进程中,需要不断调整这两个正则化因子,保持数据拟合项(Φd)、电阻率模型约束项(Φm)及畸变参数约束项(Φc)三者的平衡.
正则化因子通常可采用无偏风险预测法、广义交叉检验法、L-曲线法等方法确定,但这些方法或需要已知数据的误差水平,或需要进行大量的实验性计算,在三维反演中难以实现.近年来,一种自适应正则化因子的方法在MT反演中得到了广泛应用(Zhdanov,2002; 陈小斌等,2005; 吴小平和徐果明,2000).我们将该方法改进后拓展到双正则化因子情况.正则化因子λ1、λ2的初始值仍需在反演前根据具体情况预设,通常可设置为较大的值以保障在反演前期模型的稳定.在反演迭代过程中,当目标函数下降到小于某一阈值时(通常设置为一极小值),将正则化因子乘以某一衰减因子获得到新的正则化因子,重新计算目标函数值和梯度方向,并将搜索方向置为当前的负梯度方向,以此放宽对模型的约束,进一步拟合观测数据.衰减因子的取值并没有明确的标准,Zhdanov(2002)认为衰减因子的经验取值区间为[0.5,0.9].此外,我们在这个过程中引入了一组更新效率因子δm和δc:
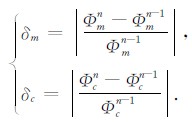
|
(15) |
式中δm和δc分别为电阻率模型和畸变参数的更新效率因子.当算法判断需要衰减正则化因子进一步拟合观测数据时,通过比较当前的两组更新效率因子自适应地判断是衰减λ1还是衰减λ2.如果电阻率模型更新效率优于畸变参数(即δm>δc),衰减λ2以放宽对畸变参数的约束,反之衰减λ1以放宽对模型参数的约束.通过采用上述自适应调整正则化因子策略,算法既能满足对观测数据的高效拟合,又能保障电阻率模型和畸变参数的稳定.
4 三维理论模型测试 4.1 模型设置与响应数据图 3所示为一个理论三维电阻率模型(mtrue).在100 Ωm的背景半空间中分布着三个电阻率分别为10 Ωm、500 Ωm和5000 Ωm的异常块体.采用交错网格有限差分算法(Staggered-Grid Finite Difference method)作正演计算(Mackie and Madden,1993),共得到225个测点的全阻抗张量数据(周期范围为1~1000 s,周期数为8).该数据不含电流畸变成分,下文中称为正常数据.由于理论模型测试的主要目的是探讨新方法在压制电流型畸变上的有效性,所以该数据中未加入任何人为噪声.

|
图 3 三维理论模型示意图 (a) 平面视图; (b) 沿测线P1的剖面视图; 白色小圆点为225个MT测点; 黑色虚线为选取的穿过模型的测线P1,白色大圆点S1为选取的一个代表性测点. Fig. 3 Sketch map of the 3-D synthetic model (a) Plan view; (b) Cross-section along the profile P1. Small circles are the location of 225 MT sites; the black dashed line represents a selected profile P1, the bigger circle S1 marks a selected site. |
为了便于比较分析,所有反演方案均采用如下设置:
电阻率模型:正、反演模型网格大小均为21×28×13,初始电阻率模型(m0)和先验电阻率模型(mprior)均为100 Ωm的均匀半空间.理想状态下,反演所得最终预测模型(m)将与理论模型(mtrue)一致.若将理论电阻率模型(mtrue)替换m代入式(7),可以得到Φm的理想值(Φmtrue)为2.761.
电流型畸变参数:根据图 1所示的电流型畸变参数的分布特征,我们随机生成了电流型畸变参数ctrue(图 7a).初始电流型畸变(c0)和先验电流型畸变(cprior)均设为单位矩阵I.理想状态下,反演所得最终预测畸变参数(c)将与ctrue一致.若将理论畸变参数(ctrue)替换c代入式(7),可以得到Φc的理想值(Φctrue)为0.094.另外,若观测数据未受到畸变影响(即ctrue为单位矩阵),此时Φc的理想值(Φctrue)为0.
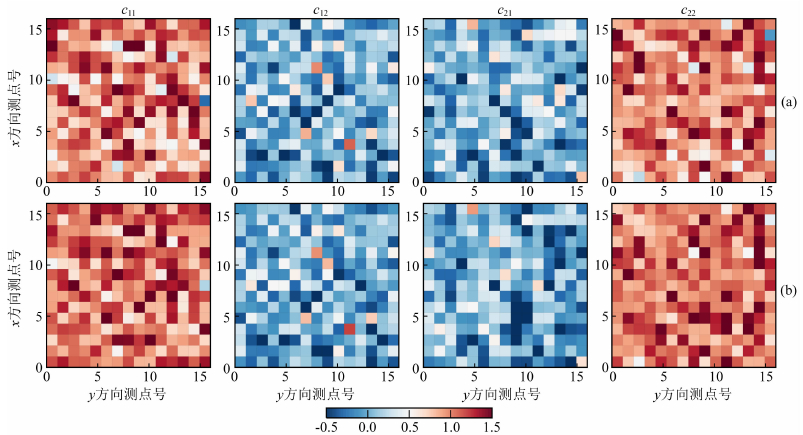
|
图 7 比较所有测点受到的电流畸变理论值与方案4所得预测值 (a) 电流型畸变参数理论值(ctrue); (b) 本文方法预测的电流型畸变参数(cpred). Fig. 7 Comparison of theoretical and predicted galvanic distortion values (a) Theoretical galvanic distortion values (ctrue); (b) Galvanic distortion values predicted by our new inversion algorithm (cpred). |
反演数据:采用全分量阻抗张量数据,各分量数据误差均设置为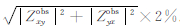
预测电阻率模型和理论模型的正演响应相等,由(6)式可得Φd为0.然而实际上,预测模型和理论模型不可能完全相等,因此通常将Φd等于1作为理想拟合值(即两者响应值之差同等于误差值).理论模型测试涉及到两类数据:
(1)正常数据:由4.1节所示模型的正演计算所得,不含电流畸变成分和任何噪音;
(2)畸变数据:将随机生成的理论畸变参数(ctrue)作用于正常数据产生的受畸变的数据(称为畸变数据).
两类反演方法:
(1)不考虑电流型畸变因素的常规三维反演方法(Kelbert et al.,2014)(称为常规方法);
(2)考虑电流型畸变因素的三维反演算法(本文方法).
测试中共设计了4种测试方案,方案1和方案2分别为常规方法和本文方法对正常数据的反演,目的是检测在无畸变条件下(即均采用正常数据)本文方法与常规方法所得结果的一致性.常规方法的可靠性已经过了大量的测试,若方案1和方案2的结果相同或接近,则表明本文方法在面对正常数据时是可靠的.方案3和方案4分别为常规方法和本文方法对畸变数据的反演,目的是表明在面对畸变数据时的常规方法的局限性以及本文方法的有效性.四种测试方案的具体情况见表 1.
|
|
表 1 四种反演方案下目标函数中各项的变化情况 Table 1 Variation of the different terms in the objective function for the four inversion strategies |
方案1:常规方法反演正常数据
方案1的目的是检测常规方法在数据未受到电流型畸变干扰情况下的反演效果.将正常数据和先验电阻率模型(mprior)的响应数据代入(6)式,可以得到数据拟合项(Φd)的初值为6.589.经过17次迭代,随着预测电阻率模型逐渐接近理论模型,Φd的值由6.589减小为1.003(图 4a中的黑色实线),达到理想拟合值1(图 4a中的黑色虚线),满足拟合条件,迭代正常终止.电阻率模型约束项(Φm)的值反映了电阻率模型的粗糙度,它的初值为0(初始和先验电阻率模型相同,均为均匀半空间),在迭代过程中随着电阻率模型逐渐偏离先验电阻率模型,Φm增大至0.455(图 4b中黑色实线),趋于其理论值2.761(图 4b中黑色虚线).图 5b、6b分别展示了方案1反演所得电阻率模型沿P1测线的剖面图及不同深度的切片图,与理论模型(图 5a、6a)对比,除了三个异常体底部由于MT方法的特性无法得到精确约束外,电阻率大小和尺度都得到了较好的还原,尤其是各块体之间的横向电性分界面清晰可辨,表明常规方法对正常数据的反演是正确有效的.
|
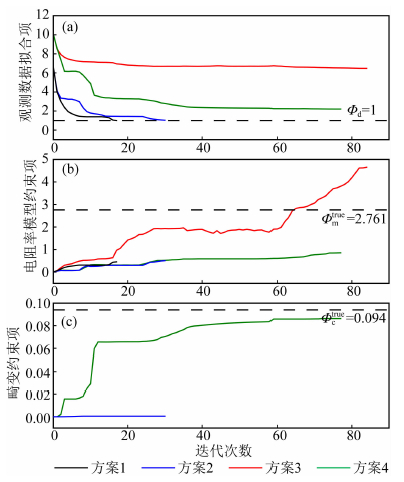
图 4 四种反演方案下Φd,Φm和Φc三项随迭代次数的变化情况 (a) 数据拟合项(Φd); (b) 电阻率模型约束项(Φm); (c) 电流型畸变参数约束项(Φc).黑色虚线为各项的理想值. Fig. 4 Variation of Φd, Φm and Φc versus iteration number for the four different inversion strategies (a) Data misfit term (Φd); (b) Resistivity model constraint term (Φm); (c) Galvanic distortion constraint term (Φc). The black dashed lines represent the theoretical values of these terms. |
|
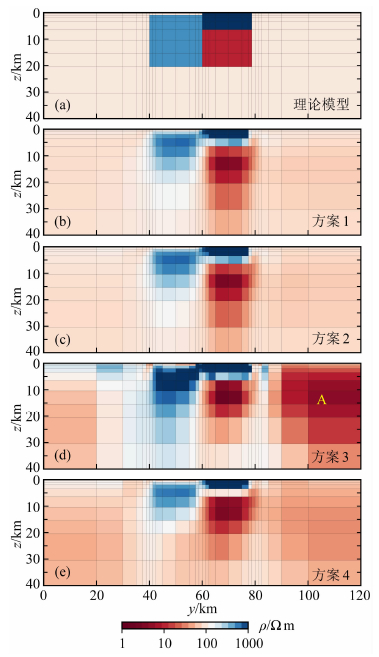
图 5 比较四种反演方案所得模型沿测线P1的电阻率剖面图 (a) 理论模型; (b) 方案1所得反演结果,较好还原了三个异常体; (c) 方案2所得反演结果,与方案1基本一致; (d) 方案3所得反演结果,严重偏离理论模型(如图中的虚假低阻异常A); (e) 方案4所得反演结果, 与方案3相比更接近理论模型, 畸变得到有效压制. Fig. 5 Comparison of resistivity cross-sections along the profile P1 derived from the four inversion strategies (a) Synthetic model; (b) Inversion result derived from strategy 1 (conventional inversion of the undistorted data); (c) Inversion result derived from strategy 2 (new algorithm inversion of the undistorted data); (d) Inversion result derived from strategy 3 (conventional inversion of the distorted data); (e) Inversion result derived from strategy 4 (new algorithm inversion of the distorted data). |
|
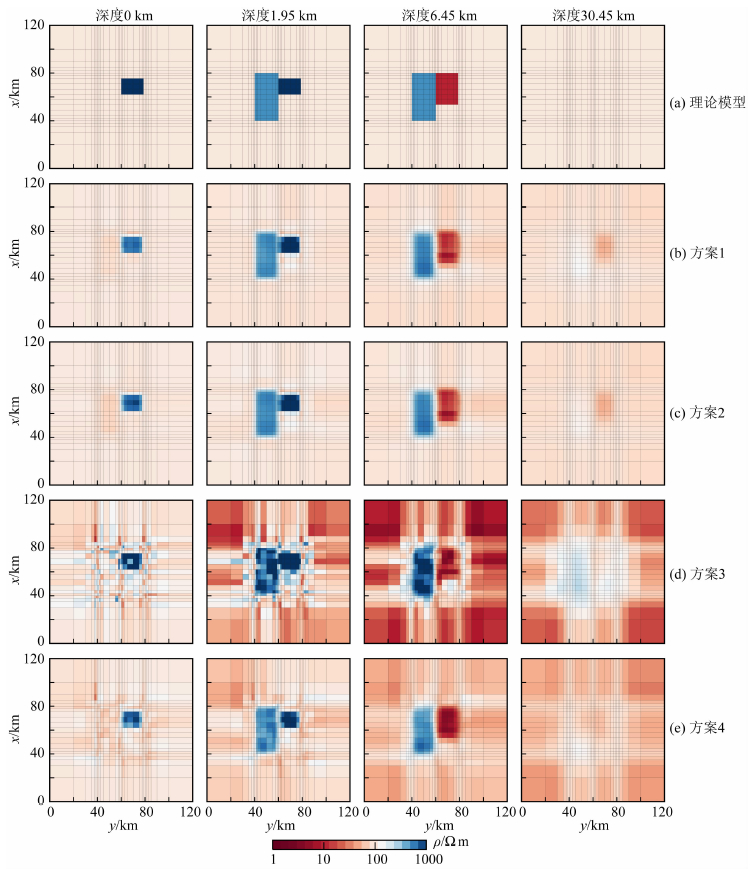
图 6 比较四种反演方案所得电阻率模型在不同深度的水平切片图 (a)—(e)与图 5相同. Fig. 6 Comparison of horizontal resistivity slices at different depths derived from the four inversion strategies (a)—(e) same as in Fig. 5. |
方案2:本文方法反演正常数据
采用本文方法同时反演电阻率模型参数与电流型畸变参数时,所面临的一种风险是可能会将一些观测数据中包含地下电性结构的信息误判为畸变作用,从而导致真实的电性结构被掩盖或者扭曲,这相当于方法本身带入了某种不确定的噪声.因此,有必要验证当数据未受畸变干扰时本文方法是否能够同样稳定地还原真实电性结构.将λ2的初值设为600,初始畸变张量(c0)和先验畸变张量(cprior)均设为单位矩阵I,其余参数与方案1保持一致.经过30次迭代后,该项由6.589减小为1.036(图 4a中蓝色实线),同样达到预期目标,反演终止.电阻率模型约束项(Φm)的终值为0.508(图 4b中蓝色实线),接近方案1结果.由于数据未受到任何畸变影响,整个反演过程中畸变参数约束项(Φc)保持为一接近于0的极小值(图 4c中的蓝色实线),符合实际.电阻率模型反演结果如图 5c、6c所示,与方案1反演结果(图 5b、6b)基本一致,三个异常体均得以成功还原,说明在没有畸变时本文方法与常规方法是一致的,没有带入附加噪声,也没有丢失有效信息.
方案3:常规方法反演畸变数据
将畸变数据和先验电阻率模型(100 Ωm的均匀半空间)的响应数据代人(6)式,得到数据拟合项(Φd)的初值为10.061.其他参数与方案1相同.经过84次迭代后陷入局部最优,反演被强行终止.数据拟合项(Φd)最终减小至6.475(图 4a中红色实线),远大于理想值1(图 4a中黑色虚线),数据拟合质量差;电阻率模型约束项(Φm)的终值为4.651(图 4b中红色实线),远大于理论值2.761(图 4b中黑色虚线),表明反演过程中常规算法对电阻率模型的约束基本失效.同时,三个异常块体的形态和电阻率幅值均遭受到严重的畸变,深部背景空间中出现了大范围的虚假低阻区域(如图 5d中的A),并且模型浅层出现了大量虚假的小异常体(图 6d).这说明,当观测数据含有电流型畸变时,常规方法的反演结果偏离真实结构.
方案4:本文方法反演畸变数据
反演参数与方案3完全相同,采用本文方法经过77次迭代后,数据拟合项(Φd)由10.061降低为2.210(图 4a中绿色实线),虽然未达到理论目标值1,但相较于方案3所得最终值(6.475),数据的拟合程度得到了显著改善;电阻率模型约束项(Φm)(图 4b中绿色实线)最终值为0.855,畸变参数模型约束项(Φc)(图 4c中绿色实线)的最终值为8.635×10-2,均趋近于理论值,表明电阻率模型和电流型畸变参数都得到了有效地约束.从反演的电阻率模型来看,尽管数据受到了畸变的干扰,本文方法仍较好地还原了理论模型中的三个异常体.与常规方法(方案3)的结果(图 5d,图 6d)比较,本文方法的结果(图 5e,图 6e)更接近理论模型,表明反演质量得到了明显改善.
4.2.2 电流型畸变参数比较分析图 7比较了所有测点所遭受的理论电流型畸变参数(ctrue)与本文方法预测的电流型畸变参数(cpred),二者整体上具有较好的一致性,说明本文方法有效地还原了电流型畸变参数.这一点对于评价本文方法的有效性相当重要,在反演过程中,电流型畸变成分如果未能得到有效的识别和还原,势必将参与到电阻率模型的还原中,从而导致电阻率模型的畸变.
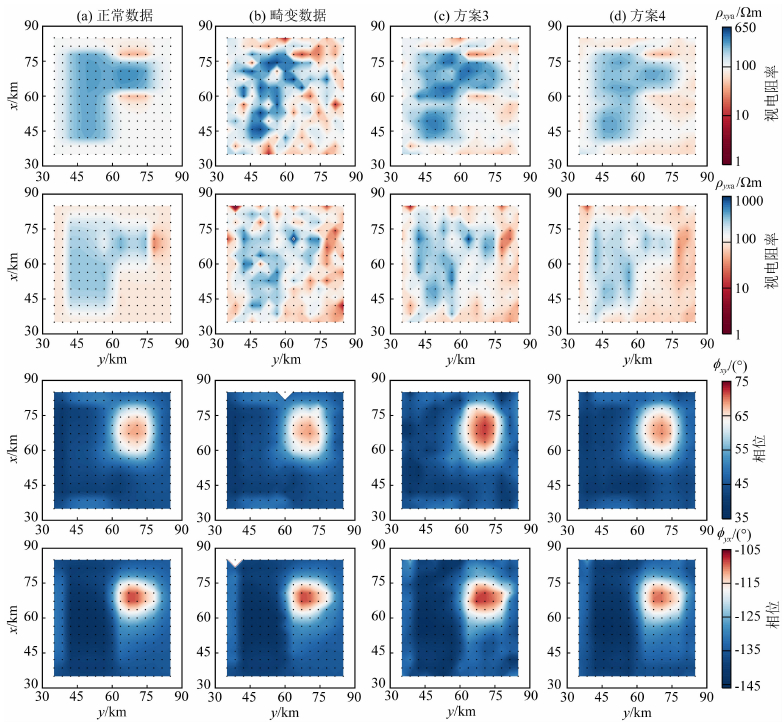
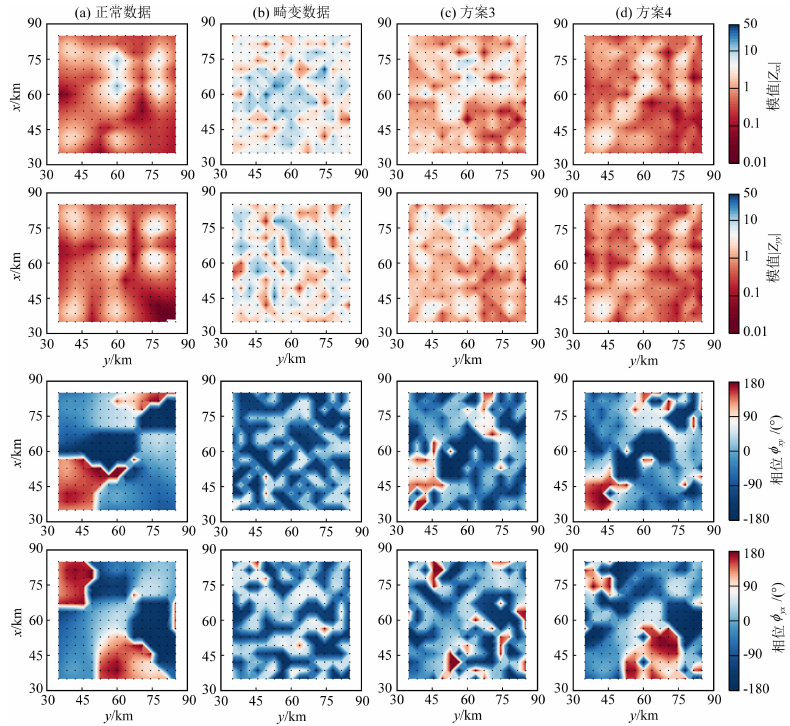
4.3 数据拟合分析仅根据数据拟合项(Φd)的取值情况并不能全面、真实地反映数据的拟合程度.图 8、图 9分别给出了所有测点阻抗张量的非对角和对角分量在周期1.389 s处的视电阻率和相位平面图.对比正常数据(图 8a,图 9a)和畸变数据(图 8b,图 9b),可以看出当三维区域阻抗张量受到畸变时,对角和非对角分量的视电阻率和相位均受到不同程度的影响,特别是对角分量受到的影响更严重.比较图 8b和图 8a,非对角分量的视电阻率受到畸变的干扰比较明显,而相位受到的影响较小,这说明即使在三维结构中,非对角分量仍主要表现为静态效应特征(即幅值变化大,而相位不变或变化很小).比较图 9b和图 9a,对角分量的模值和相位同时受到严重的畸变干扰,这是由于对角分量的模值较小,更容易受到电流型畸变的干扰.采用常规算法反演畸变数据时(方案3),数据的拟合程度很差(图 8c对比图 8a;图 9c对比图 9a).面对同样的畸变数据,本文方法显著改善了数据的拟合质量(对比图 8d和图 8a).即使对于受畸变影响严重的对角分量,本文方法的拟合质量也比常规方法好很多(对比图 9d和图 9a).
|
图 8 比较周期1.389 s处方案3和方案4预测模型响应的非对角分量拟合情况 (a) 正常数据; (b) 畸变数据; (c) 方案3预测的模型响应; (d) 方案4预测的模型响应. Fig. 8 Comparison of the off-diagonal data fits for strategy 3 and 4 at period 1.389 s (a) Synthetic data; (b) Distorted data; (c) Predicted responses by strategy 3; (d) Predicted responses by strategy 4. |
|
图 9 比较周期1.389 s处方案3和方案4预测模型响应的对角分量拟合情况 (a)—(d)与图 8相同. Fig. 9 Comparison of the diagonal data fits for strategy 3 and 4 at period 1.389 s. (a)—(d) same as in Fig. 8. |
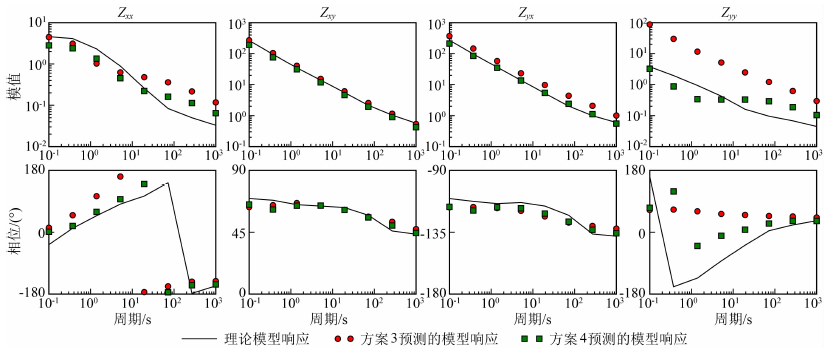
为了分析数据各频点的拟合情况,图 10给出了S1点的全阻抗张量数据随周期的变化曲线.从图中可以看出,在计算的频段范围内,与常规方法(方案3)(图 10中的红色圆点)比较,本文方法(方案4)计算的阻抗张量(图 10中的绿色三角)更接近理论值(图 10中的黑色实线).进一步表明在全频段范围内,本文方法的拟合质量明显优于常规方法.
|
图 10 比较测点S1处模型理论响应和方案3、4所得预测响应曲线 黑色实线为理论模型响应,红色圆点为方案3预测模型响应,绿色正方形为方案4预测模型响应. Fig. 10 Comparison of the theoretical and predicted response curves for strategy 3 and 4 at site S1. Solid black line: synthetic model responses; red circle: predicted responses by strategy 3; green square: predicted responses by strategy 4. |
在不考虑外界人为噪声的情况下,对大地电磁观测信号影响最严重的地质噪音当属电流型畸变(包含静位移效应).数学上来说,解决该问题的关键在于求解一个非线性的欠定问题.当区域结构可简化为一、二维时,通过阻抗张量分解等方法可以在反演前将部分畸变成分分解出来,在一定程度上缓解畸变带来的危害.然而,当区域结构具有较强的三维性时,目前尚无有效措施应对该畸变.本文试图发展一种考虑电流型畸变的三维反演算法,在反演过程中自适应地同步拟合电阻率模型和电流型畸变参数,从而达到压制畸变的影响、提升电阻率模型的可信度的目的.
与常规反演电阻率模型一样,在反演电流型畸变参数时同样面临非唯一性问题.如何在反演过程中对其进行有效约束是解决该问题的关键.基于统计分析大量实测MT数据所遭受的畸变分布特征,我们认为,在无法通过其他手段获得更精确的先验畸变信息的情况下,采用单位矩阵作为先验畸变参数并且根据预测畸变参数和先验畸变参数之差的L2范数来衡量畸变模型的复杂程度(粗糙度)是合理、有效的.
为了保障反演算法的稳定和效率,我们将二维反演中常用的自适应正则化因子策略改进后推广到双正则化因子情况中,并且通过引入新的更新效率因子,依据电阻率模型和畸变两组参数的收敛情况,在两个正则化因子之间自主选择需要衰减的因子.
在反演初期,偏重于电阻率模型和畸变两组参数的稳定性;在反演后期,当两组参数趋于稳健后,适度放宽约束,进一步拟合观测数据.需要注意的是两个正则化因子的初值仍需要在反演前根据具体情况设定并会对反演结果产生一定影响.
理论模型测试表明,对于受到电流型畸变的观测数据,常规的三维反演方法难以还原真实的电性结构.面对同等强度的畸变干扰,采用本文方法能够同时还原真实的电性结构和电流型畸变参数.最后需要指出的是,虽然理论模型测试验证了本文方法在压制电流型畸变干扰上的有效性,但地球深部的实际情况要远比理论模型复杂,面对受到各类噪声干扰的实测数据,该算法要取得理想的效果仍需要进一步的研究和改进.
致谢文中所用MT实测数据来自USARRAY项目.感谢俄勒冈大学Gary Egbert教授和Anna Kelbert博士提供MT三维正反演代码和热心帮助.匿名审稿专家提出的宝贵意见和建议对于本文的改进和提高非常重要.
| Avdeeva A, Moorkamp M, Avdeev D, et al. 2015. Three-dimensional inversion of magnetotelluric impedance tensor data and full distortion matrix. Geophysical Journal International , 202(1): 464–481. | |
| Bahr K. 1988. Interpretation of the magnetotelluric impedance tensor: regional induction and local telluric distortion. Journal of Geophysics , 62(2): 119–127. | |
| Berdichevsky M N, Dmitriev V I. 1976. Distortion of magnetic and electrical fields by near-surface lateral inhomogeneities. Acta Geodaetica, Geophysicaet Montanistica , 11(3-4): 447–483. | |
| Bibby H M, Caldwell T G, Brown C. 2005. Determinable and non-determinable parameters of galvanic distortion in magnetotellurics. Geophysical Journal International , 163(3): 915–930. | |
| Caldwell T G, Bibby H M, Brown C. 2004. The magnetotelluric phase tensor. Geophysical Journal International , 158(2): 457–469. | |
| Chave A D, Smith J T. 1994. On electric and magnetic galvanic distortion tensor decompositions. Journal of Geophysical Research: Solid Earth , 99(B3): 4669–4682. | |
| Chen X B, Zhao G Z, Tang J, et al. 2005. An adaptive regularized inversion algorithm for magnetotelluric data. Chinese Journal of Geophysics , 48(4): 937–946. doi: 10.3321/j.issn:0001-5733.2005.04.029. | |
| DeGroot-Hedlin C. 1995. Inversion for regional 2-D resistivity structure in the presence of galvanic scatterers. Geophysical Journal International , 122(3): 877–888. | |
| Egbert G D, Kelbert A. 2012. Computational recipes for electromagnetic inverse problems. Geophysical Journal International , 189(1): 251–267. | |
| Farquharson C G, Oldenburg D W. 1996. Approximate sensitivities for the electromagnetic inverse problem. Geophysical Journal International , 126(1): 235–252. | |
| Fletcher R, Reeves C M. 1964. Function minimization by conjugate gradients. The Computer Journal , 7(2): 149–154. | |
| Garcia X, Jones A G. 2002. Decomposition of three-dimensional magnetotelluric data.//Proceedings of the Second International Symposium. Amsterdam: Elsevier, 35: 235-250. | |
| Groom R W, Bailey R C. 1989. Decomposition of magnetotelluric impedance tensors in the presence of local three-dimensional galvanic distortion. Journal of Geophysical Research: Solid Earthand Planets , 94(B2): 1913–1925. | |
| Groom R W, Bailey R C. 1991. Analytic investigations of the effects of near-surface three-dimensional galvanic scatterers on MT tensor decompositions. Geophysics , 56(4): 496–518. | |
| Groom R W, Bahr K. 1992. Corrections for nearsurface effects: Decomposition of the magnetotelluric impedance tensor and scaling corrections for regional resistivities: Atutorial. Surveys in Geophysics , 13(4-5): 341–379. | |
| Hestenes M R.1951. Iterative methods for solving linear equations. NAML Report 52-9.Los Angeles, CA: National Bureau of Standards. | |
| Hestenes M R, Stiefel E. 1952. Methods of conjugate gradients for solving linear systems. Journal of Research of the National Bureau of Standards , 49(6): 409–436. | |
| Hu Z Z, Hu X Y, He Z X. 2006. Pseudo-Three-Dimensional magnetotelluric inversion using nonlinear conjugate gradients. Chinese Journal of Geophysics , 49(4): 1226–1234. doi: 10.3321/j.issn:0001-5733.2006.04.039. | |
| Jin G W, Kong X R. The Distortion and Decomposition of Magnetotelluric Impedance Tensor. (in Chinese) Beijing: Seismological Press, 2006 . | |
| Jiracek G R. 1990. Near-surface and topographic distortions in electromagnetic induction. Surveys in Geophysics , 11(2-3): 163–203. | |
| Jones A G. 1988. Static shift of magnetotelluric data and its removal in a sedimentary basin environment. Geophysics , 53(7): 967–978. | |
| Jones A G. 2011. Three-dimensional galvanic distortion of three-dimensional regional conductivity structures: Comment on "Three-dimensional joint inversion for magnetotelluric resistivity and static shift distributions in complex media" by Yutaka Sasaki and Max A. Mej. Journal of Geophysical Research: Solid Earth , 116(B12). doi: 10.1029/2011JB008665. | |
| Kelbert A, Meqbel N, Egbert G D, et al. 2014. ModEM: A modular system for inversion of electromagnetic geophysical data. Computers & Geosciences , 66: 40–53. | |
| Mackie R L, Madden T R. 1993. Three-dimensional magnetotelluric inversion using conjugate gradients. Geophysical Journal International , 115(1): 215–229. | |
| McNeice G W, Jones A G. 2001. Multisite, multifrequency tensor decomposition of magnetotelluric data. Geophysics , 66(1): 158–173. | |
| Newman G A, Alumbaugh D L. 2000. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophysical Journal International , 140(2): 410–424. | |
| Patro P K, Uyeshima M, Siripunvaraporn W. 2013. Three-dimensional inversion of magnetotelluric phase tensor data. Geophysical Journal International , 192(1): 58–66. | |
| Pellerin L, Hohmann G W. 1990. Transient electromagnetic inversion: Aremedy for magnetotelluric static shifts. Geophysics , 55(9): 1242–1250. | |
| Polak E, Ribière G. 1969. Note sur la convergence de méthodes de directions conjuguées. Revue Française d'Informatique et de Recherche Opérationnelle, 16: 35-43. | |
| Rodi W, Mackie R L. 2001. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics , 66(1): 174–187. | |
| Sasaki Y, Meju M A. 2006. Three-dimensional joint inversion for magnetotelluric resistivity and static shift distributions in complex media. Journal of Geophysical Research: Solid Earth , 111(B5). | |
| Simpson F, Bahr K. Practical Magnetotellurics. Cambridge: Cambridge University Press, 2005 . | |
| Sternberg B K, Washburne J C, Pellerin L. 1988. Correction for the static shift in magnetotellurics using transient electromagnetic soundings. Geophysics , 53(11): 1459–1468. | |
| Stiefel E.1951. Some special methods of relaxation technique.//Peoceedings of the symposium on simultaneous linear equations and the determination of eigenvalues.Washington, D.C.:U.S. Government Printing Office. | |
| Swift C M Jr.1967. A magnetotelluric investigation of an electrical conductivity anomaly in the Southwestern United States[Ph. D. thesis].Massachusetts:Massachusetts Institute of Technology. | |
| Utada H, Munekane H. 2000. On galvanic distortion of regional three-dimensional magnetotelluric impedances. Geophysical Journal International , 140(2): 385–398. | |
| Wang J Y. Inverse Theory in Geophysics. Wuhan: China University of Geosciences press, 1998 . | |
| Wu X P, Xu G M. 2000. Study on 3-D resistivity inversion using conjugate gradient method. Chinese Journal of Geophysics , 43(3): 420–427. doi: 10.3321/j.issn:0001-5733.2000.03.016. | |
| Xiao Q B, Shao G H, Jing L Z, et al. 2015. Eastern termination of the altyn tagh fault, western China: Constraints from a magnetotelluric survey. Journal of Geophysical Research: Solid Earth , 120(5): 2838–2858. | |
| Zhang L T, Unsworth M, Jin S, et al. 2015. Structure of the Central Altyn Tagh Fault revealed by magnetotelluric data: New insights into the structure of the northern margin of the India-Asia collision. Earthand Planetary ScienceLetters , 415: 67–79. | |
| Zhdanov M S. Geophysical Inverse Theory and Regularization Problems. Amsterdam: Elsevier Science, 2002 . | |
| 陈小斌, 赵国泽, 汤吉, 等. 2005. 大地电磁自适应正则化反演算法. 地球物理学报 , 48(4): 937–946. | |
| 胡祖志, 胡祥云, 何展翔. 2006. 大地电磁非线性共轭梯度拟三维反演. 地球物理学报 , 49(4): 1226–1234. | |
| 晋光文, 孔祥儒. 大地电磁阻抗张量的畸变与分解. 北京: 地震出版社, 2006 . | |
| 王家映. 地球物理反演理论. 北京: 中国地质大学出版社, 1998 . | |
| 吴小平, 徐果明. 2000. 利用共轭梯度法的电阻率三维反演研究. 地球物理学报 , 43(3): 420–427. | |
 2016, Vol. 59
2016, Vol. 59

