地下水中的氢原子被电磁场激发,会形成宏观磁矩,在地面铺设线圈可拾取宏观磁矩进动产生的核磁共振信号(Legchenko and Valla,2002; Legchenko et al.,2002;Lubczynski and Roy,2003;Roy and Lubczynski,2003;Schirov et al.,1991).信号的强弱与含水量大小有关,通过观察拾取信号的强弱可判断地下水含量.另外,不同强度的电磁场可激发地下不同深度的含水体.通过改变激发电磁场的强度,可获得地下不同深度的含水量信息.与常规的物探找水方法相比,利用核磁共振原理探寻地下水,不打钻就能确定地下含水层的深度和含水量大小等信息(林君等,2010;潘玉玲和张昌达,2000).因此,核磁共振测深(Magnetic Resonance Sounding,MRS)方法,作为一种直接探测地下水的地球物理方法(林君,2010;林君等,2012;陆其鹄等,2009;张荣等,2006),已经得到了世界上越来越多的关注.
但是,由于MRS信号非常微弱,高灵敏度的接收装置极易受到周围环境噪声的干扰(林君等,2010),MRS信号常常被淹没在噪声中,主要包括工频谐波噪声、尖峰噪声等.随着国际多通道磁共振仪器的诞生,工频谐波噪声可以通过参考通道的布设,利用其与主通道的相关性,通过自适应参考对消算法消除(Fabian,2010;Müller-Petke and Yaramanci,2010,2011a,2011b;Radic,2006;Walsh,2008;田宝凤等,2012).然而,强尖峰噪声干扰的存在,将影响自适应参考对消算法对工频噪声的剔除效果,进而阻碍MRS信号的有效提取,降低反演结果对水文地质参数解释的准确度.
尖峰噪声主要是由太阳磁暴、雷暴或者任何物体突然放电等引起的.这种尖峰噪声的主要特征是,时域上的分布和幅度具有偶然性和随机性,并且幅度大于或远大于信号幅度;频域上频率不固定,且频谱分布范围广,通常其覆盖从几赫兹到100 MHz以上,与MRS信号频率混叠在一起(林君等,2010).针对尖峰噪声对MRS信号干扰问题,国内外专家和学者进行了相应的研究.王中兴等(2009)提出差阈值替代叠加方法削弱和抑制奇异噪声,提高信号参数的提取精度;蒋川东等(2012)采用统计叠加方法去除尖峰噪声干扰;Strehl(2006),Strehl等(2006)根据尖峰噪声对MRS信号的干扰特点,提出了基于小波硬阈值变换方法去除MRS信号中的尖峰噪声.差阈值和统计叠加的方法能够判别出幅值较大的尖峰噪声,然而当尖峰噪声幅度较小时,难以判别噪声从而不能获得好的消噪效果;采用小波变换的方法进行噪声去除,其去噪效果受到分解级数和阈值策略的限制,此外,当尖峰噪声持续时间较长时,容易损失有效磁共振信号.综上,磁共振尖峰噪声处理中需要一种对其进行有效识别与去除的技术.
本文借鉴了尖峰噪声剔除方法在医学领域(Mukhopadhyay and Ray,1998)的成功应用,提出基于能量运算的磁共振信号尖峰噪声抑制方法.通过计算信号能量,突出不易识别的小幅度尖峰噪声,选取适当的阈值进行尖峰识别并剔除,进而有效提高主通道和参考道的数据相关性,为自适应参考对消算法的广泛应用奠定基础.
2 核磁共振探测噪声分析及对策 2.1 核磁共振地下水探测将发射线圈铺在地表,供入频率为拉莫尔频率的脉冲电流,形成激发磁场,当脉冲终止后,利用接收线圈接收磁共振全波信号E(t),表达式为:
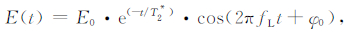
|
(1) |
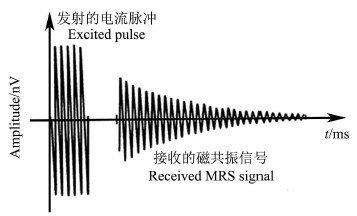
其中,E0是MRS信号的初始振幅,其大小与地下水含量成正比;T2*是平均衰减时间,与含水层介质平均孔隙度有关;φ0是初始相位;fL是拉莫尔频率.在计算机的控制下,通过有规律地改变激发脉冲电流大小可实现不同深度地下含水层探测.图 1为发射的电流脉冲与接收的磁共振信号示意图.
|
图 1 发射的电流脉冲与接收的磁共振信号示意图 Fig. 1 Excited pulse and received MRS signal |
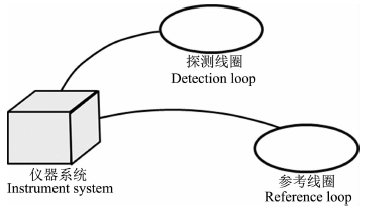
磁共振信号微弱,通常为nV级.为提高MRS信号有效获取能力,可应用参考对消算法的多通道磁共振探测系统被广泛应用.其实际工作时在距离探测线圈一定距离处,铺设一个或多个参考线圈,满足探测线圈接收含噪的磁共振信号,参考线圈只接收噪声的要求.利用探测线圈和参考线圈中噪声的相关性,采用自适应参考对消算法可有效实现噪声压制(田宝凤等,2012).图 2为带一个参考线圈的多通道磁共振探测系统的布线示意图.
|
图 2 带一个参考线圈的多通道磁共振探测系统示意图 Fig. 2 Multi-channel MRS instrumentation with a reference loop |
分析发现,影响MRS信号质量的噪声主要包括工频谐波噪声、尖峰噪声和自然噪声(林君等,2010).其中,自然噪声类似于均匀白噪声或高斯白噪声,通过多次测量,采用叠加算法即可消除,而工频谐波噪声和尖峰噪声则需要选取一定的消噪对策进行剔除.
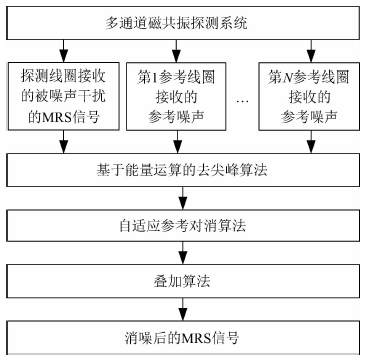
多通道核磁共振地下水探测系统可以依据噪声相关性,采用自适应参考对消方法消噪,消噪效果的好坏主要受噪声相关程度的影响(Müller-Petke and Yaramanci,2011b).研究发现,探测线圈和参考线圈中的工频谐波噪声相关性较好,而尖峰噪声相关性很差,导致自适应参考对消方法难以有效发挥作用.因此综合考虑,MRS信号的消噪对策应首先剔除尖峰噪声,再通过自适应参考对消方法压制工频谐波干扰,最后采用叠加算法剔除自然噪声影响,图 3给出了MRS信号的处理流程.
|
图 3 MRS信号处理流程图 Fig. 3 Flow chart of MRS signal processing |
用xn代表采样后离散的余弦信号,用式(2)表示:
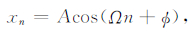
|
(2) |
式中,Ω=2πf/fs,fs是采样频率;A和ϕ分别是信号的振幅和初始相位.假定A、Ω和ϕ三个参数恒定,并选择与xn相邻的xn-1和xn+1组成方程组,得到表达式(3):
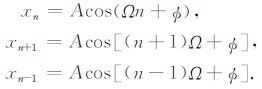
|
(3) |
根据三角函数的积化和差公式对表达式(3)进行变换,可以得出:
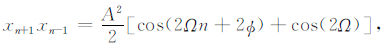
|
(4) |
再根据三角函数的二倍角公式对表达式(4)进行变换,可以得出:
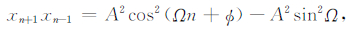
|
(5) |
式中A2cos2(Ωn+ϕ)=xn2,可以继续得到:
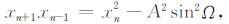
|
(6) |
整理得:
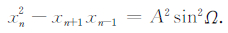
|
(7) |
当Ω<π/4,即f/fs<1/8,在误差允许的范围内,
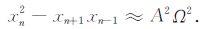
|
(8) |
由于余弦信号的能量正比于振幅的平方与频率的平方的乘积(Miller,1937),因此可用表达式(8)表示余弦信号的能量,得到:
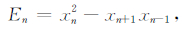
|
(9) |
式中,En即为余弦信号xn的能量.
MRS信号是呈指数规律衰减的余弦信号,因此MRS信号的振幅A是随时间按指数规律变化的.假设A=A0·e-an,Ω=Ω0,ϕ=ϕ0,可得到MRS信号为:
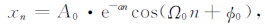
|
(10) |
利用信号能量表达式(9)计算表达式(10)所代表的MRS信号的能量,可以得到
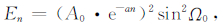
|
(11) |
同样,当采样频率大于信号频率8倍时,满足
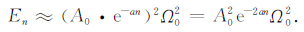
|
(12) |
从(12)式可以看出,对一个按指数规律衰减的信号xn,其能量En也是按指数规律衰减的,且信号能量的衰减速率是信号衰减速率的2倍.当A0=E0,a=1/T2*,Ω0=2πfL/fs,ϕ0=ϕ0时,表达式(10)所代表的信号xn就是MRS信号,如表达式(1)所示.
3.2 尖峰噪声的检测原理当有尖峰噪声干扰时,假设xn是接收系统采集的信号,x1n是不含尖峰噪声的MRS信号,x2n是尖峰噪声.可知,xn是x1n和x2n的线性组合,满足如下关系:
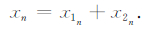
|
(13) |
假设使
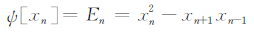
|
(14) |
成立,可以得出:
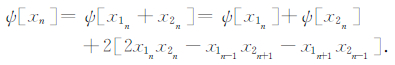
|
(15) |
如果x1n和x2n不相关,用数学期望值求信号的能量,满足如下关系:
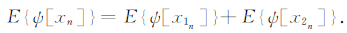
|
(16) |
引入延迟时间为2τ的x(t)的自相关函数,表达式为
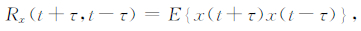
|
(17) |
式中,Rx(t+τ,t-τ)的傅里叶变换为
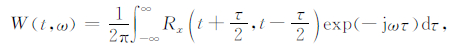
|
(18) |
式中,W(t,ω)就是该信号的谱估计.由于W(t,ω)是角频率w的偶函数
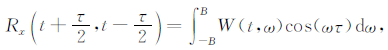
|
(19) |
式中,B是通频带宽.因此,利用公式(15)至公式(19)对表达式(14)进行变换,可以得出:
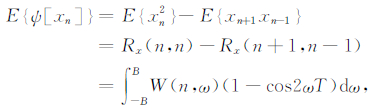
|
(20) |
式中,(1-cos2ωT)起高通滤波器的作用.假设
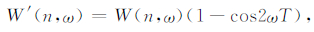
|
(21) |
可知,W(n,ω)经过高通滤波器后是W′(n,ω).由式(20)可以得到
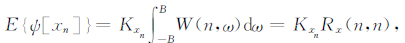
|
(22) |
其中
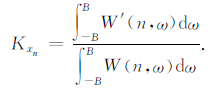
|
(23) |
由于Kxn是信号在高频部分的能量与信号总能量的比值,用于对信号在高频部分能量的测量.Kxn的变化范围是[0,2].直流信号,Kxn=0;带宽有限的白噪声,Kxn=1;带宽B=π/2T的余弦曲线,Kxn=2.Rx(n,n)是信号在nT时刻的自相关函数,表示信号在nT时刻的瞬时能量.根据表达式(22),对表达式(16)进行变换,可以得到:
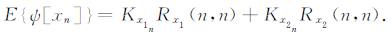
|
(24) |
可见,没有尖峰噪声时,(24)式中Kx2nRx2(n,n)的值为0.有尖峰噪声时,Kx2nRx2(n,n)起主要作用.分析可知,与MRS信号相比,尖峰噪声对瞬时能量[Rx2(n,n)]和瞬时高频[Kx2(n)]的影响更大.因此,通过计算信号的能量,以检测信号是否含有尖峰噪声.出现尖峰噪声时,信号的能量明显增加,比较信号能量的变化,识别尖峰噪声并剔除.
3.3 基于中位数的绝对偏差法剔除尖峰噪声经过上述能量运算后,尖峰噪声被突出,此时需要选取适当的阈值进行尖峰识别并剔除.
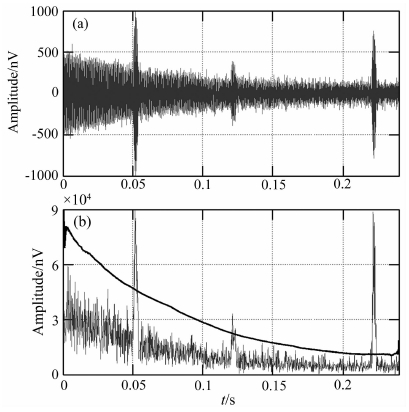
图 4a为一组受尖峰噪声干扰的MRS信号,可以看出MRS信号是按指数规律变化的衰减信号,而尖峰噪声在数据列中的表现形式为异常值,其数值多大于信号值.经过能量运算后信号如图 4b所示,可见其依然按指数规律衰减.信号和尖峰噪声的这一特点,使得选取的阈值既不能把信号最大值标记成异常值,又必须识别不明显的异常值,即幅度值小的尖峰噪声.因此,常规采用基于数据列标准差的阈值确定方法(吴石林和张玘,2010),当数据列中存在数值较大的异常值时,阈值受其影响会相对较高,进而降低了对不明显异常的检测能力.
|
图 4 峰值检测实例 (a) 受尖峰噪声干扰的MRS信号; (b) 信号能量及阈值. Fig. 4 Example of spike detection (a) MRS signal disturbed by spike noises; (b) Energy of signal and threshold. |
基于中位数的绝对偏差法(Median Absolute Deviation,MAD)(Hoaglin et al.,2000)是一种非常有效的统计学方法.对于一系列测量值为x1,x2,…,xn的数据列,计算MAD,应先求某测量值相对于其所在数据列中位数的绝对偏差,再对该绝对偏差求中位数,定义为:
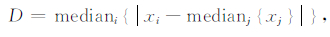
|
(25) |
式中,xi和xj代表经过能量运算后的信号;xi是该时刻某单次采集的数据点,xj为某一时刻所有单次采集的数据列,medianj{·}是求该数据列的中位数,D是计算MAD后的数值.
计算MAD后,阈值为median{x}+K·D,K是常数.根据尖峰噪声和信号在能量域中幅值的关系,以阈值能有效地标记出被突出的信号能量为标准进行选取.如图 4b所示,尖峰噪声在能量域中被突出,使用MAD方法确定的阈值既跟踪了信号的整体变化趋势,又有效地将幅度较小的尖峰噪声标记出.
将能量域中的信号与阈值进行比较,超过阈值数据视作尖峰噪声并剔除.由于实际采集的信号包含随机噪声,随机噪声中的高频成分在能量域中容易被误识别为“小尖峰”,导致增加无效的判断次数及计算量.因此,可适当地通过低通滤波器,去除随机噪声中的高频成分,以准确识别并剔除尖峰噪声.
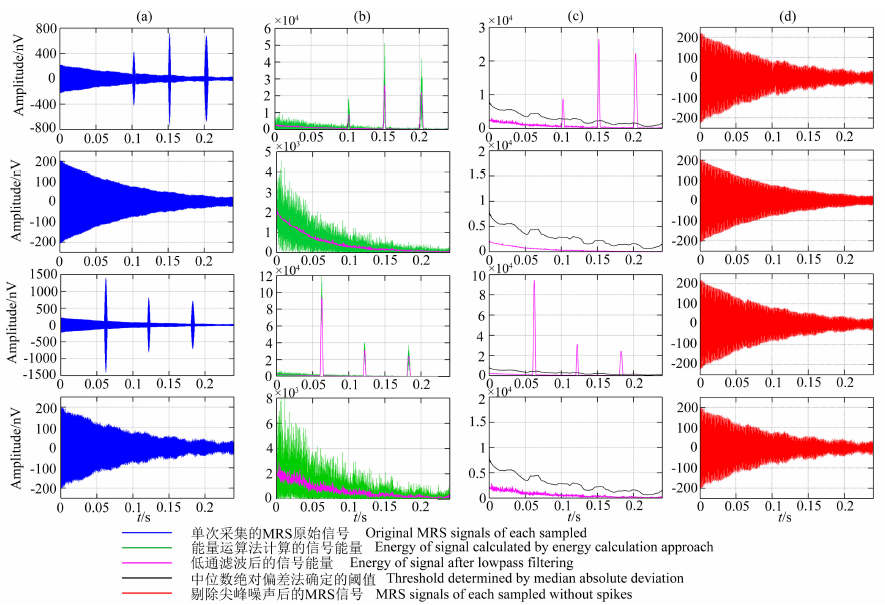
仿真一组含有16000个等精度采样点、采样频率为66667 Hz的四次叠加信号,单次采集的原始信号如图 5a所示,图中的尖峰噪声、工频谐波噪声和高斯白噪声的干扰时刻以及干扰强度均是随机的.使用能量运算法剔除尖峰噪声主要包括三个步骤:
|
图 5 基于能量运算的去尖峰算法消噪流程图 (a) 单次采集的原始信号; (b) 计算后的信号能量; (c) 中位数绝对偏差法确定的阈值; (d) 剔除尖峰噪声后的信号. Fig. 5 The workflow of energy calculation (a) Original signals of each sampled; (b) Energy of signal calculated by energy calculation; (c) Threshold determined by median absolute deviation; (d) MRS signals of each sampled without spikes. |
(1)计算单次采集信号的能量,将信号由时域转化到能量域.再将计算后的信号的能量通过低通滤波器,如图 5b所示.
(2)采用MAD方法确定阈值.
(3)将低通滤波后信号的能量与阈值进行比较,如图 5c所示,超出阈值的部分视作尖峰噪声,用该时刻无尖峰噪声的数据列的中位数进行替代,以达到剔除尖峰噪声的目的.图 5d给出了剔除尖峰噪声后的信号.
4 消噪算法仿真分析目前在磁共振信号处理中通常采用统计叠加方法进行尖峰噪声剔除(Jiang et al.,2011),其基本思想是把尖峰噪声看作统计学中的粗大误差,首先提取一个可疑的测量值,然后按t分布检验提取的测量值是否含有粗大误差,再决定其是否需要剔除,最终剔除后的数据参与到叠加运算中.
分别采用能量运算法和统计叠加法,对含有不同干扰幅度以及干扰持续时间尖峰噪声的信号进行处理,验证能量运算法的应用效果,并观察多通道系统采集中剔除尖峰噪声后,主通道和参考道数据相关性的改善情况.
除了能从波形上观察尖峰噪声的剔除效果,本文引入信噪比和标准差进行数值衡量.信噪比的定义为:
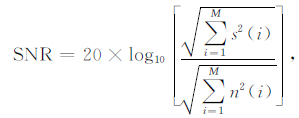
|
(26) |
式中,信噪比SNR采用了dB的表示方式.
标准差的定义为:

|
(27) |
式中,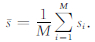
仿真信号模型参数如下:MRS信号的中心频率fL=2326 Hz,E0=200 nV,T2*=150 ms,标准差STDini=77.4495 nV,加入幅度不同的尖峰噪声干扰,使得信噪比SNR=0.9185 dB,标准差STD=95.8465 nV.图 6a为具有16000个等精度采样点的仿真含噪信号.

|
图 6 统计叠加法和能量运算法对不同幅度尖峰噪声的去噪结果 (a) 仿真的含噪信号; (b) 应用统计叠加法剔除尖峰噪声; (c) 应用能量运算法剔除尖峰噪声. 虚线是区分不同幅度尖峰噪声的标识,幅度值超过该虚线的视作大幅度尖峰噪声,反之, 视作小幅度尖峰噪声. Fig. 6 Statistical stacking approach and energy calculation approach to remove spikes of different amplitude (a) Simulated signals with spikes; (b) Remove spikes by statistical stacking approach; (c) Remove spikes by energy calculation approach. The dash line is the sign of different amplitude, data above the dash line represent big spikes, conversely, represent small spikes. |
图中具有衰减趋势的虚线,其幅度是信号幅度的1.5倍,将它作为区别不同幅度尖峰噪声的标识.幅度值超过该虚线的视作大幅度的尖峰噪声;反之,视作小幅度的尖峰噪声.分别采用统计叠加法和能量运算法对图 6a所示的仿真含噪信号进行消噪处理,图 6b和6c为对应的消噪结果.从消噪结果图中可以明显看出,应用统计叠加法后,幅值较大的尖峰噪声被剔除,但幅值较小的尖峰噪声仍然存在;而经过能量运算法后,幅值较大的尖峰噪声和幅值较小的尖峰噪声均被剔除.应用统计叠加法后,信噪比SNR=6.6617 dB,提高了5.7432 dB.另外,标准差STD=80.1300 nV,与不含尖峰噪声的MRS信号相比,标准差偏差为3.4610%.而应用能量运算法后,信噪比SNR=12.6133 dB,提高了11.6948 dB.标准差STD=77.7195 nV,标准差偏差为0.3486%.
结合统计叠加法和能量运算法的消噪原理对其消噪差异进行分析,可知,统计叠加法先剔除一个可疑的测量值,然后检验剔除的测量值是否含有粗大误差.在某些情况下,幅度值较小的干扰被认为不含有粗大误差,不予剔除.因此,统计叠加法能剔除幅度值较大的尖峰噪声,却常常忽略幅度值较小的尖峰噪声.然而,经过能量运算后,原来时域中幅度值较小的尖峰噪声在能量域中其幅度值会被增加,明显地超过信号的幅度,很容易被识别并去除.
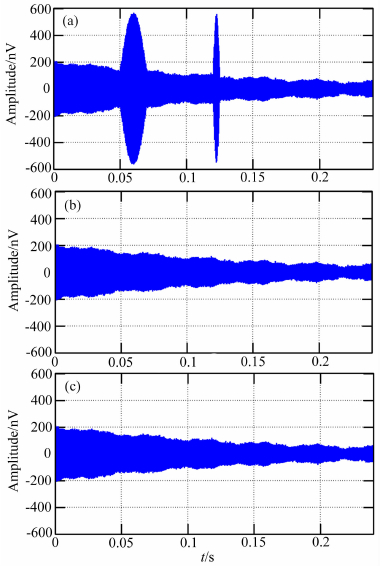
4.2 持续时间不同的尖峰噪声去噪仿真仿真信号模型参数如下:MRS信号的中心频率fL=2326 Hz,E0=200 nV,T2*=150 ms,标准差STDini=77.4495 nV,加入持续时间不同的两个尖峰噪声干扰,使得信噪比SNR=0.2261 dB,标准差STD=120.5160 nV.图 7a为具有16000个等精度采样点的仿真含噪信号.
|
图 7 统计叠加法和能量运算法对不同持续时间尖峰噪声的去噪结果 (a) 仿真的含噪信号; (b) 应用统计叠加法剔除 尖峰噪声; (c) 应用能量运算法剔除尖峰噪声. Fig. 7 Statistical stacking approach and energy calculation approach to remove spikes of different duration time (a) Simulated signals with spikes; (b) Remove spikes by statistical stacking approach; (c) Remove spikes by energy calculation approach. |
分别采用统计叠加法和能量运算法对图 7a所示的仿真含噪信号进行消噪处理,图 7b和7c为对应的消噪结果.应用统计叠加法后,信噪比SNR=18.3899 dB,提高了18.1638 dB.另外,标准差STD=77.6652 nV,与不含尖峰噪声的MRS信号相比,标准差偏差为0.2785%.而应用能量运算法后,信噪比SNR=18.3921 dB,提高了18.1660 dB.标准差STD=77.6744 nV,标准差偏差为0.2904%.从消噪结果图以及消噪后的信噪比和标准差中可以明显看出,统计叠加法和能量运算法均可剔除干扰幅度较大,持续时间较长的尖峰噪声,且不损失有效的磁共振信号,标准差偏差控制在0.3%以内,满足实际应用的需求.
4.3 多通道系统数据去噪后提高信号相关性验证模拟探测线圈采集含噪声的磁共振信号,参考线圈只采集周围环境噪声,二者共同构成多通道采集系统.参考对消算法与通道间数据相关性有关,因此需引入相关性的概念.设Pxy(f)是信号x和信号y的互相关功率谱密度,Pxx(f)是信号x的自相关功率谱密度,Pyy(f)是信号y的自相关功率谱密度.相关性的定义为:
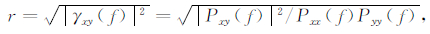
|
(28) |
式中,r介于0和1之间,当r=1时,信号x和信号y完全相关;当r=0时,信号x和信号y不相关.
仿真模型参数如下:MRS信号的中心频率fL=2326 Hz,工频谐波干扰频率f1=2250 Hz,f2=2350 Hz,参考道中工频干扰的幅度是主通道中工频干扰幅度的3倍,相位相同.主通道中随机加入幅度为150 nV到550 nV、持续时间为4 ms到15 ms的五个尖峰噪声干扰;同时,参考道中随机加入幅度为300 nV到1000 nV、持续时间为5 ms到20 ms的八个尖峰噪声干扰.使得主通道和参考道的数据相关性r=0.1369.
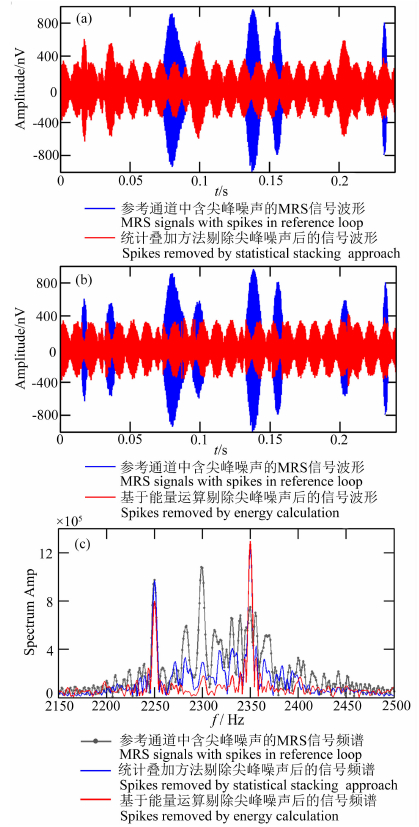
分别使用统计叠加法和能量运算法剔除主通道以及参考道中尖峰噪声.经过计算,应用统计叠加法剔除尖峰噪声后,主通道与参考道信号相关性r=0.4502,提高了0.3133.应用能量运算法剔除尖峰噪声后,主通道与参考道信号相关性r=0.4941,提高了0.3572.图 8和图 9分别给出了统计叠加法和能量运算法剔除尖峰噪声前后主通道以及参考道信号的时域波形及频谱.消噪前后信号的时域波形进一步验证了4.1和4.2节得出的结论:统计叠加法和能量运算法均可剔除干扰幅度较大,持续时间较长的尖峰噪声;另外,能量运算法可以识别并剔除干扰幅度较小的尖峰噪声.从消噪前后信号频谱图以及消噪后的相关性中可以明显看出,采用能量运算法剔除尖峰噪声后,能够显著提高主通道与参考道信号相关性,为后续应用自适应噪声对消算法更好地剔除工频谐波噪声奠定了基础.

|
图 8 使用统计叠加方法和使用基于能量运算的尖峰噪声抑制方法剔除主通道中的尖峰噪声 (a) 统计叠加方法; (b) 能量运算法; (c) 频谱结果. Fig. 8 Remove spikes by statistical stacking approach and energy calculation approach in detection loop (a) Statistical stacking approach; (b) Energy calculation approach; (c) Results in frequency domain. |
|
图 9 使用统计叠加方法和使用基于能量运算的尖峰噪声抑制方法剔除参考道中的尖峰噪声 (a) 统计叠加方法; (b) 能量运算法; (c) 频谱结果. Fig. 9 Remove spikes by statistical stacking approach and energy calculation approach in reference loop (a) Statistical stacking approach; (b) Energy calculation approach; (c) Results in frequency domain. |
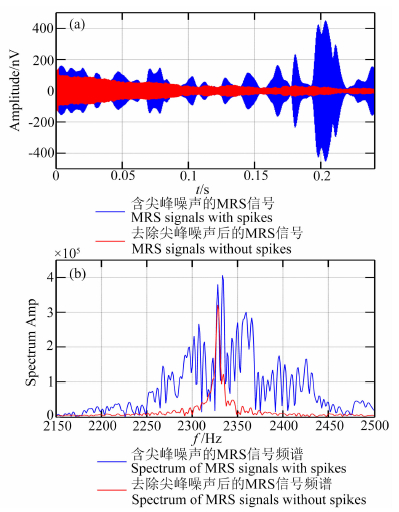
为了验证算法的实用性,在长春市郊区烧锅镇进行了野外试验.使用核磁共振地下水探测仪(林君等,2010)进行信号采集,当地的拉莫尔频率fL=2326 Hz,图 10a中蓝色线为仪器采集的原始信号时域波形图.从图中可以看出:该信号含有较多的尖峰噪声,并且从信号的时域波形上不能明显看出MRS信号指数型的衰减趋势.经计算,原始信号的信噪比SNR=-37.7090 dB.
|
图 10 基于能量运算的尖峰噪声抑制方法剔除实测数据中的尖峰噪声 (a) 剔除尖峰噪声前后的时域图; (b) 剔除尖峰噪声前后的频域图. Fig. 10 Spikes in MRS experimental data removed by energy calculation approach (a) Remove spikes in time domain; (b) Remove spikes in frequency domain. |
依次操作3.3节中使用能量运算法的三个步骤,对图 10a所示实测数据进行尖峰噪声剔除,得到消噪后的时域信号,如图 10a中红色线所示.可见,原始信号中的尖峰噪声被明显剔除,消噪后的信号呈现指数形式衰减.再从频域上进行比较,如图 10b所示,消噪后尖峰噪声的频率分量被压制,突出了信号的频率.经计算,消噪后信号的信噪比SNR1=-29.1380 dB,剔除尖峰噪声后信噪比提高了ΔSNR1=8.5710 dB.
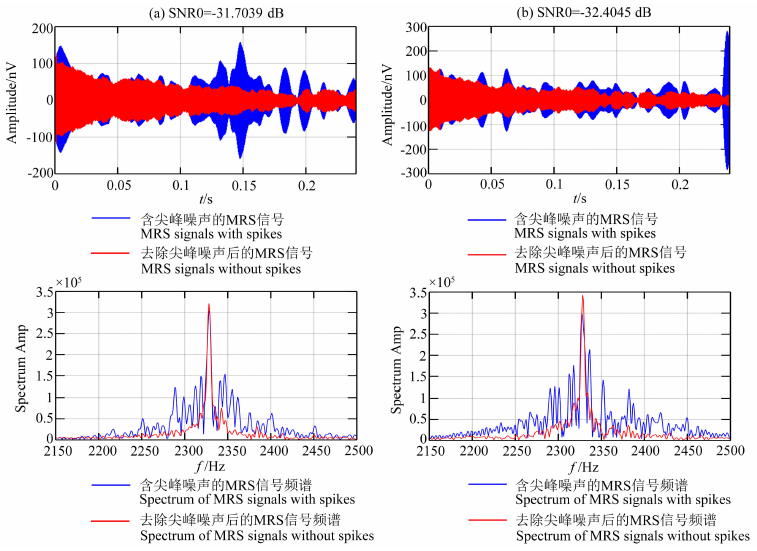
为了进一步说明方法的有效性,分别对不同信噪比下的另外两组实测数据进行处理,处理结果如图 11所示.由图 11消噪前后的时域信号及频谱可以看出,对于不同信噪比实测数据,基于能量运算的尖峰噪声抑制方法可以获得较好的消噪效果.
|
图 11 不同信噪比下实测数据处理结果 Fig. 11 Processing results of MRS signals on different SNRs |
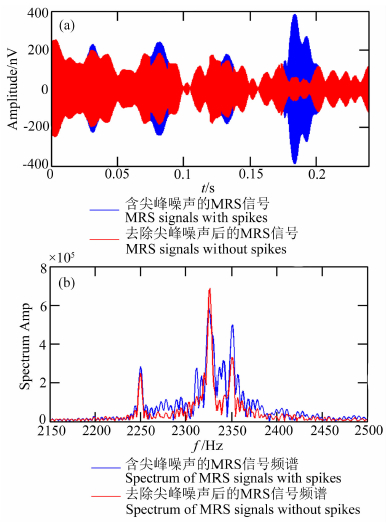
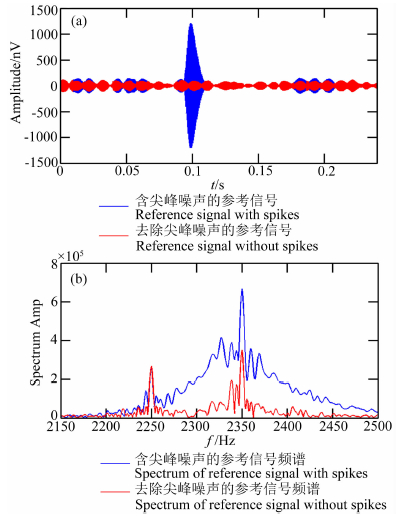
为了验证算法在多通道系统数据处理中的实用性,在长春市净月潭进行了野外试验.使用带参考线圈的核磁共振地下水探测仪进行信号采集,当地的拉莫尔频率fL=2326 Hz,受到2250 Hz和2350 Hz两个明显的工频噪声干扰.使用能量运算法剔除主通道和参考道中的尖峰噪声,结果如图 12和图 13所示.从图中可以看出:信号中的尖峰噪声被剔除,并且去除尖峰噪声后,工频噪声的频率成分更加明显.经计算,剔除尖峰噪声前,主通道和参考道的信号相关性r=0.1575;剔除尖峰噪声后,主通道和参考道的信号相关性r=0.2481.可见,对多通道磁共振探测系统,先剔除主通道和参考道中的尖峰噪声,提高信号相关性后,再应用自适应噪声对消算法去除工频谐波噪声将会取得更好的去噪效果.
|
图 12 基于能量运算的尖峰噪声抑制方法剔除主通道中的尖峰噪声 (a) 剔除尖峰噪声前后的时域图; (b) 剔除尖峰噪声前后的频域图. Fig. 12 Spikes in detection loop removed by energy calculation approach (a) Remove spikes in time domain; (b) Remove spikes in frequency domain. |
|
图 13 基于能量运算的尖峰噪声抑制方法剔除参考道中的尖峰噪声 (a) 剔除尖峰噪声前后的时域图; (b) 剔除尖峰噪声前后的频域图. Fig. 13 Spikes in reference loop removed by energy calculation approach (a) Remove spikes in time domain; (b) Remove spikes in frequency domain. |
在强尖峰噪声干扰下如何更好地实现微弱MRS信号可靠提取是核磁共振地下水探测抗干扰技术中的关键问题,它将直接影响后续应用自适应参考对消算法对工频谐波噪声的有效滤除.能量运算法可有效检测尖峰噪声并突出不易识别的小幅度尖峰噪声.本文根据能量运算法的这一特点,针对强尖峰噪声干扰问题,推导了能量域信号表达式,通过计算信号能量,有效识别尖峰噪声,然后采用基于中位数的绝对偏差法确定阈值,实现对尖峰噪声的有效剔除.与应用效果较好的统计叠加法对比研究,通过数值仿真和实测数据处理,得出如下结论:
(1) 对于干扰幅度较大,持续时间较长的尖峰噪声,能量运算法和统计叠加法均能识别并剔除,且不损失有效的磁共振信号,仿真数据去噪后信噪比提高了18 dB,标准差偏差控制在0.3%以内,满足实际应用的需求.
(2) 对于小于信号幅度1.5倍的小幅度尖峰噪声,能量运算法可有效识别并剔除,而统计叠加法无法实现.同一组仿真数据应用统计叠加法剔除尖峰噪声后,信噪比提高了5.7432 dB;应用能量运算法剔除尖峰噪声后,信噪比提高了11.6948 dB.
(3) 针对多通道系统,仿真数据经过能量运算法剔除尖峰噪声后,相关性提高了0.3572,可见剔除尖峰噪声后可明显提高主通道和参考道的数据相关性.
(4) 本文所述能量运算法不受尖峰噪声干扰幅度以及干扰持续时间限制.随机抽取三组不同信噪比的实测数据,采用能量运算法剔除尖峰噪声后,信噪比均得到大幅度提升,获得了很好的实际应用效果.
(5) 针对受工频噪声干扰的多通道磁共振探测系统的实测数据,使用本文所述能量运算法剔除主通道和参考道的尖峰噪声后,可提高数据相关性.
在核磁共振地下水实际探测应用中,除尖峰噪声之外,MRS数据还会受到工频谐波噪声和其他未知噪声等多种影响,尤其在城市周边和村庄附近探测时,高强度的工频噪声干扰会将MRS信号淹没.鉴于此,带有参考线圈的多通道探测系统被推出,自适应参考对消算法成为MRS消噪算法的主流方向.在运用本文能量运算法对MRS信号进行尖峰噪声剔除后,主通道和参考道噪声相关性的提高为后续自适应参考对消算法的有效应用奠定了基础.下一步将研究基于自适应参考对消算法对工频谐波噪声进行滤除的问题.
| Fabian N. 2010. Processing of full time series, multichannel surface NMR signals[Master's thesis]. Switzerland: ETH Zürich. | |
| Hoaglin D C, Mosteller F, Tukey J W. Understanding Robust and Exploratory Data Analysis. New York: Wiley, 2000 . | |
| Jiang C D, Lin J, Duan Q M, et al. 2011. Statistical stacking and adaptive notch filter to remove high-level electromagnetic noise from MRS measurements. Near Surf. Geophys. , 9(5): 459–468. | |
| Legchenko A, Valla P. 2002. A review of the basic principles for proton magnetic resonance sounding measurements. J. Appl. Geophys. , 50(1-2): 3–19. | |
| Legchenko A, Baltassat J M, Beauce A, et al. 2002. Nuclear magnetic resonance as a geophysical tool for hydrogeologists. J. Appl. Geophys. , 50(1-2): 21–46. | |
| Lin J, Duan Q M, Wang Y J, et al. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications. (in Chinese) Beijing: Science Press, 2010 . | |
| Lin J. 2010. Situation and progress of nuclear magnetic resonance technique for groundwater investigations. Progress in Geophysics , 25(2): 681–691. doi: 10.3969/j.issn.1004-2903.2010.02.043. | |
| Lin J, Jiang C D, Duan Q M, et al. 2012. The situation and progress of magnetic resonance sounding for groundwater investigations and underground applications. Journal of Jilin University (Earth Science Edition) (in Chinese) , 42(5): 1560–1570. | |
| Lu Q H, Wu T B, Lin J. 2009. A research report on development of instrument science for geophysics. Progress in Geophysics (in Chinese) , 24(2): 750–758. | |
| Lubczynski M, Roy J. 2003. Hydrogeological interpretation and potential of the new magnetic resonance sounding (MRS) method. Journal of Hydrology , 283(1-4): 19–40. | |
| Mukhopadhyay S, Ray G C. 1998. A new interpretation of nonlinear energy operator and its efficacy in spike detection. IEEE T. Biomed. Eng. , 45(2): 180–187. | |
| Müller-Petke M, Yaramanci U. 2010. Improving the signal-to-noise ratio of surface-NMR measurements by reference channel based noise cancellation.//16th EAGE European Meeting of Environmental and Engineering Geophysics. EAGE. | |
| Müller-Petke M, Yaramanci U. 2011a. Noise Cancellation for surface NMR: Derivation of time and frequency domain approaches.//17th EAGE European Meeting of Environmental and Engineering Geophysics. EAGE. | |
| Müller-Petke M, Yaramanci U. 2011b. Noise cancellation for surface NMR-application of time and frequency domain approaches.//17th EAGE European Meeting of Environmental and Engineering Geophysics. EAGE. | |
| Miller D C. Sound Waves: Their Shape and Speed. New York: Macmillan Company Press, 1937 . | |
| Pan Y L, Zhang C D. Theories and Methods of Surface Nuclear Magnetic Resonance. (in Chinese) Beijing: China University of Geosciences Press, 2000 . | |
| Radic T. 2006. Improving the signal-to-noise ratio of surface NMR data due to the remote reference technique.//12th EAGE European Meeting of Environmental and Engineering Geophysics. EAGE. | |
| Roy J, Lubczynski M. 2003. The magnetic resonance sounding technique and its use for groundwater investigations. Hydrogeol. J. , 11(4): 455–465. | |
| Schirov M, Legchenko A, Creer G. 1991. A new direct non-invasive groundwater detection technology for Australia. Exploration Geophysics , 22(2): 333–338. | |
| Strehl S. 2006. Development of strategies for improved filtering and fitting of SNMR-signals. Germany: Technical University of Berlin, Institute of Applied Geosciences, Department of Applied Geophysics. | |
| Strehl S, Rommel I, Hertrich M, et al. 2006. New strategies for filtering and fitting of MRS signals.//Proceedings 3rd International MRS Workshop. Madrid, Spain, 65-68. | |
| Tian B F, Lin J, Duan Q M, et al. 2012. Variable step adaptive noise cancellation algorithm for magnetic resonance sounding signal with a reference coil. Chinese J. Geophys. , 55(7): 2462–2472. doi: 10.6038/j.issn.0001-5733.2012.07.030. | |
| Walsh D O. 2008. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations. J. Appl. Geophys. , 66(3-4): 140–150. | |
| Wang Z X, Rong L L, Lin J. 2009. Spike noise elimination from surface nuclear magnetic resonance signal for underground water. Journal of Jilin University (Engineering and Technology Edition) (in Chinese) , 39(5): 1282–1287. | |
| Wu S L, Zhang Q. Error Analysis and Data Processing. (in Chinese) Beijing: Tsinghua University Press, 2010 . | |
| Zhang R, Hu X Y, Yang D K, et al. 2006. Review of development of surface nuclear magnetic resonance. Progress in Geophysics (in Chinese) , 21(1): 284–289. | |
| 林君, 段清明, 王应吉, 等. 核磁共振找水仪原理与应用. 北京: 科学出版社, 2010 . | |
| 林君. 2010. 核磁共振找水技术的研究现状与发展趋势. 地球物理学进展 , 25(2): 681–691. | |
| 林君, 蒋川东, 段清明, 等. 2012. 复杂条件下地下水磁共振探测与灾害水源探查研究进展. 吉林大学学报(地球科学版) , 42(5): 1560–1570. | |
| 陆其鹄, 吴天彪, 林君. 2009. 地球物理仪器学科发展研究报告. 地球物理学进展 , 24(2): 750–758. | |
| 潘玉玲, 张昌达. 地面核磁共振找水理论和方法. 北京: 中国地质大学出版社, 2000 . | |
| 田宝凤, 林君, 段清明, 等. 2012. 基于参考线圈和变步长自适应的磁共振信号噪声压制方法. 地球物理学报 , 55(7): 2462–2472. | |
| 王中兴, 荣亮亮, 林君. 2009. 地面核磁共振找水信号中的奇异干扰抑制. 吉林大学学报(工学版) , 39(5): 1282–1287. | |
| 吴石林, 张玘. 误差分析与数据处理. 北京: 清华大学出版社, 2010 . | |
| 张荣, 胡祥云, 杨迪琨, 等. 2006. 地面核磁共振技术发展述评. 地球物理学进展 , 21(1): 284–289. | |
 2016, Vol. 59
2016, Vol. 59


