2. 美国特拉华州立大学应用数学研究中心, 多佛 19901
2. Applied Mathematics Research Center, Delaware State University, Dover, DE 19901, USA
有限差分方法是地球物理正演模拟中重要的数值计算方法之一,它以计算精度高、算法稳定而被广泛应用于地震波(弹性波,声波)、低频电磁波和高频探地雷达正演计算(李静等,2010).在开展探地雷达复杂目标体模拟时,为了提高数值计算精度,可以对整个模型区域采用较小的离散网格,以压制网格频散现象和保持有限差分方法的计算稳定性.但模型网格剖分越细,占用计算内存将增大,计算效率降低,同时长时间的迭代计算将引起误差积累(冯德山等,2010;Li et al.,2012).采用非均匀网格划分方法可以在保证计算效率的同时有效提高计算精度.Moczo(1989)首次提出了有限差分可变网格思想,之后,研究者(赵海波等,2007;Diamanti等,2009; 黄超和董良国,2009a,2009b;孙林洁等,2011; 张慧和李振春,2011;冯德山等,2014)先后将这种思想分别应用到声波、弹性波和电磁波等地球物理方法有限差分数值模拟计算中,打破了传统固定网格方式.由介质变化程度来决定离散网格的大小,在目标区域采用细网格剖分,在背景介质区域采用较大空间网格剖分.这样的方式不仅减少了计算量,又兼顾了方法稳定性与计算精度.常用的非均匀网格包括固定方向变网格有限差分方法(Non-uniform FDTD)和粗细网格交错自适应局部亚网格有限差分方法(Adaptive Mesh Refinement Sub-grid FDTD).上述方法存在以下问题:变网格有限差分方法采用固定方向的非均匀网格,即需要在一个方向整体进行细网格划分,采用统一的时间步长,当粗细网格差距较大时需要用很小的时间步长才能满足稳定性要求,这样在一定程度上浪费了计算资源,而且难以实现对任意区域的精细目标结构的任意划分(Wang and Liang,2007,Pitarka,1999).粗细网格交错的亚网格技术虽然能自适应对任意区域划分不同的网格尺寸,并且采用不同的时间步长,但粗细网格交界的波场传递处理始终是制约该方法发展的瓶颈,特别是当网格尺寸比较大时,边界场值迭代往往出现发散,影响计算精度(谢姣,2010; Xiao et al.,2007).
如何克服以上问题,是非均匀网格有限差分方法发展的关键技术之一.本文介绍了一种新的非均匀网格有限差分方法,该方法基于麦克斯韦方程的坐标变换不变性,通过坐标变换增加目标区域参数所占的网格数目,减少背景区域网格数据以保证整体网格数目不变,达到提高计算精度的目的,这种方法被称为变换光学(transformation optics)有限差分方法.变换光学由Pendry等(2006)在Science杂志上发表了一个符合 Maxwell 方程的隐形斗篷理论(Cloak Theory).该理论提出至今,已经成了一个十分热门的研究领域,可应用于光线隐身设备设计、超透镜以及声波隐身设备等的设计和制造. Pendry等(1996)提出了基于物质结构参数变化而电磁场的传播不变性,在任意坐标变换之下,Maxwell 方程式可以维持不变,而相对介电常数与磁导率的表达式变得更复杂.对于这个坐标变换可以采用以下两种观点做解释(Chen et al,2010):第一种是空间电磁场和介质都没有变,只是坐标系改变(笛卡儿坐标换成球坐标),这是介质相对于坐标系的改变;第二种是空间、介质与电磁场都改变,但坐标系没变.变换光学方法的设计关键,即在先采用第一种观点做坐标变换,再将变换结果用第二种观点解释.变换之后的介质与原来的介质之间存在一一对应关系.变换后的相对介电常数与磁导率具有跟目标本身一样的电磁特性,只要连续地改变不同位置的目标参数,就可以建构出任何可能的电磁介质,实现坐标变换介质(transformed medium).这种方法仍然没有明确定义而暂时被称作变换光学(Transform Optics).
基于上述变换光学思想,本文推导实现了基于变换光学的二维有限差分方法并应用于探地雷达目标数值计算.针对目标体的精细结构模型,相比常规固定方向变网格、粗细网格交错局部亚网格,变换光学有限差分方法不仅很好地提高了模型的计算精度,在计算效率方面也得到了很好的改善.
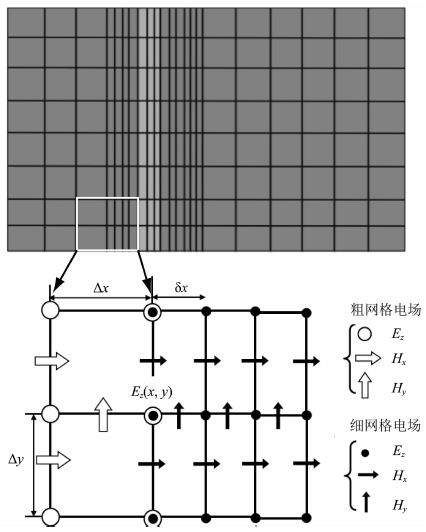
2 固定方向变网格有限差分方法固定方向变网格方法是沿固定方向对目标区域划分较细的网格,而在其他周围背景介质位置以及介质变化缓慢的区域使用较粗网格.图 1是基于垂直方向划分非均匀网格的示意图,通过非均匀网格的方法通过减少数值色散,改善了精度.这种非均匀网格差分方法采用统一的时间迭代步长,需要满足最小网格尺寸的稳定性条件.在粗细网格内部仍然采用标准的交错网格迭代形式,迭代公式与常规二阶差分格式相同(王红,2013).以y方向划分非均匀网格为例,在x方向的空间步长分别为Δx和δx,在y方向的网格尺寸统一为Δy,根据完美磁导边界的电磁场分布形式,只需要计算在网格交界面的电场分量Ez(Taflove,1995):
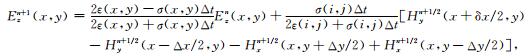
|
(1) |
|
图 1 纵向非均匀网格划分示意图 Fig. 1 The map of non-uniform gird along y direction |
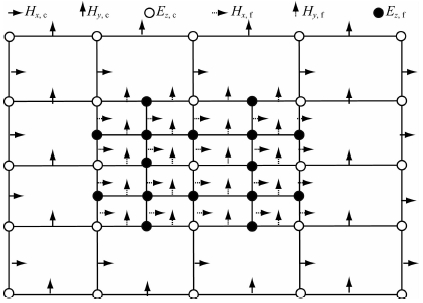
亚网格技术是在目标体的位置区域采用细网格尺寸,对于周围其他位置仍然采用粗网格尺寸,且在不同的网格区域采用不同的时间步长.通过对目标区域采用小网格尺寸能保证足够的计算精度,另外又节约内存和运行时间(Liu et al.,2009),其基本原理见附录.在粗网格和细网格区域内部仍然采用普通的均匀网格差分迭代式进行递推计算.需要注意的是,在粗细网格交界位置,由于存在网格大小的不连续性,特别是当粗细网格尺寸比例较大时,不可避免地将带来非物理性反射,影响亚网格技术稳定性,也是制约亚网格技术发展的关键因素之一.在亚网格技术研究中,如何解决粗细网格交界处的反射误差是一直以来的研究重点(Diamanti and Giannopoulos,2009).
|
图 2 二维亚网格分布示意图 Fig. 2 The map of 2D sub-grid FDTD |
基于变换光学的有限差分方法(TO-FDTD)应用坐标变换来放大局部目标区域,使得目标区域包含更多的网格单元.亚网格或非均匀网格FDTD方法要求时间上逐步迭代,并且常常会遇到时间迭代后期不稳定的问题.为了避免由变换光学引起的时间步长变小,将介质参数矩阵映射到一种色散介质模型中.时间域麦克斯韦方程组可表示为(Liu et al.,2014a)
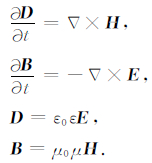
|
(2) |
将笛卡儿坐标系(x, y, z)进行坐标转换得到另一个坐标系(x’, y’, z’)之后,得到新的麦克斯韦方程组为
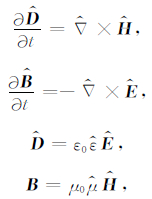
|
(3) |
式中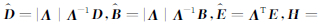
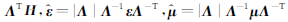
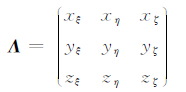
|
(4) |
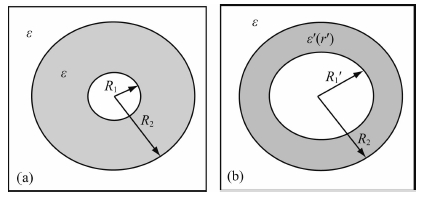
应用变换光学的方法来扩大目标区域大小,如图 3所示,在x-y平面中,半径为R1的小圆盘可以变换为一个半径为R’1的大圆盘,圆环域R1<r<R2被变换到了另一个圆环域R’1<r’<R2.将进行三次这种坐标变换:(x,y)→(r,θ)→(r’,θ’)→(x’,y’).
|
图 3 基于变换光学有限差分方法变换原理示意图 (a) 传统的FDTD; (b) 变换光学的FDTD. Fig. 3 The illustration of enlarging a small region by using transformation optics (a) Traditional FDTD; (b) Transformation optics FDTD. |
三次坐标转换的雅克比矩阵分别为
(1)由笛卡儿网格(x, y, z)转换到圆柱坐标系(r, θ, z):
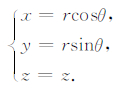
|
(5) |
其雅克比矩阵为
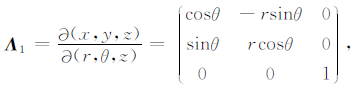
|
(6) |
(2)由(r, θ, z)到(r’, θ’, z)的坐标转换:
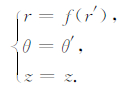
|
(7) |
其雅克比矩阵为
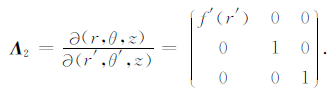
|
(8) |
如图 3所示,为了把圆环域R1<r<R2转换到另一个圆环域R’1<r’<R2,并且把圆盘r<R1扩大到r’<R’1,可以使用下列的转换函数:
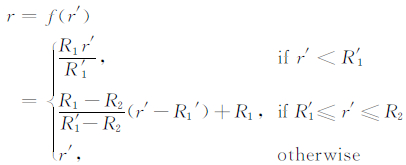
|
(9) |
(3)由圆柱坐标系(r’,θ’,z)转换为笛卡儿网格(x’,y’,z),有
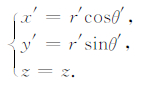
|
(10) |
雅克比矩阵为
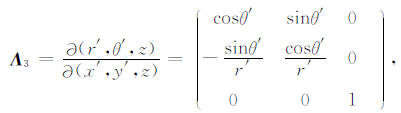
|
(11) |
结合以上三次坐标转换,得到由(x, y, z)到(x’,y’,z’)的雅克比矩阵:
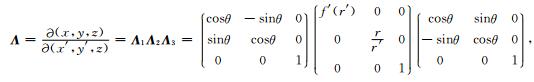
|
(12) |
一旦计算出最终的雅克比矩阵Λ,就可计算物性参数相对介电常数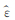
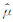
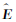
变换光学有限差分实现的基本思想可以由如图 4所示的圆形体模型解释.图 4a是在常规FDTD相对介电常数值的分布.模型网格数据为140×140,目标体和背景介质相对常数分别为81和6.圆形目标体大约占10个网格.采用变换光学有限差分模式下,圆形体目标相对介电常数变为约20,体积大小约占20个网格,其代价是周围背景介质是非均匀的渐变参数分布.为了更为直观地分析参数分布特点,垂直抽取圆心所在位置的单道相对介电常数值对比,如图 4(c、d)所示.图中标准FDTD数值分布均匀,目标与背景介质区分明显,含水圆形体相对介电常数为81,背景介质及空气层分别为6和1.TO-FDTD方法中,在坐标变换之后,环状区域的相对介电常数变成半径的函数(变换前是常数).按照上述坐标变换过程使坐标拉伸压缩.在坐标拉伸的区域,相对介电常数变小.在坐标压缩的区域,相对介电常数变大.这就是为什么中间地带(拉伸)相对介电常数变小,外环区域(压缩)变大的缘故.

|
图 4 标准FDTD和变换光学FDTD模型相对介电常数分布对比 (a) 标准FDTD二维矩阵; (b) TO-FDTD二维矩阵; (c) 标准FDTD垂直单道网格; (d) TO-FDTD垂直单道网格. Fig. 4 Model dielectric constant parameter comparison of standard FDTD and TO-FDTD (a) The 2D model of standard FDTD; (b) The 2D model of TO FDTD; (c) The single trace of standard FDTD; (d) The single trace of TO FDTD. |
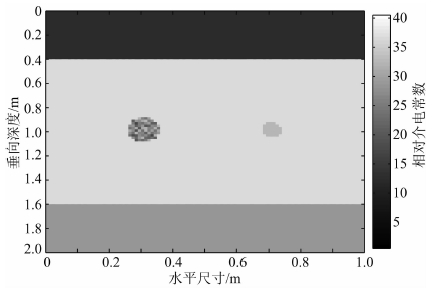
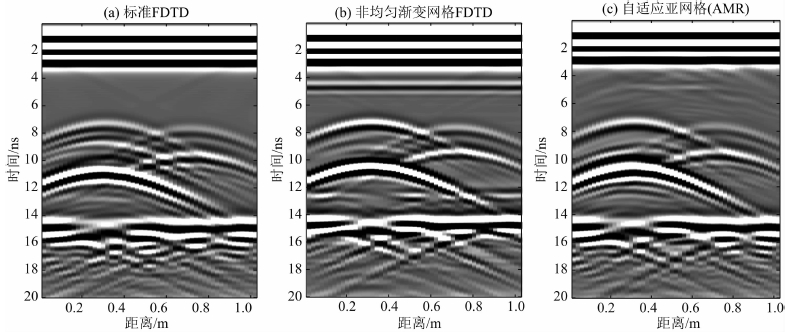
针对常规非均匀网格、自适应亚网格以及基于变换光学的有限差分方法设计不同的介质模型开展探地雷达数值模拟计算,比较不同方法在计算精度和效率方面的应用效果.图 5是两层介质模型,上层介质包含两个大小不同的随机介质圆形体.随机目标体采用混合型自相关函数生成,之所以采用随机介质目标体是为了增加模型复杂程度以测试不同方法的优缺点.模型大小为1 m×1 m.最小网格尺寸为0.01 m,上下层介质相对介电常数和电导率分别为12,6和0.01 S·m-1,0.005 S·m-1.其中随机介质目标体位于上层介质,圆形目标体半径分别为0.03 m和0.01 m,随机圆形目标相对介电常数变化范围为30~35,右侧均匀球体为30.采用天线中心频率为900 MHz的发射源,收发天线位于地表分界面.图 6为采用常规有限差分、渐变非均匀网格和自适应亚网格技术的有限差分数值模拟结果.三种方法均能够对随机圆形体目标及其层界面得到很好地模拟结果,常规有限差分结果中圆形体目标上下界面反射较为模糊,在圆形体反射信号以下存在多次波干扰,非均匀网格有限差分可以很好地压制干扰波的存在以及网格数值误差,模拟结果有更高的信噪比,目标信号清晰,杂波干扰较少.
|
图 5 不同网格划分方法测试模型 Fig. 5 The 2D test model with different FDTD method |
|
图 6 随机介质圆形体模型不同方法测试结果 (a) 常规有限差分方法; (b) 非均匀渐变网格有限差分方法; (c) 基于自适应亚网格有限差分方法. Fig. 6 The synthetic result of two random circle target model with different method (a) Standard FDTD; (b) Non-uniform FDTD; (c) AMR FDTD. |
但是,图 6b非均匀渐变网格结果在4 ns和12 ns所示的位置有固定直线反射信号,这是因为采用了横向网格加密方法,在渐变交界区域存在异常反射,网格尺寸突变造成.表 1是三种方法在相同网格尺寸条件下的计算效率对比,可以看出,基于自适应亚网格的计算时间和常规方法相当,而渐变非均匀网格在相同条件下,计算时间是常规方法的15倍左右.综合考虑计算效率和计算精度,渐变非均匀网格计算有不错的计算精度,但是计算效率较低.自适应变换亚网格计算结果在保证计算精度的同时也能较好地保证计算效率.另外,亚网格技术可以根据模型位置任意划分网格加密区域,而渐变非均匀网格只能在x或y方向整体加密网格,计算效率较低且对模型划分没有自适应亚网格方法灵活.
|
|
表 1 不同有限差分方法计算时间对比 Table 1 The comparison of computation time with different FDTD method |
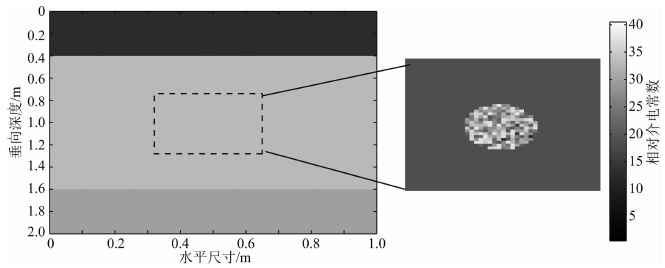
上述结果验证了常规非均匀网格在计算效率和计算精度上存在的不足.图 7是常规有限差分、自适应亚网格和基于变换光学的有限差分对比.图 7所示为两层介质模型,模型大小为1 m×1 m.最小网格尺寸为0.01 m,上下层介质相对介电常数和电导率分别为6,8和0.01 S·m-1,0.005 S·m-1.其中随机介质目标体位于上层介质.在上层模型中设计了微小随机介质圆形体模型,圆形体半径仅为0.003 m,小于网格划分的最小尺寸(0.01 m),如图 7中放大区域所示.采用天线中心频率为900 MHz的发射源,收发天线位于地表分界面.
|
图 7 局部微小随机介质模型示意图(虚框所示为局部微小目标放大) Fig. 7 The layer model with single local small random target (right figure is the zoom of the dotted box) |
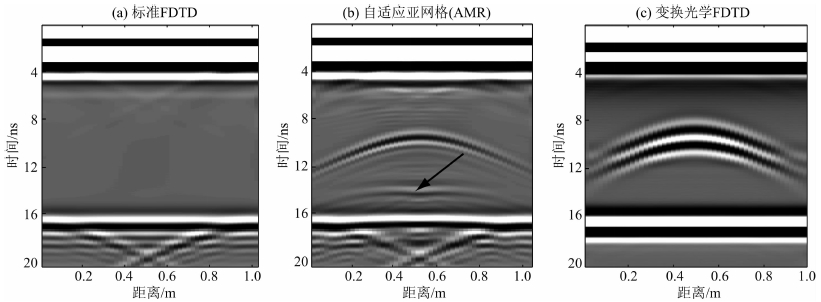
图 8所示为三种方法的计算测试结果,图 8a为常规有限差分方法模拟结果,由于目标尺寸小于最小网格,无法获得任何目标信息.在相同的条件下,采用局部亚网格有限差分,对目标区域采用Δx/4网格尺寸,图 8b中能看到明显的目标信号,箭头所示位置是因为局部粗细网格界面处理造成的计算误差,图 8c所示为采用基于变换光学的有限差分计算结果,不仅能够对模型有很好的反映,由于不需要对网格尺寸划分,即不存在亚网格技术的边界误差,显得尤为“干净”.
|
图 8 不同有限差分方法测试结果 (a) 常规有限差分方法; (b) 基于自适应亚网格有限差分方法; (c) 基于变换光学的有限差分方法. Fig. 8 The synthetic result of local small random target with different method (a) Standard FDTD; (b) AMR FDTD; (c) TO-FDTD. |
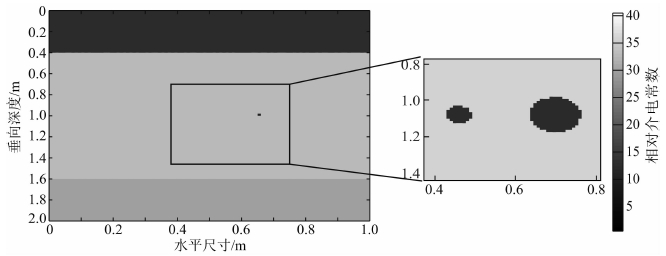
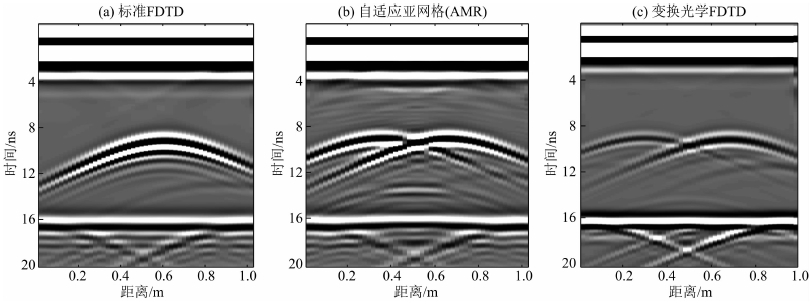
图 9所示的两个半径不同的圆形目标体,半径尺寸分别为0.003 m和0.01 m,其他参数设置与上述模型相同.采用相同的计算方式可以得到如图 10所示的计算结果,对比三种方法的结果可以看出,基于变换光学的有限差分技术通过对目标区域进行变换加密,不仅能够对微小目标有清晰的识别,而且信噪比较高,不存在边界误差干扰.层界面反射由于采用了正常的网格模式,存在的绕射干扰和多次波与常规方法和亚网格技术几乎相近.
|
图 9 局部微小随机介质模型示意图(右侧小图为黑框局部放大) Fig. 9 The layer model with two local small random target (the right figure is the zoom of the dotted box) |
|
图 10 不同有限差分方法测试结果 Fig. 10 The synthetic result of local small random target with different method |
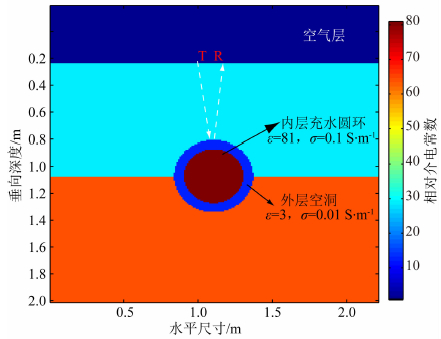
图 11为充水环状模型,通过该模型对比测试不同网格尺寸条件下变换光学和常规有限差分在计算精度和计算效率上的差异.在两层介质交界处存在一个充水环状圆形模型,圆形内半径为0.03 m,外半径为0.04 m.采用上述相同的计算参数进行数值模拟,图 12是选取收发天线位于地表中心位置的单道雷达波信号,图中分别包括最小网格尺寸为0.0025 m,0.005 m和0.01 m的常规有限差分计算结果和最小网格尺寸为0.01 m和0.015 m的变换光学有限差分计算结果.对比可以看出,常规方法在网格尺寸为0.005 m以及0.0025 m条件下计算结果与变换光学有限差分相符,而最小网格为0.01 m的结果存在明显的计算误差.表 2是不同网格尺寸的计算效率对比.相对于常规有限差分方法,基于变换光学有限差分方法可以在较大网格尺寸条件下获得与常规方法小网格相当的结果,计算效率方面却有较大的提高.例如常规方法网格为0.005 m需要52.3 s的计算时间,而变换光学有限差分网格为0.01 m时只需要35.3 s,在计算大规模长时间模型时,计算效率的优势将更加明显.
|
图 11 充水环状目标模型示意图 Fig. 11 The layer model with filling water ring |

|
图 12 采用基于变换光学有限差分和常规有限差分单道信号对比.(a) 完整单道信号; (b) 局部目标信号放大显示 Fig. 12 The comparison of single GPR signal with standard FDTD and TO-FDTD method (the right figure is the zoom of the dotted box) |
|
|
表 2 不同FDTD网格尺寸计算效率对比 Table 2 The comparison of computation time with different grid size |
基于变换光学的有限差分方法在探地雷达数值模拟中不仅能克服亚网格差分存在边界处理误差的影响,而且可以改善常规非均匀网格计算量大的问题,保持计算精度和计算效率的平衡.对于精细目标结构探地雷达模拟具有适用性,例如在探地雷达天线模拟中,馈电点的距离和天线尺寸往往存在较大的比例,特别是低频天线,馈电点的距离和天线尺寸比例接近1∶100(以馈电点1 cm,天线尺寸1 m为例),常规模拟方法为了模拟馈电点的影响,需要小于1 cm的网格尺寸,而采用本文方法,在满足稳定性条件的前提下,最小网格尺寸可选择大于1 cm.另外,变换光学也可以扩展到声波及弹性波差分方法模拟,在地震勘探大尺度目标的局部精细结构,隐形斗篷理论用于地震灾害防御(Nicoletti,2014)是当前有限差分研究的热点问题之一.
6 结论本文推导了基于变换光学的非均匀网格二维有限差分算法并应用于探地雷达正演模拟计算,对比分析了本文方法与常规FDTD方法,常规非均匀网格以及自适应亚网格(AMR)在计算效率以及计算精度上的差异.正演模拟结果表明:对于复杂随机介质模型,非均匀网格方法相对于常规有限差分可以很好地提高计算精度但是计算量也大幅度增加;自适应亚网格(AMR)有限差分方法在提高计算精度的同时可以很好地保证计算效率,但是自适应网格方法在处理粗细网格交界面时,很难避免边界反射的影响,这也是制约亚网格技术发展的瓶颈.本文提出的基于隐形斗篷理论(Cloak)的有限差分方法,通过对目标的属性参数的坐标变换,增加目标所占网格的数目,减少周围介质所占网格数目,其本质上并没有对网格进行加密,即没有增加计算量,也不存在边界反射问题.通过与常规有限差分方法对比,基于变换光学的有限差分方法在保证计算效率的同时,很好地消除了边界效应的影响,具有很好的计算精度,为探地雷达以及其他地球物理勘探方法的复杂介质精细目标结构数值模拟和参数反演提供了很好的数值计算手段.
附录A 亚网格非均匀网格原理对于二维TM模式,粗网格步长大小为Δx,Δy,时间步长为Δtc,亚网格步长为粗网格的1/nf,时间步长为Δtf=Δtc/nf.Ezn(i,j),Hxn+1/2(i,j+1/2),Hyn+1/2(i+1/2,j)表示粗网格的电磁场值,Ezfn(p,q),Hxfn+1/2(p,q+1/2),Hyfn+1/2(p+1/2,q)表示亚网格的电磁场值.当用于亚网格时,相应的电磁场值对应于Ezf,Hxf,Hyf,方程的参数与细网格区域的时间空间步长有关.电场的递推需用到周围四个磁场值.在粗细网格界面处,Ezf的计算需用到亚网格区以外的Hxf,Hyf.为了克服这个问题,在粗细网格界面附近,考虑Ez满足齐次波动方程:
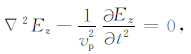
|
(A1) |
对于二维情况,可以写成
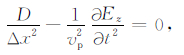
|
(A2) |
其中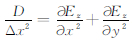

|
(A3) |
可以得到
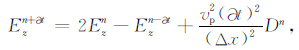
|
(A4) |
式(A4)应用于粗细网格边界.对于亚网格,从当前时刻t=nΔtc算起,需要沿时间轴往前推进nf步.在这里设nf=4,则需要分别为n+Δtf,n+2Δtf,n+3Δtf,n+4Δtf时刻,其中每一步Ezf的计算都需要用到上式.D可表示为
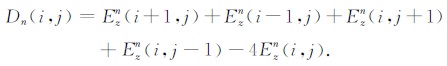
|
(A5) |
粗网格点Dn(i,j)的计算只需用到相邻粗网格点的Ezn的当前时刻值,Dn从粗网格转移到细网格需用到Taylor级数展开,对于Ezf处的点:
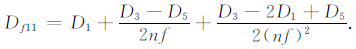
|
(A6) |
| Chen H Y, Chan C T, Sheng P. 2010. Transformation optics and metamaterials. Nat. Mater. , 9(5): 387–396. | |
| Diamanti N, Giannopoulos A. 2009. Implementation of ADI-FDTD subgrids in ground penetrating radar FDTD models. Journal of Applied Geophysics , 67(4): 309–317. | |
| Feng D S, Chen C S, Dai Q W. 2010. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chinese Journal of Geophysics , 53(10): 2484–2496. doi: 10.3969/j.issn.0001-5733.2010.10.022. | |
| Feng D S, Chen J W, Wu Q. 2014. A hybrid ADI-FDTD subgridding scheme for efficient GPR simulation of dispersion media. Chinese Journal of Geophysics , 57(4): 1322–1334. doi: 10.6038/cjg20140429. | |
| Huang C, Dong L G. 2009a. High-order finite-difference method in seismic wave simulation with variable grids and local time-steps. Chinese Journal of Geophysics (in Chinese) , 52(1): 176–186. | |
| Huang C, Dong L G. 2009b. Staggered-grid high-order finite-difference method in elastic wave simulation with variable grids and local time-steps. Chinese Journal of Geophysics , 52(11): 2870–2878. doi: 10.3969/j.issn.0001-5733.2009.11.022. | |
| Li J, Zeng Z F, Huang L, et al. 2012. GPR simulation based on complex frequency shifted recursive integration PML boundary of 3D high order FDTD. Comp. Geosci. , 49: 121–130. | |
| Li J, Zeng Z F, Wu F S, et al. 2010. Study of three dimension high-order FDTD simulation for GPR. Chinese Journal of Geophysics , 53(4): 974–981. doi: 10.3969/j.issn.0001-5733.2010.04.022. | |
| Liu J J, Brio M, Moloney J V. 2014a. Transformation optics based local mesh refinement for solving Maxwell's equations. Journal of Computational Physics , 258: 359–370. | |
| Liu J J, Brio M, Moloney J V. 2009. Overlapping Yee FDTD method on nonorthogonal grids. J. Sci. Comput. , 39(1): 129–143. | |
| Moczo P. 1989. Finite difference technique for SH-waves in 2-D media using irregular grids-application to the seismic response problem. Geophys. J. Int. , 99(2): 321–329. | |
| Nicoletti O. 2014. Seismic cloaks. Nature Materials , 13: 428. doi: 10.1038/nmat3968. | |
| Pendry J B, Schurig D, Smith D R. 2006. Controlling electromagnetic fields. Science , 312(5781): 1780–1782. | |
| Pitarka A. 1999. 3D finite-difference modeling of seismic motion using staggered grids with nonuniform spacing. Bull. seis. Soc. Am. , 89(1): 54–68. | |
| Sun C Y, Ding Y C. 2012. The precision analysis of wave equation finite difference double variable grid algorithm. Oil Geophysical Prospecting (in Chinese) , 47(4): 545–551. | |
| Sun L J, Yin X Y. 2011. A finite-difference scheme based on PML boundary condition with high power grid step variation. Chinese Journal of Geophysics , 54(6): 1614–1623. doi: 10.3969/j.issn.0001-5733.2011.06.021. | |
| Taflove A. 1995. Computational Electrodynamics: the Finite Difference Time Domain Method. USA: Artech House. | |
| Xiao K, Pommerenke D J, Drewniak J L. 2007. A three-dimensional FDTD subgridding algorithm with separated temporal and spatial interfaces and related stability analysis. IEEE Transactions on Antennas and Propagation , 55(7): 1981–1990. | |
| Wang H. 2013. Numerical modeling of acoustic wave equation with spatial varying meshes[Master thesis] (in Chinese). Changsha: Central South University. | |
| Wang L N, Liang C H. 2006. A new implementation of CFS-PML for ADI-FDTD method. Microwave and Optical Technology Letters , 48(10): 1924–1928. | |
| Xie J. 2010. Research on Subgrid Technology for FDTD[Master thesis](in Chinese). Nanjing: Nanjing University of Aeronautics and Astronautics. | |
| Zhang H, Li Z C. 2011. Seismic wave simulation method based on dual-variable grid. Chinese Journal of Geophysics , 54(1): 77–86. doi: 10.3969/j.issn.0001-5733.2011.01.009. | |
| 冯德山, 陈承申, 戴前伟. 2010. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报 , 53(10): 2484–2496. | |
| 冯德山, 陈佳维, 吴奇. 2014. 混合ADI-FDTD亚网格技术在探地雷达频散媒质中的高效正演. 地球物理学报 , 57(4): 1322–1334. | |
| 黄超, 董良国. 2009a. 可变网格与局部时间步长的高阶差分地震波数值模拟. 地球物理学报 , 52(1): 176–186. | |
| 黄超, 董良国. 2009b. 可变网格与局部时间步长的交错网格高阶差分弹性波模拟. 地球物理学报 , 52(11): 2870–2878. | |
| 李静, 曾昭发, 吴丰收, 等. 2010. 探地雷达三维高阶时域有限差分法模拟研究. 地球物理学报 , 53(4): 974–981. | |
| 孙林洁, 印兴耀. 2011. 基于PML边界条件的高倍可变网格有限差分数值模拟方法. 地球物理学报 , 54(6): 1614–1623. | |
| 王红. 2013. 变网格步长声波方程有限差分数值模拟[硕士学位论文]. 长沙: 中南大学. | |
| 谢姣. 2010. 时域有限差分方法亚网格技术的研究[硕士学位论文]. 南京: 南京航空航天大学. | |
| 张慧, 李振春. 2011. 基于双变网格算法的地震波正演模拟. 地球物理学报 , 54(1): 77–86. | |
| 赵海波, 王秀明. 2007. 一种优化的交错变网格有限差分法及其在井间声波中的应用. 科学通报 , 52(12): 1387–1395. | |
 2016, Vol. 59
2016, Vol. 59

