地球物理学报  2016, Vol. 59 Issue (6): 2266-2279   PDF    
引用本文
郑海霞, 关继腾, 薛庆忠. 2016. 基于电震耦合理论研究电极法储层岩石复电阻率频散特性. 地球物理学报, 59(6): 2266-2279, doi: 10.6038/cjg20160629.  
ZHENG H X, GUAN J T, XUE Q Z. 2016. Study on the frequency dispersion of the complex resistivity in reservoir rocks based on electroseismic coupling. Chinese J. Geophys. (in Chinese), 59(6): 2266-2279, doi: 10.6038/cjg20160629.  
基于电震耦合理论研究电极法储层岩石复电阻率频散特性
郑海霞 , 关继腾 , 薛庆忠     
中国石油大学(华东)理学院, 青岛 266580
收稿日期 2015-04-15, 2016-01-18 收修定稿
基金项目: 国家自然科学基金项目(41174101)资助.
作者简介: 郑海霞,女,1978年生,在读博士研究生,主要从事应用地球物理和电磁场理论方法研究.E-mail:zhenghx@upc.edu.cn
摘要: 复电阻率测井在识别油水层的能力上优于常规电阻率测井,然而储层岩石复电阻率特性的微观机理还没有统一完整的解释和数学模拟方法,致使复电阻率测井技术的开发缺乏足够的理论基础.本文基于孔隙介质Pride电震耦合理论,结合谐变信号激励下渗流场与电流场的耦合理论,推导出一级近似条件下的Pride电震耦合理论.采用格林函数方法建立了一维电震波场的波动方程及其解.构造了双电极法测量储层岩石复电阻率的物理模型和数学模型,从理论上阐明了岩石复电阻率频散特性的微观机制与电震效应的关系,定量分析了储层岩石复电阻率频散特性的影响因素.数学模拟结果表明:储层岩石复电阻率的频散现象是在电震快纵波和电震慢纵波的共同作用下,由孔隙介质中的电渗流机制形成的;储层岩石的复电阻率随孔隙度的增大而减小,随渗透率的增大而增大,地层水矿化度的增加或阳离子交换量的增大使得同频率的复电阻率减小.慢纵波界面极化频率受孔隙度、渗透率和地层弹性模量的影响较大,而快纵波界面极化频率受地层弹性模量的影响较大.
关键词: 复电阻率      电震效应      储层岩石      频散特性      双电极法     
Study on the frequency dispersion of the complex resistivity in reservoir rocks based on electroseismic coupling
ZHENG Hai-Xia, GUAN Ji-Teng, XUE Qing-Zhong     
College of Science, China University of Petroleum, Qingdao 266580, China
Abstract: Complex resistivity logging has a better ability to distinguish oil and water layers than normal resistivity logging. In recent years, research on this issue focused on experimental studies of factors influencing complex resistivity, while little has been done on the mechanism model and mathematical simulating method for describing complex resistivity, which makes it difficult to reveal the process of frequency dispersion from a microscopic point of view. The development of complex resistivity logging technology is impeded due to insufficient theoretical basis. In this work, mathematical models and analogy methods are developed, and the microscopic mechanism of dispersion characteristics of complex resistivity in reservoir rock is investigated. The electro-osmotic flow process and the electroseismic coupling effect are taken into account to interpret and evaluate the frequency dispersion of complex resistivity in reservoirs. The first thing is to derive a first-order approximation to the Pride electroseismic coupling theory, combining the seepage field and the current field. Next, the Green's function method is applied to build a one-dimensional wave equation and its solution. By the resulting solution, the propagating features of the electroseismic waves are analyzed. And then, according to the theory of two-electrode method measuring complex resistivity, we analyze the propagating characteristics of the current field which is influenced by the electroseismic coupling effect, and on this basis we construct physical and mathematical models of complex resistivity measured by the two-electrode method. Lastly, we clarify the influence factors on the dispersion characteristics by quantitatively analyzing the influence of porosity, permeability, salinity, cation exchange capacity, elastic modulus and core length. Simulation results show that the curve of the complex resistivity exhibits obvious frequency dispersion. The real part of the complex resistivity descends roughly in a ladder-like fashion, i.e. when the frequency is small, the real part experiences a rapid decline, then slows down. With the increasing of frequency, rapid decline happens again, and finally the curve reduces to zero. The imaginary part of W-shape shows two clear peaks. All these characteristics are formed under the combination of the electroseismic fast P-waves and electroseismic slow P-waves. When the porosity is raised, the complex resistivity value and the interfacial polarization frequency of slow-P-wave both decrease, while that of the fast P wave remains fairly constant. When the permeability is raised, the complex resistivity value and the interfacial polarization frequency of slow-P-wave both increase. Enhancing salinity contributes to the decrease of the complex resistivity value, while makes no contribution to the change of the two interfacial polarization frequencies. So does the cation exchange capacity. Changing of the elastic modulus has no effect on the complex resistivity value, while the two interfacial polarization frequencies vary with it evidently. Change of the core length has little influence on the complex resistivity value, while the two interfacial polarization frequencies both reduce with the increasing core length. Frequency dispersion is generated as a result of electroosmotic flow in porous media influenced by the combination of electroseismic fast P-waves and electroseismic slow P-wave. Correctness and reliability of this view are verified using the computing instances. It provides a new idea for the development of complex resistivity logging. Both the real part and the imaginary parts of complex resistivity curves show evident frequency dispersion. The abundant reservoir information contained in the dispersion characteristics can benefit the research of rock structure and fluid property. The value of the complex resistivity increases along with the decreasing of porosity, and the increasing of the permeability, the salinity, and the cation exchange capacity. The interfacial polarization frequencies are dominated by electroseismic wave velocity. The interfacial polarization frequency of slow P waves is found to enhance with the reducing of the porosity, and the raising of the permeability. The interfacial polarization frequency of fast-P-wave is found to vary with the elastic modulus. Both of the two interfacial polarization frequencies change little with the variation of salinity and cation exchange capacity..
Key words: Complex resistivity      Electroseismic coupling      Reservoir rocks      Frequency dispersion      Two-electrode method     
1 引言

复电阻率测井是在不同的频率条件下测量储层的电阻率，根据测量的电阻率频散信息来识别油气水层，可以较好地反映储层岩石的含油气性.近几年来，围绕着复电阻率测井技术的推广应用开展了许多研究工作，主要集中于探索复电阻率影响因素的实验研究以及复电阻率模型的数学模拟，研究方法还处于半经验半理论状态，缺少定量的数学描述，无法从微观机理上揭示储层岩石复电阻率频散特性的产生过程，造成复电阻率测井技术仍然缺乏坚实的理论基础，相关技术的开发仍然停留在试验阶段，还无法达到真正的工业化应用要求.

岩石复电阻率频散机理研究是复电阻率测井技术的研发基础.复电阻率频散特性的实验研究始于20世纪70年代，Zonge和Wynn(1975)提出剩余电磁参数可明显指示构造的含油气性，并报告了复电阻率法在油气田上的应用效果，这为复电阻率法应用于油气探测奠定了基础.Shen等(1985)研究了800~1200 MHz时岩心介电频散的特点.郑和华等(1993)运用岩石物理实验方法，在模拟地层温度和压力的条件下，在100 Hz~15 MHz频段上测量了岩石样品的复电阻率特性，从电流的角度探讨了复电阻率的频散机理.范宜仁等(1994)通过岩石频散特性的分析，认为岩石泥质含量及含油气饱和度将直接影响复电阻率的频散特性.安珊和李能根(1998)实验发现饱和盐水的泥质砂岩的复电阻率模值、复电阻率实部与复电阻率虚部均随测量电流频率、地层水矿化度以及泥质含量的升高而减小.苏庆新等(1999)采用双电极法研究了不同含水饱和度下的岩石电阻抗和界面极化频率.柯式镇等提出线圈法(柯式镇等，2003；柯式镇，2010)和电极法(柯式镇等，2006)测量复电阻率特征，并且认为线圈法与电极法频散规律可以用一定的数学模型进行描述，二者符合同一模型，具有互换性.Ulrich和Slater(2004)测量发现非胶结砂岩的复电阻率与含水饱和度有关.童茂松等(2005a，b，2007)研究了复电阻率实部频散度、模的频散度以及虚部频散度与含水饱和度的关系.肖占山等(2006a，b，2007，2009)发现泥质砂岩的复电阻率频散特性受含油饱和度、润湿性的影响较大，受地层水矿化度的影响较小.卢艳(2008)利用双电极法进行宽频带扫频测量，结果表明复电阻率的模值、虚部、模的差值和虚部差值都随含水饱和度的增加而降低.王畅等(2012)通过聚合物驱油实验结果提出复电阻率虚部同含水饱和度之间存在线性关系.张雷洁等(2013)采用双电极法观测到岩心复电阻率频散程度随着含水饱和度的增加而减弱，且界面极化频率随含水饱和度和饱和水矿化度的增加而增大.

有关岩石复电阻率数学模型的研究，不少学者通过等效电路的方式来模拟岩石的频散现象，其中比较经典的是Cole-Cole复电阻率模型.Cole和Cole(1941)为解释电介质的介电频散现象，考虑到频率域中的电子导体与电解液界面上的复超电压等效于单位面积上的复阻抗，从而提出该模型.Pelton等(1978)借用类似的等效电路模型来描述复电阻率的频谱特性，同时指出Cole-Cole模型不仅可以描述激发极化效应，还可以用来描述电磁感应频谱的低频部分，而复电阻率频散响应可以表示为多个Cole-Cole模型的组合.此后，Wait(1981)、Guptasarma(1984)、陆启行(1985)、刘崧(1988)、Xiang等(2001)、柯式镇等(2006)、程辉等(2010)、李勇等(2011)等都曾先后对Cole-Cole模型进行化简.然而Cole-Cole模型对各参数所反映的物理意义探讨的并不十分深入，该模型参数除了极化率和电阻率这两个参数得到实际应用外，频率相关系数和时间常数在实际中还没有得到充分利用(刘崧，1998).Dias(2000)对复电阻率频谱基本数学模型进行了总结，提出了一种新的激发极化模型，并对该模型中各个参数的物理意义进行了详细说明.姜恩承等(2002)根据电化学理论，应用电阻和电容网络模型来模拟电极发射法交变电场岩石阻抗，给出每个等效电路中电子元件的数学表达式，使网络模型转换成用地层参数描述的数学模型，通过阿尔奇公式得出了复电阻率公式.Jougnot等(2010)基于Maxwell-Wagner极化理论采用频谱激发极化法研究了非饱和岩石复电阻率的幅值和相位随含水饱和度的变化关系.总之，现有主流数学模型的建立大多基于等效电路的思想，理论上只要电路模型足够复杂，就可以很好地拟合实测数据.然而这类方法毕竟不是从复电阻率的物理本质出发，还不能将等效电路中的元件参数与储层岩石储渗参数和宏观电化学参数之间的关系建立起来，所以不能很好地解释岩石复电阻率的频散特性及其与岩石物性参数之间的定量关系，尚不能用于解决实际问题.

当谐变电流场作用于流体饱和孔隙介质时，在孔隙介质中激发周期性电渗流动和弹性波的传播，产生电震效应.1961年，安茨费洛夫(波达波夫，1996)通过实验证实了第二类震电效应的逆效应—电震效应. 波达波夫(1996)介绍了直流电场对地震波的影响，建立了描述孔隙介质中弹性波场和电磁场之间相互作用的数学模型，研究了周期性电流场对孔隙地层的作用，实验表明地层岩石发生了机械振动，即出现电震现象.Pride和Haartsen(1996)研究了各向同性孔隙介质中电震耦合平面波的特性.斯维托夫(陈邦彦，2006)指出：电震法的基础是含水孔隙岩层中的电渗现象，电震法可以弥补震电法的不足.近年来，国内也开展了相关的研究(石昆法，2001；周成当等，2001；刘洪，2002；苏巍等，2006).李建勇等(2001)对大庆油田1999年的实验进行了深入分析，实验发现直流电场确实改变了地震波中面波与反射波的比例.胡恒山等(2003)提出了声电效应测井时转换电场的计算公式.Hu等(2007)利用Biot理论和麦克斯韦电磁理论构成的Pride理论，研究了交变电流源激发的电声测井响应.任恒鑫等(2010)解决了层状孔隙介质震电波场数值模拟的高频不稳定性问题.张丹等(2013)讨论了不同结构模型中双力偶点源以及有限断层面源作用下产生的地震波及其伴随电磁信号的时域和频域特征.张泉滢等(2014)定量模拟了震电波的传播规律及电磁特性.资料分析表明，储层岩石的复电阻率特性和电震效应均是由谐变电流激发的电化学效应.因此可以综合考虑储层岩石电渗流过程及电震效应，有效地解释与评价储层岩石复电阻率的频散特性.

本文的研究拟解答两个问题：(1)岩石复电阻率频散特性的微观机制是什么？(2)如何构建描述复电阻率的数学模型和定量计算方法？基于以上问题，本文以孔隙介质Pride电震耦合理论为基础，采用格林函数方法建立了一维电震波场的波动方程及其解，针对双电极法构建了储层岩石复电阻率的计算公式.系统地利用数学方法阐明了岩石复电阻率频散特性的微观机制，分析了储层岩石的孔隙度、渗透率、阳离子交换量、地层水矿化度与复电阻率特性的定量关系，为提高复电阻率测井的定量解释水平提供新的思路和科学依据.

2 孔隙介质中的电震耦合理论

测量岩石复电阻率的实验室方法之一是双电极法，如图 1所示.设柱状岩心轴向为z方向，径向为r方向.由供电电极A、B向岩心供入频率为ω的谐变电流，电流密度为Je=Je0e-iωtez，测量流经岩心的电流和岩心两端的电位差即可得到岩心的复电阻率.

图 1 双电极法测量复电阻率模型 Fig. 1 Sketch of measuring complex resistivity by the two-electrode method
2.1 Pride电震耦合理论

根据电震耦合理论，当谐变电流作用于流体饱和孔隙介质时，孔隙液体中的带电离子将会受到激发而引起周期性电渗流动，致使孔隙中的液体与岩石固体骨架发生相对运动，从而在储层岩石中激发弹性波，即产生储层岩石中的电震效应.因此岩石复电阻率的微观机制中，电震耦合效应成为必不可少的微观机制之一.Pride电震波理论(Pride and Haartsen，1996)包括麦克斯韦电磁理论、孔隙介质Biot理论以及动电耦合理论.假定谐变场的时间因子为e-iωt，Pride电震耦合控制方程改为

(1)

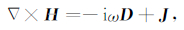
(2)

(3)

(4)

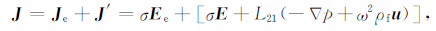
(5)

(6)

(7)

(8)

(9)

其中，ω为角频率，E、D、H和B分别表示电震相互耦合场激发的电磁场的电场强度、电位移矢量、磁场强度和磁感应强度，μ为磁导率，ε为孔隙介质介电常数，可用流体介电常数εf、基质介电常数εs表示为ε=ϕεf+(1-ϕ)εs，ϕ是孔隙度，J为岩心内的总电流密度，J′表示因电震耦合而产生的电流密度，Je和Ee分别表示外界人工电源供入岩心的电流密度和电场强度，σ为动态电导率，L12和L21分别为由谐变信号激励下渗流场与电流场的耦合理论推导出的电动耦合系数和动电耦合系数，p是流体压强，w为渗流位移，可用固相位移u和液相平均位移uf表示为w=ϕ(uf-u)，κD为动态渗透率，η为流体黏度，τ为应力张量，ρ为地层密度，可用基质密度ρs和流体密度ρf表示为ρ=ϕρf+(1-ϕ)ρs，而M、C、H和G为孔隙介质的弹性模量.

2.2 一级近似条件下的一维Pride电震耦合理论

由于岩心尺寸远小于电磁波波长，可以认为岩心内外源注入电流密度Je均匀分布且与坐标无关.在一级近似条件下，即在准静态条件下，式(2)和式(5)中可忽略位移电流和二次感应电流与震电耦合电流[σE+L21(-Δp+ω2ρfu)]的影响，即取J=Je=Je0ez，代入式(2)得：

(10)

由安培环路定律，可得磁场强度为

(11)

式中，r为岩心径向坐标，eϕ为方位角方向的单位矢量.

将式(11)代入式(1)，有：

(12)

由柱坐标系中旋度的计算公式，从式(12)中解出感应电场强度为

(13)

式(11)和式(13)为一级近似条件下电磁相互耦合产生的电磁场.将式(13)代入式(5)和式(6)，且考虑到Je=σEe，可得到二级近似条件下的电渗相互耦合公式为

(14)

(15)

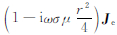
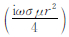
式(14)中L21(-Δp+ω2ρfu)表示由孔隙介质中的弹性振动引起的电流，相比于注入电流，这部分电流非常小可忽略不计，则式(14)中的总电流可写为J=. 若岩心半径数量级为10-2 m，电导率数量级为10-2S·m-1，则表达式中的数量级为f×10-12，在岩心复电阻率测量的频率范围内f×10-121，因此岩心中的电流密度可近似为注入电流密度，即式(14)简化为

(16)

同理，式(15)可简化为

(17)

2.3 一维电震耦合波的弹性波场响应

考虑到波沿z方向传播，则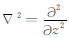，将式(9)代入式(17)，可得：

(18)

将式(8)代入式(7)，可得：

(19)

式(18)和式(19)给出了注入电流密度Je与其激发的固相位移u和渗流位移w之间的关系，然而三者的幅值关系不能简单的由此求出，原因在于这两式表示有源空间波动方程，为非齐次方程，其通解往往采用格林函数方法求得.为求解u、w，先将式(18)、(19)整理成一维电震耦合波动方程形式为

(20)

(21)

令Gu和Gw分别表示u和w对应的格林函数，则由式(20)、(21)可得单位点电流源激发的电震耦合波动方程为

(22)

(23)

利用空间域与波数域之间的一维傅里叶变换关系，其中“+”号表示沿正z轴传播的波(简称正向波)，“-”号表示沿负z轴传播的波(简称反向波)，A代表Gu和Gw，且考虑到δ函数的筛选性，式(22)和式(23)可变换为

(24)

(25)

令式(24)和式(25)的行列式为零，可得电震波波数平方为

(26)

其中，“+”号表示电震慢纵波波数平方kps2，“-”号表示电震快纵波波数平方kpf2.

由式(24)和式(25)可解得：

(27)

(28)

根据一维傅里叶反变换关系A(z)=，对式(27)和式(28)进行变换，可得：

(29)

(30)

由复变函数理论中的留数(残数)定理，可得固相位移和渗流位移的格林函数为：

(31)

(32)

令：

(33)

则式(31)和式(32)可简写为：

(34)

(35)

由格林函数方法中的一维格林函数积分公式：

(36)

(37)

则固相位移和渗流位移的解可表示为：

(38)

(39)

由于沿波的传播方向振幅衰减为零，即e∓ik∞→0，因此式(38)和式(39)可化简为：

(40)

(41)

式(40)和式(41)括号中的第一项表示电震快纵波激发的介质响应，第二项表示电震慢纵波激发的介质响应.若式中“±”号都取“+”号，表示正向波的弹性波场响应，若都取“-” 号，则表示反向波的弹性波场响应.因此，从单一波角度看，式(40)和式(41)应分为四种模式的电震波，公式为

(42)

(43)

(44)

(45)

弹性振动来源于注入岩心的电流Je0，因此岩心两端注入的电流也应分为沿正z轴传播的电流和沿负z轴传播的电流，不妨设：

(46)

(47)

可以验证，式(46)和式(47)给出的正反向波形式的电流是符合岩心中电震波传播规律的，电震波可视为正、反两个方向传播的行波.式(46)和式(47)是无界空间正反向波电流表达式，而对于岩心复电阻率测量来说，研究区域是有限的，正反向波激励源大小不同，应由边界条件确定.

3 储层岩石复电阻率的数学模拟 3.1 复电阻率的定义

根据电极法测量复电阻率原理，岩心的复电阻率可表示为

(48)

式中，ρ*(ω)为岩石复电阻率，J0为供电电流密度，ΔU为岩心两端电位差，ρR(ω)、ρI(ω)分别是复电阻率的实部和虚部(王伟男等，2004).

3.2 供电电流的传播模式

电极注入岩心的电流一部分用于激发电震快纵波，另一部分用于激发电震慢纵波，则电流密度J=Jpf+Jps，Jpf和Jps分别为快纵波的电流密度和慢纵波的电流密度.由于两种模式的电震波传播方向都与电流方向一致，则根据式(46)和式(47)电流密度可表示为

(49)

式中，Jpf0、Jps0为电流密度的振幅.由于Biot理论中激发的弹性快纵波和慢纵波的大小与储层岩石的孔隙度、渗流特性和孔隙的连通特性密切相关，Jpf0和Jps0的大小亦由岩石的孔渗特性决定.Jpf0和Jps0无法由人为激励确定，也就无法由数学方法确定.

不妨将快、慢纵波模式各自对应的电流与总激发电流的关系表示为Jpf0=Apf0J0，Jps0=Aps0J0.其中，Apf0和Aps0可理解为注入的总电流中激发快纵波模式和激发慢纵波模式的电流在总电流中所占的权重，且有Apf0+Aps0=1. 式(49)可写为

(50)

因此，设正向波和反向波的电流密度的振幅分别为J+0和J-0，岩心中任一点处总的电流密度为正反向电震波的电流之和. 因此，总电流密度可写为

(51)

根据谐变电流注入特点，在两供电电极A、B处电流密度相同，设为J0，因此：

(52)

将式(51)代入上式，且由于Apf0+Aps0=1，则在z=0处，有：

(53)

在z=L处，有：

(54)

将式(53)代入式(54)，可得到正反向电震波的电流密度振幅与总电流密度振幅之间的关系为

(55)

3.3 复电阻率的计算公式

令αξ=1σ，其中ξ=pf，ps.根据式(16)，岩心中电场强度Ee与电流密度Je的关系可表示为

(56)

由电流密度表达式(51)，岩心中的电场强度可表示为

(57)

根据电位差公式：

(58)

两电极间的电位差可表示为

(59)

对于给定长度为L的岩心，将式(59)代入式(48)，并将式(55)代入整理可得岩心的复电阻率为

(60)

由上式可看出，岩心的复电阻率与频率、岩石的电化学参数和弹性参数之间有着复杂的函数关系.

4 计算实例与分析

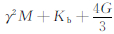
根据前述数学模型，对储层岩石复电阻率的频散特性进行数学模拟.选取的岩心基本参数如表 1所示，电动耦合系数L12、动电耦合系数L21、动态渗透率κD、电导率σ的具体表达式由于华等(2013)给出，弹性模量M、C和H的表达式由Biot-Gassman关系给出，C=γM，H=，其中，. 式中，Ks、Kf分别代表固体基质体积模量和流体体积模量，为储层已知参数；G、Kb分别代表骨架剪切模量和骨架体积模量，可以由复合介质弹性模量自洽理论(Berryman，1980)确定.

表 1 岩心复电阻率模型的基本参数表 Table 1 Basic parameters of complex resistivity of rock core
4.1 复电阻率频散特性的计算实例

除上述基本参数外，计算复电阻率还需要确定电震波中快纵波和慢纵波所占的比值.由于Apf0和Aps0无法由数学方法确定，为分析问题方便，选取三组具有代表性的权重进行模拟，取值如下：Apf0=0.8，Aps0=0.2，Apf0=0.5，Aps0=0.5，Apf0=0.2，Aps0=0.8.

考察101~106 Hz频段内复电阻率实部和虚部随频率的变化关系，如图 2所示.图中实线代表复电阻率实部，虚线代表复电阻率虚部.由模拟结果可看出，无论选取哪组快纵波和慢纵波的权重值，复电阻率曲线都显示了明显的频散现象：复电阻率实部呈“阶梯状”下降，即频率较低时，复电阻率实部先经历一次快速下降过程，然后缓慢下降，随着频率的增高，在2×104 Hz附近再一次快速下降，最后趋于零；复电阻率虚部曲线上有两个清晰的极值，曲线呈“W”型.本文复电阻率数学模型的模拟曲线虽然未能完全符合实验规律，但两次阶梯变化、两个界面极化频率等特征都与大量实验结果高度吻合(柯式镇等，1999；肖占山等，2006a，2006b；马静等，2008；Tong and Tao，2008；王畅等，2012).

图 2 复电阻率的频散特性曲线 Fig. 2 Frequency dispersion curves of complex resistivity

观察复电阻率虚部的两个极值可发现，随着慢纵波权重的增加，第一极值增大，而第二极值减小，反之，随着快纵波权重的增加，第一极值减小，而第二极值相应增大.由此可推断，复电阻率频散曲线中的两次变化分别由电震慢纵波和电震快纵波引起，其中第一次变化，即复电阻率实部第一次快速下降的位置和复电阻率虚部第一极值的位置取决于慢纵波；而第二次变化，即复电阻率实部第二次快速下降的位置和复电阻率虚部第二极值的位置取决于快纵波.由此，不妨将复电阻率虚部第一极值对应的频率称为慢纵波界面极化频率，复电阻率虚部第二极值对应的频率称为快纵波界面极化频率.某些复电阻率频散特性实验中给出的界面极化频率，实际上是快纵波界面极化频率.

图 2的模拟结果表明，无论总电流在快纵波和慢纵波模式下如何分配，都不会影响复电阻率和弹性波响应随频率的变化规律.因此为了简单但不失一般性，在后续复电阻率频散特性影响因素的讨论中取Apf0=0.5，Aps0=0.5.

4.2 复电阻率频散特性的微观机理分析

根据电震耦合理论，当谐变电流作用于流体饱和孔隙介质时，孔隙流体中的带电离子将会受到激发而引起周期性电渗流动，致使孔隙中的液体与岩石固体骨架发生相对运动，从而在储层岩石中激发弹性纵波.当弹性纵波传播时，被激发的流体带动孔隙流体中的离子相对固定电荷运动，因此产生流动电流.这个流动电流导致流体中的离子在波稀疏(密集)的地方堆积，在波密集(稀疏)的地方减少，形成了离子的浓差极化效应.

根据Δ·J=iωρe，代入式(51)和式(55)，则岩心内电荷密度ρe沿轴向的分布可表示为

(61)

令供电电流密度J0=1 A/m2，分别取频率值为10、102、103、104、105、106 Hz，根据式(61)可画出岩心长度范围内电荷密度随坐标的变化规律，如图 3所示.由图 3可看出，岩心两端电荷密度最大，正负电荷之间产生附加电场.这个由浓差极化效应产生的附加电场与流体中传导电流产生的伴随电场叠加形成岩心内的总电场.

图 3 电荷密度沿岩心轴向的分布 (a) 电荷密度的实部； (b) 电荷密度的虚部. Fig. 3 Distribution of charge density in the core along axial direction (a) Real part of the charge density; (b) Imaginary part of the charge density.

利用式(16)计算可得电场强度与电流密度之间的关系.不同频率下，岩心长度范围内电场强度随坐标的变化规律由图 4给出.图 4a表明，电场强度在岩心内呈周期性分布，其周期与注入电流的频率有关.

图 4 电场强度沿岩心轴向的分布 (a) 电场强度的实部； (b) 电场强度的虚部. Fig. 4 Distribution of electric field intensity in the core along axial direction (a) Real part of field intensity; (b) Imaginary part of field intensity.

(1)10 Hz时，电场强度的实部几乎是一条直线，场强分布与位置无关，此时岩心中的电流可视为稳恒电流，由式(48)和式(58)可知，在这一频率附近复电阻率的实部基本不变.

(2)当频率增至102 Hz时，随着频率的增加，半波长范围内电场强度大幅减弱，复电阻率实部随之迅速减小(即第一次快速下降).

(3)观察103 Hz和104 Hz曲线不难发现，电场强度变化较小，因而复电阻率变化较为缓慢.

(4)105 Hz时，电场强度在一段长度上表现为负值，场强沿坐标轴的积分应为正值部分积分S+减去负值部分积分S-，且S+随频率减小的同时，S-增大，这样二者之差迅速减小，因此复电阻率实部曲线快速下降(此即为第二次快速下降)，当S-增大到刚好等于S+时，复电阻率为零，当S-大于S+时，则复电阻率出现负值.

(5)再看106 Hz曲线，可观察到有多个完整波长，且曲线在0附近震荡，这样S-与S+在完整波长内对应抵消，对于不足一个波长的部分，若S+大于S-，则复电阻率为正值，反之，复电阻率为负值，随着频率的增大，复电阻率的正负值交替变化，因而复电阻率在高频时产生震荡现象，并且由于频率越大，不足完整波长的部分越小，因此震荡部分复电阻率的值越来越小，最终趋于零.

图 4b表明，复电阻率虚部决定于电场强度的虚部，其变化原因与实部一致.若S-增大，S+减小，则虚部绝对值增大，反之减小.当二者差值最大时，对应两个极值的情况.

由上述分析可知，复电阻率频散特性与谐变电流下的电渗流机制密切相关，然而由于岩心内电渗流的物理过程非常复杂，对其微观机理很难进行直观地描述，因此只能从电荷密度和电场强度的角度给出简单的解释.

4.3 复电阻率的频散特性与孔隙度的关系

在其他参数不变且不改变渗透率的情况下，仅改变孔隙度的大小，可以得到复电阻率与孔隙度的关系，如图 5所示，图中模数为孔隙度.从图中可看出，岩心复电阻率实部和虚部的绝对值随孔隙度的增大而减小；慢纵波界面极化频率向左推移，快纵波界面极化频率几乎不变.产生这一情况的原因在于，孔隙度越大，流体导电能力越强，因而复电阻率越小.界面极化频率与波速有关，随着孔隙度增大，慢纵波速度大幅减小，因此慢纵波界面极化频率向左移动.

图 5 复电阻率的频散特性与孔隙度的关系曲线 Fig. 5 Relationship between frequency dispersion of complex resistivity and porosity
4.4 复电阻率的频散特性与渗透率的关系

在其他参数不变且不改变孔隙度的情况下，仅改变渗透率的大小，可以得到渗透率对复电阻率频散特性的影响，如图 6所示.随着渗透率的增大，同频率下S+与S-的差值增大，因而复电阻率变大.渗透率的增大使得慢纵波速度大幅增加，因而图 6中慢纵波界面极化频率明显向右推移.

图 6 复电阻率的频散特性与渗透率的关系曲线 Fig. 6 Relationship between frequency dispersion of complex resistivity and permeability
4.5 复电阻率的频散特性与矿化度的关系

为研究地层水矿化度对复电阻率频散曲线的影响，选取了三种不同地层水矿化度(1000 mg·L-1、5000 mg·L-1和10000 mg·L-1)，如图 7所示.模拟曲线表明：随着矿化度的增加，浓度增大，溶液中导电离子增多，因此岩心复电阻率实部和虚部的绝对值都减小，而矿化度的改变并不影响波速，因此慢纵波界面极化频率和快纵波界面极化频率都不随矿化度的变化而变化.

图 7 复电阻率的频散特性与矿化度的关系曲线 Fig. 7 Relationship between frequency dispersion of complex resistivity and salinity
4.6 复电阻率的频散特性与阳离子交换量的关系

改变阳离子交换量的大小，取阳离子交换量分别为0.2 mol·L-1、0.5 mol·L-1和0.8 mol·L-1，可以得到复电阻率的频散特性与阳离子交换量的关系曲线，如图 8所示.阳离子交换量越大，储层岩石的导电能力越强，因此复电阻率的数值越小；而电震快纵波和慢纵波的波长与阳离子交换量无关，因此两个界面极化频率的位置不发生变化.

图 8 复电阻率的频散特性与阳离子交换量的关系曲线 Fig. 8 Relationship between frequency dispersion of complex resistivity and cation exchange capacity
4.7 复电阻率的频散特性与弹性模量的关系

为分析复电阻率频散特性与骨架弹性模量的关系，选取了三组弹性模量值(单位GPa)：第一组为表 1给出数据，Kf=2.25，Ks=40.7，计算得到，Kb=28.94，G=20.26；第二组Kf=2，Ks=36，Kb=0.0436，G=0.0261(周新民等，2006)；第三组Kf=2.25，Ks=35.7，Kb=3.11，G=2.45(高永新和胡恒山，2009).图 9给出模拟结果：复电阻率数值不变，原因在于弹性模量的变化不影响介质导电性；而慢纵波界面极化频率和快纵波界面极化频率都随弹性模量的改变而有明显变化，原因在于极化频率与纵波传播速度有关，而波速受到骨架弹性模量的影响.

图 9 复电阻率的频散特性与弹性模量的关系曲线 Fig. 9 Relationship between frequency dispersion of complex resistivity and elastic modulus
4.8 复电阻率的频散特性与岩心长度的关系

根据实验中岩心长度的范围，选取2.5 cm、5.0 cm和7.4 cm三种岩心长度的岩心进行数学模拟.岩心长度对电阻率频散特性的影响如图 10所示，岩心长度对导电性没有影响，因而复电阻率大小不变；当岩心长度增大时，岩心长度范围内完整波长个数增加，S+和S-的差值达到极大时对应的频率减小，因而慢纵波界面极化频率和快纵波界面极化频率都随岩心长度的增加而减小.

图 10 复电阻率的频散特性与岩心长度的关系曲线 Fig. 10 Relationship between frequency dispersion of complex resistivity and core length
5 结论

本文突破了储层岩石复电阻率研究以实验为主的现状，以Pride电震耦合理论为基础，根据双电极法特点，实现了对岩石复电阻率的定量数学描述，从微观机理上研究了储层岩石复电阻率的频散特性，通过计算实例证明了该理论的正确性和可靠性.并得到以下结论：

(1) 储层岩石复电阻率的频散现象是由孔隙介质中的电震耦合作用产生的，其微观机理的本质是电渗流作用.本文给出的复电阻率机理定量解释模型为复电阻率测井技术的开发提供了全新的思路.

(2) 一般情况下，复电阻率实部频散曲线上有两次阶梯状下降，复电阻率虚部频散曲线上有两个极值，这些特征是由电震慢纵波和电震快纵波共同作用形成的.电震波波速决定了界面极化频率出现的位置，同时对复电阻率实部和虚部的绝对值也有影响.

(3) 数学模拟结果表明，保持其他物理量不变，复电阻率的大小随着储层岩石孔隙度的增大而减小，而随着渗透率的增大而增大，地层水矿化度或阳离子交换量的增大都会使得复电阻率减小.

(4) 慢纵波界面极化频率随着孔隙度的增大而降低，而随着渗透率的增大而有较大幅度的增高；地层水矿化度和阳离子交换量对两个界面极化频率几乎没有影响；快纵波界面极化频率受弹性模量的影响较大.

由于复电阻率机理解释涉及到多孔介质的流体机制，采用不同的多孔介质流体机制模型，可得到不同的复电阻率模拟结果.本文选用的Biot双相介质物理机制模型，并不能解释所有的实验现象和物理起因.除此之外，由于实际储层岩石微观孔隙结构和渗流机制的复杂性，且储层岩石复电阻率的实验资料十分有限，文中所得结论还有待于进一步的实验验证.

致谢

感谢审稿专家提出的建设性意见，使本文的理论体系更加严谨，微观机理解释更加合理，论述更加完善.同时，感谢编辑老师细致耐心的工作！

参考文献
An S, Li N G. 1998. An investigation on multi-resistivity of aqueous rock. WLT (in Chinese) , 22(5): 315–317.
Berryman J G. 1980. Long-wavelength propagation in composite elastic media II. Ellipsoidal inclusions. The Journal of the Acoustical Society of America , 68(6): 1820–1831. doi: 10.1121/1.385171.
Chen B Y Trans. 2006. Research prospects of seismo-electromagnetic effect in the new century. Marine Geology (in Chinese) (1): 59–66.
Cheng H, Di Q Y, Li D Q. 2010. The discussion electrical properties of rocks base on frequency response characteristics. Progress in Geophysics , 25(3): 918–925. doi: 10.3969/j.issn.1004-2903.2010.03.027.
Cole K S, Cole R H. 1941. Dispersion and absorption in dielectricsⅠ. Alternating current characteristics.. Journal of Chemical Physics , 9(4): 341–351. doi: 10.1063/1.1750906.
Dias C A. 2000. Developments in a model to describe low-frequency electrical polarization of rocks. Geophysics , 65(2): 437–451. doi: 10.1190/1.1444738.
Fan Y R, Lu J M, Wang G H, et al. 1994. Experimental study on the dispersion of rock resistivity. Journal of the University of Petroleum, China (in Chinese) , 18(1): 17–23.
Gao Y X, Hu H S. 2009. Numerical simulation and analysis of seismoelectromagnetic wave fields excited by a point source in layered porous media. Chinese J. Geophys. , 52(8): 2093–2104. doi: 10.3969/j.issn.0001-5733.2009.08.018.
Guptasarma D. 1984. True and apparent spectra of buried polarizable targets. Geophysics , 49(2): 171–176. doi: 10.1190/1.1441648.
Hu H S, Guan W, Harris J M. 2007. Theoretical simulation of electroacoustic borehole logging in a fluid-saturated porous formation. The Journal of the Acoustical Society of America , 122(1): 135–145. doi: 10.1121/1.2735809.
Hu H S, Liu J Q, Wang H B, et al. 2003. Simulation of acousto-electric well logging based on simplified pride equations. Chinese J. Geophys. , 46(2): 259–264. doi: 10.3321/j.issn:0001-5733.2003.02.021.
Jiang E C, Linghu S, Ye Q Z, et al. 2002. On mathematic model of complex resistivity in frequency domain. WLT , 26(2): 98–100. doi: 10.3969/j.issn.1004-1338.2002.02.003.
Jougnot D, Revil A, Lu N, et al. 2010. Transport properties of the Callovo-Oxfordian clay rock under partially saturated conditions. Water Resources Research , 46(8): W08514. doi: 10.1029/2009wr008552.
Ke S Z. 2010. Frequency-swept measurement of electrical parameters of rock. Progress in Geophysics , 25(2): 512–515. doi: 10.3969/j.issn.1004-2903.2010.02.018.
Ke S Z, Feng Q N, He Y C, et al. 2006. Study on complex resistivity well logging with electrode antenna. Acta Petrolei Sinica , 27(2): 89–92. doi: 10.3321/j.issn.0253-2697.2006.02.019.
Ke S Z, Feng Q N, Sun Y R. 1999. A dispersion model of rock complex resistivity and its parameters algorithm. WLT , 23(6): 416–418. doi: 10.3969/j.issn.1004-1338.1999.06.003.
Ke S Z, Liu D J, Feng Q N. 2003. Study of sweep-frequency measurement system for rock complex resistivity using coil antenna. Progress in Exploration Geophysics (in Chinese) , 26(4): 309–312.
Li J Y, Tian C Z, Liu H, et al. 2001. The surface wave characteristic of seismic experiment in electric field in Daqing. Progress in Geophysics , 16(4): 29–34. doi: 10.3969/j.issn.1004-2903.2001.04.006.
Li Y, Lin P R, Zheng C J, et al. 2011. Studies of complex resistivity forward simulation and inversion over a polarization earth. Journal of Jilin University (Earth Science Edition) (in Chinese) , 41(supp.): 355–361.
Liu H. 2002. The prospective application of seismo-electric effect in natural resources exploration. Progress in Geophysics , 17(2): 211–217. doi: 10.3969/j.issn.1004-2903.2002.02.004.
Liu S. 1988. A new approximation for apparent complex resistivities. Acta Geophysica Sinica (in Chinese) , 31(6): 687–694.
Liu S. Spectral Induced Polarization. (in Chinese) Wuhan: China University of Geosciences Press, 1998 .
Lu Q X. 1985. Discussion on some problems in fitting the results of complex resistivity using Cole-Cole dispersion. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 7(1): 45–49.
Lu Y. 2008. Experimental study on complex resistivity frequency dispersion property of rocks under water flooding. World Well Logging Technology (in Chinese) (6): 39–42.
Ma J, Xiao Z S, Wang D, et al. 2008. The research progress of complex resistivity logging technology. Progress in Geophysics (in Chinese) , 23(5): 1586–1591.
Pelton W H, Ward S H, Hallof P G, et al. 1978. Mineral discrimination and removal of inductive coupling with multifrequency IP. Geophysics , 43(3): 588–609. doi: 10.1190/1.1440839.
Potapof O A. 1996. Principles of Seismo-Electric Exploration (in Chinese). Translated by Qiu W T, Li L T. Beijing: Petroleum Industry Press.
Pride S R, Haartsen M W. 1996. Electroseismic wave properties. The Journal of the Acoustical Society of America , 100(3): 1301–1315. doi: 10.1121/1.416018.
Ren H X, Huang Q H, Chen X F. 2010. Analytical regularization of the high-frequency instability problem in numerical simulation of seismoelectric wave-fields in multi-layered porous media. Chinese J. Geophys. , 53(3): 506–511. doi: 10.3969/j.issn.0001-5733.2010.03.004.
Shen L C, Savre W C, Price J M, et al. 1985. Dielectric properties of reservoir rocks at ultra-high frequencies. Geophysics , 50(4): 692–704. doi: 10.1190/1.1441944.
Shi K F. 2001. Seismo-electric effect theory and preliminary experimental results. Chinese J. Geophys. , 44(5): 720–728. doi: 10.3321/j.issn:0001-5733.2001.05.016.
Su Q X, Ke S Z, Feng Q N, et al. 1999. An experimental study on the impedance spectra of rocks saturated with oil and water in frequency 100 Hz-10 MHz. Progress in Geophysics (in Chinese) , 14(1): 93–103.
Su W, Liu C, Chen C. 2006. Progress of seismoelectric in theory and research. Progress in Geophysics , 21(2): 379–385. doi: 10.3969/j.issn.1004-2903.2006.02.007.
Tong M S, Li L, Jiang Y Z, et al. 2005b. Auto-controlled complex resistivity measurement system under modeling reservoir condition. WLT , 29(4): 364–367. doi: 10.3969/j.issn.1004-1338.2005.04.024.
Tong M S, Li L, Wang W N, et al. 2005a. Experimental study on complex resistivity of shaly sands. WLT , 29(3): 188–190. doi: 10.3969/j.issn.1004-1338.2005.03.002.
Tong M S, Tao H G. 2008. Permeability estimating from complex resistivity measurement of shaly sand reservoir. Geophysical Journal International , 173(2): 733–739. doi: 10.1111/j.1365-246X.2008.03730.x.
Tong M S, Tao H G, Ding Z, et al. 2007. Development of high-resolution complex resistivity logging tool and case study. WLT , 31(2): 166–168. doi: 10.3969/j.issn.1004-1338.2007.02.018.
Ulrich C, Slater L D. 2004. Induced polarization measurements on unsaturated, unconsolidated sands. Geophysics , 69(3): 762–771. doi: 10.1190/1.1759462.
Wait J R. 1981. Towards a general theory of induced electrical polarization in geophysical exploration. IEEE Transactions on Geoscience and Remote Sensing , GE-19(4): 231–234. doi: 10.1109/TGRS.1981.350377.
Wang C, Cheng Y, Wang L X. 2012. Study on complex resistivity experiment of water-flooded zone after polymer flooding. Journal of Heilongjiang Bayi Agricultural University , 24(6): 73–76. doi: 10.3969/j.issn.1002-2090.2012.06.019.
Wang W N, Tong M S, Chen G H, et al. The Physical Properties of Agrillaceous Sand and Logging Application. (in Chinese) Beijing: Petroleum Industry Press, 2004 .
Xiang J, Jones N B, Cheng D, et al. 2001. Direct inversion of the apparent complex-resistivity spectrum. Geophysics , 66(5): 1399–1404. doi: 10.1190/1.1487085.
Xiao Z S, Xu S Z, Luo Y Z, et al. 2006a. Complex resistivity dispersion properties experiment of shaly sands. Geological Journal of China Universities , 12(1): 123–130. doi: 10.3969/j.issn.1006-7493.2006.01.014.
Xiao Z S, Xu S Z, Luo Y Z, et al. 2006b. Study on mechanisms of complex resistivity frequency dispersion property of rocks. Journal of Zhejiang University (Science Edition) , 33(5): 584–587. doi: 10.3321/j.issn.1008-9497.2006.05.024.
Xiao Z S, Xu S Z, Luo Y Z, et al. 2007. Study on numeric simulation of complex resistivity logging. OGP (in Chinese) , 42(3): 343–347.
Xiao Z S, Zeng Z G, Zhu S H, et al. 2009. An experimental study of wettability evaluation based on frequency dispersion property of rock electric parameters. Chinese J. Geophys. , 52(5): 1326–1332. doi: 10.3969/j.issn.0001-5733.2009.05.022.
Yu H, Guan J T, Chen H, et al. 2013. Mathematical simulation on the frequency dispersion characteristics of the streaming potential in reservoir rocks. Chinese J. Geophys. , 56(2): 676–687. doi: 10.6038/cjg20130232.
Zhang D, Ren H X, Huang Q H. 2013. Numerical simulation study of co-seismic electromagnetic signals in porous media. Chinese J. Geophys. , 56(8): 2739–2747. doi: 10.6038/cjg20130822.
Zhang L J, Ke S Z, Yin C F, et al. 2013. Measurements of complex resistivity frequency dispersion of rocks in frequency 40 Hz~110 MHz//Chinese Geophysics 2013 (in Chinese). Beijing: Chinese Geophysical Society, 695-696.
Zhang Q Y, Guan J T, Zheng H X, et al. 2014. Mathematical simulation on electromagnetic properties of the plane seismoelectric waves in water-saturated porous media. Progress in Geophysics , 29(3): 1357–1368. doi: 10.6038/pg20140350.
Zheng H H, Feng Q N, Shang Z Y. 1993. Frequency property and its potential application of the complex resistance of reservoir rocks. Journal of the University of Petroleum, China (in Chinese) , 17(supp.): 23–29.
Zhou C D, Guan Z N, Yan H R, et al. 2001. Quantitative analysis of radiation energy in borehole sonic-electric transformation wave fields. Chinese J. Geophys. , 44(4): 563–572. doi: 10.3321/j.issn:0001-5733.2001.04.015.
Zhou X M, Xia T D, Xu P, et al. 2006. Seismic reflection and transmission coefficients at an air-water interface of saturated porous soil. Acta Seismologica Sinica , 28(4): 372–379. doi: 10.3321/j.issn:0253-3782.2006.04.004.
Zonge K L, Wynn J C. 1975. Recent advances and applications in complex resistivity measurements. Geophysics , 40(5): 851–864. doi: 10.1190/1.1440572.
安珊, 李能根. 1998. 含水岩石复电阻率的实验研究. 测井技术 , 22(5): 315–317.
波达波夫 O A. 1996. 震电勘探原理. 裘慰庭, 李乐天译. 北京: 石油工业出版社.
陈邦彦 译. 2006. 新世纪震电磁研究前景. 海洋地质, (1): 59-66.
程辉, 底青云, 李帝铨. 2010. 频率信号激励下岩石电性参数研究. 地球物理学进展 , 25(3): 918–925.
范宜仁, 陆介明, 王光海, 等. 1994. 岩石电阻率频散现象的实验研究. 石油大学学报(自然科学版) , 18(1): 17–23.
高永新, 胡恒山. 2009. 水平分层孔隙介质中点源激发的震电波场数值模拟及分析. 地球物理学报 , 52(8): 2093–2104.
胡恒山, 刘家琦, 王洪滨, 等. 2003. 基于简化的Pride理论模拟声电效应测井响应. 地球物理学报 , 46(2): 259–264.
姜恩承, 令狐松, 叶青竹, 等. 2002. 频率域复电阻率数学模型研究. 测井技术 , 26(2): 98–100.
柯式镇. 2010. 岩石电学参数扫频测量. 地球物理学进展 , 25(2): 512–515.
柯式镇, 冯启宁, 何亿成, 等. 2006. 电极法复电阻率测井研究. 石油学报 , 27(2): 89–92.
柯式镇, 冯启宁, 孙艳茹. 1999. 岩石复电阻率频散模型及其参数的获取方法. 测井技术 , 23(6): 416–418.
柯式镇, 刘迪军, 冯启宁. 2003. 线圈法岩心复电阻率扫频测量系统研究. 勘探地球物理进展 , 26(4): 309–312.
李建勇, 田春志, 刘洪, 等. 2001. 大庆电场地震实验资料的面波特征. 地球物理学进展 , 16(4): 29–34.
李勇, 林品荣, 郑采君, 等. 2011. 极化大地复电阻率正反演. 吉林大学学报(地球科学版) , 41(增刊1): 355–361.
刘洪. 2002. 震电效应研究在资源勘探中的应用前景. 地球物理学进展 , 17(2): 211–217.
刘崧. 1988. 计算视复电阻率的新的近似公式. 地球物理学报 , 31(6): 687–694.
刘崧. 谱激电法. 武汉: 中国地质大学出版社, 1998 .
陆启行. 1985. 复电阻率测量使用柯尔-柯尔模型拟合中若干问题的探讨. 物化探计算技术 , 7(1): 45–49.
卢艳. 2008. 水驱岩石复电阻率频散特性实验研究. 国外测井技术 (6): 39–42.
马静, 肖占山, 王东, 等. 2008. 复电阻率测井技术的研究进展. 地球物理学进展 , 23(5): 1586–1591.
任恒鑫, 黄清华, 陈晓非. 2010. 层状孔隙介质震电波场数值模拟高频不稳定性问题的解析处理方法. 地球物理学报 , 53(3): 506–511.
石昆法. 2001. 震电效应原理和初步实验结果. 地球物理学报 , 44(5): 720–728.
苏庆新, 柯式镇, 冯启宁, 等. 1999. 100 Hz~10 MHz频段含油水两相岩石电阻抗的研究. 地球物理学进展 , 14(1): 93–103.
苏巍, 刘财, 陈晨. 2006. 震电效应理论及其研究进展. 地球物理学进展 , 21(2): 379–385.
童茂松, 李莉, 姜亦忠, 等. 2005b. 模拟地层条件的复电阻率自动测量系统研制. 测井技术 , 29(4): 364–367.
童茂松, 李莉, 王伟男, 等. 2005a. 泥质砂岩的复电阻率实验研究. 测井技术 , 29(3): 188–190.
童茂松, 陶宏根, 丁柱, 等. 2007. 高分辨率复电阻率测井仪器设计及现场试验. 测井技术 , 31(2): 166–168.
王畅, 成永, 王乐新. 2012. 聚和物驱水淹层复电阻率实验研究. 黑龙江八一农垦大学学报 , 24(6): 73–76.
王伟男, 童茂松, 陈国华, 等. 泥质砂岩的物理性质及其测井应用. 北京: 石油工业出版社, 2004 .
肖占山, 徐世浙, 罗延钟, 等. 2006a. 泥质砂岩复电阻率的频散特性实验. 高校地质学报 , 12(1): 123–130.
肖占山, 徐世浙, 罗延钟, 等. 2006b. 岩石复电阻率频散特性的机理研究. 浙江大学学报(理学版) , 33(5): 584–587.
肖占山, 徐世浙, 罗延钟, 等. 2007. 复电阻率测井的数值模拟研究. 石油地球物理勘探 , 42(3): 343–347.
肖占山, 曾志国, 朱世和, 等. 2009. 基于岩石电性参数频散特性评价润湿性的实验方法研究. 地球物理学报 , 52(5): 1326–1332.
于华, 关继腾, 陈辉, 等. 2013. 储层岩石流动电位频散特性的数学模拟. 地球物理学报 , 56(2): 676–687.
张丹, 任恒鑫, 黄清华. 2013. 孔隙介质地震电磁信号的数值模拟研究. 地球物理学报 , 56(8): 2739–2747.
张雷洁, 柯式镇, 尹成芳等. 2013. 40 Hz~110 MHz岩石复电阻率频谱实验测量//中国地球物理2013. 北京: 中国地球物理学会, 695-696.
张泉滢, 关继腾, 郑海霞, 等. 2014. 水饱和孔隙介质中平面震电波电磁特性的定量模拟. 地球物理学进展 , 29(3): 1357–1368.
郑和华, 冯启宁, 尚作源. 1993. 岩石复电阻的频率特性及其应用前景. 石油大学学报(自然科学版) , 17(增刊): 23–29.
周成当, 管志宁, 严洪瑞, 等. 2001. 井中声电转换波场辐射能量定量分析. 地球物理学报 , 44(4): 563–572.
周新民, 夏唐代, 徐平, 等. 2006. 饱和土介质中地震波在水、气分界面上的反射与透射. 地震学报 , 28(4): 372–379.