2. 北京师范大学珠海分校信息技术学院, 广东珠海 519087
2. College of Information and Technology, Beijing Normal University at Zhuhai, Guangdong Zhuhai 519087, China
遥感影像土地覆盖分类是获取遥感专题信息的主要手段,在地图更新、目标识别、灾害监测、资源应用等方面有着广泛的应用和重要意义(余先川等,2014).而无需先验知识的无监督分类方法,由于其可以实现土地覆盖的自动分类(Li et al.,2010;Lü et al.,2010),与监督分类方法相比,在应急救灾等遥感应用领域中优势明显.目前,无监督分类方法主要分为硬分类和软分类两大类.遥感影像数据固有的不确定性导致分类结果具有歧义性和模糊性(承继成等,2004;Rocchini et al.,2013),因此ISODATA、K-Means等硬聚类方法处理结果不尽人意,而作为软聚类法的模糊C均值聚类(FCM)方法,往往能得到更好的结果(余先川等,2012;Zhang and Kang,2012;Xie and Zhang,2012;Huang et al.,2012).但是如果模式集各簇具有显著的密度差异,FCM的效果随着模糊指数的不同呈现显著差异(Hwang and Rhee,2007),因此基于FCM的算法在处理具有较大密度差异性和不确定性的遥感影像时难以得到满意的结果.相比一型模糊集,由于其隶属度函数为三维分布,二型模糊集可以更好地处理实际事务的不确定性问题,因而自提出伊始就倍受青睐(Rhee and Hwang,2001;陈薇和孙增圻,2005;Lucas et al.,2008;生龙,2012),其中模糊逻辑运算复杂性大大简化的区间二型模糊集的应用尤为广泛.
将区间二型模糊系统应用到实际中,首先须结合具体对象,构造合理的区间二型模糊集(纪雯等,2013),不同的区间二型模糊集将导致不同的处理结果.Hwang和Rhee(2007)在对二型模糊聚类研究的基础上,用2个不同的模糊指数构造隶属度区间,提出了区间二型模糊C均值聚类(Interval-valued type-2 fuzzy C-means clustering,IT2FCM)方法,并对多种简单数据集进行了分类实验,但降型方法过于复杂且模糊指数选择过于随意.同年,Zeng和Liu(2007)通过取一维高斯分布的均值μ和方差σ构建隶属函数区间μ=[μ,μ]=[μ-kσ,μ+kσ],k∈[0,3] 此方法有两个假设:隶属函数为高斯分布和一维高斯分布能量集中在[μ-3σ,μ+3σ].该假设往往不符合遥感影像模式集的特征.Choi和Rhee(2009)给出了启发式、基于灰度直方图特征和IT2FCM的3种区间二型模糊隶属度函数的构建方法,并通过BP神经网络分类应用验证了其有效性,不过此3种方法都存在经验依赖,比如启发式方法对初始一型隶属函数的形状和比例系数的选择敏感,特别是当比例系数选取不当时将导致区间二型隶属度函数失去不确定性描述能力;基于直方图的方法假设隶属函数呈对称的高斯分布,这常常不符合实际数据特点;基于IT2FCM的方法对模糊指数m1,m2选择敏感,而m1,m2的确定目前没有一个普适的方法(Bezdek et al.,1999),不合适的m1,m2将导致IT2FCM聚类结果比FCM更差.因此,对m1,m2的选择成为一个重要的研究领域,宫改云等(2005)经过大量研究证明从聚类有效性角度看,最佳模糊指数取值范围为[1.5,2.5].Fisher(2010)则通过将模糊指数区间[1.3,2.5]离散为13个m,然后基于某种特定的函数表达形式(如三角函数)生成某个像元取不同m时对应的这系列模糊度的集合,即二型模糊集.然而,以上各种凭经验确定的m1,m2往往不能很好地刻画待分类影像数据的模糊性,而距离度量的差异却可能导致2个地物类别区分和不能区分的差别.已有研究表明(Bezdek et al.,1999),距离度量的选择本身就存在一定的不确定性,不同的距离度量往往是从不同角度描述两个样本间的相异性,从而形成了距离度量的模糊性.De Carvalho和Camilo(2010)就样本距离度量的各向异性性质提出了自适应距离度量的概念.而遥感影像数据样本间相异性在不同的波段往往存在显著差异,即各向异性特征明显,因此本文提出基于距离度量的模糊性构建区间二型模糊集的方法.
此外,降型是二型模糊系统方法的特点和难点,其实质是一型系统中精确化运算的扩展,但通常比精确化的计算复杂性和计算量都要大很多(生龙,2012).应用中最受欢迎的是求质心的降型方法,其中Karnik-Mendel(KM)算法是一个有效的算法,成功地用来实现区间二型模糊集的降型(Karnik and Mendel,2001),不过该算法需要多次迭代,计算复杂度高,且对区间初始端点值敏感.随后研究者陆续提出多种新的区间二型模糊集降型方法,如EKM(Wu and Mendel,2009)系列算法,WM-UB(Wu and Mendel,2002),Nie-Tan(Nie and Tan,2008)方法等.到目前为止,暂没有文献对基于KM的降型方法及其他降型方法的性能做全面比较分析.不过Mendel(2013)的分析表明,在KM后提出的降型方法的计算效率通常高于KM算法,如Nie-Tan方法,而Greenfield和Chiclana(2013)对KM,WM-UB和Nie-Tan等方法的精度和评估复杂度进行的比较分析则表明,没有证据可以证明后两者优于KM算法,这表明在实际应用中,前述各种降型方法并没有从根本上突破KM算法的局限.不同于普通模糊系统框架(Mendel et al.,2006)下的降型方法,Wu和Tan(2005)则提出两种通过寻找等价一型模糊集的高效降型策略,其关键思想是将二型模糊集视为其多个代表一型模糊集的组合,因此降型就简化为如何选取等价一型模糊集.也有文献讨论降型并不一定是必须的(Mendel,2007).对于遥感影像土地覆盖分类而言,我们希望系统最后的输出是明确的.而且降型的精度与聚类输出的误差呈反相关,也即误差越小对应的降型精度越高,因此需要将误差作为参数引入到降型处理中,而Wu和Tan(2005)提出了此种实现的参考模型.
本文提出自适应区间二型模糊聚类(Adaptive interval-valued type-2 fuzzy C-means clustering,A-IT2FCM)算法,该方法的核心思想是在利用区间二型模糊集对遥感土地覆盖类别的高阶模糊不确定性建模基础上,引入自适应隶属度区间控制因子,借鉴寻找等价一型模糊集的降型思想来实现面向遥感影像分类的区间二型模糊集的降型,进而展开基于自适应区间二型模糊聚类的遥感影像土地覆盖自动分类研究.
2 自适应区间二型模糊聚类(A-IT2FCM) 2.1 基于模糊距离度量的区间二型隶属度函数构建基于二型模糊系统理论构建的区间二型模糊分类模型的不确定性体现在隶属区间的上、下边界和区间的长度3个方面(Zeng and Liu,2007),核心在于隶属度区间的构建和充分考虑隶属区间长度对分类结果的影响.
遥感影像多波段特点使得某个像元在不同波段的灰度值到某个类别中心的距离存在显著差异,我们可以依据最小的最大距离判读某个样本属于某个类别,也可以依据最大的最小距离判断某个样本不属于某个类别,而通常情况下我们采用各维距离值的代数和(平均)作为样本间距离度量值,此种处理往往抹掉了距离度量值在不同波段的差异性,即距离的各向异性,而两地物常常在特定波段具有最大的区分度,如水体和植被,在近红外波段的光谱反射值相差最明显.鉴于此,我们认为对于易区分的地物,采取平均距离度量即可,而对于在大多数波段光谱反射相近的不同地物的区分则要考虑两者的最大相异性,更合理的距离度量应该兼顾相异性的最大值和平均值,因此基于距离度量的不确定性我们构建区间二型隶属度函数如下:
已知影像数据向量X={x1,x2,…,xn},xi={xi1,xi2,…,xip},i=1,2,…,n,定义该数据集的模糊划分矩阵的上界和下界如下:
上界:
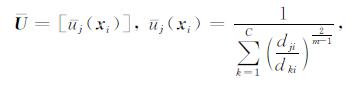
|
(1) |
下界:
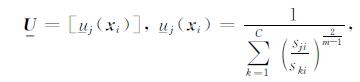
|
(2) |
其中uj(xi)和uj(xi)分别表示影像样本点xi到类别j的隶属度的上限和下限值,构成了隶属度区间[uj(xi),j(xi)],d,s分别为样本xi与类别j模糊距离度量的平均和最大度量值,即dji=mean(djiL),sji=max(djiL),L=1,2,…,p,djiL为样本xi第L维与类别j的距离,如欧氏距离,m为模糊指数,此处取m=2.5.
2.2 自适应快速降型和去模糊等价一型模糊集思路(Wu and Tan,2005),即利用最具代表性的n型模糊集表示n+1型模糊集.当n=0时,结果输出就是确定的值,也就是精确器工作.用以代表n+1型的n型模糊集必须等价于原n+1型模糊集,即能有效表示原集合的特性,通常用集合的质心来表示.假设一个区间二型模糊集Ã(其质心表示如公式(4)所示)的代表一型模糊集为A,用N个点的离散域来描述它,则其质心为:
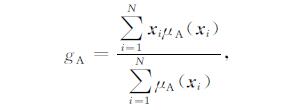
|
(3) |
其中xi 为已知样本点,要计算gA即要计算μA(xi).
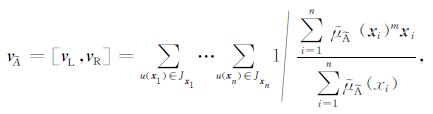
|
(4) |
其中m是模糊指数,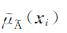
借鉴探求一型代表模糊集的思想,求解该公式中的二型模糊集的质心vÃ,本质即为求解等价的一型隶属度函数μA(xi). 为此,考虑聚类误差与降型精度的相关性,引入自适应控制因子,定义降型器如下:
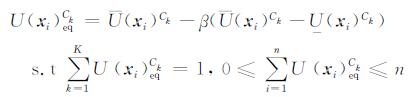
|
(5) |
其中,K为聚类数,U(xi)eqCk 为最终xi属于类别Ck 的隶属度,也即通过(5)式计算同时完成了降型和去模糊UCk和UCk 分别为原区间二型隶属度函数的上界和下界,其定义分别见公式(1)和(2),β(0≤β≤1)为隶属度区间宽度自适应控制因子,其一般定义如公式(6),其合理性证明和具体推演过程见李洪兴(1999).β的物理含义在于当类内归一化均方误差增大时,β增大,则xi属于类别Ck的等价隶属度下降,且隶属度区间长度增大,xi不属于类别Ck的可能性提高,当β=1时,U(xi)eqCk=U(xi)Ck,xi属于类别Ck的等价隶属度值取隶属度区间下界;反之,当类内归一化均方误差趋于零时,β趋于零,则xi属于类别Ck的等价隶属度逼近隶属度区间上界,xi属于类别Ck的可能性提高,当β=0时,U(xi)eqCk=U(xi)Ck,xi属于类别Ck的等价隶属度值取隶属度区间的上界.
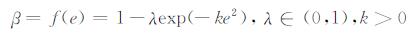
|
(6) |
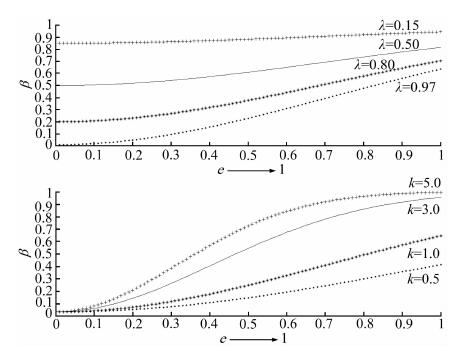
其中e为某次迭代xi所划分到的类别Ck的归一化均方误差,其定义见公式(7),常量参数λ和k对伸缩因子的影响如图 1所示.
|
图 1 常量参数对自适应伸缩因子的影响 (a) 参数对自适应控制因子的影响,k=1; (b) 参数对自适应控制因子的影响,λ=0.97. Fig. 1 The effect of constant parameters on the adaptive contraction-expansion factor |
其中,δ(xi,gk)为xi与Ck的偏差,gk为原型Ck的中心,nk为Ck的样本点数.
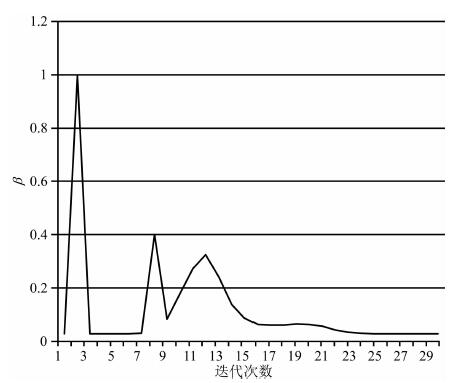
从图 1可以看出,在k(k=1)固定的情况下,λ越大,自适应控制因子β曲线越陡,即β对e变化越敏感,反之越平缓;在λ(λ=0.97)固定情况下,k≤1,β与e的变化几乎呈正线性相关,而当k=5,归一化均方误差大于0.8时,自适应因子调节能力接近饱和,即β趋于稳定值1,其意义在于当归一化均方误差较大时,xi可视为当前类别的离群点,应尽量分离出去.此处我们选择λ=0.97,k=5.在实际聚类过程中,β的值在迭代初期会有振荡,但随着归一化均方误差趋于极小值,β趋于一个稳定值,即U(xi)eqCk趋于稳定,降型完成,如图 2所示.
|
图 2 自适应降型示例 Fig. 2 An example for the adaptive contraction-expansion factor change following the clustering iteration |
A-IT2FCM算法的基本框架同IT2FCM(Hwang and Rhee,2007),算法步骤如下:
步骤1: 确定聚类数K和模糊指数m(1<m<∞),ε=10-5,迭代次数记为t,设初值t=0,初始化模糊划分Vit(1≤i≤K),自适应控制因子初始值β=0;
步骤2: 以Vt为中心,用公式(1)和(2)计算隶属度矩阵U,U;
步骤3: 用公式(7)和(6)计算Vit(1≤i≤K)归一化的类内均方误差和隶属度区间宽度自适应影响因子β;
步骤4:利用公式(5)探求等价一型隶属度,利用公式(3)更新Vt;
步骤5: 如果‖Vt+1-Vt‖<ε,转下一步,否则t=t+1,转向步骤2;
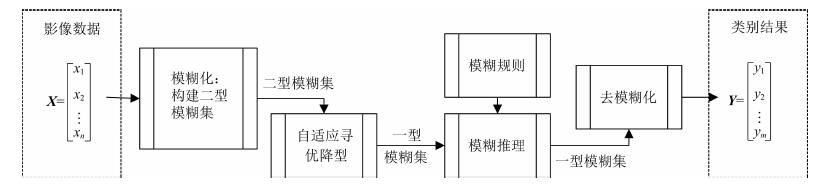
步骤6: 得到最终的聚类中心和隶属度矩阵,按最大隶属度原则去模糊化得到聚类结果.其算法流程如图 3所示.
|
图 3 自适应区间二型模糊聚类算法流程 Fig. 3 The algorithm flow of A-IT2FCM |
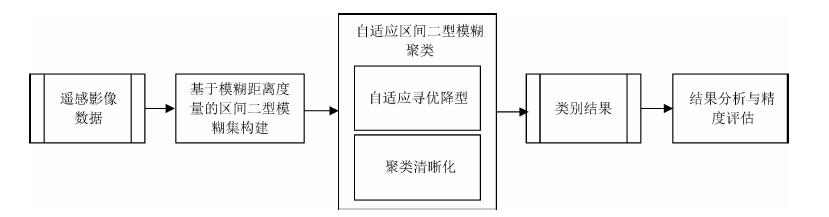
本文遥感土地覆盖自动分类实验技术流程如图 4所示,核心算法A-IT2FCM过程见2.3节算法步骤和图 3算法流程描述.
|
图 4 基于自适应区间二型模糊聚类的影像分类 Fig. 4 The overall technical process of our study in this article |
为验证A-IT2FCM算法的性能,本文进行了与基于KM(Karnik and Mendel,2001)算法降型的IT2FCM(记为KM-IT2FCM)和Tizhoosh(2005)提出的二型模糊集构建和降型方法(记为Pa-IT2FCM)及IV-FCM(余先川等,2014)的比对实验,公共参数设置保持一致以确保结果的可比性.
3.2 实验数据描述本文实验数据选自土地利用类型复杂的珠海海岸带附近(大小435×446像素,覆盖了包括一段马骝洲水道和东方高尔夫珠海球场及新围村在内的城郊区域)、北京颐和园附近(大小736×612像素,覆盖北至颐和园,南至杏石口路,西过西五环路抵北京植物园,东抵世纪城的区域)和大横琴区域(大小939×667个像素,覆盖了横琴岛及四周的大部分区域,东至澳门本岛,南到三叠泉风景区,西抵磨刀门,北至马骝洲水道以北宝盛路),见图 8a,土地覆盖有河流,农业用地、林地、人工草皮、建筑用地、园地和耕地等.该3个数据源均为SPOT5影像,包括多光谱谱段的4个波段(10 m分辨率),波谱范围为0.43至0.89 μm的可见光和近红外波段,图 5a和7a分别为前两个源影像数据1、2、3波段组合的RGB图,聚类结果类别组成情况见表 1.该3个实验数据均存在较严重的“同谱异物”现象:对于珠海海岸带附近实验数据,如图 5所示,区域A、B、C分别标识了典型的滩涂、水体和山体类,然而由于它们的光谱非常近似甚至存在混叠,很难将彼此区分开来;对于颐和园附近实验数据,如图 6a所示,影像中主要地物类别包括了:耕地、林地、水体和阴影、建筑物、主干路和草地等,覆盖面积增大,不同地物光谱混叠,且互为干扰,如林木与民房,道路与河流交错分布,相互影响,从而模糊现象更显著,典型的如图 6a中A1,A3所示,且高层建筑和林木阴影严重;而对于大横琴区域影像,两个存在明显模糊现象的区域,如图 7a中A1标示,类别包括河流、小溪、鱼塘等水域类,建筑用地和厂房等建筑用地类,人工林地类,潮湿农用地类和草皮绿地类,A2标示类别主要为建筑用地类、水域和人工草皮等.需要说明的是关于阴影的处理不在本文的讨论范畴,这里只探讨阴影的存在对本文构建的模糊分类模型性能的影响.

|
图 5 A-IT2FCM与Pa-IT2FCM及KM-IT2FCM(m1=2,m2=10)对珠海SPOT5数据的聚类分析结果 (a) 原图1、2、3波段组合; (b) Pa-IT2FCM聚类结果; (c) KM-IT2FCM (m1=2, m2=10)聚类结果; (d) A-IT2FCM聚类结果. Fig. 5 Resulting images of the SPOT5 data by Pa-IT2FCM, KM-IT2FCM (m1=2,m2=10) and A-IT2FCM |

|
图 6 A-IT2FCM与Pa-IT2FCM和KM-IT2FCM对北京颐和园附近SPOT5数据聚类分析结果 a) 原影像1、2、3波段组合RGB(736×612); (b) FCM聚类结果; (c) Pa-IT2FCM聚类结果;(d) A-IT2FCM聚类结果; (e) KM-IT2FCM (m1=2, m2=10)结果; (f) KM-IT2FCM (m1=1.5, m2=4.5)结果;(g) IV-FCM结果;(h) 区间数据建模+A-IT2FM聚类结果. Fig. 6 Resulting images of the SPOT5 data from Beijing from FCM, Pa-IT2FCM, A-IT2FCM, KM-IT2FCM (m1=2, m2=10), KM-IT2FCM (m1=1.5, m2=4.5), IV-FCM and A-IT2FCM based on the interval-valued data modeling |
|
|
表 1 聚类结果类别的组成 Table 1 Composition of the categories |

|
图 7 A-IT2FCM与IV-FCM和KM-IT2FCM对大横琴SPOT5数据聚类分析结果 (a) 大横琴SPOT5假彩色合成图(937×667); (b) IV-FCM结果; (c) KM-IT2FCM (m1=2, m2=10)结果; (d) 区间数据建模+A-IT2FM聚类结果. Fig. 7 Resulting images of the SPOT5 data from Hengqin from IV-FCM, KM-IT2FCM (m1=2, m2=10) and A-IT2FCM based on the interval-valued data modeling |
|
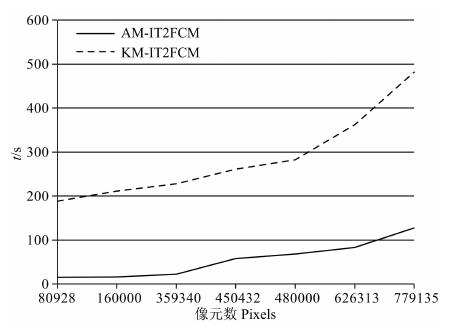
图 8 时间复杂度比较 Fig. 8 Comparison of computation complexity |
参照实验原影像数据,可以看出各种基于区间二型模糊集的模糊聚类结果,如图 5和图 6所示,对聚集效果较好地表覆盖,如图 5中的绿地、建筑用地和农业用地类和图 7中的建筑群,都得到了较好的划分结果,各个地物类别连贯且边界基本清晰可见.
而对于光谱混叠严重的区域,如图 5中的A(滩涂)、B(水体)、C(林地)的划分则有显著不同,算法Pa-IT2FCM将滩涂划到了林地类,算法KM-IT2FCM则将滩涂划到了水域类,而本文提出的A-IT2FM算法由于引入了自适应调整因子,通过聚类有效性指标将最终模糊划分矩阵导向最佳模糊划分,基本区分了3者.Pa-IT2FCM相对其他两个算法聚集能力更强,却易导致“过聚”问题,即更容易导致小目标类别消失在较大邻域类别中,而本文A-IT2FCM从样本距离度量的模糊性角度出发构建区间二型模糊集,不依赖于任何先验知识和假设,该二型模糊集模型可以更有效地描述和控制光谱混叠和干扰模糊,从而在获得聚集性好的各个类别同时可以获得混合类别结果,而不是简单地将混叠的类别划分到某个基础类别,如此处滩涂类别可以理解为水体和林地的混合,而其他两种方法要么将其划到了水域类要么将其划到了林地类.
对于北京颐和园附近SPOT5数据实验结果,光谱干扰的复杂性和显著的密度差异使得FCM结果中水域和林地类及主干路存在严重的错分现象,如图 6b所示,典型的如B1、B2和B3标示区域,且所得林地面积明显大于实际值.而A-IT2FM则依旧表现良好,得到的各个类别边界清晰,特别是主干路连贯完整,道路网和河流清晰可鉴,展现了优于传统FCM算法的分类性能,相关实验结果如图 6d所示.而KM-IT2FCM(m1=2,m2=10)对此类“同谱异物”现象严重的数据的处理显示出明显的不适应性,如图 6e所示,其结果退化到比FCM更差,验证了KM-IT2FCM对m1,m2的敏感性.重新选择m1=1.5,m2=4.5,则其结果大为改善,如图 6f所示,说明数据越复杂,KM-IT2FCM算法中对m1,m2的选取则要越谨慎.而A-IT2FM是基于模糊距离度量构建二型模糊隶属度函数,且引入了自适应控制因子调整隶属函数区间长度,显著降低了对模糊指数和先验知识的依赖,同时更有利于算法快速收敛到全局极小值得到最佳的模糊划分矩阵,结果整体上优于KM-IT2FCM,同时优于Pa-IT2FCM算法聚类结果(如图 6c所示).不过结果图也可以看出,A-IT2FM算法依旧未能很好地解决山体阴影和水体的错分问题,因为我们主要考虑地物光谱而没有考虑其空间信息和拓扑关系.
A-IT2FM处理结果(分别见图 6h和图 7d)与IV-FCM(分别见图 6g和图 7c)相比,在数据区间建模基础上进行A-IT2FCM的分类结果在保持原模型的优良特点情况下,可读性比IV-FCM更强,类别划分更清晰,尤其是对山体暗像元的抑制加强,得到了更为完整的林地类,见图 6h-H1和图 7d黄色箭头所标示区域.对于图 7a-A1中箭头所指示潮湿的草皮,IV-FCM几乎都将其划分成了水域,A-IT2FCM则得到了正确的类别划分,这说明结合了区间信息表达的区分能力和区间二型模糊集对于高阶不确定性的掌控能力,A-IT2FCM可以进一步改善模糊分类器性能.为验证本文自适应降型算法的复杂度小于KM算法,我们统计了多组实验数据的处理时间(图 8),从时间复杂度曲线看,样本点数相同时,A-IT2FM算法时间开销远小于KM-IT2FCM,且随着样本点数的增加,KM-IT2FCM的处理时间增长更快.
为从客观角度验证各对比方法分类效果,我们用GPS在地物复杂区域实测了一组样本点(每个实验区不少于50个样本点),并结合土地利用图对图 5、图 6和图 7所示结果进行了精度验证,结果如表 2所示.从表 2统计结果可以看出A-IT2FM的总体分类精度、Kappa系数均高于其他算法,这表明本文A-IT2FM聚类的性能与目视判读结果一致,有利于改善高分辨率遥感影像聚类效果,进而提高土地覆盖分类的精度,可满足更精细自动分类的需要.
|
|
表 2 分类精度和Kappa系数比较 Table 2 Comparison of the overall accuracy and Kappa for different clustering algorithms mentioned in the experiments |
二型模糊集具有比一型模糊集更强的不确定性描述和控制能力,更适于处理遥感影像土地覆盖类别存在的高阶模糊性问题.本文提出一种基于二型模糊集的建模方法:首先基于模糊距离度量构建了面向遥感影像土地覆盖分类的区间二型模糊隶属度函数;接着针对降型难题,提出了一种高效的自适应降型方法,即通过自适应影响因子探求等价一型代表模糊集以实现降型,同时去模糊化,在此基础上提出A-IT2FCM算法,最后通过三组存在较严重的“同谱异物”现象的影像自动分类实验,验证了本文基于A-IT2FCM算法的分类模型的有效性和可靠度.此外,基于模糊距离度量的区间二型模糊隶属度函数的构建不依赖参数假设和经验知识,满足自动分类的要求,而自适应模糊聚类分析可以优化分类器性能,在不同类别光谱混叠区获得比经典IT2FCM更理想的结果,即不是简单的将混叠区像元划分到某个纯净的类别,而是得到一个符合实际地表覆盖情况的类别混合结果.特别的,在数据区间建模基础上进行A-IT2FCM处理的结果较之单点数据聚类结果改进明显.不过A-IT2FCM依旧未能彻底解决阴影和水体的错分问题,我们在今后的工作中将考虑拓扑关系等空间邻域约束条件,进一步优化自适应控制因子的构造方法,以构建更有效的自动分类模型,得到更好的遥感影像土地覆盖分类结果.
致谢感谢北京师范大学空间信息处理与分析实验室的支持.感谢珠海市图形图像公共实验室的数据及地面验证支持.
| Bezdek J C, Keller J, Krisnapuram R, et al. Fuzzy Models and Algorithms for Pattern Recognition and Image Processing. US: Springer, 1999 : 183 -546. | |
| Chen W, Sun Z Q. 2005. Research on of type-2 fuzzy logic system and its application. Fuzzy Systems and Mathematics (in Chinese), 19(1): 126-135. | |
| Cheng J C, Guo H D, Shi W Z. Uncertainty of Remote Sensing Data. (in Chinese) Beijing: Science Press, 2004 . | |
| Choi B I, Rhee F C H. 2009. Interval type-2 fuzzy membership function generation methods for pattern recognition. Information Sciences, 179(13): 2102-2122. | |
| de Carvalho F A T, Camilo P T. 2010. Fuzzy K-means clustering algorithms for interval-valued data based on adaptive quadratic distances. Fuzzy Sets and Systems , 161(23): 2978–2999. | |
| Fisher P F. 2010. Remote sensing of land cover classes as type 2 fuzzy sets. Remote Sensing of Environment , 114(2): 309–321. | |
| Gong G Y, Gao X B, Wu Z D. 2005. An optimal choice method of parameter m in FCM clustering algorithm. Fuzzy Systems and Mathematics (in Chinese) , 19(1): 143–148. | |
| Greenfield S, Chiclana F. 2013. Accuracy and complexity evaluation of defuzzification strategies for the discretised interval type-2 fuzzy set. International Journal of Approximate Reasoning , 54(8): 1013–1033. | |
| Huang Q R, Wu G M, Chen J M, et al. 2012. Automated remote sensing image classification method based on FCM and SVM.//Proceedings of the 2012 2nd International Conference on Remote Sensing, Environment and Transportation Engineering. Nanjing: IEEE, 1-4. | |
| Hwang C, Rhee F C H. 2007. Uncertain fuzzy clustering: Interval type-2 fuzzy approach to C-means. IEEE Transactions on Fuzzy Systems , 15(1): 107–120. | |
| Ji W, Wang J H, Fang X K, et al. 2013. A new construction method of membership function for interval type-2 fuzzy sets. Journal of Northeastern University (Natural Science) (in Chinese) , 34(5): 618–623. | |
| Karnik N N, Mendel J M. 2001. Centroid of a type-2 fuzzy set. Information Sciences , 132(1-4): 195–220. | |
| Li B, Zhao H, Lü Z H. 2010. Parallel ISODATA clustering of remote sensing images based on MapReduce.//Proceedings of the 2010 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery. Huangshan: IEEE, 380-383. | |
| Li H X. 1999. Variable universe adaptive fuzzy control. Science in China(Series E) (in Chinese) , 29(1): 32–42. | |
| Lucas L A, Centeno T M, Delgado M R. 2008. Land cover classification based on general type-2 fuzzy classifiers. International Journal of Fuzzy Systems , 10(3): 207–216. | |
| Lü Z H, Hu Y J, Zhong H D, et al. 2010. Parallel K-means clustering of remote sensing images based on MapReduce.//Proceedings of the International Conference Web Information Systems and Mining. Sanya, China: Springer, 162-170. | |
| Mendel J M, John R I, Liu F L. 2006. Interval type-2 fuzzy logic systems made simple. IEEE Transactions on Fuzzy Systems , 14(6): 808–821. | |
| Mendel J M. 2007. Advances in type-2 fuzzy sets and systems. Information Sciences , 177(1): 84–110. | |
| Mendel J M. 2013. On KM algorithms for solving type-2 fuzzy set problems. IEEE Transactions on Fuzzy Systems , 21(3): 426–446. | |
| Nie M W, Tan W W. 2008. Towards an efficient type-reduction method for interval type-2 fuzzy logic systems.//IEEE International Conference on Fuzzy Systems, FUZZ-IEEE 2008. (IEEE World Congress on Computational Intelligence). Hong Kong: IEEE, 1425-1432. | |
| Rhee F C H, Hwang C. 2001. A type-2 fuzzy C-means clustering algorithm.//Proceedings of IFSA World Congress and 20th NAFIPS International Conference. Vancouver, BC: IEEE, 1926-1929. | |
| Rocchini D, Foody G M, Nagendra H, et al. 2013. Uncertainty in ecosystem mapping by remote sensing. Computers & Geosciences , 50: 128–135. | |
| Sheng L. 2012. Theory and application of type-II fuzzy systems[Ph. D. thesis] (in Chinese). Chengdu: University of Electronic Science and Technology of China. | |
| Tizhoosh H R. 2005. Image thresholding using type II fuzzy sets. Pattern Recognition , 38(12): 2363–2372. | |
| Wu D R, Tan W W. 2005. Computationally efficient type-reduction strategies for a type-2 fuzzy logic controller.//Proceedings of 14th IEEE International Conference on Fuzzy Systems. Reno, NV: IEEE, 353-358. | |
| Wu D R, Mendel J M. 2009. Enhanced Karnik-Mendel algorithms. IEEE Transactions on Fuzzy Systems , 17(4): 923–934. | |
| Wu H W, Mendel J M. 2002. Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems. IEEE Transactions on Fuzzy Systems , 10(5): 622–639. | |
| Xie J, Zhang X L. 2012. Clustering of hyperspectral image based on improved fuzzy C means algorithm. Journal of Convergence Information Technology , 7(12): 320–327. | |
| Yu X C, An W J, He H. 2012. A method of auto classification based on object oriented unsupervised classification. Progress in Geophys , 27(2): 744–749. doi: 10.6038/j.issn.1004-2903.2012.02.042. | |
| Yu X C, He H, Hu D, et al. 2014. Land cover classification of remote sensing imagery based on interval-valued data fuzzy C-means algorithm. Science China: Earth Sciences , 57(6): 1306–1313. | |
| Zeng J, Liu Z Q. 2007. Type-2 fuzzy sets for pattern classification: a review.//Proceedings of the IEEE Symposium on Foundations of Computational Intelligence. Honolulu, HI: IEEE, 193-200. | |
| Zhang W J, Kang J Y. 2012. Segmentation of high resolution remote sensing image using modified FCM combined with optimization method. Journal of Information and Computational Science , 9(15): 4591–4598. | |
| 陈薇, 孙增圻. 2005. 二型模糊系统研究与应用. 模糊系统与数学 , 19(1): 126–135. | |
| 承继成, 郭华东, 史文中. 遥感数据的不确定性问题. 北京: 科学出版社, 2004 : 92 -113. | |
| 宫改云, 高新波, 伍忠东. 2005. FCM聚类算法中模糊加权指数m的优选方法. 模糊系统与数学, 19(1): 143-148. | |
| 纪雯, 王建辉, 方晓柯, 等. 2013. 一种区间二型模糊隶属度函数的构造新方法. 东北大学学报(自然科学版) , 34(5): 618–623. | |
| 李洪兴. 1999. 变论域自适应模糊控制器. 中国科学: E辑 , 29(1): 32–42. | |
| 生龙. 二型模糊系统理论及应用[博士论文]. 成都: 电子科技大学, 2012 . | |
| 余先川, 安卫杰, 贺辉. 2012. 基于面向对象的无监督分类的遥感影像自动分类方法. 地球物理学进展 , 27(2): 744–749. | |
| 余先川, 贺辉, 胡丹, 等. 2014. 基于区间值模糊C-均值算法的土地覆盖分类. 中国科学: 地球科学 , 44(9): 2022–2029. | |
 2016, Vol. 59
2016, Vol. 59


