2. 二炮装备研究院, 北京 100085;
3. 中国人民解放军 63889部队, 湖南 孟州 454750
2. Equipment Research Institute of The Second Artillery, Beijing 100085, China;
3. Unit 63889 of PLA, Hunan Mengzhou 454750, China
星载干涉合成孔径雷达(InSAR)系统是高效获取全球高精度数字高程模型(DEM)最有效的工具,相关技术研究是当前世界各国在遥感与测绘领域的热点之一.继美国2000年实施航天飞机雷达地形测绘任务(SRTM)(Farr et al.,2000; Werner,2001; Rabus et al.,2003)并成功获取了DTED-2标准的DEM以来,德国研制的TerraSAR-X/TanDEM-X(Schattler et al.,2011; López-Dekker et al.,2011)双星编队InSAR系统于2011年开始工作,获取的DEM产品精度达到HRTI-3标准,成为InSAR技术发展新的里程碑.无论是在系统方案设计阶段的地面试验验证,还是在系统在轨运行阶段的定标与测试,高精度的InSAR性能评估都是不可或缺的关键技术之一.反映InSAR产品性能的技术指标主要是绝对测高精度、相对测高精度等,而直接影响DEM产品精度的干涉相位估计精度也是需要特别重视的性能指标之一.各项性能指标的高精度计算可为InSAR系统性能分析、系统误差隔离和故障诊断等提供重要的技术支持.直观上看,可以通过将InSAR处理得到的DEM与激光测量DEM等更高精度的先验DEM作比较来评估InSAR测高精度(王青松,2011).但是,亚米级的高精度DEM数据通常限于局部区域且获取困难,同时国际上公开的全球SRTM DEM数据和ASTER DEM数据格网间距较大、精度较低,无法满足现代星载InSAR系统的高精度评估需求.一些学者研究了理想干涉量的性能评估方法(Eineder,2003; 路兴强,2006; 王青松等,2009),该方法虽然理论上精度较高,但在实际应用中算法依赖的理想干涉量要全场景逐点计算,运算量非常大,同时由于系统斜距测量误差、时间同步误差等的存在及其不确定性使得理想干涉量无法得到正确计算,因此该方法无法从根本上进行客观有效的评估.
为了获得高精度、高效率和高稳健性InSAR性能评估,本文将提出一种基于虚拟特显点的性能评估方法.第2节首先介绍了基于特显点的性能评估方法,并指出该方法的优势和直接应用的技术缺陷,第3节详细介绍虚拟特显点的概念,并对评估方法加以改进,第4节对虚拟特显点InSAR性能评估方法的性能进行定量化的仿真验证与分析,最后是结论.
2 基于特显点的InSAR性能评估及其缺陷特显点InSAR性能评估方法的主要思想是在三维自然场景的SAR图像中选取高信杂比的特显点,或者在地面仿真试验中布设若干强散射的特显点目标,并以这些特显点作为评估阶段的样本点进行性能指标计算.在轨测试时,特显点可以是定标场的角反射器或者位置可精确测量的强散射地物目标,地面仿真试验中,精心布设的特显点目标i(i=1,2,…,N)的三维坐标Pi(xi,yi,hi)是已知的.为了避免旁瓣响应的相互影响,特显点两两之间的距离应不小于50个图像分辨单元.
选择特显点作为评估样本点,主要是因为可以利用其强信杂比特性精确获得它们在SAR图像中的像素位置.首先,特显点i在主、辅通道配准SAR图像中的位置(a1i,r1i)和(a2i,r2i)可以通过sinc插值方法提取局部散射幅度的最大值位置而精确得到,再根据SAR图像的慢时间基准获得对应时刻的主、辅卫星轨道位置S1i和S2i,理想的特显点干涉相位Φi可由下式计算得到,其中λ为雷达波长,
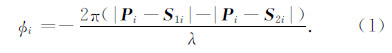
然后,利用SAR图像、干涉相位图和地面目标的对应关系,特显点的绝对干涉相位估计值 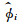 和三维坐标估计值
和三维坐标估计值 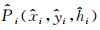 可以分别从解缠后的干涉图和InSAR生成的地理编码及投影后的DEM中插值得到.
可以分别从解缠后的干涉图和InSAR生成的地理编码及投影后的DEM中插值得到.
最后,四项主要的InSAR性能指标可用式(2)—(5)加以计算.
(1)绝对相位估计精度:
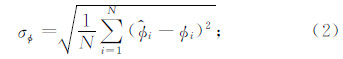
(2)相对相位估计精度:
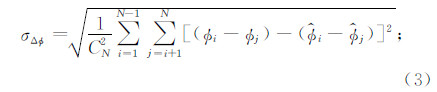
(3)绝对高程测量精度:
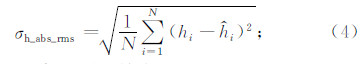
(4)相对高程测量精度:
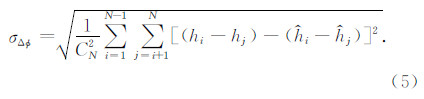
由于特显点的位置可以精确解算,因此以上各项指标的计算也是非常精确的.然而需要指出的是,计算结果尽管可以准确反映特显点处的InSAR测量性能,但却无法准确反映特显点周围一般自然场景的InSAR测量性能,尤其是与相位噪声密切相关的相对测量精度.
图 1a和图 2a分别为信杂比(SCR)为22 dB和12 dB时的特显点区域SAR图像,图 1b、1c、2b、2c分别为特显点的方位向剖面和距离向剖面,当SCR为22 dB时,峰值位置比较清晰,当SCR为12 dB时,峰值位置出现了较强的不确定性,可见高信杂比是精确获取特显点位置的必要条件.图 1d和图 2d分别为两组情况下的相干系数图,可以看出,较高的信杂比使得特显点处的相干性显著提高,这与(Ferretti et al.,2001)对永久散射体的论述是相似的.
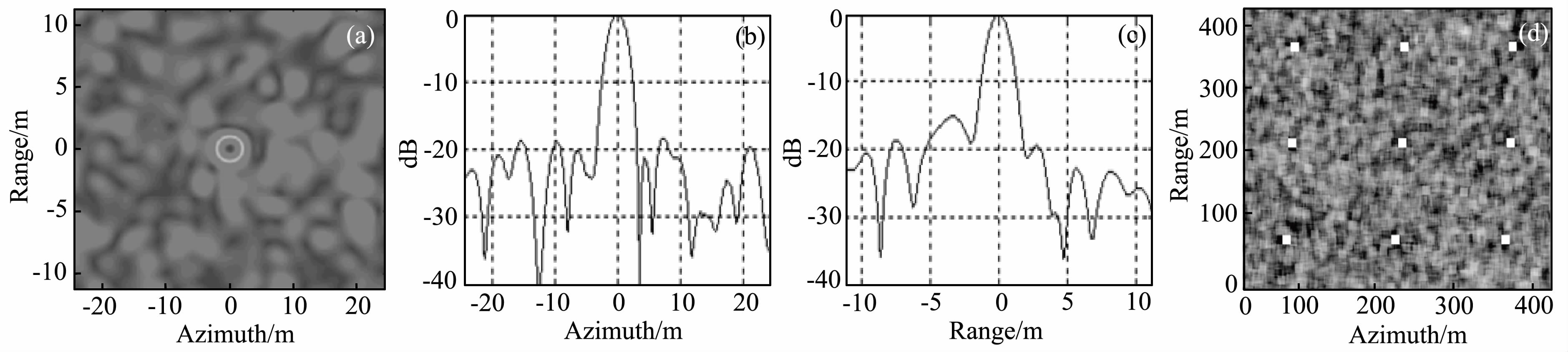 |
图 1 SCR为22 dB的特显点区域图像与相干系数图 (a) 幅度图; (b) 方位向剖面图; (c) 距离向剖面图; (d) 相干系数图. Fig. 1 Image around prominent scatterer and coherence for SCR=22 dB (a) Amplitude image; (b) Azimuth profile; (c) Range profile; (d) Coherence image. |
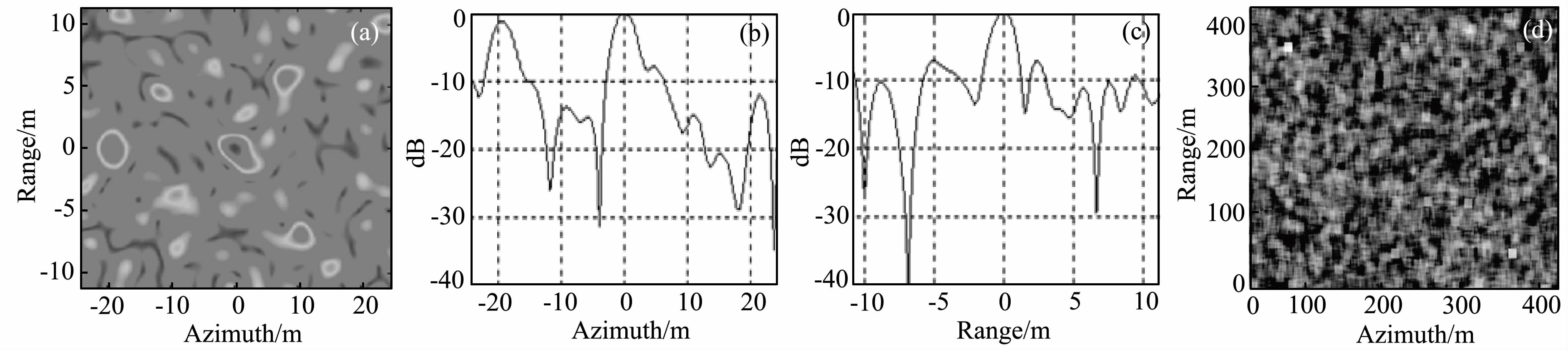 |
图 2 SCR为12 dB的特显点区域图像与相干系数图 (a) 幅度图; (b) 方位向剖面图; (c) 距离向剖面图; (d) 相干系数图. Fig. 2 Image around prominent scatterer and coherence for SCR=12 dB (a) Amplitude image; (b) Azimuth profile; (c) Range profile; (d) Coherence image. |
特显点处更高的相干性使得其InSAR测量精度显著偏高,相应的指标计算结果与其周围一般自然场景的InSAR测高性能不一致,从而无法直接用于表征InSAR产品的性能.下一节,我们引入虚拟特显点的概念,对评估方法加以改进.
3 引入虚拟特显点的高精度InSAR性能评估方法在上节中位置Pi精确已知的特显点i(i=1,2,…,N)附近相距ΔPi的位置上取得坐标为Piv的地面场景散射元,我们将它称为虚拟特显点i,如图 3所示.
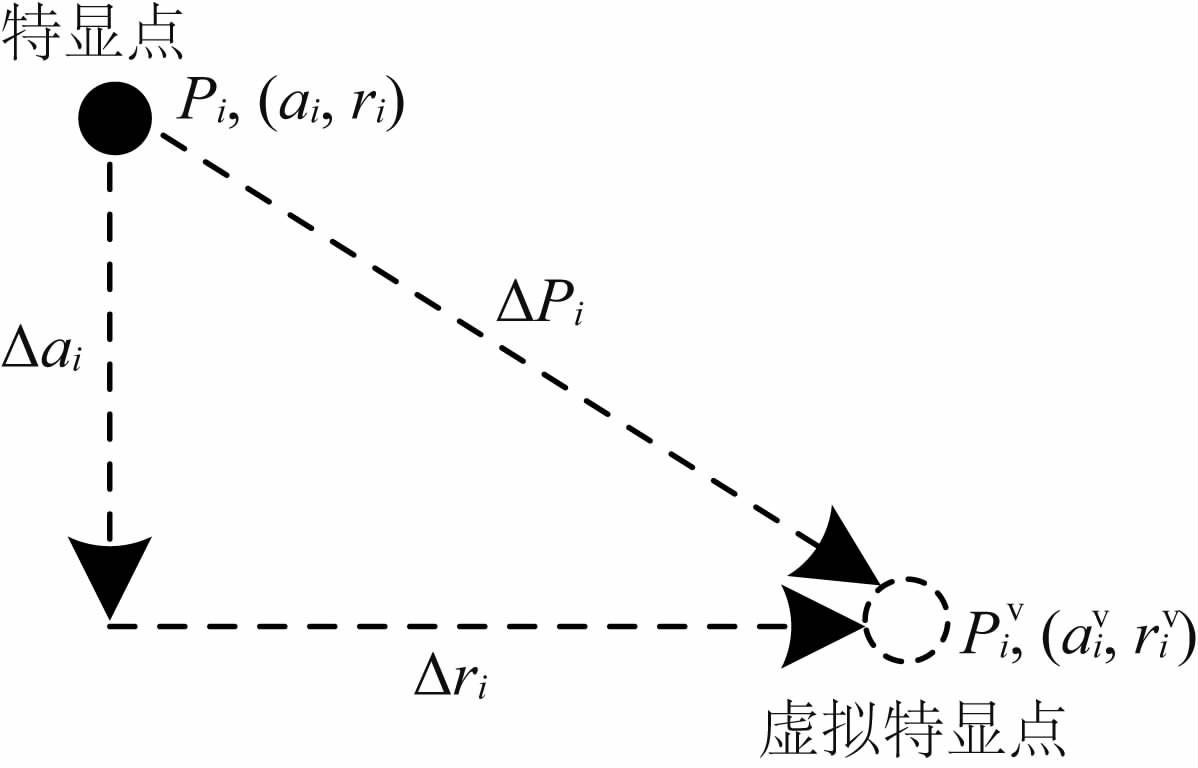 | 图 3 虚拟特显点与实际特显点的位置关系 Fig. 3 Relative position between virtual prominent scatterer and actual one |
虚拟特显点是普通的三维自然场景散射元,其干涉相位估计精度和DEM测量精度可用于客观表征InSAR产品的性能.根据第2节,特显点由于信杂比较高其图像位置坐标(ai,ri)可以精确计算,而为了获得精确的InSAR指标计算结果,还必须准确获取虚拟特显点在SAR图像中的位置(aiv,riv).但是,虚拟特显点不是真正的高信杂比特显点,其图像坐标无法直接通过插值方法提取出来.
由图 3,如果可以准确计算SAR图像中虚拟特显点和实际特显点的相对位置(Δai,Δri),那么虚拟特显点的位置(aiv,riv)也就可以精确确定了.下面我们利用距离多普勒模型方程,采用SAR图像几何定位技术(Schreier,1993; Roth et al.,2005)解决这一问题.
主、辅图像的多普勒方程和斜距方程分别如式(6)—(11)所示:
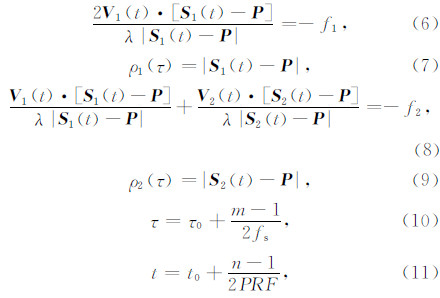
其中,τ和τ0分别为距离向第m个像元和第一个像元的快时间,fs为雷达信号采样频率;t和t0分别为方位向第n个像元和第一个像元的慢时间,PRF为雷达方位向脉冲重复频率;S1(t)、S2(t)、P分别为主星、辅星及地面散射点的位置矢量,V1(t)、V2(t)分别为主星、辅星的速度矢量,ρ1(τ)、ρ2(τ)分别为地面散射点在两幅SAR图像中的斜距,f1、f2分别为主、辅通道的多普勒中心频率.
以上方程组已知雷达参数、卫星轨道、虚拟特显点及相应实际特显点的地面位置,可以采用非线性迭代的计算方法,精确解算出图像像元坐标.记第i(i=1,2,…,N)个虚拟特显点及相应实际特显点的图像位置坐标分别为 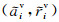 和
和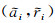 .实际中,尽管受卫星轨道测量误差、雷达斜距测量误差、时间同步误差等多种系统误差的影响,
.实际中,尽管受卫星轨道测量误差、雷达斜距测量误差、时间同步误差等多种系统误差的影响,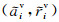 和
和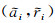 的计算误差较大,但是由于各项系统误差源通常具有时空缓变的特性,在较小的局部区域内,虚拟特显点相对于实际特显点的图像相对位置坐标可以由下式精确计算.
的计算误差较大,但是由于各项系统误差源通常具有时空缓变的特性,在较小的局部区域内,虚拟特显点相对于实际特显点的图像相对位置坐标可以由下式精确计算.
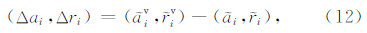
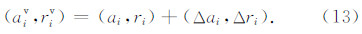
进一步,采用第2节的指标计算方法即可将虚拟特显点作为评估样本点,利用式(2)—(5)计算四项InSAR性能指标.
需要指出的是,图 3中虚拟特显点和实际特显点的相对位置ΔPi应尽量控制在50~100个分辨单元内,一方面偏小的间距容易引入实际特显点旁瓣能量的影响,另一方面偏大的间距将使得图像相对位置的计算误差增大.
4 仿真实验与分析实验采用一发双收的双星编队InSAR系统方案,卫星和雷达参数参考TanDEM-X系统,如表 1所示.实验的仿真场景为3 km×3 km的山地,平均坡度小于10°,场景中均匀布设100个特显点,间距大于150 m,各特显点的后向散射系数设为20 dBm2.实验中仅考虑了两种主要的系统误差,即不同去相干条件下的干涉相位误差和10 mm的视线向基线测量误差,InSAR系统模糊高度约32.73 m.
| | 表 1 卫星与雷达系统参数 Table 1 Parameters of satellite and radar system |
仿真实验流程如图 4所示,编队卫星的InSAR回波数据模拟、SAR成像和InSAR数据处理均采用天基雷达先进仿真器(SBRAS)(Wang et al.,2007; Chen et al.,2012)实现,其中三维自然场景的散射建模与回波仿真方法可参考文献(Ulaby and Dobson,1989; Franceschetti et al.,1992; Eineder,2003).
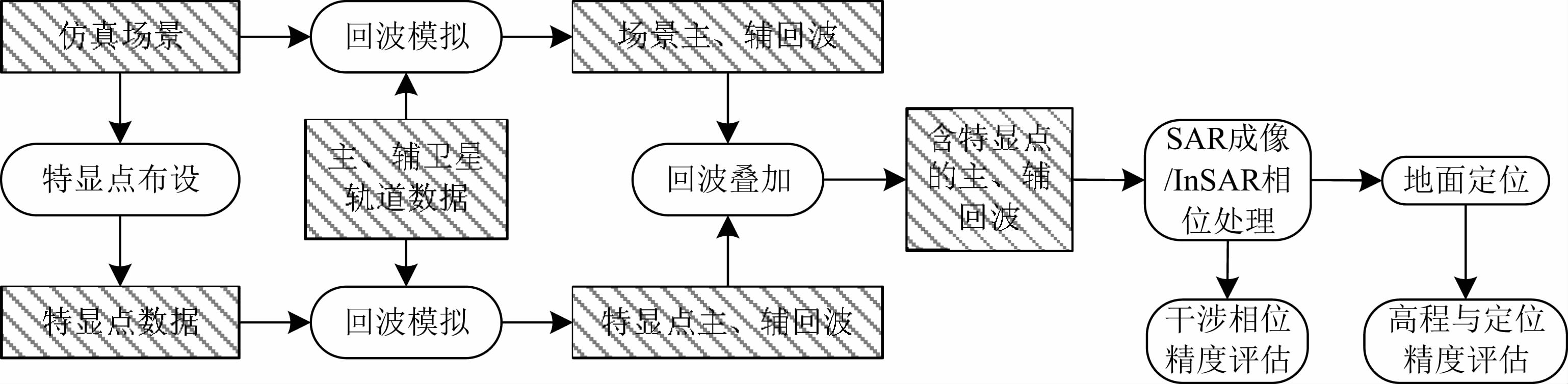 | 图 4 InSAR性能评估的仿真实验流程 Fig. 4 Diagram of InSAR performance evaluation simulation experiment |
图 5和图 6分别为地面三维自然场景和解缠后的干涉相位图.四组不同平均相干系数下的仿真实验结果如图 7所示,图中不同的曲线分别对应各项指标的理论预估结果、特显点评估结果(PS)和虚拟特显点评估结果(VPS).理论值是根据InSAR系统参数及文献(张永俊,2011)的性能预估模型获得,其中模型中的干涉相位滤波等效视数取16.可以看出,特显点方法的评估结果与理论值相差较大,尤其是相位估计精度和相对测高精度明显偏高,并且指标值随着相干系数的变化表现过缓,无法准确反映相干性与相对测高精度的变化关系;而改进后的虚拟特显点方法则有效避免了特显点强散射特性的影响,其四组性能指标计算结果与理论分析曲线均很好地吻合,充分说明了新方法的优越性.需要说明的是,图 7c中PS方法似乎与理论值更为接近,这是因为绝对测高精度不同于其他三组InSAR性能指标,其误差来源主要是10 mm的视线向基线误差,而受信号相干性影响较小,因此实验中该指标难以在评估方法上形成显著差异.图中三条曲线在指标数值上已非常接近,曲线之间的细微差异主要是理论模型的近似和仿真计算的随机性引起的,完全可以忽略不计.
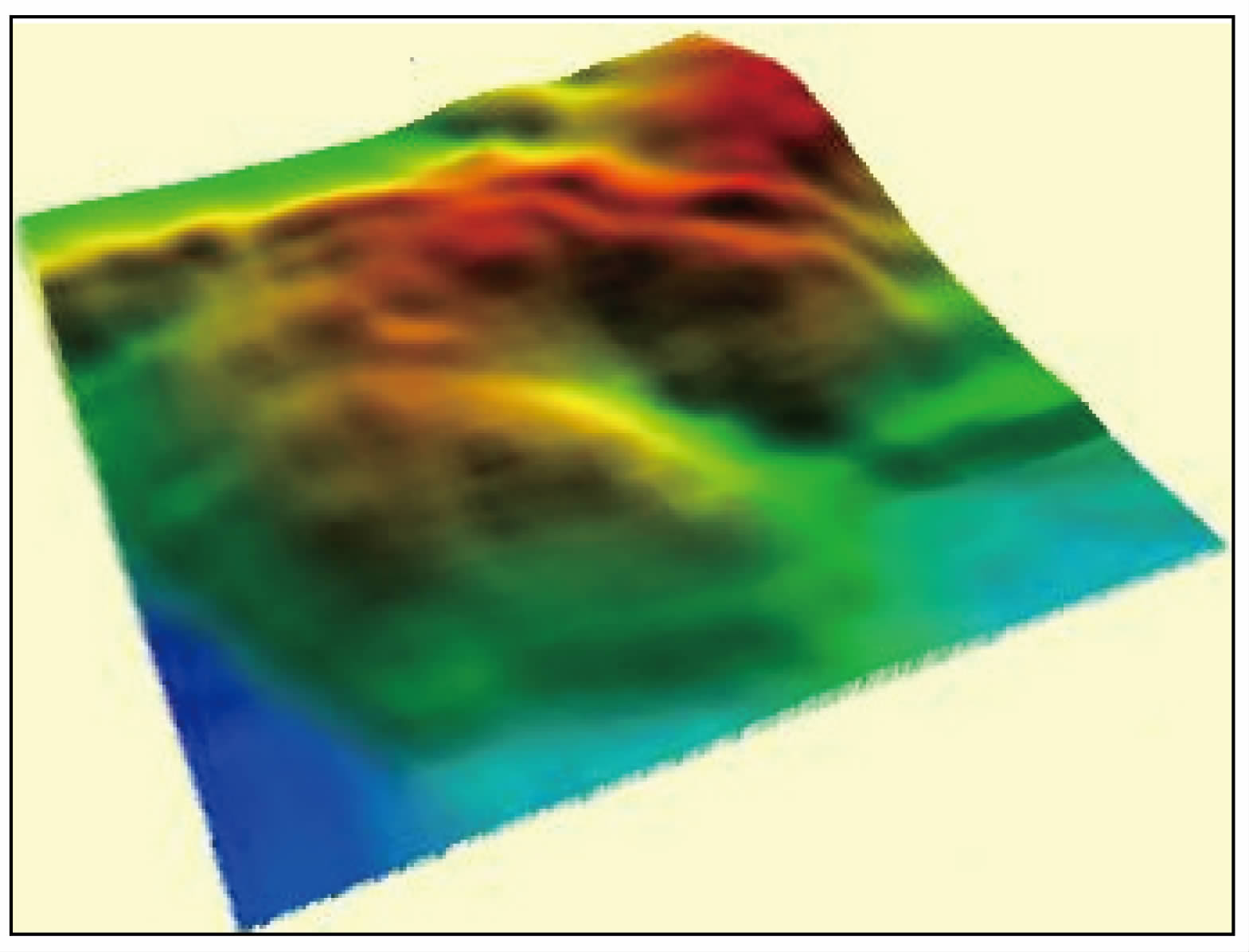 | 图 5 仿真输入的三维场景 Fig. 5 3D scene simulation input |
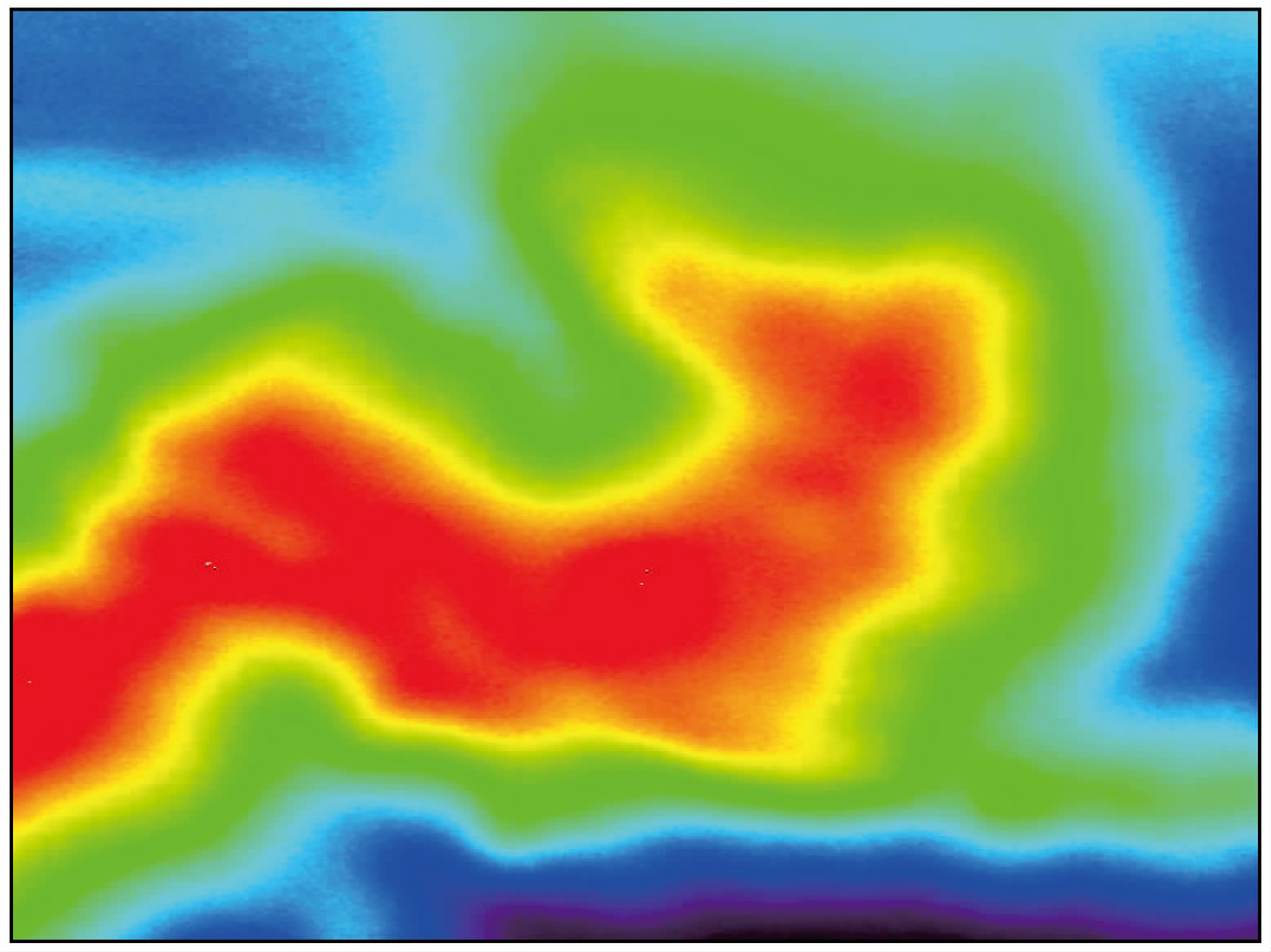 | 图 6 解缠后的干涉相位图 Fig. 6 Unwrapped interferometric phase |
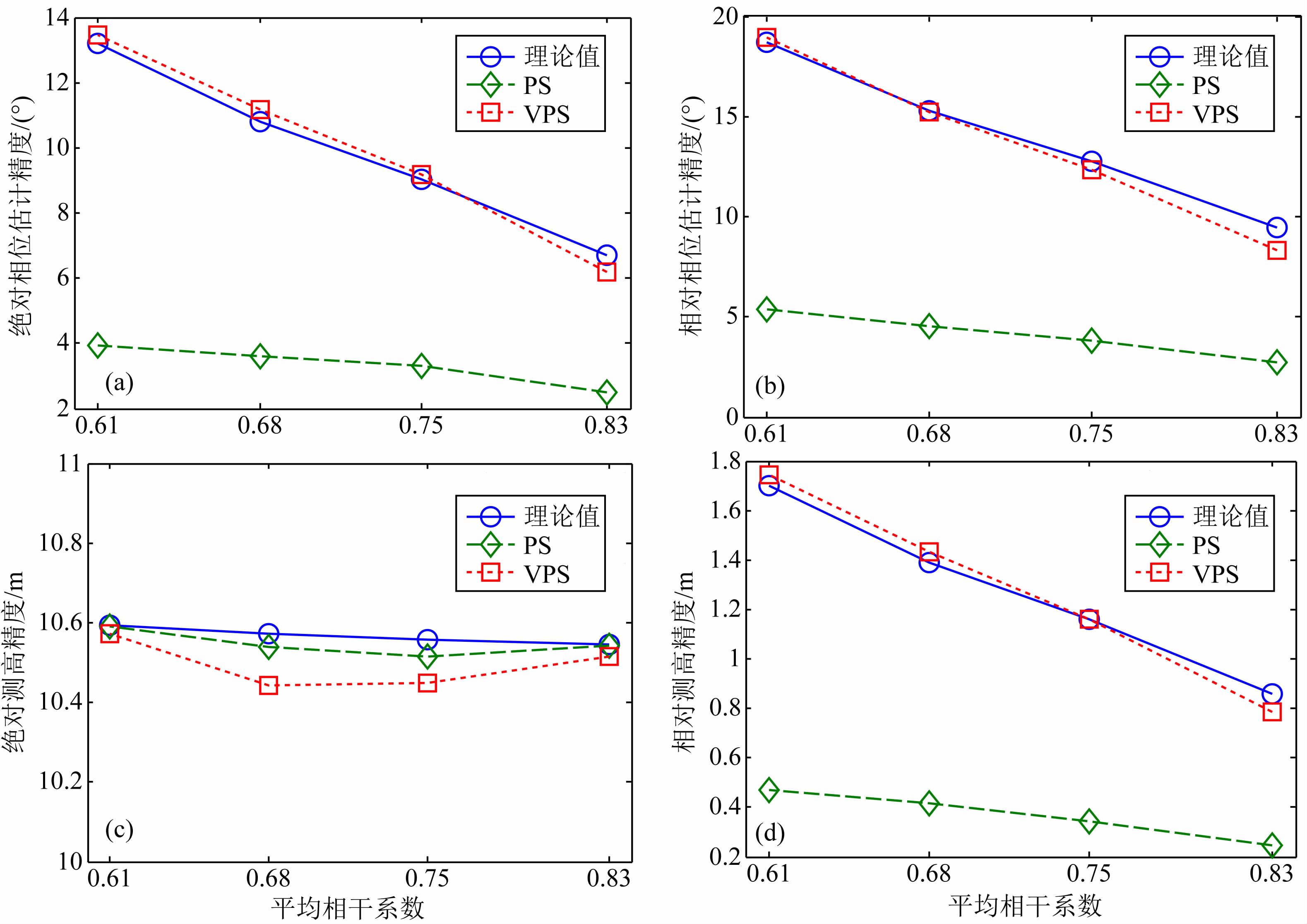 |
图 7 不同平均相干系数下的InSAR性能评估结果 (a) 绝对相位估计精度; (b) 相对相位估计精度; (c) 绝对测高精度; (d) 相对测高精度. Fig. 7 InSAR performance evaluation results for four different coherences (a) Absolute phase accuracy; (b) Relative phase accuracy; (c) Absolute height accuracy; (d) Relative height accuracy. |
本文研究了基于特显点的分布式卫星InSAR性能评估方法,一方面指出了特显点的高信杂比特性有助于SAR图像位置的精确计算,分析了高信杂比带来的相干性提高使得InSAR性能指标偏高的技术缺陷,进一步提出在实际特显点邻域引入虚拟特显点作为评估样本点的改进方法,实现了高精度、高效率和高稳健的InSAR性能指标计算.最后,全流程的分布式卫星InSAR信号仿真实验对评估方法进行了充分验证.本文成果可广泛应用于InSAR系统的地面仿真试验,以及在轨InSAR系统的性能评估、外定标、误差隔离和故障诊断等.
| [1] | Chen Q, Yu A X, Sun Z Y, et al. 2012. A multi-mode space-borne SAR simulator based on SBRAS.//2012 IEEE International Geoscience and Remote Sensing Symposium(IGARSS). Munich:IEEE, 4567-4570. |
| [2] | Eineder M. 2003. Efficient simulation of SAR interferograms of large areas and of rugged terrain. IEEE Transactions on Geoscience and Remote Sensing, 41(6):1415-1427. |
| [3] | Farr T G, Hensley S, Rodriguez E, et al. 2000. The shuttle radar topography mission.//CEOS SAR Workshop. Paris:European Space Agency, 361-363. |
| [4] | Ferretti A, Prati C, Rocca F. 2001. Permanent scatterers in SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing, 39(1):8-20. |
| [5] | Franceschetti G, Migliaccio M, Riccio D, et al. 1992. SARAS:A synthetic aperture radar(SAR) raw signal simulator. IEEE Transactions on Geoscience and Remote Sensing, 30(1):110-123. |
| [6] | López-Dekker P, Prats P, De Zan F, et al. 2011. TanDEM-X first DEM acquisition:A crossing orbit experiment. IEEE Geoscience and Remote Sensing Letters, 8(5):943-947. |
| [7] | Lu X Q. 2006. Study on modeling and simulation of distributed spaceborne InSAR[Ph. D. thesis](in Chinese). Changsha:National University of Defense Technology. |
| [8] | Rabus B, Eineder M, Roth A, et al. 2003. The shuttle radar topography mission-a new class of digital elevation models acquired by spaceborne radar. ISPRS Journal of Photogrammetry and Remote Sensing, 57(4):241-262. |
| [9] | Roth A, Huber M, Kosmann D. 2005. Geocoding of TerraSAR-X data. DLR TerraSAR-X Tech. Report. |
| [10] | Schattler B, Kahle R, Metzig R, et al. 2011. The joint TerraSAR-X/TanDEM-X ground segment.//2011 IEEE International Geoscience and Remote Sensing Symposium(IGARSS). Vancouver, BC:IEEE, 2298-2301. |
| [11] | Schreier G. 1993. SAR Geocoding:Data and Systems. Karlsruhe:Wichmann-Verlag. |
| [12] | Ulaby F T, Dobson M C. 1989. Handbook of Radar Scattering Statistics for Terrain. Norwood:Artech House. |
| [13] | Wang M, Liang D N, Huang H F, et al. 2007. SBRAS:An advanced simulator of spaceborne radar.//2007 IEEE International Geoscience and Remote Sensing Symposium(IGARSS). Barcelona:IEEE, 4942-4944. |
| [14] | Wang Q S, Huang H F, Dong Z, et al. 2009. Fast simulation of InSAR ideal interferometric phase and precision analysis. Journal of System Simulation(in Chinese), 21(18):5951-5954. |
| [15] | Wang Q S. 2011. Research on high-efficiency and high-precision processing techniques of spaceborne interferometric synthetic aperture radar[Ph. D. thesis](in Chinese). Changsha:National University of Defense Technology. |
| [16] | Werner M. 2001. Shuttle radar topography mission(SRTM) mission overview. Frequenz, 55(3-4):75-79. |
| [17] | Zhang Y J. 2011. Study on error analysis and DEM precision improvement methods of spaceborne distributed InSAR[Ph. D. thesis](in Chinese). Changsha:National University of Defense Technology. |
| [18] | 路兴强. 2006. 天基分布式InSAR系统建模与仿真研究[博士论文]. 长沙:国防科学技术大学. |
| [19] | 王青松, 黄海风, 董臻等. 2009. INSAR理想干涉相位计算的快速方法及精度分析. 系统仿真学报, 21(18):5951-5954. |
| [20] | 王青松. 2011. 星载干涉合成孔径雷达高效高精度处理技术研究[博士论文]. 长沙:国防科学技术大学. |
| [21] | 张永俊. 2011. 星载分布式InSAR系统的误差分析与DEM精度提高方法研究[博士论文]. 长沙:国防科学技术大学. |
 2016, Vol. 59
2016, Vol. 59

