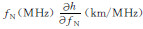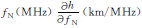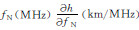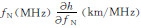电离层是由太阳高能电磁辐射、宇宙射线和沉降粒子作用于地球的高层大气使之电离而产生的,处于离地面以上约60~2000 km之间,是近地空间环境的一个重要组成部分.电离层由于含有足够多的自由电子,会对无线电波的传播产生一定的影响,其中影响最严重的是短波信号(Felgate和Golley,1971),这些影响携带了电离层结构组成及当时状态的特征信息,因此,人们常利用短波信号对电离层的特性进行实时监测,以全面了解电离层的结构形态及变化、扰动等.
电离层短波垂直探测(简称垂测)(Hunsucker,1991)是一种历史最悠久、至今仍然很重要的常规电离层探测手段,通过垂直向上发射不同频率的电磁波,测量电磁波从电离层折回的时间能够获得反映电离层虚高与频率关系的垂测电离图.利用对垂测 电离图自动度量(Reinisch和Huang,1983;Galkin等,1996;Gilbert和Smith,1988;柳文等,2009;Scotto和Pezzopane,2004)获得的垂测描迹可以反演电离层电子浓度剖面(电离层高度与等离子体频率或电子浓度的对应关系),它能够提供详细的电离层结构和变化的信息,对研究电离层结构、电离层波传播问题、空间气象应用等具有重要意义,因此,垂测电离图的反演一直以来受到人们十分广泛的重视.
目前,垂测电离图反演方法可以归纳为以下两种:①直接计算法,该方法直接利用实测虚高计算对应频率的真实反射高度(简称真高),主要有分片法(Titheridge,1959)、单一多项式法(Titheridge,1961)、重叠多项式法(Titheridge,1967)等,这些方法中有的是通过建立真高和虚高的联立方程组,直接根据实测虚高求解出真高,如分片法和单一多项式法,有的是从较低的频率到较高的频率,通过计算逐步确定各个频率对应的真高,如重叠多项式法,分片法也可以采用此方法,基于直接计算法的思想,Titheridge开发了垂测电离图自动反演的POLAN 程序(Titheridge,1985);②模式法(Dyson和Bennett,1988;丁宗华等,2007;Jiang等,2014; Reinisch和Huang,1983;Scotto,2009;郑传青,1992),该方法假设电离层剖面可用某种模型表征,通过寻找使基于该模型合成的垂测描迹与实测描迹在某种意义上最佳吻合的模型参数来确定电离层剖面,相较于直接计算法,模式法对于电离图质量要求不那么苛刻,并且反演效果也不错,应用较为普遍,国内外学者利用不同的探测数据发展了多种基于模式法的电离层参数反演方法.
基于模式法思想,Reinisch和Huang公开了一种基于移位切比雪夫多项式模型反演电离层剖面的方法(Reinisch和Huang,1983),并开发了垂测电离图自动反演NHPC程序应用于电离图实时自动度量(ARTIST)系统中.该方法将F层建模为移位切比雪夫多项式,求解满足计算虚高与实测虚高在最小二乘意义上最佳吻合的多项式系数,从而确定电离层剖面,后来,针对回波描迹中明显有F1层描迹的情况,做了模型上的一些改进,即将F1层和F2层分别用不同的移位切比雪夫多项式表示(Reinisch等,1988),但该方法更适用于F1层充分发展的情况,对于F1层未充分发展的情况,基于反演结果合成的垂测电离图与实测电离图在F1层临频附近会有一些差异,另外,未考虑层与层连接处的光滑性问题也是该方法的不足之处.
F1层未充分发展,即F1层峰高处电子浓度剖面梯度为有限数值,此时,垂测描迹上表现为F1层到F2层的平滑过渡,而不是F1层充分发展时出现的尖点.这一情况,在垂测电离图中经常出现,王世凯等(2010)也给出了F1层未充分发展时基于QPS(准抛物段)模型的反演方法.本文针对F1层未充分发展情况,并从电离层剖面的光滑性考虑,在Reinisch和Huang(1983)、Reinisch等(1988)提出的电离层剖面反演方法的基础上,建立了F1层未充分发展时电离层模型,详细描述了反演流程,并基于仿真和实测数据对反演算法的有效性进行了验证.
2 F1层未充分发展的剖面模型现有常用的电离层模型,无论是QPS模型(Dyson和Bennett,1988)、IRI(国际参考电离层)模型(Bilitza,1990),还是Reinisch和Huang(1983)、Reinisch等(1988)提出的移位切比雪夫多项式模型,所描述的电子浓度剖面在每层的峰高处都近似为抛物形状,此处梯度剖面为无穷大,也即较低一层剖面在抛物顶点处达到该层电子浓度的最大值,然后到达较高一层,如图 1a给出的剖面示意图中红色实线所示(红色虚线给出的是该处的抛物形状),当F1层充分发展时,上述模型描述F1层剖面是恰当的,此时回波描迹表现为在F1层临频处“冲上去”,形成一个尖点,如图 1b给出的回波描迹示意图中红色实线所示,然而对于F1层未充分发展情况,较低一层剖面未到达抛物顶点处就已经达到该层电子浓度的最大值,然后到达较高一层,剖面梯度为一个有限的数值,如图 1a给出的示意图中蓝色实线所示(蓝色虚线给出的是该处的抛物形状),此时回波描迹表现为F1层到F2层描迹的平滑过渡,如图 1b给出的回波描迹示意图中蓝色实线所示,对于F1层未充分发展情况,上述常用模型将不能很好地描述F1层未充分发展情况剖面的变化特征.
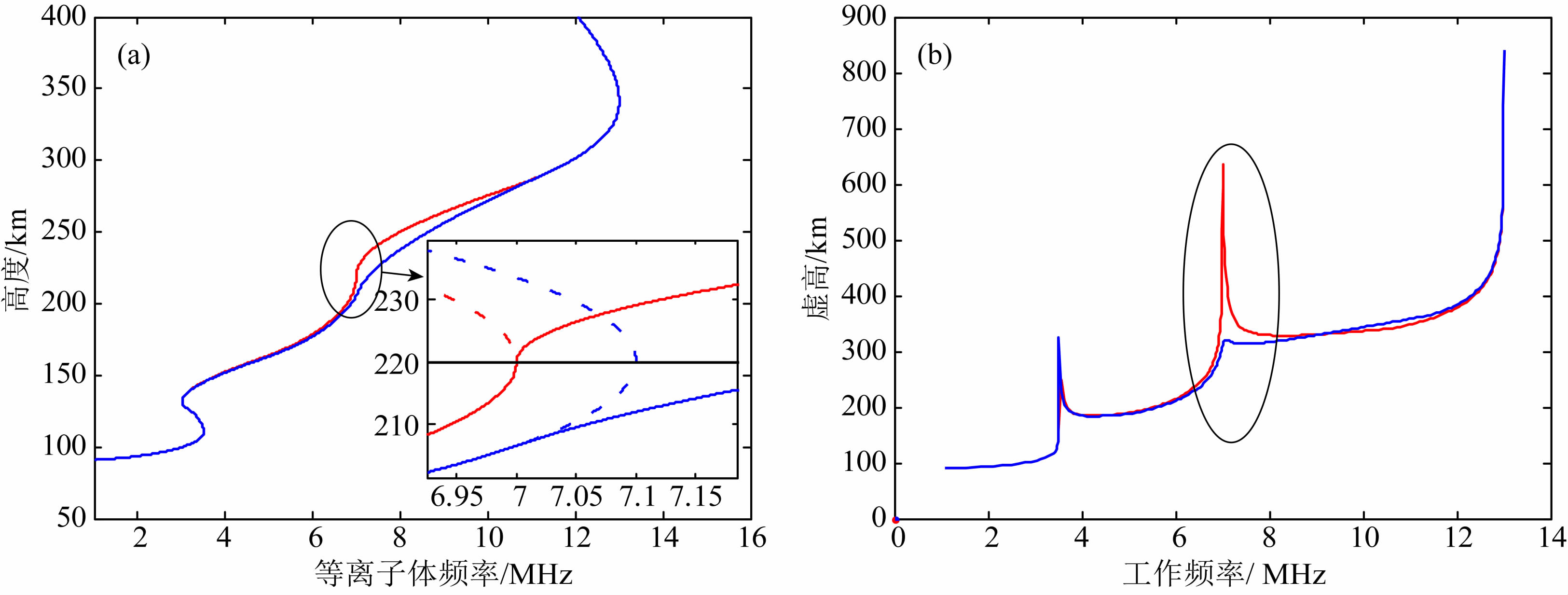 | 图 1 F1层未充分发展时剖面和回波描迹示意图 (a) 剖面示意图;(b) 回波描迹示意图.Fig. 1 The diagram of the profile and the echo trace of incompletely developed F1 layer (a) The diagram of the profile; (b) The diagram of the echo trace. |
针对上述分析的F1层是否充分发展时剖面存在的差异,本文引入F1层模型设定临频这一参数,基于Reinisch和Huang(1983)、Reinisch等(1988)提出的移位切比雪夫多项式模型建立了F1层未充分发展情况的电离层模型,下面给出新建模型的详细描述.
基于Reinisch和Huang(1983)、Reinisch等(1988)提出的移位切比雪夫多项式模型,将电离层建模为包含E层、谷层、F1层、F2层的四层模型,E层和谷层剖面用抛物模型表示,F1层和F2层剖面用移位切比雪夫多项式模型表示,电离层电子浓度剖面具有式(1)所示形式:
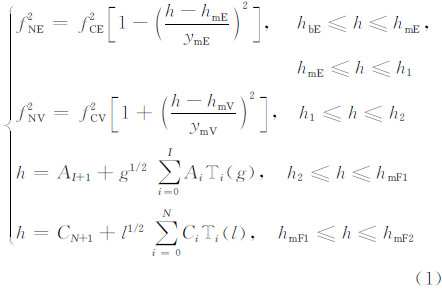
(1)E层:
fNE表示E层等离子体频率;fCE表示E层临频; hmE 表示E层峰高; ymE 表示E层半厚; hbE=hmE-ymE 表示E层底高;
(2)谷层:
fNV表示谷层等离子体频率;fCV表示谷层最小等离子体频率;hmV表示谷层等离子体频率为fCV时对应的电离层高度;ymV表示谷层半厚; h2=hmE+W,W 定义为谷层宽度;
(3)F1层:
Ti(g)为移位切比雪夫多项式,具有式(2)所示 形式:
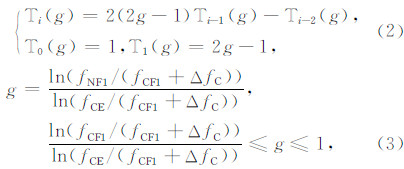
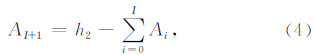
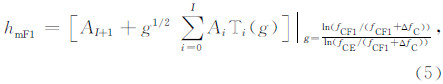
(4)F2层:
移位切比雪夫多项式Ti(l)中的l具有式(6)所示形式:
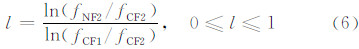
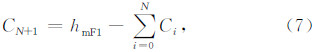

为了使建立的电子浓度剖面满足连续光滑特性,在层与层的连接点处,基于连接点以上及以下电离层模型分别计算的等离子体频率(平方)值以及剖面梯度(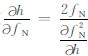 ,fN表示等离子体频率)应该相等,根据这一条件,限定相关参数之间的内在关系,即
,fN表示等离子体频率)应该相等,根据这一条件,限定相关参数之间的内在关系,即
(1)在 h=hmF1 处,有
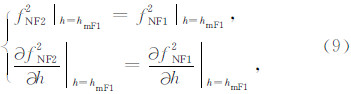
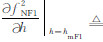
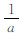 ,则由式(9)中的下式可得
,则由式(9)中的下式可得 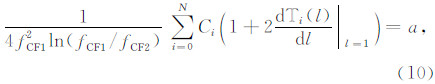
(2)在 h=h2 处,有
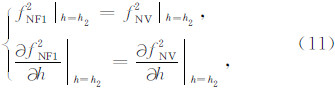
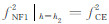 ,并且令
,并且令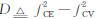 以及
以及 ,即
,即 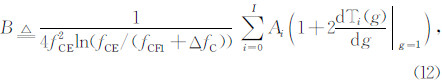
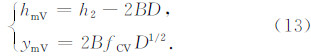
(3)在 h=h1 处,有
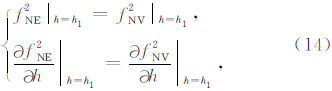
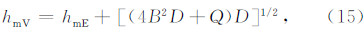
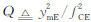 ,式(15)结合式(13)中的上式以及 W 可以进一步得到
,式(15)结合式(13)中的上式以及 W 可以进一步得到 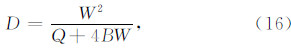
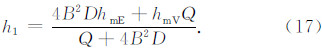
在这一节中,通过计算各层反射回波虚高,得到计算虚高与实测虚高的误差量,从而用于实现后续基于最小化误差量的各层参数反演.在计算过程中,出于简化计算过程,同时又不会引入很大的误差的考量,仍然采用Reinisch和Huang(1983)使用的方法,即在计算电波在E层和谷层传播的群距离时没有考虑地磁场的影响,在计算电波在F1层和F2层传播的群距离时假设地磁场为一定值,即任意位置处的地磁场与垂测站上空300 km高度处的地磁场一致.
(1)E层回波虚高的计算
对于频率小于等于fCE的电波将在E层反射,回波虚高计算公式为
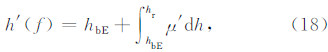
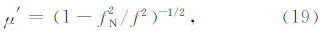
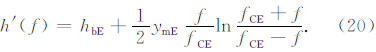
(2)F1层回波虚高的计算
对于频率大于fCE、小于等于 fCF1 的电波将在F1层反射,回波虚高计算公式为
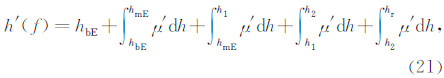
计算Δh′ E(f),Δh′ J(f),Δh′ V(f)时用到的 μ′ 仍然具有式(19)的形式,计算结果分别为
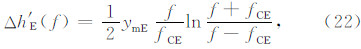
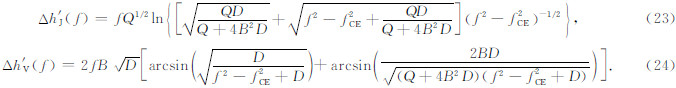
计算Δh′ F1(f)时用到的 μ′ 采用Huang和Reinisch(1982)给出的形式,计算结果为

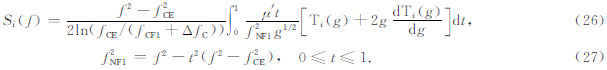
(3)F2层回波虚高的计算
对于频率大于 fCF1、小于等于fCF2 的电波将在F2层反射,回波虚高计算公式为
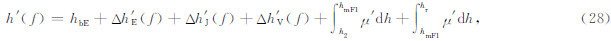
此时,Δh′ E(f)、Δh′ J(f)、Δh′ V(f)仍然可分别用式(22)、式(23)、式(24)计算,Δh′ F1(f)仍然可以采用式(25)计算,但由于此时电波在F2层反射,其中的 Si(f)的计算公式变为
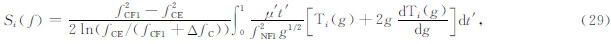

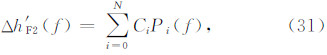
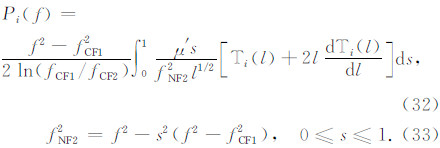
在本节中,基于对所选数据点的计算得到的虚高和实测虚高的差的平方和最小化准则,实现各层参数的反演,即实现最小二乘意义上的参数最优化.
(1)E层参数的反演
由式(1)中上式可知,决定E层剖面的三个参数主要是fCE、hmE(或hbE)、ymE,本文采用一种区域搜索的方法实现E层参数的反演,虽然fCE可由垂测电离图智能判读软件(柳文等,2009)自动给出,误差小于0.2 MHz,但考虑到进一步提高反演精度,本文对fCE也在一定范围进行搜索,确定最优值.
假设垂测电离图智能判读得到的E层描迹有 K 个点,其对应的工作频率和虚高分别为 fk和h″(fk),读出的E层临频和最小虚高分别记为 fCEr和h″ minE,则对参数fCE、hbE、ymE分别在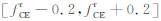 、
、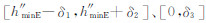 (其中δ1、δ2和δ3 是搜索范围控制量)以一定步进取值得到不同组参数,每一组参数根据式(20)计算得到 K 个点的 h′(fk ),然后计算实测虚高和计算虚高的误差平方和:
(其中δ1、δ2和δ3 是搜索范围控制量)以一定步进取值得到不同组参数,每一组参数根据式(20)计算得到 K 个点的 h′(fk ),然后计算实测虚高和计算虚高的误差平方和:
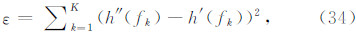
(2)设定ΔfC时谷层参数的反演
由式(13)、式(15)和式(16)可知,得到E层参数后,谷层只要确定 B和W 两个参数,谷层剖面就可以确定,因此,谷层参数反演即确定 B和W 两个参数.本文基于搜索、迭代方法实现谷层 B和W 两个参数的反演.
在谷层参数的反演过程中,选择F1层描迹中大于E层临频和F1层描迹最小虚高(记为h″ minF1)对应的频率之间的数据用于确定谷层参数,因为这部分描迹点对谷层参数比较敏感,假设共有 K 个点,其对应的工作频率和虚高分别为 fk和h″(fk).
谷层参数反演的基本步骤如下.
① 设定 W=0;
② 设定 B=0,I=7;
③ 基于最小二乘法计算F1层剖面系数 Ai(i=0~I+1);
④ 检查计算的系数 Ai(i=0~I)是否满足F1层剖面单调递增特性,(a)如果不满足,则 I=I-1,如果 I < 0,则执行⑤,否则,执行③;(b)如果满足,对 AI+1和前一次迭代记录的值进行比较,如果二者之差小于某一较小值(例如0.5 km),则计算 K 个点实测虚高和计算虚高的误差平方和,记录当前 B、W 以及计算的误差平方和的值,否则,在没有超过限定的最大迭代次数情况下,根据 Ai(i=0~I)自动调整 I,按照式(12)更新 B 的值,执行③,若超过限定的最大迭代次数,则执行⑤;
⑤ W=W+1(单位为km),如果 W 小于设定的搜索范围(例如0.7 h″ minF1-hmE),则执行②,否则,执行⑥;
⑥ 找出记录的误差平方和的最小值,该最小值对应的 B、W 即确定为谷层参数,如果没有记录下有效的 B和W,则W=0,B=0.
其中,上述步骤③的具体方法为:
根据式(21)给出 K 个点实测虚高 h″(fk)和计算虚高 h′(fk)的误差平方和:
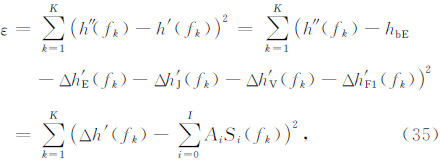
 Δh′ V(fk). 要使 ε 达到最小,即求解满足式(36)的系数 Ai(i=0~I):
Δh′ V(fk). 要使 ε 达到最小,即求解满足式(36)的系数 Ai(i=0~I): 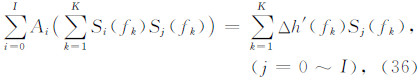
(3)设定ΔfC 时F1层参数的反演
选取F1层描迹中F1层描迹最小虚高对应的频率到 fCF1 之间的数据(或者是全部F1层描迹数据)用于确定F1层参数,假设共有 K 个数据点,其对应的工作频率和虚高分别为 fk和h″(fk). 在读取了 fCF1(由垂测电离图智能判读软件自动给出)的情况下,F1层剖面由系数 Ai(i=0~I+1)完全确定,可采用类似反演谷层参数时用到的方法来计算这些系数,这里需要注意的是,在谷层参数确定后,谷层与F1层交点处的剖面梯度也已经确定,那么,根据当前数据计算出的系数 Ai(i=0~I)必须满足式(12),因此,F1层参数的反演实际上是一个约束优化问题,即
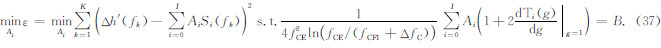
可采用拉格朗日法求解上述问题进行F1层参数的反演,具体的步骤为:
①根据式(37)建立一个新的函数:
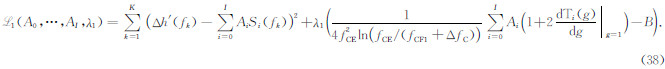
② 对式(38)中各个自变量求偏导数,建立方程组:
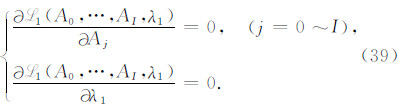
③ 求解上述方程组,得到系数 Ai(i=0~ I),检查计算的系数 Ai(i=0~I)是否满足F1层剖面 单调递增特性,(a)如果不满足,则 I=I-1,如果 I < 0,执行④,否则,执行①;(b)如果满足,执行④;
④ 按照式(4)计算 AI+1.
(4)设定ΔfC 时F2层参数的反演
F2层描迹中的数据用于确定F2层参数,假设共有 K 个数据点,其对应的工作频率和虚高分别为 fk和h″(fk). 在读取了 fCF2 的情况下,F2层剖面由系数 Ci(i=0~ N+1)完全确定,在F1层参数确定后,F1层与F2层交点处的剖面梯度也已经确定,那么,根据当前数据计算出的系数 Ci(i=0~ N)必须满足式(10),因此,F2层参数的反演同样是一个约束优化问题,可采用类似反演F1层参数时用到的方法来计算这些系数:
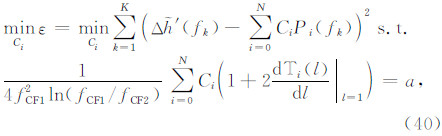
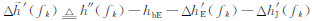
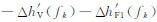 . 同样,采用拉格朗日法求解上述问题进行F2层参数的反演.
. 同样,采用拉格朗日法求解上述问题进行F2层参数的反演.
(5)谷层、F1层、F2层参数的最终确定
当F1层未充分发展时,垂测电离图智能判读软件自动给出的 fCF1 相对于F1层模型设定临频的偏差ΔfC 是一个未知量,理论上,ΔfC 的取值可以介于 0~fCF2-fCF1 之间,因此,在反演谷层、F1层、F2层参数时,将ΔfC 在 0~fCF2-fCF1 内遍历,选取使所有数据点计算虚高与实测虚高误差和最小的ΔfC 对应的谷层、F1层、F2层参数作为最终的谷层、F1层、F2层参数.
图 2给出了整个反演算法的流程框图.
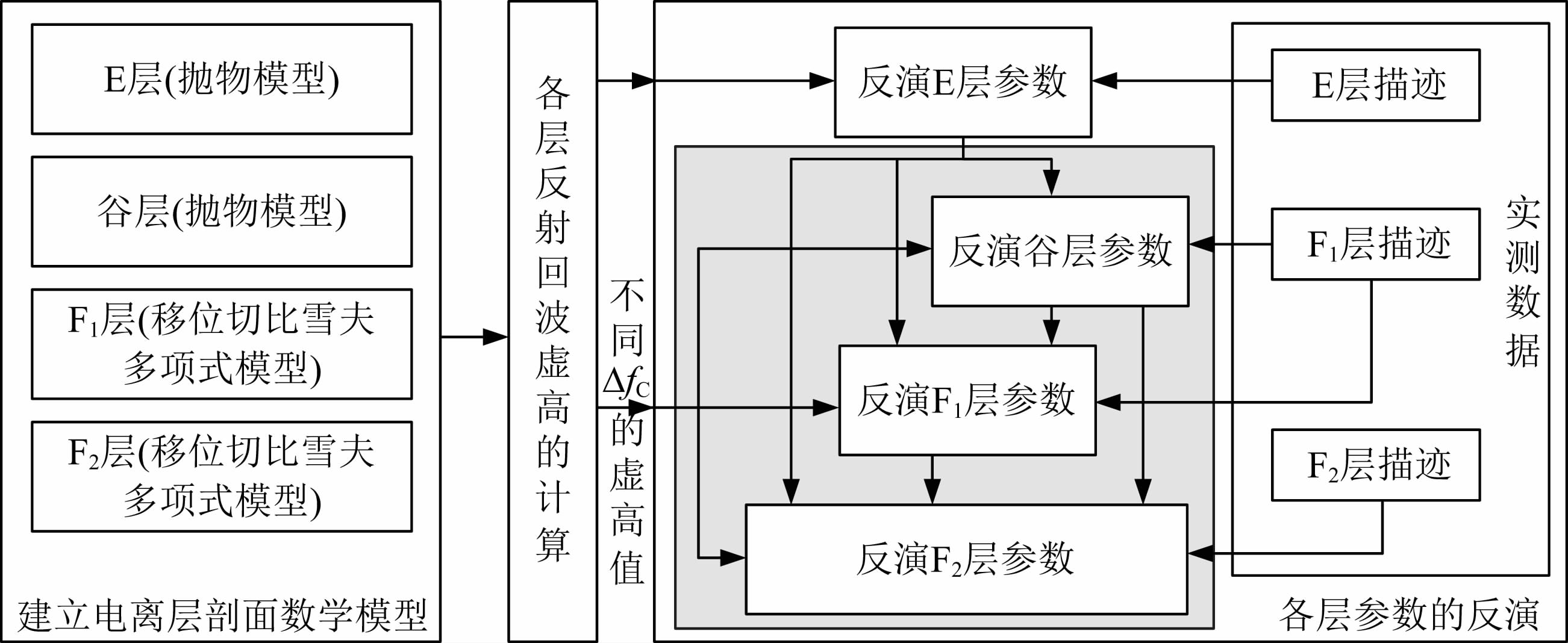 | 图 2 反演算法流程框图Fig. 2 The inversion flowchart of the vertical incidence ionogram |
本节主要是基于仿真实例对建立的电离层模型和反演算法进行仿真分析.仿真分析的思路是:假定电离层剖面参数,依此形成真实的电子浓度剖面,基于真实的电子浓度剖面仿真得到真实的回波描迹数据,然后基于真实的回波描迹数据采用不同的反演算法反演电子浓度剖面,将反演得到的剖面和真实电子浓度剖面进行比较来验证反演算法的有效性.
表 1给出了两个仿真实例的电离层参数,假定F1层充分发展时的临频为7MHz,二者的区别主要是F1层的发展程度不同.图 3和图 4分别给出了两个仿真实例反演算法的结果比较.
| | 表 1 仿真实例电离层参数 Table 1 The ionospheric parameters of the simulation examples |
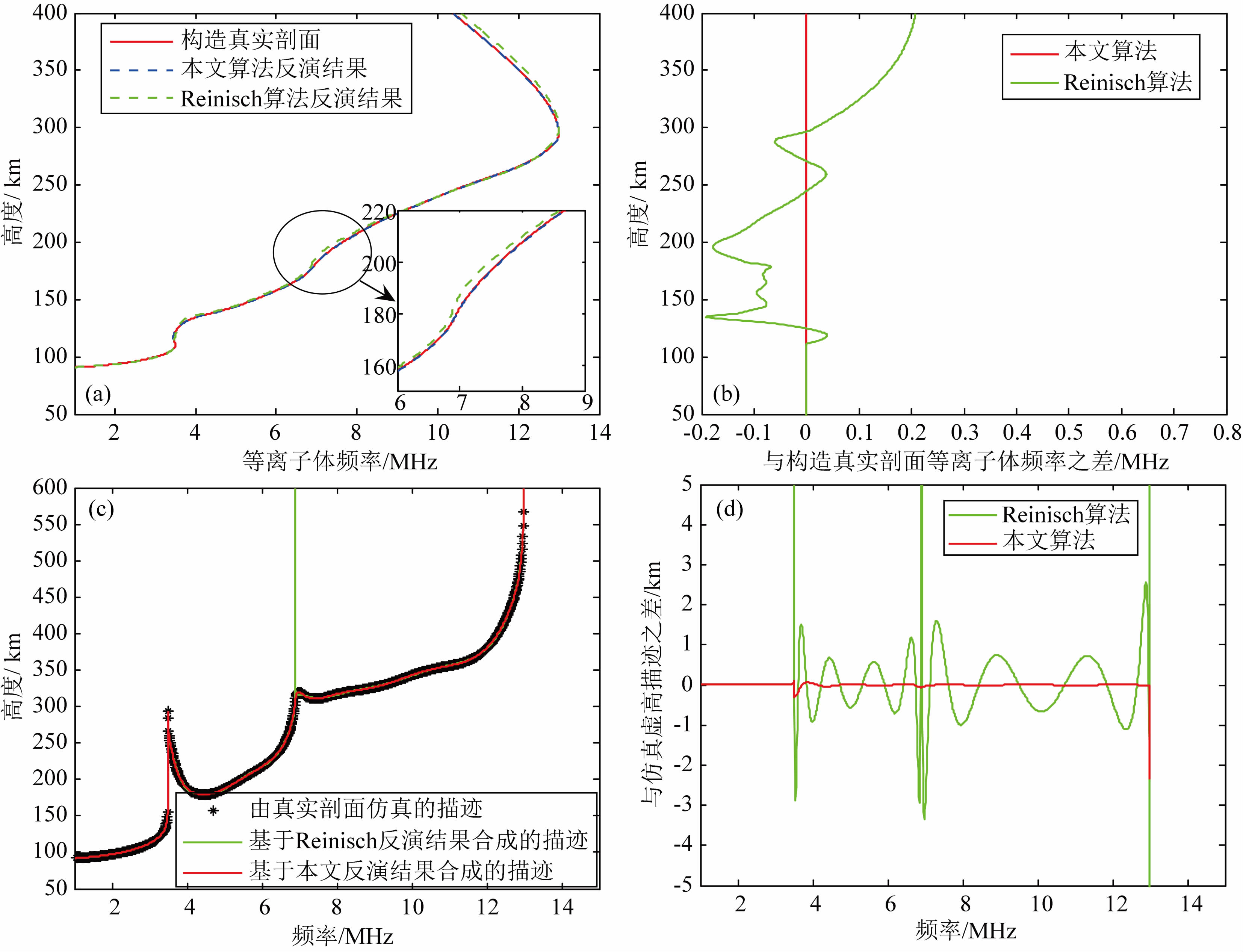 | 图 3 仿真实例1反演算法比较 (a) 剖面比较; (b) 剖面误差; (c) 虚高描迹比较; (d) 虚高误差. Fig. 3 The comparison of inversion results for example 1 (a) The comparison of profiles; (b) Profile errors; (c) The comparison of synthesized traces; (d) Virtual height errors. |
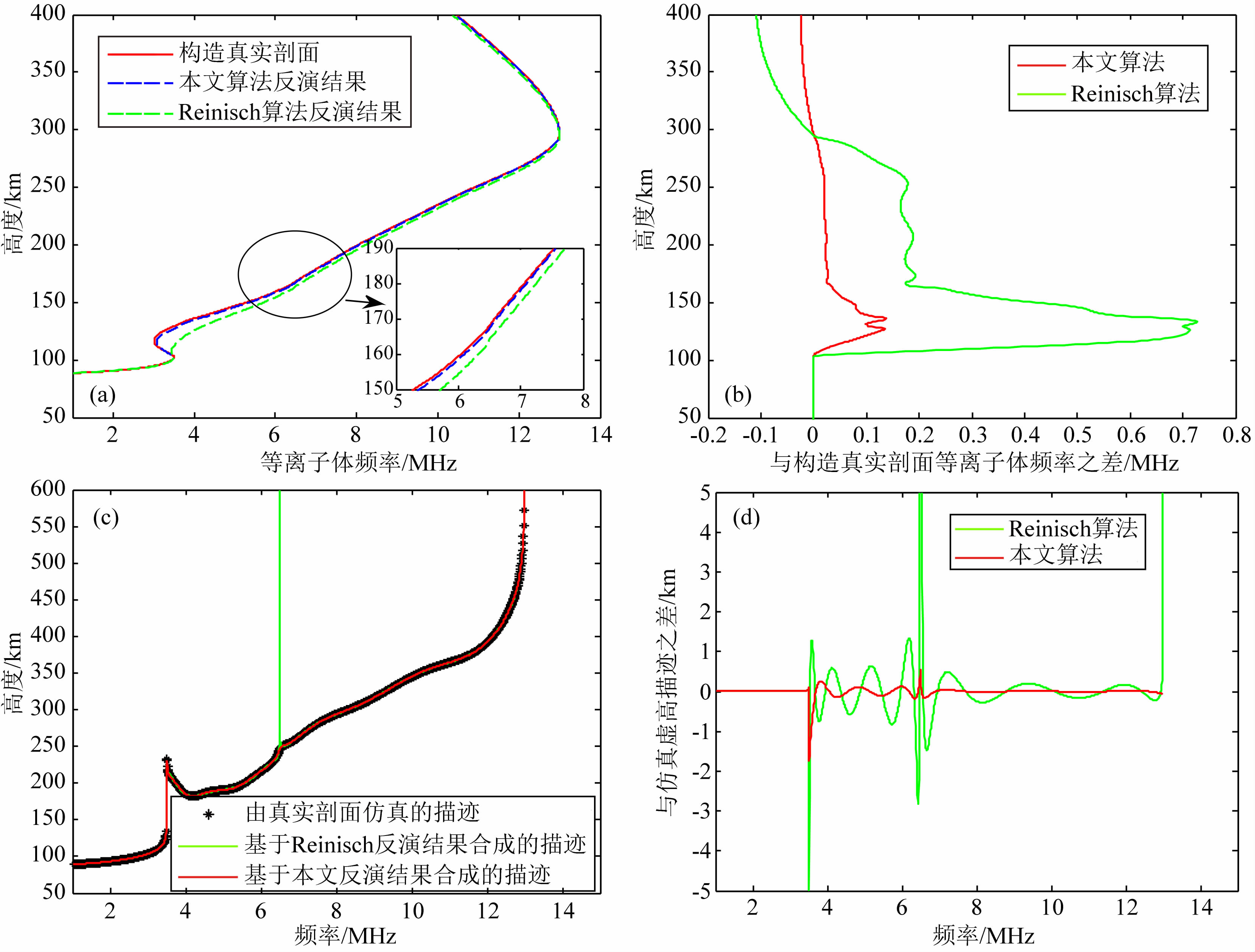 | 图 4 仿真实例2反演算法比较 (a) 剖面比较; (b) 剖面误差; (c) 虚高描迹比较; (d) 虚高误差. Fig. 4 The comparison of inversion results for example 2 (a) The comparison of profiles; (b) Profile errors; (c) The comparison of synthesized traces; (d) Virtual height errors. |
图 3a和图 4a给出的是反演剖面和真实剖面的比较结果,其中红色实线是真实电子浓度剖面,绿色虚线和蓝色虚线分别是基于Reinisch和Huang(1983)以及Reinisch等(1988)提出算法(后续简记为Reinisch算法)和本文算法反演的电离层电子浓度剖面.由图中可以看出,本文反演算法反演的电子浓度剖面和真实剖面误差较小,图 3b和图 4b中红色实线给出了本文算法反演剖面与构造真实剖面等离子体频率之差;而Reinisch算法反演的电子浓度剖面和真实剖面误差相对要大一些,如图 3b和图 4b中绿色实线所示,其中在F1层临频(峰高)附近,与真实剖面误差(绝对值)约为0.2 MHz,这主要是因为,Reinisch算法给出的F1层模型剖面在F1层临频处接近抛物形状,对应的剖面梯度为无穷大,而这与F1层未充分发展情况是不一致的.在仿真实例2中,Reinisch算法反演谷层剖面和真实剖面的最大误差(绝对值)约为0.7 MHz,这主要是由于反演过程存在解的不唯一性导致.而本文反演算法,要基于不同的F1层模型设定临频值得到对应的谷层、F1层和F2层参数,然后从这些参数中选取使合成F1层、F2层虚高和真实回波描迹虚高误差和最小的一组作为最终的电离层参数,降低了选择错误解的概率.
图 3c和图 4c给出的是真实回波描迹虚高和基于反演结果合成虚高的比较结果,图 3d和图 4d给出了两种算法反演结果合成虚高与真实回波描迹虚高之差,由图中可见,基于本文算法反演结果合成的虚高描迹与真实回波描迹误差较小,两个仿真实例 对应的误差(绝对值)均值分别为0.01 km和0.04 km,而基于Reinisch算法反演结果合成的虚高描迹与真实回波描迹误差较大,两个仿真实例对应的误差(绝对值)均值分别为14.22 km和3.32 km,并且基于Reinisch算法反演结果合成的虚高描迹在F1层临频处“冲了上去”,与真实回波描迹明显不一致,这也是F1层充分发展和未充分发展的区别所在.
本文算法在反演F1层参数、F2层参数时均附加了该层与前一层交点处的剖面梯度保持不变这一 约束条件,保证了反演剖面的连续光滑性,而Reinisch 算法只保证了剖面的连续性.表 2和表 3分别给出了基于Reinisch算法和本文反演算法反演剖面在各层连接点处的等离子体频率值和剖面梯度值,用以说明反演剖面的连续性和光滑性.表中“-”表示在“对应高度-0”处的值,“+”表示在“对应高度+0”处的值.由表中数值可以看出,在连接点以上和以下趋近于连接点的位置处,等离子体频率都相等,证明了两种反演算法得到的剖面都是连续的;Reinisch算法反演剖面在h2和hmF1处剖面梯度出现了跳变,即左右导数不相等,如表 2中黑色加粗数据所示,说明反演的剖面不光滑,而本文算法反演剖面在各个连接点处的左右导数都相等(稍许误差是数值计算误差所致),说明了反演的剖面在各个连接点处保持了光滑性.
| | 表 2 Reinisch算法反演剖面各层连接点处计算结果 Table 2 The results at the connection points of the layers based on Reinisch′s inversion profile |
| | 表 3 本文算法反演剖面各层连接点处计算结果 Table 3 The results at the connection points of the layers based on inversion profile presented in this paper |
基于中国电波传播研究所记录的大量垂测数据对反演算法进行了验证,本节选取了7组数据对算法的有效性加以说明.选取的数据均为典型三层(F1层未充分发展)电离层情况.
图 5给出了典型三层(F1层未充分发展)电离层情况实测电离图(左列图)以及垂测反演结果(右列图),在右列图中,黑色“*”描迹给出的是垂测电离图智能判读软件对实测电离图的判读结果,蓝色虚线和玫红色虚线分别是基于Reinisch算法和本文算法反演的电离层电子浓度剖面,绿色实线和红色实线分别是基于上述两种算法反演的电子浓度剖面合成的垂测虚高描迹.
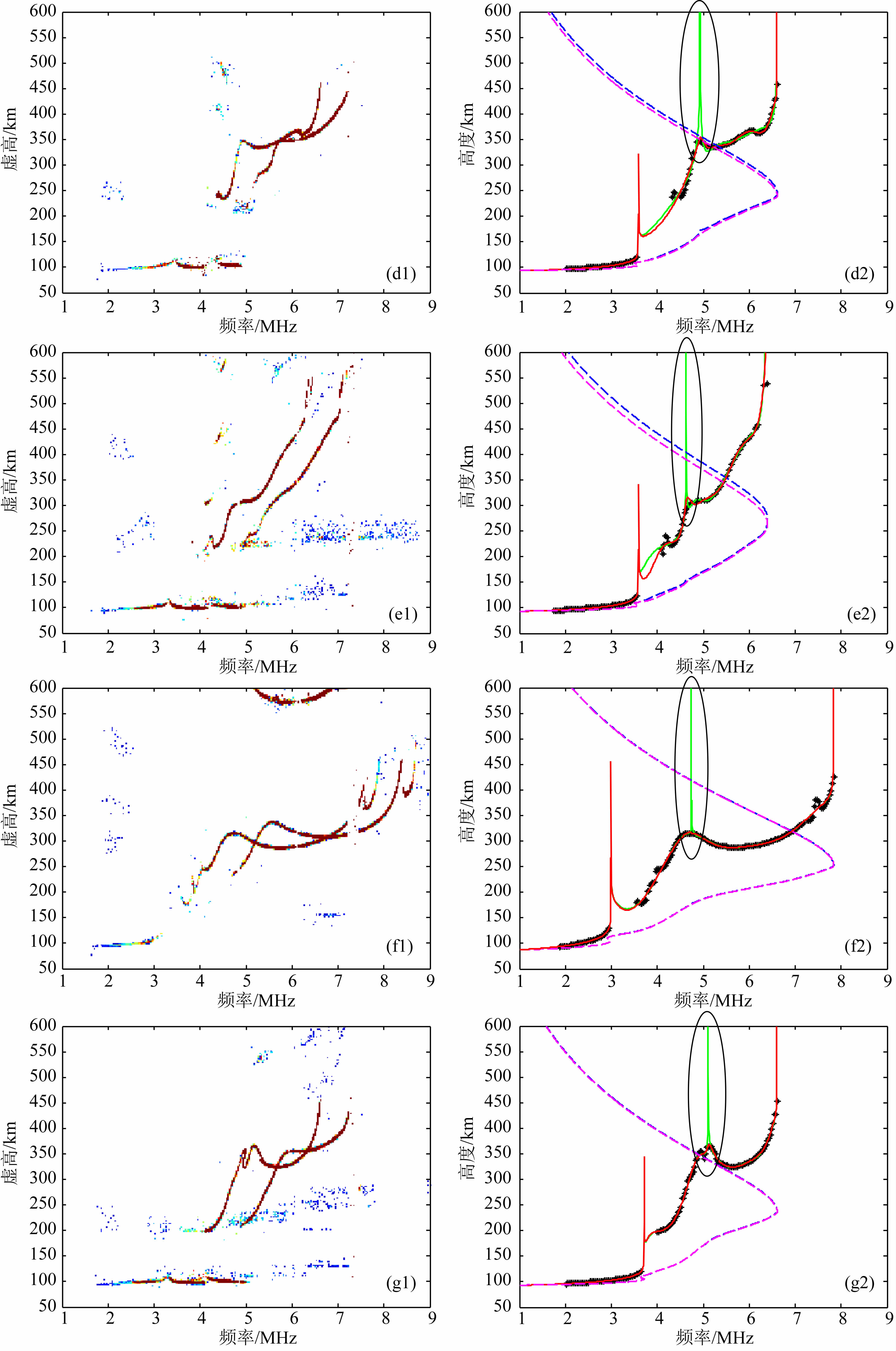 | 图 5 典型三层电离层情况垂测电离图和垂测反演结果 (a)—(g)分别为2014年08月03日12时06分、2014年12月11日15时00分、2015年08月23日13时48分、2015年08月23日14时03分、2015年08月23日14时33分、2015年08月23日16时33分和2015年08月24日12时18分的结果,左侧为实测电离图、右侧为 反演剖面. Fig. 5 The ionograms and inversion profiles for typical three layers ionosphere (a)—(g) are the results on 3 August 2014 at 12 : 06 LT, on 11 December 2014 at 15 : 00 LT, on 23 August 2015 at 13 : 48 LT, on 23 August 2015 at 14 : 03 LT, on 23 August 2015 at 14 : 33 LT, on 23 August 2015 at 16 : 33 LT and on 24 August 2015 at 12 : 18 LT, respectively;the left panels are measured ionograms and the right panels are the inversion profiles. |
Reinisch算法没有考虑F1层未充分发展情况,基于反演算法得到的电子浓度剖面合成的垂测描迹在F1层临频附近均与实测描迹有很大差别,如图 5中黑色椭圆框入的绿色实线所示,而本文算法考虑了F1层未充分发展情况,基于反演算法反演的剖面合成的回波描迹与实测描迹在F1层临频附近都吻合得较好,如图 5中红色实线所示.
图 5(c1)—5(g1)中的实测电离图显示,此时F1层或者F2层均存在一定程度的扰动,两种算法对于频率间变化比较缓慢的扰动均具有一定的鲁棒性,本文算法性能更好一些,如图 5(d2)所示.但是对于明显存在附加电离层的扰动,如图 5(c1)和5(f1)所示,出现了F0.5层和F3层,此时基于两种反演算法反演剖面合成的描迹都没有表现出实测描迹的扰动特征,因此,对于这类情况,还需要在电离层模型上增加扰动项模型,进行进一步的改进.
由于Es层遮蔽或者吸收的影响,F1层低端常常会出现描迹严重缺失,如图 5(a2)和5(d2)所示,此种情况下,两种算法均能自动反演出电子浓度剖面,实现对提取的实测描迹在最小二乘意义上的最佳拟合,但对应区域反演剖面可能存在一定的差别.而由于实测数据的缺失以及没有真实剖面的比对,无法说明哪种反演算法对这一区域的反演结果更加准确.因此,对于描迹缺失问题,应该考虑增加具有实际物理意义的缺失数据补偿算法,这也是进一步提高反演精度的必要条件.
在中纬度地区、中午前后,F2层临频东西向的梯度一般较小(Davies和Rush,1985).因此,对于中纬度地区东西向1000 km左右的链路,中午前后,电子浓度剖面均匀分布的假设近似成立.在此基础上,选取了符合上述条件的一条斜测链路,基于本文算法反演的电子浓度剖面,在电子浓度剖面为均匀分布的假设下,利用自研的基于三维数字射线追踪(Jones和Stephenson,1975;柳文等,2008)和离散电子浓度网格的斜测描迹合成软件,合成对应该斜测链路的斜测描迹与实测电离图进行对比,对反演电子浓度剖面的准确性做进一步的验证.
图 6给出了对比结果,其中,玫红色点迹表示基于本文提出反演算法反演电子浓度剖面合成的斜测描迹.由图中可以看出,合成描迹E层低角的群距离和实测数据吻合得较好,误差在斜向探测一个距离分辨率之内(7.5 km);图 6a中实测F1层描迹大部分缺失,但根据描迹的趋势可以判断合成的描迹与已有描迹是一致的.图 6b中没有观察到明显的F1层描迹,合成F1层描迹群距离与对应频率上的实测描迹有一些差别,偏差最大达30 km,这主要是由于电子浓度均匀分布的假设和实际情况有一定的出入所致;图 6a中合成F2层描迹高低角波都与 实测结果一致,图 6b中随着频率的增大,合成F2层描迹群距离与实测值逐渐接近,但MUF比实测值略低,这 些差别也主要是由于电子浓度分布的不均匀性造成的.
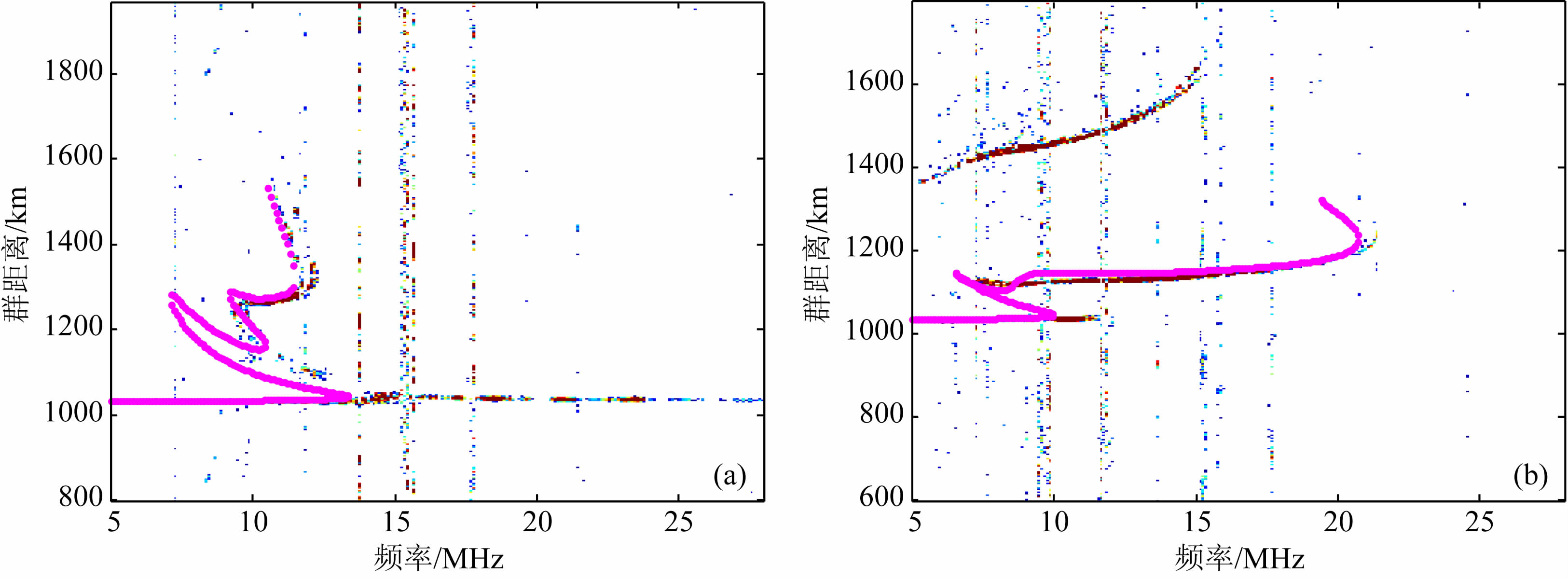 | 图 6 基于垂测反演结果合成的斜测描迹与实测电离图对比情况 (a) 2014年08月03日12时06分; (b) 2014年12月11日15时00分. Fig. 6 The comparison between the synthesized oblique traces and the recorded traces (a) On 3 August 2014 at 12: 06 LT; (b) On 11 December 2014 at 15: 00 LT. |
综上,由实测数据和基于反演结果合成的描迹的对比可知,对于F1层未充分发展情况,本文算法能够根据提取的垂测描迹较为准确地给出上空电离层状态.
6 结论本文在Reinisch和Huang(1983)、Reinisch等(1988)提出的一种基于移位切比雪夫多项式模型反演电离层剖面的方法的基础上,针对F1层未充分发展情况,引入F1层模型设定临频这一参数,建立了F1层未充分发展时的电离层模型,提出了约束优化F1层参数、F2层参数的垂测电离图反演方法,该方法重新归纳如下:利用E层描迹数据,通过局部寻优实现E层参数的反演;给出一个F1层模型设定临频值,利用F1层较低频率区域的数据,基于搜索、迭代的方法实现谷层参数的反演,得到谷参数后,选取F1层较高频率区域回波描迹数据(或者全部F1层回波描迹数据),在保证剖面连续光滑的约束条件下,计算F1层剖面多项式系数.同样,在保证剖面连续光滑的约束条件下,选取F2层回波描迹数据,计算F2层剖面多项式系数;然后,改变F1层模型设定临频值,重复上述过程,得到每个F1层模型设定临频值对应的各层剖面参数;最后,基于F1层、F2层描迹点的计算虚高和实测虚高误差和最小准则,选取对应的F1层模型设定临频下得到的剖面参数,最终确定电离层剖面.
本文提出的反演算法能够对F1层未充分发展的垂测电离图进行有效反演,并且反演的电子浓度剖面具有连续光滑特性,反演有效性利用仿真和实测数据进行了验证.需要说明的是,本文提出反演算法只是针对F1层未充分发展情况,因为在反演F1层和F2层参数时使用了约束优化方法,因此,对于F1层充分发展情况,式(40)中的约束条件为a=∞,将无法结合约束条件计算出F2层参数,因此,需要反演算法增加预处理单元,判断此时F1层的发展情况.
另外,在本文反演模型中加入扰动项,将有助于对存在扰动情况的电离图反演精度的进一步提高;对于回波描迹缺失问题,考虑增加具有实际物理意义的缺失数据补偿算法;以及考虑使用O波、X波联合反演进一步提高反演算法的稳定性;等等.以上这些都是使算法更适合实际工程应用需要改进的地方,这也是今后需要进一步努力的方向.
| [1] | Bilitza D. 1990. The international reference ionosphere. NSSDC/WDC-A-R & S Report 90-22. National Space Science Data Center. Greenbelt,Maryland. |
| [2] | Dyson P L,Bennett J A. 1988. A model of the vertical distribution of the electron concentration in the ionosphere and its application to oblique propagation studies. Journal of Atmospheric and Terrestrial Physics,50(3):251-262. |
| [3] | Davies K,Rush C M. 1985. High-frequency ray paths in ionospheric layers with horizontal gradients. Radio Science,20(1):95-110. |
| [4] | Ding Z H,Ning B Q,Wan W X. 2007. Real-time automatic scaling and analysis of ionospheric ionogram parameters. Chinese Journal of Geophysics,50(4):969-978. |
| [5] | Felgate D G,Golley M G. 1971. Ionospheric irregularities and movements observed with a large aerial array. Journal of Atmospheric and Terrestrial Physics,33(9):1353-1369. |
| [6] | Galkin I A,Reinisch B W,Ososkov G A,et al., 1996. Feedback neural networks for ARTIST ionogram proceedings. Radio Science,31(5):1119-1128. |
| [7] | Gilbert J D,Smith R W. 1988. A comparison between the automatic ionogram scaling system ARTIST and the standard manual method. Radio Science,23(6):968-974. |
| [8] | Huang X Q,Reinisch B W. 1982. Automatic calculation of electron density profiles from digital ionograms 2. True height inversion of topside ionograms with the profile-fitting method. Radio Science,17(4):837-844. |
| [9] | Hunsucker R D. 1991. Radio Techniques for Probing the Terrestrial Ionosphere. Springer-Verlag. |
| [10] | Jiang C H,Yang G B,Zhao Z Y,et al., 2014. A method for the automatic calculation of electron density profiles from vertical incidence ionograms. Journal of Atmospheric and Solar-Terrestrial Physics,76:20-29. |
| [11] | Jones R M,Stephenson J J. 1975. A versatile three-dimensional ray tracing computer program for radio waves in the ionosphere. OT Report 75-76. US Department of Commerce,Office of Telecommunications,US Government Printing Office. Washington,USA, 185 pp. |
| [12] | Liu W,Jiao P N,Wang S K,et al., 2008. Short wave ray tracing in the ionosphere and its application. Chinese Journal of Radio Science (in Chinese),23(1):41-48. |
| [13] | Liu W,Kong Q Y,Chen Y,et al., 2009. Method on ionogram autoscaling based on IRI model. Chinese Journal of Radio Science(in Chinese),24(2):218-223. |
| [14] | Reinisch B W,Huang X Q. 1983. Automatic calculation of electron density profiles from digital ionograms 3. Processing of bottomside ionograms. Radio Science,18(3):477-492. |
| [15] | Reinisch B W,Gamache R R,Huang X Q,et al., 1988. Real time electron density profiles from ionograms. Advances in Space Research,8(4):63-72. |
| [16] | Scotto C,Pezzopane M. 2004. Software for the automatic scaling of critical frequency foF2 and MUF(3000)F2 from ionograms applied at the ionospheric observatory of gibilmanna. Annales Geophysicae,47(6):1783-1790. |
| [17] | Scotto C. 2009. Electron density profile calculation technique for autoscala ionogram analysis. Advances in Space Research,44(6):756-766. |
| [18] | Titheridge J E. 1959. The calculation of real and virtual heights of reflection in the ionosphere. Journal of Atmospheric and Terrestrial Physics,17:96-109. |
| [19] | Titheridge J E. 1961. A new method for the analysis of ionospheric records. Journal of Atmospheric and Terrestrial Physics,21:1-12. |
| [20] | Titheridge J E. 1967. The overlapping-polynomial analysis of ionograms. Radio Science,2(10):1169-1175. |
| [21] | Titheridge J E. 1985. Ionogram analysis with the generalized program POLAN. Report UAG-93. World Data Center A for Solar-Terrestrial Physics. Boulder,Colorado. |
| [22] | Wang S K,Liu W,Li S L,et al., 2010. Inversion method of F1 layer on vertical sounding ionogram. Chinese Journal of Radio Science(in Chinese),25(1):172-177. |
| [23] | Zheng C Q. 1992. The inversion of the vertical sounding ionogram. Chinese Journal of Radio Science(in Chinese),7(4):64-74. |
| [24] | 丁宗华,宁百齐,万卫星. 2007. 电离层频高图参数的实时自动度量与分析. 地球物理学报,50(4):969-978. |
| [25] | 柳文,孔庆颜,陈跃等. 2009. 基于IRI模型的垂测电离图自动判读算法. 电波科学学报,24(2):218-223. |
| [26] | 柳文,焦培南,王世凯等. 2008. 电离层短波三维射线追踪及其应用研究. 电波科学学报,23(1):41-48. |
| [27] | 王世凯,柳文,李书苓. 2010. 垂测电离图F1层反演方法研究. 电波科学学报,25(1):172-177. |
| [28] | 郑传青. 1992. 垂直探测频高图的反演. 电波科学学报,7(4):64-74. |
 2016, Vol. 59
2016, Vol. 59