2. 南京信息工程大学, 江苏省大气环境与装备技术协同创新中心, 南京 210044;
3. 南京信息工程大学, 大气物理学院, 南京 210044;
4. 南京信息工程大学, 电子与信息工程学院, 南京 210044;
5. 南京信息工程大学, 物理与光电工程学院, 南京 210044;
6. 南京市气象局, 南京 210000
2. Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology, Nanjing University of Information Science & Technology, Nanjing 210044, China;
3. School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing 210044, China;
4. School of Electronic & Information Engineering, Nanjing University of Information Science & Technology, Nanjing 210044, China;
5. School of Physics & Optoelectronic Engineering, Nanjing University of Information Science & Technology, Nanjing 210044, China;
6. Nanjing Meteorology Bureau, Nanjing 210000, China
高空气象要素的精确探测对于天气预报(Posada et al., 2013)、气候诊断预测(肖存英等, 2008; Dai et al., 2011)、大气环境监测(李刚等, 2015)以及气象灾害预警与减灾而言均具有重要的意义.无线探空仪是高空气象要素探测的主要手段之一.尽管目前已将飞机、火箭和卫星等应用于高空探测,但无线探空仪以其价格低廉和操作方便等优势仍被普遍应用于全球气象探空观测站.例如,我国120个探空站每天的常规探测全部采用无线探空仪实施高空探测.由此可见,无线探空仪提供的历史或将来的高空气象要素数据对天气预报与气候研究具有极其重要的参考价值.无线探空仪高空测量中温度、气压、风速等均具有较高测量精度,但湿度测量精度较低,而高空湿度的准确测量对预报是否降水及降水量大小均起关键性作用.探空湿度测量误差来自多方面,值得注意的是,高空中太阳辐射加热效应导致的误差由于相关研究尚不充分而往往被忽视.实际上,由于湿度传感器测量空气相对湿度,当空气绝对湿度不变而温度升高时,所测量的相对湿度值会变小.在低温环境下温度每增加10 ℃,饱和水汽压将升高一倍(李英干和范金鹏, 1990),导致相对湿度降为原来的50%.可见,探空湿度传感器测量准确的湿度值与感知准确的环境温度值有很大关联.
一般探空湿度测量时,为防止高空下雨或者雨云的干扰,在湿度传感器上通常加防雨罩,如Vaisala公司的RS80探空仪、韩国JinYang探空仪以及国内GTS1型探空仪.虽然防雨罩能起到一定的防雨效果,但通风效果变差会带来较大的延迟效应(Leiterer et al., 2005; Verver et al., 2006),且防雨罩在太阳辐射下被加热也会导致罩内湿度传感器及周围温度升高(Ciesielski et al., 2009).为避免雨水和高空低温结露的影响,Vaisala公司推出的新型RS92探空仪的湿度测量采用双加热湿度传感器.它使用交替加热和测量的方式解决了雨水及结露的问题,同时也保持了良好的通风效果,但两个湿度传感器均完全暴露在太阳辐射下,辐射加热引起传感器上的温度升高不可避免(Yoneyama et al., 2008; Bock and Nuret, 2009; Kottayil et al., 2012).因此,无论上述哪种方式,均由于太阳辐射导致湿度传感器衬底温度比周围大气温度有所升高,从而提高了湿度传感器感湿材料周围空气的饱和水汽压,使得测量的相对湿度值偏干(Guichard et al., 2000).太阳辐射对湿度测量准确性影响显著,这制约了与高空湿度相关的天气预报与气候变化预估预警等研究水平的提高.
近些年来,国内外专家针对太阳辐射引起探空湿度测量误差的问题开展了一些相关研究.在实验方面,Vömel等(2007)最早提出太阳辐射偏干误差SRDB (Solar Radiation Dry Bias)的概念,并给出了一种太阳辐射误差实验修正方法.随后Cady-Pereira等(2008)、Nuret等(2008)、Rowe等(2008)、Ciesielski等(2009, 2010)对RS80、RS90和RS92探空仪的测湿误差进行了研究,主要采用的方法是将其测量的数据与CFH (Cryogenic Frost-point Hygrometer)进行对比研究得出湿度误差修正系数.国内张立功等(2007)、姚雯等(2008)、Bian J C等(2011)、颜晓露等(2012)对我国目前使用的L波段无线探空仪与国外的探空仪以及CFH进行一系列对比试验,均发现我国GTS1型探空仪高空湿度测量有偏干现象,但文中仅对其简单阐述,未进行详细分析或提出相关的修正理论方法.在理论方面,国内已有部分专家开始采用计算流体动力学CFD (computational fluid dynamics)软件对探空温度传感器模型进行数值模拟与分析(刘清惓等, 2012, 2013; Luo et al., 2014).本文作者前期采用流体动力学方法建立了湿度测量简化系统的稳态模型,并初步得出太阳辐射加热效应引起高空湿度测量值偏干的结论.同时着重研究了由此引起的湿度相对误差与海拔高度、湿度传感器尺寸、衬底材料及反射率等因素之间的关系(冒晓莉等, 2014),而文献(冒晓莉等, 2015)则进一步研究发现由太阳辐射引起的偏干相对误差与观测地点、施放气球时间等因素均有密切关系.总体上讲,目前关于湿度的数值模拟方法仅研究了湿度传感器基本模型的稳态分析,正如前文所述,为了减少云雨等因素的影响,探空仪实际业务应用中使用的湿度传感器通常带有防雨/防辐射罩,或者采用双加热的湿度测量方式.因此,为更加真实研究太阳辐射和云雨对探空仪湿度测量的影响,本文将结合我国探空站使用的GTS1型探空仪中的湿度测量系统作为研究模型,该探空湿度测量结构带有一个盒状的防雨/防辐射罩.结合改进的太阳辐射计算模型,本文通过CFD方法研究太阳辐射和云雨对其测量湿度产生的影响,着重研究防雨/防辐射罩对于提高探空湿度测量精度的实际效果.同时以南京探空站2014年的部分典型湿度测量数据作为具体研究和修正对象,以期本文研究结果为探空湿度测量太阳辐射偏干误差的有效修正提供有益参考.
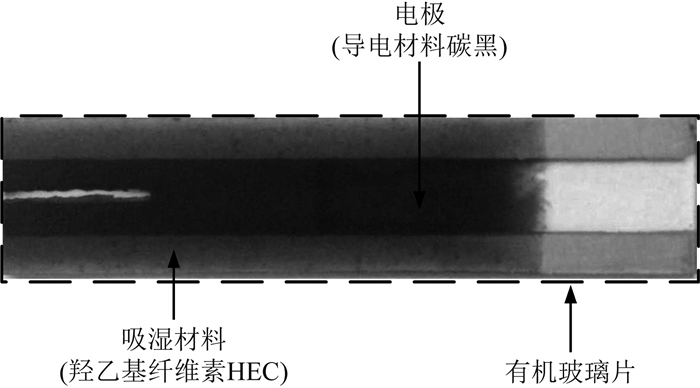
2 GTS1测湿原理及太阳辐射相关理论 2.1 GTS1探空仪湿度测量原理数字探空仪GTS1于1998年由上海长望气象科技有限公司研发成功,如今广泛应用于我国探空站.图 1为南京探空站所用探空仪GTS1中的湿度传感器实物照片,该传感器采用型号为XGH-02的高分子湿敏电阻,具有测湿范围广、互换性好,响应速度快,体积小等优点.从图 1可以看出,XGH-02湿敏电阻是一片带有电极的有机玻璃基片,其片上浸渍了按一定比例混合搅拌后的羟乙基纤维素HEC (吸湿材料)、碳黑(导电材料)、Tx-100和三梨醇(涨力辅助材料).电阻表面感应材料为黑色,可以吸附和释放水分子,当达到动态平衡时,电阻值反应外界大气的相对湿度,故湿敏电阻传感器是通过测量电阻来间接获得大气的相对湿度.理论上讲,为充分与大气交换水汽,感应材料应直接裸露在空气中.
|
图 1 GTS1探空仪电阻式湿度传感器 Fig. 1 Resistive humidity sensor of the GTS1 radiosonde |
图 2给出了GTS1探空仪的俯视图,温度传感器为能与空气充分接触,其直接裸露在空气中.虽然湿度传感器也需充分与空气接触,但为避免空中雨云和雨滴直接影响,故在湿度传感器上端安装了防雨罩.为反射太阳辐射和大气辐射,防雨罩内部涂黑,从而起到了防辐射功能,所以一般称之为防雨/防辐射罩,其在一定程度上阻碍了湿度传感器与空气的充分接触.为解决通风问题,图 2中当防雨/防辐射罩放下时,右边上方盖子留有一个进气口,下方斜坡设计将气流导向湿度传感器方向,而左侧采用缺口设计作为出气口.此设计使得GTS1探空仪在上升过程中,空气可快速且较充分地与湿度传感器接触交换水汽.

|
图 2 GTS1探空仪的俯视图 Fig. 2 The top view of the GTS1 radiosonde |
湿度表示大气干燥程度,可用绝对湿度、相对湿度、比较湿度、混合比、饱和差以及露点等物理量来表示.探空仪上湿敏电阻感测的是大气的相对湿度RH(Relative Humitidy),其为大气的实际水汽压e与饱和水汽压es之比.这里要注意的是饱和水汽压与大气温度有关,当温度T升高,饱和水汽压es变大,在相同的实际水汽压e下大气相对湿度RH变小.因而严格来说,相对湿度是一定温度下的相对湿度,可用RH(T)来表示.对于湿敏电阻而言,若由于某种原因,使得基片温度T1比环境温度T0高,则湿度传感器给出的相对湿度值RH(T1)会出现偏干现象,即RH(T1) < RH(T0).而在实际的探空湿度测量中,太阳辐射加热会使探空湿度传感器的衬底温度升高,因而输出湿度值出现显著偏干现象,该偏干误差被称为太阳辐射偏干误差SRDB.根据文献(冒晓莉等, 2014)可知,如若得到环境温度T0和太阳辐射加热后湿度传感器上的温度T1,则湿度测量时由太阳辐射引起的相对误差er为
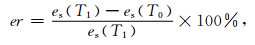
|
(1) |
式中es(T0)、es(T1)分别为温度T0和T1下的饱和水汽压.不难理解,若已知实测湿度值RH(T1),则修正后湿度值RHc为
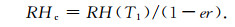
|
(2) |
在上文中提到探空仪GTS1设置了防雨/防辐射罩,但防雨/防辐射罩的防辐射效果到底如何?结合下面提出的改进的太阳辐射计算模型,本文将利用计算流体动力学方法研究该防雨/防辐射罩具体的防辐射能力.
2.3 改进的太阳辐射计算模型本文需研究太阳辐射对湿度传感器的加热影响,因而太阳辐射量是重点设置参数.太阳辐射包括直射量IDN和散射量Id,在很多流体动力学的计算中,均将它们设为常数.实际上IDN和Id均与时空有着密切关系,观测地不同的经纬度和不同的海拔高度,观测日期以及观测的时刻等均对其产生影响.目前,太阳辐射相关的计算模型也较丰富,例如,Bird and Hulstrom模型(1980年)、Heliosat-1模型(1995年)、MAC模型(1987年)、METSTAT模型(1998年)、MLWT2模型(2003年)、MRM-5模型(2008年)等.本文中我们采用了一种新的改进型太阳辐射计算模型(Dai and Fang, 2014),结合南京探空站GTS1探测的相关参数,通过Fluent仿真计算获得太阳辐射引起的湿度测量误差.具体的改进型太阳辐射计算模型如下:
大气层外的太阳常数年平均为1367 W·m-2,由于地球绕太阳轨道为椭圆形,一年中第d天(一年中的1月1号,d=0)大气层外的太阳常数ISUN为
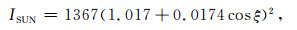
|
(3) |
这里ξ代表圆的不规则度,可由下式得到

|
(4) |
其中M=2dπ/365.
在无云理想状态下,随海拔高度降低,太阳直射通量呈现逐渐变小的趋势.海平面太阳直射通量为总太阳辐射量的80%,从大气层外到海平面损失近20%,这主要归因于大气分子、水汽等的吸收与散射.不同海拔高度太阳直射通量IDN和散射通量Id可由下式得到:
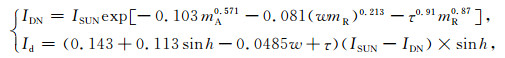
|
(5) |
其中w为垂直水汽柱,τ为气溶胶光学厚度,在美国标准大气中分别取值1.416 cm和0.2688,其余参数如太阳高度角h、空气相对质量mR和绝对质量mA定义如下.
根据文献(Liou, 2004)得知,太阳高度角h可由下式得到:
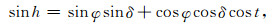
|
(6) |
式中φ为观测地纬度,北纬为正,南纬为负;t为地方时角,正午为0;δ为太阳赤纬,式(7)为其计算公式:
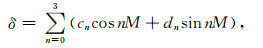
|
(7) |
其中系数cn和dn见文献(Liou, 2004).
空气的相对质量mR和绝对质量mA计算公式为
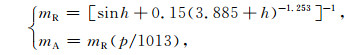
|
(8) |
其中p为气压,可由无线探空仪同步测量提供.
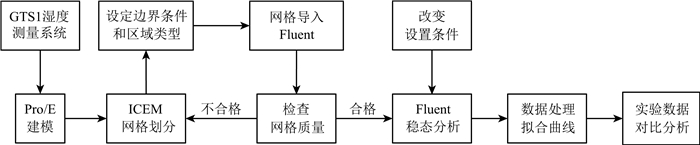
3 建模及研究方法 3.1 流体动力学湿度测量误差修正研究流程图 3为本文采用计算流体动力学方法研究探空湿度测量时太阳辐射偏干误差的流程图.首先确定探空仪GTS1湿度测量系统为研究对象,采用Pro/E (Pro/Engineer)进行建模,然后采用Ansys软件包中的前处理软件ICEM CFD (The Integrated Computer Engineering and Manufacturing code for Computational Fluid Dynamics)进行网格划分,接着导入国际主流的CFD软件Ansys Fluent中进行传热数值模拟,在准确获得太阳辐射下湿度传感器上的温度场分布之后,结合Goff-Gratch饱和水汽压逼近公式,通过数据处理获得上述太阳辐射偏干误差理论推导的湿度测量时的相对误差,最后与部分实验结果进行对比分析.下文给出各个步骤的具体信息.
|
图 3 基于计算流体动力学的湿度测量误差修正流程图 Fig. 3 The flow chart of the correction for humidity measurement errors based on CFD |
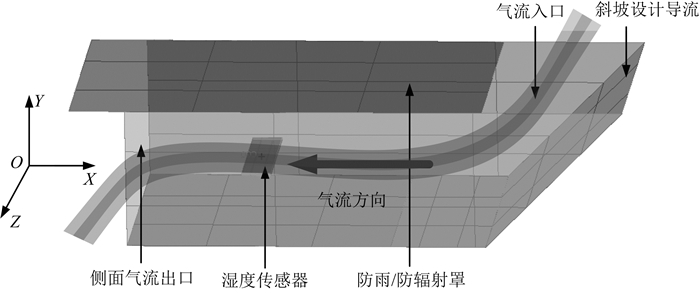
Pro/E作为一种当前最流行的高端三维CAD (Computer Aided Ddsign)软件,越来越受到人们的青睐.根据上述GTS1湿度测量结构简化模型的实际尺寸,采用Pro/E建立GTS1湿度测量结构计算模型,如图 4所示.根据实际测量,防雨/防辐射罩的总尺寸为170 mm×87 mm×47.5 mm,上方气流入口尺寸48 mm×47.5 mm,斜坡角度45°,传感器尺寸为43 mm×10.06 mm×1 mm.图 4中标出了气流入口、气流出口、导流斜坡以及防雨/防辐射罩,湿度传感器位于防雨/防辐射罩下方.需要说明的是,本文主要考虑的是湿敏电阻周围区域的温度场分布,如果模型过于复杂,不仅计算量急剧增加,也不能很好地反映局部细节情况,故将湿度测量结构模型进行一定的简化.经过前期分析计算得知,防雨/防辐射罩下方的电路盒子与湿度传感器的安装座对罩内气流和温度场的影响较小,因而这里将其省略.此外,由于湿敏电阻传感器的衬底有机玻璃厚度为1 mm左右,而感湿膜和电极的厚度在微米量级,对整体与外界热交换影响甚小,为了简化模型,采用衬底直接代替湿敏电阻作为温度场分析主体(冒晓莉等, 2014).
|
图 4 GTS1探空仪湿度测量结构计算模型 Fig. 4 The structure model of humidity measurement system of the GTS1 radiosonde |
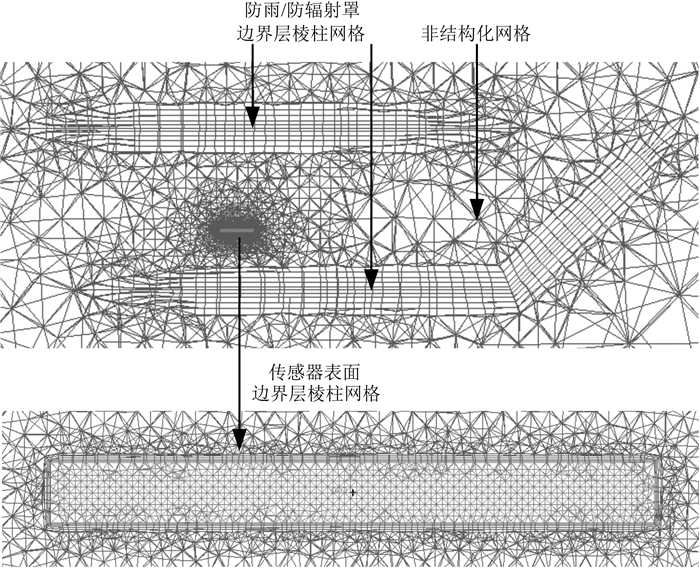
为了进行有限元分析,仿真计算前需采用前处理软件ICEM对Pro/E所建实体模型进行网格划分.由于防雨/防辐射罩外形尺寸与壁面厚度悬殊较大,若采用常规的网格划分技术,计算量将倍增,且未必取得较好的计算结果.针对该问题,本文提出了运用面网格代替体网格的网格划分方法.在Pro/E建模时,防雨/防辐射罩暂采用一个无厚度的面代替,在ICEM中作为面划分网格,而在后续的Fluent计算中,可设置此面的尺寸为0.55 mm,这样既可提高计算精度,计算量又较适中.网格划分可采用六面体和四面体,这里采用适应性较强的非结构化四面体网格.在权衡了计算规模和计算精度的前提下,为更好地捕捉边界层处的流体情况,采用了局部加密及边界层棱柱网格,通过加强边界层的处理以获得更真实的计算结果.如图 5所示,不难发现防雨/防辐射罩及传感器周围的边界层均为5层棱柱网格.
|
图 5 GTS1探空仪湿度测量结构网格划分情况 Fig. 5 The mesh of humidity measurement model of the GTS1 radiosonde |
Ansys Fluent是当前国际主流的CFD软件,是求解流体流动和传热问题强有力的工具.本文采用Fluent仿真软件建立探空仪GTS1湿度测量系统的稳态传热模型,对其施加外部复杂对流-太阳辐射耦合热边界条件,进行流固耦合传热分析.通过Fluent仿真分析,研究不同条件下湿敏电阻传感器(简化为衬底)上的温度场分布,求解太阳辐射加热引起的湿敏电阻上的温度变化,再通过公式(1)推导湿敏电阻测量湿度时由太阳辐射引起的相对误差.
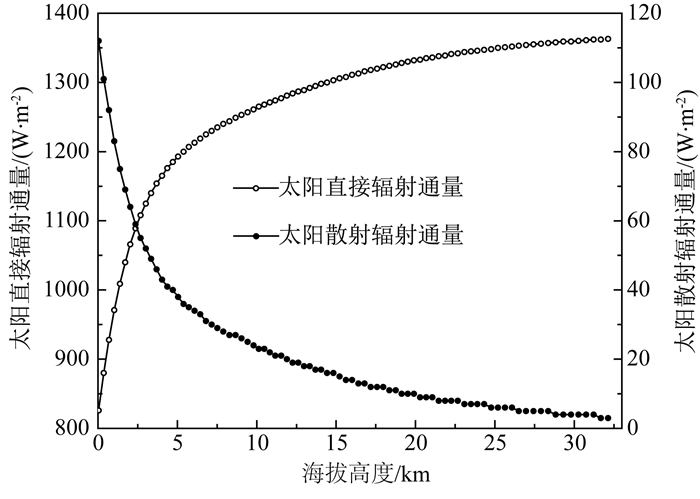
本文中太阳辐射方向的设置采用了软件自带的“solar calculation”功能自动计算出太阳高度角和方位角.经过调研分析得知,探空仪GTS1上升过程中在各种气流作用下做复杂的二维摆动(张恩红等, 2013),姿态也各异,这里为了简化计算过程,暂假设探空仪上升姿态固定(冒晓莉等, 2014),设模型坐标中X方向为北,Z方向为东,Y方向为天顶方向,即气流入口方向.南京探空站经纬度为东经118.5°,北纬32°,时区为东八区;日期根据选定数据设立,时间设为探空仪在空中的实际时刻(气球上升过程是连续的,但模拟仿真过程是离散的,这里将探空仪上升过程以1 min进行平均以获取离散数据).关于太阳辐射量,软件中有两个备选模式:“Theoretical Maximum”和“Fair Weather Condition”.但是无论是哪种模式均只能针对地面的情况,换言之,软件无法给出高空的具体数值.本文采用上文阐述的改进的太阳辐射通量的计算方法,计算出从地面到高空32km左右太阳辐射的直射通量和散射通量值.以南京2014年9月6日为例,早上七点半施放气球,太阳直接辐射通量和散射辐射通量随海拔高度(随上升时间)的关系如图 6所示.由图 6可知,太阳直接辐射通量随海拔高度的升高而急剧增大,原因有两个:第一,同一时刻,太阳直接辐射通量随海拔的升高而增大;第二,随着探空仪的上升,时间的推移,太阳高度角变高,也会导致太阳直接辐射通量增加.太阳散射辐射通量正好相反,低空较大,海拔10 km以上可忽略.由此可见,太阳散射通量的准确设置在低空尤为重要.
|
图 6 2014年9月6日南京太阳辐射通量与海拔高度的关系 Fig. 6 The relationship between solar flux and altitude at Nanjing in September 6, 2014 |
此外,本文主要对探空仪GTS1湿度测量模型在太阳辐射下的传热进行分析,材料传热系数及流体流速均对传热过程影响较大,根据实际情况,传感器的衬底有机玻璃和防雨/防辐射罩的传热系数均设定为0.2 W·m-1·K-1.探空仪在随气球上升过程中,忽略空气本身的垂直和水平运动,探空仪与空气存在垂直方向的相对运动,则假设探空仪静止在空中不动而设定气流垂直向下.GTS1探空仪上升速度为5~9 m·s-1,相当于气流的流速为5~9 m·s-1,由于流速较低,空气可设为不可压缩理想气体(彭小勇等, 2004).另外,湿度测量系统简化模型迎风面尺寸达到170 mm×87 mm,气流在流动中形成湍流,湍流模型采用k-ε标准模型,压力和速度解耦采用SIMPLE算法.湍流尺度即水力直径D由防雨/防辐射罩尺寸计算得到.湍流强度I=0.16×Re-0.125,其中雷诺数Re根据气流密度、速度、动力黏度及特征尺寸得到.
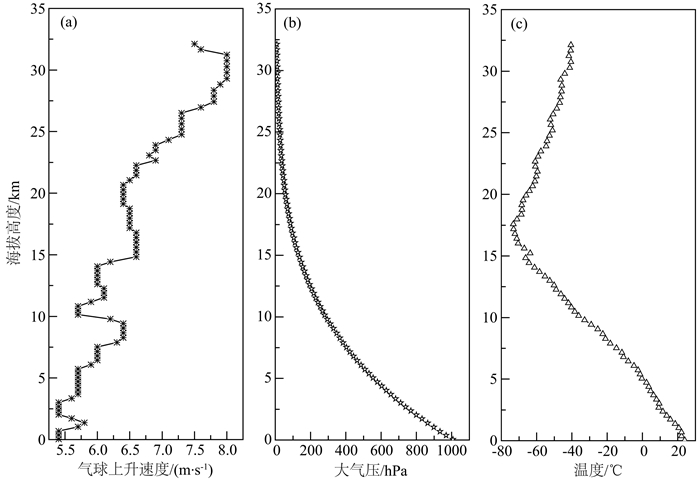
软件设置中对传热分析影响较大的另一个参数设置是边界层参数,传感器表面因为被防雨/防辐射罩遮挡,不直接接受太阳辐射,故表面吸收率设为0,防雨/防辐射罩反射率设定为70%.气流进口采用速度入口边界条件,速度利用探空仪上升过程中每分钟的平均速度,如图 7a所示.由该图可见,低空速度较小,随着气球膨胀等原因,高空气球的上升速度逐渐变大,但在海拔10 km的地方,探空仪上升速度出现先下降再上升的过程.气流出口采用压力出口,大气压以探空仪同球的压力传感器所测大气压为准,2014年9月6日的大气压随海拔高度的曲线如图 7b所示,压力随海拔高度的升高而单调下降.温度也设置为同球探空仪温度传感器测量的温度值,如图 7c所示,温度随海拔增加先下降再上升,分界处位于对流层和平流层的过渡层,初步判定南京9月份的对流层顶大概在17~18 km之间.结合南京全年的探空数据发现,南京四季的对流层顶均在16~19 km之间.
|
图 7 2014年9月6日南京探空站探空仪GTS1观测的部分气象参数与海拔高度的关系曲线 Fig. 7 The relationship between partial meteorological parameters measured by the GTS1 radiosonde and altitude at Nanjing sounding station in September 6, 2014 |
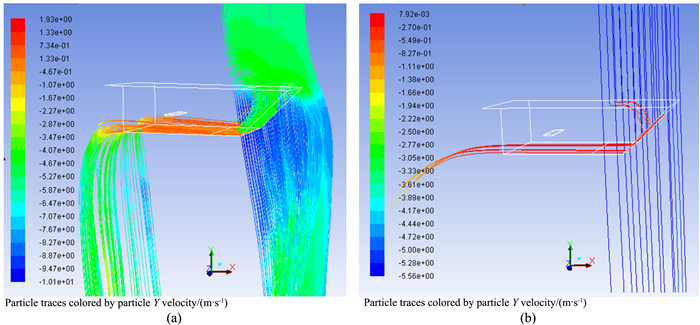
探空仪在高空探测湿度时,空中雨滴和云滴均会对湿度测量产生严重影响,为解决该问题,探空仪GTS1的湿度测量系统安装防雨设备,如图 2所示,探空仪GTS1湿度传感器虽然隐藏在防雨罩下方,但雨滴和云滴是否随着气流流经湿度传感器从而影响湿度测量?下面通过仿真计算湿度传感器上捕捉云雨滴的情况来分析此问题.典型云滴半径为10 μm,密度为108m-3,而典型雨滴半径为1 mm,密度为103m-3,根据计算可得无论是雨滴还是云滴下体积率均小于10%,不属于气粒耦合问题,符合离散相计算条件.因此本文在气流入口上方设置不同的云滴和雨滴面源,通过fluent模拟仿真典型云滴和典型雨滴的运动轨迹.这里给出了流体动力学仿真的南京2014年9月6日海拔2 km处探空仪防雨罩的防雨情况,图 8(a, b)分别为典型云滴和典型雨滴在垂直方向速度分量仿真图.由图不难发现,由于雨滴尺寸较大,气流几乎不影响它的运行轨迹,碰到防雨罩之后顺着壁面从罩内流出.由于典型云滴尺寸较小,气流改变了它们的运行轨迹.但是传感器表面捕捉粒子数均为0.云底高度位于400 m至几公里,云层最高可延伸至对流层顶,根据计算模型在不同海拔高度下的仿真数据发现,湿度传感器表面均未捕捉到雨滴和云滴粒子,说明GTS1探空仪的防雨罩确实起到了很好的防雨效果.
|
图 8 云雨滴轨迹仿真 (a)典型云滴垂直方向速度仿真图;(b)典型雨滴垂直方向速度仿真图. Fig. 8 The simulation map of trajectories of cloud-and rain-drops (a) The simulation map of the typical cloud droplet velocity in the vertical direction; (b) The simulation map of the typical raindrop velocity in the vertical direction. |
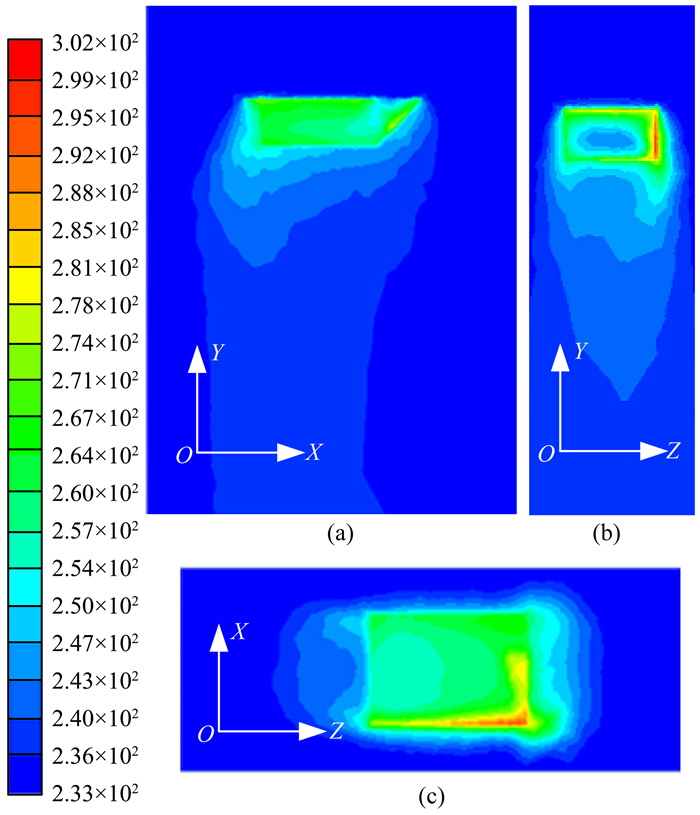
图 9给出了南京探空站2014年9月6日探空仪上升83 min后,到达最高点(海拔高度32.126 km)气球爆炸时太阳辐射下防雨/防辐射罩上的温度场分布.图 9a为防雨/防辐射罩与XOY平面平行的侧面上温度场分布,由图可见此侧面上温度场分布较均匀,这主要是由于忽略了探空仪在空中的摆动,该侧面没有直接接受太阳辐射的原因.图 9b为水平气流方向剖面图,从防雨/防辐射罩内部的温度场分布可看出内部的温度明显比外界环境温度高,但从防雨/防辐射罩壁面到中间温度逐渐降低,这与流速场仿真结果相吻合.中间区域气流流速较强,因而带走热量的能力较强,从这个角度来看,湿敏电阻的放置位置尽量处于温度场较低的中间区域.图 9c为防雨/防辐射罩上表面的温度场分布俯视图,由于设置X方向为北,Z方向为东,所以由图中可清楚看出,此时太阳辐射在-X和Z方向之间,根据设置可知,这属于东南方向,而实际在7:30时施放气球,83 min后即接近9:00时,太阳的方位角显然仍在东南方向,因而本文仿真结果与实际情况吻合.
|
图 9 2014年9月6日探空仪GTS1湿度测量系统在海拔32.126 km的温度场分布 (a) XOY平面;(b) YOZ平面;(c) XOZ平面. Fig. 9 The temperature distribution of humidity measurement system from GTS1 radiosonde at altitude of 32.126km at Nanjing in September 6, 2014 (a) The plane of XOY; (b) The plane of YOZ; (c) The plane of XOZ. |
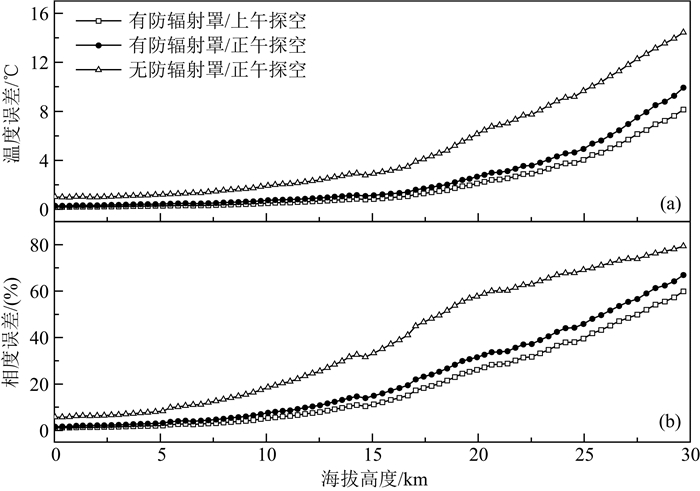
由上述分析可看出,在太阳辐射下防雨/防辐射罩内的温度明显高于周围环境的温度,说明其不可能消除太阳辐射的影响,但是否具有一定的防辐射效果呢?下面以南京2014年6月6日的相关数据为例,通过对比有无防辐射罩时湿度传感器上的温度场分布进行讨论分析.一方面,如果将GTS1的防辐射罩去掉,将湿敏电阻完全暴露在空气中,在太阳辐射加热下,由图 10a可知湿敏电阻上的温度与环境温度的差异明显高于有防辐射罩时的情形,由此引起的湿度测量相对误差也存在明显差别(图 10b所示).通过上述分析可知GTS1的防辐射罩具备一定的防辐射能力,但它并不能完全消除太阳辐射加热对湿度测量结果的影响.另一方面,若施放气球的时间改为同一天的11:30,即探空仪在空中的时间为正午前后,通过仿真分析发现此时太阳辐射加热引起的相对误差比早上7:30施放气球时要高很多,该研究结果表明太阳辐射加热对湿度测量误差的影响与施放气球的时间有直接关联,根本原因在于正午前后太阳高度角较高,太阳辐射量较大,因而太阳辐射加热效果较明显.一般情况下,国内将8:00时和20:00时(实际施放气球的时间较8:00时和20:00时提前30 min左右)作为常规探测时间.但实际上,由于夏天短时对流天气较明显,且50%以上的雷暴大风、局部强降雨等天气生消在两次常规探测之间(廖晓农等,2007).所以,即使正午前后太阳辐射误差较大,仍可通过增加14:00时的高空探测来提高短时临近潜势预报的准确率.同时,应用这些高空观测资料也可检验和修正前期预报结果.随着技术的发展,根据实际研究或者应用中的需求,我国将会与国际接轨,将2:00时和14:00时的两次探测也列为常规探测.
|
图 10 GTS1防辐射罩防辐射效果图 (a)温度差与海拔高度的关系;(b)相对误差随海拔高度的关系. Fig. 10 The anti-radiation effect of radiation shield of GTS1 (a) The relationship between temperature error and altitude; (b) The relationship between the relative error of RH and altitude. |
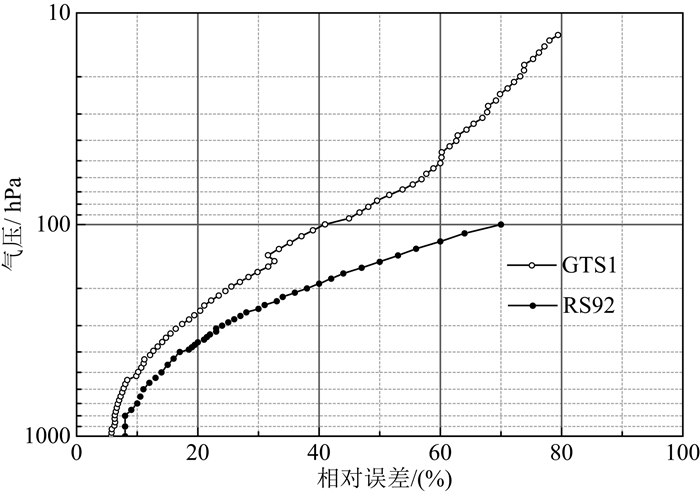
RS92作为Vaisala新一代探空仪,湿度测量采用双加热式湿度传感器,其轮流加热交替测量的方法有效避免了传感器表面结冰导致测量失效的问题.图 11给出了GTS1与RS92由于太阳辐射引起的湿度测量相对误差随气压变化的曲线.无论是GTS1还是RS92,其相对误差均随气压降低而呈单调递增关系,即海拔高度越高,相对误差越大.原因可归纳为以下两点:(1)海拔越高,太阳的直接辐射通量增大,导致辐射加热效应增强,湿度传感器与环境的温度差变大从而使得湿度相对误差也逐渐变大;(2)海拔高度增加后,大气密度急剧减小,直接导致传热能力降低.值得注意的是,虽然随海拔高度增加,风速增大和气体黏度下降均会导致传热增强,但相比较前两个因素而言影响较小,于是总体表现为温差依然增大,因而相对湿度测量时相对误差显著增加.
|
图 11 太阳辐射条件下GTS1与RS92湿度测量的相对误差的比较曲线 Fig. 11 The curve of the relative error of RH respectively from GTS1 and RS92 considering the solar radiation |
由图 11还可清楚看出,与GTS1相比,RS92的偏干现象更为严重,该仿真结果符合实际情况.RS92采用双加热湿度传感器,它们完全暴露在空气之中,优点是直接与空气充分接触,减小了延迟时间.但缺点也很明显,由于传感器上无遮挡,太阳辐射直接对其进行加热,使传感器上的温度高于周围环境温度.而GTS1的防雨/防辐射罩在很大程度上阻挡了太阳辐射的直接加热,起到了一定的防辐射功能.例如,气压100 hPa处,RS92的相对误差高达70%,而GTS1的误差约为40%.需要说明的是,尽管防雨/防辐射罩对太阳辐射能起到一定的防护作用,但还不能完全消除其影响,为提高湿度观测数据的准确性,因此探空仪GTS1湿度测量的历史或将来的数据仍需进行太阳辐射误差修正.为进一步验证本文提出的基于流体动力学的太阳辐射偏干误差修正模型的有效性,下文将该模型的计算结果与GTS1的实验结果做具体的对比分析.
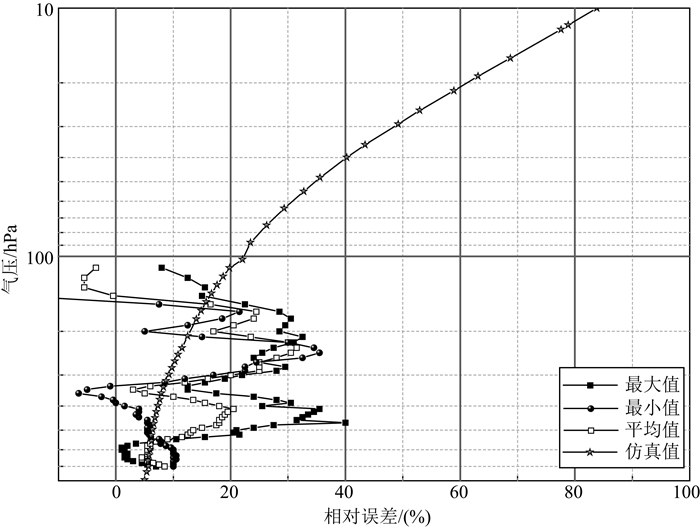
4.4 昆明实验与流体动力学仿真比较2009年8月7日至13日卞建春等在昆明(北纬25.01°,东经102.65°,海拔1.889 km)对探空仪GTS1、RS80以及CFH进行了湿度测量的对比实验(Bian et al., 2011).实验结果表明GTS1和RS80的湿度传感器(带有防辐射罩)与CFH相比均表现出偏干现象,且GTS1的偏干更显著.文中还分别给出了白天和夜晚GTS1与CFH湿度测量的相对误差曲线,通过曲线不难发现白天的偏干现象明显高于夜晚,而事实上白天与夜晚GTS1湿度传感器本身的误差变化很小,最大的区别在于有无太阳辐射,这表明白天与夜晚偏干值之差主要来源于太阳辐射加热效应.通过将白天和夜晚GTS1与CFH湿度测量的相对误差相减,本文间接获取了GTS1由于太阳辐射引起的湿度测量相对误差的最小值、最大值和平均值.如图 12所示,500 hPa以下GTS1湿度测量由太阳辐射引起的平均相对偏差在10%以内,而500 hPa以上误差急剧增加,到310 hPa时平均相对偏差达30%.接近100 hPa时,由于温度较低,GTS1很容易结冰,导致无法正常测量湿度值,由图 12可知这个区域出现了明显不正常的偏湿现象.
|
图 12 太阳辐射下昆明实验GTS1观测的湿度数据相对误差与流体动力学仿真值的比较 Fig. 12 The comparison of relative error of RH between the measurement datum from GTS1 in Kunming and the simulation results using CFD under similar conditions of solar radiation |
利用本文建立的GTS1的湿度测量模型,在Fluent中严格按照昆明的地理位置,施放气球的时间等进行相应设置和模拟计算.通过图 12比较数值分析结果和实验结果可知,基于流体动力学的仿真值随海拔高度增加而单调递增,而实验结果中相对误差的波动范围较大,且随海拔高度呈现非单调递增关系.尽管如此,仿真值基本落在实验相对误差范围内,尤其是300 hPa以下吻合度较好.当气压在200~300 hPa范围内时,实验结果的相对误差急剧增加达到30%,而此时仿真值仅约10%.除了实验测量本身会存在一定的误差外,两者产生偏差的原因还可能在于:(1)由于文献(Bian et al., 2011)给出的湿度观测数据是多天测量的结果,且未给出具体的温度和气压值,在本文实际计算中温度和气压采用标准大气的相关参数;(2)从计算量的角度出发,本文对GTS1湿度测量计算模型进行了简化处理;(3)在本文的流体动力学计算中,忽略了水平侧风的影响.若考虑侧风,GTS1探空仪将做复杂二维摆动,在这种情况下,气流与防雨/防辐射罩的入口面会形成不同的角度,导致通风效果变差,其变差程度与摆动半径成正比.而文献(张恩红等, 2013)的实验结果表明摆动半径与侧风风速成正比.一般情况下,气压在200~300 hPa范围内时,侧风将达到最大值,因此该范围内防雨/防辐射罩的通风效果最差,这导致了显著的太阳辐射偏干误差.为了充分说明这一问题,本文在暂不考虑探空仪复杂二维摆动的前提下,结合一般的高空侧风数据,最大的侧风一般出现在200 hPa左右高度,此时气流与防雨/防辐射罩的入口面的夹角几乎为零.在这种通风效果最差的静态条件下,通过流体动力学计算发现太阳辐射偏干误差为55%~70%.实际上,在探空仪上升的动态过程中,不同海拨的侧风均不同,防雨/防辐射罩会做复杂的二维摆动因而太阳辐射偏干误差比上面计算的静态值小.我们将在后续的工作中开展复杂二维摆动方面的研究.但从总体上可以看出,本文基于流体动力学计算的修正值和实验修正范围吻合较好,这在一定程度上表明本文数值分析法的有效性.
4.5 南京探空站GTS1数据分析比较南京探空站每天早晚使用GTS1探空仪实施8:00时和20:00时两次常规探测,从而获取高空温度、湿度、气压、风速风向等气象要素.国内专家对高空湿度测量的相关实验研究表明(Bian J C et al., 2011;颜晓露等,2012),GTS1湿度测量白天呈现明显的偏干现象,且主要为太阳辐射加热导致的偏干现象.采用基于流体动力学的太阳辐射误差修正方法,现选取2014年南京具有代表性的四天(3月12日、6月6日、9月6日、12月11日)进行数值模拟仿真.具体结合GTS1湿度测量系统的简化模型,在Fluent软件中设置南京探空站的地理位置和时区,施放气球时间为上午7:30,日期分别设置为3月12日、6月6日、9月6日、12月11日,气流速度按照气球上升速度设置,温度、气压按照探空仪实测数据进行相应设置.通过Fluent模拟仿真太阳辐射下湿度传感器上的温度场分布,再通过公式(1)推导湿度测量的太阳辐射相对误差,四天的比较曲线如图 13所示.由图 13可以看出,四条曲线均随海拔高度的升高而单调递增;6月6日的相对误差最大、9月6日的次之、12月11日的最小.这主要归因于一年中6月份的太阳高度角最大,太阳直接辐射通量最大;12月份的太阳高度角最小,太阳直接辐射通量最小,故太阳高度角直接影响太阳辐射对防雨/防辐射罩的加热效应.我国对施放气球的高度要求是26 km,南京探空站年平均在28.5 km左右,一般情况下秋冬季较高,由图 13中可以看出9月份的施放气球的高度最大,达到32 km以上.

|
图 13 不同季节南京探空站GTS1湿度测量的太阳辐射相对误差 Fig. 13 The solar radiation dry error of humidity measurement by GTS1 in different seasons at Nanjing sounding station |
图 14为相对湿度的绝对误差比较曲线,由图可知,绝对误差与海拔高度基本呈现递增关系,但由于不同海拔高度的相对湿度值RH区别较大,绝对误差呈现了一定的波动,如6月份在对流层上部波动较大.总体上讲,GTS1相对湿度测量精度较低,要求温度高于-25 ℃时误差≤5%RH,温度低于-25 ℃时,误差≤10%RH.虽然从图 14中不难看出,海拔高度25 km以下基本能满足要求,但25 km以上,误差基本在10%RH以上,且最高已达20%RH,这严重制约了我国高空湿度的测量精度.鉴于这种现状,结合实际观测数据,基于流体动力学数值方法对25 km以下湿度测量的误差进行修正可进一步提高湿度测量的精度,而对25 km以上湿度测量太阳辐射偏干误差实现修正则可显著提升我国湿度探空高度.

|
图 14 不同四天的探空湿度测量的绝对误差 Fig. 14 The absolute error of sounding humidity measurement in different four days |
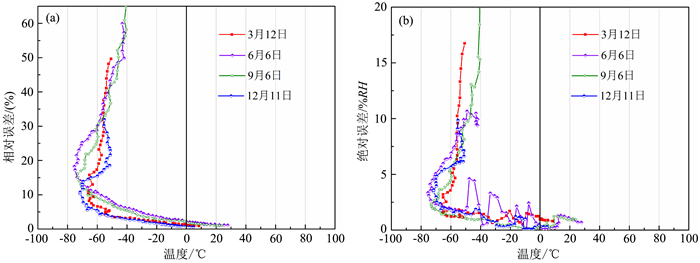
图 15反映了湿度测量误差与温度之间的关系.图 15a是湿度测量的相对误差随环境温度变化的关系曲线,当温度高于-40 ℃时,相对误差较小,反之误差较大.温度-60 ℃以下一般在对流层顶和平流层下部15~20 km左右,相对误差较大,在10%~30%之间.温度在-40~-60 ℃区间,太阳辐射相对误差不确定,因为该温度区间海拔高度对应着对流层下部和平流层中部,而这两层的相对误差差异很大.如图 15b所示,湿度绝对误差的变化规律与相对误差类似,区别为6月6日的绝对误差波动较大.
|
图 15 湿度测量的误差与环境温度的关系 Fig. 15 The relationship between humidity measurement error and ambient temperature |
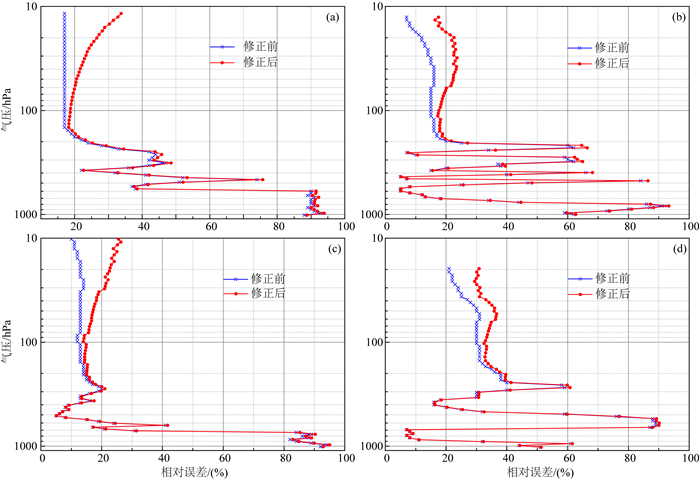
本文最后对南京探空站探空仪GTS1的湿度实测数据实施了流体动力学太阳辐射偏干误差修正.图 16反映了不同的四天修正前后的湿度廓线对比曲线.对比四天的湿度廓线不难发现,200 hPa以下(对流层)大气的相对湿度较高,且波动较大,尤其是6月6日湿度的波动较多.200 hPa以上(平流层)大气的相对湿度较小,属于典型低温低湿区域,波动也较小.不难发现,不同季节的对流层湿度廓线修正前后曲线变化不明显,而平流层湿度廓线修正后的曲线与修正前的曲线相差较大,该结果表明这个区域的偏干现象较为严重.值得注意的是,2014年3月12日平流层的湿度测量值出现固定不变的值,这可能是由于湿敏电阻结冰导致测量失效引起的,因此平流层湿度的准确测量目前仍是个难点.但总的来说,前面与RS92相对误差以及昆明实验结果的对比研究,均表明了基于流体动力学的太阳辐射误差修正方法是可靠有效的,其能够在一定程度上提升我国探空湿度测量精度.由图 16中太阳辐射误差修正前后的湿度廓线对比可知,100 hPa (海拔16.5 km)以下区域测量精度提高2%RH左右,而100 hPa以上区域测量精度可提高2%~21%RH,该结果同时表明太阳辐射误差修正对于对流层顶(16~19 km)以上的高空湿度测量更为重要.
|
图 16 不同季节GTS1观测的湿度廓线修正前后的曲线 (a) 2014年3月12日;(b) 2014年6月6日;(c) 2014年9月6日;(d) 2014年12月11日. Fig. 16 The vertical humidity profiles in different seasons (corrected vs uncorrected) from GTS1 (a) March 12, 2014; (b) June 6, 2014; (c) September 6, 2014; (d) December 11, 2014. |
结合改进的太阳辐射计算模型,通过计算流体力学CFD软件Fluent对探空仪GTS1湿度测量结构模型在太阳辐射加热下温湿度场分布进行了数值模拟,着重探讨了GTS1湿度测量系统的防雨和防辐射效果,并最终选取南京探空站2014年不同季节的四天的观测数据作为模拟仿真参数进行相关计算和修正.经过对数值模拟的数据与实验测试结果进行对比研究分析得到如下结论:
(1)探空仪GTS1的防雨/防辐射罩有很好的防雨效果,防辐射效果也较明显,但尚不能消除太阳辐射的影响,特别是100 hPa以上的高空.而本文提出的基于流体动力学的太阳辐射偏干误差修正方法可在一定程度上提高湿度测量精度,100 hPa以下区域提高2%RH左右,而100 hPa以上区域可提高2%~21%RH;
(2)由于太阳辐射加热影响,探空仪GTS1虽然设有防辐射罩,但湿度测量仍存在明显偏干现象.流体动力学计算得到的湿度测量偏干程度随海拔高度的升高而增加,这与太阳辐射引起Viasala探空仪RS92湿度偏干现象一致;
(3)基于流体动力学方法,以南京探空站2014年3月12日、6月6日、9月6日、12月11日四天为例,计算得到的太阳辐射加热引起的探空仪GTS1湿度测量的相对误差er随海拔高度单调递增,而绝对误差RH%随海拔高度非单调递增;
(4)太阳辐射加热对探空仪湿度测量的偏干影响与环境温度存在非单调关系,在对流层,环境温度越低,偏干程度越大;在平流层,环境温度越低,偏干程度越小.
本文也给出了理论计算与实验测量存在一定差异的原因,其中水平侧风引起探空仪做复杂二维摆动是最重要的原因,在后续工作中我们将考虑这一复杂因素对探空湿度测量太阳辐射偏干误差的具体影响.总之,本文提出的研究方法及获得的计算结果对探空湿度测量太阳辐射偏干误差的有效修正等方面的研究具有一定的参考价值.
| Bian J C, Chen H B, Vömel H, et al. 2011. Intercomparison of humidity and temperature sensors: GTS1, vaisala RS80, and CFH. Adv. Atmos. Sci., 28(1): 139-146. DOI:10.1007/s00376-010-9170-8 | |
| Bock O, Nuret M. 2009. Verification of NWP model analyses and radiosonde humidity data with GPS precipitable water vapor estimates during AMMA. Wea. Forecasting, 24(4): 1085-1101. DOI:10.1175/2009WAF2222239.1 | |
| Cady-Pereira K E, Shephard M W, Turner D D, et al. 2008. Improved daytime column-integrated precipitable water vapor from vaisala radiosonde humidity sensors. J. Atmos. Ocean. Technol., 25(6): 873-883. DOI:10.1175/2007JTECHA1027.1 | |
| Ciesielski P E, Johnson R H, Wang J H. 2009. Correction of humidity biases in vaisala RS80-H sondes during NAME. J. Atmos. Ocean. Technol., 26(9): 1763-1780. DOI:10.1175/2009JTECHA1222.1 | |
| Ciesielski P E, Chang W M, Huang S C, et al. 2010. Quality-controlled upper-air sounding dataset for TiMREX/SoWMEX: Development and corrections. J. Atmos. Ocean. Technol., 27(11): 1802-1821. DOI:10.1175/2010JTECHA1481.1 | |
| Dai A G, Wang J H, Thorne P W, et al. 2011. A new approach to homogenize daily radiosonde humidity data. J. Climate, 24(4): 965-991. DOI:10.1175/2010JCLI3816.1 | |
| Dai Q M, Fang X D. 2014. A simple model to predict solar radiation under clear sky conditions. Adv. Space Res., 53(8): 1239-1245. DOI:10.1016/j.asr.2014.01.025 | |
| Guichard F, Parsons D, Miller E. 2000. Thermodynamic and radiative impact of the correction of sounding humidity bias in the tropics. J. Climate, 13(20): 3611-3624. DOI:10.1175/1520-0442(2000)013<3611:TARIOT>2.0.CO;2 | |
| Kottayil A, Buehler S A, John V O, et al. 2012. On the importance of vaisala RS92 radiosonde humidity corrections for a better agreement between measured and modeled satellite radiances. J. Atmos. Ocean. Technol., 29(2): 248-259. DOI:10.1175/JTECH-D-11-00080.1 | |
| Leiterer U, Dier H, Nagel D, et al. 2005. Correction method for RS80-A humicap humidity profiles and their validation by Lidar backscattering profiles in tropical cirrus clouds. J. Atmos. Ocean. Technol., 22(1): 18-29. DOI:10.1175/JTECH-1684.1 | |
| Li G, Tan Y K, Li C Y, et al. 2015. The distribution characteristics of total ozone and its relationship with stratospheric temperature during boreal winter in the recent 30 years. Chinese J. Geophys., 58(5): 1475-1491. DOI:10.6038/cjg20150502 | |
| Li Y G, Fan J P. Humidity Measurement 1.Beijing: China Meteorological Press, 1990: 466-470. | |
| Liao X N, Yu X D, Tan Y Z. 2007. Improvement of convective weather forecasting with enhanced 1400 BST sounding data. Meteor. Mon., 33(3): 28-32. | |
| Liou K N. 2004. An Introduction to Atmospheric Radiation (in Chinese). 2nd ed. Guo C L, Zhou S J Trans. Beijing: China Meteorological Press, 45-54. | |
| Liu Q Q, Yang J, Yang R K, et al. 2012. CFD Analysis and heating strategy design of heated twin humidity sensor. Chin. J. Sens. Actuators, 25(8): 1039-1044. | |
| Liu Q Q, Dai W, Yang R K, et al. 2013. Fluid dynamics analysis on solar radiation error of radiosonde temperature measurement. Plateau Meteor., 32(4): 1157-1164. | |
| Luo Y, Kun Y, Shi Y B, et al. 2014. Research of radiosonde humidity sensor with temperature compensation function and experimental verification. Sens. Actuators A, 218: 49-59. DOI:10.1016/j.sna.2014.07.015 | |
| Mao X L, Xiao S R, Liu Q Q, et al. 2014. Fluid dynamic analysis on solar heating error of radiosonde humidity measurement. Acta Phys. Sin., 63(14): 144701. DOI:10.7498/aps.63.144701 | |
| Mao X L, Xiao S R, Zhang J H, et al. 2015. The research on spatial and temporal distribution of solar radiation error of radiosonde humidity sensor. Sci. Technol. Eng., 15(10): 1-9. | |
| Nuret M, Lafore J P, Guichard P, et al. 2008. Correction of humidity bias for vaisala RS80-A sondes during the AMMA 2006 observing period. J. Atmos. Ocean. Technol., 25(11): 2152-2158. DOI:10.1175/2008JTECHA1103.1 | |
| Peng X Y, Gu W L, Liu J X, et al. 2004. A theoretical analysis of incompressibility of the low speed gas flow. J. Nanhua Univ. (Sci. Technol.), 18(3): 34-35. | |
| Posada R, García-Ortega E, Sánchez J L, et al. 2013. Verification of the MM5 model using radiosonde data from Madrid-Barajas Airport. Atmos. Res., 122: 174-182. DOI:10.1016/j.atmosres.2012.10.018 | |
| Rowe P M, Miloshevich L M, Turner D D, et al. 2008. Dry bias in vaisala RS90 radiosonde humidity profiles over antarctica. J. Atmos. Ocean. Technol., 25(9): 1529-1541. DOI:10.1175/2008JTECHA1009.1 | |
| Verver G, Fujiwara M, Dolmans P, et al. 2006. Performance of the vaisala RS80A/H and RS90 humicap sensors and the meteolabor "snow white" chilled-mirror hygrometer in paramaribo, suriname. J. Atmos. Ocean. Technol., 23(11): 1506-1518. DOI:10.1175/JTECH1941.1 | |
| Vömel H, Selkirk H, Miloshevich L, et al. 2007. Radiation dry bias of the vaisala RS92 humidity sensor. J. Atmos. Ocean. Technol., 24(6): 953-963. DOI:10.1175/JTECH2019.1 | |
| Xiao C Y, Hu X, Tian J H. 2008. Analysis and comparison of deriving winds from satellite temperature data. Chinese J. Geophys., 51(2): 325-336. DOI:10.3321/j.issn:0001-5733.2008.02.005 | |
| Yan X L, Zheng X D, Li W, et al. 2012. Inter-comparision and application of atmospheric humidity profiles measured by CFH and Vaisala RS80 radisondes. J. Appl. Meteor. Sci., 23(4): 433-440. | |
| Yao W, Ma Y, Xu W J. 2008. Relative humidity error of L-band electronic radiosonde and its application. J. Appl. Meteor. Sci., 19(3): 356-361. | |
| Yoneyama K, Fujita M, Sato N, et al. 2008. Correction for radiation dry bias found in RS92 radiosonde data during the MISMO field experiment. SOLA, 4: 13-16. DOI:10.2151/sola.2008-004 | |
| Zhang E H, Cao Y C, Li H, et al. 2013. Research on the method of data processing of the wind sounding by Bei Dou radiosonde.//The Fourth China Satellite Navigation Conference (in Chinese). Beijing: China Satellite Navigation Conference Organizing Committee. | |
| Zhang L G, Chen Z B, Wang Y, et al. 2007. Comparison of radiosonde observation and L-band radar data and 59-701 system. Meteor. Sci. Technol., 35(1): 123-125. | |
| 李刚, 谭言科, 李崇银, 等. 2015. 近30年北半球冬季臭氧总量分布特征及其与平流层温度的关系. 地球物理学报, 58(5): 1475–1491. DOI:10.6038/cjg20150502 | |
| 李英干, 范金鹏. 湿度测量1.北京: 气象出版社, 1990: 466-470. | |
| 廖晓农, 俞小鼎, 谭一洲. 2007. 14时探空在改进北京地区对流天气潜势预报中的作用. 气象, 33(3): 28–32. | |
| Liou K N著. 2004.大气辐射导论. 2版.郭彩丽, 周诗健译.北京:气象出版社, 45-54. | |
| 刘清惓, 杨杰, 杨荣康, 等. 2012. 双加热湿度传感器的CFD分析与加热策略设计. 传感技术学报, 25(8): 1039–1044. | |
| 刘清惓, 戴伟, 杨荣康, 等. 2013. 探空温度测量太阳辐射误差的流体动力学分析. 高原气象, 32(4): 1157–1164. | |
| 冒晓莉, 肖韶荣, 刘清惓, 等. 2014. 探空湿度测量太阳辐射误差修正流体动力学研究. 物理学报, 63(14): 144701. DOI:10.7498/aps.63.144701 | |
| 冒晓莉, 肖韶荣, 张加宏, 等. 2015. 探空湿度测量太阳辐射误差时空分布特征研究. 科学技术与工程, 15(10): 1–9. | |
| 彭小勇, 顾炜莉, 柳建祥, 等. 2004. 低速气体流动不可压缩性理论解析. 南华大学学报(自然科学版), 18(3): 34–35. | |
| 肖存英, 胡雄, 田剑华. 2008. 利用卫星温度资料计算风场的方法分析与比较. 地球物理学报, 51(2): 325–336. DOI:10.3321/j.issn:0001-5733.2008.02.005 | |
| 颜晓露, 郑向东, 李蔚, 等. 2012. 两种探空仪观测湿度垂直分布及其应用比较. 应用气象学报, 23(4): 433–440. | |
| 姚雯, 马颖, 徐文静. 2008. L波段电子探空仪相对湿度误差研究及其应用. 应用气象学报, 19(3): 356–361. | |
| 张恩红, 曹云仓, 李黄等. 2013.北斗探空仪测风的数据处理方法研究.//第四届中国卫星导航学术年会电子文集.北京:中国卫星导航学术年会组委会. | |
| 张立功, 陈志斌, 王勇, 等. 2007. L波段雷达-电子探空仪系统对比观测分析. 气象科技, 35(1): 123–125. | |
 2016, Vol. 59
2016, Vol. 59


