航空电磁法(Airborne Electromagnetic简称AEM)是一种以飞行器为载体,对地下目标体进行勘探的地球物理方法.它凭借速度快、成本低、便捷高效等优势,特别适合地形复杂地区(如高山、沙漠、湖泊沼泽等)地球物理勘查.时间域航空电磁法作为AEM的一个重要分支,其工作原理是通过人工激发脉冲信号,观测地下介质中涡流在On-time和Off-time产生的电磁响应,进而了解地下介质的电性分布.目前该方法主要应用于地质填图、矿产勘查、环境工程和地下水等领域(殷长春等,2015).时间域航空电磁用于高阻极化区域勘探过程中经常观测到电磁负响应,由于对该类数据的产生机理缺乏了解,严重地影响数据处理和解释.
通常认为时间域电磁数据的负响应是由激发极化效应产生的.激发极化效应(Induced Polarization简称IP)主要包括电子导体和离子导体激发极化效应.电子导体的激电效应是由于电子导体与溶液界面上的双电层在外界电流的作用下发生电子和离子的定向移动,并在断电后产生的放电现象;离子导体的激电效应是由于岩石颗粒和周围溶液分界面上存在的双电层在外界电流作用下发生变形,并在外界电流断电后产生离子放电.目前该方法已广泛应用于金属矿产、油气勘查及水文环境地质调查等领域(Börner et al., 1996;Kemna et al., 2000;Slater and Lesmes, 2002;Hördt et al., 2007;Williams et al., 2009).与传统的地面激发极化法相比,航空激电法(Airborne Induced Polarization简称AIP)作为一种新的勘探方法,将航空电磁法和激电法的优势结合起来,解决了传统激电法中高阻覆盖地区接地电阻过大和复杂地形等问题.Hohmann等(1970)提出在磁性源下探测激电异常的方法,并指出航空激电法的理论可行性.Pelton等(1978)等基于大量的岩矿石的测量结果,提出的一种用来描述岩矿石激电效应的数学模型,即Cole-Cole模型;Spies (1980)在瞬变电磁实测数据中发现符号反转现象,对此Spies给出几种不同的解释,并认为其中最可能是由于IP效应引起的.Weidelt (1982)证明了重叠回线装置下,如果地下介质的电导率是非频散的,那么无论地下介质电导率如何分布,瞬变电磁响应都不会出现符号反转.对重叠(或中心)回线瞬变电磁响应中的符号反转现象引起了许多学者的讨论.在排除几何效应、介电常数和磁导率频散等因素后,一致认为这是由于电化学的极化机制引起的电导率频散现象.另外,学者们对重叠(或中心)回线瞬变电磁法的激发极化机制也进行深入的研究和讨论(Smith and West, 1988;Smith et al., 1988;Flis et al., 1989).其中,Smith等(1988)为了快速计算时间域极化介质电磁响应,提出一种近似褶积算法.然而,由于其在理论计算过程中忽略与极化电流相关的耦合项,得到的极化电流为近似极化电流,与感应电流方向相反.
本文以时间域航空电磁法正演理论为基础,通过引入Cole-Cole模型,并根据Smith等(1988)对极化电流的定义,正演得到频率域响应,经过汉克尔变换得到时间域响应.为了计算实际极化电流密度,我们以极化介质的复电阻率和高频极限电阻率代替常规电阻率,分别经过正演计算得到总电流密度和感应电流密度,其差值即为极化电流密度.与前人研究不同的是,为了研究实际极化电流的扩散特征,我们考虑了与极化电流相关的耦合项的影响.通过研究极化介质中感应电流和极化电流的分布特征,对航空瞬变电磁法中负响应的产生机理给出合理解释.本文研究有利于加深激电效应对航空电磁信号影响特征的了解.
2 航空瞬变电磁激电效应正演理论 2.1 Cole-Cole模型Cole-Cole模型是Pelton等(1978)等人提出的用于描述岩石激电效应的数学模型.其数学表达式如下
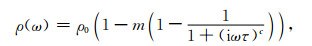
|
(1) |
其中,ρ0为零频电阻率,m为充电率,τ为时间常数,c为频率相关系数,ω为角频率,i为虚数单位.对(1)式两边取倒数,得到Cole-Cole模型的复电导率形式

|
(2) |
式中σ∞为高频极限电导率,其倒数为ρ∞,其中
本文以垂直磁偶极子为发射源,将发射源设在直角坐标系原点正上方h=30 m处,z轴垂直向下,x、y轴位于地表水平面.发射磁偶极矩大小为1 Am2,发射电流为负阶跃波.刘云鹤(2011)给出含源全空间层状介质的电磁场表达式,其中垂直磁偶极子在任意位置(x,y,z)产生的电场水平分量为
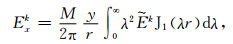
|
(3) |
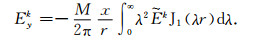
|
(4) |
式中M为发射偶极矩,
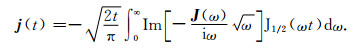
|
(5) |
式中J1/2为半整数阶贝塞尔函数,可以通过Yin等(2008)给出的160点汉克尔滤波系数计算得到.
根据Smith等(1988)的理论有
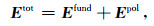
|
(6) |
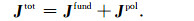
|
(7) |
式中,E tot、J tot分别为极化介质中频率域总电场和总电流密度,E fund、J fund分别为极化介质中频率域基本电场和基本电流密度(不存在激电效应),剩余部分即为频率域极化电场E pol和频率域极化电流密度J pol.
根据欧姆定律,总电流密度和基本电流密度为
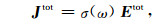
|
(8) |
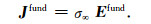
|
(9) |
由上式可知,总电流密度J tot与σ(ω)相关,基本电流密度J fund与σ∞相关,通常又称作感应电流密度.
综合公式(2)、(6)、(7)、(8)、(9)可以得到极化电流密度J pol的数学表达式
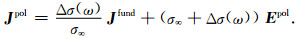
|
(10) |
上式第二项表示与极化电流相关的耦合项(Smith et al., 1988).不同于Smith等(1988)给出的近似极化电流密度,本文极化电流正演计算中包含该耦合项的影响,为实际极化电流密度.上述不同电流频率域结果经反傅氏变换可得到时间域电流密度.
3 理论模型正演 3.1 精度验证为了验证时间域电流密度正演响应的准确性,我们将本文计算结果与Raiche等(2007)的算法结果进行对比.以两种不同电阻率大小的均匀极化半空间模型为例,发射源为垂直磁偶极子,磁偶极矩为1 Am2,发射源高度30 m,测点为地下(50 m,0 m,50 m)处,分别计算该点总电流密度、感应电流密度及极化电流密度随时间变化的曲线,图 1展示了精度验证结果(虚线表示负电流密度),可以看出本文的计算结果与Raiche的算法结果吻合很好,不考虑电流密度在变号时刻附近的误差,低阻极化模型(图 1a)的误差均在3%以内,高阻极化模型(图 1b)的误差均在5%以内.
|
图 1 精度验证. (a)低阻极化模型,ρ0=20 Ωm,ρ∞=10 Ωm,m=0.5,τ=0.001 s,c=0.9;(b)高阻极化模型,ρ0=500 Ωm,ρ∞=250 Ωm,m=0.5,τ=0.001 s,c=0.9. Fig. 1 Accuracy verification for the polarizable model of (a) ρ0=20 Ωm, ρ∞=10 Ωm, m=0.5, τ=0.001 s, c=0.9; (b) ρ0=500 Ωm, ρ∞=250 Ωm, m=0.5, τ=0.001 s, c=0.9. |
针对低阻极化模型,可以看到早期极化电流密度为正,晚期变为负值.对于高阻极化体,由于其中电流扩散速度快,正向极化电流很早衰减完,因此图 1b所示的时间范围内实际极化电流没有发生变号.因为实际极化电流的变化规律不会随着电阻率大小改变而改变,如能准确计算更早时间道的极化电流密度值,对于高阻极化模型,我们仍会发现早期极化电流为正,晚期变为负值.
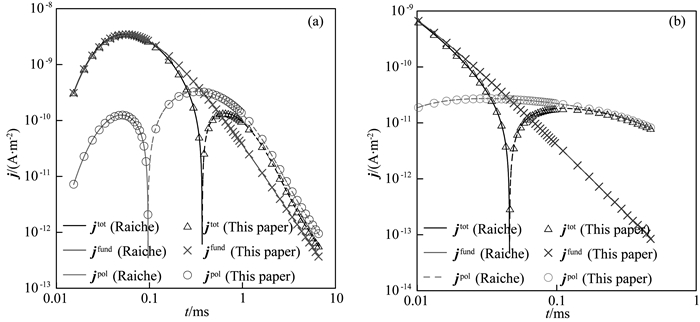
3.2 耦合项的影响为了分析(10)式中耦合项对极化电流密度的影响,我们针对图 1的两种极化模型,在地下(50 m,0 m,50 m)处,分别计算近似极化电流密度(Smith et al., 1988)、耦合项及实际极化电流密度.图 2分别展示了低阻极化模型和高阻极化模型中耦合项的影响.对于低阻极化模型(图 2a),耦合项在早期时间道为正值,其大小相对于近似极化电流密度较大,因此实际极化电流在早期为正值,之后变为负值;对于高阻极化模型,如图 2b所示,其耦合项相对于近似极化电流较小(0.01 ms以后),故极化电流为负值.从图 2可以看出,早期时间道耦合项的影响均较大,而晚期道耦合项的影响基本可以忽略.由于早期道耦合项是造成实际极化电流出现变号的关键,故本文实际极化电流正演模拟过程中均考虑耦合项的影响.
|
图 2 极化电流耦合项的影响特征(模型同图 1) (a)低阻极化模型;(b)高阻极化模型 Fig. 2 Influence of coupling term of polarizable current for model (a) and (b) of Fig. 1 |
为了研究时间域航空电磁激电效应对电磁扩散的影响,我们针对表 1给出5种模型的激电参数计算地下电流分布.为提高计算效率,正演计算中采用OpenMP并行技术.通过分析极化模型中感应电流、极化电流及总电流的分布特征,阐述激发极化的充放电过程,并对航空瞬变电磁中负响应产生机理给出合理的解释.此外,还对比分析不同充电率m、高频极限电导率σ∞及层状极化介质对电磁扩散特征的影响.
|
|
表 1 均匀半空间模型参数 Table 1 Parameters for a homogeneous half-space model |
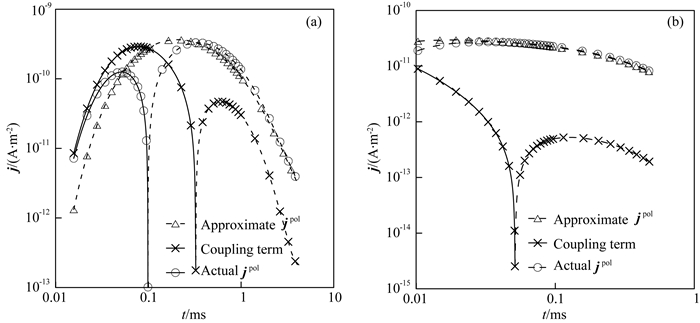
为了分析极化介质中感应电流与极化电流的变化规律并解释时间域航空电磁负响应产生机理,我们以模型1为例,计算极化介质中感应电流jfund、极化电流j pol及总电流j tot的时间域分布结果.图 3给出4个不同时刻(0.02 ms、0.1 ms、1.0 ms、2.0 ms)模型1中感应电流、极化电流及总电流的XZ分布图(y=0 m).图 4a为模型1中不同位置极化电流jpol随时间变化曲线,图 4b为模型1中测点为地下(100 m,0 m,100 m)处的jtot、j fund和j pol随时间变化曲线.

|
图 3 模型1中(a)感应电流密度;(b)极化电流密度;(c)总电流密度的XZ分布图(y=0 m).图中正负值只表示不同电流流动方向 Fig. 3 Distribution on the XZ-plane (y=0 m) for (a) induced current; (b) polarization current; (c) total current for Model 1. The positive and negative values indicate the directions of current flow |
|
图 4 (a)模型1在不同测点处极化电流随时间变化特征;(b)测点(100 m,0 m,100 m)处感应电流密度、极化电流密度和总电流密度随时间变化特征 Fig. 4 (a) Polarization current versus time for Model 1 at different locations; (b) induced current, polarization current, and the total current at location (100 m, 0 m, 100 m) versus time |
从图 3a的感应电流分布可以看出,感应电流总是沿正方向流动,随着时间不断向下和向外扩散,强度发生衰减,形成“烟圈”效应.与感应电流相比,极化电流具有独特的扩散特征,从图 3b和4a可以看出:(1)早期极化电流沿着正方向流动,强度先增加后减弱,表征充电过程;(2)随时间推移,充电过程达到饱和,极化电流变为零;(3)充电过程结束后开始放电,极化电流变为负向;(4)极化电流在整个扩散过程中,充电时段其扩散特征与感应电流相同,呈现“烟圈”特征;然而,在放电时段,反向极化电流不具有“烟圈”扩散特征--随时间推移,反向极化电流虽然不断向外扩大,强度减弱,但其极大值一直处于源中心在地表投影处.这种现象可以做出如下解释:对(10)式两边取散度可得
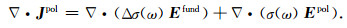
|
(11) |
对于均匀极化半空间,上式可改写成
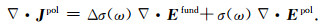
|
(12) |
从上式可以看出,极化电流的散度包括感应电场的散度和极化电场的散度.由于感应电场为螺线管场,即

|
(13) |
同时由于极化电场是由离子定向移动产生的有源场,故其散度不为零,因此极化电流的散度也不为零.在早期充电阶段,感应电场占主导地位,极化电流呈现“烟圈”扩散特征;而在晚期放电阶段,极化电场逐渐占主导地位,极化电流呈现非“烟圈”扩散特征.图 3c给出总电流分布特征.由于总电流包含感应电流和极化电流,在早期呈现与感应电流相同的扩散特征,而在晚期负向极化电流占主导地位,总电流呈现非螺线管场的极化电流扩散特征.
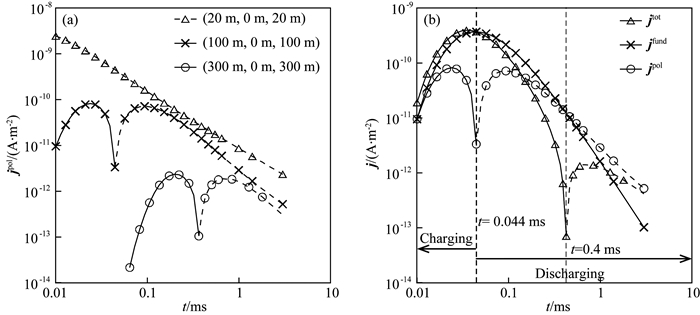
根据上述感应电流和极化电流的充放电过程,我们可以对极化介质出现电流负响应给出物理解释.早期感应电流对整个极化半空间进行充电,极化电流与感应电流流动方向相同(均为正方向),并呈“烟圈”向下和向外扩散.随着时间推移,感应电流逐渐衰减;当感应电流衰减至无法维持充电状态时,极化体达到充电饱和,此时极化电流为零.之后开始放电过程,极化电流变为负向,其强度先增加再减小,如果某一时刻极化电流值大于感应电流值,那么极化介质中总电流变为负向,此时航空电磁系统有可能观测到负电磁响应.
必须指出,尽管地下为极化介质,且晚期道存在负向总电流,但时间域航空电磁系统中仍有可能观测不到负响应数据.这是因为航空电磁响应与系统的Footprint有关(Yin et al., 2014),当晚期道Footprint影响区域中既包括正向电流又包括负向电流(图 3c),如果负向电流的响应远大于正向电流的响应,则航空电磁系统观测到负电磁响应;反之,如果该区域负向电流的响应小于正向电流的响应,则航空电磁系统中观测不到负响应数据.通常情况,高阻极化区由于感应电流衰减快,更容易观测到由激电效应引起的电磁负响应.从图 4b给出的模型1中测点(100 m,0 m,100 m)处的感应电流、极化电流和总电流随时间变化特征可以看出,大约在t=0.044 ms充电达到饱和,此时极化电流为零,之后该点极化电流变为负方向,开始放电过程;当极化电流大于感应电流时,总电流变为负方向.图中显示大约在t=0.4 ms时,该点总电流变为负值.
为进一步加深对极化介质中电磁扩散过程的了解,图 5展示了模型1中感应电流、极化电流及总电流的三维空间分布(以t=1.0 ms为例).图中通过引入时间因子实现动态描述(动画可从相关网页下载).从电流动态分布图中,我们可以更直观地看到极化电流和感应电流的不同扩散特征及时间域航空电磁系统电流发生变号的过程.
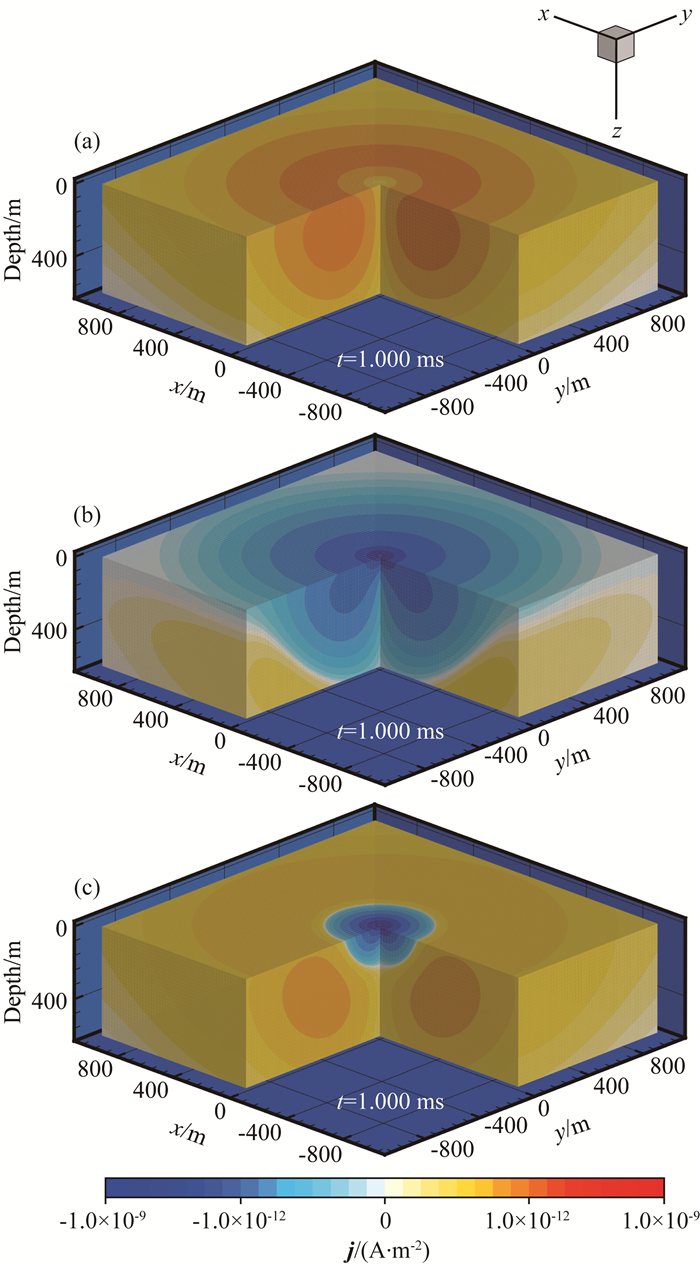
|
图 5 模型1中(a)感应电流密度;(b)极化电流密度;(c)总电流密度的三维分布.图中正负值只表示电流不同流动方向 Fig. 5 Three-dimensional distribution for (a) induced current; (b) polarization current; (c) total current for Model 1. The positive and negative values indicate the directions of current flow |
本节为研究充电率m对电磁扩散的影响,我们对比不同充电率模型的电流分布特征.图 6展示了模型1-3中总电流密度的XZ分布图(y=0 m),其中模型3为均匀非极化半空间模型.从图中可以看出,不同充电率模型均存在电流随时间扩散的现象.其中,非极化半空间瞬变电流呈现“烟圈”效应(图 6c),而极化半空间由于存在激电效应(图 6(a, b)),电流在扩散过程中出现变号,随时间向下和向外扩散.此外,不同充电率模型中早期电流扩散特征相似,这是因为早期极化模型中的感应电流占主导地位,激电效应不明显.随着时间推移,极化电流开始占主导地位,激电效应变的明显,随之极化介质中开始出现负向电流.从图 6和图 7给出的不同充电率模型的电流衰减曲线可以看出,充电率越大,负响应幅值越大且出现越早,影响范围也越大.

|
图 6 不同充电率模型中总电流密度的XZ分布图(y=0 m).图中正负值只表示不同电流流动方向 Fig. 6 Total current at the XZ plane (y=0 m) for different models. The positive and negative values indicate the directions of current flow |
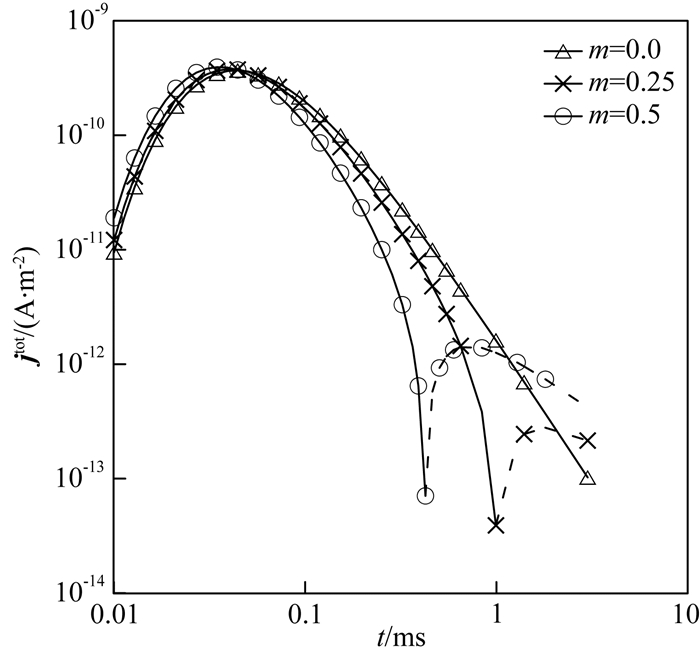
|
图 7 极化模型中测点(100 m,0 m,100 m)处总电流密度随时间变化特征 Fig. 7 Total current at location (100 m, 0 m, 100 m) versus time for different m |
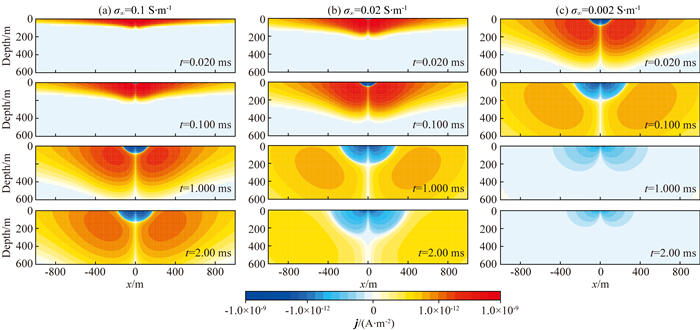
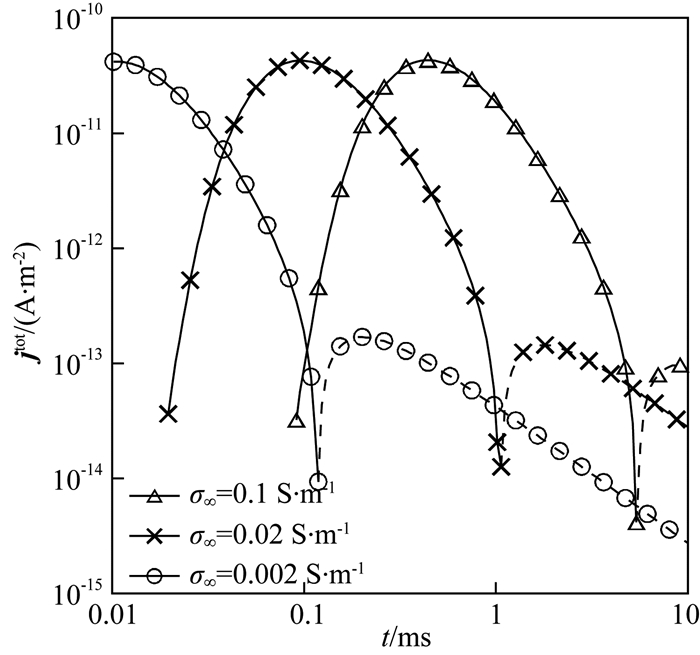
为了研究极化介质中σ∞对电磁扩散的影响.图 8展示了模型1、4和5中总电流密度的XZ分布图(y=0 m).从图中可以看出,对于均匀极化半空间模型,σ∞越小(高阻极化介质),电流扩散速度越快,负向电流出现越早,相同时刻负向电流影响范围越大.图 9给出不同σ∞模型在同一测点处的总电流密度j tot随时间变化结果.从图中可以看出,σ∞越小,电流出现变号时间越早,负向电流影响范围越大,这也说明了高阻极化区激电效应更明显.
|
图 8 模型1、4和5总电流密度的XZ分布图(y=0 m).图中正负值只表示不同电流流动方向 Fig. 8 Total current at the XZ plane (y=0 m) for Model 1, 4 and 5. The positive and negative values indicate the directions of current flow |
|
图 9 极化模型中测点(200 m,0 m,100 m)处电流密度随时间变化特征 Fig. 9 Total current at location (200 m, 0 m, 100 m) versus time for different σ∞ |
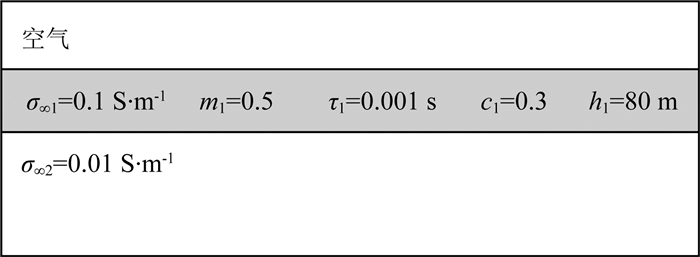
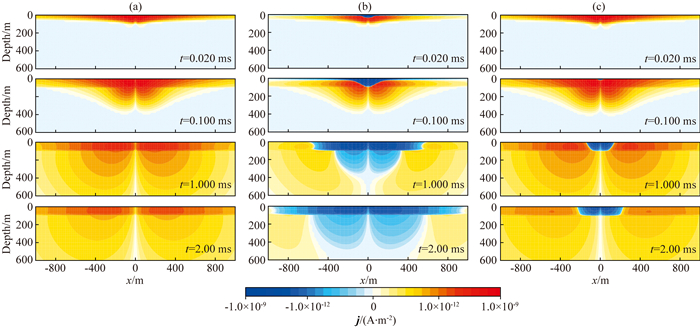
为考虑层状介质电性分界面对电磁扩散的影响,我们以两层介质模型为例,表层为极化层,基底为非极化半空间.图 10给出层状介质模型参数.图 11给出4个不同时刻层状介质中感应电流、极化电流及总电流的XZ分布图(y=0 m).从图 11可以看出,相对于均匀半空间模型,由于层状介质存在电性分界面,其电流密度在电性分界面两侧呈现不连续性.从图 11a可以看出,感应电流从表层穿透分界面保持正方向流动;从图 11b可以看出,极化电流只产生于表层极化介质中,非极化基底不产生极化电流.随着时间推移,表层介质中的极化电流向下传播,穿透电性分界面并在非极化半空间中扩散.图 11b也非常明显地展示了层状介质中极化电流的充放电过程.考虑到总电流为感应电流和极化电流的综合效应,图 11c表明随时间总电流仅在表层极化层中发生变号现象,在非极化基底中感应电流始终占主导地位,总电流没有发生变号.
|
图 10 层状模型示意图 Fig. 10 A layered earth model |
|
图 11 层状介质中(a)感应电流密度;(b)极化电流密度;(c)总电流密度的XZ分布图(y=0 m),图中正负值只表示不同电流流动方向 Fig. 11 Distribution on the XZ-plane (y=0 m) for (a) induced current; (b) polarization current; (c) total current for the layered earth in Fig. 10, The positive and negative values indicate the directions of current flow |
本文以时间域航空电磁激电效应理论和算法为基础,通过分析均匀半空间模型中感应电流和极化电流的分布特征,阐述激发极化的充放电过程,对航空瞬变电磁中负响应产生机理给出解释.通过对比分析不同激电参数对时间域航空电磁法电磁扩散的影响,得出以下结论:
(1)极化介质中既存在感应电流,又存在极化电流.早期感应电流影响较大,激电效应不明显,而晚期极化电流占主导地位,激电效应变的明显.
(2)早期充电过程中极化电流呈现类似于感应电流的“烟圈”扩散特征,而晚期的极化电流受离子/电子放电影响为有源场,不呈现“烟圈”扩散特征.
(3)极化介质的充电率越大,电流出现变号时间越早,负向总电流幅值也越大,影响范围越大.
(4)极化介质的电导率σ∞越小,电流出现变号时间越早,负向电流幅值及激电效应影响越大.
(5)在极化区,实际航空电磁勘探中能否观测到电磁负响应取决于测区电阻率、激电参数、电磁系统的Footprint和观测时间等因素.高阻极化区更容易观测到电磁负响应,而低阻极化区有可能观测不到电磁负响应.
通过本文极化介质中电磁扩散过程的研究和激发极化产生负电磁响应机理的探讨,希望加深对航空电磁系统激电效应的理解,促进极化区航空电磁数据的合理解释.
致谢作者向吉林大学电磁“千人计划”研究团队成员在文章的准备过程中提供的帮助表示感谢.特别对审稿人和编辑对本文提出的修改建议表示感谢.
| Börner F D, Schopper J R, Weller A. 1996. Evaluation of transport and storage properties in the soil and groundwater zone from induced polarization measurements. Geophysical Prospecting, 44(4): 583-601. DOI:10.1111/gpr.1996.44.issue-4 | |
| Chave A D. 1983. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion. Geophysics, 48(12): 1671-1686. DOI:10.1190/1.1441448 | |
| Flis M F, Newman G A, Hohmann G W. 1989. Induced-polarization effects in time-domain electromagnetic measurements. Geophysics, 54(4): 514-523. DOI:10.1190/1.1442678 | |
| Hohmann G W, Kintzinger P R, Van Voorhis G D, et al. 1970. Evaluation of the measurement of induced electrical polarization with an inductive system. Geophysics, 35(5): 901-915. DOI:10.1190/1.1440136 | |
| Hördt A, Blaschek R, Kemna A, et al. 2007. Hydraulic conductivity estimation from induced polarisation data at the field scale-the Krauthausen case history. Journal of Applied Geophysics, 62(1): 33-46. DOI:10.1016/j.jappgeo.2006.08.001 | |
| Kemna A, Binley A, Ramirez A, et al. 2000. Complex resistivity tomography for environmental applications. Chemical Engineering Journal, 77(1-2): 11-18. DOI:10.1016/S1385-8947(99)00135-7 | |
| Liu Y H. 2011. Research on 3-D controlled source electromagnetic method inversion using nonlinear conjugate gradients (in Chinese). Changchun: Jilin University. | |
| Pelton W H, Ward S H, Hallof P G, et al. 1978. Mineral discrimination and removal of inductive coupling with multifrequency IP. Geophysics, 43(3): 588-609. DOI:10.1190/1.1440839 | |
| Raiche A, Sugeng F, Wilson G. 2007. Practical 3D EM inversion? The P223F software suite. ASEG Extended Abstracts, 2007(1): 1-5. | |
| Slater L, Lesmes D P. 2002. Electrical-hydraulic relationships observed for unconsolidated sediments. Water Resources Research, 38(10): 31-1-31-13. | |
| Smith R S, Walker P W, Polzer B D, et al. 1988. The time-domain electromagnetic response of polarizable bodies: An approximate convolution algorithm. Geophysical Prospecting, 36(7): 772-785. DOI:10.1111/gpr.1988.36.issue-7 | |
| Smith R S, West G F. 1988. Inductive interaction between polarizable conductors: An explanation of a negative coincident-loop transient electromagnetic response. Geophysics, 53(5): 677-690. DOI:10.1190/1.1442502 | |
| Spies B R. 1980. A field occurrence of sign reversals with the transient electromagnetic method. Geophysical Prospecting, 28(4): 620-632. DOI:10.1111/gpr.1980.28.issue-4 | |
| Weidelt P. 1982. Response characteristics of coincident loop transient electromagnetic systems. Geophysics, 47(9): 1325-1330. DOI:10.1190/1.1441393 | |
| Williams K H, Kemna A, Wilkins M J, et al. 2009. Geophysical monitoring of coupled microbial and geochemical processes during stimulated subsurface bioremediation. Environmental Science & Technology, 43(17): 6717-6723. | |
| Yin C, Smith R S, Hodges G, et al. 2008. Modeling results of on-and off-time B and dB/dt for time-domain airborne EM systems.//70th Annual EAGE Conference and Exhibition. Extended Abstract, 1-4. | |
| Yin C C, Huang W, Ben F. 2013. The full-time electromagnetic modeling for time-domain airborne electromagnetic systems. Chinese J. Geophys., 56(9): 3153-3162. DOI:10.6038/cjg20130928 | |
| Yin C C, Huang X, Liu Y H, et al. 2014. Footprint for frequency-domain airborne electromagnetic systems. Geophysics, 79(6): E243-E254. DOI:10.1190/geo2014-0007.1 | |
| Yin C C, Zhang B, Liu Y H, et al. 2015. Review on airborne EM technology and developments. Chinese J. Geophy., 58(8): 2637-2653. DOI:10.6038/cjg20150804 | |
| 刘云鹤. 2011.三维可控源电磁法非线性共轭梯度反演研究.长春:吉林大学. | |
| 殷长春, 黄威, 贲放. 2013. 时间域航空电磁系统瞬变全时响应正演模拟. 地球物理学报, 56(9): 3153–3162. DOI:10.6038/cjg20130928 | |
| 殷长春, 张博, 刘云鹤, 等. 2015. 航空电磁勘查技术发展现状及展望. 地球物理学报, 58(8): 2637–2653. DOI:10.6038/cjg20150804 | |
 2016, Vol. 59
2016, Vol. 59


