2. 中南大学有色金属成矿预测与地质环境监测教育部重点验室, 长沙 410083;
3. Department of Geology and Geophysics, University of Utah, Salt Lake City, Utah, USA
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals of Ministry of Education, Central South University, Changsha 410083, China;
3. Department of Geology and Geophysics, University of Utah, Salt Lake City, Utah, USA
航空电磁法(AEM)分为频率域航空电磁(AFEM)和时间域航空电磁或航空瞬变电磁(ATEM)两种,其中频率域方法发展较早,研究成果相对较多(Alumbaugh and Alumbaugh, 1995;Cox and Zhdanov, 2008;Yin et al., 2014).但AFEM效率较低、探测深度较小,而ATEM探测效率较高,能够获取较多的地质信息.早在20世纪六七十年代,Wait (1969)、Nabighian (1970)、Ghosh (1972)、Fraser (1972)、Singh (1973)等研究了时间域电磁(TEM)电磁场的传播特征.但由于TEM探测方法的理论相对复杂,在二维和三维的反演方面研究进展缓慢,主要工作集中在二维、三维正演模拟(王华军和罗延钟,2003; Commer and Newman, 2004;熊彬和罗延钟,2006;李建慧,2011;周俊杰,2011;王宇航,2013;强建科等,2015;殷长春等,2015)和一维反演与定性解释方面(Yin and Fraser, 2004;Yin and Hodges, 2007;Viezzoli et al., 2008;陈斌等,2014).然而地下真实情况往往是二维和三维结构,一维ATEM的反演和解释不能满足实际工作需要,因此有必要继续研究高维ATEM的反演问题.
三维时间域电磁正反演最大的障碍是内存和时间消耗巨大,目前仍然处于理论研究阶段(Haber et al., 2007;Cox et al., 2012;Zaslavsky et al., 2012;Oldenburg et al., 2013),而2.5维ATEM正反演相对于三维而言,对计算资源和时间的消耗要小许多,也是最有可能实现突破的.截至目前,对于航空瞬变电磁法2D、2.5D的反演研究相对较少.Farquharson (1995)提出了频率域中基于伴随场的灵敏度矩阵的计算方法,为高维电磁法反演中灵敏度矩阵的求解提供理论依据.熊彬等(2004)利用原始场和辅助场之间的点乘和面积积分求得电磁响应值对地下空间电导率的偏导数矩阵,但其反演算法仍在研究中.Wilson (2006)实现了基于阻尼特征参数法的频率域2.5维航空电磁数据反演.Guillemoteau (2012)利用玻恩近似和经验判断的方法进行快速2D航空瞬变电磁法的反演研究.余小东(2014)分别使用阻尼特征参数反演法与阻尼最小二乘反演法实现了2.5D航空瞬变电磁反演算法,并对比研究了两种方法的反演结果.
非线性共轭梯度法(Non-linear Conjugate Gradient,NLCG)不需要对最优化问题进行线性化,在反演时间和内存的耗费上相对较低,非常适合解决高维电磁反演问题.自Newman和Alumbaugh (2000)提出采用非线性共轭梯度方法解决电磁反演问题以来,该方法已经应用在大地电磁法、可控源电磁法的反演解释中(Rodi and Mackie, 2001;Newman and Boggs, 2004;Kelbert et al., 2008;Commer and Newman, 2009;翁爱华等,2012).本文将非线性共轭梯度方法应用到2.5D时间域航空电磁反演中.在正演过程中,我们利用有限单元法求解基于拉氏傅氏域中异常电磁场的微分方程,再通过逆拉氏逆傅氏双变换得到时间域的瞬变电磁响应.反演过程中,采用伴随方程法求解灵敏度矩阵,通过二次插值向后追踪法求解最佳步长.通过对理论模型数据进行反演,验证了时间域航空电磁2.5维非线性共轭梯度反演的有效性.此外,讨论了噪声、不同初始模型对反演结果的影响.
2 正演理论由Maxwell方程组出发,同时将总感应场划分为背景场和异常场:

|
(1) |
式中e和h分别代表时间域中电场和磁场,下标a代表异常场,下标b代表背景场.将时间域Maxwell方程组经过拉氏变换得到相应背景场的偏微分方程:

|
(2) |

|
(3) |
式中E和H分别代表拉氏域中的电场和磁场,ε代表介电常数,σ代表介质电导率,μ代表磁导率,s代表拉氏域变量,J代表场源电流密度矢量.
由总场等于背景场和异常场之和可得到异常场的偏微分方程:

|
(4) |

|
(5) |
其中J a=σa E b.对式(4)、(5)的偏微分方程进行y方向的一维傅里叶变换便可得到拉氏傅氏域中的偏微分方程,并利用有限单元法求解得到异常场.本文中的有限单元法采用三角形网格剖分技术;对于最终形成的大型线性方程组,采用Pardiso_64位直接解法求解器进行求解,该方法的优点在于求解精度高,多源情况下能实现并行回代.
经过以上有限元法求解得到的是拉氏傅氏域中的异常场,需要再经过逆傅氏变换和逆拉氏变换才能得到时间域中的异常场值.在逆傅氏变换中,由于采用汉克尔变换的滤波系数过多,计算量过大,本文采用三次样条插值技术,从而在保证计算精度的情况下大大减少计算量.在逆拉氏变换中,采用Gaver-Stehfest变换技术,其优点是计算量小,纯实数运算(罗延钟和昌彦君,2000).最后将得到时间域中的异常场,与解析法计算得到的时间域背景场相加就得到了总感应场.
为了验证该正演算法的有效性与准确性,将计算结果与层状模型的半解析解(罗延钟等,2003)进行了比较.收发装置采用水平共面装置(如图 1),飞行高度为30 m,收发距为10 m,发射波形为阶跃波,层状模型的第一层、第三层电导率均为0.01 S·m-1,第二层电导率为0.05 S·m-1,第一层、第二层的厚度均为100 m,图 2a所示为层状模型得到的数值解与半解析解对比情况.从图 2b可以看出,最大相对误差2.40%,平均相对误差1.49%.由此可知,在时间为1 μs到10 ms的范围内数值解与半解析解吻合较好,精度较高.

|
图 1 模型示意图 Fig. 1 Sketch of model |

|
图 2 层状模型的数值解与解析解的对比结果 (a)垂直磁场数值解与解析解对比;(b)数值解与解析解的相对误差. Fig. 2 Comparison of numerical and analytic solutions on the layering model (a) Comparison of numerical and analytic solutions for vertical magnetic field; (b) Relative errors of numerical and analytic solutions. |
反演问题的目标函数可以写成如下形式:

|
(6) |
式中,d为N维观测数据向量,m为M维的模型空间向量,而F为正演算子,Ψ表示目标函数,W m为模型加权矩阵,W d为数据加权矩阵,λ为正则化因子,上标T表示转置.目标函数的梯度为

|
(7) |
式中,A m为灵敏度矩阵.目标函数Ψ(m)的最小值通过NLCG进行求解,每次反演迭代可写成以下形式:

|
(8) |
式中,k为迭代次数,αk为迭代步长,p k是迭代方向矢量.
正则化因子λ在反演中约束步长的大小,每减小一次λ导致正则化部分在目标函数的比重变小,模型修正空间变大,可以搜索较大的步长.这里正则化因子λ的选择方法是借鉴Zhdanov (2009)的自动化选取λ值的方法.首先给定一个初始值λ0,计算λk=λ0qk-1,q>0,k=1,2,3,…,K代表反演的迭代次数.
3.2 灵敏度矩阵的分析灵敏度是指电磁响应对模型参数的一阶导数,即构成灵敏度矩阵A的元素,其计算方法对于梯度类的最优化反演算法有着相当重要的作用,本文采用伴随方程法求解垂直磁场的灵敏度.拉氏域中垂直磁场的灵敏度为(龙剑波,2014)

|
(9) |
式中的E为人工源区域V内的电场空间分布函数,而E +为伴随单位磁偶源激发的伴随电场函数.因为体积分的被积函数中ϕj只在对应的第j个网格内不为0,所以每一个灵敏度矩阵的元素只需在相应的单元内进行积分即可.反演中只需计算一次灵敏度矩阵,灵敏度矩阵求解只需要计算2次正演,从而节约了反演计算时间.
公式(9)可以进一步简化为:

|
(10) |
该式就是空间域中走向方向y=0处,场值Hz对电导率的偏导数计算式.为研究灵敏度的分布规律,设计如下均匀半空间模型,地下电导率为0.01 S·m-1,发射线框位于地面,边长为20 m,电流强度为10 A,选取采样时间点分别为t1=0.0020 ms,t2=0.0056 ms,t3=0.0155 ms,t4=0.0431 ms,t5=7.1876 ms,t6=20.0000 ms.图 3给出了各个时间点场值Hz对空间每个单元电导率的灵敏度分布特征(图中数据为灵敏度幅值的对数).在时间上,灵敏度的幅值从早期(t1)到晚期(t6)不断衰减,这种变化与场值在时间上的衰减类似;在空间上,灵敏度幅值则从场源附近向四周迅速衰减,在早期t1~t4,灵敏度从浅部到深部的衰减较快,而在较晚期时间点t5~t6,灵敏度衰减速率相对变慢,在200 m内已没有较明显的“轮廓线”.这表明,相对于晚期,早中期时间点的灵敏度对介质更敏感.

|
图 3 异常体正上方(Offset=0)垂直磁场的灵敏度(绝对值)对数值的空间、时间变化 Fig. 3 Temporal and spatial variations of logarithm values in sensitivity of vertical magnetic field (absolute value) above the anomaly body (offset=0) |
在NLCG主循环迭代过程中,由于目标函数Ψ(m k+αk p k)不仅仅是迭代步长α的二次函数(至少高于二次),通常需要用迭代法获得最佳步长αk, best,这样会增加时间消耗.本文结合前人的研究成果(刘云鹤和殷长春,2013;Newman and Alumbaugh, 2000),采用二次插值向后追踪方法(Backtracking)计算最佳步长.在Wolfe准则中,目标函数充分下降需要满足两个不等式

|
(11) |

|
(12) |
式(11)称为充分下降条件,式(12)为曲率条件,其中的常数c1、c2为0到1之间的正数.本文采用的步长搜索过程中最关键的是求取NLCG最佳步长αk, best:
1)求得Ψ(mk, 1)、g(m k, 1)、p(m k, 1),并计算:

|
(13) |
然后取αt=min [1.0, 1.01×temp_α ],min表示最小值;并计算f1=Ψ(m k, 0+αt p k, 0).
2)若αt满足下降条件:l=f1-f0-g k, 0 p k, 0αt≤0,其中f0=Ψ(mk, 0),则αk, best=αt,结束搜索,令

|
(14) |
3)若αt不满足下降条件,进行向后追踪,令
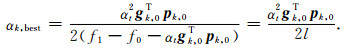
|
(15) |
验证αk, best是否满足不等式(11),若满足,则结束搜索;若不满足,则令αt=αk, best,并重复循环,直到满足设计要求.
4 理论数据反演 4.1 反演算法稳定性为了测试反演算法的稳定性与有效性,对理论模型正演的数据加入5%的高斯噪声再进行反演.模型如图 4a所示,在背景电阻率为100 Ωm的均匀介质中,嵌入一个大小为100 m×20 m、电阻率为50 Ωm、埋深为20 m的低阻异常体.采用水平共面装置(如图 1),飞行高度为30 m,收发距为10 m,发射波形为阶跃波.测点为15个,测点间距为30 m,采样时间范围为1.2 μs~10 ms,采样时间点为10个.正演测道曲线见图 4b,早期测道平缓,晚期道电磁响应变化明显.

|
图 4 反演算法稳定性测试 (a)低阻体模型;(b)低阻体正演响应测道曲线图;(c)低阻体模型的反演结果;(d)反演迭代过程中RMS变化曲线. Fig. 4 Tests of inversion algorithm stability (a) Low resistivity model; (b) TEM response of low resistivity model; (c) Inversion result of the low resistivity model; (d) RMS variation curve during iteration inversion. |
由反演结果(图 4c)看出,低阻异常体得到很好的还原,低阻体的埋深、横向和纵向尺寸以及位置都能得到较准确的反映,电阻率值也大致与理论模型的电阻率值相一致,可以较为清晰地反映地下真实电性结构.
图 4d给出了迭代过程中均方相对误差(RMS)的变化情况.从图中可以看出,①加入5%噪声后对反演有影响,但不是很大,说明算法比较稳定;②迭代开始时,均方相对误差较大,但下降较快,从第9次迭代往后,误差下降速率减慢,有一段较长的平缓趋势,这反映了非线性共轭梯度反演收敛比较稳定.收敛误差约20%左右,相比较其他的物探方法来说,这个误差是很大的,主要原因在于瞬变电磁的原始数据是二次衰变感应场,最大数据和最小数据相差5~6个数量级,这样的数据体计算的拟合误差一般较大,因此说,评价瞬变电磁反演效果时,均方相对误差仅作参考.
4.2 初始模型对反演结果的影响为了测试反演算法的适应性,我们设计了一个低阻与高阻混合的较复杂模型,目的是检验反演算法对电性差异较大异常体的分辨能力,以及不同初始模型对反演结果的影响.复杂模型如图 5a所示,背景电阻率为100 Ωm,低阻异常体大小为100 m×30 m、电阻率为20 Ωm、埋深为20 m,高阻异常体大小为100 m×20 m、电阻率为300 Ωm、埋深为20 m.采用水平共面装置(如图 1),飞行高度为30 m,收发距为10 m,发射波形为阶跃波,横向测点为17个,点距为30 m,初始模型电阻率分别设为150 Ωm、100 Ωm、50 Ωm.

|
图 5 不同初始模型反演结果 (a)复杂模型;(b)初始模型为150 Ωm;(c)初始模型为100 Ωm;(d)初始模型为50 Ωm. Fig. 5 Inversion results of different initial models (a) Complicated model; (b) Initial resistivity model of 150 Ωm; (c) Initial resistivity model of 100 Ωm; (d) Initial resistivity model of 50 Ωm. |
在反演中,当初始模型选择为150 Ωm时(大于实际模型的背景电阻率100 Ωm),反演结果见图 5b,低阻与高阻异常基本得到还原,但低阻异常体的晕圈范围较大,低阻电阻率值偏高于真实低阻异常体;高阻异常体的电阻率值偏低于真实值.
当初始模型设为100 Ωm时(等于实际模型的背景电阻率100 Ωm),反演结果见图 5c,低阻与高阻异常基本得到还原,而且低阻异常体的晕圈范围变小一点,低阻电阻率值和高阻电阻率值都比较接近于真实的模型电阻率值,反演结果较好.
当初始模型选择为50 Ωm时(小于实际模型的背景电阻率100 Ωm),反演结果见图 5d,大致能够反映出低阻与高阻异常的中心位置,但低阻异常体的晕圈范围变大了许多,对低阻体的反演结果变差,对高阻体反演结果影响不大,而且浅部出现了局部小异常.
通过以上比较可以看出,当选择的初始模型电阻率值与真实背景电阻率值差别不大时,能够得到稳定的反演结果.
4.3 正演与反演时间消耗由于时间域电磁法数值计算需要多次变换,导致计算时间较长.本次研究在PC机上完成,计算机处理器为Intel Core i7-2600,主频3.4 GHz,内存16 GB.采用Fortran语言实现正演与反演算法程序.
模型网格剖分为72×79,拉氏域波数为12个,汉克尔变换系数采用250个,时间采样点为10个,测点数为17个.通过分析,程序各模块的耗时差异较大:数据文件输入与输出和背景垂直磁场计算环节时间消耗很少,可忽略不计.在反演流程中,正演程序是关键,每调用一次正演程序需要约272 s,在形成灵敏度矩阵时需要约632 s,这部分比较耗时;进入正常反演迭代后,平均每次迭代耗时约614 s,总体反演时间随迭代次数线性增加,一般迭代约10次即可(表 1),大约需要1.97 h.由此看出,2.5D ATEM反演非常耗时,投入实用化前必须解决并行运算问题.
|
|
表 1 ATEM反演算法各模块耗时统计 Table 1 Time-consumption statistics for the ATEM inversion module contained in inversion algorithm |
ATEM的实测数据来自于Cox等(2012)论文,是关于Reid-Mahaffy实验场采用MEGATEM II系统获取的L40测线d B/dt垂直分量数据,由于本反演算法速度所限,对实测数据进行了抽稀处理,即抽取的测点尽量落在异常密集部位(图 6a).MEGATEM Ⅱ系统设置为90 Hz基频、42%占空比的半正弦发射波形,系统记录20道信号,包括沿x和z方向的d B/dt和感应磁场.我们反演时仅采用了断电后的dBz/dt数据,最后一道的时间是5.5 ms.沿测线方向网格间距30 m,深度方向网格间距10 m到50 m不等,网格大小为82×91,迭代20次,拟合误差从87%下降到34.3%.从反演结果看,得到了三个明显的低阻异常体,但异常中心收敛不集中,反演深度总体偏浅,基本与Cox等(2012)采用积分方程的方法反演的结果一致,证明本算法是正确的,但在计算时间和精度方面还需要继续优化改进.

|
图 6 来自MEGATEM仪器的L40测线dB/dt的反演结果 (a) dB/dt的垂直分量曲线图;(b)反演电阻率结果. Fig. 6 Inversion results of dB/dt data from survey line L40 using instrument MEGATEM (a) Vertical component of observed data; (b) Inversion results of resistivity. |
本文采用NLCG方法,实现了2.5D ATEM反演算法.采用将背景场和异常场分离的办法,用解析法计算背景场,用有限单元法计算异常场,从而消除了场源处的奇异性问题.此外,采用快速、高精度的直接解法求解线性方程组,以及Gaver-Stehfest变换技术求解逆拉氏变换和三次样条插值方法求解逆傅氏变换,从而保证正演算法的计算精度和计算效率.在处理灵敏度矩阵时,采用伴随方程法进行求解,从而提高反演计算效率.在计算最佳迭代步长时,采用二次插值向后追踪方法(Backtracking),为反演迭代的稳定性提供了保障.理论模型计算表明,反演结果能够基本反映地下真实电性结构.反演得到的低阻异常体较真实异常体的范围略大,可能与正演算法的计算精度、反演过程中灵敏度的计算以及迭代步长选取等多种因素有关,还需要进一步优化算法.同时,研究了选择不同初始模型情况下得到的反演结果,当选择的初始模型电阻率值与真实背景电阻率值相吻合时,得到的反演结果最好.此外,目前反演存在计算耗时较大的问题,还需要通过并行算法提高计算效率.
致谢感谢外审专家给予了详细的点评和中肯的修改意见.
| Newman G A, Alumbaugh D L. 1995. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences. Geophysical Prospecting, 43(8): 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 | |
| Chen B, Mao L F, Liu G D. 2014. The estimated prospecting depth of CHTEM-I system by the method of diffusion electric field. Chinese J. Geophys., 57(1): 303-309. DOI:10.6038/cjg20140126 | |
| Commer M, Newman G A. 2004. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics, 69(5): 1192-1202. DOI:10.1190/1.1801936 | |
| Commer M, Newman G A. 2009. Three-dimensional controlled-source electromagnetic and magnetotelluric joint inversion. Geophysical Journal International, 178(3): 1305-1316. DOI:10.1111/gji.2009.178.issue-3 | |
| Cox L H, Zhdanov M S. 2008. Advanced computational methods of rapid and rigorous 3-D inversion of airborne electromagnetic data. Communications in Computational Physics, 3(1): 160-179. | |
| Cox L H, Wilson G A, Zhdanov M S. 2012. 3D inversion of airborne electromagnetic data. Geophysics, 77(4): WB59-WB69. DOI:10.1190/geo2011-0370.1 | |
| Farquharson C G. 1995. Approximate sensitivities for the multi-dimensional electromagnetic inverse problem [Ph. D. thesis]. Vancouver: University of British Columbia. | |
| Fraser D C. 1972. A new multicoil aerial electromagnetic prospecting system. Geophysics, 37(3): 518-537. DOI:10.1190/1.1440277 | |
| Ghosh M K. 1972. Interpretation of airborne EM measurements based on thin sheet models [Ph. D. thesis]. Toronto: University of Toronto. | |
| Guillemoteau J, Sailhac P, Behaegel M. 2012. Fast approximate 2D inversion of airborne TEM data: Born approximation and empirical approach. Geophysics, 77(4): WB89-WB97. DOI:10.1190/geo2011-0372.1 | |
| Haber E, Oldenburg D W, Shekhtman R. 2007. Inversion of time domain three-dimensional electromagnetic data. Geophysical Journal International, 171(2): 550-564. DOI:10.1111/gji.2007.171.issue-2 | |
| Kelbert A, Egbert G D, Schultz A. 2008. Non-linear conjugate gradient inversion for global EM induction: resolution studies. Geophysical Journal International, 173(2): 365-381. DOI:10.1111/gji.2008.173.issue-2 | |
| Li J H. 2011. 3D numerical simulation for transient electromagnetic field excited by large source loop based on vector finite element method [Ph. D. thesis] (in Chinese). Changsha: Central South University. | |
| Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data. Chinese J. Geophys., 56(12): 4278-4287. DOI:10.6038/cjg20131230 | |
| Long J B. 2014. Non-linear conjugate gradient inversion for 2.5D airborne transient electromagnetic data [Master's thesis] (in Chinese). Changsha: Central South University. | |
| Luo Y Z, Chang Y J. 2000. A rapid algorithm for G-S transform. Chinese J. Geophys., 43(5): 684-690. DOI:10.3321/j.issn:0001-5733.2000.05.012 | |
| Luo Y Z, Zhang S Y, Wang W P. 2003. A research on one-dimension forward for aerial electromagnetic method in time domain. Chinese J. Geophys., 46(5): 719-724. | |
| Nabighian M N. 1970. Quasi-static transient response of a conducting permeable sphere in a dipole field. Geophysics, 35(2): 303-309. DOI:10.1190/1.1440093 | |
| Newman G A, Alumbaugh D L. 2000. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophysical Journal International, 140(2): 410-424. DOI:10.1046/j.1365-246x.2000.00007.x | |
| Newman G A, Boggs P T. 2004. Solution accelerators for large-scale three-dimensional electromagnetic inverse problems. Inverse Problems, 20(6): S151-S170. DOI:10.1088/0266-5611/20/6/S10 | |
| Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics, 78(1): E47-E57. DOI:10.1190/geo2012-0131.1 | |
| Qiang J K, Zhou J J, Man K F. 2015. Synthetic study of 2.5-D ATEM based on finite element method. Geophysical and Geochemical Exploration, 39(5): 1059-1062. | |
| Rodi W L, Mackie R L. 2001. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics, 66(1): 174-187. DOI:10.1190/1.1444893 | |
| Singh S K. 1973. Electromagnetic transient response of a conducting sphere embedded in a conductive medium. Geophysics, 38(5): 864-893. DOI:10.1190/1.1440381 | |
| Viezzoli A, Christiansen A V, Auken E, et al. 2008. Quasi-3D modeling of airborne TEM data by spatially constrained inversion. Geophysics, 73(3): F105-F113. DOI:10.1190/1.2895521 | |
| Wait J R. 1969. Electromagnetic induction in a solid conducting sphere enclosed by a thin conducting spherical shell. Geophysics, 34(5): 753-759. DOI:10.1190/1.1440045 | |
| Wang H J, Luo Y Z. 2003. Algorithm of a 2.5 dimensional finite element method for transient electromagnetic with a central loop. Chinese J. Geophys, 46(6): 855-862. | |
| Wang Y H. 2013. The research on HTEM 2.5D forward modeling and curve analysis [Master's thesis] (in Chinese). Chengdu: Chengdu University of Technology. | |
| Weng A H, Liu Y H, Jia D Y, et al. 2012. Three-dimensional controlled source electromagnetic inversion using non-linear conjugate gradients. Chinese J. Geophys., 55(10): 3506-3515. DOI:10.6038/j.issn.0001-5733.2012.10.034 | |
| Wilson G A, Raiche A P, Sugeng F. 2006. 2.5D inversion of airborne electromagnetic date. Exploration Geophysics, 37(4): 363-371. | |
| Xiong B, Luo Y Z, Qiang J K. 2004. Methods for calculating sensitivities for 2.5D transient electromagnetic inversion (Ⅰ). Progress in Geophysics, 19(3): 616-620. | |
| Xiong B, Luo Y Z. 2006. Finite element modeling of 2.5-D TEM with block homogeneous conductivity. Chinese J. Geophys., 49(2): 590-597. | |
| Yin C C, Fraser D C. 2004. The effect of the electrical anisotropy on the response of helicopter-borne frequency-domain electromagnetic systems. Geophysical Prospecting, 52(5): 399-416. DOI:10.1111/gpr.2004.52.issue-5 | |
| Yin C C, Hodges G. 2007. Simulated annealing for airborne EM inversion. Geophysics, 72(4): F189-F195. DOI:10.1190/1.2736195 | |
| Yin C C, Huang X, Liu Y H, et al. 2014. Footprint for frequency-domain airborne electromagnetic systems. Geophysics, 79(6): E243-E254. DOI:10.1190/geo2014-0007.1 | |
| Yin C C, Zhang B, Liu Y H, et al. 2015. 2.5-D forward modeling of the time-domain airborne EM system in areas with topographic relief. Chinese J. Geophys., 58(4): 1411-1424. DOI:10.6038/cjg20150427 | |
| Yu X D. 2014. Inversion of 2.5 dimensional time domain helicopter airborne electromagnetic method [Master's thesis] (in Chinese). Chengdu: Chengdu University of Technology. | |
| Zaslavsky M, Druskin V, Abubakar A, et al. 2012. Large-scale Gauss-Newton inversion of transient controlled-source electromagnetic data using the model reduction approach.//SEG Technical Program Expanded Abstracts 2012. SEG: 1-6. | |
| Zhdanov M S. 2009. Geophysical Electromagnetic Theory and Methods. New York: Elsevier. | |
| Zhou J J. 2011. Research on airborne transient electromagnetic 2.5-D forward modeling [Master's thesis] (in Chinese). Changsha: Central South University. | |
| 陈斌, 毛立峰, 刘光鼎. 2014. 用扩散电场法估算CHTEM-I系统的探测深度. 地球物理学报, 57(1): 303–309. DOI:10.6038/cjg20140126 | |
| 李建慧. 2011.基于矢量有限单元法的大回线源瞬变电磁法三维数值模拟[博士论文].长沙:中南大学. http://cdmd.cnki.com.cn/Article/CDMD-10533-1012476266.htm | |
| 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究. 地球物理学报, 56(12): 4278–4287. DOI:10.6038/cjg20131230 | |
| 龙剑波. 2014. 2.5维航空瞬变电磁数据的非线性共轭梯度反演[硕士论文].长沙:中南大学. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014396119.htm | |
| 罗延钟, 昌彦君. 2000. G-S变换的快速算法. 地球物理学报, 43(5): 684–690. DOI:10.3321/j.issn:0001-5733.2000.05.012 | |
| 罗延钟, 张胜业, 王卫平. 2003. 时间域航空电磁法一维正演研究. 地球物理学报, 46(5): 719–724. | |
| 强建科, 周俊杰, 满开峰. 2015. 时间域航空电磁法2.5维有限元模拟. 物探与化探, 39(5): 1059–1062. | |
| 王华军, 罗延钟. 2003. 中心回线瞬变电磁法2.5维有限单元算法. 地球物理学报, 46(6): 855–862. | |
| 王宇航. 2013.吊舱式时间域直升机航空电磁2.5维正演及响应曲线分析[硕士论文].成都:成都理工大学. http://cdmd.cnki.com.cn/Article/CDMD-10616-1013263554.htm | |
| 翁爱华, 刘云鹤, 贾定宇, 等. 2012. 地面可控源频率测深三维非线性共轭梯度反演. 地球物理学报, 55(10): 3506–3515. DOI:10.6038/j.issn.0001-5733.2012.10.034 | |
| 熊彬, 罗延钟, 强建科. 2004. 瞬变电磁2.5维反演中灵敏度矩阵计算方法(Ⅰ). 地球物理学进展, 19(3): 616–620. | |
| 熊彬, 罗延钟. 2006. 电导率分块均匀的瞬变电磁2.5维有限元数值模拟. 地球物理学报, 49(2): 590–597. | |
| 殷长春, 张博, 刘云鹤, 等. 2015. 2.5维起伏地表条件下时间域航空电磁正演模拟. 地球物理学报, 58(4): 1411–1424. DOI:10.6038/cjg20150427 | |
| 余小东. 2014. 时间域直升机航空电磁法2.5维反演[硕士论文]. 成都: 成都理工大学. http://cdmd.cnki.com.cn/Article/CDMD-10616-1015536447.htm | |
| 周俊杰. 2011.航空瞬变电磁法2.5维正演模拟研究[硕士论文].长沙:中南大学. | |
 2016, Vol. 59
2016, Vol. 59


