2. 中原油田分公司物探研究院, 河南濮阳 457001
2. Geophysical Exploration Research Institute, Zhongyuan Oilfield Company, Henan Puyang 457001, China
地震偏移技术是现代地震勘探数据处理的三大基本技术之一,在油气地震勘探中占有重要地位.逆时偏移(McMechan,1983;刘红伟等,2010)是目前较为精确的偏移成像方法,但仍属于常规偏移的范畴,其偏移算子是线性Born正演算子的共轭转置,而不是它的逆(Claerbout,1992).当地震数据采集不足或不规则、地下构造情况复杂以及波场带宽有限时,常规偏移方法只能对地下构造模糊成像,无法满足岩性油气藏勘探开发的需求.最小二乘偏移(Least-Square Migratin, LSM)将成像看作是最小二乘意义下的反演问题,通过不断拟合观测数据与反偏移模拟数据之间的误差泛函,可以得到振幅保真性更好、分辨率更高、偏移噪声更少的成像结果(Tarantola,1984;Nemeth et al., 1999).早期的最小二乘偏移主要基于射线理论(Dai et al., 2011;刘玉金等,2013;黄建平等,2013)和单程波理论(Kühl and Sacchi, 2003;Clapp et al., 2005;杨其强和张叔伦,2008;Tang,2009;沈雄君和刘能超,2012;周华敏等,2014),近年来基于双程波理论的LSRTM得到了广泛的研究和关注,然而计算量过于庞大限制了其进一步推广应用(Wong et al., 2011;Dai et al., 2012;郭振波和李振春,2014;黄建平等,2014;李振春等,2014).
正演模拟是LSRTM的基本单元,高效精确的正演模拟算法对LSRTM有着举足轻重的作用.有限差分法(Finite-Difference Method,FDM)是当前应用较为广泛的数值模拟算法,FDM中常用的两套网格系统分别为规则网格(Not Staggered Grids,NSG)和交错网格(Standard Staggered Grids,SSG).规则网格一般使用二阶标量声波方程,而交错网格常采用一阶速度-应力方程(Virieux,1986).研究表明,交错网格相比于规则网格,不仅易于处理变密度介质,且具有更高的数值模拟精度、更快的收敛速度、能更好地压制数值频散等,因而交错网格在正演模拟中取得了巨大成功(董良国等,2000).
不过,鉴于常规网格的原理简单且易于实现等优点,目前LSRTM的理论框架大多是基于二阶常密度标量声波方程建立的.然而,实际地下介质是变密度的,基于波形匹配策略的常规LSRTM算法无法考虑密度变化引起的振幅变化,从而也就无法得到保真的成像结果,丧失了LSRTM的关键优势.一阶速度-应力方程可方便地处理非均匀变密度介质,更加符合实际地质情况,但基于交错网格的一阶速度-应力方程LSRTM算法还处在探索阶段.由于常规LSRTM是基于二阶标量声波方程建立的,因而简单地将一阶速度-应力方程推广到LSRTM的波场延拓中是否合适仍值得深入探讨.
本文从一阶速度-应力波动方程入手,推导了相应的线性化波动方程和伴随方程,进而利用伴随状态法给出了梯度公式和更新流程,最终建立了一阶速度-应力方程LSRTM的整套理论框架.研究发现,基于二阶标量声波方程的常规LSRTM算法和基于一阶速度-应力方程的LSRTM算法存在很大的差异,前者的伴随方程和波动方程相同,而后者的伴随方程与波动方程迥然不同.常规LSRTM算法在处理变密度介质时,会得到失真成像结果,进而对后续的解释会产生错误的指导,而基于一阶速度-应力方程的LSRTM可以很好地考虑密度变化造成的影响,在非均匀变密度介质下仍能得到真振幅成像结果,且由于其多变量、多方程特性,也会对未来的弹性波LSRTM有一定的启发意义.
考虑到基于一阶速度-应力方程的LSRTM算法计算量仍然较大,通过引入动态相位编码技术(Romero et al., 2000),将多炮数据编码组合为一个超道集,可有效减小计算量.不过,当前的多震源LSRTM算法(Mulit-source LSRTM,MLSRTM)忽略了梯度和步长的随机性,收敛速度仍太慢.为了进一步提高计算效率、压制串扰噪声,本文将随机最优化思想推广到基于一阶速度-应力方程的MLSRTM中,本算法考虑了梯度的随机特性,每次迭代的梯度都是之前迭代梯度的指数衰减加权平均,通过合并之前的信息,从而减小了梯度的随机波动.模型试算证实本方法比传统相位编码LSRTM方法收敛更快,因而可节省计算成本、提高计算效率.
2 一阶速度-应力方程LSRTM非均匀各向同性介质的二维声波一阶速度-应力方程为
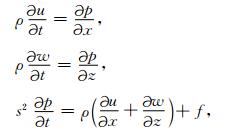
|
(1) |
其中,u, w表示质点速度,p表示声压,ρ为介质密度,s为介质慢度,即速度的倒数,f为震源项.
为了便于表示,令矩阵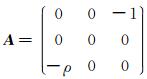

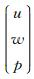
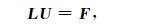
|
(2) |
其中L=A∂x+ B ∂z+ C ∂t为正演算子,F=(0 0 f)T为震源矩阵,上标T表示转置.
2.1 线性化波动方程假设慢度场的平方s2可以分解为背景慢度场平方s02与扰动慢度场平方Δs2的叠加,即
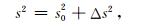
|
(3) |
由场的叠加原理可知,原始波场U可理解为由背景介质产生的背景波场U 0和由扰动介质产生的扰动波场U s叠加而成,即
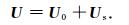
|
(4) |
原始波场与背景波场都满足波动方程,将公式(3)与(4)代入公式(1),并与背景波场的波动方程相减后应用Born近似,用背景波场U 0替代总波场U,即可得到扰动波场U s的控制方程:
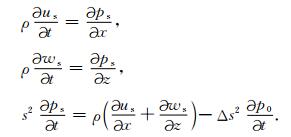
|
(5) |
写成矩阵的形式为
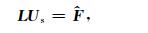
|
(6) |
其中,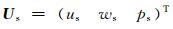
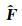
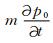
基于反演的成像方法寻求最优的地下介质模型,以使得反偏移模拟波场与观测波场残差的模最小,是一个最小范数问题,定义目标泛函为

|
(7) |
其中,‖ ‖22代表向量的L2范数,Uobs为观测记录.
采用梯度导引类算法求解公式(7),需要计算目标泛函关于模型参数的梯度:

|
(8) |
其中
梯度公式(8)中的偏导数波场可以通过对扰动波场的控制方程(公式(6))两边相对于模型参数求导得到:
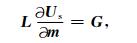
|
(9) |
其中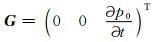
直接求取公式(9)中的偏导数波场是不可取的,因为对于地下任一点的偏导数波场都需要一次正演过程,目前的计算设备无法承受.本文借助伴随状态法(Wang et al., 2012)计算后续的目标泛函梯度,在此我们首先推导一阶速度-应力方程对应的伴随算子及相应的伴随波场控制方程.
由伴随状态法可知:
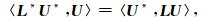
|
(10) |
其中L *为L的伴随算子, U *为伴随波场.
将公式(9)代入公式(8),并应用伴随状态法(公式(10))可得
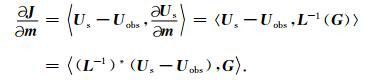
|
(11) |
可以看出,若定义伴随波场U *满足方程
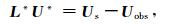
|
(12) |
则公式(11)中标量乘的左项可直接用伴随波场U *表示,进而梯度可快速计算得到.
将L的表达式带入公式(10),并进行标量乘的积分展开,然后应用分步积分和初始、边界条件,即可推出L *的表达式:
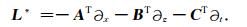
|
(13) |
将公式(13)代入公式(12),并将其展开可得伴随波场的控制方程:
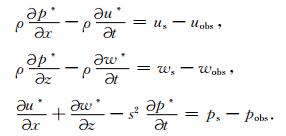
|
(14) |
从公式(14)可以看出,基于一阶速度-应力方程推导出的伴随方程,相比于原始波动方程(公式(1))有很大的改变,而基于二阶声波方程推导的伴随方程则与原始波动方程相同,这是两种LSRTM的本质区别.也就是说,本文从理论上证明了在LSRTM中,若波场的正传采用一阶速度-应力方程(公式(1)和(5)),则其数据残差的反传方程应该是对应的伴随方程(公式(14)),而不再是原始的波动方程.同样说明:将一阶速度-应力方程直接应用于常规LSRTM算法的正反传波场延拓中是不合适的,即使能得到相应的成像结果,也是缺乏理论依据的,这也从侧面证实了本文工作的意义.
需要指出的是,大多数陆上勘探记录到的地震数据只是声压p,因而公式(14)中的速度分量残差是不存在的,即公式(14)中前两个式子的右端都为0,反传的只是声压残差.伴随波场主要是为了求取后续的梯度,而梯度更多的是强调更新方向,因而在只有声压的情况下本文算法与常规LSRTM相同,可以得到正确的结果.不过,海上勘探不仅可以记录声压场,海底电缆等装置还可以记录两个速度分量,此时常规声波LSRTM仍然只能利用声压数据,而本文一阶速度-应力方程LSRTM算法可同时利用所有数据,由于所用到的波场信息更多,反演结果相对更可靠,这也从另一方面说明了本文算法的优势.
由伴随波场的控制方程(公式(12))可求得伴随波场为
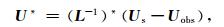
|
(15) |
将公式(15)代入(11),可进一步简化梯度公式为
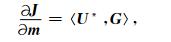
|
(16) |
将上式展开,即可得到相应的梯度计算公式
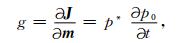
|
(17) |
利用最速下降法可对模型进行迭代更新,其更新过程为
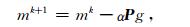
|
(18) |
其中,α为更新步长,P为预处理算子.最优的预处理算子应为Hessian矩阵的逆,但计算量巨大,直接求取并不现实.本文用背景波场的能量来近似Hessian矩阵的对角元素,在减少计算量的同时加速了收敛速度.
3 随机最优化相位编码技术由于LSRTM需要多次迭代,且每次迭代都是常规逆时偏移计算量的2.5倍,因而庞大的计算量限制了该方法的推广应用.考虑到其计算量与炮数成线性关系,因而与面炮偏移(张叔伦和孙沛勇,2002;赵景霞等,2006)思想类似,通过相位编码技术(Romero et al., 2000)将多个炮集组合成一个超道集,可有效地减小计算量,在此基础上应用共享存储并行编程(OpenMP)技术,可进一步提高计算效率.相比于静态编码技术,动态编码在迭代过程中可以更好地压制由于相位编码引入的串扰噪声(Schuster et al., 2011).本文选用的编码方式为震源极性编码,编码函数为
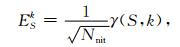
|
(19) |
其中,Nnit为总迭代次数,S为当前炮号,k为当前迭代次数,γ为随机的±1,在每次迭代中随机生成.
利用上述编码函数组合得到的超道集可表示为

|
(20) |
其中,S为炮号,ES为编码函数,dS为第S炮的数据,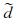


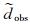
Moghaddam等(2013)研究发现相位编码算法的目标泛函是真实目标泛函的随机无偏估计,其梯度也是如此.由于相位编码LSRTM的梯度是随机的,因而其步长也应该是随机的.然而,目前相位编码LSRTM求解时仍然采用与传统LSRTM算法相同的确定性最优化解法,例如最速下降法、共轭梯度法等,忽略了梯度和步长的随机性.随机最优化解法是一类考虑了搜索方向随机性的迭代算法,主要有三种实现方案:一是加权平均之前的更新模型,二是加权平均之前的梯度,三是加权平均Hessian算子.Moghaddam等将随机最优化解法应用到全波形反演中,得到了较好的效果.本文借鉴随机最优化的思想,将其推广到基于一阶速度-应力方程的MLSRTM中,通过加权平均之前和梯度,从而减小了梯度的随机波动.
鉴于当前迭代次数下计算的梯度相比之前迭代计算的梯度更加准确,因而简单的算术平均是不可取的,研究发现指数衰减加权平均是一种较为合适的方案.优化后的梯度表达式为
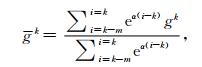
|
(21) |
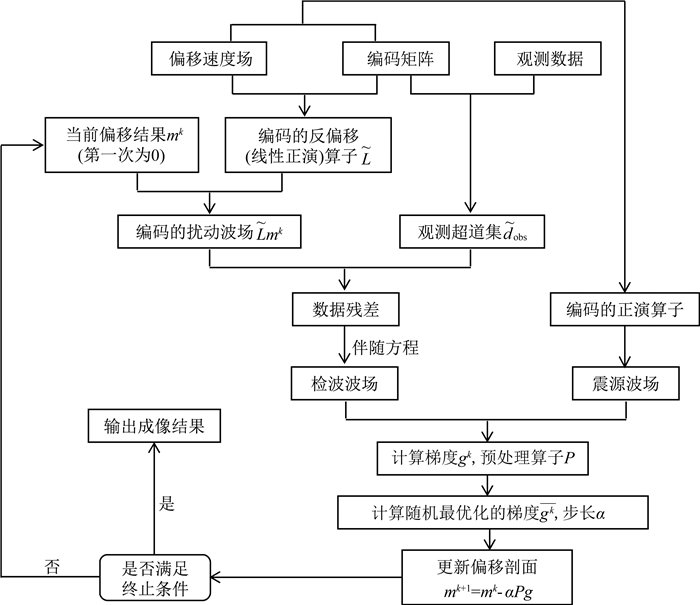
其中,k为当前迭代次数;m为加权的前期迭代次数,综合考虑效率和效果,令其等于10;α为衰减因子,经过大量试算,取为0.4,具体的计算流程如图 1所示.
|
图 1 相位编码LSRTM计算流程图 Fig. 1 Flowchat of LSRTM with phase-encoding |
本文以SEG/EAGE盐丘模型为例,来验证算法的正确性及有效性.盐丘速度场如图 2a所示,对应的扰动模型如图 2b所示,采用Gardner公式给出相应的密度场,计算公式为ρ=0.31ν0.25.从图 2可以看出,盐丘模型中存在高速异常体,通过对盐下弱照明区域的成像分析,可用于检验成像算法的优劣.模型参数如下:横向网格点数为645,纵向网格点数为150,纵横向网格间距都是20 m.计算参数为:在地表以40 m间隔均匀分布320炮,每炮都是645个检波点全接收,震源为主频18 Hz的雷克子波,时间采样间隔1.4 ms,最大记录时间4.2 s.

|
图 2 盐丘模型(a)速度场; (b)扰动模型. Fig. 2 Salt model (a) Velocity model; (b) Slowness perturbation. |
需要说明的是,在相同计算参数下,交错网格相比规则网格算法不仅频散压制更好,且精度更高,同相轴更加清晰.因而在相同精度和频散要求下,交错网格算法允许的空间网格步长更大,可在一定程度上节省计算量.进一步来说,对相同的观测记录进行LSRTM成像时,由于交错网格算法精度更高,因而可允许的计算参数较宽松;若交错网格和规则网格都采用相同的计算参数,则可能规则网格算法由于精度低、频散等,而不能很好地匹配观测数据,从而得不到好的成像效果.
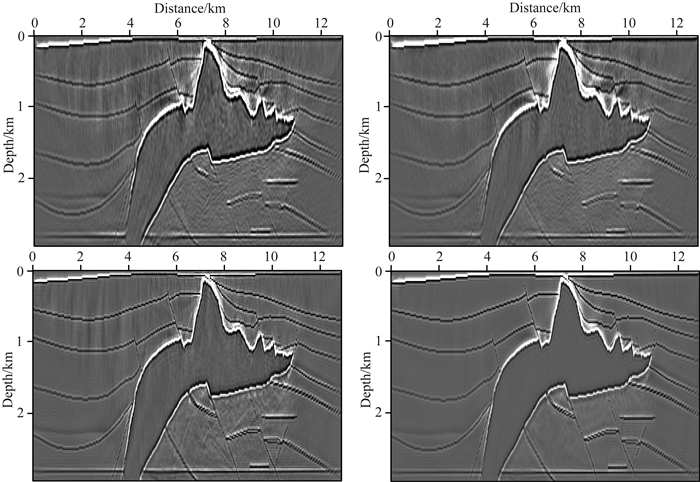
首先进行成像试算,用以测试算法的正确性和有效性.为了减小计算量、提高计算效率,利用动态编码技术将320炮组合为一个超道集.对相同的正演数据(考虑密度的影响),分别采用常规LSRTM和本文算法做成像试算,两种算法的所有计算参数都一样,得到的结果如图 3所示.图 3左栏为常规LSRTM迭代20次和80次结果,右栏为本文一阶方程LSRTM迭代20次和80次结果.对比图 3左、右两栏可以看出,常规LSRTM结果中存在很多噪声,即使随着迭代次数的增大,由相位编码引入的高频串扰噪声得到有效压制,但在盐丘的上下仍然存在较强的偏移噪声,这是由于没有考虑密度变化所产生的影响.而本文算法随着迭代次数的增多,低频噪声和高频串扰噪声都得到了有效压制,且照明补偿效果明显,盐下成像得到很大的提高,成像分辨率也较高,与真实反射率模型十分接近.
|
图 3 成像结果.左栏:常规LSRTM,右栏:本文算法.上下分别为第20次和第80次迭代结果 Fig. 3 Image result. Left: convertional LSRTM, Right: our method. Top and Bottom is the 20th and 80th times iteration respectively |
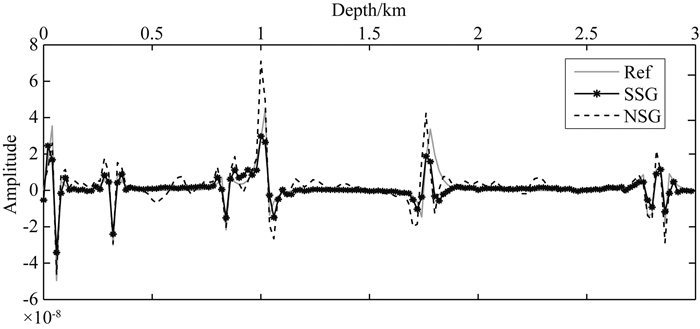
图 4为横向6 km处的单道波形对比图,其中实线为真实反射率曲线,破折线为常规LSRTM迭代80次结果,点线为本文算法迭代80次结果.从中可以看出,本文算法得到的慢度扰动曲线逐渐向真实曲线靠拢,而常规LSRTM由于没有考虑密度的影响,在迭代过程中将振幅差异都归咎于慢度扰动,因而得到的慢度扰动曲线振幅比真实曲线更大.此外,从图 4还可以看出,常规LSRTM在真实曲线的零振幅处存在较大的非零波动,对应于图 3左下图中的盐丘上、下部的偏移噪声,究其原因主要有两个方面:一是相同计算参数下常规网格比交错网格频散更为严重;二是由于不考虑密度的常规LSRTM数据匹配更慢,而相位编码技术在较好的匹配数据下能够更快地压制串扰噪声,因而图 4中的非零波动也包括相位编码引入的串扰噪声.上述试算验证了在处理变密度介质时,本文算法相比常规LSRTM具有更高的保真性,有利于后续的反演解释.
|
图 4 成像结果与真实慢度扰动曲线对比 Fig. 4 Comparsion of image result and true slowness perturbation |
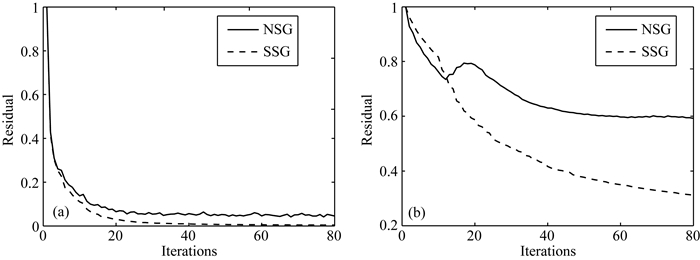
图 5为归一化后的数据残差(图 5a)和模型残差(图 5b)随迭代次数的变化曲线,其中实线(图中NSG)为常规LSRTM,破折线(图中SSG)为本文算法.可以看出,随着迭代次数的增加,两种算法的残差都逐渐减小,且一开始下降趋势明显,随着迭代次数的进一步增大,下降趋势减慢.由于目标泛函是数据空间的拟合,因而数据残差相比模型残差能收敛到更低的值.本文算法相比常规LSRTM,不论是数据残差还是模型残差都能更快地收敛到较低的值,尤其是模型残差曲线更能反映出本文算法的优势,由于考虑了密度的影响,能够完全匹配实际的振幅,从而可以得到更好的结果.
|
图 5 残差曲线(a)数据残差; (b)模型残差. Fig. 5 The normalized error residual (a) The data residual; (b) The model residual. |
以上模型试算所考虑的都是变密度介质,若假设密度为常数,则常规LSRTM和本文LSRTM得到的结果基本相同,只是由于相同计算参数下规则网格的频散更严重,对结果略有影响,为此在常规LSRTM中采用更高阶的空间精度延拓算子,得到的成像结果和图 3右下图(本文LSRTM)近乎相同,从而说明了在常密度假设下,常规LSRTM能够得到真振幅的成像结果,本文算法的优势主要体现在非均匀变密度介质下,且对弹性波LSRTM有一定的指导意义.
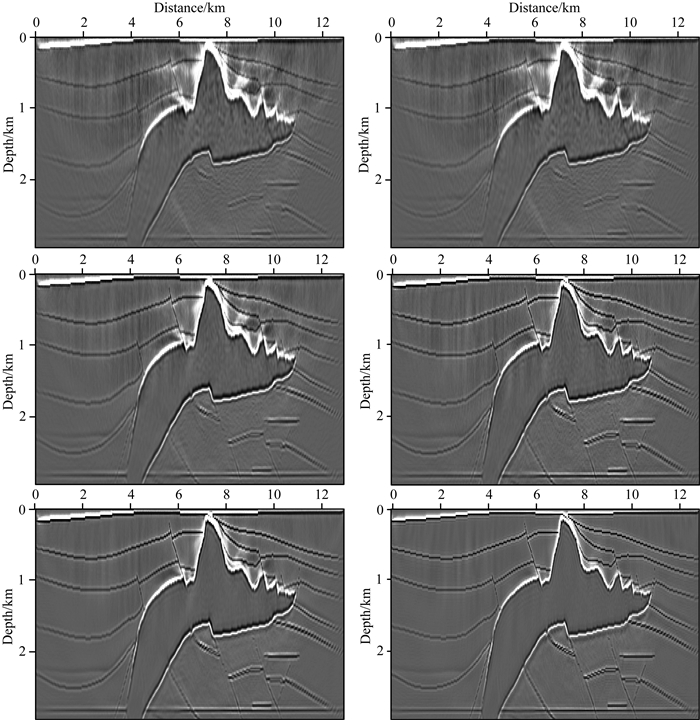
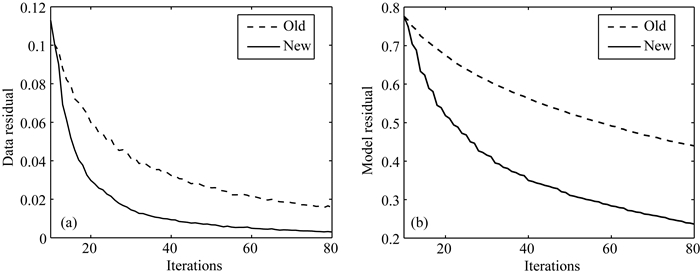
4.2 随机最优化MLSRTM本节仍然以SEG/EAGE盐丘模型为例,来验证本文随机最优化相位编码LSRTM算法的正确性和有效性.计算参数和4.1节完全相同,采用传统极性编码得到的第10次、第30次和第80次LSRTM结果分别如图 6左栏所示,图 6右栏从上到下依次为随即最优化极性编码LSRTM迭代10次、30次和80次反演成像结果.对比图 6可知,两种算法的第10次迭代结果完全相同,这是由于本文优化算法的梯度是前10次迭代梯度的加权平均(即公式(21)中m=10),因而从第11次开始才有所改变.对比两种算法在第30次和第80次的成像结果,可以看出,优化算法相比传统算法成像效果有了明显改善,尤其是在盐丘顶部,不仅成像分辨率得到提高,且低频噪声得到更好的压制.相应的两种算法的数据残差和模型残差曲线,分别如图 7a和7b所示,其中虚线为传统算法,实线为本文算法.从图 7可以清楚发现,本文算法的误差收敛更快,尤其是模型残差曲线,在第30次迭代时的成像效果已经优于传统算法第80次的成像效果,即采用本文算法所需迭代次数更少,从而可显著节约计算量、提高计算效率.
|
图 6 相位编码LSRTM反演成像结果左栏:传统算法,右栏:随机最优化算法.从上到下依次为第10次、第30次和第80次结果. Fig. 6 Image result of the MLSRTM Left: convertional LSRTM, Right: our method. Top and Bottom is the 10th、30th and 80th times iteration respectively. |
|
图 7 (a)数据残差曲线; (b)模型残差曲线 Fig. 7 The normalized error residual. (a) is the data residual, (b) is the model residual |
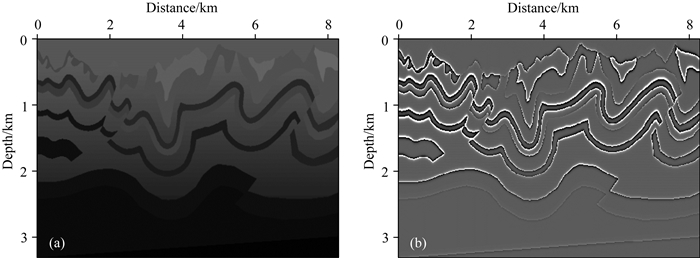
逆掩断层模型作为标准复杂速度模型,存在较为明显的近地表起伏和强横向变速,可验证算法在复杂介质情形下的可行性和适用性.其速度场如图 8a所示,对应的扰动模型如图 8b所示.本文采用Gardner公式给出相应的密度场,计算公式为ρ=0.31ν0.25,由于需要考虑密度的影响,因而常规LSRTM算法不再适用,而本文算法则可以非常方便地处理非均匀变密度介质.模型参数如下:横向网格点数为834,纵向网格点数334,网格间距为10 m.计算参数为209炮均匀分布于地表,炮间距为40 m,每炮834道,道间距10 m.震源采用主频30 Hz的雷克子波,时间采样间隔为0.7 ms,最大记录时间为4.2 s.
|
图 8 逆掩断层模型(a)速度场; (b)扰动模型. Fig. 8 Overthrust model (a) Velocity model; (b) Slowness perturbation. |
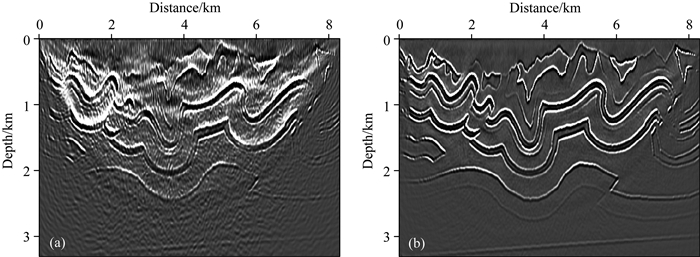
同样将209炮编码组合为一个超道集,然后采用本文一阶方程LSRTM算法迭代更新,图 9a、9b分别为第10次和80次迭代结果.对比图 9可知,可以得到相同的结论,随着迭代次数的增加,成像分辨率提高、低频噪声和串扰噪声减小、振幅保真性增强,且逆掩构造刻画非常清晰,从而验证了本文算法对复杂模型的适用性.
|
图 9 本文算法LSRTM成像结果(a)第10次迭代结果; (b)第80次迭代结果. Fig. 9 Image result obtined by our method (a) 10 times iteration; (b) 80 times iteration. |
本文推导并实现了基于一阶速度-应力方程的多震源最小二乘逆时偏移算法.通过理论分析和模型试算,得到了如下几点结论与认识:
(1)目前的LSRTM研究大多是基于二阶常密度标量声波方程展开的,无法处理非均匀变密度介质.本文提出的算法由于可采用交错网格,因而相比于规则网格算法具有更高的精度,能够更好压制数值频散,且更易于处理强非均匀变密度介质,从而更加符合地下实际情况,有一定的研究价值.
(2)一阶速度-应力方程LSRTM算法相比于常规二阶方程LSRTM算法的最大不同在于伴随算子的差异,常规LSRTM的伴随方程与正演方程相同,而一阶方程LSRTM则不然,因而直接将一阶速度-应力方程简单地用于常规LSRTM的波场延拓中是不合适的.
(3)随机最优化算法考虑了梯度的随机特性,每次迭代的梯度都是之前迭代梯度的指数衰减加权平均,减小了梯度的随机波动,相比传统相位编码算法收敛更快,因而可节省计算成本、提高计算效率.
虽然本文算法的优势较为明显,但也应该看到,本文仅仅是初步推导了基于一阶速度-应力方程的LSRTM算法,未来还需深入研究.例如,研究如何将其推广到GPU等快速计算设备(刘红伟等,2010)上,进一步提高计算效率;研究预条件和正则化算子等,增加算法的稳定性和加快收敛速度;考虑如何将其应用于实际资料中.由于本算法采用一阶速度应力方程,因而具有多变量和多方程的特性,这为弹性波LSRTM奠定了一定的基础,这也是本文未来的研究方向.
致谢感谢Madagascar软件(http://www.reproducibility.org)提供的绘图支持,特别感谢两位评审专家为本文完善提出的宝贵意见,感谢贵刊编辑对本文修改给予的帮助.
| Claerbout J F. Earth Soundings Analysis: Processing Versus Inversion.Boston: Blackwell Scientific Publications, 1992. | |
| Clapp M L, Clapp R G, Biondi B L. 2005. Regularized least-squares inversion for 3-D subsalt imaging.//75th Annual International Meeting, SEG, Expanded Abstracts, 1814-1817. | |
| Dai W, Wang X, Schuster G T. 2011. Least-squares migration of multisource data with a deblurring filter. Geophysics, 76(5): R135-R146. DOI:10.1190/geo2010-0159.1 | |
| Dai W, Fowler P, Schuster G T. 2012. Multi-source least-squares reverse time migration. Geophysical Prospecting, 60(4): 681-695. DOI:10.1111/gpr.2012.60.issue-4 | |
| Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys., 43(3): 411-419. | |
| Guo Z B, Li Z C. 2014. True-amplitude imaging based on least-squares reverse time migration. Oil Geophysical Prospecting, 49(1): 113-120. | |
| Huang J P, Li Z C, Kong X, et al. 2013. A study of least-squares migration imaging method for fractured-type carbonate reservoir. Chinese J. Geophys., 56(5): 1716-1725. DOI:10.6038/cjg20130529 | |
| Huang J P, Cao X L, Li Z C, et al. 2014. Least square reverse time migration in high resolution imaging of near surface. Oil Geophysical Prospecting, 49(1): 107-112. | |
| Kühl H, Sacchi M D. 2003. Least-squares wave-equation migration for AVP/AVA inversion. Geophysics, 68(1): 262-273. DOI:10.1190/1.1543212 | |
| Li Z C, Guo Z B, Tian K. 2014. Least-squares reverse time migration in visco-acoustic medium. Chinese J. Geophys., 57(1): 214-228. DOI:10.6038/cjg20140118 | |
| Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys., 53(7): 1725-1733. DOI:10.3969/j.issn.0001-5733.2010.07.024 | |
| Liu Y J, Li Z C, Wu D, et al. 2013. The research on local slope constrained least-squares migration. Chinese J. Geophys., 56(3): 1003-1011. DOI:10.6038/cjg20130328 | |
| McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 31(3): 413-420. DOI:10.1111/gpr.1983.31.issue-3 | |
| Moghaddam P P, Keers H, Herrmann F J, et al. 2013. A new optimization approach for source-encoding full-waveform inversion. Geophysics, 78(3): R125-R132. DOI:10.1190/geo2012-0090.1 | |
| Nemeth T, Wu C J, Schuster G T. 1999. Least-squares migration of incomplete reflection data. Geophysics, 64(1): 208-221. DOI:10.1190/1.1444517 | |
| Romero L A, Ghiglia D C, Ober C C, et al. 2000. Phase encoding of shot records in prestack migration. Geophysics, 65(2): 426-436. DOI:10.1190/1.1444737 | |
| Schuster G T, Wang X, Huang Y, et al. 2011. Theory of multisource crosstalk reduction by phase-encoded statics. Geophysical Journal International, 184(3): 1289-1303. DOI:10.1111/gji.2011.184.issue-3 | |
| Shen X J, Liu N C. 2012. Split-step least-squares migration. Progress in Geophysics, 27(2): 761-770. DOI:10.6038/j.issn.1004-2903.2012.02.044 | |
| Tang Y X. 2009. Target-oriented wave-equation least-squares migration/inversion with phase-encoded hessian. Geophysics, 74(6): WCA95-WCA107. DOI:10.1190/1.3204768 | |
| Tarantola A. 1984. Linearized inversion of seismic reflection data. Geophysical Prospecting, 32(6): 998-1015. DOI:10.1111/gpr.1984.32.issue-6 | |
| Virieux J. 1986. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics, 51(4): 889-901. DOI:10.1190/1.1442147 | |
| Wang J, Zhou H, Tian Y K, et al. 2012. A new scheme for elastic full waveform inversion based on velocity-stress wave equations in time domain.//82st Annual International Meeting, SEG, Expanded Abstract, 1-5. | |
| Wong M, Ronen S, Biondi B. 2011. Least-squares reverse time migration/inversion for ocean bottom data: A case study.//81st Annual International Meeting, SEG, Expanded Abstracts, 2369-2373. | |
| Yang Q Q, Zhang S L. 2008. Least-squares Fourier finite-difference migration. Progress in Geophysics, 23(2): 433-437. | |
| Zhang S L, Sun P Y. 2002. A fast pre-stack depth migration on areal shot records. Oil Geophysical Prospecting, 37(4): 333-338. | |
| Zhao J X, Zhang S L, Sun P Y, et al. 2006. 3-D parallel prestack depth migration of synthetic source records. Chinese J. Geophys., 49(1): 225-233. | |
| Zhou H M, Chen S C, Ren H R, et al. 2014. One-way wave equation least-squares migration based on illumination compensation. Chinese J. Geophys., 57(8): 2644-2655. DOI:10.6038/cjg20140823 | |
| 董良国, 马在田, 曹景忠, 等. 2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411–419. | |
| 郭振波, 李振春. 2014. 最小平方逆时偏移真振幅成像. 石油地球物理勘探, 49(1): 113–120. | |
| 黄建平, 李振春, 孔雪, 等. 2013. 碳酸盐岩裂缝型储层最小二乘偏移成像方法研究. 地球物理学报, 56(5): 1716–1725. DOI:10.6038/cjg20130529 | |
| 黄建平, 曹晓莉, 李振春, 等. 2014. 最小二乘逆时偏移在近地表高精度成像中的应用. 石油地球物理勘探, 49(1): 107–112. | |
| 李振春, 郭振波, 田坤. 2014. 黏声介质最小平方逆时偏移. 地球物理学报, 57(1): 214–228. DOI:10.6038/cjg20140118 | |
| 刘红伟, 李博, 刘洪, 等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报, 53(7): 1725–1733. DOI:10.3969/j.issn.0001-5733.2010.07.024 | |
| 刘玉金, 李振春, 吴丹, 等. 2013. 局部倾角约束最小二乘偏移方法研究. 地球物理学报, 56(3): 1003–1011. DOI:10.6038/cjg20130328 | |
| 沈雄君, 刘能超. 2012. 裂步法最小二乘偏移. 地球物理学进展, 27(2): 761–770. DOI:10.6038/j.issn.1004-2903.2012.02.044 | |
| 杨其强, 张叔伦. 2008. 最小二乘傅立叶有限差分偏移. 地球物理学进展, 23(2): 433–437. | |
| 张叔伦, 孙沛勇. 2002. 快速面炮记录叠前深度偏移. 石油地球物理勘探, 37(4): 333–338. | |
| 赵景霞, 张叔伦, 孙沛勇, 等. 2006. 三维并行合成震源记录叠前深度偏移. 地球物理学报, 49(1): 225–233. | |
| 周华敏, 陈生昌, 任浩然, 等. 2014. 基于照明补偿的单程波最小二乘偏移. 地球物理学报, 57(8): 2644–2655. DOI:10.6038/cjg20140823 | |
 2016, Vol. 59
2016, Vol. 59

