地震波数值模拟中,首先要做的就是对模型进行网格剖分,网格质量对方程求解的精度和效率都起着至关重要的作用.传统意义下好的网格性质,如大小均匀、长宽适当、相互正交等,有时并不能获得精确的数值解.人们通过研究证实,依据物理问题中参数的变化来构造网格,往往能够获得与物理问题更相适应、更高精度的数值解.用变分法来构造网格的思想最早由Barfield (1970)提出.Brackbill和Saltzman (1982)基于Barfield (1970)的思想,给出了描述网格疏密性、正交性和光滑性的泛函.Antonios (1988)对Brackbill和Saltzman (1982)的方法进行了改进,提出了一种带方向控制的泛函来控制网格走向的方法.在国内也有很多人对该方法进行了相关研究.康红文等(2002)对自适应网格中的权函数进行了研究.于明(2004)在前人的基础上改进了光滑性控制的变分表达式,使其与疏密程度和正交性控制方程具有一致的量纲,并且添加了网格正规性的控制方程.
满足地质模型要求的曲线网格生成后,就需要在这些离散点上计算波场.有限差分法简单灵活,是地球物理中最常用的数值计算方法.有限差分法地震波数值模拟由Alterman和Karal (1968)提出.Boore (1972)和Kelly等(1976)将该方法推广至非均匀介质.但是他们的有限差分法存在计算精度低,容易导致计算不稳定等问题.Madariaga (1976)首次提出了在交错网格中求解一阶速度-应力弹性波方程的算法来提高有限差分法的精度和稳定性.Virieux (1984)将该方法推广到非均匀介质地震波数值模拟中.Crase (1990)给出了基于交错网格系统的高阶差分格式.传统有限差分法采用矩形网格对模型进行网格剖分,由于矩形网格自身的限制,起伏的海底界面只能由一系列的阶梯状折线代替,从而造成数值模拟过程中的人为虚假绕射波.此外,在模拟液-固构造下的地震波场时,如果界面与网格线不一致,则在界面处需要更细的网格才能得到精确的结果(van Vossen et al., 2002).因此,对于传统的规则网格有限差分法需要对整个计算区域采用较密的网格,而这不仅增加了内存需求而且降低了计算效率.为了解决上述问题,Moczo (1989)提出了可变网格的思想;Jastram和Behle (1992)将变网格的思想运用到声波方程数值模拟中;Jastram和Tessmer (1994)将该思想运用到弹性波数值模拟中,提出了纵向网格步长逐渐变化的算法;朱生旺等(2007)将该算法的空间差分精度进一步提高,使该算法的模拟精度和灵活性更高.但由于它们依旧是基于规则网格实现的,并不能从根本上消除阶梯状网格引起的虚假绕射波.为此人们发展了不规则网格有限差分法.Opršal和Zahradniík (1999)给出了非规则介质中的二阶波动方程的矩形不规则网格差分方法.Pitarka (1999)提出了各项同性介质中矩形不规则网格的有限差分方法.张剑锋(1998)通过坐标映射得到了非规则网格差分方法.但是他们的方法计算精度较低.
为了有效消除人为虚假绕射波,本文将基于变分原理的自适应网格生成技术引入到起伏海底速度模型的网格剖分中,采用曲线坐标系下的高阶仿真型有限差分法对声波方程进行了数值模拟.该方法生成的网格具有以下特点:(1)可以更加准确地描述模型界面; (2)可以尽量保证网格的光滑性和正交性; (3)网格剖分更加合理.高阶仿真型有限差分法可以有效压制数值频散、提高计算精度.
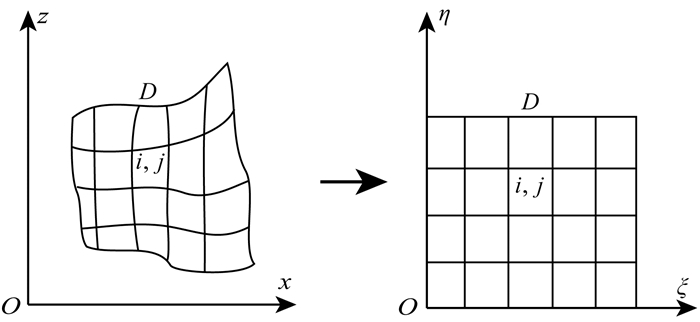
2 方法原理 2.1 自适应网格生成考虑任意形状的物理域(x, z)通过坐标变换可以转换到直角四边形的计算域(ξ, η)(如图 1),那么存在坐标系变换的Jacobi式J=xξzη-xηzξ,并且成立坐标变换
|
图 1 网格映射示意图 Fig. 1 The sketch map of grid mapping |
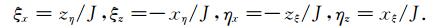
|
(1) |
根据微分几何理论,J表示两个坐标系中面积微元之比,即dxdz=|J|dξdη. |J|的大小能反映网格疏密程度,可以用J和一个用来调节网格疏密的权函数w(x, z)的乘积来调节整个物理域网格的疏密性(Brackbill,1982):
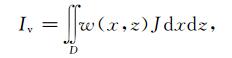
|
(2) |
式中w(x, z)为加权函数,D为整个模型区域.
定义表示映射后坐标光滑性的泛函:
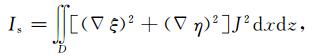
|
(3) |
定义表示网格正交性的泛函:
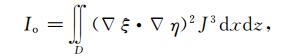
|
(4) |
通常,生成自适应网格时需要同时考虑所有性质.故加权组合上述泛函取极小值时的Euler方程展开式,可得(见附录A):
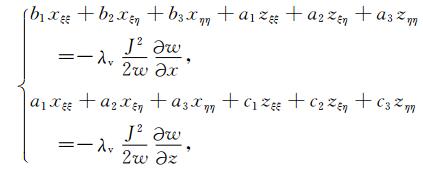
|
(5) |
式中

|
λv, λs, λo为正的加权系数(可以根据问题的需要来选择数值大小).
式(5)即为最终得到的自适应网格生成控制方程,可以采用Gauss-Seidel法来求解.权函数w(x, z)可以根据具体问题选取, 本文以速度模型的梯度来构造权函数.可令权函数为
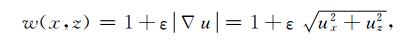
|
(6) |
式中ε为用来调整权函数的大小的系数,ux是速度的横向梯度,uz是速度的纵向梯度.
2.2 曲线坐标系下的高阶仿真型有限差分设物理平面(x, z)和计算平面(ξ, η)存在如下的一一对应关系:
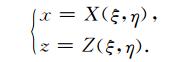
|
(7) |
根据链式法则,变量u的一阶导数和二阶导数可表示成如下形式:
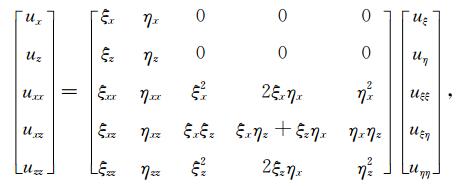
|
(8) |
式中,下角标ξ表示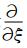
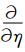
利用这些导数可以求得梯度(GRID)、散度(DIV)和拉普拉斯(LAP)算子的差分近似,但是该方法不仅方程复杂而且很难保证解的物理性质.因此我们用映射法和支撑算子法来建立不规则坐标系下的DIV和GRID的仿真型有限差分近似.
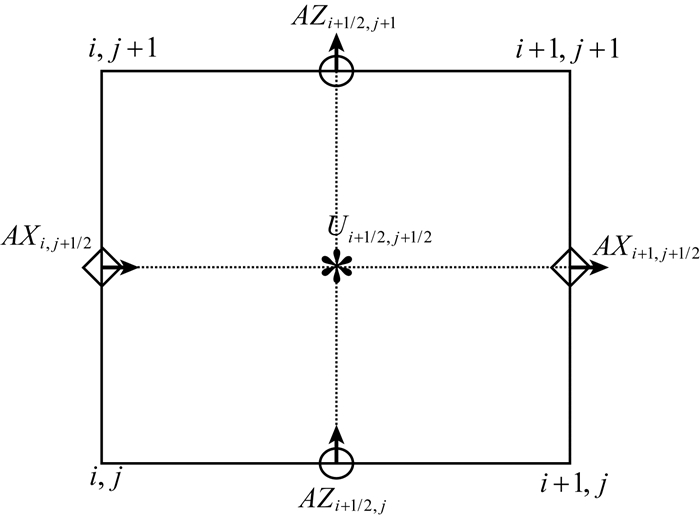
定义离散函数空间Hξ和Hη来表示向量A=(AX, AZ)的水平分量和垂直分量;定义离散空间HC表示标量U.它们在笛卡尔坐标系下的分布如图 2所示.
|
图 2 离散函数的空间分布 Fig. 2 The spatial distribution of the discrete function |
为了获得二维曲线坐标系下DIV和GRAD差分近似,我们需要一维差分算子和映射算子.∂/∂ξ的差分算子可分为如下两种类型:
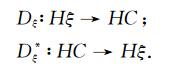
|
则四阶差分算子的具体形式如下(Castillo et al, 2000):

|
(9) |
式中Aξ表示向量A的水平分量,U表示标量.
同理我们可以得到差分算子Dη和Dη*:
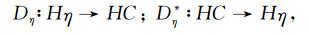
|
具体形式如下:
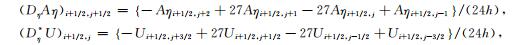
|
(10) |
式中Aη表示向量A的垂直分量,U表示标量.
定义映射算子:
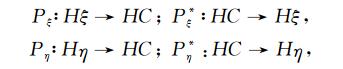
|
具体形式如下:

|
(11) |
如果我们知道坐标系转换关系及其导数,那么我们就可以得到二维曲线坐标系下DIV的四阶差分近似:
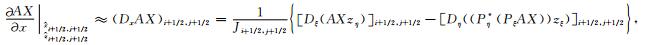
|
(12) |
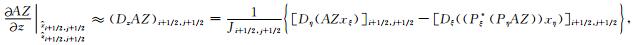
|
(13) |
式中AX, AZ是向量A的水平分量和垂直分量,
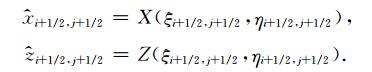
|
利用支撑算子法得到GRID的离散近似(见附录B).
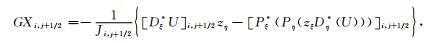
|
(14) |
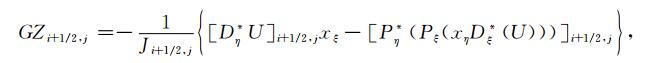
|
(15) |
式中GXi, j+1/2, GZi+1/2, j为梯度的水平分量和垂直分量.
3 曲线坐标系下的声波方程数值求解非均匀各项同性介质中的一阶声波方程为
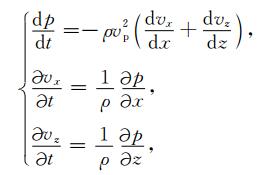
|
(16) |
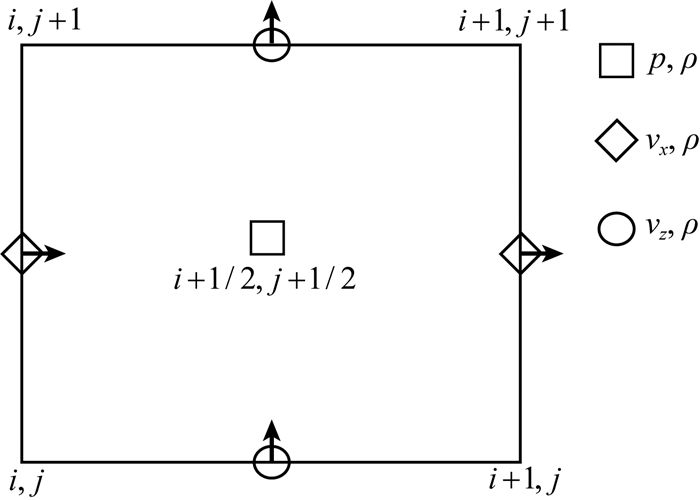
其中,p为压强,vx,vz为质点速度,ρ是密度,vp是纵波速度.它们在笛卡尔坐标系下的分布如图 3.
|
图 3 一阶声波方程的变量分布 Fig. 3 The variable distribution of first-order acoustic equation |
利用四阶仿真型有限差分求解方程(16)中的空间导数得

|
(17) |
把方程(16)改写成如下形式:
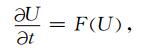
|
(18) |
式中U=(p, vx, vz),F是关于波场变量U的函数.
令Un=U(nΔt),则可用p步显式Runge-Kutta算法对方程(19)进行迭代求解(Bogey,2004):
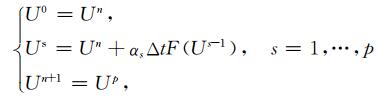
|
(19) |
其中,αs是Runge-Kutta算法的系数,Δt是时间步长.
4 模型试算下面给出五个模型算例,用以验证本文方法的精度、有效性和适用性.第一个是均匀半空间速度模型,通过与解析解对比,用来验证本文方法的精度.第二和第三个是起伏海底两层速度模型,通过与规则网格有限差法对比,来验证方法的有效性.第四个和第五个是复杂海底速度模型,用来验证本文方法的适应性.
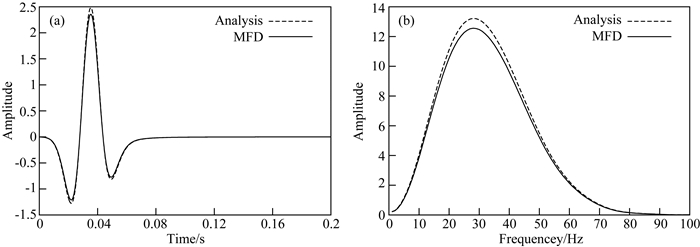
4.1 均匀速度模型首先利用本文方法对均匀半空间速度模型进行模拟.模型速度为2000 m·s-1,密度为1000 kg·m-3.数值解所用空间网格大小为10 m,时间采样间隔为1 ms, 震源是主频为30 Hz的雷克子波,位于(20 m, 20 m)处,检波点位于(120 m, 10 m).图 4a为相应的波形对比,图中Analysis曲线为Cagniard-De Hoop算法得到的解析解,MFD曲线为采用本文方法得到的数值解.由图可见, 本文方法得到的直达波与解析解基本吻合.图 4b为直达波振幅谱对比.由图可见,本文方法得到的直达波振幅谱和解析解的振幅谱基本一致.
|
图 4 均匀半空间速度模型中解析解和MFD得到的数值解对比(a)波形对比; (b)振幅谱对比. Fig. 4 The contract of analytical and MFD solution in the homogeneous half-space velocity model (a) The contract of waveform; (b) The contract of amplitude spectrum. |
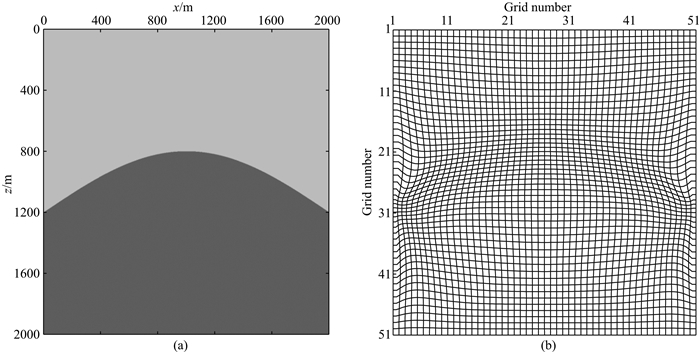
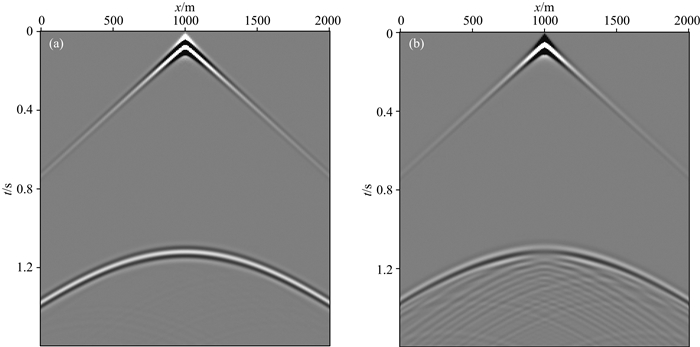
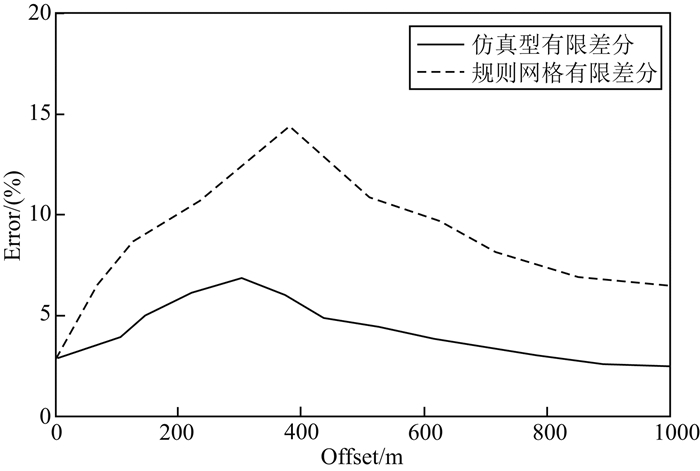
图 5a为海底单背斜速度模型,模型大小为2000 m×2000 m, 第一层速度为1500 m·s-1,第二层速度为2000 m·s-1,密度为1000 m·s-1.计算域中的空间网格尺寸为10 m,时间采样间隔为1 ms,最大记录时间为1.6 s, 震源采用主频为30 Hz的雷克子波,位于(1000 m, 20 m)处,检波点深度为10 m.图 5b为利用本文方法得到的自适应网格示意图,由图可以看出,利用本文方法对海底背斜模型进行自适应网格剖分不仅可以更准确描述海底界面, 而且在界面附近有很好的密集性、光滑性和正交性.图 6为波场快照对比、图 7为模拟地震记录对比,由图可以看出,相对与规则网格有限差分法,本文方法可以有效消除阶梯状网格引起的人为虚假绕射波.图 8为不同方法得到的反射波最大振幅与解析解的误差对比;实线表示利用本文方法得到的反射波最大振幅误差,虚线表示规则网格有限差分法得到的反射波最大振幅误差.由图可以看出,相对与规则网格有限差分法,本文方法在模拟起伏海底反射波时具有更高的计算精度.
|
图 5 海底单背斜模型(a)和自适应网格示意图(b) Fig. 5 The single anticline model under the sea (a) and the sketch map of adaptive grid (b) |

|
图 6 0.8 s时的波场快照对比(a)本文方法;(b)规则网格有限差分法. Fig. 6 The contract of wavefield snapshot at 0.8 s (a) Our method; (b) Regular grid finite-difference method. |
|
图 7 模拟地震记录对比(a)本文方法;(b)规则网格有限差分法. Fig. 7 The contract of seismic record (a) Our method; (b) Regular grid finite-difference method. |
|
图 8 本文方法和规则网格有限差分法得到的反射波最大振幅误差 Fig. 8 The errors of the maximum amplitude of the reflected waves by the proposed method and the MFD method |
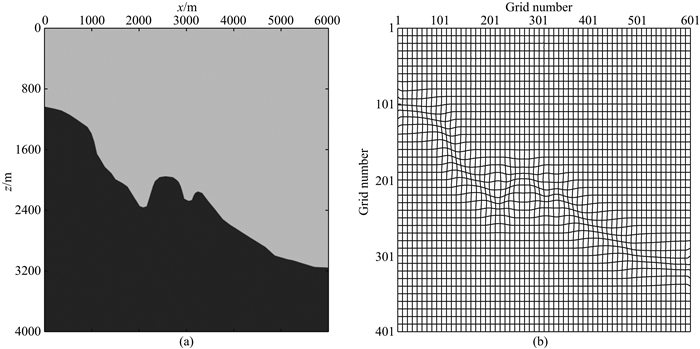
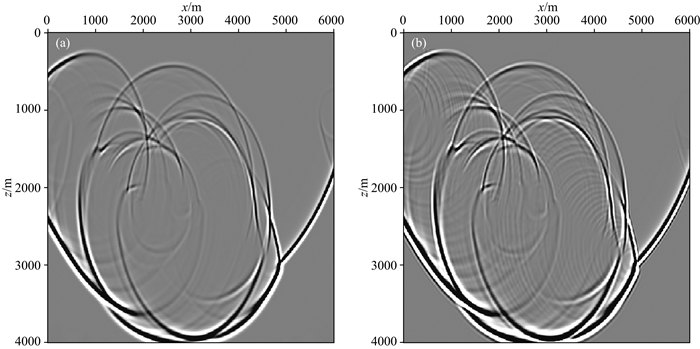
图 9a为起伏海底速度模型,模型大小为6000 m× 4000 m,第一层速度为1500 m·s-1,第二层速度为2000 m·s-1,密度为1000 m·s-1.计算域中的空间网格尺寸为10 m,时间采样间隔为1 ms,最大记录时间为6 s, 震源是主频为30 Hz的雷克子波,位于(1000 m, 20 m)处,检波点深度为10 m.图 9b为利用本文方法得到的自适应网格示意图,由图可以看出,本文提出的网格剖分法对剧烈的起伏海底同样有很好的适应性.图 10为波场快照对比,图 11为模拟地震记录对比.由图可见,本文方法相对与规则网格有限差分法不仅可以消除虚假绕射波,而且可以有效压制数值频散.
|
图 9 起伏海底模型(a)和自适应网格示意图(b) Fig. 9 Rough seabed model (a) and the sketch map of adaptive grid (b) |
|
图 10 1.2 s的波场快照对比(a)本文方法;(b)规则网格有限差分法. Fig. 10 The contract of wavefield snapshot at 1.2 s (a) Our method; (b) Regular grid finite-difference method. |

|
图 11 模拟地震记录对比(a)本文方法;(b)规则网格有限差分法. Fig. 11 The contract of seismic record (a) The seismic record of our method; (b) Regular grid finite-difference method. |
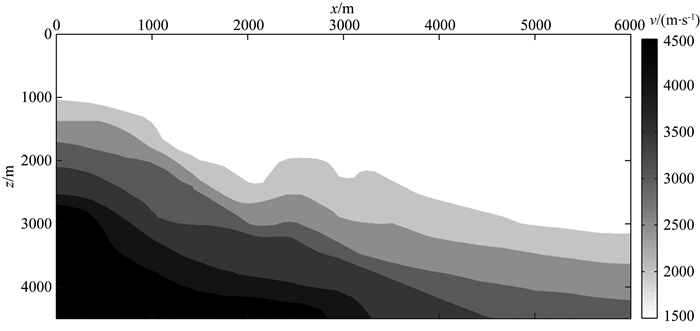
图 12为起伏海底多层模型,模型大小为6000 m× 4500 m,速度分布如图所示.计算域中的空间网格尺寸为10 m,时间采样间隔为1 ms,最大记录时间为6 s, 震源是主频为30 Hz的雷克子波,位于(3000 m, 20 m)处,检波点深度为10 m.图 13为利用本文方法得到的自适应网格示意图,由图可见,利用本文提出的自适应网格剖分法对复杂海底模型进行网格剖分不仅可以更好地描述每一层界面,而且在每个界面附近网格明显密集,从而提高了网格的分辨率.图 14为利用本文方法得到的模拟地震记录和2 s时的波场快照.由图可见,本文方法对复杂海底模型同样有很好的适应性.
|
图 12 复杂海底模型 Fig. 12 The complex sea bottom model |

|
图 13 复杂海底模型自适应网格示意图 Fig. 13 The sketch map of adaptive grid of complex seabed model |

|
图 14 本文方法得到的复杂海底模型模拟地震记录(a)和2 s时的波场快照(b) Fig. 14 The seismic record (a) and snapshot at 2 s (b) of complex seabed velocity model |
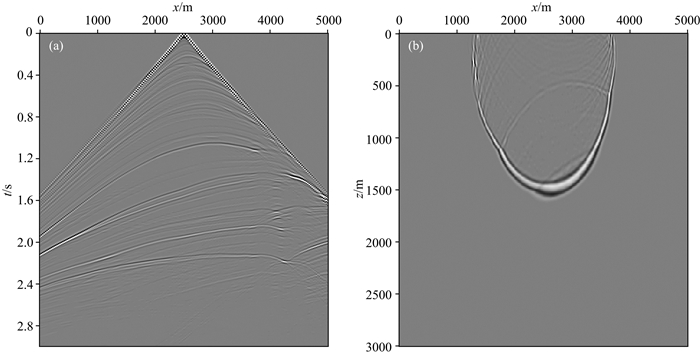
图 15为Marmousi速度模型,模型大小为10000 m×3000 m.计算域中的空间网格尺寸为10 m,时间采样间隔为1 ms,最大记录时间为3 s,震源是主频为30 Hz的雷克子波.图 16为利用本文方法得到的自适应网格示意图.由于数据量较大网格细节不能清晰展现, 但从整体上可以看出网格线在模型梯度大的区域颜色较深呈密集分布, 而在梯度小的区域颜色较浅网格线相对稀疏.图 17a为利用本文方法得到的单炮模拟地震记录,炮点位置为(3000 m, 20 m), 道间距为20 m, 一共是250道.图 17b为0.8 s时刻的波场快照.由图可以看出, 利用本文方法对Marmousi模型进行数值模拟不仅可以消除阶梯状网格引起的虚假绕射波,而且可以有效压制数值频散提高计算精度,从而验证了本文方法对复杂海底模型的强适应性.

|
图 15 Marmousi速度模型 Fig. 15 Marmsousi velocity model |

|
图 16 Marmousi模型自适应网格示意图 Fig. 16 The sketch map of adaptive grid of Marmousi |
|
图 17 Marmousi模型单炮模拟地震记录(a)和0.8 s时的波场快照(a) Fig. 17 Single-shot seismic record (a) and snapshot at 2 s (b) of Marmousi model |
为了有效消除规则网格有限差分法引起的虚假绕射波,本文将自适应网格生成技术引入到地震波数值模拟的网格剖分中,采用仿真型有限差分法对曲线坐标系下的声波方程进行了数值模拟.通过理论分析与模型试算可以得到以下结论:(1)利用自适应网格对起伏海底进行网格剖分相对与规则网格,不仅可以更准确描述界面起伏,而且在界面附近可以加密网格.从而在不增加计算量的前提下消除阶梯状网格引起的虚假绕射波.(2)高阶仿真型有限差分法相对于规则网格有限差分法可以有效降低数值频散、提高计算精度.(3)相对于规则网格有限差分法,本文方法在相对较大的网格间距下同样可以有效消除阶梯网格引起的绕射波,从而可以有效减少内存,提高计算效率.
6 附录A 自适应网格生成方法定义表示映射后坐标疏密性的泛函(Brackbill, 1982)
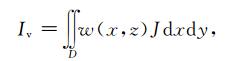
|
(A1) |
式中(x, z)为物理平面上的网格点,w(x, z)为加权函数,J为雅克比行列式,D为整个模型区域.
对式(A1)变量代换,该泛函变为
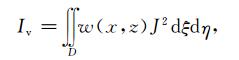
|
(A2) |
泛函(A2)对应变分问题的Euler方程为
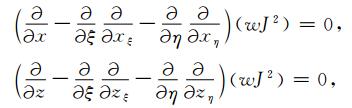
|
(A3) |
将(A3)式展开后化成标准形式方程:

|
(A4) |
式中(x, z)是物理平面上的点,(ξ, η)是计算平面上的点
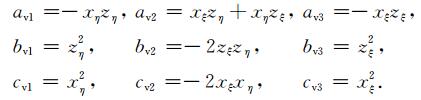
|
(A5) |
定义一个表示映射后坐标光滑性的泛函
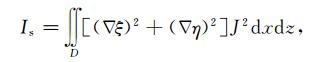
|
(A6) |
对式(A6)进行变量代换,该泛函变成
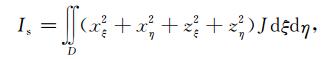
|
(A7) |
如果网格光滑性好,则式(A7)取极小值.故式(A7)的Euler方程为
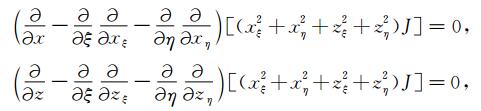
|
(A8) |
将式(A8)展开化简得
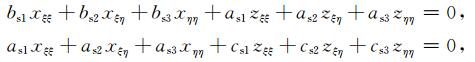
|
(A9) |
式中
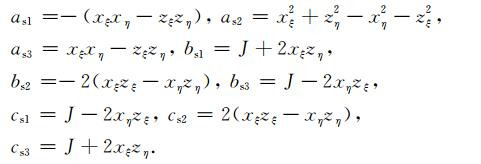
|
(A10) |
在考虑网格的正交性,定义表示坐标正交程度的泛函
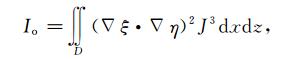
|
(A11) |
对式(A11)变量代换,该泛函变成
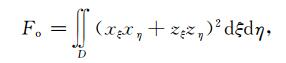
|
(A12) |
式(A12)变分问题的Euler方程为
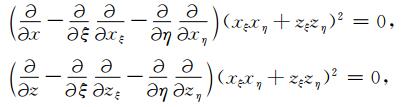
|
(A13) |
将式(A13)展开并化成标准形式方程
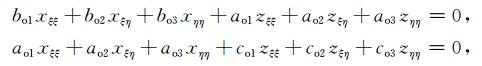
|
(A14) |
式中
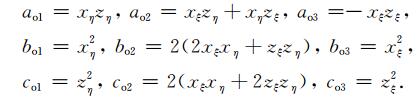
|
(A15) |
通常,生成自适应网格时需要同时考虑所有性质.设表示网格疏密性,光滑性和正交性的正的加权系数λv, λs, λo,做代数运算λv×(A4)+λs×(A9)+λo×(A14)得
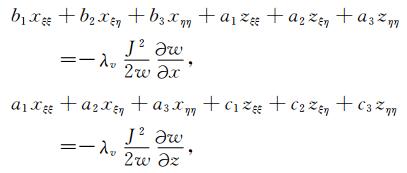
|
(A16) |
式中
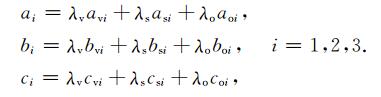
|
在支撑算子法中散度和梯度满足如下的积分关系:
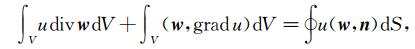
|
(B1) |
式(B1)的左边积分也可以写成如下内积形式:
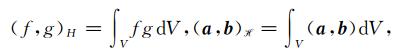
|
(B2) |
如果方程在边界上的积分等于零则(B1)式变为

|
(B3) |
因此微分算子div和grad互为负共轭:
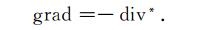
|
(B4) |
根据链式法则向量A=(AX, AZ)在(ξ, η)坐标系下的散度为
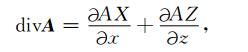
|
(B5) |
式中
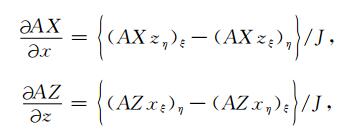
|
(B6) |
把(B5)式带到(B1)式的第一项中得
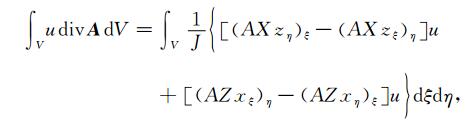
|
(B7) |
把(B6)式的第二项写成如下形式:
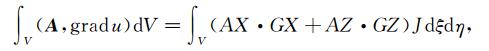
|
(B8) |
利用分步积分法求(B7)并与(B8)比较得
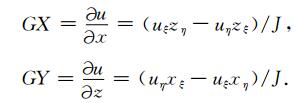
|
(B9) |
| Alterman Z, Karal F C. 1968. Propagation of elastic waves in layered media by finite difference methods. Bulletinof the Seismological Society of America, 58(1): 367-398. | |
| Antonios E G, Antonie J E. 1988. Directional control in grid generation. Journal of Computational Physics, 74(2): 422-439. DOI:10.1016/0021-9991(88)90086-1 | |
| Barfield W D. 1970. An optimal mesh generator for Lagrangian hydrodynamic calculations in two space dimensions. Journal of Computational Physics, 6(3): 417-429. DOI:10.1016/0021-9991(70)90040-9 | |
| Bogey C, Bailly C. 2004. A family of low dispersive and low dissipative explicit schemes for flow and noise computations. Journal of Computational Physics, 194(1): 194-214. DOI:10.1016/j.jcp.2003.09.003 | |
| Boore D M. 1972. Finite difference methods for seismic wave propagation in heterogeneous materials. Methods in Computational Physics, 11: 1-37. | |
| Brackbill J U, Saltzman J S. 1982. Adaptive zoning for singular problems in two dimensions. Journal of Computational Physics, 46(3): 342-368. DOI:10.1016/0021-9991(82)90020-1 | |
| Castillo J E, Hyman J M, Shashkov M J, et al. 2000. High-order mimetic finite difference methods on nonuniform grids.//Proceedings of the Third International Conference on Spectral and High Order Methods. Houston, Texas: Special Issue of Houston Journal of Mathematics. | |
| Crase E. 1990. High-order (space and time) finite-difference modeling of the elastic wave equation.//60th SEG Annual Meeting.San Francisco, California: Society of Exploration Geophysicists, 987-991. | |
| Jastram C, Behle A. 1992. Acoustic modelling on a grid of vertically varying spacing. Geophysical Prospecting, 40(2): 157-169. DOI:10.1111/gpr.1992.40.issue-2 | |
| Jastram C, Tessmer E. 1994. Elastic modelling on a grid with vertically varying spacing. Geophysical Prospecting, 42(4): 357-370. DOI:10.1111/gpr.1994.42.issue-4 | |
| Kang H W, Gu X Q, Liu C J. 2002. Study on weigh functions of adaptive grid technique. Acta Mechanica Sinica (in Chinese), 34(5): 790-795. | |
| Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms: A finite-difference approach. Geophysics, 41(1): 2-27. DOI:10.1190/1.1440605 | |
| Madariaga R. 1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666. | |
| Moczo P. 1989. Finite-difference technique for SH-waves in 2-D media using irregular grids-application to the seismic response problem. Geophysical Journal International, 99(2): 321-329. DOI:10.1111/gji.1989.99.issue-2 | |
| Opršal I, Zahradník J. 1999. Elastic finite-difference method for irregular grids. Geophysics, 64(1): 240-250. DOI:10.1190/1.1444520 | |
| Pitarka A. 1999. 3D elastic finite-difference modeling of seismic motion using staggered grids with nonuniform spacing. Bulletin of the Seismological Society of America, 89(1): 54-68. | |
| van Vossen R, Robertsson J O A, Chapman C H. 2002. Finite-difference modeling of wave propagation in a fluid-solid configuration. Geophysics, 67(2): 618-624. DOI:10.1190/1.1468623 | |
| Virieux J. 1984. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics, 49(11): 1933-1942. DOI:10.1190/1.1441605 | |
| Yu M. 2004. Generation of 2-D adaptive structured grids by variational methods. Chinese Journal of Computational Physics (in Chinese), 21(1): 27-34. | |
| Zhang J F. 1998. Non-orthogonal grid finite-difference method for numerical simulation of elastic wave propagation. Acta Geophysica Sinica (in Chinese), 41(S): 357-366. | |
| Zhu S W, Qu S L, Wei X C, et al. 2007. Numeric simulation by grid-various finite-difference elastic wave equation. Oil Geophysical Prospecting (in Chinese), 42(6): 634-639. | |
| 康红文, 谷湘潜, 柳崇健. 2002. 自适应网格技术中的权函数问题研究. 力学学报, 34(5): 790–795. | |
| 于明. 2004. 二维自适应结构网格的变分生成方法. 计算物理, 21(1): 27–34. | |
| 张剑锋. 1998. 弹性波数值模拟的非规则网格差分法. 地球物理学报, 41(S): 357–366. | |
| 朱生旺, 曲寿利, 魏修成, 等. 2007. 变网格有限差分弹性波方程数值模拟方法. 石油地球物理勘探, 42(6): 634–639. | |
 2016, Vol. 59
2016, Vol. 59


