2. 地球空间环境与大地测量教育部重点实验室, 武汉 430079;
3. 地球空间信息技术协同创新中心, 武汉 430079;
4. 国家测绘地理信息局卫星测绘应用中心, 北京 100048
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China;
3. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China;
4. Satellite Surveying and Mapping Application Center, NASA, Beijing 100048, China
GRACE卫星从2002年发射至今,已经运行了十多年的时间,为静态重力场建模以及时变重力场信号的分析研究提供了重要的技术手段.在400 km左右的空间分辨率上,GRACE卫星能提供大地水准面精度达到2~3 mm的月重力场时间序列(Tapley et al., 2004),为时变重力场研究及其解释提供了坚实的基础,并在水文现象特殊地区获得了大量有价值的科学研究成果(Chambers et al., 2004; Chen et al., 2006; Velicogna and Wahr, 2006),成功地将卫星重力学与水文学、冰川学以及全球气候变化问题紧密联系起来.典型的应用区域如亚马逊流域,由于该地区河流众多,雨量充沛,地表浅层水的GRACE反演结果呈现出很强的年度和季节性特征(Wahr et al., 2004).
利用GRACE任务的观测数据,研究时变重力场主要有两种方法.一种是基于Stokes位系数的分析法(Wahr et al., 1998),通过引力位系数的时间序列提取重力场时变信息,表达方式有等效水高或者大地水准面等,本文简称为位系数法,这种研究思路目前在时变重力场领域应用最为广泛.从本质上讲,采用位系数方法研究重力场时变,是基于Level 2级别产品进行的,即首先获得长时间的重力场模型时间序列,然后由位系数的时变分析地表物质迁移.另一种时变研究的方法则是本文要探讨的MASCON (Mass Concentration)方法.
MASCON方法最早是在行星重力场研究中提出的一种方法,用以研究行星表面的“质量瘤”,也就是质量异常(Muller and Sjogren, 1968).自然地,也可以将地表的物质迁移看作一种质量异常加以对待.因此,MASCON方法的思想也可以用于GRACE卫星任务的数据分析,该方法由JPL (Jet Propulsion Laboratory)的研究人员引入并实现(Watkins et al., 2005; Rowlands et al., 2005).其显著特点是在建模过程中把地表物质迁移参数化,建立起对应的引力场变化模型,并主要通过GRACE卫星的高精度星间观测数据,把质量变化对应的等效水高直接作为参数解算.MASCON方法与位系数法有很大不同,在位系数方法中,由于球谐系数是定义在整个球面上,需要利用全球的观测数据解算重力场模型,在重力场模型序列的基础上才能开展时变研究.理论上,MASCON方法则更为灵活,可以针对感兴趣的区域直接引入参数建模.另外,在GRACE任务的数据处理中,由于GRACE卫星的编队特点,直接利用位系数法反演的时变信号中存在严重的南北条带误差,需要根据位系数的误差特征,选择合适的滤波器才能获得最终的时变结果(Swenson and Wahr, 2006),在一定程度上影响了真实信号的提取.而MASCON方法直接将质量变化作为参数引入到观测方程中进行求解,但在目前的MASCON方法研究中,有许多关键问题需要解决,包括加速度计校准,加入空间/时间限制条件等等.总体而言,在区域范围内,星间距离变率数据对重力场变化非常敏感,并有着极强的空间对应关系,因此MASCON方法有可能更便捷地获取区域时变信号.并且,对于GRACE卫星的极轨设计,星下点的数据分布由赤道向两极逐渐加密,位系数法很难顾及这种特征,但在MASCON方法中,可以灵活地选择质量异常的空间分辨率.国外各大研究机构在JPL之后,逐步开展了MASCON方法的研究,除JPL最新提出的基于动力法的MASCON方法外,还有基于能量法和在轨视线法等MASCON方法(Luthcke et al., 2006; Rowlands et al., 2010; Sabaka et al., 2010; Ivins et al., 2011; Luthcke et al., 2013).可以说,MASCON方法的特点吸引了众多的研究力量,使得这个领域有可能成为卫星重力时变研究方向的新热点.
MASCON方法在实现上,需要以时变/静态重力场模型解算技术为基础,难度较大.我国在时变重力场研究领域,目前仍然以位系数方法为主,但在MASCON的研究方面,最近也取得了一定的进展.在方法仿真方面,已经有多家单位采用动力法做了研究(李琼,2014;郭飞霄等,2014),李琼(2014)在亚马逊流域还进行了试算,做了很好的探索研究.此外,在高亚洲冰川质量变化研究中,也有研究人员借鉴了MASCON方法的思想,实现过程则是基于已有的位系数模型序列进行参数估计(朱传东等,2015),该方法可以简单概括为以位系数模型序列作为观测值估计MASCON参数,也是MASCON方法研究中的有益尝试.需要指出的是该文所采取的研究思路与这里所讲的一般意义上的MASCON方法不同.本文的MASCON方法将直接从卫星跟踪卫星观测数据估计MASCON参数.
以JPL的代表性工作以及国内目前展开的情况看,MASCON方法的技术过程可以概括为两个关键步骤:(1)获得星载加速度计的校准参数.由于在MASCON方法的参数估计过程中这些参数要固定下来,如何校准是一个重要的技术难点.就GRACE任务而言,这些参数没有全部公布,本文将自行估计所有与加速度计有关的校准参数.(2)利用研究区域的星间距离变率数据解算MASCON参数,并引入空间/时间限制条件,增强解算结果的可靠性,关键问题在于如何合理定权.针对JPL所提的MASCON方法(Rowlands et al., 2010),本文主要探讨两个问题:(1)在校准加速度计阶段,该方法提出在校准模型中引入沿轨方向周期特征为每转一周(CPR: Cycle Per Revolution)的参数;(2)轨道数据只在加速度计校准过程中使用,在MASCON参数解算过程中并不使用.在已有的位系数法研究中,GRACE卫星加速度计校准模型中是不存在沿轨方向的CPR参数的(Wu and Kruizinga, 2004;邹贤才等,2015),因此JPL的做法只能看做是一种经验性的做法.如果采用纯动力法,不引入经验参数是否也能获得可靠的结果?轨道数据在MASCON方法中是否属于可有可无的观测值,也是值得探讨的问题--利用动力法反演MASCON参数,只采用星间观测值时,由于星间距离变率是相对观测量,估计双星的轨道初值属于病态问题.如果不估计轨道初值,则轨道初值的误差直接通过轨道积分影响星间观测值的计算值,进而影响MASCON参数的估计.
为此,本文将联合轨道数据一起解算MASCON参数.尽管已有的仿真分析表明MASCON参数对轨道的影响,在空间位置上相对MASCON参数所在的区域有一定的滞后(李琼,2014),但是GRACE卫星给出的时变信号无疑主要来自星间观测数据,通过合理的定权完全可以把轨道当作一种新形式的限制条件,利用卫星相对地心的绝对位置加强图形结构.这样,不仅可以估计卫星的轨道初值,也可以减小空间限制条件的权重,进而拓展动力法求解MASCON的灵活性,充分发挥动力法在力模型精化、参数反演上的优势.简言之,本文的目的是在动力法的框架下,以方法研究为主,改进现有技术模式,通过仿真以及GRACE实际数据处理探讨地表物质迁移的MASCON方法,使之与标准的GRACE卫星重力场模型解算过程更接近,并以亚马逊流域为例,对研究结果的有效性进行验证,与目前广泛采用的位系数法进行对比.
2 MASCON参数的动力法反演模型与仿真验证 2.1 基于动力法的MASCON方法反演模型利用MASCON方法反演地表质量变化的基本原理是将一定区域内的地表质量变化假定为覆盖于该区域表面的薄层,通过背景场模型与薄层的叠加,获得地球外部引力场.不难看出,MASCON方法需要建立该薄层与卫星跟踪观测数据的联系.在实际的任务数据反演中一定存在空间分辨率限制,因此在某个区域范围内,可以把地表物质变化看作有一定密度、厚度相同的单层.为方便解释,如果假定单层的密度为水的密度,则该单层的厚度为等效水高.对GRACE任务来讲,研究浅层水文现象的时变效应是其特长,因此在大多数情况下,我们用等效水高来表示特定区域的质量变化.
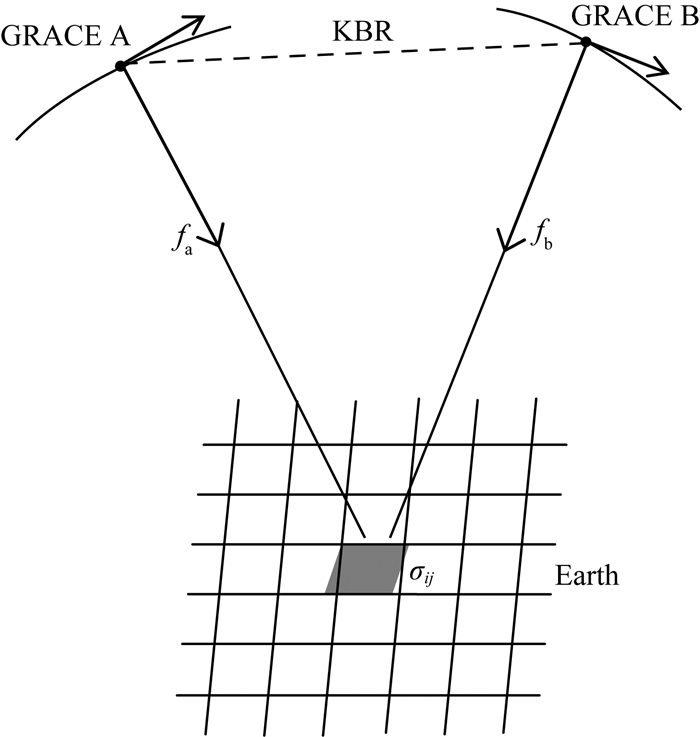
根据上面的分析,首先给出地表MASCON参数与地球外部扰动引力之间的泛函关系.假定在研究区域内做了规则的空间划分,区域编号为(i, j)的单层密度为σij,对应的等效水高为δhij,如图 1所示,根据文献(Chao et al., 1987)有式.
|
图 1 MASCON方法研究地表物质迁移的原理图 Fig. 1 Fundamental principle on the surface mass flux determination using the MASCON method |
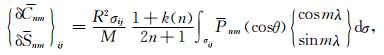
|
(1) |
其中,n, m分别代表球谐函数的阶和次,θ和λ为球面面元的余纬和经度,Pnm(cosθ)为缔合的Legendre函数,R为地球平均半径,M为地球总质量,k(n)为负荷Love数.顾及标准条件下水的密度ρw与单层密度σij的关系有
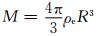
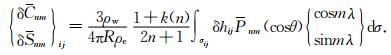
|
(2) |
质量异常对两颗GRACE卫星的引力差异会影响两颗卫星的运动,通过高精度的星间测量设备可以观测到这种微小的变化.在MASCON方法中,直接建立地表质量变化与地球重力场引力位系数变化之间的关系,如式(2)所示.式(1)和式(2)建立了地表物质变化对外部引力场球谐系数的扰动关系.在给定区域,由该区域地表质量变化可以导出对引力场参数的贡献之和δCnm和δSnm.按照卫星跟踪数据分析中的动力法原理,通过卫星轨道积分过程,这项改正可以转换为对卫星跟踪观测值的影响.从而可以通过状态转移矩阵,对观测方程线性化,反演地表质量变化参数.
在具体的算法设计上,参数δhij采用二维编码.力模型偏导数计算中,主要包括三类,分别是对位置、速度和参数的偏导数.对于保守力模型而言,对速度的偏导数恒为零,对位置的偏导数与地球引力场模型完全一致.求取力f对MASCON模型参数的偏导数时,有下列关系:
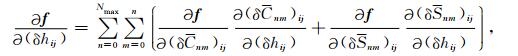
|
(3) |
式(3)给出的是一个求和式,其中Nmax是选定的截断阶,对GRACE而言,一般选择60.实际上是遍历所有阶次位系数,计算力对等效水高参数偏导数之和.计算某个特定阶次位系数对MASCON参数的偏导数时,可由(2)式导出.
MASCON方法中的另一个重要问题是限制条件.如果把MASCON参数δhij按某个约定的次序编号为(H1, H2, …, Hndim), 其中,ndim为参数的个数.∀H1, H2, …, Hndim,附加如下的参数限制条件(Rowlands et al., 2005):
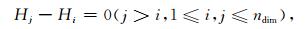
|
(4) |
按照上述要求,限制条件的总数为ndim×(ndim-1)/2.对应的权为
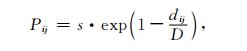
|
(5) |
其中,s表示限制条件的比例系数,可以看作限制条件的相对权重.dij表示MASCON参数Hi, Hj之间的空间距离,D为相关距离.附加限制条件的意义可以简单概括为:邻近的MASCON参数,等效水高趋向相等,它起到的是空间平滑效果.
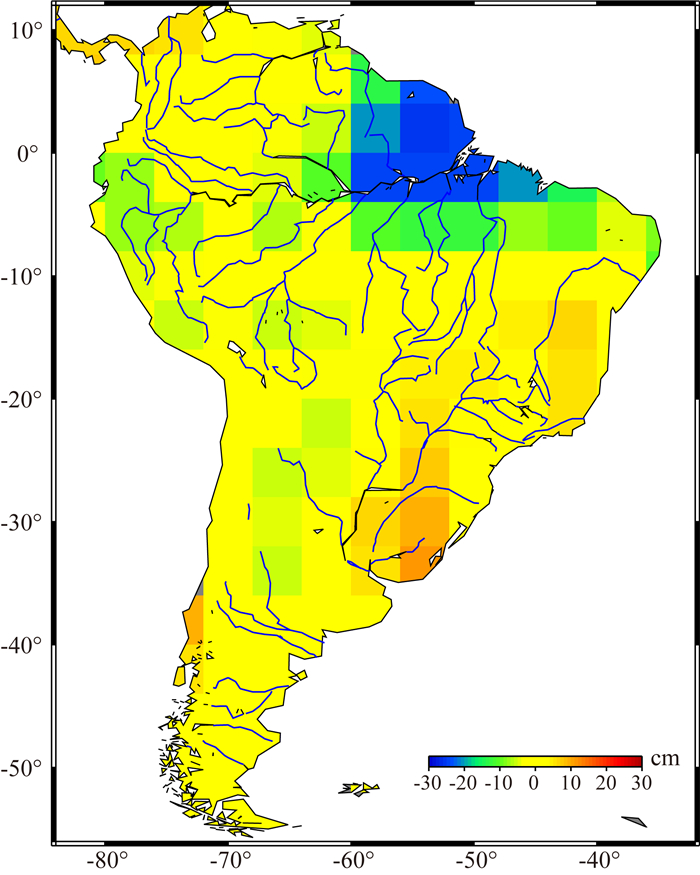
2.2 基于动力法的MASCON方法仿真为了让仿真研究更符合实际的情形,本文从全球陆面数据同化系统(Global Land Data Assimilation System, GLDAS) (Rodell et al., 2004)中提取亚马逊流域作为研究区域,如图 2所示.选取2009年11月数据,将其计算的等效水高进行单位统一、格式转换后,模拟为GRACE任务期间的地表浅层水变化.从图 2可以看出,在整个研究区域,南部的水文信号相对较弱,主要集中在北部地区.在此基础上,联合其他必要的卫星动力学模型以及基本参数(邹贤才,2007),积分生成GRACE双星的精密轨道,获得星间距离变率数据,由此可以分析局部MASCON参数对GRACE观测值的影响,包括量级、与MASCON参数的空间关系等.
|
图 2 GLDAS水文数据2009年11月亚马逊地区陆地水储量等效水高变化 Fig. 2 The EWH change in Amazon basin by GLDAS in Dec. 2009 |
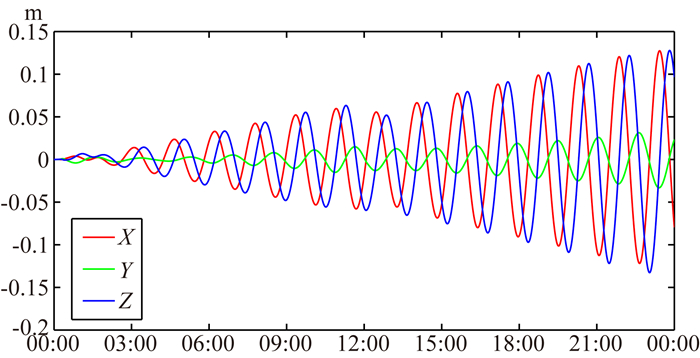
首先分析地表浅层水变化对轨道积分的影响.在轨道积分中,固定轨道初值、重力场模型位系数等与轨道积分有关的参量,分别做两次卫星观测值模拟.一是假定没有地表物质迁移,二是假定一定的MASCON分布(来自GLDAS模型,见上),则两次仿真所造成的差异完全是MASCON参数引起的,因此可以从数值上分析MASCON信号对轨道积分的影响.图 3显示了MASCON参数对地心惯性系中卫星轨道三个坐标分量的影响.可以看出,一天之内,轨道差异的最大值接近15 cm,呈现明显的趋势项、周期振荡组合特征.说明本文在正演研究中,MASCON参数所表征的物质迁移,通过式(2)对引力场产生扰动,轨道差异明显呈现重力场模型的影响特点.因此图 3从数值上说明在一定的条件下(比如本文的24 h的弧段),在当前厘米级的定轨水平下,卫星精密轨道也是有可能用于探测MASCON现象的.
|
图 3 MASCON参数对轨道积分的影响(单位:m) Fig. 3 The effects of MASCON parameters on the integration of orbit (Unit: m) |
上述分析进一步说明,在利用卫星重力数据求解MASCON参数时,轨道对MASCON参数的反演也是有价值的.如果需要研究全球MASCON参数的求解,轨道数据的作用不可忽略,有必要顾及轨道信息.JPL最新的研究成果中(Watkins et al., 2015),已经采用了星载GPS的高低跟踪数据,事实上采用了轨道观测值.考虑将来课题组也需要在全球MASCON模型解算上进行研究,同时为了做好区域与全球模式的一致处理,本文提出在局部MASCON的研究中也使用轨道数据.另外一个重要原因,如果仅采用星间距离变率数据,估计初始位置、速度是一个病态问题,联合轨道观测数据可以有效克服这个缺点.当然,为了不影响MASCON信号主要来自星间距离变率这一基本原则,本文通过方差分量估计的方式,通过定权合理使用轨道观测值.
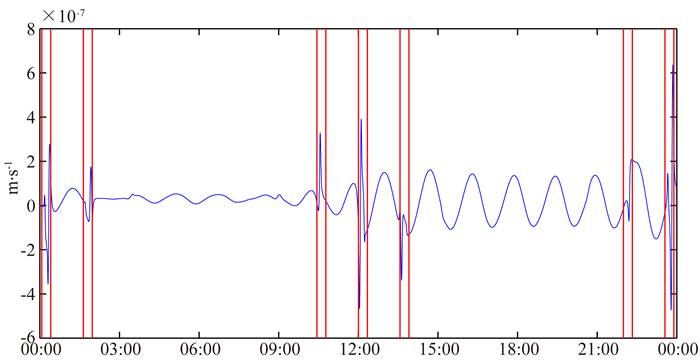
以上分析是在一个较为广阔的区域内模拟水文数据,更加符合实际情况.下面具体分析较局部区域内的时变信号对星间距离变率的影响特征,从而为实测数据的处理提供必要思路.如图 4所示,在2009年11月2日,GRACE卫星经过亚马逊流域(范围请参见图 2)的时间为00 : 04 : 25T00 : 24 : 40、01 : 38 : 20T01 : 58 : 35、10 : 26 : 20T10 : 46 : 35、12 : 00 : 15T12 : 20 : 30、13 : 34 : 10T13 : 54 : 25、21 : 59 : 15T22 : 19 : 30、23 : 33 : 10T23 : 53 : 25(均为GPS时间),每次通过将近20 min的飞行时间.图中以红线表示卫星的通过时间区间.可以看出,星间距离变率出现的异常也正好在这些时间段,两者之间高度吻合,表明星间距离变率与MASCON参数在空间位置有强相关性,成为利用星间距离变率反演局部地表物质迁移的重要依据.
|
图 4 2009年11月2日内MASCON参数对星间距离变率的影响(单位:m·s-1) Fig. 4 The effects of MASCON parameters on the inter-satellite range-rate on Nov. 2, 2009 (Unit: m·s-1) |
最后利用上述模拟的含有时变信号的观测数据,反演了MASCON参数.由于研究的是正反算问题,在仿真中并没有加入空间限制条件,反演结果与原值的差值分布如图 5所示,其结果与真值高度一致(与真值之差量级在10-8),可以认为在整个研究区域内差值为零.上述仿真确认了本文所提思路的有效性,也可以看作对本文所开发软件的一种可靠性检验.

|
图 5 MASCON参数恢复结果与真值之间的差异 Fig. 5 The difference between the results recovered by MASCON method and the original values |
在本文讨论的局部MASCON方法中,由于卫星经过的时间段,数据观测量相对而言较少,故必须控制好数据质量.以图 6为例,在某次卫星通过中,联合轨道与星间距离变率的对比结果,可以判定星间距离变率的时间序列中存在一处明显的粗值,不能运用于MASCON数据处理,否则,在观测数据少、星间距离变率权重大,且与MASCON空间位置高度相关的情况下(参见图 4),对MASCON解算的影响会非常显著.

|
图 6 星间距离变率中的异常观测值实例(单位:m·s-1) Fig. 6 The outliers in the inter-satellite range-rate measurements (Unit: m·s-1) |
仿真分析与实测数据处理采用的均为作者自研的动力法软件(邹贤才等, 2015; 邹贤才和李建成, 2016).在总的步骤上,与文献(Rowlands et al., 2005)一致.首先是加速度计校准阶段,静态重力场模型采用EIGEN6C4,估计60阶次.并顾及了重力场低阶时变、N体引力、相对论改正、固体潮、海潮、极潮以及AOD1B的时变改正信号等,具体参见表 1.关于动力法的基本原理,观测方程的组建等可以参见专门论述该问题的文章(邹贤才等, 2016).其次是采用本文给出的方法,在研究区域内,解算MASCON参数.式(5)中的相对权s最终取值为3.0×10-11.
|
|
表 1 动力学模型以及参数配置方案 Table 1 Configuration on the dynamic force models |
非保守力由加速度计提供.在加速度计校准方面,本文的目的是采用与位系数法一致的处理方式,因此并没有在加速度计校准模型中额外增加与CPR周期参数有关的改正项,所有结果都是基于标准的线性-偏差校准模型,在同时估计重力场模型的过程中完成(Wu and Kruizinga, 2004; 邹贤才等, 2015, 2016).
3.2 数值结果与精度分析为验证本文局部MASCON方法反演水储量变化的可靠性,选取了GLDAS水文模型计算的水储量变化、CSR RL05球谐系数反演的水储量变化,并且与由JPL采用MASCON方法解算的水储量变化结果进行了比较.其中,GLDAS水储量变化采用Noah模式驱动的1°×1°月平均陆面同化数据,减去2004年1月至2009年12月的平均值得到;CSR RL05水储量变化由JPL GRACE Tellus提供,采用了CSR解算的RL05版本GRACE时变重力场球谐系数,替换一阶和二阶项,减去2004年1月至2009年12月平均值,再进行300 km的高斯滤波和去条纹滤波得到,空间分辨率为1°×1°(Swenson, 2012);JPL MASCON水储量变化由JPL GRACE Tellus提供,采用球冠质量凝集方程直接解算月重力场变化得到,通过引入实际的地球物理信息避免了后续的高斯滤波和去条纹等滤波进行高频噪声和相关误差的处理,解算结果为3°×3°等面积格网,提供数值结果为0.5°×0.5°格网(Wiese, 2015; Watkins et al., 2015).为深入分析本文计算水储量变化的可靠性,从各方法计算的月平均水储量变化时间序列,由此提取的水储量变化的季节性周期,以及直接的月水储量变化分布三个方面进行了比较.
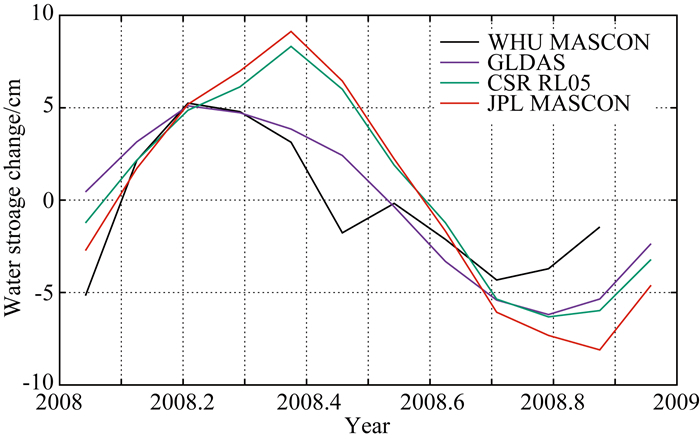
图 7给出了几种方法解算的亚马逊地区陆地水储量变化月均时间序列.从图中可以看出,本文利用MASCON方法解算的水储量变化与其他三种结果具有较好的一致性,与GLDAS水文模型符合最好.与GLDAS、CSR、JPL三种结果的相关性分别为0.89、0.77、0.76.在本文的解算过程中,GRACE任务的6月和12月数据存在质量问题.其他月份的迭代计算收敛后,轨道和星间距离变率的单位权中误差接近,数值约2.2×10-7.但是6月和12月的对应结果为8.2×10-7和5.4×10-5,表明高低和低低跟踪数据之间的一致性存在问题.除去这两个月份,本文计算结果与GLDAS、CSR和JPL三种结果的相关性分别为0.97、0.90、0.88.
|
图 7 不同方法解算的亚马逊地区陆地水储量变化月均时间序列 Fig. 7 The monthly time series of EWH change in Amazon basin by different methods in 2008 |
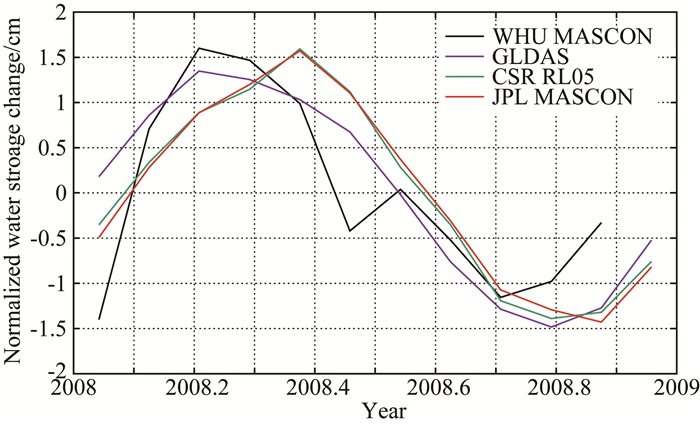
由于CSR RL05时变重力场解算的水储量变化是相对2004年1月至2009年12月平均值的差值,与GLDAS和本文计算结果有一定系统偏差.因此,将这几种时间序列进行了规格化处理,结果如图 8.可以看出,除去6月和12月的结果,几种方法计算的亚马逊地区陆地水储量变化时间序列具有很好的一致性.
|
图 8 规格化后亚马逊地区陆地水储量变化月均时间序列 Fig. 8 The normalized monthly time series of EWH change in Amazon basin by different methods in 2008 |
上述几种方法计算的2008年亚马逊地区陆地水储量变化月均时间序列,由于整体观测时间只有一年,无法提取周年变化信号,故利用趋势项和半周年变化参数进行最小二乘拟合,计算得到各方法对应的半周年周期,如表 2.从表中可以看出,四种数据计算的半周年变化特征在其误差范围内符合较好,特别是半周年相位,本文计算结果的中误差更小;而半周年振幅,本文计算结果与GLDAS结果符合最好,与CSR RL05球谐系数计算结果和JPL MASCON计算结果在其误差范围内保持一致.
|
|
表 2 亚马逊地区陆地水储量变化半周年周期特征 Table 2 The semi-annual cycles of EWH change in Amazon basin by different methods |
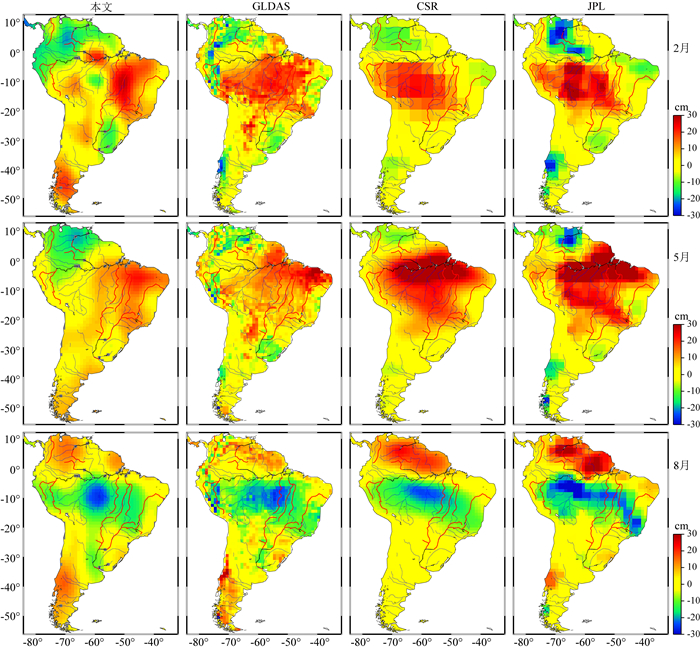
上述给出了亚马逊地区水储量的月均变化特征及各种结果的对比分析,为更深入分析几种结果的关系,选取2月、5月和8月,给出了四种方法对应的水储量变化,如图 9.可以看出,四种方法在这三个月计算的水储量变化空间分布具有一定的相似性,水储量变化最大和最小的区域基本一致,其中,本文计算结果与GLDAS结果最为符合,CSR RL05结果与JPL MASCON结果符合最好,由于GLDAS结果未进行空间滤波,表现出较多的高频信息,而JPL MASCON结果虽然在变化最大和最小区域上与CSR RL05结果符合很好,但在其他区域出现了较大的极值高频信号.
|
图 9 四种方法计算的亚马逊地区2008年2月、5月和8月陆地水储量变化 (从上到下依次为2月、5月和8月,从左到右依次为本文、GLDAS、CSR和JPL计算结果) Fig. 9 The EWH change in Amazon basin by different methods in February, May and August, 2008 (From upper to lower are February, May and August, respectively; from left to right are the results of this paper, GLDAS, CSR RL05 and JPL MASCON, respectively) |
本文提出了改进JPL局部MASCON参数反演方法的思路,引入轨道观测数据加强解算过程的稳定性,并修改了原方法中加速度计的校准策略,使MASCON研究与通常的位系数解算过程基本保持一致,解算策略上的一致性对位系数法与MASCON的深入对比研究提供了基础.本文的仿真研究从数值上指出卫星轨道与星间距离变率均受到了MASCON参数显著的摄动影响,并且,星间距离变率与MASCON参数具有较强的空间相关性.
作为方法研究的进一步验证,本文利用MASCON方法试算了亚马逊地区2008年的浅层地表水储量变化,并与GLDAS水文模型,以及基于CSR RL05球谐系数时变重力场和JPL MASCON方法计算的水储量变化结果进行了对比分析,四种方法获得的水储量变化时间序列吻合较好,剔除异常值后,本文结果与其他三者相关性分别达到0.97、0.90、0.88,同时提取的半周年相位一致性高,而半周年振幅因参考基准不一致有一定差异,在选定的三个月份内,四种方法得到的水储量变化空间变化分布基本一致,通过比较验证了本文所提方法的正确性和可靠性.由于MASCON方法解算中涉及大量计算,本文仅给出了一年的试验结果,但已足以证明方法的正确性,后续将改进计算方法,进行大规模的研究应用.
致谢感谢NASA JPL提供的GRACE任务观测数据,感谢NASA MEaSUREs Program提供的球谐系数和MASCON方法计算GRACE陆地水储量变化数据(http://grace.jpl.nasa.gov [2016-03-25]),感谢NASA GSFC提供的GLDAS水文模型.
| Chambers D P, Wahr J, Nerem R S. 2004. Preliminary observations of global ocean mass variations with GRACE. Geophysical Research Letters, 31(13): L13310. | |
| Chao B F, O'Connor W P, Chang A T C, et al. 1987. Snow load effect on the Earth's rotation and gravitational field, 1979-1985. Journal of Geophysical Research, 92(B9): 9415-9422. DOI:10.1029/JB092iB09p09415 | |
| Chen J L, Wilson C R, Tapley B D. 2006. Satellite gravity measurements confirm accelerated melting of Greenland ice sheet. Science, 313(5795): 1958-1960. DOI:10.1126/science.1129007 | |
| Guo F X, Xiao Y, Wang F F. 2014. MASCON inversion method of earth surface mass anomaly using GRACE range rate data. Progress in Geophysics (in Chinese), 29(6): 2494-2497. DOI:10.6038/pg20140602 | |
| Ivins E R, Watkins M M, Yuan D N, et al. 2011. On-land ice loss and glacial isostatic adjustment at the Drake Passage: 2003-2009. Journal of Geophysical Research, 116(B2): B02403. | |
| Li Q. 2014. Earth's surface mass transport recovered from temporal gravity field and its applications [Ph. D. thesis](in Chinese). Wuhan: Wuhan University. | |
| Luthcke S B, Rowls D D, Lemoine F G, et al. 2006. Monthly spherical harmonic gravity field solutions determined from GRACE inter-satellite range-rate data alone. Geophysical Research Letters, 33(2): L02402. | |
| Luthcke S B, Sabaka T J, Loomis B D, et al. 2013. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global MASCON solution. Journal of Glaciology, 59(216): 613-631. DOI:10.3189/2013JoG12J147 | |
| Muller P M, Sjogren W L. 1968. MASCONs: lunar mass concentrations. Science, 161(3842): 680-684. DOI:10.1126/science.161.3842.680 | |
| Rodell M, Houser P R, Jambor U, et al. 2004. The global land data assimilation system. Bulletin of the American Meteorological Society, 85(3): 381-394. DOI:10.1175/BAMS-85-3-381 | |
| Rowlands D D, Luthcke S B, Klosko S M, et al. 2005. Resolving mass flux at high spatial and temporal resolution using GRACE intersatellite measurements. Geophysical Research Letters, 32(4): L04310. | |
| Rowlands D D, Luthcke S B, Mccarthy J J, et al. 2010. Global mass flux solutions from GRACE: A comparison of parameter estimation strategies-Mass concentrations versus Stokes coefficients. Journal of Geophysical Research, 115(B1): B01403. | |
| Sabaka T J, Rowls D D, Luthcke S B, et al. 2010. Improving global mass flux solutions from Gravity Recovery and Climate Experiment (GRACE) through forward modeling and continuous time correlation. Journal of Geophysical Research, 115(B11): B11403. DOI:10.1029/2010JB007533 | |
| Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data. Geophysical Research Letters, 33(8): L08402. | |
| Swenson S C. 2012. GRACE monthly land water mass grids NETCDF RELEASE 5.0.Ver.5.0.PO.DAAC, CA, USA. Dataset accessed at http://dx.doi.org/10.5067/TELND-NC005. http://podaac.jpl.nasa.gov/dataset/TELLUS_LAND_NC_RL05 | |
| Tapley B D, Bettadpur S, Ries J C, et al. 2004. GRACE measurements of mass variability in the Earth system. Science, 305(5683): 503-505. DOI:10.1126/science.1099192 | |
| Velicogna I, Wahr J. 2006. Measurements of time-variable gravity show mass loss in Antarctica. Science, 311(5768): 1754-1756. DOI:10.1126/science.1123785 | |
| Wahr J, Molenaar M, Bryan F. 1998. Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE. Journal of Geophysical Research, 103(B12): 30205-30229. DOI:10.1029/98JB02844 | |
| Wahr J, Swenson S, Zlotnicki V, et al. 2004. Time-variable gravity from GRACE: first results. Geophysical Research Letters, 31(11): L11501. | |
| Watkins M M, Yuan D N, Kuang D, et al. 2005. GRACE harmonic and MASCON solutions at JPL. Eos Trans. AGU, 86(52), Fall Meet. Suppl., Abstract G22A-04, San Francisco, Calif. | |
| Watkins M M, Wiese D N, Yuan D N, et al. 2015. Improved methods for observing Earth's time variable mass distribution with GRACE using spherical cap mascons. Journal of Geophysical Research, 120(4): 2648-2671. | |
| Wiese D N. 2015. GRACE monthly global water mass grids NETCDF RELEASE 5.0.Ver.5.0.PO.DAAC, CA, USA. Dataset accessed at http://dx.doi.org/10.5067/TEMSC-OCL05. http://grace.jpl.nasa.gov/data/get-data/jpl_global_mascons/ | |
| Wu S, Kruizinga G. 2004. Algorithm theoretical basis document for GRACE Level-1B data procesing. JPL D-27672, Version 1.0.California. | |
| Zhu C D, Lu Y, Shi H L, et al. 2015. Trends of glacial mass changes in High Asia from satellite gravity observations. Chinese J. Geophys., 58(3): 793-801. DOI:10.6038/cjg20150309 | |
| Zou X C. 2007. Theory of satellite orbit and earth gravity field determination [Ph. D. thesis](in Chinese). Wuhan: Wuhan University. http://www.oalib.com/references/18979432 | |
| Zou X C, Li J C, Zhong L P, et al. 2015. Calibration of the accelerometers onboard GRACE with the dynamic method. Geomatics and Information Science of Wuhan University (in Chinese), 40(3): 357-360. | |
| Zou X C, Li J C. 2016. Study on the earth gravity modeling by GOCE in individual accelerometer mode. Chinese J. Geophys. (in Chinese), 59(4): 1260-1266. DOI:10.6038/cjg20160408 | |
| Zou X C, Zhong L P, Li J C. 2016. Simultaneous solution for precise satellite orbit and earth gravity model. Chinese J. Geophys. (in Chinese), 59(7): 2413-2423. | |
| 郭飞霄, 肖云, 汪菲菲. 2014. 利用GRACE星间距离变率数据反演地球表层质量变化的MASCON方法. 地球物理学进展, 29(6): 2494–2497. DOI:10.6038/pg20140602 | |
| 李琼. 2014.地表物质迁移的时变重力场反演方法及其应用研究[博士学位论文].武汉:武汉大学. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528749.htm | |
| 朱传东, 陆洋, 史红岭, 等. 2015. 高亚洲冰川质量变化趋势的卫星重力探测. 地球物理学报, 58(3): 793–801. DOI:10.6038/cjg20150309 | |
| 邹贤才. 2007.卫星轨道理论与地球重力场模型的确定[博士学位论文].武汉:武汉大学. | |
| 邹贤才, 李建成, 衷路萍, 等. 2015. 动力法校准GRACE星载加速度计. 武汉大学学报:信息科学版, 40(3): 357–360. | |
| 邹贤才, 李建成. 2016. 单加速度计模式下的GOCE卫星重力场建模方法研究. 地球物理学报, 59(4): 1260–1266. DOI:10.6038/cjg20160408 | |
| 邹贤才, 衷路萍, 李建成. 2016. 卫星精密定轨与重力场建模的同解法. 地球物理学报, 59(7): 2413–2423. | |
 2016, Vol. 59
2016, Vol. 59


