2. 低渗透油气田勘探开发国家工程实验室, 西安 710018
2. National Engineering Laboratory for Exploration and Development of Low-Permeability Oil & Gas Fields, Xi'an 710018, China
非常规致密砂岩是指其储层覆压渗透率小于0.1 mD (1mD=0.987×10-3 μm2)的岩石,它与常规高渗孔隙砂岩储层的地质特征有很大不同(邹才能等,2011), 因此, 两者的岩石物理模型亦有很大的差异, 这就需要研究致密砂岩储层的岩石物理模型.岩石是由固体岩石骨架和流动孔隙流体组成的多相介质,其有效弹性性质常用以下4个等效弹性参数来描述:基质模量、干岩石骨架模量、孔隙流体模量和环境因素(包括压力、温度、声波频率等).岩石物理理论模型旨在建立这些模量之间相互关系,并在一定的假设条件下对实际储层进行简化,以便定量分析不同储层物性参数(孔隙度、饱和度等)与有效弹性性质之间的关系.岩石物理理论模型可以分为有效介质模型理论和波传播理论两大类(陈颙等,2009;刘浩杰,2009;杨志芳和曹宏,2009;马淑芬等,2010;巴晶,2013).有效介质模型理论是在已知组成岩石各相的相对含量、分布特征和矿物弹性模量条件下,根据几何平均物理模型,以适当方式定量求取岩石的等效弹性模量.尚若用理论方法来预测地下岩石的等效弹性模量,如果只知道各构成矿物组分的体积含量和各矿物的弹性模量特征,这时只能预测出弹性模量的上下限,要精确的预测具体值,还需了解其孔隙的几何特征.Reuss (1929)提出了“等应力平均”模型,类似于串联模型,它给出了当构成成分有相等应力时,平均应力与平均应变的比值;Voigt (1910)提出了“等应变平均”模型,类似于并联模型,它给出了当构成成分假设有相等应变时,应力与平均应变的比值;Voigt-Reuss-Hill平均模型(Hill, 1952)是将Voigt上限和Reuss下限取算数平均来估算岩石的等效弹性模量;通过交换岩石两种构成成分材料计算的Hashin和Shtrikman (1963)界限模型,相对来说是当岩石的孔隙几何细节未知情况下最窄的可容许上下界限.
当地震波通过含有流体的复杂孔隙介质时,不同地质条件下的岩石会对通过的地震波做出响应,这也为我们利用地震波传播理论预测和计算多孔岩石介质弹性模量提供的另一种思路.
国外学者在孔隙介质理论建立方面做了很多创新性的工作,Biot (1956a, b)首次建立了含饱和流体的多孔介质理论,其最大的贡献是预测了慢纵波的存在.White (1975)首次提出了基于介观尺度的含球形气包的孔隙岩石中地震速度频散与能量衰减理论.Eshelby (1957)、Walsh (1965)、O′Connell和Budiansky (1974)、Kuster和Toksöz (1974)Hudson (1980, 1981, 1994)先后利用孔隙度和裂隙密度作为有效模型的函数来直接估计孔裂隙介质的弹性性质,并推导了各种表达式来计算含有孔隙和裂隙的岩石弹性性质.Dutta和Odé(1979)将Biot理论应用到White模型中,在取消White模型中的假设条件下,系统推导了含饱和流体中固体和流体的耦合运动关系,定量化给出了衰减系数随频率、气体饱和度和气包大小的变化趋势.Pride和Berryman (2003a, b)从波的控制方程和声学衰减、流体的运动方程两方面讨论了双孔双渗的线性动力学特征.Mavko和Nur (1975)认为在微观尺度下地震波通过含有孔隙-裂隙系统的流体饱和岩石时,可能会发生流体喷射现象,由此,建立了比奥-喷射(BISQ)模型理论,该理论在一定程度上能更加合理和有效的解释实际地震资料中P波和S波的频谱能量衰减和速度频散.国内学者巴晶等拓展了双孔岩石中介观流体流动的模拟,并推论波场衰减可能来自介观流体的流体和宏观Biot流扩散.巴晶等(2012)进一步从经典的哈密尔顿原理出发,采用Rayleigh理论刻画由纵波激励产生的非饱和岩石中气包的局部流体扰动,进而得到了Biot-Rayleigh双孔介质波动方程.杨顶辉和陈小宏(2001)研究了含流体多孔介质的BISQ模型.聂建新等(2010)研究含泥质低孔渗各向异性黏弹性介质中的波频散和衰减.
实验室进行岩石物理测量是最直观的地球物理数据来源,通过实验室数据测定声波参数(施行觉等,1995;蒋立新和施行觉,1998;伍向阳等,2000;王大兴等,2006)求得岩石的各种弹性参数和岩石模量.其主要流程:(1) 选取目标区岩心,进行实验室测量及结果分析,建立测量物理参数(孔隙度,饱和度,密度)和弹性参数(速度,泊松比等)之间关系;(2) 尝试进行流体替换,研究岩石不同孔隙流体对速度和衰减影响;(3) 建立合理且简化的岩石物理模型,并将应用到实际勘探中.
岩石物理建模主要任务是解决弹性参数(如横波等)预测、储层流体替换、优选甜点敏感参数,进而建立岩石物理模版,目的是为储层预测和流体检测提供依据,减小预测的风险,提高地震储层预测的可靠性.目前,在砂泥岩层中岩石物理模型研究主要选用Xu和White (1995, 1996)提出一种砂泥岩混合模型,该模型综合考虑了岩石孔隙度、孔隙几何形状和粘土含量来预测声波速度.然而,致密砂岩储层渗透率低、孔隙度小,与Xu-White的砂泥岩模型有差异(白俊雨等,2012;赵立新等,2012),要建立致密砂岩岩石物理模型就必须重新分析研究骨架参数和Brie等(1995)指数e值的变化规律,其与实际测量的数据的吻合度直接影响岩石参数计算的准确性(姜仁等,2015).
本文就是详细分析和研究鄂尔多斯盆地苏里格致密气田岩石物理实测的多组数据,并通过致密砂岩储层Brie等(1995)模型中指数的变化进行拟合分析,建立适合该区致密含气砂岩储层的岩石物理模型,根据其岩石物理参数随含气饱和度变化规律,指导苏里格气田勘探和开发生产中的储层和含气性预测.
2 致密砂岩气储层岩石物理模型建立 2.1 实验数据分析鄂尔多斯盆地苏里格气田是典型的“低孔、低渗、低压”致密气田,储层与非储层地球物理差异小(杨华等,2013),为了深入研究该区岩石地球物理参数之间的关系,我们收集整理分析了苏里格气田上古生界二叠系石盒子组盒8段以往实测和新测的共17口井51块岩样超声波实验数据,共获得304组不同孔隙度、不同含水饱和度(Sw,单位:%)下对应的纵波速度、横波速度、泊松比等弹性参数,见表 1、2、3和4.这次通过不同孔隙度下含气饱和度与纵波速度、横波速度、泊松比、纵波Q值和横波Q值等因子的关系统计研究,建立苏里格地区储层岩石物理模型,为储层预测提供理论依据.实验室岩石物理测定与文献(伍向阳等,2000;王大兴等, 2006)中的方法和实验条件基本类似.实验中选取苏里格气田的地层条件为温度105 ℃、压力29 MPa.纵波的测量精度为1%,横波的测量精度为2%,根据纪录的波形用频谱振幅比法计算Q值,误差约为10%.用超声波脉冲透射法测得的,其频率为1 MHz,而地震波的频率在100 Hz以下,其间存在频散.根据Sothcott等(2000)的研究表明,在高频和低频条件下,岩石中波速及衰减随流体含量变化的幅度虽然不同,但其总的变化趋势和关系是相似的.
|
|
表 1 苏里格地区岩样测量结果统计表 Table 1 Statistics of measurements of rock samples from Sulige area |
根据统计数据分析的目的,对测量结果按孔隙度范围进行重新选排,得到孔隙度(φ,单位:%)区间分别为3.81~4.20、4.96~5.62、6.44~7.19、8.27~8.48、9.7~10.8的5组实验数据,并分别对这5组数据做纵波速度(VP,单位m·s-1)、横波速度(VS, 单位m·s-1)、泊松比(σ,无量纲)、纵波品质因子Q值(Qp,无量纲)、横波品质因子Q值(Qs,无量纲)与含气饱和度Sg(1-Sw,单位:%)的交会图,剔除部分异常样点后,按孔隙度分类的5组实验数据分析如下:
(1) 纵横波速与含气饱和度的关系
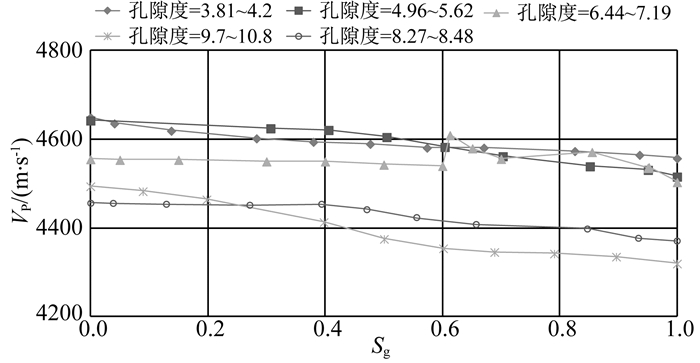
图 1中相对大孔隙度组的纵波速度随含气饱和度的增加而下降的梯度大,纵波速度明显比小孔隙度组变小.图 2表明横波速度整体随孔隙度变小而略增加,随含气饱和度增加的变化趋势不明显.
|
图 1 5组实验样品纵波速度VP随含气饱和度Sg的变化曲线 Fig. 1 P-wave velocity (VP) versus gas saturation (Sg) from five-set rock samples |

|
图 2 5组实验样品横波速度VS随含气饱和度Sg的变化曲线 Fig. 2 S-wave velocity (VS) versus gas saturation (Sg) from five-set rock samples |
(2) 吸收衰减与含气饱和度的关系
从图 3可以看出,对于纵波而言,孔隙度越大,纵波品质因子越小,也就是吸收衰减就越强烈;孔隙度6.44~7.19中个别数据跳跃应为测量误差,剔除其异常点外,看总体趋势,同一孔隙度范围内,纵波品质因子随含气饱和度的增大先是减小,到含气饱和度达到一定值(60%~70%)时,纵波品质因子达到最小值,随后随着含气饱和度的增加,纵波品质因子略有点增加.

|
图 3 5组实验样品纵波品质因子Qp随含气饱和度Sg的变化曲线 Fig. 3 Quality factors of the P-wave (Qp) versus gas saturation (Sg) from five-set rock samples |
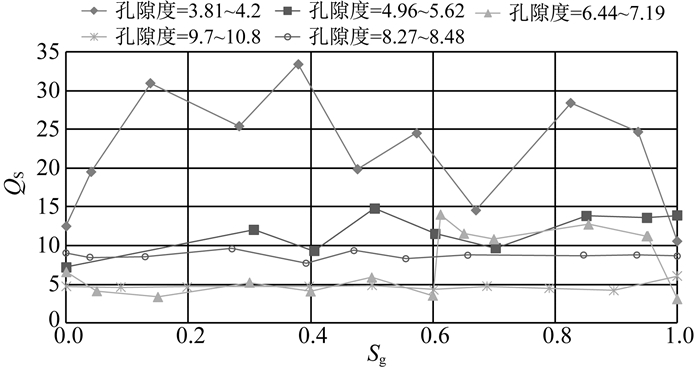
图 4表明横波品质因子在孔隙度3.81~4.2时,横波品质因子随着含气饱和度的增加而减小.在孔隙度4.96~7.19时,横波品质因子随Sg的变化关系较为复杂,个别数据跳跃应为测量误差.含气饱和度对横波品质因子的影响不明显,影响横波品质因子的主要因素为岩石的孔隙度.
|
图 4 5组实验样品横波品质因子Qs随含气饱和度Sg的变化曲线 Fig. 4 Quality factors of the S-wave (Qs) versus gas saturation (Sg) from five-set rock samples |
(3) 泊松比与含气饱和度的关系
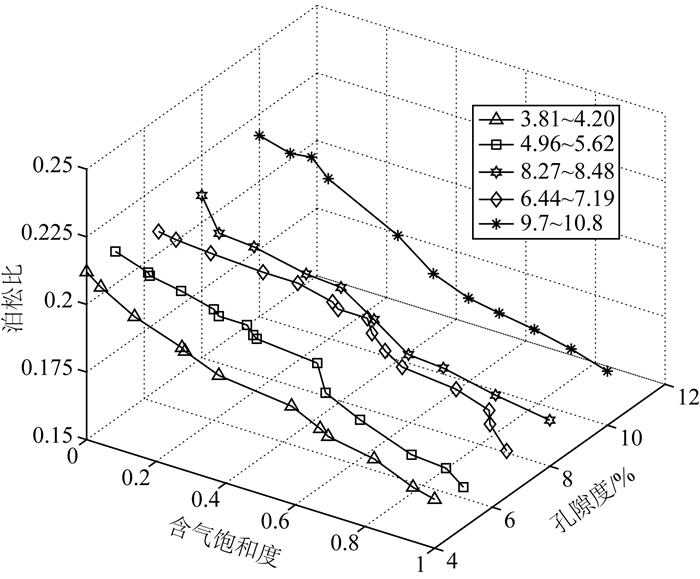
含气饱和度相同时,5组样品数据的泊松比分布在较大的变化范围,见图 5,且这种变化规律比较复杂,但整体表现为含气饱和度越大,泊松比越小,且含气饱和度较小(小于40%)时,减小较慢;含气饱和度较大(大于40%)时,减小较快.综合统计分析这5组实验数据,可发现如下规律:
|
图 5 5组实验样品泊松比σ随孔隙度φ和含气饱和度Sg的变化曲线 Fig. 5 Poisson′s ratio (σ) versus porosity (φ) and gas saturation (Sg) based on five-set rock samples |
①孔隙度φ越大,纵波速度VP越小;含气饱和度Sg越大,纵波速度VP越小;
②孔隙度φ越大,横波速度VS亦越小;但在同一孔隙度下,含气饱和度Sg增大时,横波速度VS会略有增大;
③孔隙度φ越大,纵波品质因子Qp越小;在同一孔隙度下,含气饱和度Sg增大时,纵波品质因子Qp减小;
④孔隙度φ越大,横波品质因子Qs越小;在同一孔隙度下,当含气饱和度Sg增大时,横波品质因子Qs变化不明显;
⑤不同孔隙度φ组中,含气饱和度Sg越大,泊松比σ越小.
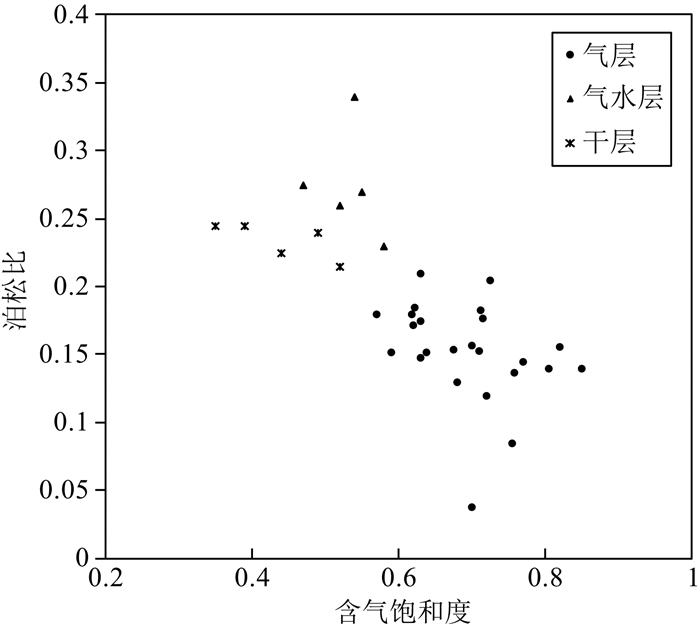
上述实验岩石物理表明:致密砂岩储层的纵横波速度衰减和泊松比与储层的孔隙度及含气饱和度呈近似负线性关系,由此,结合这些岩石物理关系,利用地震属性进行储层含气性预测是可行的.同样利用苏里格气田盒8段储层的19口测井34个层点的测井岩石物理分析数据,统计泊松比与含气饱和度的关系如图 6,也表明随含气饱和度的增加泊松比降低,气层的泊松比要比干层和气水层更低.上述岩石物理实验数据和测井岩石物理分析两方面的结论不但为苏里格地区致密砂岩储层预测奠定了的实验基础,而且为该区致密砂岩岩石物理模型,确定模型参数提供了重要的实验数据来源.
|
图 6 苏里格气田测井岩石物理分析的泊松比与含气饱和度关系图(利用19口井共34个层点) Fig. 6 Poisson′s ratio (σ) versus gas saturation (Sg) based on the rock physics data using 34 points from 19 wells in Sulige gas field |
地层的岩石性质是由组成它的矿物成分所决定的,由测井资料对地层进行评价研究可以得到地层的泥质含量、孔隙度、渗透率、含油饱和度、束缚水饱和度等地层参数.据此结果,有两种预测地层弹性参数的方法:一是分析地层各矿物组分构成的弹性模量特征,甚至是各构成组分矿物颗粒相互胶结在一起的几何细节特征,建立一个等效介质模型或有效介质模型,计算得到对应的干岩石弹性模量特征,在这里我们称之为岩石物理理论模型方法;二是如果条件不够完善,不能准确的获得地层各构成矿物组分的弹性模量特征和矿物颗粒相互胶结在一起的几何细节特征,可根据实验室岩心超声波测量结果建立起弹性参数和地层矿物含量、岩石孔隙度等的相关方程式,我们称之为岩石物理经验模型方法,这是较直接的解决问题的方法,操作也很简单,只是实验的代价较高.而实际研究中,常常把两种方法结合起来,即通过岩石物理岩心测量实验建立目标区所求弹性参数与岩石物性参数的经验关系值,再利用符合实际地质条件的有效介质模型来预测该目标区的弹性参数.
(1) 致密储层的岩石物理模型
传统的岩石物理模型是由Wood (1955)提出的,它的假设是岩石的孔隙比较大(20%~30%及以上),连通性较好,且为均匀饱和状态.这一经典模型(又称Reuss平均模型)表征中高孔渗储层模型是合适的, 即均匀饱和状态的Wood模型,公式为
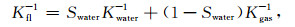
|
(1) |
其中,Kgas、Kwater分别为气、水的体积模量,Sgas、Swater分别为气、水的饱和度,且Sgas+Swater=1,下同.
1977年,Domenico指出当岩石孔隙较小(10%左右及以下),且流体不是在孔隙尺度均匀时,Wood模型就不适合某些实验数据(Domenico,1977),为此,按建立一种气液混合的方法来计算两相混合流体的体积模量,公式为
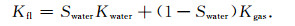
|
(2) |
随后,Brie等(1995)研究大量测井岩石物理数据后,发现致密砂岩储层有类似的情况,并对上式作了修正,建立新的模型公式为(Brie方程)(Brie et al., 1995)
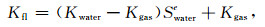
|
(3) |
其中,Kgas、Kwater分别为气、水的体积模量,Swater为含水饱和度,e是经验系数.
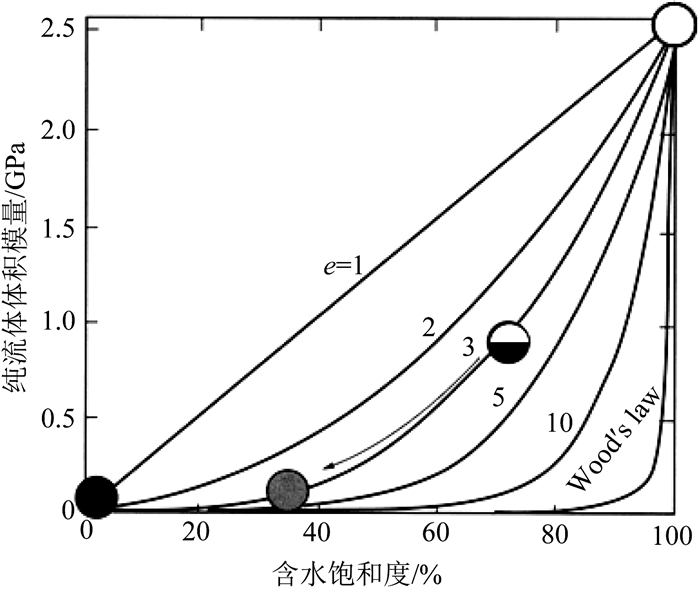
根据两相(气、水)混合流体的模型公式(3),在一般情况下纯气和纯水的体积模量相差约2.5 GPa,见图 7.通常致密储层含气饱和度低、孔隙度小,气层和背景储层的体积模量差异为0.8 GPa (黄绪德和李明,2012;杨华等,2013).鄂尔多斯盆地苏里格气田上古生界的致密含气砂岩与气水砂岩相差0.9 GPa,与干砂岩相差1.3 GPa (杨华等,2013).
|
图 7 Brie方程中流体饱和度与体积模量关系(来自Brie et al., 1995) Fig. 7 Relationship between fluid saturation and bulk modulus in the Brie equation (from Brie et al., 1995) |
(2) 致密储层岩石物理模型的经验参数
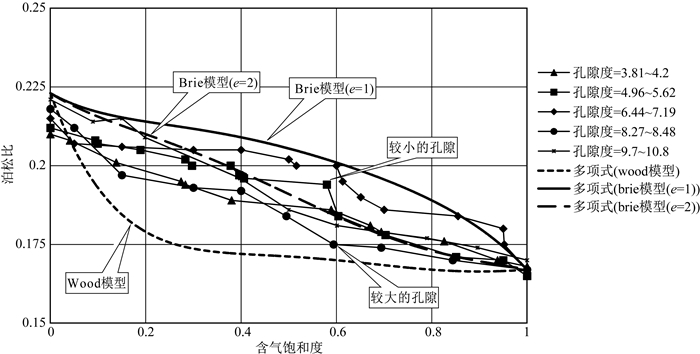
对于两相或多相混合流体弹性属性的计算用Brie方程公式(3)来计算,在e指数较大的情况下相当于Wood公式描述的流体饱和度与体积模量关系(图 8),不同e指数情况下流体含水饱和度与体积模量关系差异很大,用来模拟不同饱和状态下的混合流体特征.一般地,e指数在1~3之间,但严格数值仍需要根据大量实测岩石物理资料进行标定.根据前面的实验室岩石物理实际测定资料分析,重新优选计算体积模量和泊松比与含气饱和度的关系,表明鄂尔多斯盆地上古生界致密砂岩储层的模型与Brie模型(e=2)相似度最高.因此,Brie (e=2)模型能更好的表征致密岩石储层物理参数随含气饱和度变化规律.
|
图 8 苏里格气田盒8致密砂岩泊松比与含气饱和度的关系 Fig. 8 Poisson′s ratio (σ) versus gas saturation (Sg) of H8 tight sandstone formation in the Sulige gas field |
鄂尔多斯盆地北部的苏里格气田属于典型的大型岩性气藏,二叠系上古生界下石盒子组盒8分上下两段,以盒8下段分流河道沉积的石英砂岩为主,石英含量较高,一般90%以上,盒8砂岩的孔隙度是4%~14%,平均孔隙度为8.8%;渗透率主要为0.05×10-3~5×10-3 μm2,平均渗透率为0.73×10-3 μm2,属于典型的低孔、低渗致密储层(杨华等,2013).根据盒8段岩性及岩石结构特点,选择有效介质模型来建立岩石物理模型(Xu-White模型等);岩石主要由骨架和流体组成,岩石骨架包括泥质骨架和砂岩骨架,其中泥质骨架的矿物成份为干粘土,砂岩骨架的矿物成分为石英和碳酸钙,选择Voigt-Reuss-Hill平均模型计算混合骨架的弹性属性,然后根据苏里格气田盒8岩石结构特征,利用微分等效介质模型逐渐将骨架矿物组分相关孔隙、充填矿物相关孔隙加入,与混合岩石骨架再次进行混合计算,得到干岩的弹性属性;流体部分首先根据Han和Batzle (2004)算法模拟气藏状态下的单相流体属性,然后根据致密储层岩石物理实验室统计分析,两相(气、水)混合流体的模型公式(3)中的经验参数e选取为2,利用Brie方程来计算两相或多相混合流体弹性属性(Brie et al., 1995),最后采用Gassmann流体替换技术,模拟得到各向同性岩石在饱含流体条件下的弹性响应特征.
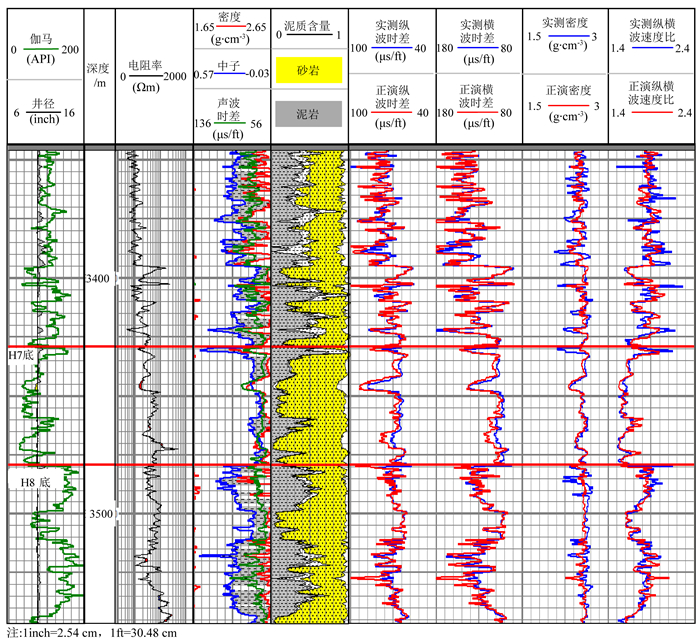
3.1 弹性参数正演预测在建立了岩石物理模型后,可以用常规测井资料预测有关弹性曲线(赵立新等,2012;杨华等, 2013),该岩石物理模型也可以进一步开展流体替换研究和侵入校正工作.根据以上岩石物理建模流程和先前解释得到的岩石物理体积模型,对苏里格气田Sxx井的正演弹性曲线与实测曲线进行了对比(图 9).第1至4道分别为测井原始的伽马和井径;深浅电阻率;密度、补偿中子和声波时差;泥质含量和岩性解释剖面.而第5道至第8道依次为纵波时差、横波时差、密度和纵横波速度比的正演与实测结果对比,其中蓝色实线代表实测曲线,红色实线代表正演拟合曲线;拟合曲线与实测曲线相关性很高,仅仅在极个别的井径扩径段正演拟合曲线与实测曲线略有稍微差异,说明了岩石物理正演模型和正演拟合结果的可靠性.
|
图 9 苏里格气田Sxx井正演弹性曲线与实测曲线对比 其中8条曲线框的说明:1.伽马(绿色)和井径;2.深浅电阻率;3.密度(红色)、补偿中子(兰色)和声波时差(绿色);4.泥质含量和砂泥岩剖面;5.实测纵波时差(兰色)和正演纵波时差(红色);6.实测横波时差(兰色)和正演计算横波时差(红色);7.实测密度(兰色)和正演密度(红色);8.实测纵横波速度比和正演纵横波速度比. Fig. 9 Comparison of elastic curve from forward modeling and measurement in Well Sxx in the Sulige gas field 1.Gamma (green) and caliper; 2. Resistivity; 3.Density (red) compensated neutron (blue), acoustic slowness (green); 4. Shale content and shale profile; 5. Slowness of P-wave from measures (blue) and slowness of P-wave from forward model (red); 6. Slowness of S-wave from measures (blue) and slowness of S-wave from forward model (red); 7. Density from measures (blue) and density from forward model (red); 8. VP/VS from measures (blue) and VP/VS from forward model (red). |
岩石物理分析的重要任务之一就是从一种流体饱和的岩石地震速度分析中,预测另外一种流体饱和岩石的地震速度.同样说来,干岩骨架的弹性模量是固定的,那么在孔隙中用一种流体(比如水)的弹性模量,代替另一种流体(比如气)的弹性模量,预测不同流体的岩石速度,这就是孔隙流体的替换.Biot-Gassmann方程是大多数岩石物理模型所采用的流体置换方法.一般地,地震波穿过岩石时,会诱发孔隙压力的增加,孔隙压力的增加会阻止进一步的压缩,进而增加了岩石刚性,低频Biot-Gassmann模型通过下列方程预测所产生的饱和岩石有效体积模量的增加,公式为
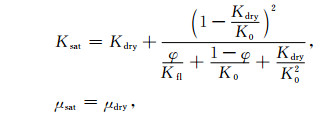
|
(4) |
其中Kdry为岩石骨架的有效体积模量,Ksat为饱和岩石的有效体积模量,K0为组成岩石矿物的体积模量,φ为孔隙度,μdry为岩石骨架的有效剪切模量,μsat为饱和岩石的有效剪切模量.
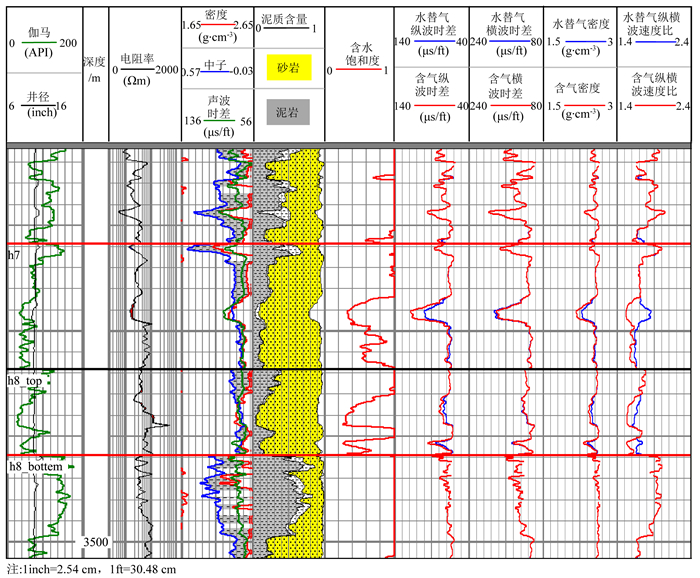
根据苏里格气田实际气藏温度、压力情况,正演计算在特定各矿物含量、孔隙度、饱和度情况下地层的弹性响应.图 10是用Biot-Gassmann模型公式(4)对该气田Sxx井盒8地层进行流体置换正演结果.第1至4道为测井原始的伽马、井径;深浅电阻率;密度、补偿中子和声波时差;泥质含量和岩性解释剖面.而第5道至第9道依次为含水饱和度、纵波时差、横波时差、密度、和纵横波速度比的流体替换前后的结果对比,其中,红色实线代表原状地层岩石饱含气情况下的弹性响应;蓝色实线代表地层岩石100%含水情况下的弹性响应.对比可以发现100%含水与原状地层岩石饱含气情况下岩石的纵波速度的差异为400 m·s-1左右,纵、横波速度比的差异在0.1左右.由此可见,盒8原状储层的气层替换为水层后纵波速度、密度和纵横波速度比在气层段变化最为明显,而横波速度基本没变化.
|
图 10 苏里格气田Sxx井流体置换正演结果 其中9条曲线框的说明:1.伽马(绿色)和井径;2.深浅电阻率;3.密度(红色)、补偿中子(兰色)和声波时差(绿色);4.泥质含量和砂泥岩剖面;5.含水饱和度;6.含气纵波时差(红色)和水替代气的纵波时差(兰色);7.含气横波时差{红色}和水替代气的横波时差(兰色);8.含气密度(红色)和水替代气密度(兰色);9.含气纵横波速度比(红色)和水替代气的纵横波速度比(兰色). Fig. 10 Forward modeling results of fluid substitution for Well Sxx in the Sulige gas field 1. Gamma (green) and caliper; 2. Resistivity; 3. Density (red) compensated neutron (blue), acoustic slowness, 4. Shale content and shale profile; 5. Water saturation; 6. Slowness of P-wave with gas-bearing (red) and slowness of P-wave with water-bearing (blue); 7. Slowness of S-wave with gas-bearing (red) and slowness of S-wave with water-bearing (blue); 8. Density with gas-bearing (red) and density with water-bearing (blue); 9. VP/VS with gas-bearing (red) and VP/VS with water-bearing (blue). |
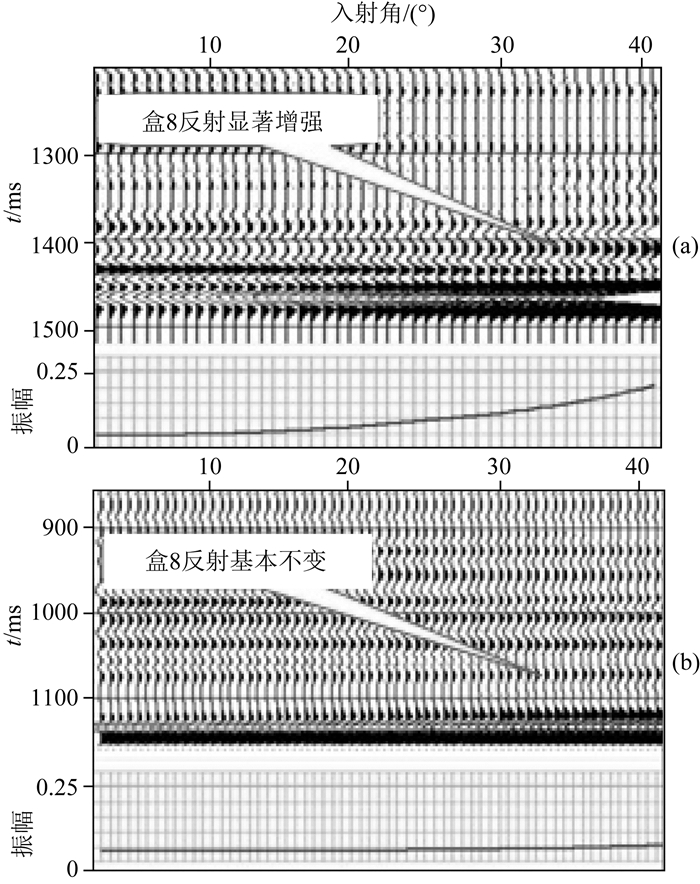
通过苏里格气田盒8储层流体替换前后AVO模型正演分析可见(图 11),盒8原状储层为气层(图 11a)时,盒8砂岩反射振幅随入射角增大而幅度显著增强;而将盒8原状地层的气层替换为水层后(图 11b),盒8砂岩反射振幅随入射角增大而幅度变化不明显(基本不变).图 11中盒8储层反射振幅在流体替换前后的变化,说明苏里格气田盒8含气砂岩为典型的第Ⅲ类AVO响应特征,这为苏里格气田寻找“亮点”型气藏,用AVO技术预测储层的含气性提供了依据.
|
图 11 苏里格气田流体替换的地震AVO正演分析 (a)盒8砂岩储层孔隙流体为气;(a)盒8砂岩储层孔隙流体为水. Fig. 11 AVO forward modeling analysis of fluid replacement in sulige gas field (a) Gas saturation of H8 reservoir; (b) Water saturation of H8 reservoir. |
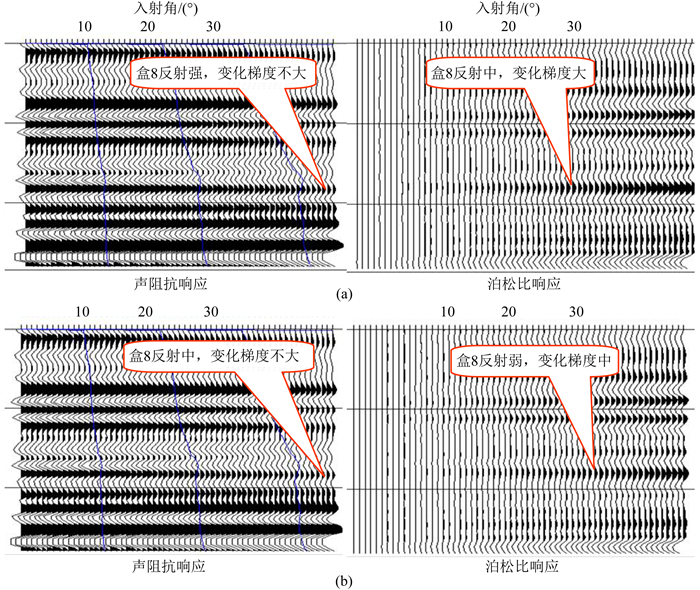
同样,根据Hilterman (2006)的理论,苏里格气田盒8砂岩储层孔隙流体原状为气替换为水后,见图 12.盒8储层声阻抗反射振幅替换前后由强振幅变为中振幅,但随入射角的变化梯度不大;盒8储层泊松比反射振幅替换前后由中振幅变为弱振幅,但随入射角的变化梯度由大变为中等,说明小入射角声阻抗对气水的响应比较敏感,大入射角泊松比对气水响应比较敏感.由此,验证了致密储层岩石物理模型中,储层的声阻抗和泊松比(或纵横波速度比)响应是影响反射振幅随偏移距变化的主要因素.声阻抗和泊松比地震响应属性是两个独立的弹性参数,两者的综合应用将在后面实际生产储层预测中发挥重要的作用.
|
图 12 苏里格气田盒8砂岩储层孔隙流体置换前后的随入射角变化的声阻抗响应和泊松比响应分析 (a)盒8砂岩储层孔隙流体为气;(b)盒8砂岩储层孔隙流体为水. Fig. 12 Analysis of acoustic impedance and Poisson′s ratio response before and after fluid replacement of H8 reservoir in sulige gas field (a) Gas saturation of H8 reservoir; (b) Water saturation of H8 reservoir. |
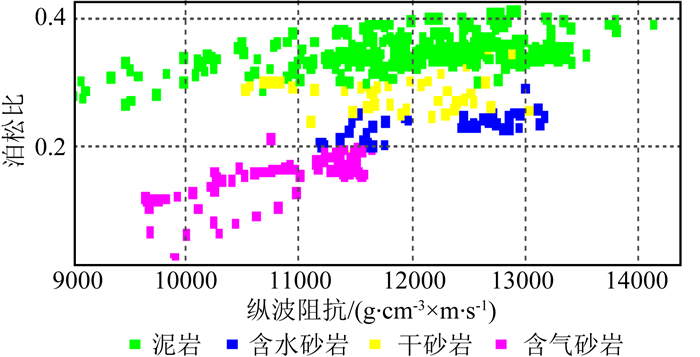
从苏里格气田盒8段地层的泊松比及与纵波阻抗交会图(图 13)分析看出,泊松比是岩性敏感的主要参数,它可以较好的区分砂岩和泥岩(泥岩和砂岩的泊松比界限在0.24左右);泊松比和声阻抗为储层响应敏感的参数:含气砂岩表现出低的泊松比(小于0.20)和声阻抗降低(小于12000 g·cm-3×m·s-1),因此,应用叠前地震反演获得的泊松比,以及泊松比与声阻抗交会能够较好的预测岩性、储层和含气性(杨华等,2013;王大兴等,2014).
|
图 13 苏里格气田泊松比及与纵波阻抗交会 Fig. 13 Poisson′s ratio versus P-wave impedance in Sulige gas field |
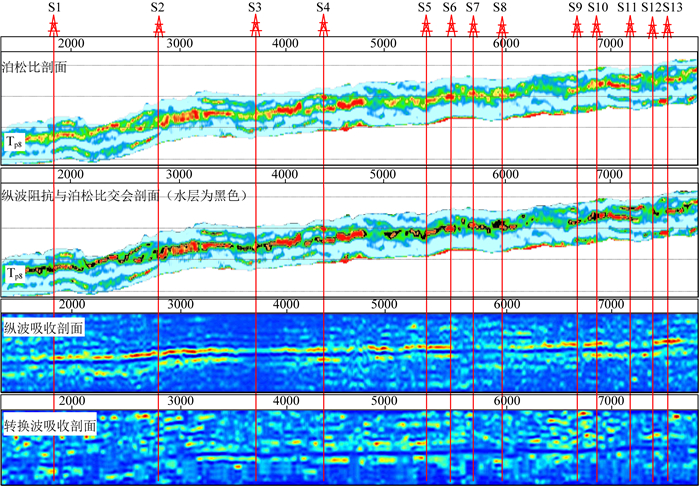
苏里格气田位于鄂尔多斯盆地北部的沙漠区,气田北部表层条件优越,共采集了全数字三分量三维103 km2和全数字三分量二维5360 km的的地震资料,通过多波处理特别是转换波成像处理技术攻关(杨华等,2013;王大兴等,2014),获得了高品质的纵横波叠前分偏移距叠加剖面,根据苏里格气田建立的致密砂岩储层岩石物理模型研究成果,充分利用纵横波联合叠前反演及参数交会以及纵横波吸收衰减,对储层的气水分布进行探索性预测.图 14为苏里格气田某多波测线叠前反演泊松比及与波阻抗交会、纵横波吸收剖面,其中,泊松比剖面能够很好的指示岩性,可以较好的区分砂岩(红色、黄色和绿色部分)和泥岩(浅蓝色和蓝色部分);泊松比与波阻抗交会剖面,可以较好的预测含气异常,也就是可以区分含气层(红色部分)和含水层(黑色部分);纵横波吸收剖面中纵波对含流体比较敏感,呈现出含气层有规律的分布特征,而横波对流体不敏感,呈现出的规律性不强,高异常(黄色和红色)表现出高孔隙砂岩分布非均质性极强的特征.该剖面共计有13口(S1-S13)检验井,分为气井、气水井、低产井和水井四种类型,典型代表了苏里格气田气水分布特征.通过地震属性参数泊松比、泊松比与波阻抗交会,以及纵横波吸收验证,苏里格致密砂岩储层岩石物理模型指导下的储层预测和流体检测,仅有2口井验证不符合,表明岩石物理模型理论应用与实际生产中流体检测结合取得了较好的效果.
|
图 14 苏里格气田某多波测线叠前反演泊松比及与波阻抗交会、纵横波吸收剖面 Fig. 14 Sections of Poisson′s ratio, P-wave impedance versus Poisson′s ratio, P-wave attenuation, and S-wave attenuation in Sulige gas field |
根据图 14剖面上的四类储层流体特征(气井、气水井、低产井和水井),建立了四种地震属性响应模式,其详细表述如下:
(1) 储层为优质气层型,试气为工业流井和高产气流井:地震属性响应为低泊松比、纵波阻抗与泊松比交会大正异常、高纵波吸收、高横波吸收.如图 14中,S6和S13试气均为高产工业流井(井口产量气分别为14.7和9.8万方/日).唯S7井纵横波吸收都不明显,但井口产量试气为4.5万方/日工业气流,与地震预测不相符.
(2) 储层为气水同层型,试气为产气水井;地震属性响应为低泊松比、纵波阻抗与泊松比交会中异常、高纵波吸收、中高横波吸收.如图 14中,S4和S9钻遇气水层,试气为产气水井(井口产量气分别为2.1和3.1万方/日,产水分别为18和4.5方/日).S11井虽然也为产气水井(井口产量气2.0,产水7.5方/日),但纵横波吸收不明显,地震预测不符合.
(3) 储层为差气层型,试气均为低产气流井:地震属性响应为中低泊松比、纵波阻抗与泊松比交会无异常、中高纵波吸收、中低横波吸收,表明物性差.如图 14中,S2、S8、S10和S12钻遇差气层,试气均为低产气流井(井口产量气分别为0.108、0.8、1.4和1.5万方/日).
(4) 储层为产水层型,试气均为产水井;地震属性响应为中低泊松比、纵波阻抗与泊松比交会负异常、中高纵波吸收、中低横波吸收,表明含水.如图 14中,S1、S3和S5钻遇含气水层,试气均为产水井(井口产量气分别为1.5、0.27、0.36万方/日,产水分别为42、21.5和3方/日).
4 结论通过对苏里格气田上古生界二叠系石盒子组盒8致密砂岩实验室岩石物理测定的大量数据按孔隙度分组进行系统分析,详细研究了不同孔隙度下各类弹性参数随含气饱和度的变化情况,在此基础上,认为低孔隙度下Brie (e=2)模型能够表征苏里格气田致密储层物理参数随含气饱和度变化的规律,如泊松比随含气饱和度呈近似负线性关系,而非高孔高渗的Wood模型中含气饱和度大于20%时地震弹性属性无法预测其含气饱和度的变化,为致密含气储层预测提供了理论和实验基础.根据这一岩石物理模型研究成果,应用纵横波联合叠前反演和致密储层敏感参数交会分析,以及纵横波吸收衰减特征研究等手段,对比苏里格气田盒8致密储层的四类流体特征建立了四种地震属性的响应模式,对储层的气水分布进行了探索性预测,取得了理论模型与实际预测结合较好的验证成果.
致谢本文方法研究中蔡克汉工程师参与了部分图件制作,在此致谢!
| Ba J. Progress and Review of Rock Physics.Beijing: Tsinghua University Press, 2013. | |
| Ba J, Carcione J M, Cao H, et al. 2012. Velocity dispersion and attenuation of P waves in partially-saturated rocks: Wave propagation equations in double-porosity medium. Chinese J. Geophys., 55(1): 219-231. DOI:10.6038/j.issn.0001-5733.2012.01.021 | |
| Ba J, Yan X F, Chen Z Y, et al. 2013. Rock physics model and gas saturation inversion for heterogeneous gas reservoirs. Chinese J. Geophys., 56(5): 1696-1706. DOI:10.6038/cjg20130527 | |
| Bai J Y, Song Z X, Su L, et al. 2012. Error analysis of shear-velocity prediction by the Xu-White model. Chinese J. Geophys., 55(2): 589-595. DOI:10.6038/j.issn.0001-5733.2012.02.021 | |
| Biot M A. 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid.I. Low-frequency range. The Journal of the Acoustical Society of America, 28(2): 168-178. DOI:10.1121/1.1908239 | |
| Biot M A. 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid.II. Higher frequency range. The Journal of the Acoustical Society of America, 28(2): 179-191. DOI:10.1121/1.1908241 | |
| Brie A, Pampuri F, Marsala A F, et al. 1995. Shear sonic interpretation in gas-bearing sands.//SPE Annual Technical Conference and Exhibition. Dallas, Texas: SPE. | |
| Chen Y, Huang T F, Liu E R. Rock Physics.Hefei: Press of University of Science and Technology of China, 2009. | |
| Domenico S N. 1977. Elastic properties of unconsolidated porous sand reservoirs. Geophysics, 42(7): 1339-1368. DOI:10.1190/1.1440797 | |
| Dutta N C, Odé H. 1979. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model, ) Part I-Biot theory. Geophysics, 44(11): 1777-1788. DOI:10.1190/1.1440938 | |
| Eshelby J D. 1957. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 241(1226): 376-396. DOI:10.1098/rspa.1957.0133 | |
| Gao J H, Yang S L, Wang D X. 2008. Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data. Chinese J. Geophys., 51(3): 853-861. | |
| Han D H, Batzle M L. 2004. Gassmann's equation and fluid-saturation effects on seismic velocities. Geophysics, 69(2): 398-405. DOI:10.1190/1.1707059 | |
| Hashin Z, Shtrikman S. 1963. A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of the Mechanics and Physics of Solids, 11(2): 127-140. DOI:10.1016/0022-5096(63)90060-7 | |
| Hill R. 1952. The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society, Section A, 65(5): 349-354. DOI:10.1088/0370-1298/65/5/307 | |
| Hilterman F J. 2006. Seismic Amplitude Interpretation (in Chinese). Sun X P, Zhao L W, et al., trans. Beijing: Petroleum Industry Press. | |
| Huang X D, Li M. Poroelastic and Hydrocarbon Detection.Beijing: Petroleum Industry Press, 2012. | |
| Hudson J A. 1980. Overall properties of a cracked solid. Mathematical Proceedings of the Cambridge Philosophical Society, 88(2): 371-384. DOI:10.1017/S0305004100057674 | |
| Hudson J A. 1981. Wave speeds and attenuation of elastic waves in material containing cracks. Geophysical Journal International, 64(1): 133-150. DOI:10.1111/j.1365-246X.1981.tb02662.x | |
| Hudson J A. 1994. Overall properties of a material with inclusions or cavities. Geophysical Journal International, 117(2): 555-561. DOI:10.1111/gji.1994.117.issue-2 | |
| Jiang L X, Shi X J. 1998. Relation between wave velocity in sandstone and fluid content in porous medium under high frequency condition. OGP, 33(3): 355-362. | |
| Jiang R, Zeng Q C, Huang J Q, et al. 2015. Tight gas saturation detection by most sensitive AVO attributes with rock physics analysis. Science Technology and Engineering, 15(1): 163-167. | |
| Kuster G T, Toksöz M N. 1974. Velocity and attenuation of seismic waves in two-phase media: Part I, Theoretical formulations. Geophysics, 39(5): 587-606. DOI:10.1190/1.1440450 | |
| Li W X, Shi G, Wang H, et al. 2007. The study on the relationships of elastic properties of rock physics. Progress in Geophysics, 22(5): 1380-1385. | |
| Liu H J. 2009. Summarization of seismic rock physics research. Petroleum Geophysics, 7(3): 1-8. | |
| Ma S F, Han D K, Gan L D, et al. 2010. A review of seismic rock physics models. Progress in Geophys., 25(2): 460-471. DOI:10.3969/j.issn.1004-2903.2010.02.012 | |
| Mavko G, Nur A. 1975. Melt squirt in the asthenosphere. Journal of Geophysical Research, 80(11): 1444-1448. DOI:10.1029/JB080i011p01444 | |
| Nie J X, Yang D H, Ba J. 2010. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay. Chinese J. Geophys., 53(2): 385-392. DOI:10.3969/j.issn.0001-5733.2010.02.016 | |
| O'Connell R J, Budiansky B. 1974. Seismic velocities in dry and saturated cracked solids. Journal of Geophysical Research, 79: 5412-5426. DOI:10.1029/JB079i035p05412 | |
| Pride S R, Berryman J G. 2003a. Linear dynamics of double-porosity dual-permeability materials.I. Governing equations and acoustic attenuation. Physical Review E, 68(3): 036603. DOI:10.1103/PhysRevE.68.036603 | |
| Pride S R, Berryman J G. 2003b. Linear dynamics of double-porosity dual-permeability materials.II. Fluid transport equations. Physical Review E, 68(3): 036604. DOI:10.1103/PhysRevE.68.036604 | |
| Reuss A. 1929. Berechnung der Flieβgrenzen von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Zeitschrift für Angewandte Mathematik und Mechanik, 9(1): 49-58. DOI:10.1002/(ISSN)1521-4001 | |
| Shi G, Shen W L, Yang D Q. 2003. The relationship of wave velocities with saturation and fluid distribution in pore space. Chinese J. Geophys., 46(1): 138-142. | |
| Shi X J, Xu G M, Jin P, et al. 1995. The laboratory study of influence of water saturation on rock's velocity and attenuation. Acta Geophysica Sinica, 38(Suppl. I): 281-287. | |
| Sothcott J, McCann C, O'Hara S G. 2000. The influence of two different pore fluids on the acoustic properties of reservoir sandstones at sonic and ultrasonic frequencies.//SEG Technical Program Expanded Abstracts. SEG: 1883-1886. | |
| Voigt W. Lehrbuch der Kristallphysik.Leipzig: Teubner, 1910. | |
| Walsh J B. 1965. The effect of cracks on the compressibility of rock. J. Geophys. Res., 70(2): 381-389. DOI:10.1029/JZ070i002p00381 | |
| Wang D X, Xin K F, Li Y M, et al. 2006. An experimental study of influence of water saturation on velocity and attenuation in sandstone under stratum conditions. Chinese J. Geophys., 49(3): 908-914. | |
| Wang D X, Zhang M B, Chen J, et al. 2014. Application of multi-wave seismic in tight sandstone gas reservoir exploration. OGP, 49(5): 946-953, 1005. | |
| White J E. 1975. Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics, 40(2): 224-232. DOI:10.1190/1.1440520 | |
| Wood A B. A Textbook of Sound.New York: the MacMillan Co, 1955. | |
| Wu X Y, Chen Z A, Wei J X. 2000. A technique for measuring ultrasonic velocity and attenuation spectra. Chinese Journal of Rock Mechanics and Engineering, 19(S1): 895-898. | |
| Xu S Y, White R E. 1995. A new velocity model for clay-sand mixtures. Geophysical Prospecting, 43(1): 91-118. DOI:10.1111/gpr.1995.43.issue-1 | |
| Xu S Y, White R E. 1996. A physical model for shear-wave velocity prediction. Geophysical Prospecting, 44(4): 687-717. DOI:10.1111/gpr.1996.44.issue-4 | |
| Yang D H, Chen X H. 2001. BISQ model for fluid-filled, porous medium. OGP, 36(2): 146-159. | |
| Yang H, Wang X S, Wang D X, et al. Sulige Gas Field Multi-Wave Seismic Exploration in a Key Technology.Beijing: Petroleum Industry Press, 2013. | |
| Yang Z F, Cao H. 2009. Review of progresses in seismic rock physics. Progress in Geophys., 24(3): 893-899. DOI:10.3969/j.issn.1004-2903.2009.03.011 | |
| Zhao L X, Chen K G, Wang W W, et al. New Technology of Acoustic Logging and Application Practice.Beijing: Petroleum Industry Press, 2012. | |
| Zou C N, Tao S Z, Hou L H, et al. Unconventional Oil and Gas Geology.Beijing: Geological Publishing House, 2011. | |
| 巴晶. 岩石物理学进展与评述.北京: 清华大学出版社, 2013. | |
| 巴晶, CarcioneJ M, 曹宏, 等. 2012. 非饱和岩石中的纵波频散与衰减:双重孔隙介质波传播方程. 地球物理学报, 55(1): 219–231. DOI:10.6038/j.issn.0001-5733.2012.01.021 | |
| 白俊雨, 宋志翔, 苏凌, 等. 2012. 基于Xu-White模型横波速度预测的误差分析. 地球物理学报, 55(2): 589–595. DOI:10.6038/j.issn.0001-5733.2012.02.021 | |
| 陈颙, 黄庭芳, 刘恩儒. 岩石物理学.合肥: 中国科学技术大学出版社, 2009. | |
| Hilterman F J. 2006.地震振幅解释.孙夕平, 赵良武等译.北京:石油工业出版社. | |
| 黄绪德, 李明. 孔隙弹性与油气预测.北京: 石油工业出版社, 2012. | |
| 蒋立新, 施行觉. 1998. 高频条件下砂岩波速与多孔隙介质流体含量关系的研究. 石油地球物理勘探, 33(3): 355–362. | |
| 姜仁, 曾庆才, 黄家强, 等. 2015. 基于岩石物理分析的致密砂岩流体检测方法研究. 科学技术与工程, 15(1): 163–167. | |
| 刘浩杰. 2009. 地震岩石物理研究综述. 油气地球物理, 7(3): 1–8. | |
| 马淑芬, 韩大匡, 甘利灯, 等. 2010. 地震岩石物理模型综述. 地球物理学进展, 25(2): 460–471. DOI:10.3969/j.issn.1004-2903.2010.02.012 | |
| 聂建新, 杨顶辉, 巴晶. 2010. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究. 地球物理学报, 53(2): 385–392. DOI:10.3969/j.issn.0001-5733.2010.02.016 | |
| 施行觉, 徐果明, 靳平, 等. 1995. 岩石的含水饱和度对纵、横波速及衰减影响的实验研究. 地球物理学报, 38(增刊1): 281–287. | |
| 王大兴, 辛可锋, 李幼铭, 等. 2006. 地层条件下砂岩含水饱和度对波速及衰减影响的实验研究. 地球物理学报, 49(3): 908–914. | |
| 王大兴, 张盟勃, 陈娟, 等. 2014. 多波地震技术在致密砂岩气藏勘探中的应用. 石油地球物理勘探, 49(5): 946–953, 1005. | |
| 伍向阳, 陈祖安, 魏建新. 2000. 一种测量岩石声波速度和衰减谱的技术. 岩石力学与工程学报, 19(S1): 895–898. | |
| 杨顶辉, 陈小宏. 2001. 含流体多孔介质的BISQ模型. 石油地球物理勘探, 36(2): 146–159. | |
| 杨华, 王喜双, 王大兴, 等. 苏里格气田多波地震勘探关键技术.北京: 石油工业出版社, 2013. | |
| 杨志芳, 曹宏. 2009. 地震岩石物理研究进展. 地球物理学进展, 24(3): 893–899. DOI:10.3969/j.issn.1004-2903.2009.03.011 | |
| 赵立新, 陈科贵, 王文文, 等. 声波测井新技术及应用实践.北京: 石油工业出版社, 2012. | |
| 邹才能, 陶士振, 侯连华, 等. 非常规油气地质.北京: 地质出版社, 2011. | |
 2016, Vol. 59
2016, Vol. 59

