跨孔雷达是一种高效的浅层地球物理探测技术,能够提供两个钻孔之间的高分辨率地质剖面图像(Pettinelli et al., 2009; Liu and Sato, 2002;Liu et al., 2011, 2014).波形反演可以得到精准的地下介质物性参数,其分辨率达到亚波长级别.结合跨孔雷达和波形反演,能得到准确且高分辨率的地下介质物性信息.探地雷达波形反演起步较晚,早期Moghaddam等(1991)在Tarantol (1984)的全波形反演技术上对小目标体介电常数成像做了一些尝试,但没有取得满意的效果,这主要是因为缺乏先验信息来保证收敛.之后Kuroda等(2005)和Ernst等(2007b)分别使用全波形反演的方法对跨孔雷达数据成像,并取得了较好的效果.不同的是,Kuroda等的方法只考虑了介电常数,而Ernst等采用级联更新的办法同时考虑介电常数和电导率.Meles等(2010)提出了矢量全波形反演技术,并且在反演过程中同时迭代介电常数和电导率.Belina等(2012)对全波形反演中源的子波估计部分进行了一些分析.国内方面,吴俊军等(2014)对全波形反演的理论基础进行了详细的推导,使用最速下降法来更新模型参数;周辉等(2014)提出了一种不需要提取源子波的波形反演方法,但只考虑介电常数.
在实际数据的波形反演中,由于源子波未知,通常的办法是在反演过程中加入源子波这一变量,并随着反演的进行更新.当反演结果与真实模型相同时,则估计得到的源子波与真实源子波相同.该方法在处理合成数据时十分有效,但在实际数据反演中表现不佳.这可能是因为实际数据对应的地下介质复杂度高,且数据本身的信噪比较低.在地震波形反演中,已有许多不依赖于源子波的波形反演方法.原理大致可以分成两类:在频率域,利用一道参考波形对数据进行归一化处理,在此过程中自然消除源子波的影响(Lee and Kim, 2003;Xu et al., 2006);另一种为对实际数据和正演数据同时分别卷乘参考道的实际和正演数据,这样新数据中同时包含实际子波和理论子波,从而摆脱源子波的影响(Choi et al., 2005).在探地雷达波形反演中,周辉等(2014)借助已知源子波、地质模型和采集系统的正演数据,将实际数据转换成给定源子波的信号,以避免激发脉冲的求取.
本文实现了一种不依赖于源子波的跨孔雷达时间域波形反演.我们首先对实际数据和一道来自正演数据的参考道做褶积,同样的,对正演数据和一道来自实际数据的参考道做褶积.新的目标函数建立在褶积波场之上,理论上,不论正演过程使用哪种激发脉冲,新的褶积波场都共用相同的源子波.新目标函数的另一个重要特征是正演波场使用的源子波对褶积波场起到低通滤波作用,因此不依赖源子波的时间域波形反演很容易实现多尺度策略.文中使用求导的方法详细推导了不依赖源子波的时间域波形反演的梯度和步长公式,实现了介电常数和电导率的同步反演.不同于Meles等(2010)根据扰动来推导梯度,求导法更加简洁易懂.之后,我们将该方法应用到三组合成数据和两组实际数据中.
2 理论 2.1 目标函数通常情况下,目标函数为实际数据和正演数据之间的l2范数:
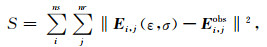
|
(1) |
式中,Ei, j(ε, σ)和Ei, jobs分别为第i个发射在第j个接收位置的正演数据和实际数据,ns和nr分别为源的数目和接收器的数目.将(1)式写成格林函数与源子波的褶积形式,则
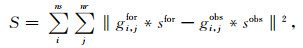
|
(2) |
g和s分别为格林函数和源子波,上角标for和obs分别代表正演数据和实际数据;*号表示褶积过程.波形反演即通过更新模型参数使(2)式所代表的误差最小,但在实际数据处理过程中,源子波sobs必须在反演过程中估计.
为了避免在反演过程中对源子波的估计,本文实现一种不依赖源子波的波形反演.对于同一个源下的所有接收数据,正演数据与一道取自实际数据的参考道褶积;同样的,实际数据也与一道取自正演数据的参考道褶积.新的目标函数为:
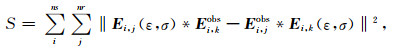
|
(3) |
这里,Ei, k(ε, σ)和Ei, kobs分别为第i个源下取自正演数据和实际数据的参考道,k为参考道对应的接收器位置.同样将(3)式写成格林函数和源子波的褶积形式:
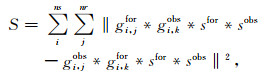
|
(4) |
在(4)式中,等号右端的两项共用了相同的新源子波sfor*sobs.基于褶积过程的自然线性特征,源子波的影响被消去了.因此,建立在(4)式基础上的波形反演不再依赖于源子波.
2.2 目标函数对应的梯度(3)式的l2范数写成点乘形式为:
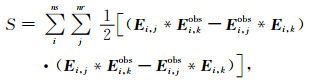
|
(5) |
为简略起见将正演数据E (ε, σ)缩写为E,在之后的推导中不再说明.目标函数对应的梯度由(5)式对模型参数p(ε和σ)的求导来获得:
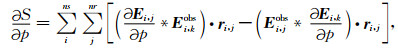
|
(6) |
其中,ri, j=Ei, j* Ei, kobs-Ei, jobs* Ei, k.
我们将(6)式右端第一项写成积分形式:
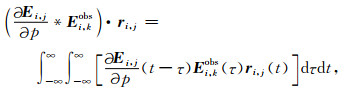
|
(7) |
令t-τ=ξ,则dτ=-dξ.(7)式可以重新写成:

|
(8) |
式中,r′ i, j(ξ)为残差与实际数据参考道的互相关.可以看出(8)式为电场对模型参数的一阶偏导(∂Ei, j/∂p)与互相关残差(r′ i, j)之间点乘后积分的结果,与传统目标函数下波形反演的梯度公式类似.
根据附录A,(8)式重写为:
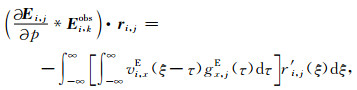
|
(9) |
式中,需要注意的有:vi, xE和gx, jE下角标不同,这是因为虚拟源v是对应发射,而格林函数g则是对应接收;vi, xE和gx, jE对应的时间不同,是因为我们将褶积写成了积分形式.再次的,令ξ-τ=t,则dτ=-dt.重新整理(9)式:
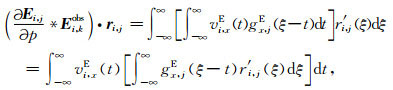
|
(10) |
格林函数gx, jE满足互易定理,即gx, jE=gj, xE.因此,互相关∫-∞∞gx, jE(ξ-t)r′ i, j(ξ) dξ可以被认为是相关残场r′ i, j的后向传播过程.由于(10)式中的后向传播场∫-∞∞gx, jE(ξ-t)r′ i, j(ξ) dξ在时间上是倒置的,因此(10)式也可以被认为是后向传播场与虚拟源之间的零相位褶积.这跟逆时偏移的成像条件类似,区别在于后向传播场的源不同.
(6)式的第二项采用相同的形式推导:
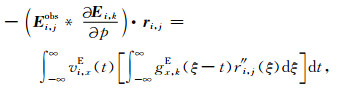
|
(11) |
其中
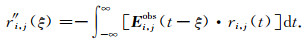
|
(12) |
在(11)式和(12)式中,需要注意的是第二个相关残场r″ i, j只应在第k个参考道位置后向传播.
因此,不依赖源子波的时间域波形反演对应的目标函数梯度的后向传播残场源的第一项为:
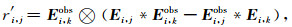
|
(13) |
对应在每个接收器位置j.第二项后向传播残场源为:
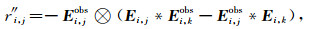
|
(14) |
只在第k个参考道位置后向传播.由于第一项和第二项后向传播是在同一时间进行的,因此只需要一次正演即可完成.在(13)和(14)式中,⊗代表互相关.对于(13)式,只有实际数据的参考道与残场的每一项进行相关;而在(14)式中,为实际数据和残场之间逐道之间的相关.在实际操作中,(14)式对应的第二项后向传播残场源被累加在一起作为一道信号在参考道位置k处反向传播.
最后,给出最终的梯度表达式:
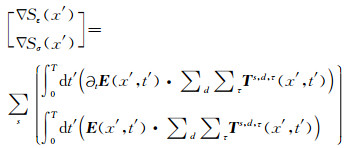
|
(15) |
其中
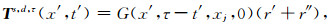
|
(16) |
T为后向传播场,(16)式中的格林函数G表明了其在时间上的反向传播.
2.3 迭代步长的求解在本文的波形反演中,分别沿着介电常数和电导率的负梯度方向寻找最佳步长,实现两者的同步反演.第n次反演对应的目标函数为:
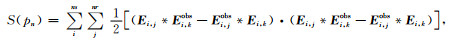
|
(17) |
这里,p代表模型参数(ε和σ).则第n+1次目标函数为:
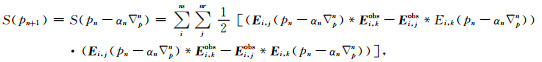
|
(18) |
其中,Eobs为实际数据,E为正演数据,Δpn为第n次迭代的梯度,且有:
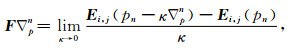
|
(19) |
F代表电场E在模型参数p处的线性因子.由于本文按照负梯度方向搜索步长,因此:
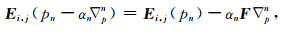
|
(20) |
将(20)式代入(18)式:
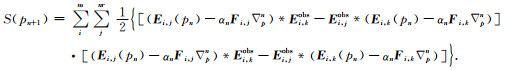
|
(21) |
注意,在(21)式中,Ei, j和Ei, k的下标不同,但对应的为同一个梯度方向Δpn.重新整理(21)式:
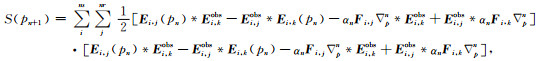
|
(22) |
当S(pn+1)最小时,满足
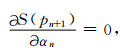
|
(23) |
这时,αn为最佳步长:
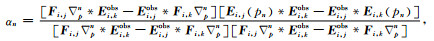
|
(24) |
在同步反演中,分别沿负ΔSε和ΔSσ方向各自寻找最佳步长,因此需要给定两个不同的小稳定因子κε和κσ.将(19)式代入(24)式,则具体的步长公式为:
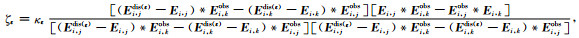
|
(25) |
其中,Ei, jdis (ε)=[Ei, j(ε+κεΔSε)-Ei, j(ε)].
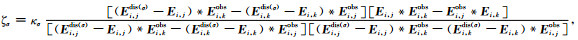
|
(26) |
其中,Ei, jdis (σ)=[Ei, j(σ+κσΔSσ)-Ei, j(σ)].
迭代公式为:
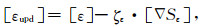
|
(27) |
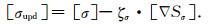
|
(28) |
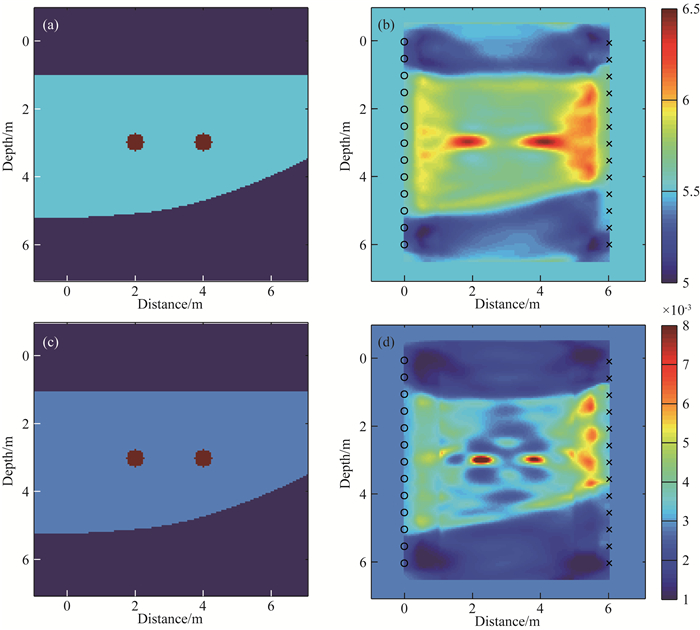
本节给出复杂模型下,同步反演介电常数和电导率的结果.模型如图 1所示,图 1a为介电常数模型,图 1c为电导率模型.该模型分为三层,其中第一层和第三层介质相同,相对介电常数为5,电导率为0.001 S·m-1.中间层的相对介电常数为5.5,电导率为0.0028 S·m-1.中间层埋藏了两个管状异常体,它们的直径为0.5 m,间隔2 m,相对介电常数为7,电导率为0.008 S·m-1.发射和接收器的位置分别用圆圈和叉表示.初始模型为均匀地层,其相对介电常数为5.5,电导率为0.0028 S·m-1,与中间层相同.
|
图 1 (a)介电常数真实模型;(b)介电常数反演结果;(c)电导率真实模型;(d)电导率反演结果 Fig. 1 (a) True model of permittivity; (b) Permittivity from source-independent waveform inversion; (c) True model of conductivity; (d) Conductivity from source-independent waveform inversion |
图 1b和图 1d分别为同时反演的介电常数和电导率结果,图中上下两个界面清晰,也能够分辨出两根管状异常体的大小和位置.从整体上看,电导率的反演结果要优于介电常数,表现在两个管状异常体的电导率反演结果在形状和数值上都与真实模型更接近.但反演结果中出现了较多的假异常,这是由于本文的波形反演在梯度计算过程中包含了数据之间的褶积和互相关处理,提高了反演过程的非线性程度.加上本节算例中模型的复杂度较高,且在反演过程中介电常数和电导率之间互相作用,导致源的近场干扰更加强烈.
3.2 实际数据--贵州数据采集地位于中国西南的贵州省,地貌属于高原山地,并且境内喀斯特地貌发育丰富,岩溶分布范围广泛.采集过程使用中心频率为100 MHz的MALA钻孔雷达系统,探测的两个钻孔之间的水平距离为18 m.反演中使用的数据包含40组发射,其中发射源以1 m等间隔分布在9 m至48 m深度范围内.接收器的总覆盖范围为0 m至47 m,但每个源对应的接收器范围和数目都不相同.由于缺乏对应地质资料,无法获得钻孔所在地详细的地质信息.初始模型分别由走时成像和重心频率下降法(Liu et al., 1998)得到.
在对实际数据进行波形反演之前,首先对实际数据进行了一系列的预处理,包括提取数据、滤波.之后,采用Ernst等(2007a)的办法对实际数据做三维校正,另外在实际数据的波形反演过程中,共进行了三次源子波估计.
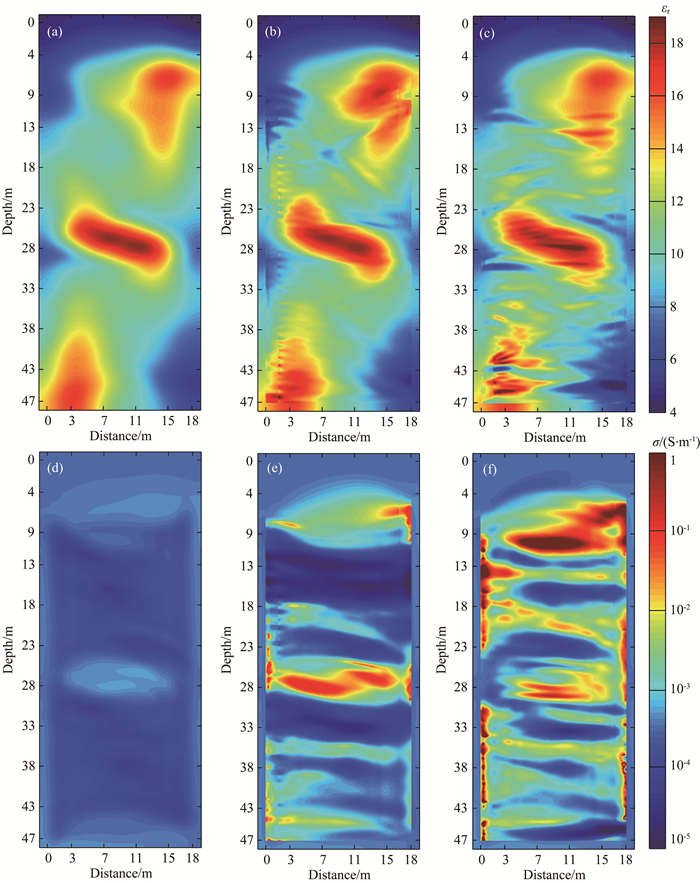
图 2a和图 2b为反演中使用的介电常数和电导率初始模型,分别由走时成像和重心频率下降法得到.走时成像得到的介电常数效果较好,而重心频率下降法得到的电导率只能反映出地层中异常体的相对变化,其数值是不准确的.图 2b和图 2e为使用反褶积法估计源子波的时间域波形反演结果,图 2c和图 2f为不依赖源子波的时间域波形反演结果.从整体来看,由波形反演得到的电导率结果分辨率更高,反映了地下介质的精细结构,而且与介电常数的反演结果吻合较好,都表现出左下和右上区域在数值上较高的特征.对比图 2c和图 2f,发现两者相对于图 2a变化较小,这主要是因为走时成像技术十分成熟,其结果已经较为准确.尽管图 2b和图 2c中均体现了更多的细节,这些细节难以解释.我们认为图 2c的结果更为准确,比如图 2c在深度43 m处的异常与电导率一致,而图 2b中无这种特征.对比图 2e和图 2f,两者都反映了地层特征,如深度18 m处、深度35 m处及深度45 m处.但图 2f的结果更加清晰,分辨率更高.除此之外,图 2f中在深度13 m位置有一水平薄层,而图 2e中无体现.我们认为不依赖源子波的时间域波形反演结果更加准确可靠,优于使用估计源子波的时间域波形反演.
|
图 2 贵州实际数据 (a)介电常数初始模型;(b)使用估计源子波的介电常数反演结果;(c)不依赖源子波的介电常数反演结果;(d)电导率初始模型;(e)使用估计源子波的电导率反演结果;(f)不依赖源子波的电导率反演结果. Fig. 2 Field data of Guizhou (a) Initial model of permittivity; (b) Permittivity from inversion using estimated source wavelets; (c) Permittivity from source-independent inversion; (d) Initial model of conductivity; (e) Conductivity from inversion using source wavelets; (f) Conductivity from source-independent inversion. |
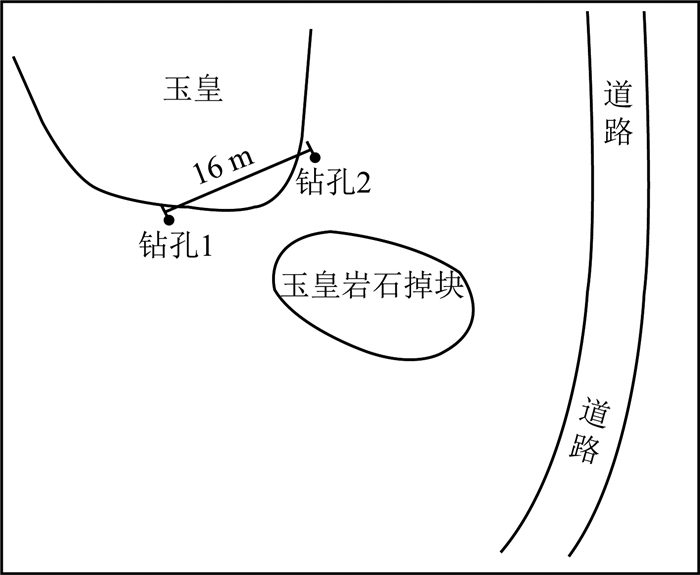
岫岩位于辽东半岛北部,是我国著名的玉石产地之一.1995年,于岫岩哈达碑镇发现世界最大玉体--‘玉皇’.‘玉皇’高25 m,最大直径30 m,总体积达2.4×104 m3,总重量约6×104 t.本次数据采集位置在巨型玉石‘玉皇’脚下,目的是探测地基稳定状况、采空区层数、充填情况及稳定状况.采集过程使用基于矢量网络分析仪的自制钻孔雷达天线系统,中心频率为100 MHz.两个钻孔之间的距离为16 m,如图 3所示.共有32个发射源,范围从29.5 m到67.5 m等间隔分布,每组发射对应28个接收器.接收器序列1 m等间隔排列,且随源的每次下移整体向下移动1 m.
|
图 3 ‘玉皇’现场照片及钻孔位置示意图 Fig. 3 Scene photo of 'Yuhuang' and schematic diagram of borehole location |
图 3中,开裂的岩体为‘玉皇’,人站立的位置为岩石掉块.根据已有的地质资料,我们得知:‘玉皇’巨型玉体下部0~100 m深度范围内存在五层以上的巷道,分属不同的矿山.这些巷道中,有的已经坍塌,有的尚在使用中.
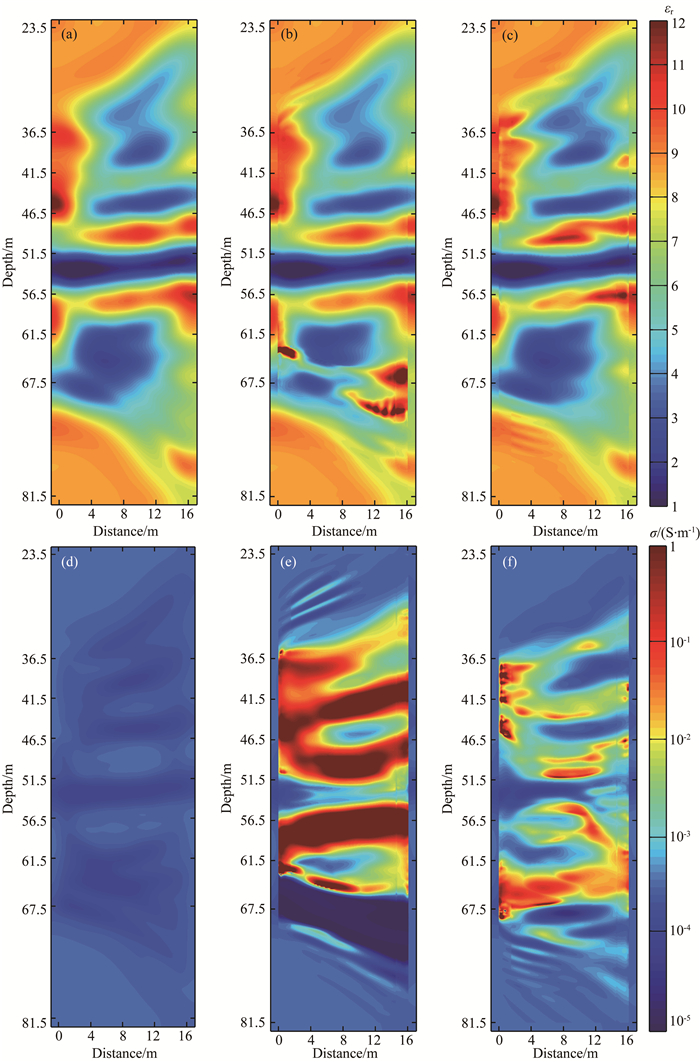
图 4a和图 4d分别为走时成像和重心频率下降法得到的介电常数和电导率分布图像.图 4b和图 4e为使用估计源子波的时间域波形反演结果,图 4c和图 4f为不依赖源子波的时间域波形反演结果.由于该组实际数据的信噪比不高,在使用反褶积估计源子波时仅使用了部分数据(深度62.5~67.5 m).在使用估计源子波的整个反演过程中共进行三次源子波估计,但后两次仅用来修正估计源子波的振幅.由于只使用了部分数据估计源子波,在反演过程中缺乏对源子波相位的修正,图 4b中深度67.5 m处的异常可能是由估计源子波和真实源子波之间的相位差异造成的.图 4e的电导率反演结果的最大值超过了1 S·m-1,最小值低于0.01 mS·m-1,这种不合理反映了估计源子波在振幅上是不准确的.这种不准确表现在两个互相矛盾的方面:以深度61.5 m处为分界线,上半部分表明估计源子波的振幅较小,因而整体电导率结果较大;下半部分表明估计源子波的振幅较大,所以电导率的结果较小.造成这种现象的原因在于数据质量不高,反褶积法无法得到可靠的源子波.图 4f与图 4e在整体上表现一致,但图 4f在数值上更为合理,这是因为消除了源的影响.图 4f在深度61.5至67.5 m范围内表现出电导率较高的层状结构,图 4e在相同位置也有所体现.因此,在实际数据质量不高的情况下,使用估计源子波的波形反演难以得到好的反演结果,不依赖源子波的波形反演具有更大的优势.
|
图 4 岫岩实际数据 (a)介电常数初始模型;(b)使用估计源子波的介电常数反演结果;(c)不依赖源子波的介电常数反演结果;(d)电导率初始模型;(e)使用估计源子波的电导率反演结果;(f)不依赖源子波的电导率反演结果. Fig. 4 Field data of Xiuyan (a) Initial model of permittivity; (b) Permittivity from inversion using source wavelets; (c) Permittivity from source-independent inversion; (d) Initial model of conductivity; (e) Conductivity from inversion using source wavelets; (f) Conductivity from source-independent inversion. |
本文实现了一种不依赖源子波的时间域跨孔雷达波形反演,其原理是建立一个新的基于褶积波场的目标函数.在该目标函数中,通过褶积使实际数据和正演数据共用相同的新源项,从而消去了源子波的影响.通过求导的方式详细推导了目标函数对应的梯度和步长公式,并引入地震波形反演中的虚拟源概念.
为了验证文中不依赖源子波的波形反演效果,同时对一个合成数据模型反演介电常数和电导率,结果表明该方法能够重建亚波长尺寸的异常体和地层结构.最后,我们将该方法应用到两组实际数据中.其中贵州实际数据质量较好,使用估计源子波和不依赖源子波两种波形反演均能得到可靠的反演结果,但通过对比我们认为不依赖源子波的波形反演效果更佳,这可能是估计得到的源子波与实际源子波仍存在差异造成的.而岫岩实际数据的信号质量较差,使用反褶积法估计源子波具有很大的难度,最终的反演结果较差.在这种情况下,更能体现出不依赖源子波波形反演的价值.
尽管不依赖源子波的波形反演在理论上更加先进,这种方法也带来一些问题.最主要的是该方法在梯度计算过程中需要进行褶积和互相关运算,较大地提高了反演的非线性,因此需要更好的初始模型和反演策略来保证收敛.由于在频率域更易于实现多尺度策略,未来我们考虑研究频率域不依赖源子波的波形反演.
附录A 虚拟源原理对于Maxwell方程:
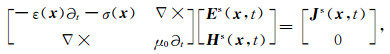
|
(A1) |
在时间域,我们可以简写成:
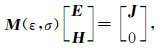
|
(A2) |
(A2)式两端分别对模型参数p求导,并忽略磁场项:
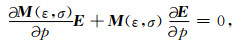
|
(A3) |
整理可得:
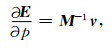
|
(A4) |
其中
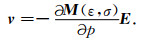
|
(A5) |
v为虚拟源(Pratt et al., 1998; Shin et al., 2001),对于不同的模型参数(ε,σ)具有不同的表达式;M-1等同于格林函数g.对于时间域Maxwell方程而言,有
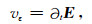
|
(A6) |
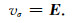
|
(A7) |
对于(A2)式,如果忽略磁场项,写成包含格林函数的形式:
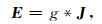
|
(A8) |
则对比(A2)(A4)(A5)(A8)可以得出:
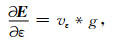
|
(A9) |
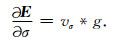
|
(A10) |
| Belina F A, Irving J, Ernst J R, et al. 2012. Waveform inversion of crosshole georadar data: influence of source wavelet variability and the suitability of a single wavelet assumption. IEEE Transactions on Geoscience and Remote Sensing, 50(11): 4610-4625. DOI:10.1109/TGRS.2012.2194154 | |
| Choi Y, Shin C, Min D J, et al. 2005. Efficient calculation of the steepest descent direction for source-independent seismic waveform inversion: An amplitude approach. Journal of Computational Physics, 208(2): 455-468. DOI:10.1016/j.jcp.2004.09.019 | |
| Ernst J R, Green A G, Maurer H, et al. 2007a. Application of a new 2D time-domain full-waveform inversion scheme to crosshole radar data. Geophysics, 72(5): J53-J64. DOI:10.1190/1.2761848 | |
| Ernst J R, Maurer H, Green A G, et al. 2007b. Full-waveform inversion of crosshole radar data based on 2-D finite-difference time-domain solutions of Maxwell's equations. IEEE Transactions on Geoscience and Remote Sensing, 45(9): 2807-2828. DOI:10.1109/TGRS.2007.901048 | |
| Kuroda S, Takeuchi M, Kim H J. 2005. Full waveform inversion algorithm for interpreting cross-borehole GPR data.//75th Annual International Meeting, SEG, Expanded Abstracts: 1176-1180. | |
| Lee K H, Kim H J. 2003. Source-independent full-waveform inversion of seismic data. Geophysics, 68(6): 2010-2015. DOI:10.1190/1.1635054 | |
| Liu L B, Lane J W, Quan Y L. 1998. Radar attenuation tomography using the centroid frequency downshift method. Journal of Applied Geophysics, 40(1-3): 105-116. DOI:10.1016/S0926-9851(98)00024-X | |
| Liu S X, Sato M. 2002. Electromagnetic logging technique based on borehole radar. IEEE Transactions on Geoscience and Remote Sensing, 40(9): 2083-2092. DOI:10.1109/TGRS.2002.803847 | |
| Liu S X, Wu J J, Zhou J F, et al. 2011. Numerical simulations of borehole radar detection for metal ore. IEEE Transactions on Geoscience and Remote Sensing, 8(2): 308-312. DOI:10.1109/LGRS.2010.2066545 | |
| Liu S X, Lei L L, Fu L, et al. 2014. Application of pre-stack reverse time migration based on FWI velocity estimation to ground penetrating radar data. Journal of Applied Geophysics, 107: 1-7. DOI:10.1016/j.jappgeo.2014.05.008 | |
| Meles G A, van der Kruk J, Greenhalgh S A, et al. 2010. A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole/borehole-to-surface GPR data. IEEE Transactions on Geoscience and Remote Sensing, 48(9): 3391-3407. DOI:10.1109/TGRS.2010.2046670 | |
| Moghaddam M, Chew W C, Oristaglio M. 1991. Comparison of the born iterative method and Tarantola's method for an electromagnetic time-domain inverse problem. International Journal of Imaging Systems and Technology, 3(4): 318-333. DOI:10.1002/(ISSN)1098-1098 | |
| Pettinelli E, Di Matteo A, Mattei E, et al. 2009. GPR response from buried pipes: Measurement on field site and tomographic reconstructions. IEEE Transactions on Geoscience and Remote Sensing, 47(8): 2639-2645. DOI:10.1109/TGRS.2009.2018301 | |
| Pratt G, Shin C, Hicks G L. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x | |
| Shin C, Jang S, Min D J. 2001. Improved amplitude preservation for prestack depth migration by inverse scattering theory. Geophysical Prospecting, 49(5): 592-606. DOI:10.1046/j.1365-2478.2001.00279.x | |
| Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 | |
| Wu J J, Liu S X, Li Y P, et al. 2014. Study of cross-hole radar tomography using full-waveform inversion. Chinese J. Geophys. (in Chinese), 57(5): 1623-1635. DOI:10.6038/cjg20140525 | |
| Xu K, Greenhalgh S A, Wang M Y. 2006. Comparison of source-independent methods of elastic waveform inversion. Geophysics, 71(6): R91-R100. DOI:10.1190/1.2356256 | |
| Zhou H, Chen H M, Li Q Q, et al. 2014. Waveform inversion of ground-penetrating radar data without needing to extract exciting pulse. Chinese J. Geophys.(in Chinese), 57(6): 1968-1976. DOI:10.6038/cjg20140627 | |
| 吴俊军, 刘四新, 李彦鹏, 等. 2014. 跨孔雷达全波形反演成像方法的研究. 地球物理学报, 57(5): 1623–1635. DOI:10.6038/cjg20140525 | |
| 周辉, 陈汉明, 李卿卿, 等. 2014. 不需提取激发脉冲的探地雷达波形反演方法. 地球物理学报, 57(6): 1968–1976. DOI:10.6038/cjg20140627 | |
 2016, Vol. 59
2016, Vol. 59


