地球物理学报  2016, Vol. 59 Issue (12): 4457-4463   PDF    
引用本文
闫述, 薛国强, 陈明生. 2016. 磁性层状介质的CSAMT电场分量响应特征. 地球物理学报, 59(12): 4457-4463, doi: 10.6038/cjg20161208.  
Yan S, Xue G Q, Chen M S. 2016. Response of CSAMT electromagnetic component in the magnetized layered earth. Chinese J. Geophys. (in Chinese), 59(12): 4457-4463, doi: 10.6038/cjg20161208.  
磁性层状介质的CSAMT电场分量响应特征
闫述1 , 薛国强2 , 陈明生3     
1. 江苏大学计算机科学与通信工程学院, 江苏镇江 212013;
2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 中煤科工集团西安研究院有限公司, 西安 710054
收稿日期 2015-12-02, 2016-10-22 收修定稿
基金项目: 国家重大科研装备研制项目“深部资源探测核心装备研发”（ZDYZ2012-1）-05子项目“多通道大功率电法勘探仪”-04课题“M-TEM资料处理及偏移成像软件研制”，国家自然科学基金（41374129，41474095）联合资助
作者简介: 闫述, 女, 1953年生, 教授, 主要从事电磁场与微波技术研究.E-mail:yanshu@ujs.edu.cn
通讯作者: 薛国强, 男, 1966年生, 研究员, 主要从事电磁探测方法研究.E-mail:ppxueguoqiang@163.com
摘要: 在传统的勘探电磁学理论中，往往把岩层磁导率近似看成空气中的磁导率，从而得到简化后的电磁场响应式，主要用于指导非磁性介质情况下的电磁探测.本文开展了磁性介质的电磁响应理论、数值模拟和特征分析等研究，以便实现对磁性矿体的电磁精细探测.首先推导出磁性层情况下的电磁响应表达式；然后，计算了几种典型磁性介质地质断面的响应曲线，并对其响应特征进行了分析；研究结果表明：当磁性层位于地表时，当表层相对磁导率μr>1.2，磁性层对电磁测深曲线具体明显的影响；当岩层为中间层时，只要μr>1.2，对H型、A型曲线中段会有影响.对H型曲线，主要表现在使极小值处的曲线抬高、变宽，以致使曲线形态发生变化；当磁性层处于最后一层时，不论岩层的磁导率是多少，对各类二、三层曲线来讲，不会影响曲线的形态，只是使渐近线前第一个极值点的位置右移，极值点至渐近线之间的线段变得较为陡峭.
关键词: 电磁学      磁导率      勘探      响应      曲线     
Response of CSAMT electromagnetic component in the magnetized layered earth
YAN Shu1, XUE Guo-Qiang2, CHEN Ming-Sheng3     
1. Telecommunication Engineering, Jiangsu University, Jiangsu Zhenjiang 212013, China;
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. CCTEMG xi an research institute, Xi'an 710054, China
Abstract: In the traditional exploration electromagnetic theory, the rock permeability is usually regard as the air permeability approximately. As a result, the electromagnetic field response can be derived simply. However, study on electromagnetic response considering rock permeability is required for fine electromagnetic detection of magnetic ore bodies. In this paper, electromagnetic field response expressions of the magnetic layered earth is deduced at first, then the response curves of several kinds of typical magnetic medium geological sections are calculated. The research results show that electromagnetic sounding curves are heavily affected by the rock permeability layer when the earth is covered by a magnetic layer with rock permeability μr>1.2. While as H-type and A-type curves are heavily affected by rock permeability (μr>1.2) for the middle layer. On the other hand, when the magnetic layer is buried as the basement, electromagnetic sounding curves are slightly affected by the rock permeability layer..
Key words: Electromagnetic research      Permeability      Exploration      Response      Curve     
1 引言

勘探电磁法是通过观测不同类型的电磁信号以获取地下目标体的电性信息以达到探测的目的，传统的电磁法主要考虑了岩石多种物理特性中的一种，即导电性.目前广泛应用的电磁场理论、勘探技术及数据解释手段也大部分是在该基础上形成的.然而，随着电磁法应用领域的越来越广，人们对勘探精度要求的越来越高，仅仅基于岩石电阻率特性的数据解释在许多情况下已不能满足特定的勘探需求.这就要求考虑多方面的岩石物理特性，以更加全面地解释观测信号，提取更加丰富的岩石物性信息.

磁导率作为岩石的另一种重要物性参数，在通常的理论研究和实际应用中一般不予考虑不同岩石矿物的不同，而将其设定为与空气磁导率一样的常数.这样的处理方式对于那些具有顺磁性或逆磁性的岩石矿物来说差别微乎其微；但是对于那些具有铁磁性或超顺磁性的矿物，当外加磁场与之作用时，将会产生较强的附加磁场，并被接收装置记录，若同样不考虑磁导率带来的这些变化，将会严重影响后期数据处理解释的精度(Ward and Hohamnn, 1991).事实上，相当一部分的岩矿石具有较高的相对磁导率，如磁铁矿和基性岩发育区的矿层和岩层的相对磁导率往往大于1.

对于岩矿石磁性对电磁法带来的影响，很早就引起了人们的注意, 特别是磁性物质对瞬变电磁响应的影响的研究较为深入.Buselli (1982)研究了近地表超顺磁物质对瞬变电磁测深数据的影响；Lee (1984a, 1984b)研究了超顺磁性大地的瞬变电磁响应特性；牛之琏(1985)引用Cole-Cole模型研究了瞬变电磁张弛效应，指出瞬变电磁张弛效应的衰减速度要比导电体瞬变涡流效应慢的多，在晚期有可能测出瞬变电磁张弛效应，磁张弛效应作为一种附加效应，可能成为限制电磁法探测深度的地质噪声源，但是在有利的地质条件下也可以利用磁张弛效应评价复杂磁异常；Kozhevnikov和Antonov (2008, 2009, 2011)分别对均匀大地、两层大地及多层大地的磁张弛效应对瞬变电磁数据的影响进行了研究；殷伟伟(2013)针对稀疏浸染状铁矿的瞬变电磁响应特征进行了分析，并指出了针对此类铁矿石的瞬变电磁探测方法.对于磁性介质对频域响应的影响，国内外的研究主要集中于频域航空电磁法中(Huang and Fraser, 2002; 高亮等，2009).习建军(2010)和王卫平等(2013)都针对基于磁导率和电阻率的频率域航空电磁法的正反演进行了研究.其他的研究还包括：闫述和陈明生(1997)从全场区出发，研究了频率域测深中磁性层对水平电场响应及视电阻率带来的影响，指出磁性层的存在不可忽视，会对视电阻率曲线带来较大的影响.

可控源音频大地电磁法(CSAMT)的波区理论相对比较成熟，近年来，CSAMT单分量观测模式的发展，使得CSAMT的观测从单一的远区平面波区拓展至近区(Xue et al., 2015).为了获取更加精确的解释成果，解决更加复杂的地质勘探任务，特别是实现大深度磁性铁矿的精细探测，非常有必要研究岩矿石磁性特征给CSAMT观测数据及数据解释带来的影响.本文首先推导了考虑磁性层的全场区水平电场频率域表达式以及对应的视电阻率表达式，然后研究了不同相对磁导率情况下的视电阻率变化特点.本文的研究对于识别野外实测CSAMT数据中的磁异常效应，提高数据解释精度具有一定的理论和实际意义.

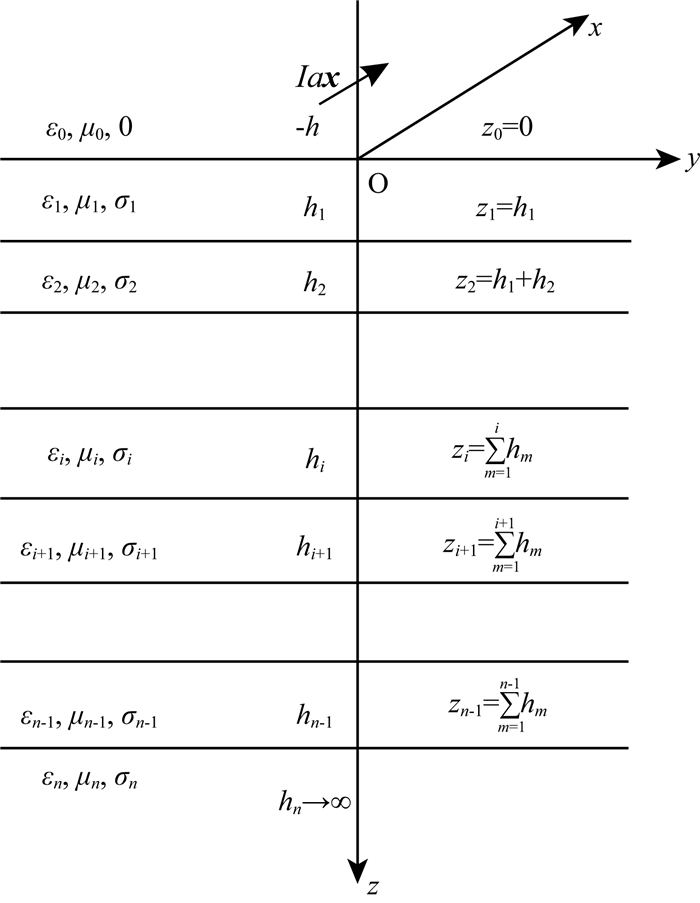
2 水平磁性层电磁响应理论

设空气的磁导率为μ0，分层大地各层的磁导率分别为μ1, μ2, …, μn.在距地面高度为h的(0, 0, h)点放置一个谐变水平电偶极子Iax (见图 1)，x表示单位矢量.

图 1 水平磁性分层介质 Fig. 1 Diagram of layered earth with magnetic permeability

在各层介质的分界面上，例如第层i与第i+1层分界面上引入边界条件：电场强度的切向分量总是连续的；当分界面上无自由面电流时磁场强度的切向分量也是连续的，即

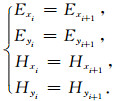
(1)

引入矢量位A求解E和H (张秋光，1983)，公式为

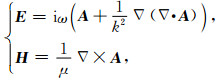
(2)

式中，ω为角频率，A为矢量位，E代表电场矢量，H代表磁场矢量，下标代表不同方向的分量，k为波数，k2=ω2με+iωμσ, 其中，μ、σ和ε分别表示每一层的磁导率、电导率和介电常数.

根据(1)式，矢量位A的边界条件方程可写为

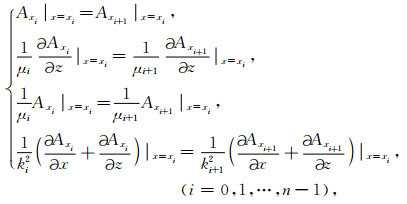
(3)

考虑到边界条件以及Axi, Axi+1, Azi, Azi+1均满足齐次亥姆赫兹方程，由此可确定矢量位的解为

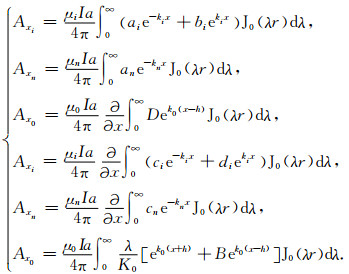
(4)

式中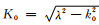，，J0为0阶第一类Bessel函数，λ为积分变量，物理意义是r方向的波矢量，r是接收点到发射源的距离.

利用(3)可求出(4)式中的4n个待定系数，再根据公式(2)及Ay=0可导出Ex为

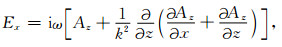
(5)

由此确定了个场强分量的具体表达式.当h=0时水平分层大地表面上电场强度Ex分量为

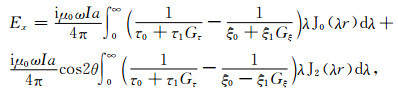
(6)

其中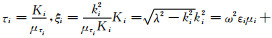，iωμiσi，Gτ和Gξ为地层因子，μτi是第i层的相对磁导率，θ是谐变线电流元Ia x与到xoy平面上任一点P(x, y)的矢径所形成的夹角(图 2).

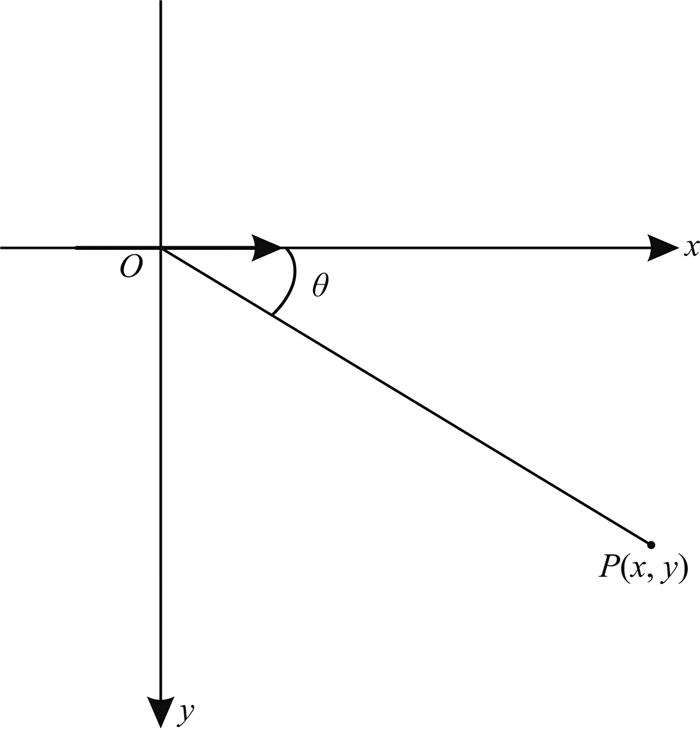
图 2 θ角示意图 Fig. 2 Sketch of angle θ

得到水平电场Ex后，就可以求取Ex定义的视电阻率为

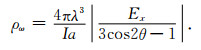
(7)

3 含磁性岩层的视电阻率响应曲线

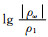
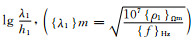
图 3-图 5分别为根据(7)式计算的G型、D型和H型模型不同层位具有不同相对磁导率情况下的视电阻率曲线示意图.曲线的纵坐标为，横坐标为.曲线上的数值表示磁导率异常地层的相对磁导率，各模型的参数如图中所示，取源中轴线的点作为观测点，r表示观测点到源中心的距离.

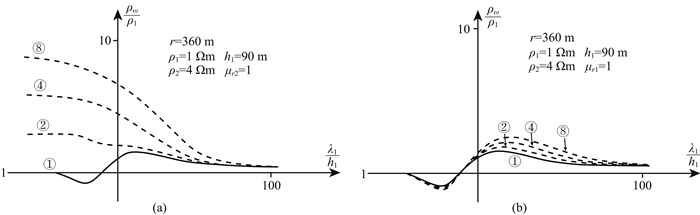
图 3 G型断面视电阻率曲线 (a)第一层磁导率不同；(b)第二层磁导率不同. Fig. 3 Apparent resistivity curves of G-type model (a) Different permeability of the first layer; (b) Different permeability of the second layer.
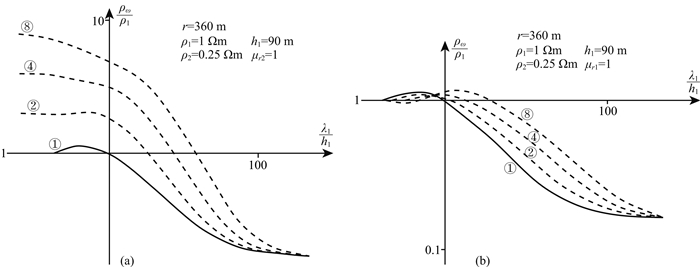
图 4 D型断面视电阻率曲线 (a)第一层磁导率不同；(b)第二层磁导率不同. Fig. 4 Apparent resistivity curves of D-type model (a) Different permeability of the first layer; (b) Different permeability of the second layer.
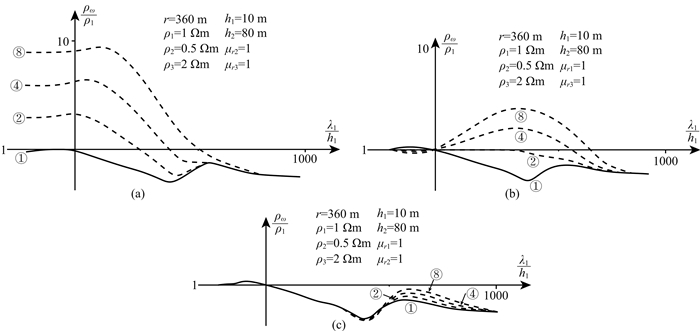
图 5 H型断面视电阻率曲线 (a)第一层磁导率不同；(b)第二层磁导率不同；(c)第三层磁导率不同. Fig. 5 Apparent resistivity curves of H-type model (a) Different permeability of the first layer; (b) Different permeability of the second layer; (c) Different permeability of the third layer.

从以上各图可以看出，当最下面一层岩层为磁性层时，不论是二层曲线还是三层曲线，对应视电阻率曲线的影响都没有第一层或中间层具有磁性时那么明显了，即随着基底磁导率的增大，视电阻率的增大幅度较小，而且随着频率的降低逐渐与μr3=1(基底无磁性)时视电阻率曲线尾部渐近线相重合.

4 含磁性岩层的视电阻率响应特征

磁性层的视电阻率曲线响应特征基本上在二层G、D和三层H型曲线上表示了出来.当某一层的相对磁导率增大时，对应的视电阻率值也随之增大.

(1)磁性层位于顶层时

当第一层岩层为磁性层时，对应的视电阻率曲线的首部反映最为明显.其增大的幅度为第一层岩层真电阻率的μr倍.具体分析如下：

电场强度Ex的公式(6)在远区场情况下，可简化为

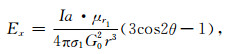
(8)

而不考虑磁性层时的远区场公式为

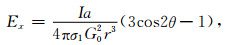
(9)

(8)式与(9)式相比可知，因此视电阻率值是原来的μr1倍.

(2)当中间层为磁性层时，视电阻率曲线的变化比较明显.对于三层曲线，当相对磁导率达到一定程度，如大于4时，曲线形态都变得与K型曲线类似.

(3)磁性层位于底层时

当底部岩层为磁性层时，对应的视电阻率曲线的反映不明显.具体分析如下：

如果低频时已进入频率测深近区场(k3r≤1)，则公式(6)变为

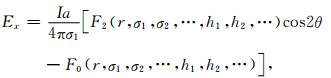
(10)

其中，Fn为直流测深中已知的函数.在三层情况下，其表达式为

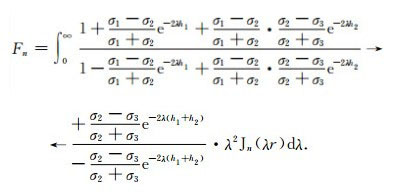
(11)

采用非线性数字滤波方法计算上式中的汉克尔变换(Ward and Hohmann, 1991).此时的近区场已变得与同装置的直流电偶极子的场一样，电场强度已与磁导率无关.故最后一层岩层为磁性层时，其视电阻率曲线也总要与非磁性层的曲线尾部渐近线相重合.

可见，为了探测埋深较深的磁性岩层，应该使相应的视电阻率曲线段保持在远区或中区，以达到能探测磁性基底的效果.但是，在事先不知岩层参数的情况下，单纯从曲线上仍然不易发现磁性层的存在，除了依赖地质信息和物性信息外，还可以通过对比的方法，掌握磁性层响应特性.下面以磁铁矿为例进行说明.

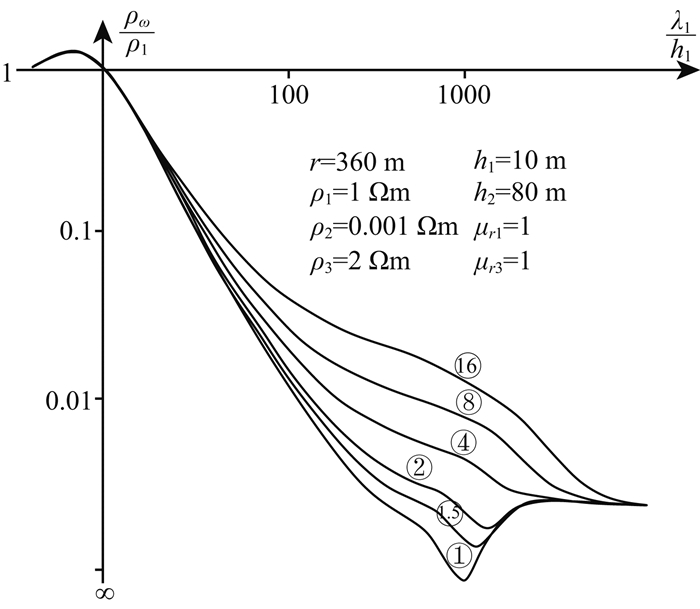
设铁磁性矿层位于模型的中间层，电阻率为0.001 Ωm，厚度为80 m，上覆地层电阻率为1 Ωm，厚度为10 m，基底电阻率为2 Ωm.图 6给出了中间磁层相对磁导率不同情况下的正演视电阻率曲线.从图中可以看出，由于磁铁矿是具有极低电阻率的矿层，当μr=2时极小值的位置已有很大的移动，达到8时则使曲线形态明显改变了.此时如果将磁性层作为探测目标时从上面对含磁性岩层分层大地频率测深视电阻率计算结果所绘曲线看出，磁性岩层的存在有着明显的视电阻率响应.可以此特征为解释依据，将会获得好的磁铁矿探测效果.

图 6 铁磁性矿层对H型曲线的影响特征 (曲线上的数值表示第二层的μr2值) Fig. 6 Effect of a ferromagnetic layer on apparent resistivity curves of H-type cross section (The μr2 of the second layer is represented by the numerical value of the curve)
5 结论

(1)仅从公式所含的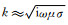明显看出，μ和σ有着同等地位，不考虑其他方面，对视电阻率应有相近的贡献.因此，在有磁性岩层存在的地区，应考虑磁性层对频率测深视电阻率的影响.本文开展磁性介质的电磁响应研究，推导出磁性层情况下的电磁响应表达式.

(2)通过对磁性层响应分析可知：磁性层埋藏深度越小，磁化特性表现越明显，磁性层埋藏深度越大，磁化特性表现越不明显；磁性层的电阻率越大，磁化特性表现越不明显，磁性层的电阻率越小，磁化特性表现越明显；远场情况下，磁化特性表现比较明显，近场情况下，磁化特性基本没有表现.

(3)具体地，(1)当磁性层位于地表时，当表层相对磁导率μr>1.2，磁性层对电磁测深曲线具体明显的影响；(2)当岩层为中间层时，只要μr>1.2，对H型、A型曲线中段会有影响.对H型曲线，主要表现在使极小值处的曲线抬高、变宽，以致使曲线形态发生变化；(3)当磁性层处于最后一层时，不论岩层的磁导率是多少，对各类二、三层曲线来讲，不会影响曲线的形态，只是使渐近线前第一个极值点的位置右移，极值点至渐近线之间的线段变得较为陡峭.此时磁性层的影响已趋于减弱了，特别对于μr < 2的基性岩、超基性岩已无明显影响.此时如将磁性岩层做为探测目标，则是徒劳的.

(4)在实际情况中，制约岩矿石磁导率的因素很多，对于不同的地质环境，铁磁岩矿石的磁导率在其平均值的附近有一个较大的变化范围.本文计算时所采用的岩石物性参数值只具有一般性，但是计算结果不影响对磁性介质响应特性的分析.另外，利用磁性层对频率测深视电阻率曲线的响应，可探测近于水平的磁性岩层赋存；基性岩、超基性岩在地中的分布有许多是成水平层状的，或者是可以看成是水平层状的.铁质石英岩也可以在一个比较广的区域成层状分布.因此由水平层状介质计算出来的磁性层响应特征曲线能很好地反映这类磁性岩石的分布.对于陡产状及不规则产状的磁铁矿床，尽管他们的相对磁导率非常大，μr=2.2~25，但不能套用水平情况下得出的结论，只是有助于定性方面的分析.

参考文献
Buselli G. 1982. The effect of near-surface superparamagnetic material on electromagnetic measurements. Geophysics, 47(9): 1315-1324. DOI:10.1190/1.1441392
Gao L, Hu X Y, Wang W Y, et al. 2009. A study of frequency airborne electromagnetic forward under magnetic condition. Chinese Journal of Engineering Geophysics (in Chinese), 6(4): 399-403.
Huang H P, Fraser D C. 2002. Dielectric permittivity and resistivity mapping using high-frequency, helicopter-borne EM data. Geophysics, 67(3): 727-738. DOI:10.1190/1.1484515
Kozhevnikov N O, Antonov E Y. 2008. The magnetic relaxation effect on TEM responses of a uniform earth. Russian Geology and Geophysics, 49(3): 197-205. DOI:10.1016/j.rgg.2008.02.004
Kozhevnikov N O, Antonov E Y. 2009. The magnetic relaxation effect on TEM responses of a two-layer earth. Russian Geology and Geophysics, 50(10): 895-904. DOI:10.1016/j.rgg.2009.02.001
Kozhevnikov N O, Antonov E Y. 2011. Magnetic relaxation of a horizontal layer: effect on TEM data. Russian Geology and Geophysics, 52(4): 398-404. DOI:10.1016/j.rgg.2011.03.002
Lee T J. 1984a. The effect of a superparamagnetic layer on the transient electromagnetic response of a ground. Geophysical Prospecting, 32(3): 480-496. DOI:10.1111/gpr.1984.32.issue-3
Lee T J. 1984b. The transient electromagnetic response of a magnetic or superparamagnetic ground. Geophysics, 49(7): 854-860. DOI:10.1190/1.1441731
Niu Z L. 1985. The effect of transient magnetic relaxation and its significance in evaluating the anomaly of complex magnetism. Journal CSIMM (in Chinese)(2): 79-85.
Wang W P, Zeng Z F, Wu C P, et al. 2013. Frequency domain airborne electromagnetic dual-frequency inversion method based on magnetic permeability. Geological Science and Technology Information (in Chinese), 32(2): 181-186.
Ward S H, Hohmann G W. 1991. Electromagnetic theory for geophysical exploration.//Nabighian N ed. Electromagnetic Methods in Applied Geophysics. Tulsa, Oklahoma: Society of Exploration Geophysics, 121-223.
Xi J J. 2010. A study of forward and inversion for frequency-domain airborne electromagnetic method in terms of permeability and resistivity[Master thesis] (in Chinese). Changchun: Jilin University.
Xue G Q, Yan S, Gelius L J, et al. 2015. Discovery of a major coal deposit in china with the use of a modified CSAMT method. Journal of Environmental & Engineering Geophysics, 20(1): 47-56.
Yan S, Chen M S. 1997. The responsibility of apparent resistivity curves on frequency sounding for magnetic layers. Geology and Prospecting (in Chinese), 33(3): 38-42.
Yin W W. 2013. Analysis on the response characteristic of the transient electromagnetic method to detect the sparse disseminated iron ore[Master thesis] (in Chinese). Taiyuan: Taiyuan University of Technology.
Zhang Q G. Field Theory (in Chinese).Beijing: Geology Press, 1983.
高亮, 胡祥云, 王卫一, 等. 2009. 磁性条件下频率域航空电磁法正演研究. 工程地球物理学报, 6(4): 399–403.
牛之琏. 1985. 瞬变磁张弛效应及其在评价复杂磁异常中的意义. 中南矿冶学院学报(2): 79–84.
王卫平, 曾昭发, 吴成平, 等. 2013. 基于磁导率的频率域航空电磁法双频反演方法. 地质科技情报, 32(2): 181–186.
习建军. 2010.基于磁导率和电阻率的频率域航空电磁法正反演研究[硕士学位论文].长春:吉林大学.
闫述, 陈明生. 1997. 频率测深中磁性层的视电阻率响应. 地质与勘探, 33(3): 38–42.
殷伟伟. 2013.稀疏浸染状铁矿瞬变电磁响应特征分析[硕士学位论文].太原:太原理工大学.
张秋光. 场论.北京: 地质出版社, 1983.