2. 蒙城地球物理国家野外科学观测研究站, 安徽 蒙城 233500
2. National Geophysical Observatory at Mengcheng, Anhui Mengcheng 233500, China
塌方、沉陷、突水等地质灾害易发生于煤和矿产资源的地下开采、隧道和地铁等城建工程,对安全生产造成严重威胁,并带来巨大的损失.此类地质灾害的主要诱因是含水导水地质构造,以及各种隐伏的不稳定构造,如断层及破碎带等.为了预防突发性地质灾害的发生,需要开展巷道超前探测工作,提前确定掌子面前方不良地质体.直流电阻率法具有对低阻异常反应灵敏的特点,且易于在巷道中施工,在空区积水、含水断层、富水岩层等危险地质构造的超前探测工作中取得了一定效果.李学军(1992)根据理论分析提出煤井下定点源梯度法,并指出可以通过所获得的视电阻率区分含水与非含水构造.王进杰(1995)通过获得成功的实例,推断了直流电法在煤矿巷道应用的可能性.韩德品等(1997)论述了采煤工作面单极-双极直流电透视原理和解释方法,指出垂直和平行两种观测方式均能有效反映工作面顶和底板围岩的影响.刘青雯(2001)阐述了井下电法超前探测工作原理,对避免掘进头后方巷道和地层电性变化的影响并重点突出巷道前方地质异常进行了研究.李玉宝(2002)结合实例进行技术经验总结,分析了电法超前探测工作的影响因素、技术效果.张乃宏和李定鹏(2003)将井下工作面侧帮超前探测技术应用于采煤工作面内部陷落柱预防,表明该技术能探测陷落柱位置及其富水性.王国华等(2003)介绍了矿井直流电法超前探测工作步骤,展示了实际应用效果.屈有恒等(2007)对井地有限线源三维电阻率反演进行了研究.张彦湘等(2008)综合介绍了矿井电磁勘探技术在煤矿安全领域的应用,指出矿井电磁勘探技术探明巷道周围地质构造的独特优势.杨庭伟等(2009)提出了三种聚焦电流法电极布置方式,并用导电纸实验模拟了聚焦电流法巷道超前探测.刘斌等(2009,2012)基于全空间球体含水构造超前探测解析公式实现了阻尼最小二乘反演,并将其与改进遗传算法非线性反演相结合.张平松等(2009,2013)指出点电源电场球壳理论存在的问题,通过改进观测系统增强对前方含水异常体的综合认识及预测能力.强建科等(2010)根据电流密度分布特点,研究了三维巷道直流聚焦法电极组合.张力等(2011)利用同性电流相斥原理,参考垂向测深和侧向测井技术设计出适合巷道的垂直聚焦电位和梯度电位超前探测方案.石学锋和韩德品(2012)介绍了直流电法超前探测技术在某矿实际生产中的应用,李冰(2015)也介绍了直流电法超前探测技术在某矿含水断层构造探测中的应用.
目前直流电法巷道超前探测主要采用单极-双极装置,即利用点电极A在掌子面处供电,电极B置于无穷远处,并使用接收电极MN在掌子面后方反向一定范围观测,针对产生的等电位球面异常,利用几何交汇法基于地下均匀全空间电场分布简单模型推断和解释掌子面前方的地质情况.由于巷道空腔本身的存在,使空间内电场分布产生畸变,影响原本就复杂的异常响应,导致后期解释具有不确定性,偏差和误报皆有可能发生,直流电法巷道超前探测面临挑战(高致宏等,2006;强建科等,2011;程久龙等,2014).由此可见,只有建立基于实际情况的三维巷道模型,并在计算中考虑巷道空腔本身的影响,才有可能通过超前探测工作预知巷道掘进前方地质情况.岳建华和李志聃(1993,1997,1999)通过物理实验和边界元数值模拟,通过不同矿井直流电法的全空间效应和巷道影响特征给出了巷道影响系数的经验公式.程久龙等(2000)采用解析方法给出了全空间中倾斜断层的点电源电位解析解,介绍了单极-双极法超前探测原理、工作方法,并重点讨论了巷道前方存在含水断层这一有代表性地质体.王大庆等(2003)应用有限差分法对均匀围岩介质中点源电流场的巷道影响进行模拟研究,以巷道底板供电为例,根据计算结果初步总结了巷道的影响规律.刘志新等(2003)和刘树才等(2004)应用有限元法对矿井直流电透视方法进行三维正演,并总结了不同数值计算方法的特点,指出了矿井直流电法三维正演模拟面临的问题.王志刚等(2006a,2006b)在直流电法基本微分方程基础上,采用有限差分法进行井地电法三维数值模拟研究.黄俊革等(2005,2006,2007)使用有限元法分别对巷道电阻率测深和超前预报的异常响应进行研究,给出了更为准确的全空间板状体模型点电源电位解析解.韩光等(2009)通过沙槽实验给出了矿井直流电法超前预报球体构造的经验公式.阮百尧等(2009,2010)通过轴对称电性介质二维异常电位有限元数值模拟方法,对聚焦观测条件下巷道模型进行了模拟计算,并对影响巷道超前探测的旁侧异常和观测方式进行研究.王小龙等(2011)采用COMSOL Multiphysics多物理场仿真软件进行矿井巷道超前探测正演,并研究了巷道前方存在不同形状异常体时矿井超前探测视电阻率形态及极值点位置.柳建新等(2012)通过电阻率法有限元数值模拟计算,对影响巷道直流聚焦法超前探测距离的主要因素及该方法的超前探测距离进行研究.翟培合等(2014)利用ANSYS有限元分析软件对起伏巷道超前探测进行研究,巷道起伏会使视电阻率极小值和异常范围减小.
综上所述,目前普遍的直流电法超前探测方法是通过视电阻率观测曲线的最小值位置预测掌子面前方低阻异常体的距离,并且有相应的预测经验公式(程久龙等,2000;黄俊革等,2006;韩光等,2009).总体上,国内的巷道超前探测技术面临迫切的生产需求,促进了电阻率数值模拟和物理实验条件的发展,但实际地下地质结构复杂,异常大小不定且任意分布,而且可能存在有电阻率各向异性,使得目前由简单模型实验或数值模拟获得的预测公式不确定性较大,而且其准确性和可靠性难于评价.
Monte Carlo方法用随机化思想解决非确定性问题(Metropolis and Ulam,1949;Rubinstein and Kroese,2011),已逐渐应用于地球物理领域(Sambridge and Mosegaard,2002;吴文圣和黄隆基,2004;朱守彪和石耀霖,2007;魏超等,2008).本文利用电阻率三维非结构有限元数值模拟(Wang et al.,2013),在使用比值法消除巷道空腔影响的基础上,给出了巷道超前探的线性预测模型.然后,引入Monte Carlo方法,随机化生成大量电阻率任意分布的地下巷道模型,与并行算法相结合,对生成的大量随机模型进行电阻率三维数值模拟并行计算,得到每个巷道模型前方低阻异常体位置的预测结果并进行统计处理,获得各预测模型的准确度及可靠性的估计,为巷道超前探测准确性和可靠性的定量化描述提供新思路.同时,由于煤层存在电阻率各向异性,因此在巷道超前探测中考虑介质各向异性的影响也很有必要,对地下巷道的安全生产有重要的实际意义.
2 超前探测数值模拟Wang等(2013)实现了基于非结构有限单元的各向异性电阻率有限元数值模拟.为了进一步提高求解精度,我们采用异常电位法进行计算,即将模型内各电导率 σ 分成背景电导率 σp 和异常电导率 σs, 分别产生一次场 vp 和二次场 vs, 总场为二者叠加:
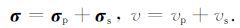
|
(1) |
当计算域为全空间时,点电源产生的一次场 vp 为:
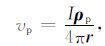
|
(2) |
其中, I 为点电源的电流强度, ρp=$\frac{1}{{{\sigma }_{P}}}$为围岩背景电阻率, r=(x,y,z) 为位置矢量.需要注意的是,当巷道位于地下浅层时,无法再将计算域视为全空间,需要引入镜像源(Li and Uren,1997)进行等效计算,镜像源位置 rm=(xm,ym,zm) 满足:
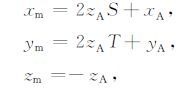
|
(3) |
其中,点源A的位置 rA=(xA,yA,zA). 若各向异性电阻率
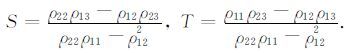
|
(4) |
为了简化方程,令
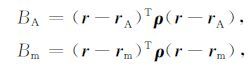
|
(5) |
则点电源产生的一次场 vp 为
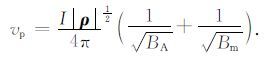
|
(6) |
对于二次场,将公式(1)代入以下电势控制方程:
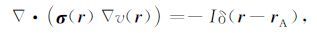
|
(7) |
变换后可得二次场控制方程:

|
(8) |
直流电法的地表(记为Γ0)法方向电流密度 jn=0, 故有
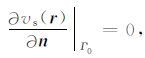
|
(9) |
通常将地下计算区域取为半径 R 足够大的半空间球体,其边界记为 ΓR, 有
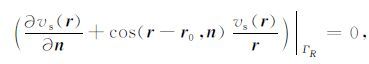
|
(10) |
为混合边界条件(第三类边界条件).在数值模拟中,可在模型设计时保持主要计算区域与边界距离较大,从而忽略其边界影响.
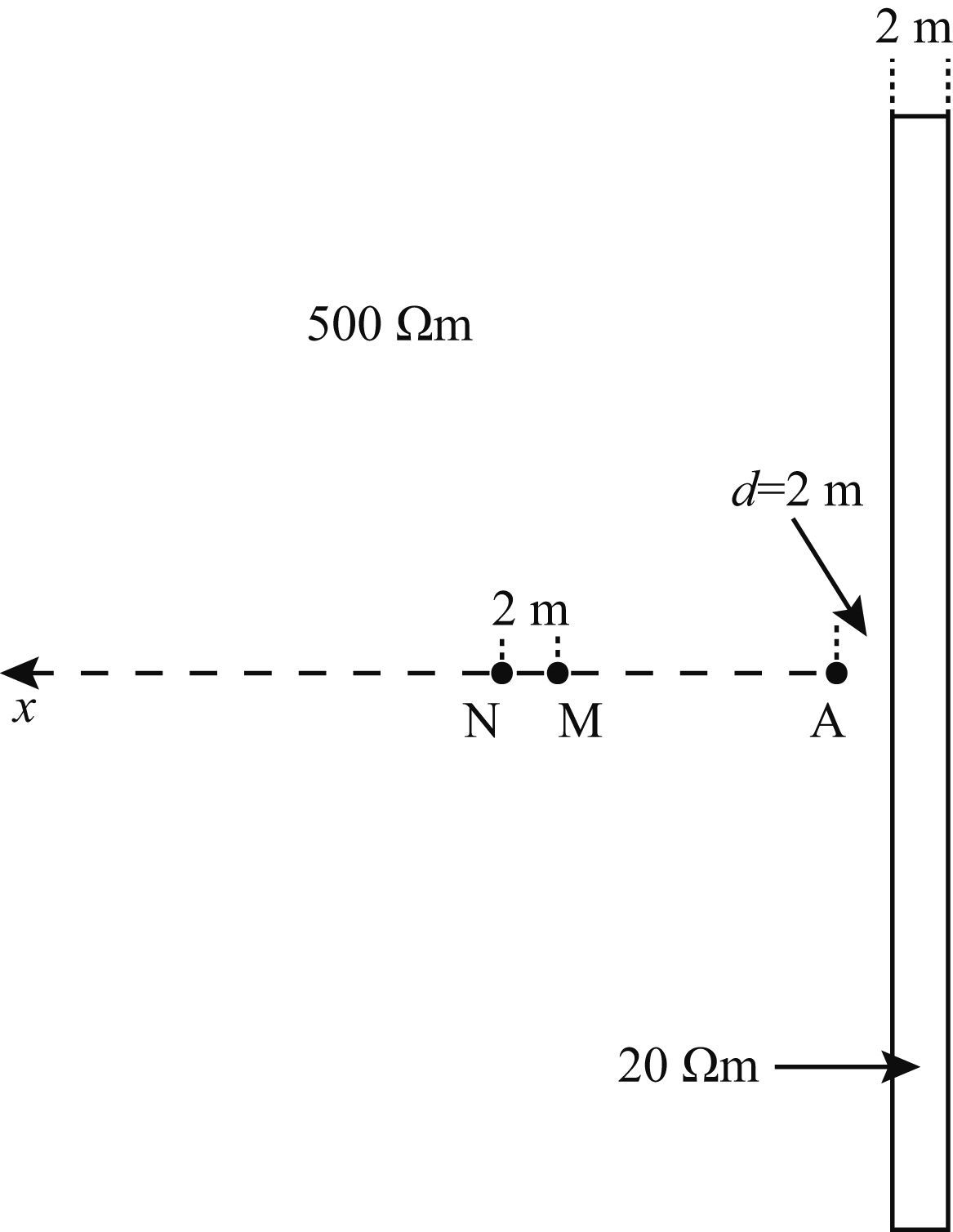
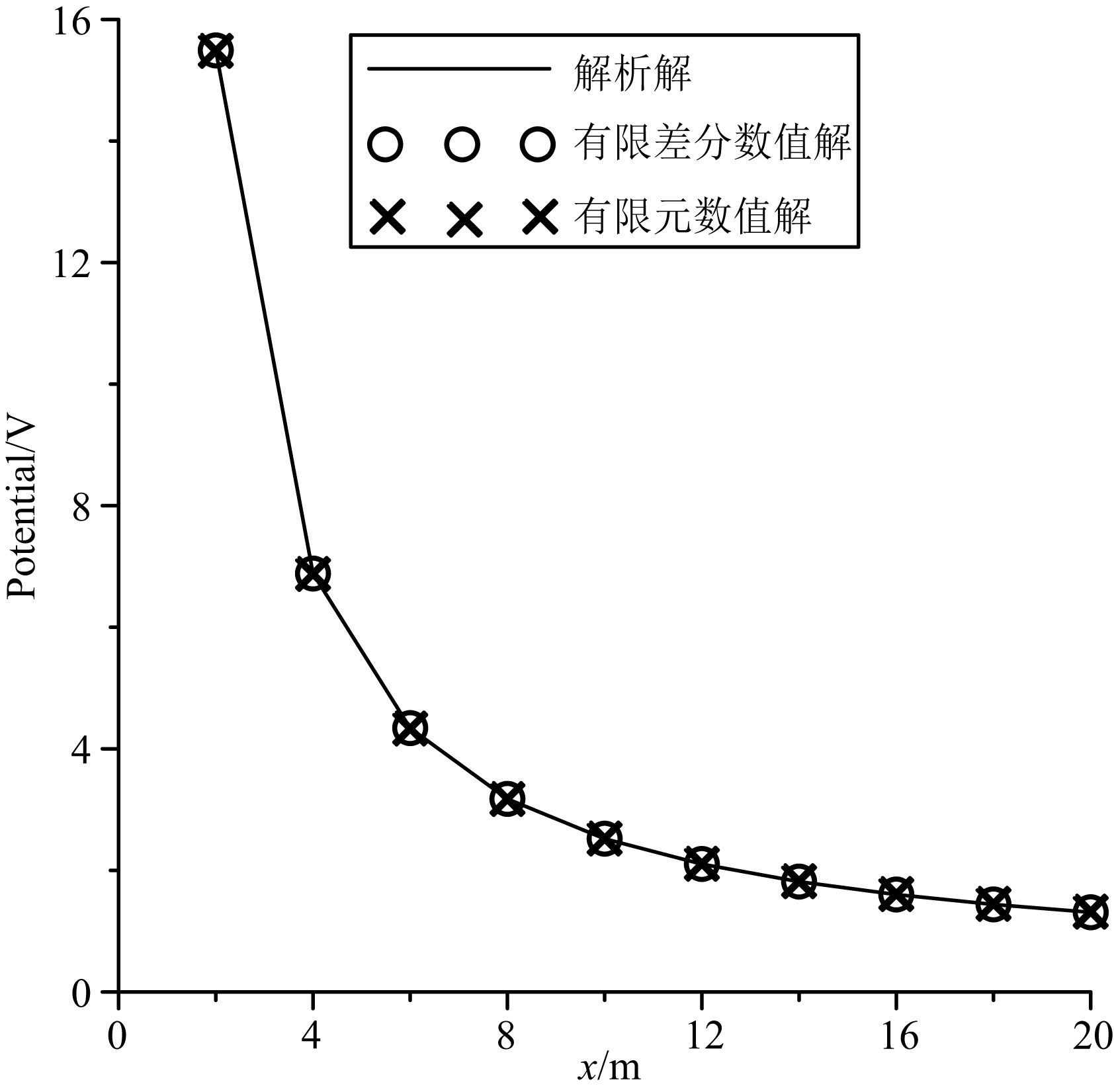
黄俊革等(2006)给出了全空间板体模型的电位异常响应解析解,并通过比值法(傅良魁,1983)消除巷道空腔的影响.鲁晶津和吴小平(2013)使用基于多重网格的有限差分算法(Lu et al.,2010)对巷道超前探测进行有效模拟,其计算精度与解析解吻合良好.我们将本文的有限元数值模拟与该有限差分数值模拟进行比较,对全空间板体模型(如图 1)进行数值模拟:背景电阻率为500 Ωm,板体厚2 m,电阻率为20 Ωm,到原点距离d=2 m.采用单极-单极装置,点电源A位于原点,电流强度为1 A,测线长20 m,其测点间隔2 m.图 2为数值解与解析解的电位值对比,本文的有限元数值模拟误差不超过0.8%.
|
图 1 板体模型示意图 Fig. 1 Schematic diagram of a plate model |
|
图 2 数值解与解析解对比 Fig. 2 Comparison of numerical and analytical solutions |
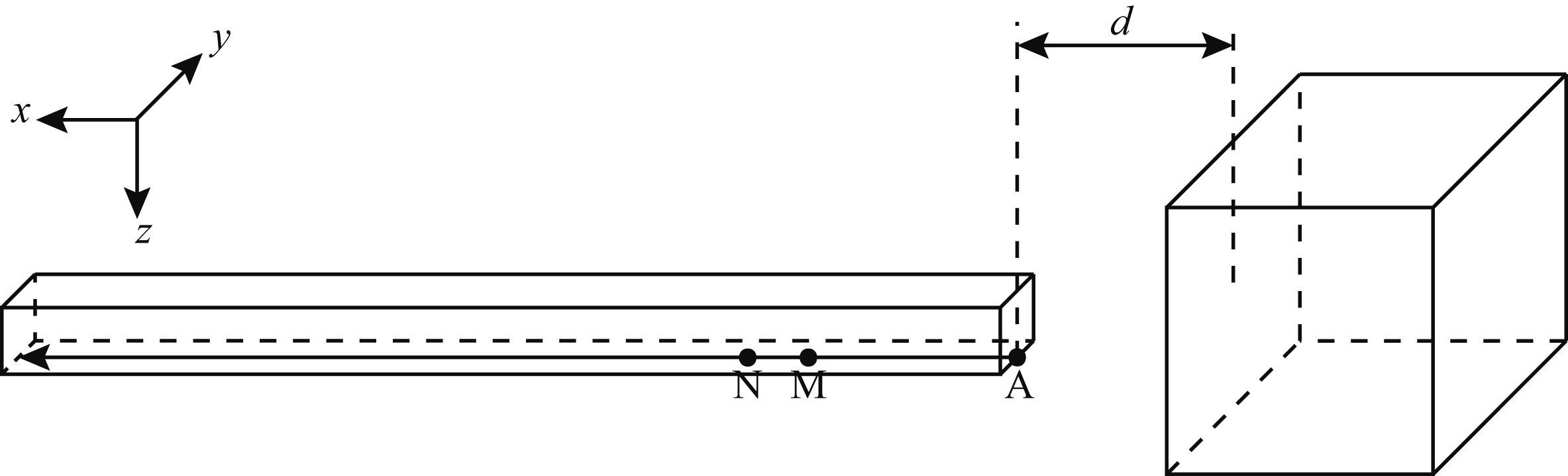
图 3为巷道超前探测基本模型:地下围岩背景电阻率为500 Ωm,巷道存于地下深处,巷道空腔尺寸为200 m×2 m×2 m,巷道空腔内空气电阻率取为1010 Ωm,巷道掌子面正前方存在低阻异常体,尺寸为20 m×20 m×20 m,电阻率为20 Ωm,设异常体距离掌子面的距离为d.采用单极-双极装置,点电源A置于巷道掌子面底部,同时也是坐标原点;测线沿着巷道掘进方向反向布置于巷道底部,其测点间隔2 m,从中依次选取MN,极距为2 m.
|
图 3 巷道模型示意图 Fig. 3 Schematic diagram of a tunnel model |
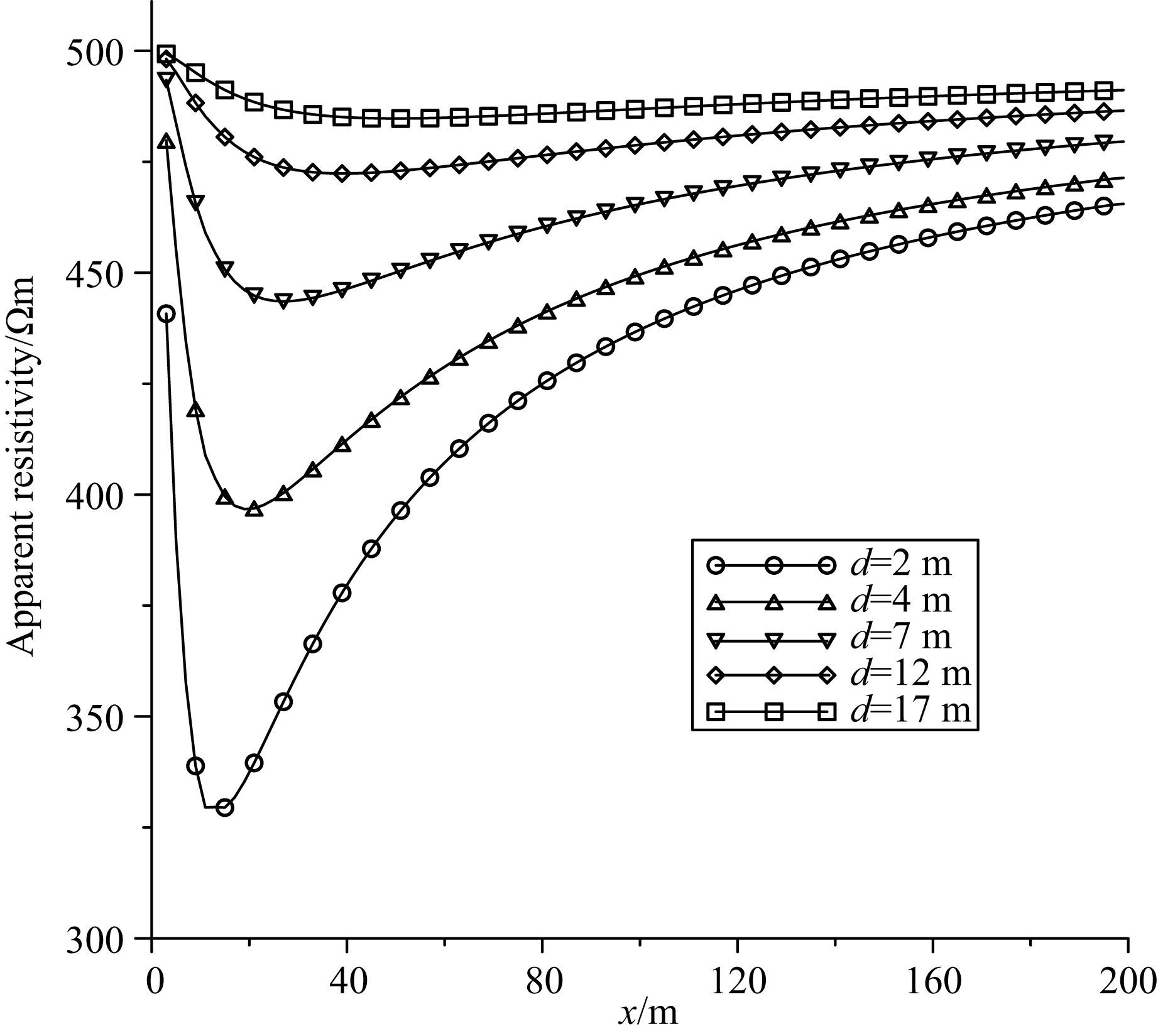
依次取d=2 m、d=4 m、d=7 m、d=12 m和d=17 m,分别绘制单极-双极装置观测的视电阻率对于MN中点坐标的曲线,并采用比值法消除巷道空腔的影响(如图 4).相对于围岩背景电阻率500 Ωm,d=2 m时低阻异常体引起的视电阻率相对异常幅值达34%;随着低阻异常体远离掌子面,其引起的视电阻率异常逐渐减小,在d=12 m时视电阻率相对异常幅值大于5%,低阻异常仍然较明显;d=17 m时视电阻率相对异常幅值仍大于3%,低阻异常仍然可观测.异常体和围岩电阻率确定时,视电阻率相对异常幅值还与低阻异常体的大小有关,鲁晶津(2010)模拟了地下500 Ωm均匀介质中存在电阻率为20 Ωm的无限大板体超前探模型,在d=50 m时视电阻率相对异常幅值可达5%.实际上,王国华等(2003)、石学锋和韩德品(2012)、李冰(2015)等大量工程实际应用表明,采用巷道内单极-双极装置能够成功观测到掌子面前方异常地质体引起的视电阻率相对异常.
|
图 4 单极-双极装置观测的视电阻率曲线 Fig. 4 Apparent resistivity curve of a pole-dipole array |
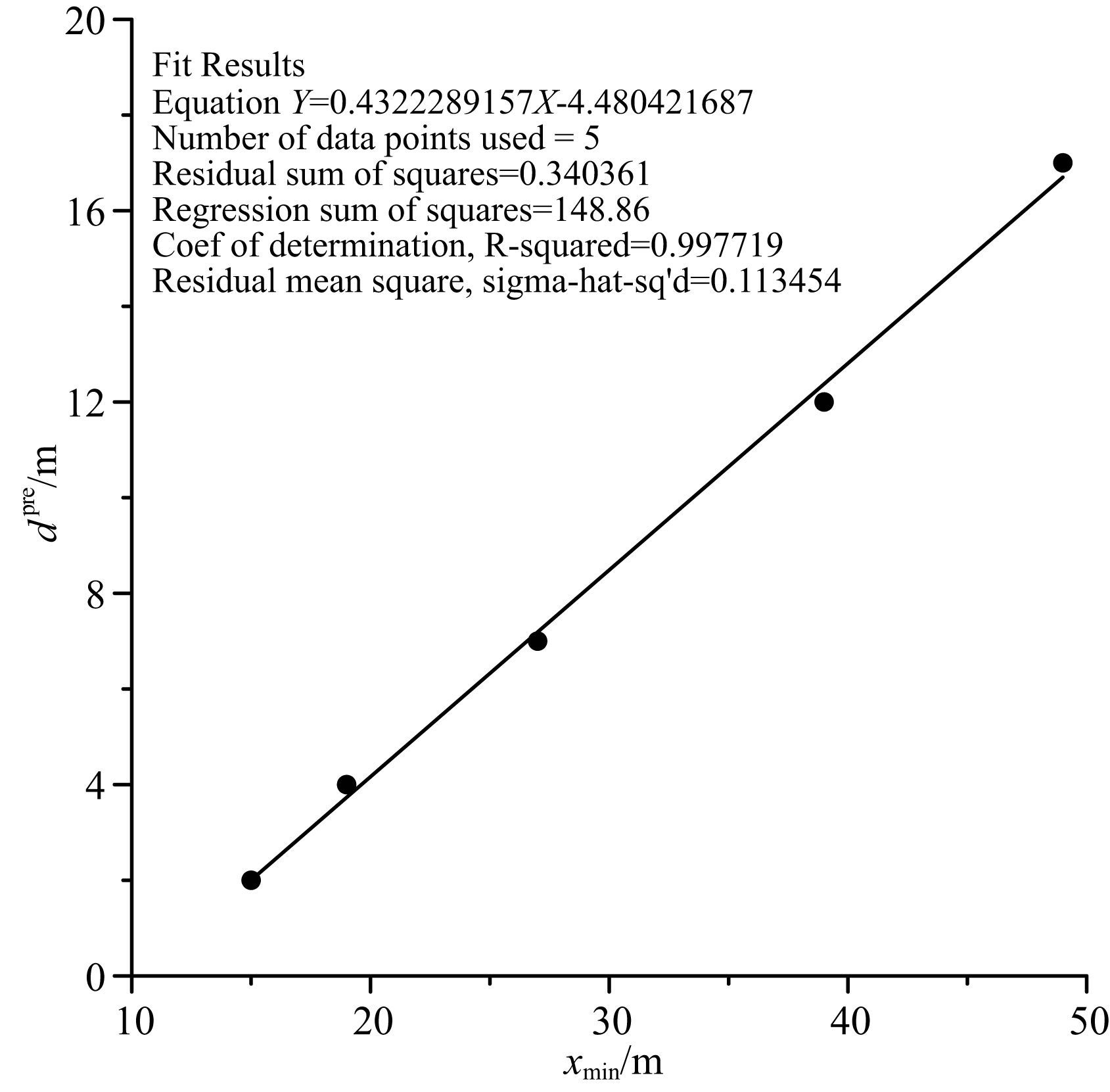
图 5显示了视电阻率曲线最小值位置xmin与异常体真实距离d的对应关系,通过线性拟合,给出超前探线性预测模型如下:
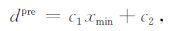
|
(11) |
|
图 5 视电阻率曲线最小值位置与异常体真实距离的关系 Fig. 5 Relationship between position of least value on the curve of apparent resistivity and real distance of anomaly body |
其中,dpre为预测的异常体距离,c1=0.432,c2=-4.480.
程久龙等(2000)建立超前探测实际地电模型,通过同心球壳等位面几何作图法将经验公式(11)的线性关系系数c1取为0.8~1.0,c2取为0.0;黄俊革等(2006)推导出全空间板体模型的解析解,并通过有限元数值模拟获得超前探线性预测公式,其c1取为0.1~0.25,c2取为0.0;韩光等(2009)通过沙槽模拟实验对巷道超前探测技术理论进行验证,总结得到线性预测公式,其c1为0.8,c2为-4.0.
以上经验公式普遍应用于巷道超前探测工作中,可通过视电阻率曲线最小值位置来估计掌子面前方异常体的真实距离.考虑到真实地质构造复杂、异常不规则,此类针对特定异常模型的经验公式均缺乏足够的理论支撑.而且实际地质结构中电阻率各向异性现象普遍存在,也对超前探测经验公式的可靠性提出挑战.因此必须通过巷道超前探测数值模拟对大量模型进行试算,并充分考虑异常的不规则、电阻率各向异性等影响因素,才能对经验公式的可靠性进行客观的评估.针对传统的评估方法难以处理模型的多样化及其普适性问题,我们采用Monte Carlo方法用随机化思想处理异常的不规则和电阻率各向异性,充分发挥基于有限元的直流各向异性电阻率巷道超前探测数值模拟的效率优势,对大量不同异常模型进行验算,通过统计所预测的异常体距离分布,量化展示超前探测模型经验公式的准确度及可靠性.
3 电阻率各向异性的影响
近年来,地质结构中普遍存在的各向异性现象逐渐受到重视,具有层理结构的岩石电阻率具有极其明显的方向性(陈峰等,2003).为了获得各向异性地质条件的电位分布,基于各向异性电阻率的数值模拟发展迅速(Yin and Weidelt,1999; Yin and Maurer,2001;Li and Spitzer,2005;Zhou et al.,2009).各向异性电阻率可以由主分量ρ0=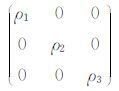
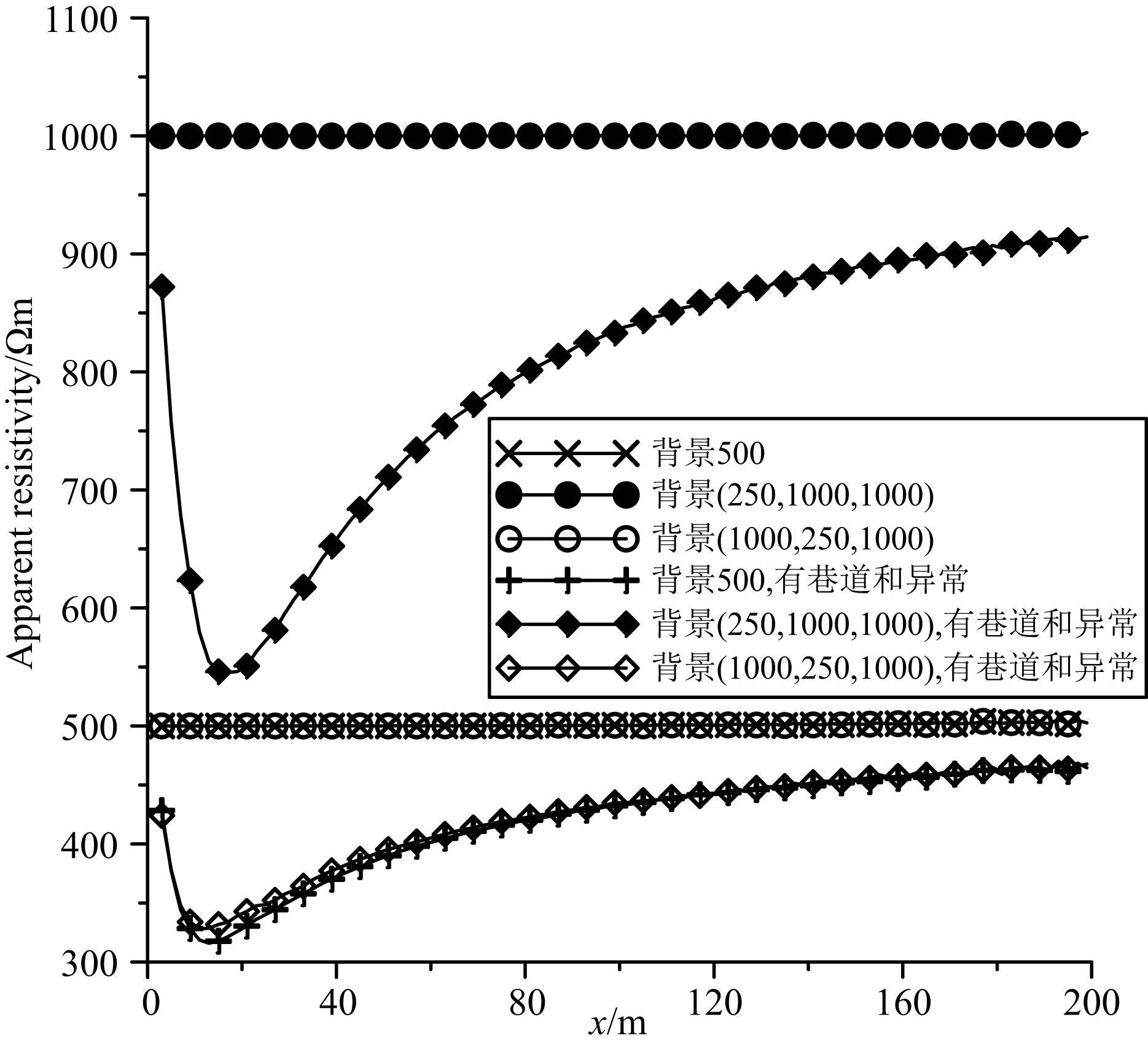
我们首先考虑全空间背景电阻率各向异性的情况,依旧采用单极-双极装置观测.分别取背景电阻率为各向同性ρ=500 Ωm、各向异性 ρ=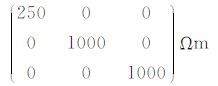


|
图 6 各向异性反常现象 Fig. 6 Unusual phenomenon of anisotropy |
Monte Carlo方法是一种统计试验法或随机模拟法,可以通过随机变量的统计试验、随机模拟,获得问题的近似解.其特点是用数学方法在计算机上模拟实际概率过程,然后加以统计处理(朱守彪和石耀霖,2007).基本原理如下:
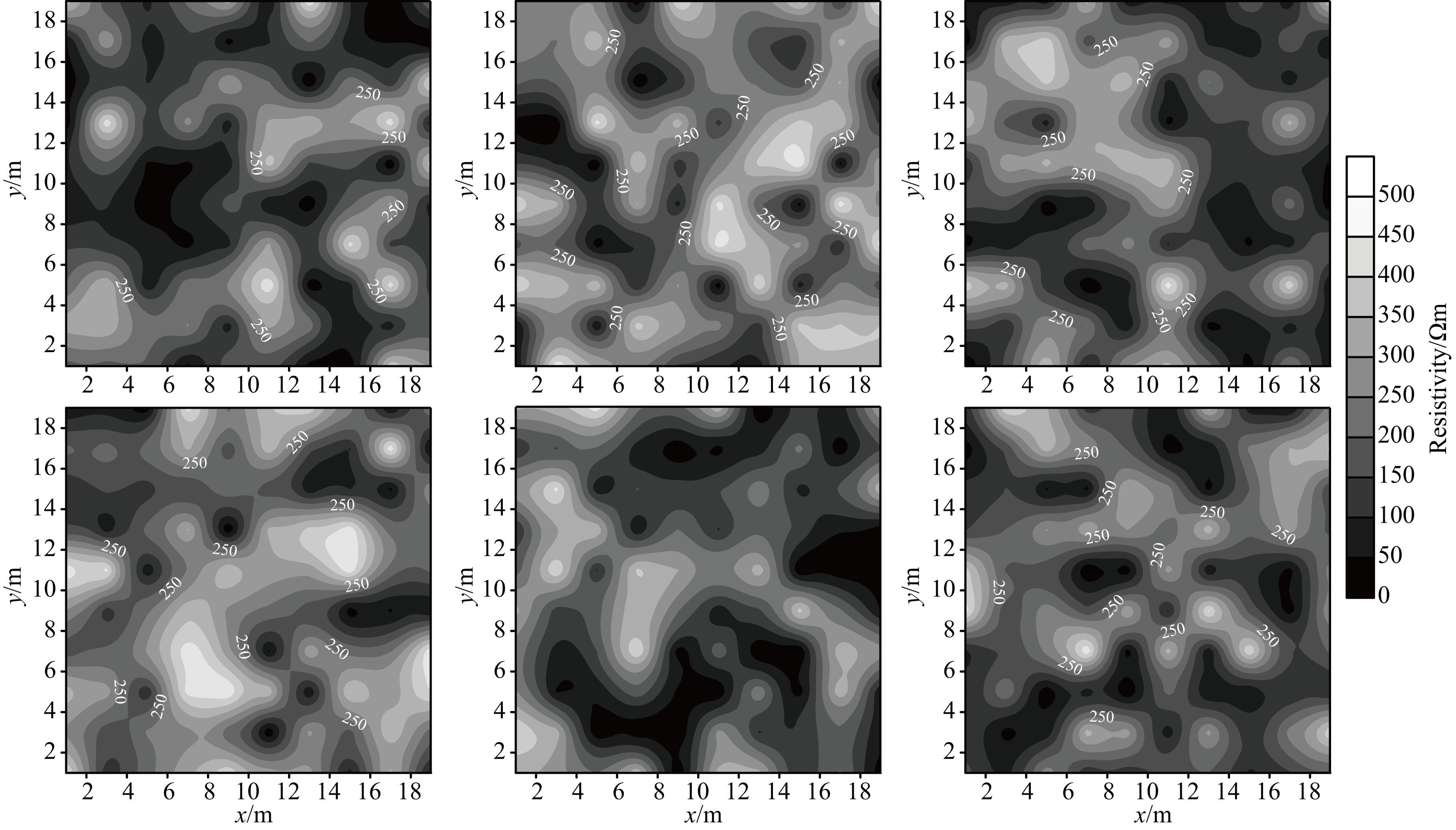
将Monte Carlo方法应用于巷道超前探测数值模拟,随机化生成大量不同电阻率分布的低阻异常结构:将前述20 m×20 m×20 m的低阻异常区域划分为10×10×10的1000个立方体单元,各单元电阻率在小于背景电阻率为500 Ωm的条件下随机生成,即形成具有低阻特性的电阻率随机分布.图 7展示了6个随机生成的电阻率分布断面图,模拟实际地层含水特点.对于同样的观测装置而言,只有低阻异常体的电阻率分布影响超前探测预测结果,预测函数为:
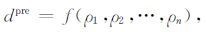
|
(12) |
|
图 7 随机生成电阻率分布 Fig. 7 Distribution of randomly generated resistivity |
其中,各单元电阻率变量 ρ1,ρ2,…,ρn 的概率分布已知,这里n=1000; f 为如公式(11)的线性预测算子.在实际问题中,前方异常体的真实位置往往是未知的.蒙特卡罗方法利用一个随机数发生器通过直接或间接采样取出每一组随机变量 ρ1,ρ2,…,ρn的值(ρ1i,ρ2i,…,ρni),然后按dpre对于ρ1,ρ2,…,ρn 的关系式确定函数 dpre的值dipre:
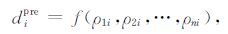
|
(13) |
反复独立采样多次(i=1,2,…,m)便可得到函数dpre的一批采样数据 d1pre,d2pre,…,dmpre. 当模拟次数足够多时,统计处理模拟结果,便可给出与实际情况相近的函数 dpre 的概率分布及误差估计,据此考察不同预测模型的可靠性及准确度.
考虑到Monte Carlo方法随机化生成大量不同的地电模型,这些不同电性结构的巷道超前探测三维数值模拟又是相互独立的,计算量巨大,必须进行并行化处理.近年来CPU产业发展迅速,整体趋势也逐渐从高频向多核转变,推动了并行计算的发展.小到移动工作站,大到集群服务器和超级计算机,都有多个CPU计算核心,只有并行计算才能充分发挥其计算能力.基于CPU的并行计算在地球物理领域已获得重视和发展(Tan et al.,2006;Lin et al.,2009;胡祥云等,2012;李焱等,2012),我们采用OpenMP实现并行Monte Carlo方法,其Fortran伪代码如下:
!$use omp_lib
! 预处理,开辟存储空间,使模型相互独立
!$omp parallel
!$omp do
do i = 1,n ! n为模型数量
! 对Monte Carlo方法生成的模型进行数值模拟
end do
!$omp end do
!$omp end parallel
经过并行化的程序可以充分发挥多核CPU的性能,且遵循OpenMP标准,可以方便地置于集群服务器和超级运算中心运行.
我们对大量随机模型进行并行计算,并在合成视电阻率数据中引入最大值为1%高斯误差(Box and Muller,1958),然后逐个利用经验公式(11)预测异常体到掌子面的距离,四个经验公式的c1和c2分别取自程久龙等(2000)、黄俊革等(2006)、韩光等(2009)以及本文线性模型的拟合值,并统计其预测的异常体到掌子面距离dpre的概率分布情况,从而获得各种预测模型可靠性和准确度的量化描述.
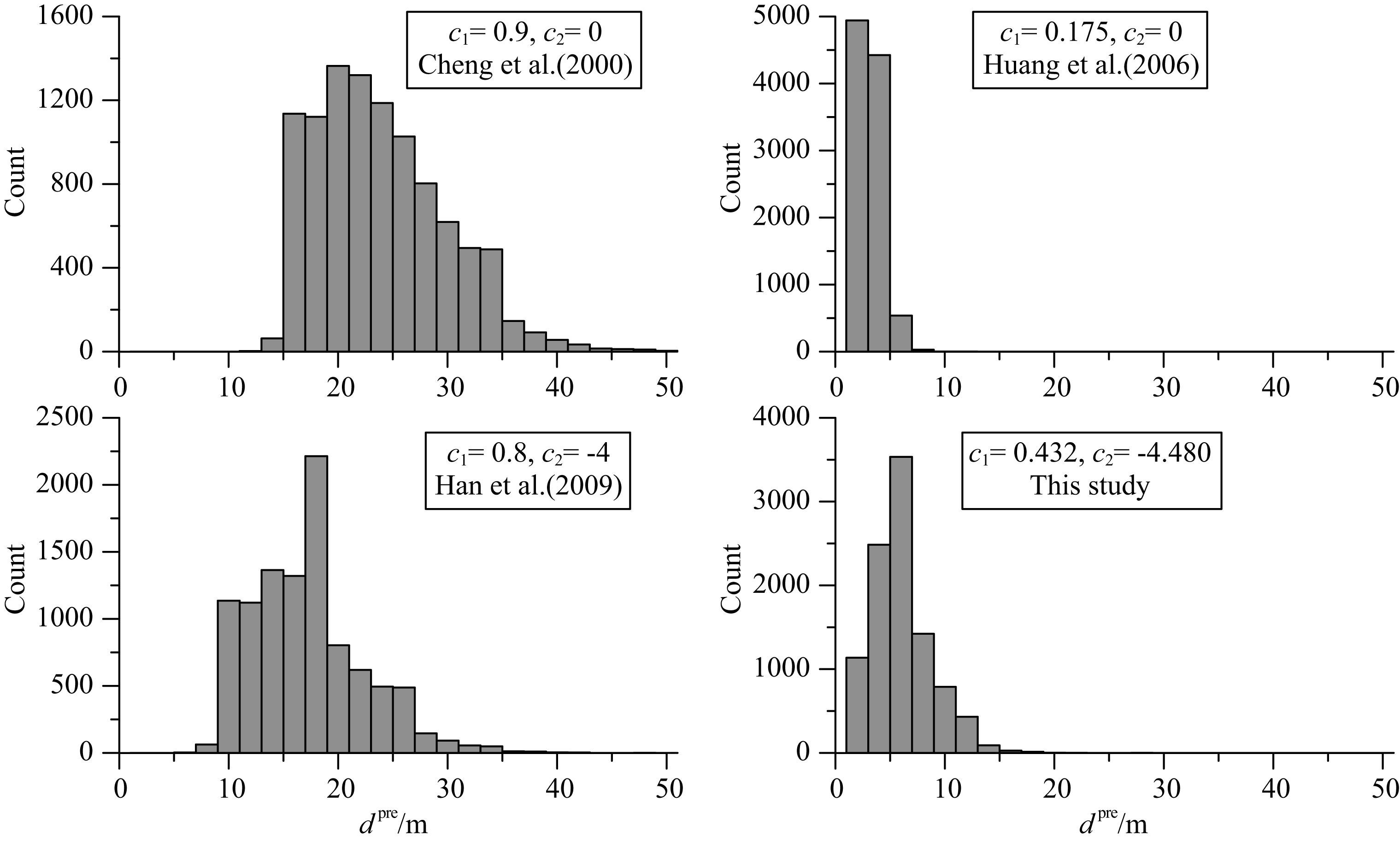
4.2 Monte Carlo方法应用于巷道超前探测结果模型设计类似于图 3:地下围岩背景电阻率为500 Ωm,巷道存于地下深处,巷道空腔尺寸为200 m×2 m×2 m,巷道空腔内空气电阻率取为1010 Ωm,依旧在巷道内观测,其单极-双极装置保持不变.我们用Monte Carlo方法对掌子面前方的低阻异常体进行模拟:低阻异常不再固定位置和尺寸,而是随机出现在20 m×20 m×20 m区域内,该区域距离掌子面距离d=7 m.区域内电阻率在不大于背景的500 Ωm的前提下,随机分布.即低阻异常体可以不止一个,电阻率也可以不连续.我们对10000组随机模型进行处理,图 8为四个经验公式的预测结果:横坐标为经验公式预测的异常到掌子面距离dpre,纵坐标为模型个数统计.本文的经验公式预测dpre集中在真实的d=7 m附近,而其余三个经验公式预测的dpre存在误差.其中,第一个和第三个经验公式由于c1较大,预测的dpre比真实的d大,可能在实际生产中迟报,带来安全隐患.
|
图 8 当d=7 m时,经验公式预测的异常到掌子面距离dpre分布 Fig. 8 Distribution of dpre from the experience when d=7 m |
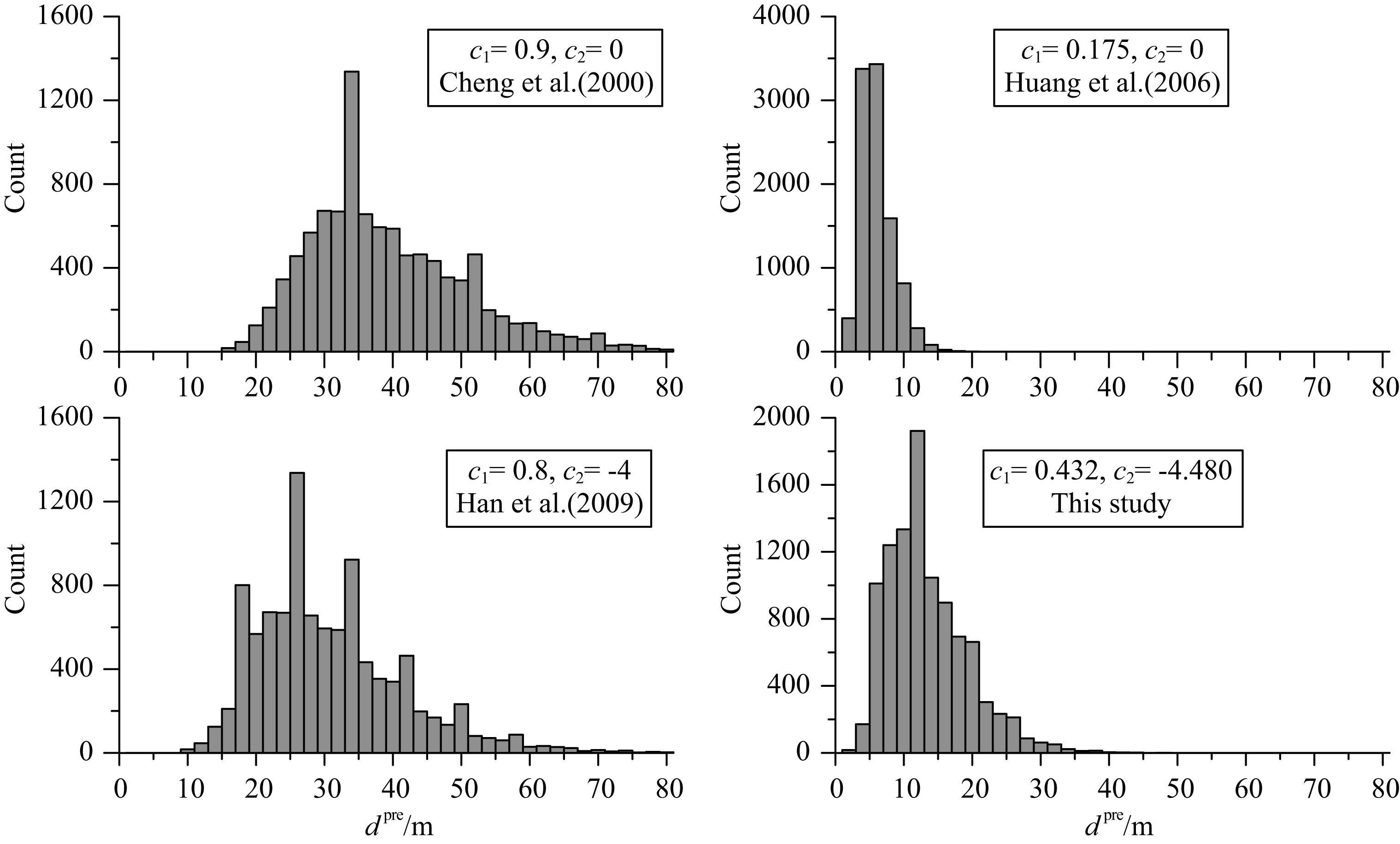
我们将可能出现随机异常的区域调整到距离掌子面d=12 m,重复以上工作.图 9展示了对10000组随机模型统计处理,结果表明:随着低阻异常体距离掌子面越远,预测准确性下降,四个经验公式的预测结果分布都变得更分散.相比之下,本文的经验公式预测的异常到掌子面距离dpre集中在12 m附近,更为准确.
|
图 9 当d=12 m时,经验公式预测的异常到掌子面距离dpre分布 Fig. 9 Distribution of dpre from the experience when d=12 m |
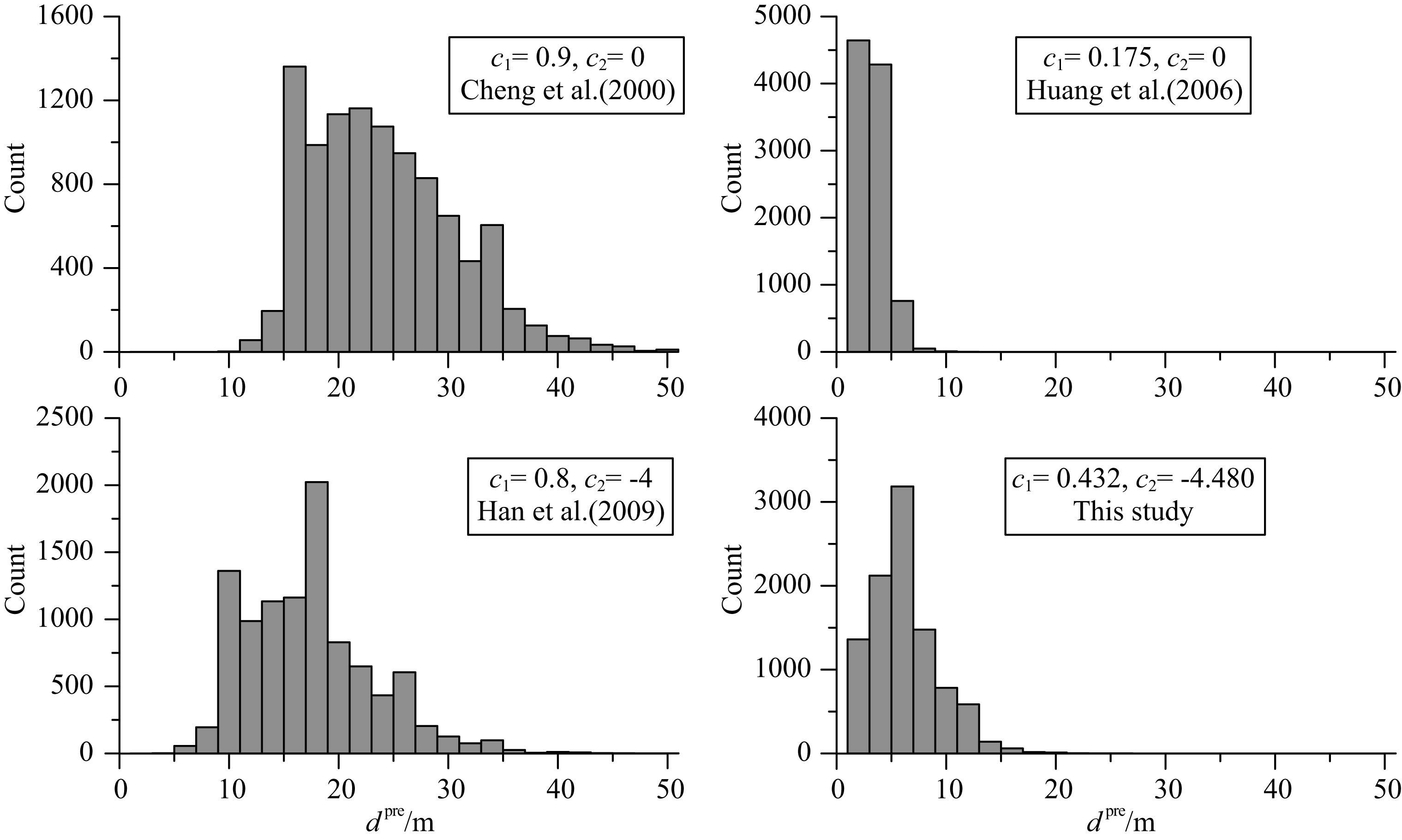
我们进一步考虑电阻率各向异性的影响.将可能出现异常的区域移至d=7 m处,使异常区域的电阻率具有各向异性.这里采用横向各向同性模型,随机选择层理结构方向,并随机生成ρL和ρT,限制条件为平均电阻率 ρ′=$\sqrt{{{\rho }_{L}}{{\rho }_{T}}}$不大于背景电阻率的500 Ωm,并限制各向异性系数 λ=$\sqrt{{{\rho }_{L}}/{{\rho }_{T}}}$位于1.0~3.0之间.图 10显示了对10000组随机模型的处理结果:多数情况下,本文的经验公式预测dpre集中在真实的d=7 m附近,而其余三个经验公式预测的dpre存在误差.对比图 8可知,掌子面前方异常区域的电阻率各向异性对巷道超前探测工作影响不明显.
|
图 10 当d=7 m且异常区域为各向异性时,经验公式预测的异常到掌子面距离dpre分布 Fig. 10 Distribution of dpre from the experience when anisotropic anomaly and d=7 m |
我们再考虑背景电阻率各向异性的情况:模型设置同上,使围岩背景电阻率具有各向异性.仍采用横向各向同性模型进行数值模拟,随机选择围岩背景的层理结构方向,并保持其平均电阻率 ρ′ 为500 Ωm,随机生成位于1.0~3.0之间各向异性系数λ.
图 11展示了对10000组随机模型统计处理结果,可见四个经验公式预测的异常到掌子面距离dpre基本都远大于真实的距离d=7 m,在实际生产中这种电阻率各向异性的影响造成的迟报、误报,将导致很大的危险.对比图 8可知,围岩背景的电阻率各向异性对巷道超前探测工作影响很明显.
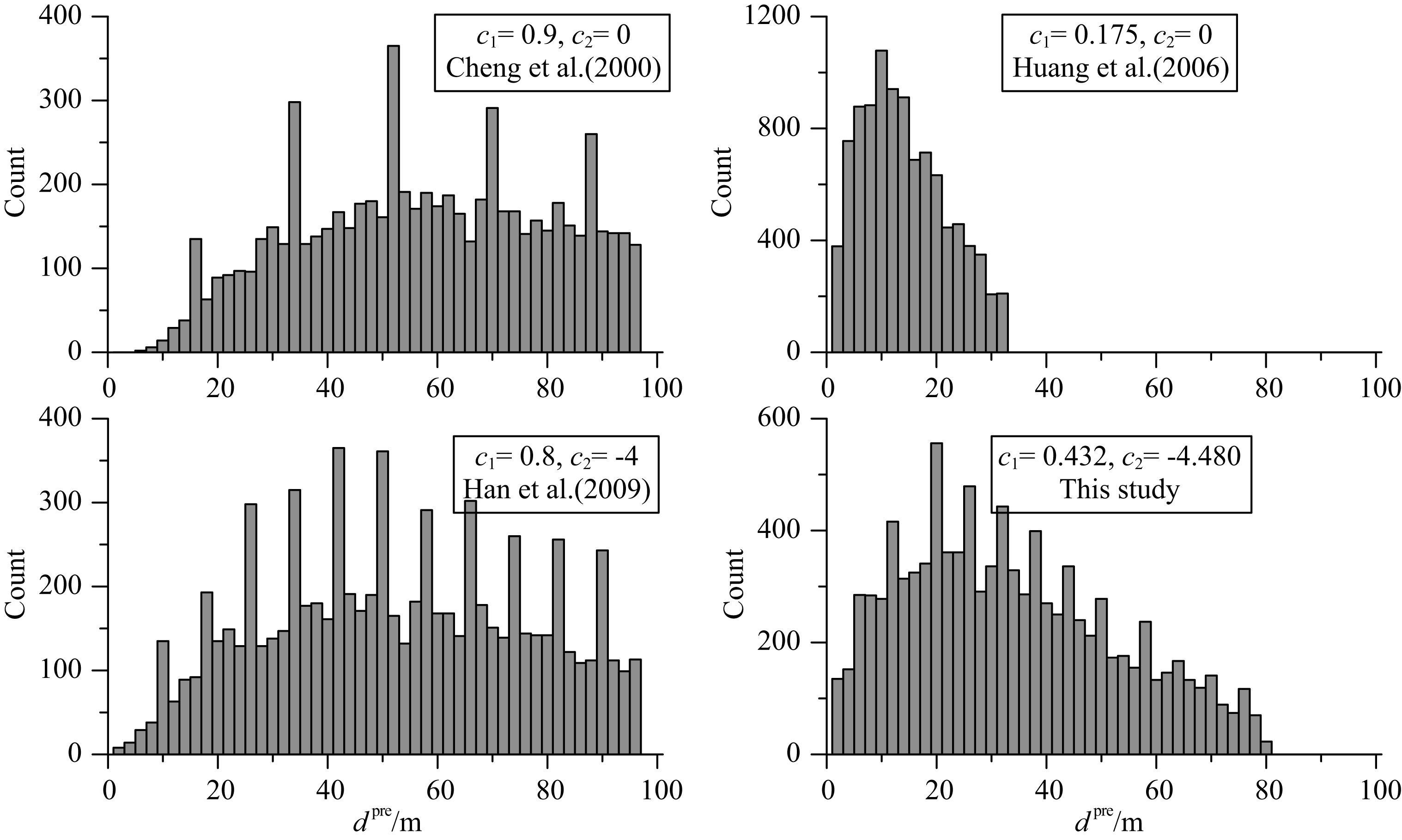
|
图 11 当d=7 m且围岩背景为各向异性时,经验公式预测的异常到掌子面距离dpre分布 Fig. 11 Distribution of dpre from the experience when background is anisotropic and d=7 m |
以上几类数值模拟中,采用本文的并行Monte Carlo方法,对每类10000组模型进行计算,每个模型的非结构网格节点数约50000,在PC上耗时不超过三小时(CPU为四核i5-3.2 GHz,内存为8 G).可见,并行Monte Carlo方法高效地解决了大量复杂模型电阻率三维有限元数值模拟,巨大计算量的并行化处理也是本文的关键.
5 总结本文利用电阻率三维有限元数值模拟进行直流电法巷道超前探测研究,给出了超前探线性预测模型.由于现有各种超前探经验预测公式多从简单地电模型的物理实验或数值模拟实验得到,不能反映实际地下结构的复杂性.我们引入Monte Carlo方法,随机生成10000个复杂地电模型,对各模型进行电阻率三维有限元数值模拟并行计算,然后利用已有的几种经验预测公式估计掌子面前方低阻异常体的距离,最后对估计的距离进行统计处理,获得各种经验预测模型的准确度及可靠性.统计结果表明,本文提出的经验公式预测的低阻异常体到掌子面距离更为准确,可靠性更好.Monte Carlo方法为巷道超前探测准确性和可靠性的定量化描述提供了新思路.
我们进一步考虑电阻率各向异性对超前探测的影响,结果表明,围岩背景的电阻率各向异性对巷道超前探测工作影响很明显,已有的四个经验公式预测的异常体到掌子面距离均远大于真实的距离,在实际生产中将导致很大的危险.因此,必须建立起基于电阻率各向异性介质的超前探预测模型,并在大量工程实际应用中不断修正和完善.
| Box G E P, Muller M E. 1958. A note on the generation of random normal deviates. The Annals of Mathematical Statistics , 29 (2) : 610-611. DOI:10.1214/aoms/1177706645 | |
| Chen F, An J Z, Liao C T. 2003. Directional characteristic of resistivity changes in rock of original resistivity anisotropy. Chinese Journal of Geophysics (in Chinese) , 46 (2) : 271-280. | |
| Cheng J L, Wang Y H, Yu S J, et al. 2000. The principle and application of advance surveying in roadway excavation by resistivity method. Coal Geology & Exploration (in Chinese) , 28 (4) : 60-62. | |
| Cheng J L, Li F, Peng S P, et al. 2014. Research progress and development direction on advanced detection in mine roadway working face using geophysical methods. Journal of China Coal Society (in Chinese) , 39 (8) : 1742-1750. | |
| Fu L K. Electrical Prospecting Tutorial (in Chinese). Beijing:Geological Publishing House. (in Chinese) 1983 . | |
| Gao Z H, Yan S, Wang X C, et al. 2006. Application status of advance detection with electric method in underground laneway and discussion about several issues. Coal Technology (in Chinese) , 25 (5) : 120-121. | |
| Habberjam G M. 1972. The effects of anisotropy on square array resistivity measurements. Geophysical Prospecting , 20 (2) : 249-266. DOI:10.1111/gpr.1972.20.issue-2 | |
| Habberjam G M. 1975. Apparent resistivity, anisotropy and strike measurements. Geophysical Prospecting , 23 (2) : 211-247. DOI:10.1111/gpr.1975.23.issue-2 | |
| Han D P, Zhang T M, Shi Y D, et al. 1997. The principle and interpretation method of the monopolar dipole DC penetration at working face. Coal Geology & Exploration (in Chinese) , 25 (5) : 32-35. | |
| Han G, Zhuang D Y, Tian J, et al. 2009. Primary theory on the mine direct current method to pilot predict sphere structure and study on san trough simulation experiment. Coal Engineering (3) : 69-72. | |
| Hu X Y, Li Y, Yang W C, et al. 2012. Three-dimensional magnetotelluric parallel inversion algorithm using data space method. Chinese Journal of Geophysics (in Chinese) , 55 (12) : 3969-3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 | |
| Huang J G, Bao G S, Ruan B Y. 2005. A study on anomalous bodies of DC resistivity sounding in tunnel. Chinese Journal of Geophysics (in Chinese) , 48 (1) : 222-228. DOI:10.1002/cjg2.v48.1 | |
| Huang J G, Wang J L, Ruan B Y. 2006. A study on advanced detection using DC resistivity method in tunnel. Chinese Journal of Geophysics (in Chinese) , 49 (5) : 1529-1538. | |
| Huang J G, Ruan B Y, Wang J L. 2007. The fast inversion for advanced detection using DC resistivity in tunnel. Chinese Journal of Geophysics (in Chinese) , 50 (2) : 619-624. | |
| Li B. 2015. Application of DC law ahead detection technology in detection of moisture fault structure. Coal Technology (in Chinese) , 34 (3) : 113-115. | |
| Li P, Uren N F. 1997. Analytical solution for the point source potential in an anisotropic 3-D half-space. 1. Two-horizontal-layer case. Mathematical and Computer Modelling , 26 (5) : 9-27. | |
| Li X J. 1992. Study and experiment on heading detecting by fixed electric source gradient method in underground. Coal Geology & Exploration (in Chinese) , 20 (4) : 59-62. | |
| Li Y, Hu X Y, Yang W C, et al. 2012. A study on parallel computation for 3D magnetotelluric modeling using the staggered-grid finite difference method. Chinese Journal of Geophysics (in Chinese) , 55 (12) : 4036-4043. DOI:10.6038/j.issn.0001-5733.2012.12.015 | |
| Li Y B. 2002. Mine electric method pilot detection technology. Coal Science and Technology (in Chinese) , 30 (2) : 1-3. | |
| Li Y G, Spitzer K. 2005. Finite element resistivity modelling for three-dimensional structures with arbitrary anisotropy. Physics of the Earth and Planetary Interiors , 150 (1-3) : 15-27. DOI:10.1016/j.pepi.2004.08.014 | |
| Lin C H, Tan H D, Tong T. 2009. Parallel rapid relaxation inversion of 3D magnetotelluric data. Applied Geophysics , 6 (1) : 77-83. DOI:10.1007/s11770-009-0010-5 | |
| Linde N, Pedersen L B. 2004. Evidence of electrical anisotropy in limestone formations using the RMT technique. Geophysics , 69 (4) : 909-916. DOI:10.1190/1.1778234 | |
| Liu B, Li S C, Li S C, et al. 2009. Study of advanced detection of water-bearing geological structures with DC resistivity method. Rock and Soil Mechanics (in Chinese) , 30 (10) : 3093-3101. | |
| Liu B, Li S C, Nie L C, et al. 2012. Advanced detection of water-bearing geological structures in tunnels using 3D DC resistivity inversion tomography method. Chinese Journal of Geotechnical Engineering (in Chinese) , 34 (10) : 1866-1876. | |
| Liu J X, Deng X K, Guo R W, et al. 2012. Numerical simulation of advanced detection with DC focus resistivity in tunnel by finite element method. The Chinese Journal of Nonferrous Metals (in Chinese) , 22 (3) : 970-975. | |
| Liu Q W. 2001. Underground electrical lead survey method and its application. Coal Geology & Exploration (in Chinese) , 29 (5) : 60-62. | |
| Liu S C, Liu Z X, Jiang Z H, et al. 2004. Some problems in 3D forward simulation of mine direct current method. Geophysical & Geochemical Exploration (in Chinese) , 28 (2) : 170-172. | |
| Liu Z X, Xu X G, Yue J H. 2003. 3D finite element simulation for mine DC electrical method-research of the dc penetration method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 25 (4) : 302-307. | |
| Lu J J. 2010. Studies of multigrid algorithm for 3D geo-electromagnetic modeling and its applications[Ph. D. thesis] (in Chinese). Hefei:University of Science and Technology of China. | |
| Lu J J, Wu X P, Spitzer K. 2010. Algebraic multigrid method for 3D DC resistivity modelling. Chinese Journal of Geophysics , 53 (3) : 700-707. DOI:10.3969/j.issn.0001-5733.2010.03.025 | |
| Lu J J, Wu X P. 2013. 3D numerical modeling of tunnel DC resistivity for in-advance detection. Coal Geology & Exploration (in Chinese) , 41 (6) : 83-86. | |
| Metropolis N, Ulam S. 1949. The Monte Carlo method. Journal of the American Statistical Association , 44 (247) : 335-341. DOI:10.1080/01621459.1949.10483310 | |
| Qiang J K, Ruan B Y, Zhou J J. 2010. Research on the array of electrodes of advanced focus detection with 3D DC resistivity in tunnel. Chinese Journal of Geophysics (in Chinese) , 53 (3) : 695-699. DOI:10.3969/j.issn.0001-5733.2010.03.024 | |
| Qiang J K, Ruan B Y, Zhou J J, et al. 2011. The feasibility of advanced detection using DC three-electrode method in coal-mine tunnel. Progress in Geophysics (in Chinese) , 26 (1) : 320-326. DOI:10.3969/j.issn.1004-2903.2011.01.038 | |
| Qu Y H, Zhang G B, Zhao L F, et al. 2007. Study on 3-D resistivity inversion for infinite surface-borehole line current source. Progress in Geophysics (in Chinese) , 22 (5) : 1393-1402. | |
| Ruan B Y, Deng X K, Liu H F, et al. 2009. Research on a new method of advanced focus detection with DC resistivity in tunnel. Chinese Journal of Geophysics (in Chinese) , 52 (1) : 289-296. | |
| Ruan B Y, Deng X K, Liu H F, et al. 2010. Influential factors and optimum survey method of advanced focus detection with DC resistivity in tunnels. Progress in Geophysics (in Chinese) , 25 (4) : 1380-1386. DOI:10.3969/j.issn.1004-2903.2010.04.029 | |
| Rubinstein R Y, Kroese D P. 2007. Simulation and the Monte Carlo Method. New Jersey:John Wiley & Sons. | |
| Sambridge M, Mosegaard K. 2002. Monte Carlo methods in geophysical inverse problems. Reviews of Geophysics , 40 (3) : 3-1. | |
| Shi X F, Han D P. 2012. The application of DC resistivity method in coal mine tunnel advanced exploration. Safety in Coal Mines (in Chinese) , 43 (5) : 104-107. | |
| Tan H D, Tong T, Lin C H. 2006. The parallel 3D magnetotelluric forward modeling algorithm. Applied Geophysics , 3 (4) : 197-202. DOI:10.1007/s11770-006-4001-5 | |
| Wang D Q, Xu X G, Yue J H. 2003. Simulation research drift influence of point-source current field in the medium of uniform wallrock. Coal Geology of China (in Chinese) , 15 (2) : 55-58. | |
| Wang G H, Yang J Y, Yu J Q. 2003. Application of mine DC current method to pilot probing in mining gateway excavation face. Coal Science and Technology (in Chinese) , 31 (F08) : 42-45. | |
| Wang J J. 1995. The application of D-C method in looking for water in mine tunnels. Journal of Hebei Mining and Civil Engineering Institute (in Chinese) , 12 (1) : 28-32. | |
| Wang W, Wu X P, Spitzer K. 2013. Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids. Geophysical Journal International , 193 (2) : 734-746. DOI:10.1093/gji/ggs124 | |
| Wang X L, Feng H, Li P, et al. 2011. Application of COMSOL multiphysics to pilot detection positive evolution of mine resistivity. Coal Science and Technology (in Chinese) , 39 (11) : 112-117. | |
| Wang Z G, He Z X, Liu Y. 2006a. Research of three-dimensional modeling and anomalous rule on borehole-ground DC method. Chinese Journal of Engineering Geophysics (in Chinese) , 3 (2) : 87-92. | |
| Wang Z G, He Z X, Wei W B. 2006b. Study on some problems upon 3D modeling of DC borehole-ground method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 28 (4) : 322-327. | |
| Wei C, Li X F, Zhang M G. 2008. The geophysical inverse method based on quantum Monte Carlo. Chinese Journal of Geophysics (in Chinese) , 51 (5) : 1494-1502. | |
| Wu W S, Huang L J. 2004. Monte Carlo simulation of three-detector density logging. Chinese Journal of Geophysics (in Chinese) , 47 (1) : 164-170. | |
| Yang T W, Ruan B Y, Zhou L, et al. 2009. Simulating focused-current advanced detection in tunnels by conductive paper test. Mineral Resources and Geology (in Chinese) , 23 (4) : 362-366. | |
| Yin C, Maurer H M. 2001. Electromagnetic induction in a layered earth with arbitrary anisotropy. Geophysics , 66 (5) : 1405-1416. DOI:10.1190/1.1487086 | |
| Yin C C, Weidelt P. 1999. Geoelectrical fields in a layered earth with arbitrary anisotropy. Geophysics , 64 (2) : 426-434. DOI:10.1190/1.1444547 | |
| Yin C C. 2000. Geoelectrical inversion for a one-dimensional anisotropic model and inherent non-uniqueness. Geophysical Journal International , 140 (1) : 11-23. DOI:10.1046/j.1365-246x.2000.00974.x | |
| Yue J H, Li Z D. 1993. Study and model experiments of tunnel influence on electric curves in coal mines. Coal Geology & Exploration (in Chinese) , 21 (2) : 56-59. | |
| Yue J H, Li Z D. 1997. Mine DC electrical methods and application to coal floor water invasion detecting. Journal of China University of Mining & Technology (in Chinese) , 26 (1) : 94-98. | |
| Yue J H, Li Z D. 1999. Roadway influence on electrical prospecting in underground mine. Journal of China Coal Society (in Chinese) , 24 (1) : 7-10. | |
| Zhai P H, Liu Y, Niu C, et al. 2014. Numerical simulation of advanced detection with DC resistivity in fluctuation tunnel. Safety in Coal Mines (in Chinese) , 45 (2) : 138-140. | |
| Zhang L, Ruan B Y, Lu Y Z, et al. 2011. Study of full-space numerical modeling of advanced exploration in tunnel with DC Focus resistivity method. Chinese Journal of Geophysics (in Chinese) , 54 (4) : 1130-1139. DOI:10.3969/j.issn.0001-5733.2011.04.029 | |
| Zhang N H, Li D P. 2003. Application of mine electrical method in exploring the break-out-water collapse column in Renlou Mine. Coal Geology & Exploration (in Chinese) , 31 (6) : 56-57. | |
| Zhang P S, Liu S D, Cao Y. 2009. A study on stereo electric method advance prediction technology in tunnel excavation. Coal Geology of China (in Chinese) , 21 (2) : 50-53. | |
| Zhang P S, Li Y S, Hu X W. 2013. Application and discussion of the advanced detection technology with DC resistivity method in tunnel. Chinese Journal of Underground Space and Engineering (in Chinese) , 9 (1) : 135-140. | |
| Zhang Y X, Han D P, Zhao P. 2008. Application status quo and progressing of mine electromagnetic technique in coalmine security domain. Coal Geology of China (in Chinese) , 20 (12) : 60-63. | |
| Zhdanov M S, Keller G V. 1994. The Geoelectrical Methods in Geophysical Exploration. New York:Elsevier Science Limited. | |
| Zhou B, Greenhalgh M, Greenhalgh S A. 2009. 2.5-D/3-D resistivity modelling in anisotropic media using Gaussian quadrature grids. Geophysical Journal International , 176 (1) : 63-80. DOI:10.1111/gji.2008.176.issue-1 | |
| Zhu S B, Shi Y L. 2007. Error analysis of strain rates from GPS measurements based on Monte Carlo method. Chinese Journal of Geophysics (in Chinese) , 50 (3) : 806-811. | |
| 陈峰, 安金珍, 廖椿庭. 2003. 原始电阻率各向异性岩石电阻率变化的方向性. 地球物理学报 , 46 (2) : 271–280. | |
| 程久龙, 王玉和, 于师建, 等. 2000. 巷道掘进中电阻率法超前探测原理与应用. 煤田地质与勘探 , 28 (4) : 60–62. | |
| 程久龙, 李飞, 彭苏萍, 等. 2014. 矿井巷道地球物理方法超前探测研究进展与展望. 煤炭学报 , 39 (8) : 1742–1750. | |
| 傅良魁. 电法勘探教程. 北京: 地质出版社, 1983 . | |
| 高致宏, 闫述, 王秀臣, 等. 2006. 巷道超前(电法)探测的应用现状与存在的问题. 煤炭技术 , 25 (5) : 120–121. | |
| 韩德品, 张天敏, 石亚丁, 等. 1997. 井下单极-偶极直流电透视原理及解释方法. 煤田地质与勘探 , 25 (5) : 32–35. | |
| 韩光, 庄德玉, 田劼, 等. 2009. 矿井直流电法超前预报球体构造的初步理论及沙槽实验研究. 煤炭工程 (3) : 69–72. | |
| 胡祥云, 李焱, 杨文采, 等. 2012. 大地电磁三维数据空间反演并行算法研究. 地球物理学报 , 55 (12) : 3969–3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 | |
| 黄俊革, 鲍光淑, 阮百尧. 2005. 坑道直流电阻率测深异常研究. 地球物理学报 , 48 (1) : 222–228. | |
| 黄俊革, 王家林, 阮百尧. 2006. 坑道直流电阻率法超前探测研究. 地球物理学报 , 49 (5) : 1529–1538. | |
| 黄俊革, 阮百尧, 王家林. 2007. 坑道直流电阻率法超前探测的快速反演. 地球物理学报 , 50 (2) : 619–624. | |
| 李冰. 2015. 直流电法超前探测技术在含水断层构造探测中的应用. 煤炭技术 , 34 (3) : 113–115. | |
| 李学军. 1992. 煤矿井下定点源梯度法超前探测试验研究. 煤田地质与勘探 , 20 (4) : 59–62. | |
| 李焱, 胡祥云, 杨文采, 等. 2012. 大地电磁三维交错网格有限差分数值模拟的并行计算研究. 地球物理学报 , 55 (12) : 4036–4043. DOI:10.6038/j.issn.0001-5733.2012.12.015 | |
| 李玉宝. 2002. 矿井电法超前探测技术. 煤炭科学技术 , 30 (2) : 1–3. | |
| 刘斌, 李术才, 李树忱, 等. 2009. 隧道含水构造直流电阻率法超前探测研究. 岩土力学 , 30 (10) : 3093–3101. | |
| 刘斌, 李术才, 聂利超, 等. 2012. 隧道含水构造直流电阻率法超前探测三维反演成像. 岩土工程学报 , 34 (10) : 1866–1876. | |
| 柳建新, 邓小康, 郭荣文, 等. 2012. 坑道直流聚焦超前探测电阻率法有限元数值模拟. 中国有色金属学报 , 22 (3) : 970–975. | |
| 刘青雯. 2001. 井下电法超前探测方法及其应用. 煤田地质与勘探 , 29 (5) : 60–62. | |
| 刘树才, 刘志新, 姜志海, 等. 2004. 矿井直流电法三维正演计算的若干问题. 物探与化探 , 28 (2) : 170–172. | |
| 刘志新, 许新刚, 岳建华. 2003. 矿井电法三维有限元正演模拟——直流电透视方法技术研究. 物探化探计算技术 , 25 (4) : 302–307. | |
| 鲁晶津. 2010. 地球电磁三维数值模拟的多重网格方法及其应用研究[博士论文]. 合肥:中国科学技术大学. | |
| 鲁晶津, 吴小平. 2013. 巷道直流电阻率法超前探测三维数值模拟. 煤田地质与勘探 , 41 (6) : 83–86. | |
| 强建科, 阮百尧, 周俊杰. 2010. 三维坑道直流聚焦法超前探测的电极组合研究. 地球物理学报 , 53 (3) : 695–699. DOI:10.3969/j.issn.0001-5733.2010.03.024 | |
| 强建科, 阮百尧, 周俊杰, 等. 2011. 煤矿巷道直流三极法超前探测的可行性. 地球物理学进展 , 26 (1) : 320–326. DOI:10.3969/j.issn.1004-2903.2011.01.038 | |
| 屈有恒, 张贵宾, 赵连锋, 等. 2007. 井地有限线源三维电阻率反演研究. 地球物理学进展 , 22 (5) : 1393–1402. | |
| 阮百尧, 邓小康, 刘海飞, 等. 2009. 坑道直流电阻率超前聚焦探测新方法研究. 地球物理学报 , 52 (1) : 289–296. | |
| 阮百尧, 邓小康, 刘海飞, 等. 2010. 坑道直流电阻率超前聚焦探测的影响因素及最佳观测方式. 地球物理学进展 , 25 (4) : 1380–1386. DOI:10.3969/j.issn.1004-2903.2010.04.029 | |
| 石学锋, 韩德品. 2012. 直流电阻率法在煤矿巷道超前探测中的应用. 煤矿安全 , 43 (5) : 104–107. | |
| 王大庆, 许新刚, 岳建华. 2003. 均匀围岩介质中点源电流场的巷道影响模拟研究. 中国煤田地质 , 15 (2) : 55–58. | |
| 王国华, 杨居友, 于景泉. 2003. 井下直流电法在掘进工作面超前探测中的应用. 煤炭科学技术 , 31 (F08) : 42–45. | |
| 王进杰. 1995. 直流电法在煤矿巷道找水中的应用. 河北煤炭建筑工程学院学报 , 12 (1) : 28–32. | |
| 王小龙, 冯宏, 李萍, 等. 2011. 矿井电阻率超前探测正演模拟. 煤炭科学技术 , 39 (11) : 112–117. | |
| 王志刚, 何展翔, 刘昱. 2006a. 井地直流电法三维数值模拟及异常规律研究. 工程地球物理学报 , 3 (2) : 87–92. | |
| 王志刚, 何展翔, 魏文博. 2006b. 井地直流电法三维数值模拟中若干问题研究. 物探化探计算技术 , 28 (4) : 322–327. | |
| 魏超, 李小凡, 张美根. 2008. 基于量子蒙特卡罗的地球物理反演方法. 地球物理学报 , 51 (5) : 1494–1502. | |
| 吴文圣, 黄隆基. 2004. 三探测器密度测井的Monte Carlo模拟. 地球物理学报 , 47 (1) : 164–170. | |
| 杨庭伟, 阮百尧, 周丽, 等. 2009. 聚焦电流法隧道超前探测导电纸 模拟. 矿产与地质 , 23 (4) : 362–366. | |
| 岳建华, 李志聃. 1993. 巷道空间对矿井电测曲线影响的模型实验研究. 煤田地质与勘探 , 21 (2) : 56–59. | |
| 岳建华, 李志聃. 1997. 矿井直流电法及在煤层底板突水探测中的应用. 中国矿业大学学报 , 26 (1) : 94–98. | |
| 岳建华, 李志聃. 1999. 矿井直流电法勘探中的巷道影响. 煤炭学报 , 24 (1) : 7–10. | |
| 翟培合, 刘玉, 牛超, 等. 2014. 起伏巷道直流电阻率法超前探测数值模拟. 煤矿安全 , 45 (2) : 138–140. | |
| 张力, 阮百尧, 吕玉增, 等. 2011. 坑道全空间直流聚焦超前探测模拟研究. 地球物理学报 , 54 (4) : 1130–1139. DOI:10.3969/j.issn.0001-5733.2011.04.029 | |
| 张乃宏, 李定鹏. 2003. 矿井电法探测突水陷落柱在任楼煤矿的应用. 煤田地质与勘探 , 31 (6) : 56–57. | |
| 张平松, 刘盛东, 曹煜. 2009. 坑道掘进立体电法超前预报技术研究. 中国煤炭地质 , 21 (2) : 50–53. | |
| 张平松, 李永盛, 胡雄武. 2013. 巷道掘进直流电阻率法超前探测技术应用探讨. 地下空间与工程学报 , 9 (1) : 135–140. | |
| 张彦湘, 韩德品, 赵镨. 2008. 矿井电磁技术在煤矿安全领域的应用现状及进展. 中国煤炭地质 , 20 (12) : 60–63. | |
| 朱守彪, 石耀霖. 2007. 基于Monte Carlo方法的由GPS观测计算地应变率的误差分析. 地球物理学报 , 50 (3) : 806–811. | |
 2016, Vol. 59
2016, Vol. 59


