2. 国家海洋局海底科学重点实验室, 杭州 310012;
3. 浙江大学地球科学学院, 杭州 310027
2. Key Laboratory of Submarine Geosciences, State Oceanic Administration, Hangzhou 310012, China;
3. School of Earth Sciences, Zhejiang University, Hangzhou 310027, China
地震数据采集是整个地震勘探流程的基础,采集技术水平的提高对整个地震勘探的发展具有重要的意义.当前的地震数据采集是基于信号处理学科中的Fourier变换和Nyquist采样定理的(Marks,1991; Oppenheim et al.,1989).然而,该理论指导下的信息获取、存储、融合、处理及传输等方面已经成为目前信息领域技术发展的主要瓶颈之一,在地震数据采集中的表现也很明显.这主要是因为:1)根据Nyquist采样定理,若要使采样得到的信号能不失真地保持原信号的信息,必须以不低于待研究信号最高频率两倍的采样频率进行规则采样(否则就会产生假频),因而在进行地震勘探数据采集系统设计时,空间测网的采样间隔(包括检波器测网的线距、点距和炮点测网的线距、点距)与地震记录的时间间隔必须分布均匀且密集;2)勘探目标的复杂程度和精细化程度要求的提高也迫使人们在地震勘探中不仅要提高采集的地震数据的精度,还要进行“两宽一高”(宽频带、宽方位和高密度)采样(Cordsen and Galbraith,2002; Regone,2006; Sirgue et al.,2009; ten Kroode et al.,2013; Vermeer,2003; VerWest and Lin,2007)、多波多分量(Allen and Brown,1995; Bloom and Marscher,1996; Mohan and Singh,2002)和大面积地震数据采集以实现对地下构造的高精度成像.这就导致常规地震数据采集的时间越来越长、采集成本也越来越高,给后续的数据处理、数据质控、数据安全存储和管理带来了新的挑战.因此,在满足数据采集要求的前提下,如何经济高效地进行数据采集是当前地震勘探方法技术研究中一个十分迫切的问题,得到了地球物理学家们的广泛关注.
压缩感知是应用数学和信号处理领域近十年来的最新研究成果,是一种建立在矩阵分析、拓扑几何、优化、统计概率论、运筹学和泛函分析等学科上信息获取与处理的全新的理论体系.它在信号具有稀疏性的先验假定下,通过对信号“精挑细选”的采样数据,把经典的基于Nyquist采样理论的信号采样(Signal Sampling)转变为对信号中的信息采样(Information Sampling),通过求解一个特定的最优化问题就可以从这些极少量的采样数据恢复出原始信号.所谓稀疏性,是指一个信号(向量)中除了少数部分元素不为零之外,其他大部分的元素都为零(或非常接近于零);若该信号不满足此要求,但对其进行某种变换(可以是正交变换,也可以是非正交变换),变换后的系数满足此要求,则也称该信号具有稀疏性(或变换域稀疏性),则这个变换对于该信号而言就称为稀疏变换.信号的稀疏性是进行采样的基础,信号的采样间隔取决于信息在信号中的结构与分布,从而打破了基于Fourier变换和Nyquist采样定理的常规采样方法的诸多限制,为信号的高效采样方案的研究与设计以及从本质上解决常规采样方法引起的信息冗余、采样效率低的问题提供了理论依据.因压缩感知利用的是信号的稀疏性,因此在本文中又称为基于稀疏性的信号采样理论.近年来,随着该理论在医疗成像(Lustig et al.,2007)、无线通信(Mamaghanian et al.,2011)、模式识别(Wright et al.,2010)、雷达探测(Herman and Strohmer,2009)与图像超分辨重建(Park et al.,2003; Yang et al.,2010)等领域的高度关注及应用研究的深入,地球物理工作者也将其应用到地震勘探数值模拟、数据压缩、数据重建和非线性反演等方面(Hennenfent et al.,2010; Hennenfent and Herrmann,2006,2008; Herrmann,2010; Herrmann and Hennenfent,2008; Lin et al.,2008; Wang et al.,2010; 唐刚,2010; 王薇等,2013),但在地震数据高效采集领域的应用研究还处于起步阶段.Lin和Herrmann(2009)提出了把压缩感知应用于多源地震数据采集的思路,Moldoveanu(2010)对海上数据采集的随机观测方法进行了积极的探索,Milton等(2011)提出了把常规规则密集布置炮点的地震采集方式改为随机稀疏布置炮点的数据采集方式(注:他们使用多维插值方法来重构数据).马坚伟(2011)的“稀疏促进地震勘探”观点提出了利用压缩感知降低野外采集数据量的构想,陈生昌等(2012,2015)报告了应用压缩感知理论进行地震数据高效采集方法研究的初步框架.Mosher等(2012)基于压缩感知理论提出了一种非均匀优化采样的地震数据观测系统设计,表明可以使用相同数量的仪器设备获得更高的空间分辨率或者可以完成更大面积的采集任务.以上研究对基于压缩感知的高效采集进行了有益的探索,为利用地震波场的稀疏性进行地震数据的高效采集提供了基本思路.
综上所述,基于稀疏性的地震数据高效采集方法是一种正在发展且有着广阔前景的采集方法,国内外还没有系统地开展地震数据高效采集方法理论的研究,其中存在的许多问题尚需解决,如方法应用的理论基础、具体实施方案以及数据重建方案等.本文在深入调研当前地震数据高效采集方法的基础上,从高效采集方法理论和具体实施策略两方面开展基于稀疏性的地震数据高效采集方法研究.其中,高效采集方法理论研究主要包括以下三个部分:1)地震数据的稀疏性理论依据以及适合地震数据时间-空间特征的最稀疏变换方法;2)地震数据的高效采集测网(测线、测点分布)设计方法;3)规则密集测网上的地震数据的重构方法.高效采集具体实施策略研究主要包括以下三个部分:1)在常规规则密集测网的基础上,根据炮点和检波点在测网布置中的各种分布情况,利用上述稀疏约束的随机采样方法开展了高效采集测网设计方法研究,提出高效采集测网的设计方案;2)根据稀疏约束地震数据重建理论,提出了对应高效采集得到的三种类型的地震数据的重建方法流程;3)对高效采集地震数据的直接偏移成像方法进行了研究,通过高效采集数据的直接成像和重建数据的偏移成像结果的对比,验证数据重建方法的有效性.
2 地震数据高效采集方法理论发展一种新的采样方法的一般途径包括以下三点:1)在对信号进行采样前需要有待研究信号的先验知识; 2)根据待研究信号的先验知识来确定采样方案;3)采集到的数据必须是待研究信号的真实反映,即由采集数据必须能准确地重构信号.陈生昌等(2015)讨论并指出了带限信号Nyquist采样的局限性,即Nyquist采样是在假定信号频带有限的情况下确定的均匀规则的采样方案,采样间隔必须满足一定的要求;当带限信号的频谱是稠密地分布在整个频带范围内时,Nyquist采样方法是高效的,反之则是非高效的.接下来,我们将根据上述三个认识开展地震数据高效采集方法的研究.
2.1 地震数据的稀疏性与稀疏变换地震数据是否具有稀疏性是开展地震数据高效采集方法理论的前提和基础.波动方程描述了地震波在介质中的传播规律和传播特征,因而根据波动方程的解的一般表示式进行地震数据的稀疏性的数学物理依据研究是一条必要且可行的研究路径.密度均一介质、脉冲震源激发条件下的声波波动方程为
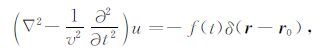
|
(1) |
其中, r0=x0i+y0j+z0k 为震源位置, u 为地震波场, -f(t)δ(r-r0) 为震源函数.该方程的Green函数 G(r,t|r0,t0) 可以表示为(杜世通,2009):
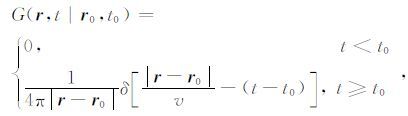
|
(2) |
式(2)表明,空间 r0 处的一个单位脉冲震源在 t0 时刻开始激发,所产生的球面波在 t>t0 时间向四周空间扩散,在 t 时刻,波传播到以 r-r0 为半径的球面上,随着波的传播,其振幅值按照 14πr-r0 的比例因子衰减.
通过Green函数(2)式可以把非其次方程
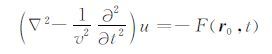
|
(3) |
的解表示成如下的形式(杜世通,2009):
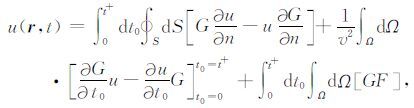
|
(4) |
其中, t+为t+ε 的微量时间段, ε 为任意一个微量, Ω 为求解区域, S 为 Ω 区域的边界, F(r0,t) 为震源.
待研究信号的基本特征与变换的基本波形越接近,则信号就可以取得越稀疏的变换系数(Chen et al.,1998; Starck et al.,2010).从(4)式可以看到,波动方程的解是一个以Green函数(2)为主体的积分表达式,而Green函数(2)式则包含了一个空间上以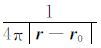
曲波变换可以表示如下:
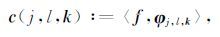
|
(5) |
其中,φj,l,k 为Curvelet函数, j,l,k 分别为位置参量(对于二维数据来说, k=(k1,k2) 为变换参数), 〈〉 表示内积.(5)式表明,曲波变换能够实现信号的多尺度、多方向分解.Curvelet变换具有如下性质:
1) 它是一个紧的框架,能够通过(6)式
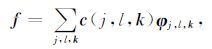
|
(6) |
完成信号的重建,并满足Parseval关系:
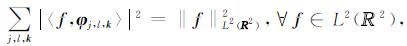
|
(7) |
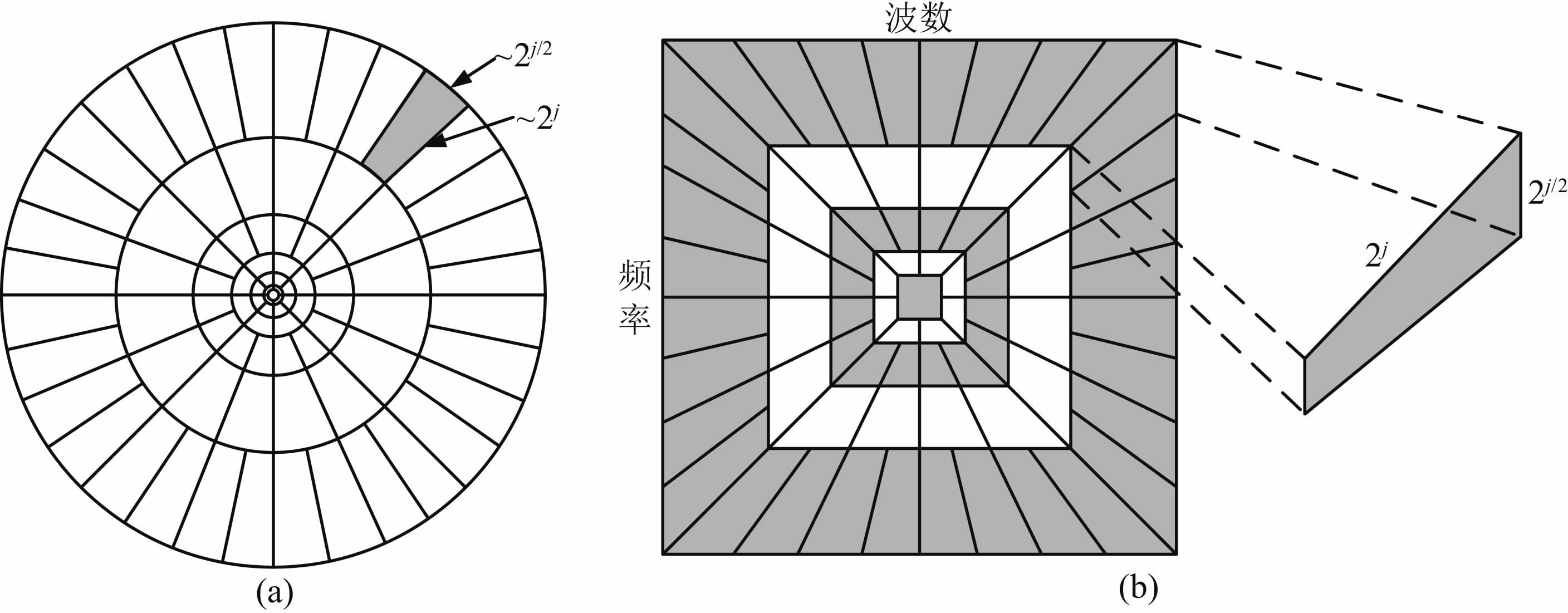
2) 各向异性——抛物尺度关系:曲波变换是在频率域中实现的,连续Curvelet变换基于极坐标系,离散Curvelet变换基于笛卡儿坐标系,图 1是连续Curvelet变换和离散Curvelet变换的频率空间分块图,整个频率空间是一些抛物楔形组成的,楔形的有效长度length和宽度width服从以下各向异性尺度关系(Candès et al.,2006b):
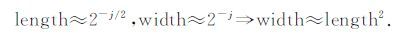
|
(8) |
|
图 1 曲波变换频率空间分块图 (a)连续曲波变换;(b)离散曲波变换.在频率空间,曲波近似由抛物楔形来支撑(如图a中箭头所示和图b中放大的部分). Fig. 1 Schematic curvelet tiling of the f-k plane (a)Continuous curvelet transform;(b)Discrete curvelet transform. In the f-k domain,the curvelets are supported by angular “parabolic” wedges. |
3) 多方向性:Curvelet变换是一种多方向变换,除了粗尺度下的Curvelet是无方向之外,其他尺度上都有很好的方向选择性.
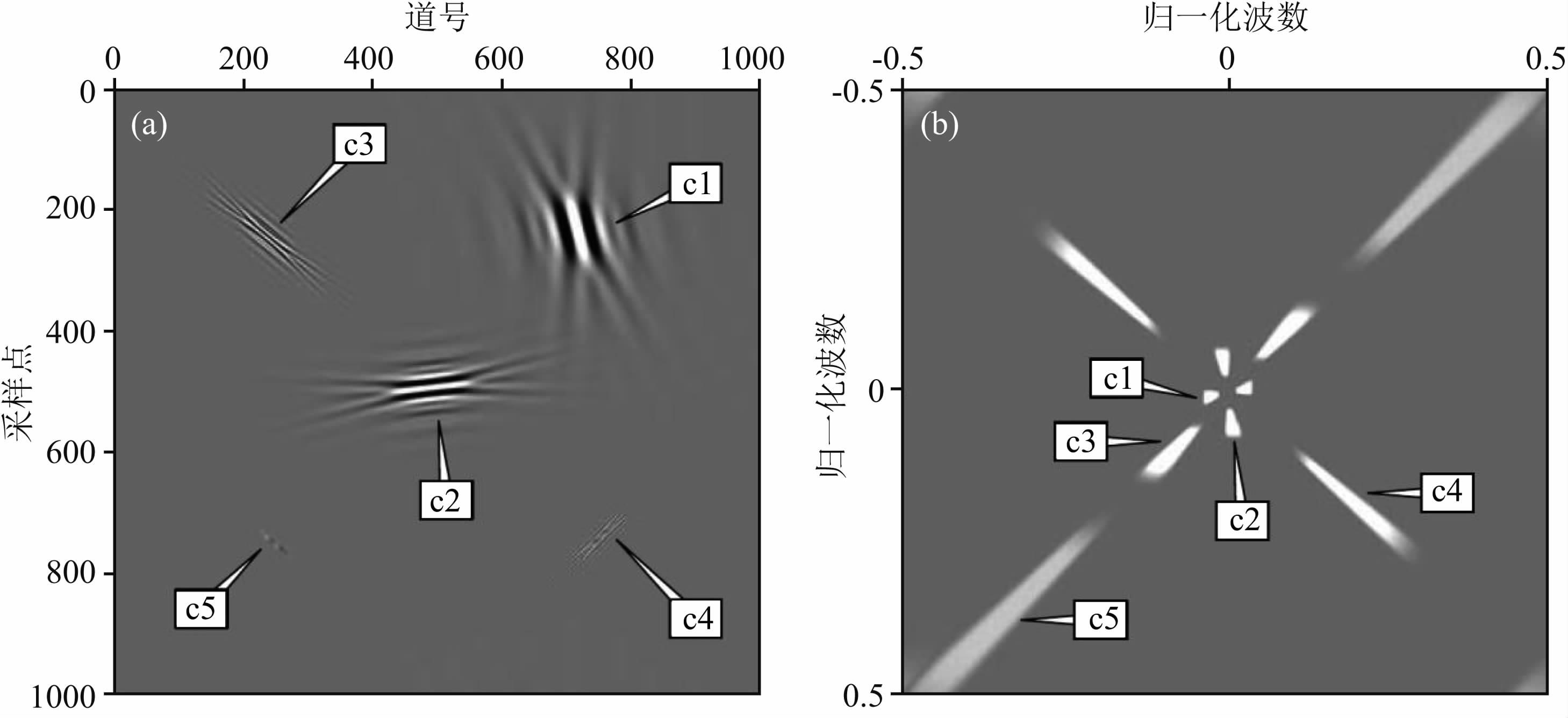
Curvelet是一种各向异性小波,具有与地震波前的形态非常相似曲线状的基元.图 2是几个不同的Curvelets及其在频率中的分布图,多尺度、多方向性可以很好地进行区分.由此可知,Curvelet变换能更好地捕捉到曲线状的奇异特征,也就可以为地震数据提供最稀疏的表示(Candès and Donoho,2004; Candès et al.,2006b).
|
图 2 Curvelets示例 (a)为5个不同尺度、不同方向的曲波;(b)为(a)所对应的5个曲波的振幅谱.引自Hennenfent等(2010). Fig. 2 Sample curvelets (a)Five real curvelets at different scales and angles;(b)Amplitude spectrum of(a)annotated only for the positive frequencies due to symmetry around DC. Cited from Hennenfent et al.(2010). |
地震数据的采集过程可以表示为:
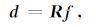
|
(9) |
其中,f∈RM 为原始地震数据, d∈Rn 为采集到的地震数据,通常有 n <M,R∈Rn×M 是采样矩阵.设 C为f 的稀疏变换,即 f=CHm, 则式(9)就可以转化为:
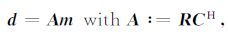
|
(10) |
其中,上标H代表Hermitian转置, m∈RN 是f
在实际中,方程(10)大都表现为一个欠定方程而难以对其进行求解.研究表明,只要 n×N 的矩阵 A 的任何一个子集 S (记为 AS,为n×|S| 阶子矩阵, S 为 A 中所有可能的 |S|≤k 列元素的组合, S是S 的基数, k <N为m 中非零元素的个数)近似表现为一个正交基(Candès et al.,2006a; Herrmann,2010),则仍然可以对问题(10)进行求解,前提条件是必须能找到一个使 AS 满足(11)式(受限等距特性,RIP)的受限等距参数 0 <δk<1:
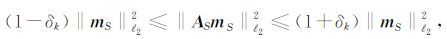
|
(11) |
其中, δk≤(k-1)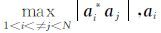
AS 的非唯一性意味着一个稳定、成功的解 m 的获得依赖于 AS 列之间的非相干性.随机理论表明,具有独立同分布(independent and identically distributed,i.d.d.)的高斯随机矩阵满足此要求,且当稀疏度 k 满足
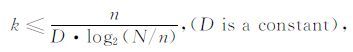
|
(12) |
时,式(11)总是成立的(Herrmann,2010).也就是说,在稀疏变换的帮助下,只需要利用按照超定采样比 n/k≈D·log2N 进行采样的结果就可以完成稀疏域中的 k 个非零系数的恢复,且 k 越小,实际所需的采样数 n 也就越少.
综上所述,若 A 为随机矩阵,在变换矩阵 C 确定的情况下,采样矩阵 R 也必须是随机矩阵,因而采样方法的设计也就成为一个关键问题.
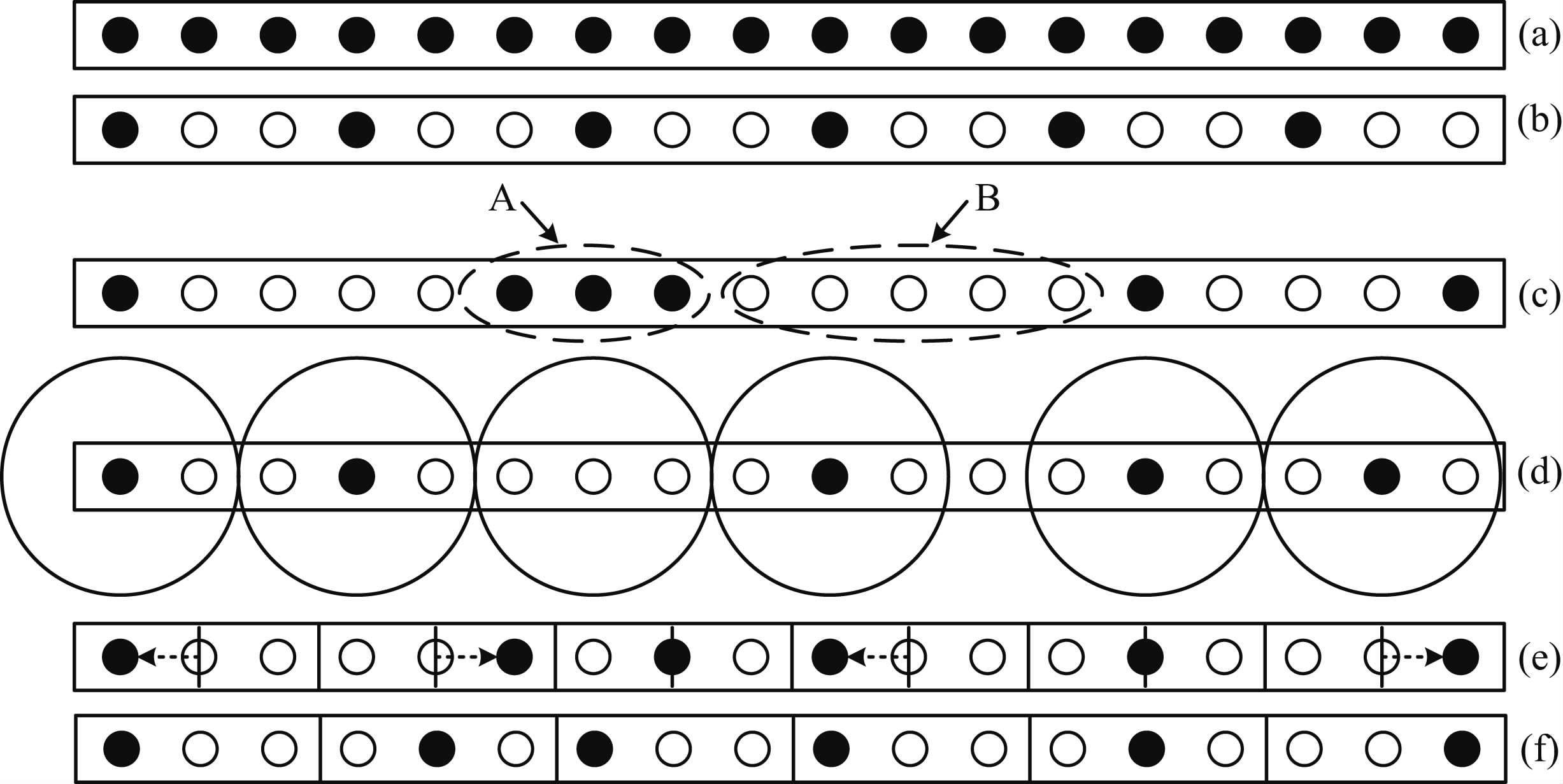
2.2.2 随机采样及改进的分段采样随机采样方法可以克服常规规则欠采样(图 3b)引起的假频,这也是随机采样能够用于采样信号的重建的内在原因.图 3列出的几种采样方法中,高斯随机采样容易造成采样点过于聚集或者分散的情况(如图 3c中A、B箭头所示),引起部分区域采样信息的冗余或者缺失,给后续数据恢复处理带来困难.
|
图 3 采样方法对比示意图(在18个样点中抽取6个样点) (a)所有样点;(b)规则欠采样;(c)高斯随机欠采样;(d)泊松碟欠采样;(e)Jittered采样;(f)分段随机采样. 其中,实心点代表实际采样点,空心圆圈代表总的样点. Fig. 3 Schematic diagram of sampling method(6 points are sampled from 18 points) (a)All points;(b)Regular undersampling;(c)Gaussian random undersampling;(d)Poisson disk undersampling;(e)Jittered random undersampling;(f)Piecewise-random undersampling. Solid points represent sampled points. Hollow circles represent total samples. |
为解决上述问题,人们发展了多种随机且均匀的采样方法,常用的有以下几种:1)泊松碟随机采样(Dunbar and Humphreys,2006; Tang et al.,2009; 唐刚,2010)——通过在相邻采样点周围设置一些具有一定半径的圆盘来控制采样间隔(圆盘区域不能重叠,如图 3d所示);2)Jittered采样(Hennenfent and Herrmann,2008)——首先对所有样点进行均匀分段,然后在每个段内以中心样点为基准做随机“抖动”来选取采样点(图 3e),该方法要求每个段内的样点数为奇数;3)分段采样(Wang et al.,2011)——对所有样点先分段,然后在每个子段内随机选取一个作为采样点(图 3f).
为了了解上述采样方法的特性与差异,这里以Fourier变换作为稀疏变换,利用褶积矩阵
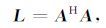
|
(13) |
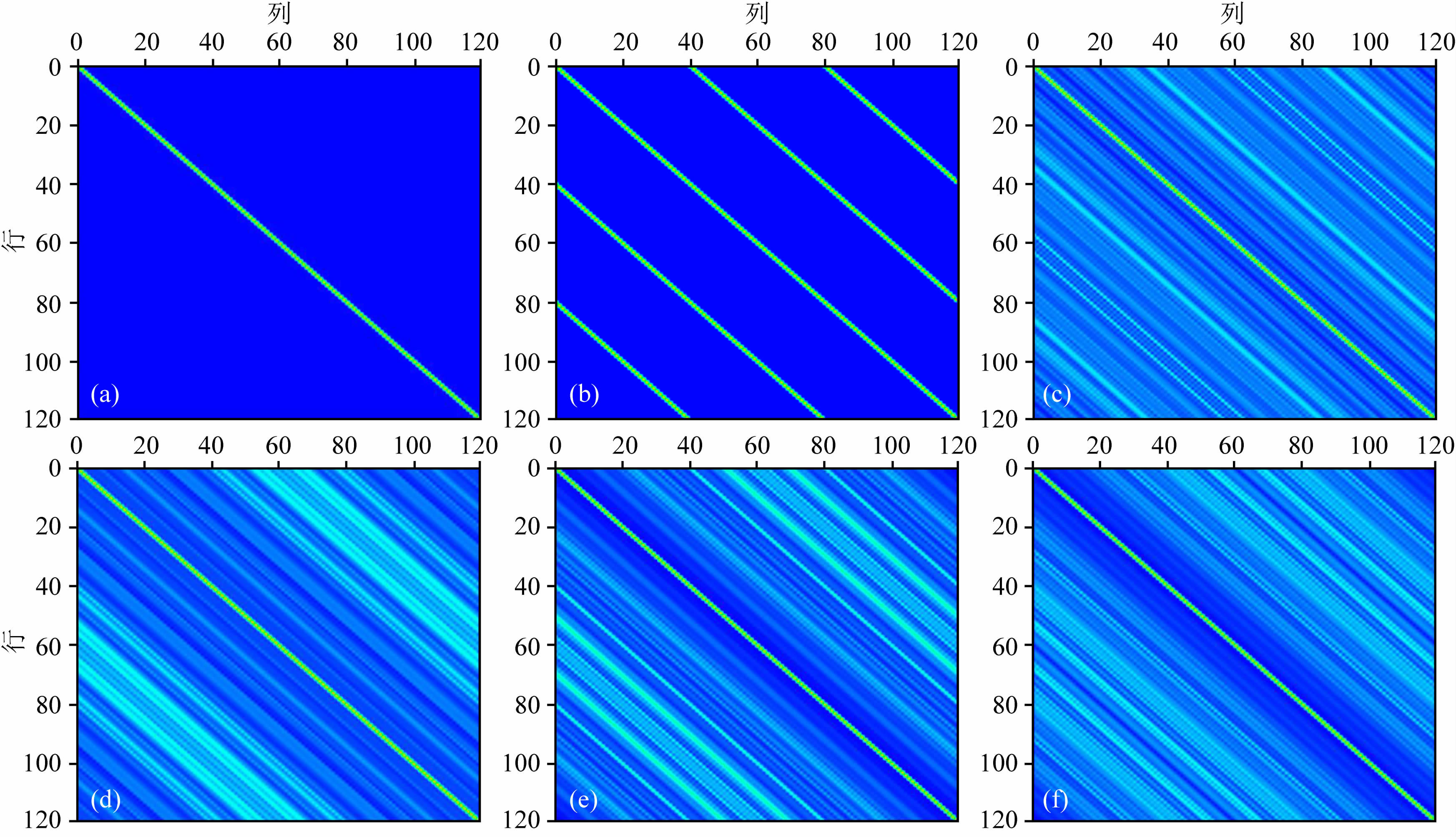
进行对比分析研究. L 可以表示出采样方法本身“泄漏”信号的特性:1)当进行全采样时(图 4a), L=I, 对应采样矩阵的元素(主对角线)为1,其他为0;2)当进行规则欠采样时(图 4b), L 主对角线上的元素幅值降低,产生了平行于主对角线的、振幅具有一致性的频率泄漏(Donoho,2006;Verdú,1998; Xu et al.,2005);3)当进行随机欠采样时(对应高斯随机欠采样、泊松碟采样、Jittered采样和分段随机采样的矩阵分别如图 4c、4d、4e和4f所示),假频被转化为低幅值随机噪声, L 中泄漏频率成分的分布具有一定的随机性.高斯随机采样泄漏的频率分布比较均匀,而其他三种随机且均匀的采样方法(图 4d、4e、4f)则可以压制主要信号周围的噪声,具有明显的“蓝色噪声”频谱特征,且分段随机采样泄漏的频率成分在主对角线附近的信息更少且弱,更易于有用信号与噪声的分离处理.
|
图 4 不同采样方法的矩阵 L 对比 (a)完全采样;(b)规则欠采样;(c)高斯随机欠采样;(d)泊松碟欠采样;(e)Jittered采样;(f)分段随机采样. Fig. 4 Matrix L corresponding to different sampling methods (a)Total sampling;(b)Regular undersampling;(c)Gaussian random undersampling;(d)Poisson disk undersampling;(e)Jittered undersampling;(f)Piecewise random undersampling. |
由此可知,分段随机采样方法除了具有更为优越的“蓝色噪声”频谱分布特征、特别适合具有稀疏性先验信息的信号的采样之外,分段采样方法还突破了Jittered采样对段内样点为奇数的限制,具有更好的灵活性.然而,和Jittered采样相类似,当总样点不是采样点数整数倍时,分段随机采样会受到剩余样点问题的困扰(图 5a).针对这种状况,这里提出一种改进分段采样方法(图 5b),主要过程如下:
1) 对所有样点分段.假设总的样点为n0,需要采样点数为ns,先对总的样点分为ns段,每个段内有 int(n0/ns) 个样点,剩余的样点数为 nr (图 5a虚线椭圆区域),很明显 nr <ns. 这里 int() 表示取整.
2) 段内样点数调整.从 ns 个段中随机选取 nr 个段,并把分段后剩余的 nr 个样点放入选好的 nr 个段中,调整后会有 nr 个段的样点数目会增加一个,如图 5a箭头所示.

|
图 5 (a)常规分段随机采样方法,(b)改进的分段随机采样方法.例子中,在20个样点中抽取了6个样点 Fig. 5 (a)Conventional piecewise random sampling,(b)Improved piecewise random sampling. Six points are sampled from 20 points |
3) 采样.从 ns 个段中各随机地抽取一个样点作为采样点,共 ns 个采样点.
这种改进的分段采样方法在保持分段随机采样的优点的同时解决了剩余样点的问题,可以根据实际情况按任意采样比例(采样的道数和总道数之比)进行采样,提高了实际地震数据采集系统设计的灵活性.
2.3 稀疏约束下高效采集数据的重建由高效采集得到的不规则稀疏测网地震数据恢复出规则密集测网地震数据的实质是一个欠定线性反问题的求解过程,某种意义上也可以视为一种数据插值问题(Abma,2009; 刘喜武等,2004).
由(10)式可知, m 可以通过求解下面的稀疏优化问题获得:
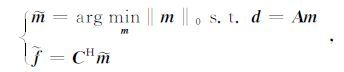
|
(14) |
式中,波浪线~表示信号的估计值,l0 范数是一种伪范数(定义式: ‖m‖0∶=#{m,mi≠0}), 是信号稀疏性的最佳度量, mi表示向量m的第i 项.
利用Lagrange乘子法把具有约束的问题转化为下面的无约束优化问题:
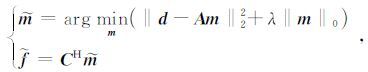
|
(15) |
其中, λ>0 为拉格朗日乘子.由于在实际求解中,l0 范数约束造成了问题的非凸性,求解比较困难,一般用l1 范数代替l0 范数,使问题转化为凸优化问题,即
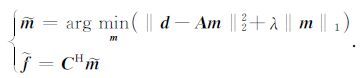
|
(16) |
上述稀疏优化问题的求解方法与策略主要包括:(1)贪婪类算法,如(正交)匹配追踪法(Chen et al.,1998; Tropp and Gilbert,2007)等;(2)基于l1 范数最小约束的预条件共轭梯度(Koh et al.,2007)、凸集梯度法(Abma and Kabir,2006)等,但该类方法涉及到矩阵计算问题,不适合大规模问题求解;(3)阈值类方法(Daubechies et al.,2004),该方法简单易行,避免了矩阵求逆运算而能适应大规模问题的求解.这里我们使用迭代阈值法进行求解,并考虑到提高迭代的稳定性,引入了加速迭代阈值法(Blumensath,2012; Daubechies et al.,2008),其迭代格式如下:
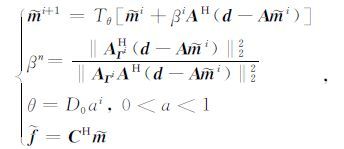
|
(17) |
其中, i 为迭代次数, θ 为阈值, θ0 为初始阈值,并随着迭代次数按指数衰减, βn 为迭代步长,保证了迭代过程的稳定性, Γi 是 mi 的支撑集, Tθ 为硬阈值算子,其定义如下:
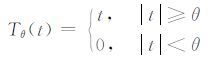
|
(18) |
通过式(17)的迭代就可以得到满足一定精度要求的全局最优稀疏解 , 进而得到重建地震数据的估计值$\tilde{f}$. 上述加速迭代阈值方法求解稀疏优化问题的迭代式构造简单、计算稳定,并且可以适宜大规模计算,可以比较方便地用于叠前地震数据的重建.
3 地震数据高效采集实施策略本文第2节对地震数据高效采集理论进行了一定程度上的改进和探索研究,本节将在地震波场稀疏性的先验信息基础上,利用2.2节提出的改进的分段采样方法对常规采集系统的规则、密集的震源和检波点进行随机采样,得到非规则、稀疏的高效采集测网,再利用2.3节发展的稀疏重建方法对使用上述高效采集测网采集的地震数据进行重建.本节力求将高效采集方法理论与地震采集系统的测网设计相结合,探讨高效采集的具体实施方法策略问题.
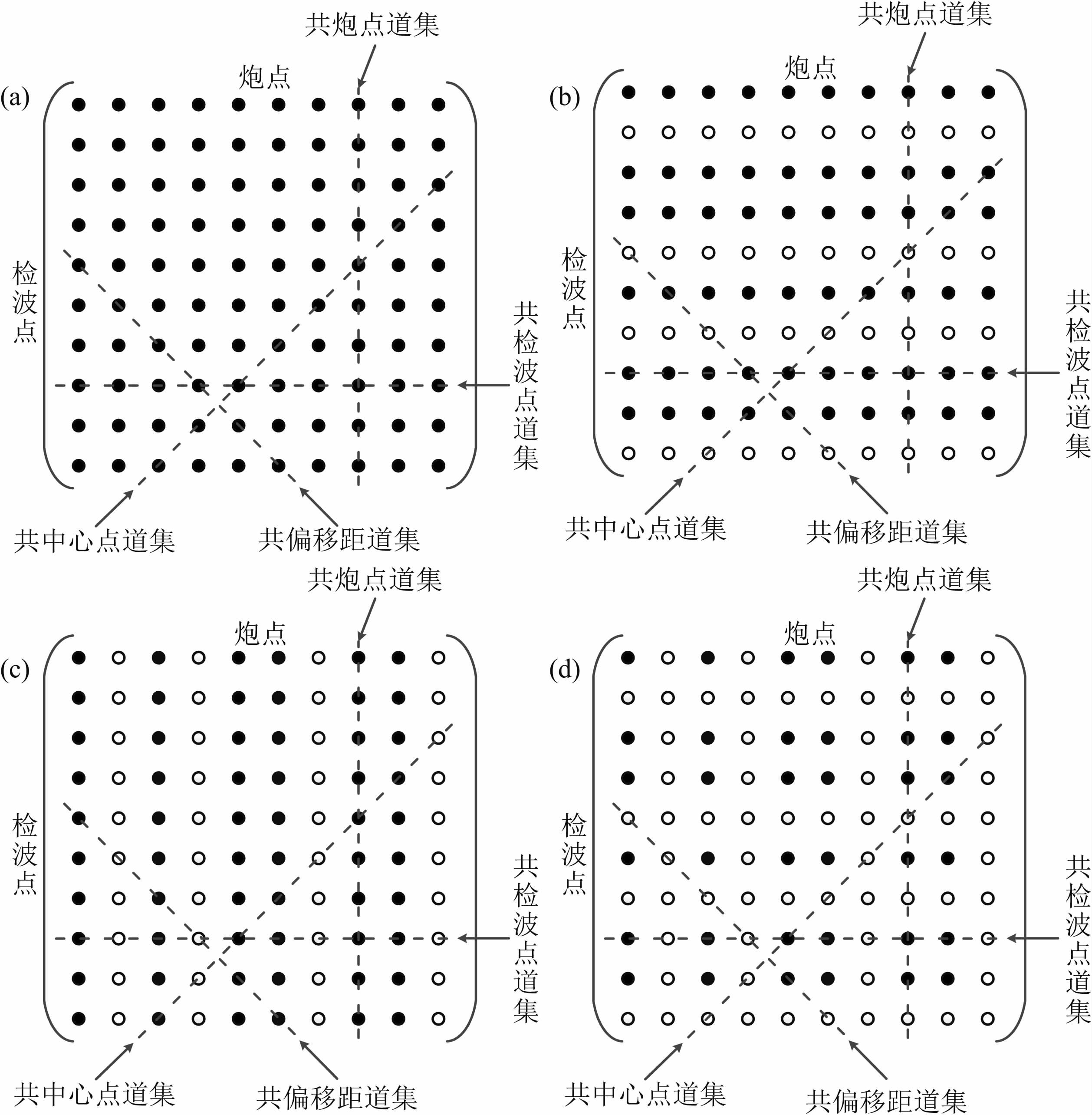
Berkhout和Pao(1982)指出,在频率域地震数据(2D或3D)可以通过一个数据矩阵 P 来表示,其元素 Pi,j 表示和检波器i、震源 j 对应的复值.设 ng 为所有的检波器数目, ns 为所有的激发炮数, P 如图 6a所示,每一行代表一个共检波点道集,每一列代表一个共炮点道集,每条对角线代表一个共偏移距道集,每条反对角线代表一个共中心点道集.频率域常规单震源地震数据采集模型(Berkhout et al.,2008)可以写为:
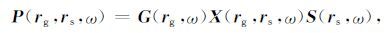
|
(19) |
其中, ω 为圆频率, rs 为震源的位置, rg 为检波点的位置, S 为震源,每一列代表一个震源排列, X(rg,rs,ω) 为地下地震波场传播算子, G(rg,ω) 代表检波器矩阵,代表一个频率分量检波器特性,每一行代表一个检波器排列, P(rg,rs,ω) 为接收到的地震数据.
3.1 稀疏约束下的高效采集测网布置方法基于地震数据采集中的炮点和检波点之间的关系,按照稀疏性约束的地震数据采样矩阵设计的要求设计服从独立同分布的随机矩阵对震源矩阵 S 和检波器矩阵 G 加以改变,就可以得到不同参数的地震数据观测系统.
3.1.1 规则炮点、随机检波点(DsRg)高效采集按照稀疏性约束的地震数据采样矩阵设计的要求,设计检波器随机采样矩阵 Θg∈Rng′×ng, 其中, ng′ 为选取的检波器数目,且 ng′ <ng.通过Θg 作用于(19)式中的 G 可得:
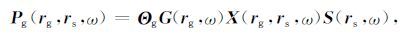
|
(20) |
式(20)就是按照规则布置炮点、随机稀疏布置检波点的方式进行采集的数学模型, Pg 为接收到的地震数据,下标g表示检波点随机布置,其数据矩阵的结构如图 6b所示.
3.1.2 随机炮点、规则检波点(RsDg)高效采集按照稀疏性约束的地震数据采样矩阵设计的要求,设计炮点随机采样矩阵为 Θs∈Rns′×ns, 其中, ns′ 为按照一定的随机策略选取的炮点数目(且 ns′ <ns).通过Θs 对(19)式中的 S 加以改变,可得:

|
(21) |
式(21)就是按照随机布置炮点、规则布置检波点的方式进行采集的数学模型, Ps 为接收到的地震数据,下标s表示震源随机布置,其数据矩阵的结构如图 6c所示.
|
图 6 常规规则密集采集和高效采集的地震数据矩阵示意图 (a)常规规则密集采集方式;(b)DsRg采集方式;(c)RsDg采集方式;(d)RsRg采集方式.矩阵中黑点表示数据矩阵的元素,为某一个频率成分的复值;空心圈表示非采样元素. Fig. 6 Schematic diagram of seismic data matrix corresponding to conventional and highly efficient acquisition (a)Conventional acquisition;(b)DsRg acquisition;(c)RsDg acquisition;(d)RsRg acquisition. Black dots represent the elements of the data matrix,one of which is a complex value of a certain frequency component. Hollow circles represent unsampled points. |
该采集方式实际上是前面两种采集方式的综合,即对激发炮数和检波器数目都进行随机采样.按照稀疏性约束的地震数据采样矩阵设计的要求,设计检波器随机采样矩阵 Θg∈Rng′×ng 和炮点随机采样矩阵 Θs∈Rns′×ns,其中ng′和ns′ 分别是按照特定的随机策略选取的检波器的数目和炮点的数目,且 ng′ <ng、ns′<ns. 通过 Θg和Θs对(19)式中的G和S 都加以改变,可得:
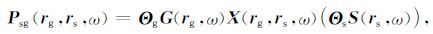
|
(22) |
式(22)就是按照随机布置炮点、随机检波点的方式进行采集的数学模型,数据矩阵 Psg 的结构如图 6d所示.
定义DsRg、RsDg和RsRg高效采集方法的效率参数 μg、μs和μsg 如下:
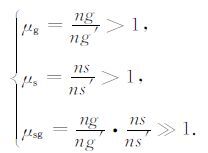
|
(23) |
该参数可以从理论上用来描述高效采集方法的优势,参数值越大,采集效率就越高.
根据上述高效采集方法的数学模型,我们提出使用地震数据高效采集的具体步骤如下:
1) 常规规则密集测网设计:根据勘探目标的情况和勘探工作的要求,应用常规的观测系统设计方法设计规则密集的观测测网(测线、测点和源线、源点),作为下一步进行高效采集测网设计的基准测网;
2)高效采集测网设计:选择合适的高效采集方法,并设置合适的效率参数;应用稀疏约束的随机矩阵设计方法设计检波点采样矩阵和炮点采样矩阵(或其中之一),按预先设定好的采样比率对步骤1)设计的规则密集网格的检波点和炮点(或其中之一)进行随机抽样,得到相应类型的非规则大间距分布的高效采集测网;
3) 执行高效采集任务:按照步骤2)设计出的高效采集测网进行地震数据采集,得到相应类型的地震数据.
常规地震数据采集方法的测网是按照Nyquist采样定理的要求而设定的规则密集、且采样间隔(空间、时间)符合采样定理的要求的网格,高效采集方法的测网是在上述测网的基础上通过随机抽样得到的大间距分布的网格,对炮点、检波点以及两者同时随机布置分别得到了不同的高效采集方法,对于提高地震数据采集效率具有重要的意义.
3.2 高效采集地震数据的重建因为观测系统的差异,通过3.1节提出的三种采集方法获得的地震数据就具有不同的结构,如何恢复为规则密集测网上的地震数据是本节的研究内容.
3.2.1 DsRg高效采集地震数据重建相比常规方法采集到的地震数据,使用DsRg高效采集方法采集到的地震数据总的炮数不变,只是在每炮包含的是分布不规则、随机布置稀疏测网上的地震道.该类地震数据的重建过程如下(如图 7所示):

|
图 7 DsRg高效采集地震数据重建流程图示 Fig. 7 Flow chart of reconstruction of seismic data from DsRg highly efficient acquisition |
1) 根据检波点采样矩阵把高效采集数据中缺失道的位置填充为零;
2) 根据本文稀疏性约束的地震数据重建方法,选择合适的稀疏变换在共炮域逐炮恢复各炮缺失的地震道.
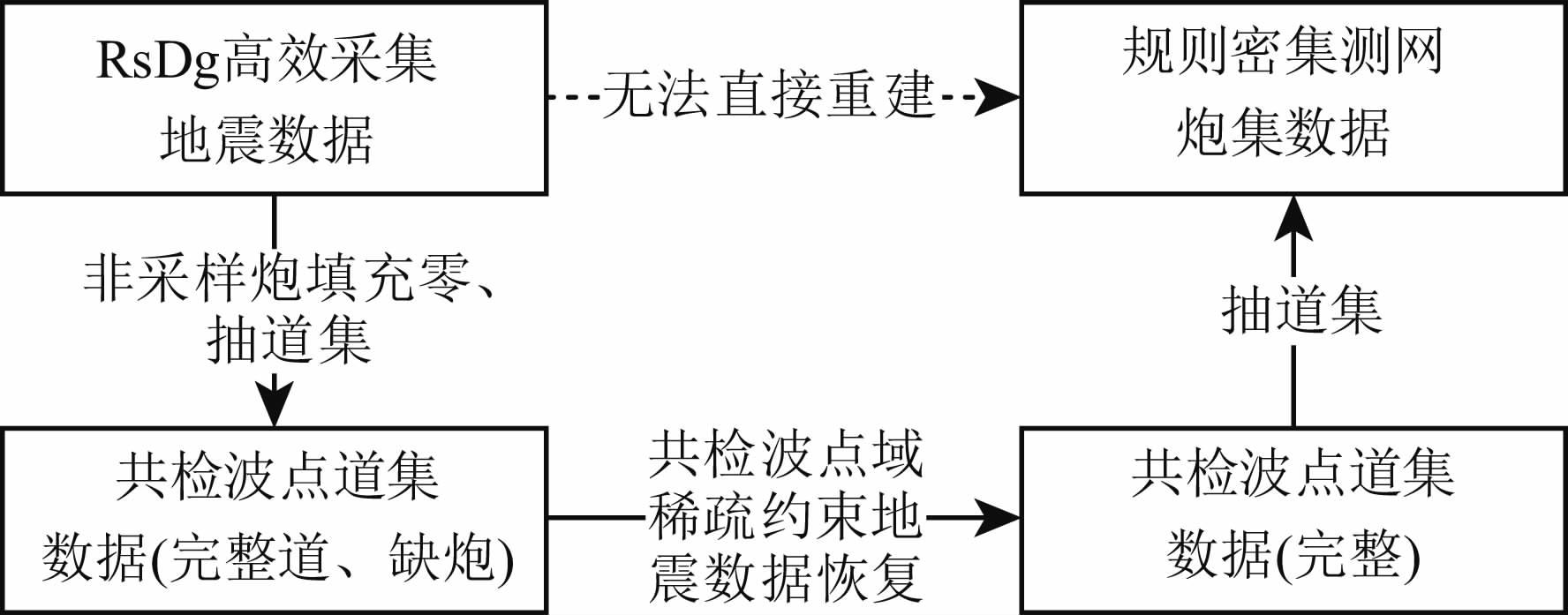
3.2.2 RsDg高效采集地震数据重建相比常规方法采集到的地震数据,使用RsDg高效采集方法采集到的地震数据总的道数不变,只是按照分布不规则、随机布置的源点测网激发了部分炮.该类地震数据的重建过程如下(图 8):
|
图 8 RsDg高效采集地震数据重建流程图示 Fig. 8 Flow chart of reconstruction of seismic data from RsDg highly efficient acquisition |
1) 根据炮点采样矩阵,把缺失的地震炮集数据填充为零,然后通过抽道集把共炮点道集转换为共检波点道集,此时每个共检波点道集表现为随机缺失数据的特征;
2) 根据本文稀疏性约束的地震数据重建方法,在共检波点域逐个道集恢复缺失的数据;
3) 把步骤2) 得到的完整的共检波点道集数据再通过抽道集转换为共炮点道集数据,就得到了常规规则密集测网上的地震数据.
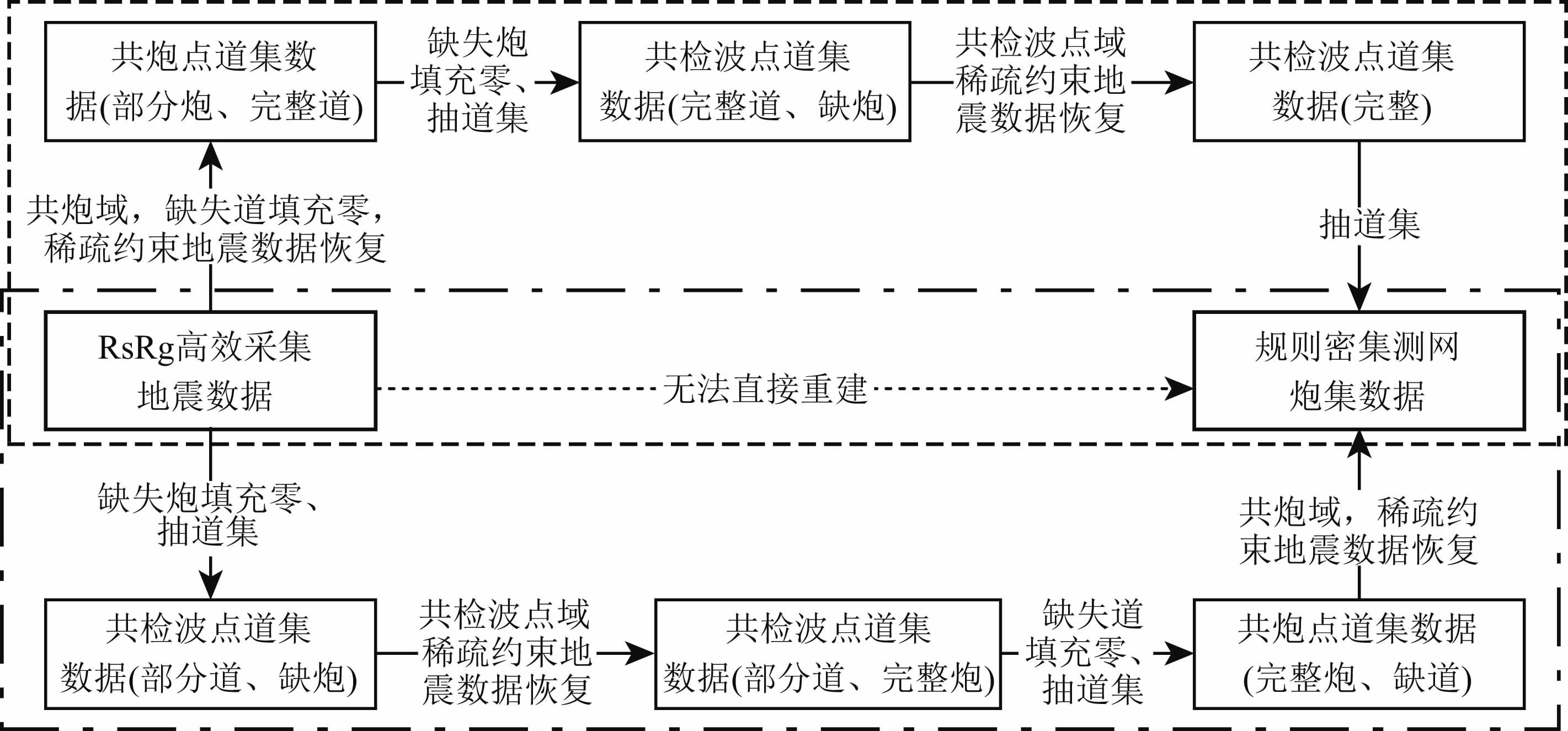
3.2.3 RsRg高效采集地震数据重建相比常规方法采集到的地震数据,RsRg高效采集方法在分布不规则的、稀疏炮点和稀疏检波点测网上激发了部分炮,并使用部分道接收了极少量的地震数据.因为RsRg高效采集地震数据是在源点网格和检波点网格上都经过随机采样的,因此需要在震源和检波点两个方向上进行恢复处理,根据两个方向上恢复次序的不同,高效采集地震数据重建过程也就可以分为两种途径(图 9):
|
图 9 RsRg高效采集地震数据重建流程图示 其中,虚线框包围的区域表示先在共炮域恢复,然后在共检波点域恢复的方法,点划线框包围的区域表示先在检波点域恢复,然后在共炮域恢复的方法. Fig. 9 Flow chart of reconstruction of seismic data from RsRg high efficient acquisition The area surrounded by dashed box represents the recovery firstly in common source domain and then in the common detector domain. Dotted box denotes the recovery in the reverse order. |
方法1,共炮域-共检波点域重建策略(如图 9虚线框区域所示),具体步骤如下:
1) 根据检波点采样矩阵,把缺失的地震道填充为零,并根据第2.3节讲述的稀疏性约束的地震数据重建方法在共炮域逐个炮集恢复缺失的地震道;
2)根据炮点采样矩阵,把步骤1)的恢复结果中缺失炮数据填充为零,并通过抽道集转换为共检波点道集,此时各共检波点道集数据表现为随机缺炮的特征;
3) 再使用稀疏性约束的地震数据重建方法,在共检波点域逐个道集恢复缺失的数据;
4)通过抽道集把步骤3)得到共检波点道集数据转换为共炮点道集数据,即得到了重建地震数据.
方法2,共检波点域-共炮域重建(如图 9点划线框区域所示),具体步骤如下:
1)根据炮点采样矩阵,把RsRg高效采集数据的缺失炮集数据填充为零,并通过抽道集转换为共检波点道集数据;此时每个共检波点道集表现为随机缺失数据的特征;
2)使用稀疏性约束的地震数据重建方法,在共检波点域逐个道集恢复缺失的数据;
3)根据检波点采样矩阵,把步骤2)得到的数据中缺失道填充为零,并通过抽道集转换为共炮点道集数据;
4)再使用稀疏性约束的地震数据重建方法,在共炮域逐个炮集恢复缺失的地震道,即得到重建地震数据.
第二步重建是以第一步为基础的,重建次序的确定要以第一步得到好的恢复结果为前提,可以依据采样数据的采样比(炮域或道域)以及统计稀疏性(炮域或道域)来确定.一般来说,统计稀疏性越好、采样比越高、采样的样本基数越大对恢复越有利.
3.3 高效采集地震数据的偏移成像为证明本文提出的重建方法的有效性,本文使用波动方程叠前偏移成像方法对高效采集地震数据及其重建地震数据的成像效果进行对比分析,处理流程如图 10所示.

|
图 10 高效采集地震数据偏移成像策略示意图 Fig. 10 Sketch of migration imaging strategy for seismic data from highly efficient acquisition |
从高效采集过程来看,高效采集在常规规则密集震源测网和检波点测网(或者其中之一)上做了随机采样,只是炮集数量以及每个炮集中道的数量有一定的减少,并未从本质上影响到地震数据采集的三个过程:1)震源激发、2)波场传播以及3)地震数据接收.因此高效采集数据和常规规则密集地震数据的偏移成像的流程是一致的.
设 rs 为震源位置, ng 为常规观测系统总的检波点个数, rg 为检波点的位置, r=(x,z) 为地下成像点位置.深度方向上用下行波方程正向外推震源波场,即利用波场算子(陈生昌等,2001) W(r,rs) 将震源波场从 rs 传播到 r; 同时用上行波方程反向外推记录波场,即利用 W*(r,rg) 将检波器波场从 rg 反向传播到 r .经过两步外推,也就获得了位置 r 上的震源波场 S(r,ω) 和检波器波场 P(r,ω), 这个过程可以表示为:
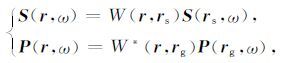
|
(24) |
其中, ω 表示频率, * 表示复共轭.应用时间一致性成像原理提取偏移成像结果,则位置 r 处的像可以由(25)式给出:
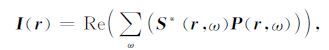
|
(25) |
式中, Re 表示取实部运算, I(r) 表示位置 r 处的成像.
由以上可知,高效采集地震数据虽然不完整,但仍然可以按照常规方法进行外推并成像,只需要按照实际情况在偏移过程中确定实际采集数据的震源和检波点的位置即可.
4 地震数据高效采集数值试验本节将基于理论模型对高效采集方法理论进行数值试验,以检验本文高效采集方法的可行性与有效性.
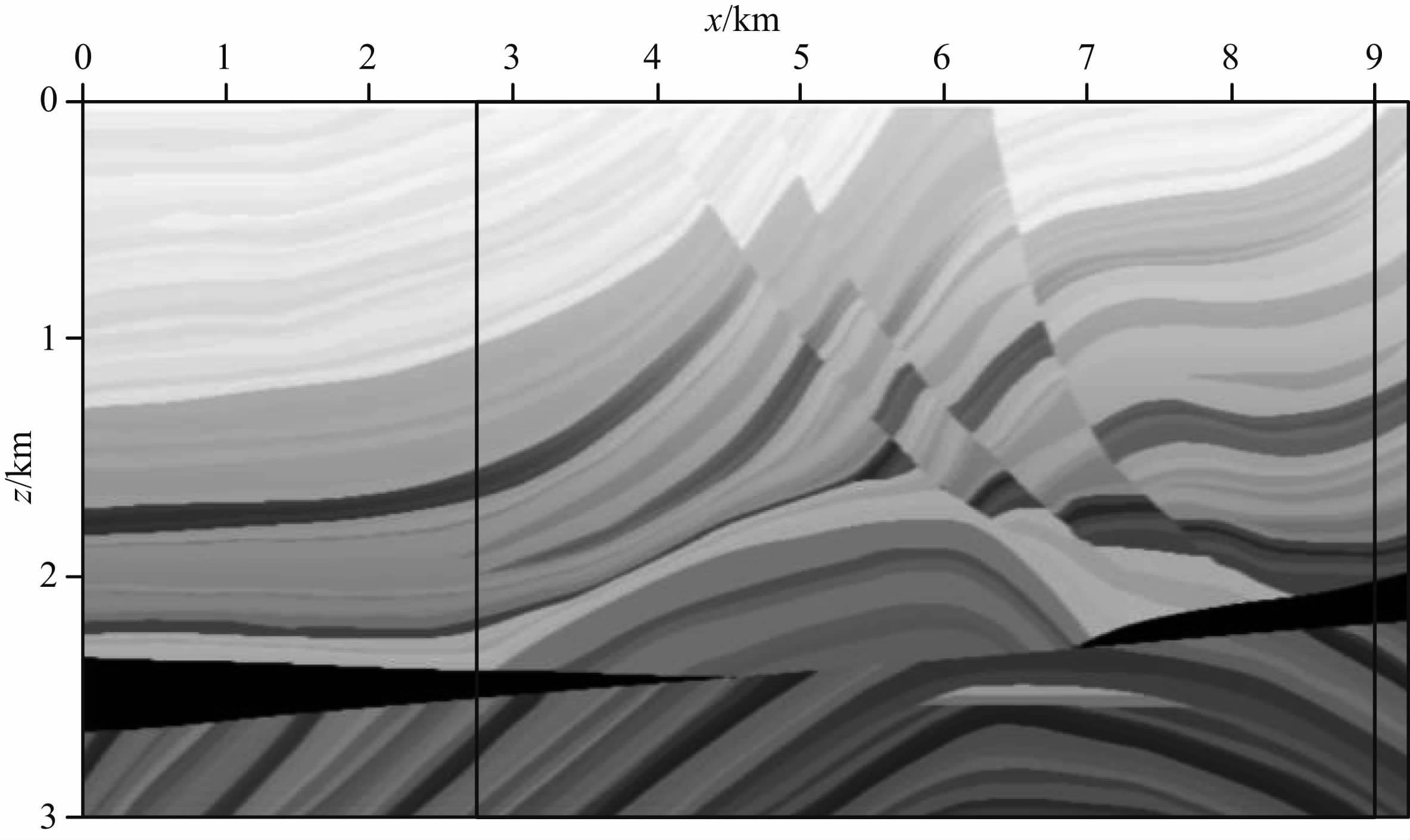
4.1 试验模型Marmousi模型是法国石油研究院推出的国际标准模型数据(速度模型如图 11所示),该模型具有典型的复杂断层构造,对实际勘探区非常具有代表性.本文基于此数据开展高效采集模型试验以检验方法的有效性和适应性.该模型大小为nx=737、nz=750,网格间距dx=12.5 m、dz=4 m.
|
图 11 Marmousi 速度模型 Fig. 11 Marmousi velocity model |
按照第2节所述的高效地震数据采集的具体操作步骤,首先进行常规观测测网的设计:总炮数为400,炮间距为12.5 m,第一炮位置为3375 m;采用固定检波器的观测方式,第一个检波器的位置为2750 m,检波点数为500,道间距为12.5 m,排列长度为6237.5 m,观测范围如图 11中线框区域.在此基础上进行后续高效采集方法的数据采集与数据重建相关试验.
为了表示采集数据的重建效果,这里定义第 i 个道集的恢复信噪比SNRi为:
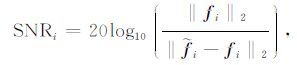
|
(26) |
为了表示多个道集的恢复效果(多个共炮道集或多个共检波点道集),这里定义整体恢复信噪比SNRt如下:
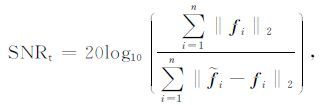
|
(27) |
其中, i=1,2,…,n,fi 为常规采集方法得到的第 i 个道集数据, i 为高效采集地震数据重建处理之后得到的对应第 i 个道集的数据, ‖‖2为l2 范数运算.
4.2 DsRg高效采集试验本节基于Marmousi模型开展DsRg高效采集试验.常规密集测网如4.1节所述,按照第2.2节所述理论,基于改进的分段采样方法设计DsRg高效采集网格如下:源点网格不变,总的激发炮数还是400炮,在规则检波点网格的基础上,随机布置50%的地震道(即250道),效率系数μg=2,提高了数据采集的效率.
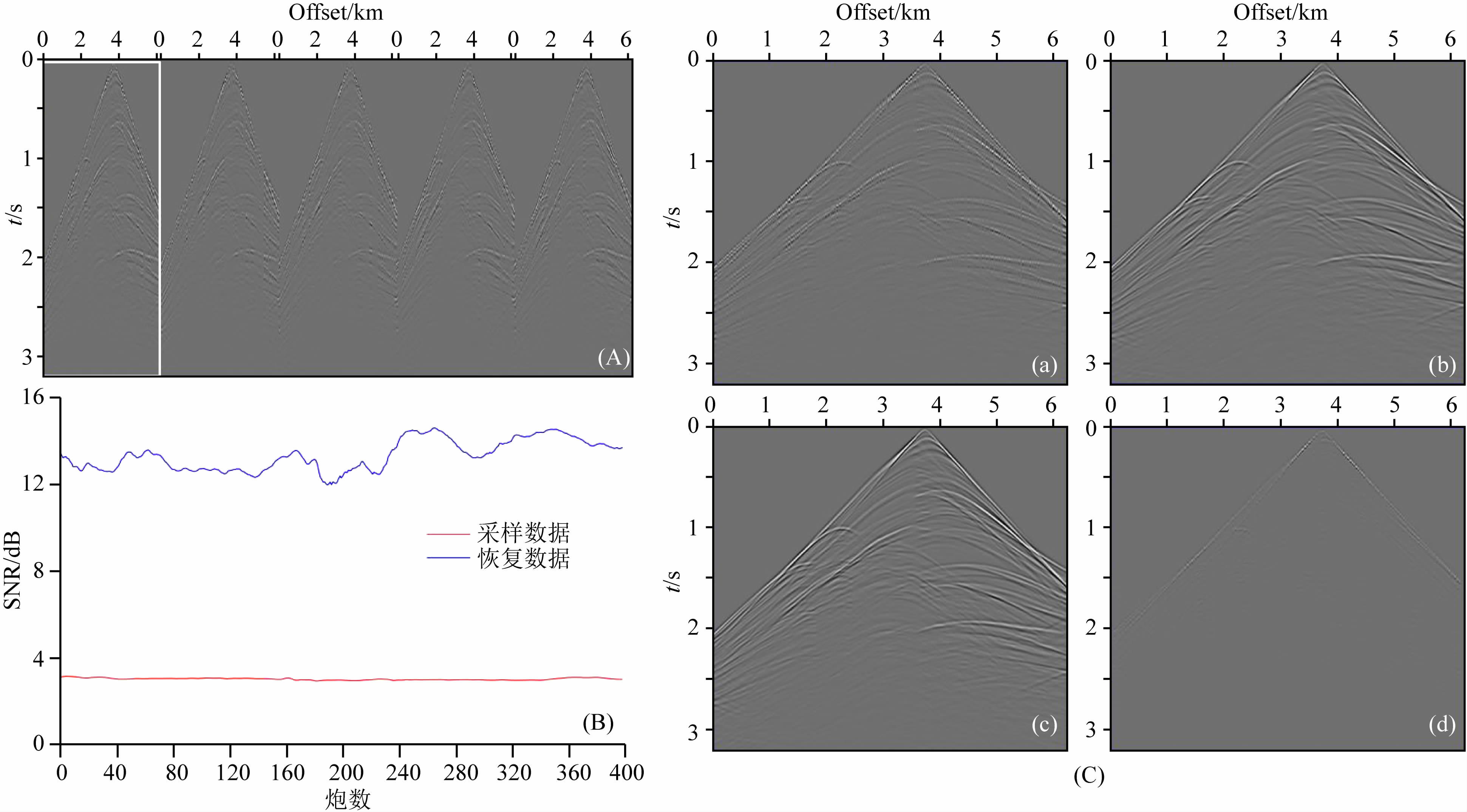
使用DsRg高效采集方法进行采集,得到了400炮、每炮含随机布置250道的高效采集地震数据,图 12A显示了其中第251~255炮数据,可以看到DsRg高效采集地震数据缺道比较严重,造成了大量同相轴间断.按照本文3.2.1 节所述的DsRg高效采集地震数据的重建方法对400炮随机采样的地震数据逐炮进行恢复,并最终得出所有炮的恢复结果,总体恢复信噪比如图 12B所示.其中,第251炮(即图 12A中白色线框所示的炮)的恢复情况如图 12C所示,可以看出采集到的含缺失道的地震数据经过重建处理得到了很好地重建,信噪比达到了14.46 dB,接近于常规采集地震数据,在局部大幅值区域误差稍大.从图 12B和图 12C所示的恢复情况可以看出,DsRg高效采集在采样率为50%的情况下,利用本文重建方法仍得到了可以和常规方法采集数据十分接近的结果.
|
图 12 基于图 11所示Marmousi模型的DsRg高效采集地震数据及其重建结果 规则网格为400炮、500道,稀疏网格为400炮、250道;检波点的采样率是50%,整体重建信噪比为13.25 dB.(A)采集的251~255炮记录;(B)400炮数据的恢复信噪比.最高为14.55 dB,最低为11.93 dB,平均为13.25 dB;(C)图 12A中白色线框所示炮(第251炮)重建结果,其中,(C—a)为采集数据,(C—b)为重建结果,重建信噪比为14.46 dB,(C—c)为对应的常规方法采集的炮数据,(C—d)为重建误差. Fig. 12 Seismic data from DsRg highly efficient acquisition and its reconstruction results based on Marmousi model shown in Fig. 11 Regular acquisition network comprise 400 sources and 500 receivers. Sparse acquisition network consists of 400 sources and 250 receivers. Receiver sampling rate is 50%. Overall recovery SNR is 13.25 dB.(A)Acquired data of shots 251~255.(B)Recovered SNR of 400 shots data with the maximum of 14.55 dB,minimum of 11.93 dB and average of 13.25 dB.(C)Shot shown as white rectangle in Fig. 12A(shot 251)and its reconstruction results,where(C—a)is acquisition data,(C—b)is reconstruction results (SNR: 14.46 dB),(C—c)is the conventional seismic data,(C—d)is reconstruction error. |
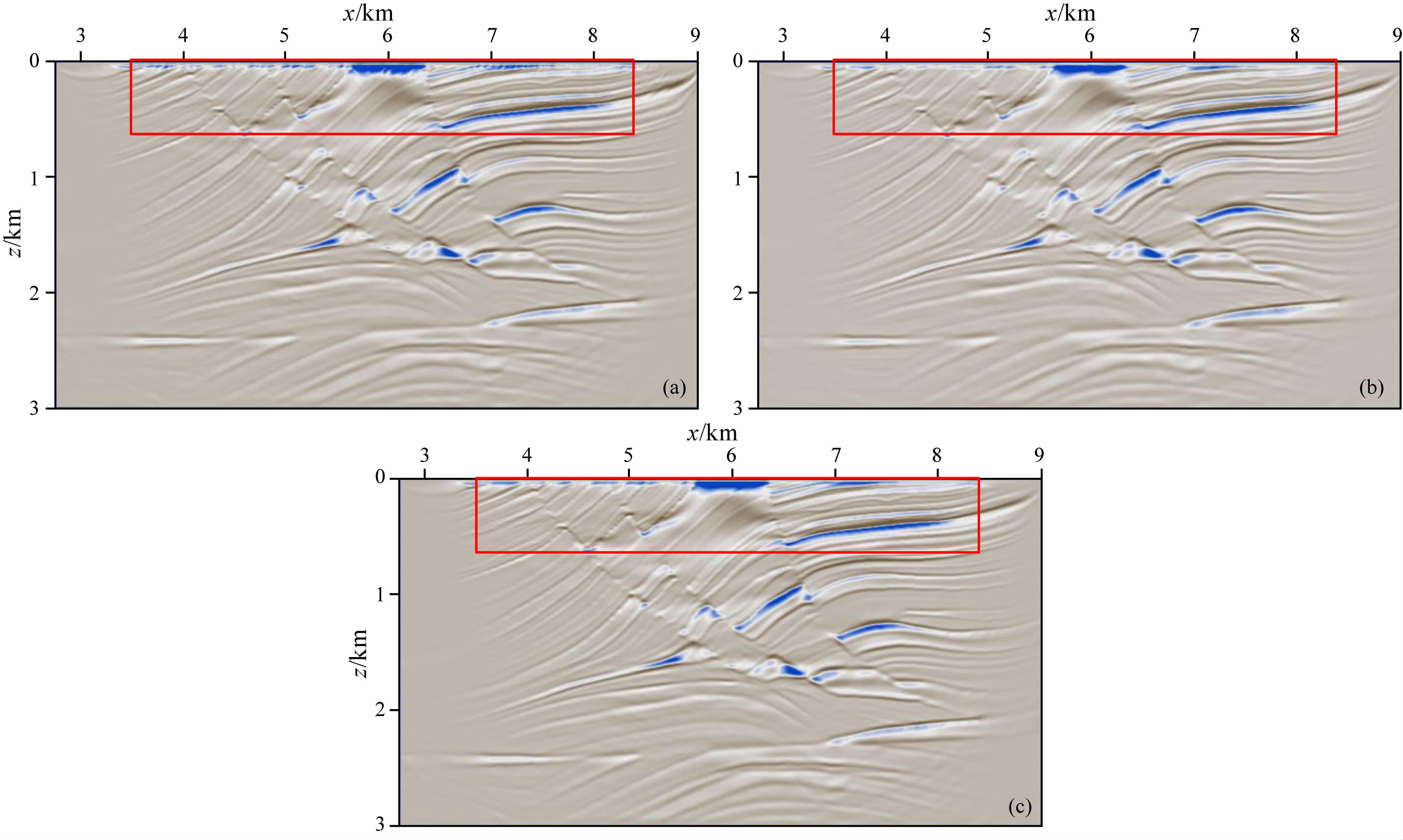
为了进一步验证DsRg采集方法和本文恢复方法的有效性,这里对高效采样数据和恢复数据进行了偏移成像处理,结果分别如图 13a、13b所示,对比常规地震数据偏移成像结果(图 13c)可以看出:1)由于缺少有效的信息支撑,高效采集数据的直接偏移成像结果在浅层会有大量随机假象产生(参见图 13a红色线框区域),而重建数据补充了缺失数据信息,增强了整体有效信息,其偏移成像结果更接近常规地震数据成像结果;2)高效采集数据、重建数据和常规采集数据的偏移成像结果在深层差别不大,主要是因为通过地震波场在深层有着更多的叠加,从而降低了随机缺失数据对成像结果的影响.由此可知,从成像效果上也可以证明DsRg高效采集方法具有理论与实际可行性.
|
图 13 DsRg高效采集数据成像试验结果 (a)高效采集数据成像结果;(b)重建数据成像结果;(c)常规规则密集数据成像结果.其中,规则网格为400炮、500道,稀疏网格为400炮、250道,检波点的采样率是50%. Fig. 13 Imaging tests of DsRg highly efficient acquisition (a)Imaging result of DsRg acquisition data.(b)Imaging result of reconstruction data.(c)Imaging result of conventional data. Regular acquisition network is made up of 400 sources and 500 receivers. Sparse acquisition network is constituted by 400 sources and 250 receivers. Receiver sampling rate is 50%. |
本节基于Marmousi模型开展RsDg高效采集试验.RsDg高效采集方法实质上是在常规采集方法的基础上随机布置了少量的炮点,根据波场的互易原理,RsDg和DsRg高效采集数据的恢复方法具有一致性.常规密集测网如4.1节所述,按照本文2.2节的理论,基于改进的分段采样方法设计RsDg高效采集网格如下:在密集源点网格(共400炮)的基础上随机激发200炮,同时保持500接收道不变,效率系数μs=2,大大提高地震数据采集效率.
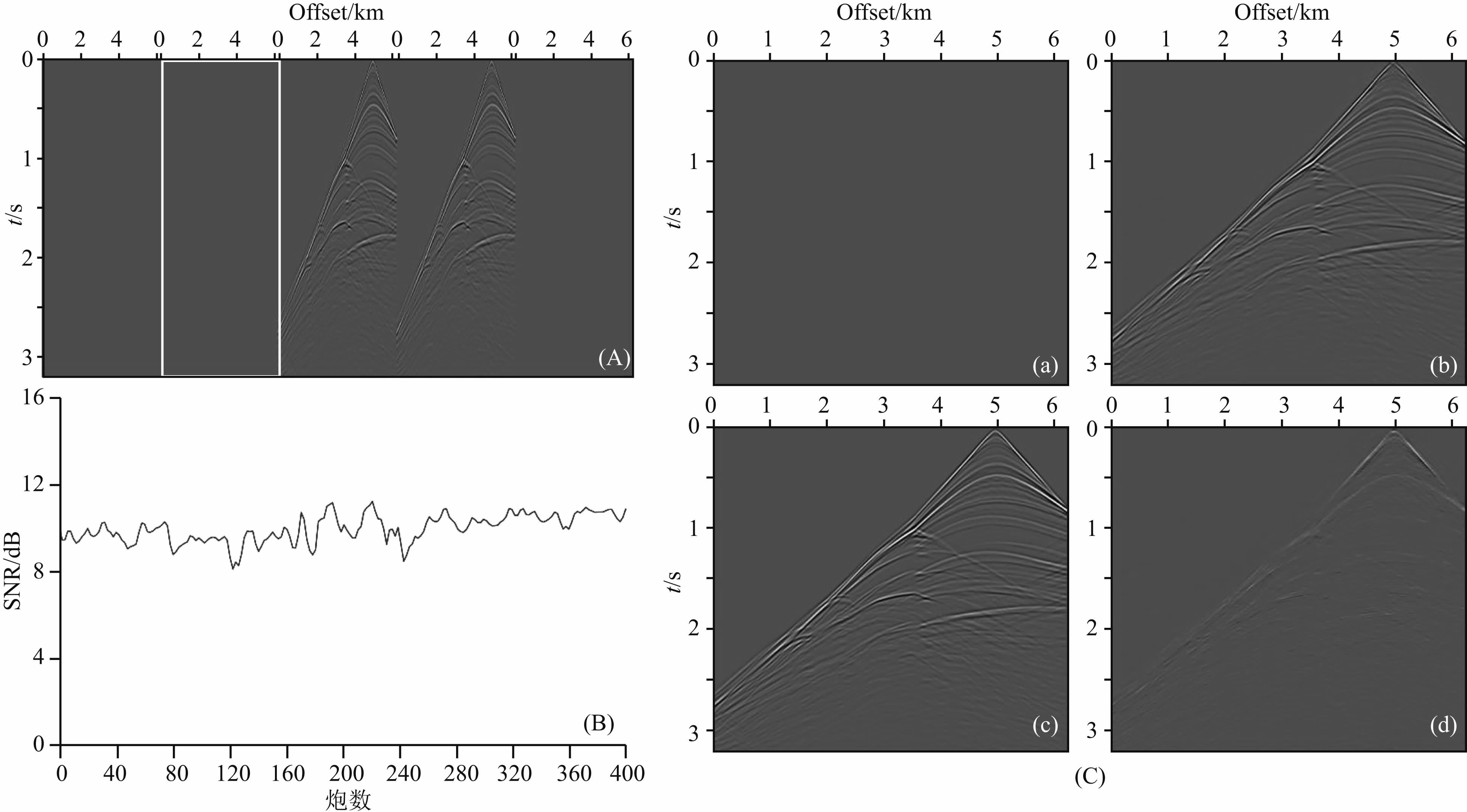
使用RsDg高效采集方法进行采集,得到了随机激发的200炮、每炮含500道的高效采集地震数据,其中第176和177炮如图 14A所示(这两炮对应常规采集的350和351炮;作为对比,没有采集的空白炮也显示在相应的位置上).按照本文3.2.2 节所述的RsDg高效采集地震数据的重建策略对本次采集数据进行重建处理,得到了缺失的200炮地震数据,信噪比如图 14B所示.以图 14A中白色线框所示的缺失炮为例(对应常规采集数据的第349炮),重建结果如图 14C—b所示,和图 14C—c所示的常规规则地震数据非常接近,信噪比为10.77 dB,图 14C—d为恢复误差.从图 14B和图 14C所示的恢复结果中可以看出,通过50%的激发炮得到的重建结果(完全重建)和常规直接采集数据仍具有很高的一致性,证明了DsRg高效采集方法和本文恢复方法也是可行的.
|
图 14 基于图 11所示Marmousi模型的RsDg高效采集地震数据及其重建结果 规则网格为400炮、500道,稀疏网格为200炮、500道,炮采样率是50%,整体重建信噪比为10.05 dB.(A)采集的176和177炮,对应常规采集的350和351炮,图中空白炮为非采集炮;(B)完全重建的200炮数据的信噪比;最高为11.27 dB,最低为8.08 dB,平均为10.05 dB;(C)图 14A中白色线框所示的炮的重建情况(对应第349炮常规地震数据),其中(C—a)为非采集炮数据,(C—b)为重建结果,重建信噪比为10.77 dB,(C—c)为对应的常规方法采集的炮数据,(C—d)为重建误差. Fig. 14 Seismic data form RsDg efficient acquisition and its reconstruction results based on Marmousi model shown in Fig. 11 Regular acquisition network is constituted by 400 sources and 500 receivers. Sparse acquisition network is constituted by 200 sources and 500 receivers. Source sampling rate is 50%. Overall recovery SNR is 10.05 dB.(A)Acquired data of shots 176 and 177 corresponding to conventional shots 350 and 351. Blank shot represents unacquired shot.(B)SNRs of 200-shot data reconstructed completely,with maximum of 11.27 dB,minimum of 8.08 dB and average of 10.05 dB.(C)Reconstruction of unacquired shot in white rectangle of Fig. 14A(corresponding to conventional shot 349).(C—a)Unacquired data,(C—b)Reconstruction result with SNR 10.77 dB,(C—c)Conventional seismic data,(C—d)Reconstruction error. |
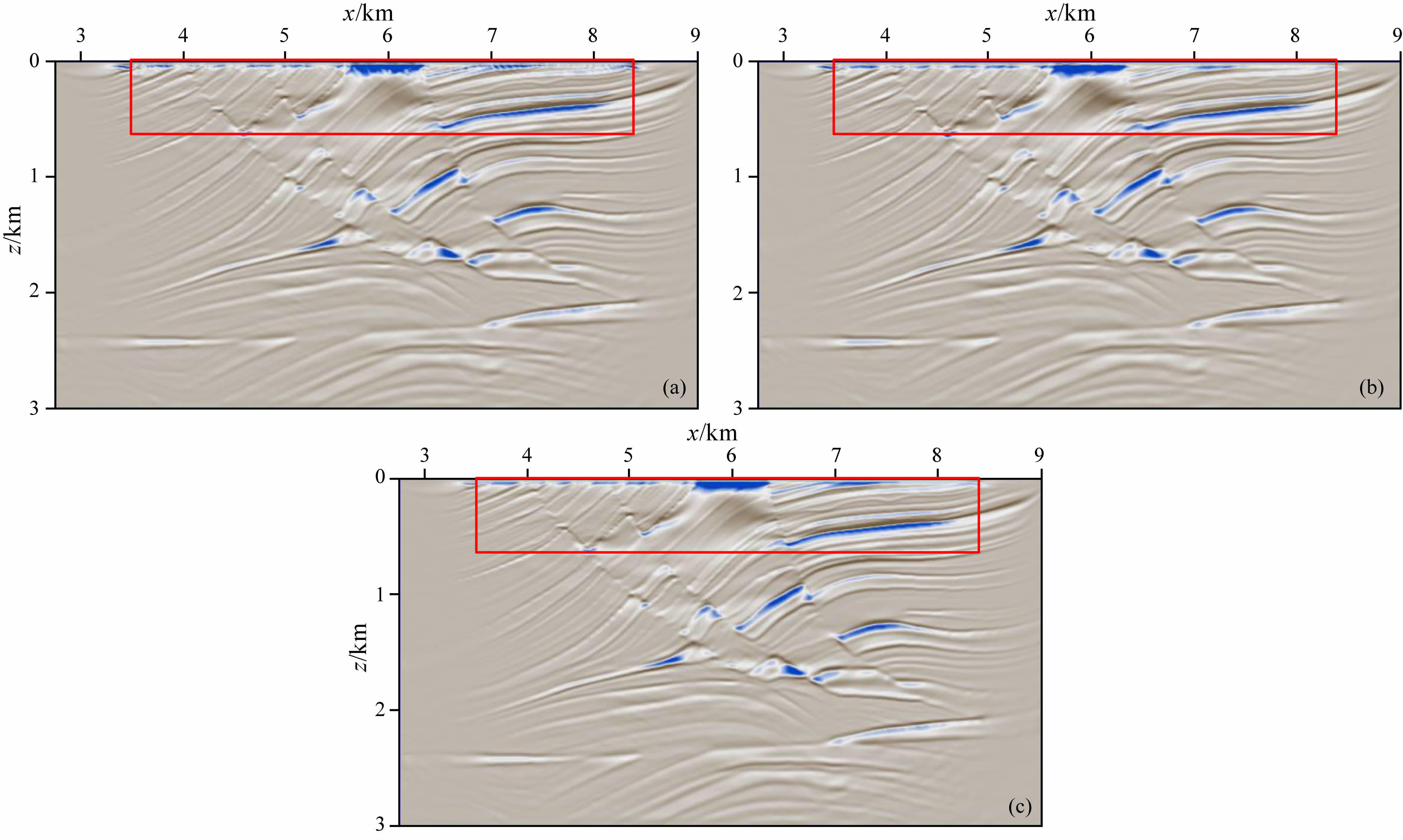
接着,再对高效采集数据和恢复数据进行偏移成像处理,结果分别如图 15a、15b所示,通过和图 15c所示的常规地震数据偏移成像结果比较可以看出:1)在成像剖面的浅层,高效采集数据的直接成像结果中会有大量随机假象产生(参见图 15a红色线框区域),而重建数据的偏移成像结果中这些假象被大大压制(甚至消除),更接近常规地震数据成像结果;2)采样数据和恢复数据在深层都可以得到比较好的成像效果.由此可知,本节偏移成像试验取得了和4.2节DsRg高效采集地震数据成像相似的结论,即随机布置炮点或检波点造成了严重的采集数据的缺失,都会在成像结果中造成假象,而恢复数据成像与常规地震数据成像更为接近,效果较好.
|
图 15 RsDg高效采集数据成像试验结果 (a)高效采集数据成像结果;(b)重建数据成像结果;(c)常规规则密集数据成像结果.其中,规则网格为400炮、500道,稀疏网格为200炮、500道,炮的采样率是50%. Fig. 15 Imaging tests of RsDg seismic data (a)Imaging result of highly efficient acquired data.(b)Imaging result of reconstructed data.(c)Imaging result of conventional data. Regular acquisition network is constituted by 400 sources and 500 receivers. Sparse acquisition network is constituted by200 sources and 500 receivers. Source sampling rate is 50%. |
本节基于Marmousi模型开展RsRg高效采集试验.常规密集测网如4.1节所述,按照第2.2节所述理论,基于改进的分段采样方法设计RsRg高效采集网格如下:在密集测网网格(400炮、500道)的基础上随机激发200炮、随机布置250道检波器,效率系数μsg=4,极大地提高了地震数据采集的效率.
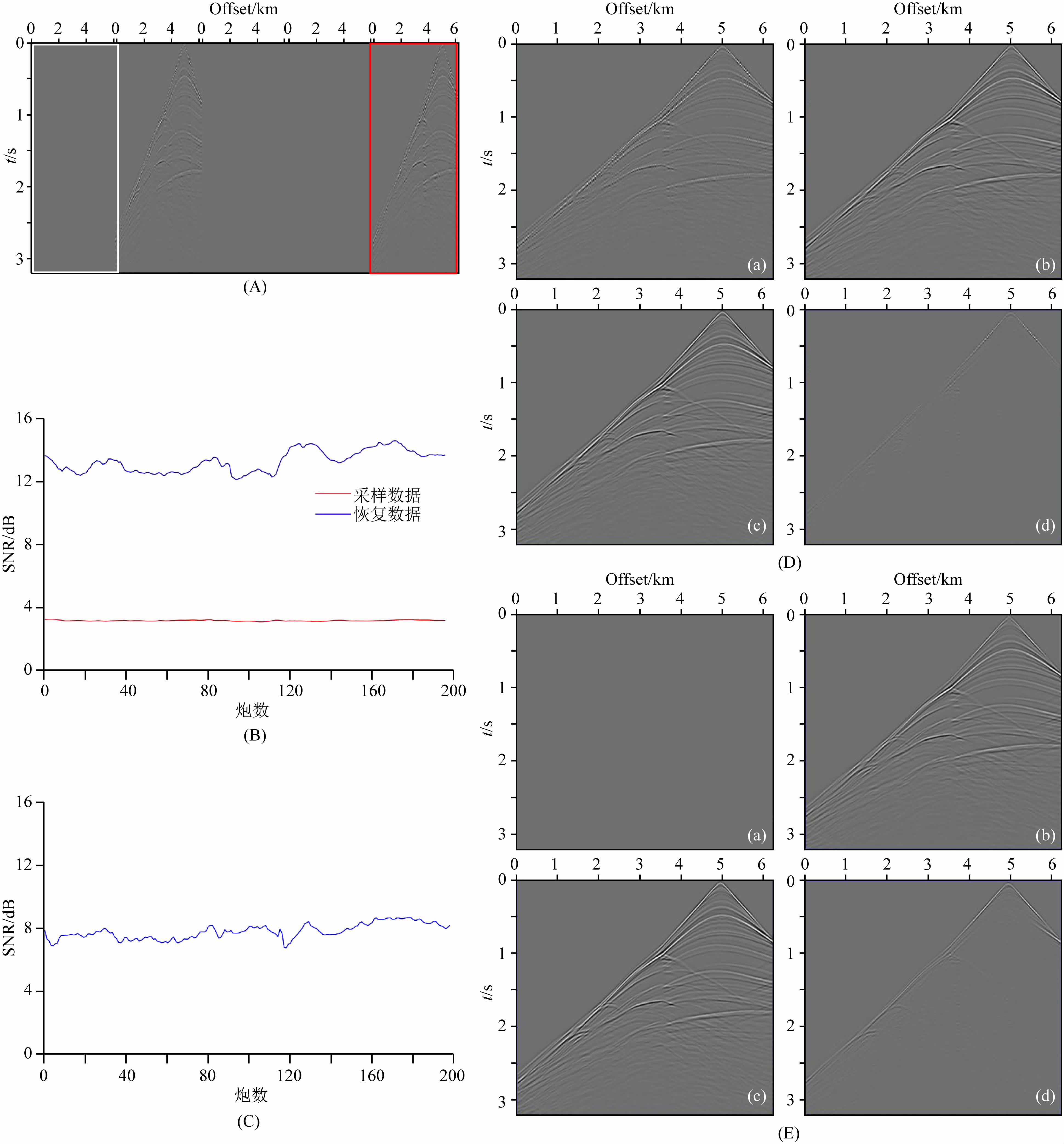
使用RsRg高效采集方法进行采集,得到了随机激发的200炮、每炮含随机布置的250道的高效采集地震数据,其中第174和175炮如图 16A所示,这两炮对应常规采集的349和352炮(空白炮表示没有采集,但作了显示).根据地震数据的互易原理,共炮点道集数据和共检波点道集数据具有相同的传播特性,因而在同一种稀疏变换中具有相同的稀疏度;在炮和检波器采样率一致(都为50%)的情况下,鉴于共炮域的采样基数大于共检波点域的采样基数,这里选择先进行炮域恢复再进行检波点域恢复的重建顺序.使用本文3.2.3 节所述的RsRg高效采集地震数据的重建方法对本次采集数据进行重建处理,恢复效果可以从激发炮和完全重建炮两类数据来分析,200激发炮记录和200完全重建炮记录的恢复信噪比如图 16B和16C所示,其中第173激发炮(即图 16A中红色线框所示的炮,对应第352炮常规数据)的恢复结果见图 16D,完全重建炮(即图 16A中白色线框所示的炮,对应第349炮常规数据)的恢复情况见图 16E.从恢复结果中可以看出,激发炮因为包含了部分数据信息(随机布置的250道),恢复效果比较好,而完全重建炮的恢复效果稍微差一些(特别是大幅值同相轴附近).由以上可知,25%的整体采样率的RsRg高效采集方法大大提高了采集效率,整体平均恢复信噪比达到了9.68 dB,和前述试验类似,在局部大幅值同相轴附近恢复误差较大,从而验证了RsRg高效采集方法的优势以及实际可操作性.
|
图 16 基于图 11所示Marmousi模型的RsRg高效采集地震数据及其重建结果 规则网格为400炮、500道,稀疏网格为200炮、250道,炮点和检波点的采样率都是50%.在25%数据整体采样率的情况下,整体平均恢复信噪比为9.68 dB.(A)第174和175炮,对应常规采集的349和352炮,图中空白炮为非采集炮,为便于比较这里也做了显示;(B)RsRg高效采集数据激发炮恢复试验恢复信噪比结果:最高为14.60 dB,最低为12.21 dB,平均为13.22 dB;(C)RsRg高效采集数据非激发炮恢复试验恢复信噪比结果:最高为8.63 dB,最低为6.70 dB,平均为7.77 dB;(D)RsRg高效采集地震数据(随机缺道地震数据)的重建结果(对应第352炮常规地震数据),其中,(D—a)为非采集炮数据(图 16A中红色线框所示),(D—b)为(D—a)的重建结果,(D—c)为常规方法采集的炮,(D—d)为(D—b)的恢复误差,恢复信噪比为14.53 dB;(E)RsRg高效采集地震数据对非采样地震数据的重建结果(对应第349炮常规地震数据),(E—a)为非采集炮数据(图 16A中白色线框所示),(E—b)为重建结果,(E—c)为常规方法采集的炮,(E—d)为(E—b)的恢复误差,恢复信噪比为8.56 dB. Fig. 16 Seismic data from RsRg highly efficient acquisition and its reconstruction results based on Marmousi model shown in Fig. 11 Regular acquisition network is constituted by 400 sources and 500 receivers. Sparse acquisition network is constituted by 200 sources and 250 receivers. Both source and receiver sampling rates are 50%. Overall recovery SNR is 9.68 dB in the condition of 25% sampling rate.(A)RsDg seismic data of shots 174 and 175,corresponding to shots 349 and 352 of conventional data. Blank data is shown for contrast.(B)SNRs of recovered RsRg data with maximum of 14.60 dB,minimum of 12.21 dB and average of 13.22 dB.(C)SNRs of recovered DsRg data with maximum of 8.63 dB,minimum of 6.70 dB and average of 7.77 dB.(D)RsRg data(red rectangle shown in Fig. 16A,corresponding to conventional shot 352)and its reconstruction results.(D—a)Unacquired data,(D—b)Reconstruction result of(D—a),(D—c)Conventional seismic data,(D—d)Reconstruction error. The recovery SNR is 14.53 dB.(E)Blank shot 349(unacquired,white rectangle in Fig. 16A)and its reconstruction results.(E—a)Unacquired data,(E—b)Reconstruction result of(E—a),(E—c)Conventional seismic data,(E—d)Reconstruction error. The recovery SNR is 8.56 dB. |
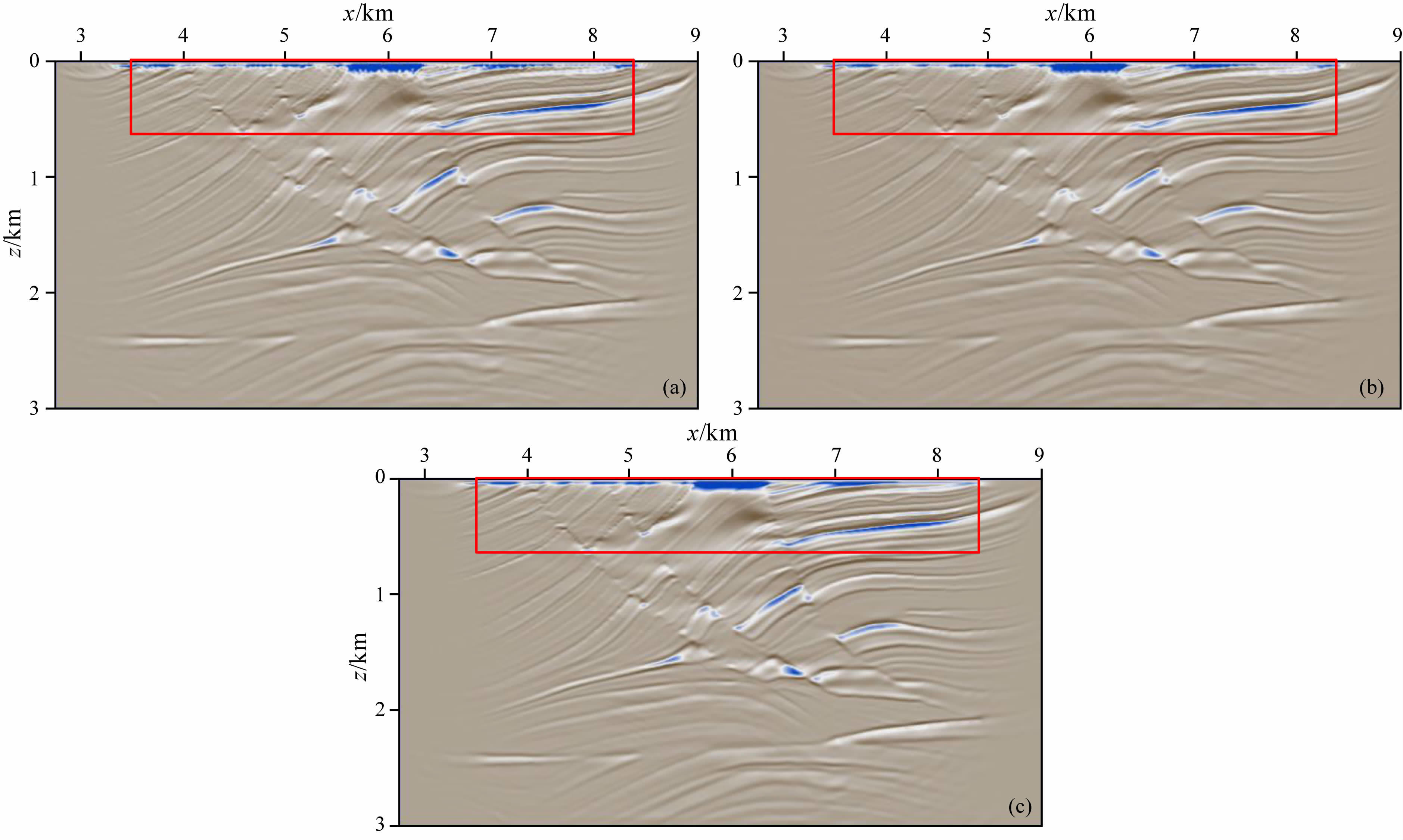
和前面两个试验一样,这里也对高效采样数据和恢复数据进行了偏移成像处理,以进一步检验高效采集和重建算法的效果.所有成像结果见图 17.从成像结果中可以看出:1)高效采集地震数据的浅层有假象产生,且比前面DsRg、RsDg两种高效采集数据的直接成像结果中的假象更严重(见图中红色方框区域);2)相比高效采集数据的直接成像,恢复数据的成像结果明显得到了改善,残留假象得到了部分压制;3)本方法由于采集到的数据比DsRg、RsDg两种高效采集方法更少,因而重建效果及其成像效果也有所下降.由此也可以看出RsRg高效采集方法具有一定的可行性,但在实际高效采集中一定要注意采集效率和恢复效果的平衡.
|
图 17 RsRg高效采集数据单程波偏移成像结果 (a)高效采集数据成像结果;(b)重建数据成像结果;(c)常规规则密集数据成像结果.规则网格为400炮、500道,稀疏网格为200炮、250道,炮点和检波点的采样率都是50%. Fig. 17 Migration imaging results of RsRg highly efficient acquisition data (a)Imaging result of RsRg acquisition data.(b)Imaging result of reconstruction data.(c)Imaging result of conventional data. The regular acquisition network is constituted by 400 sources and 500 receivers. Sparse acquisition network is constituted by 200 sources and 250 receivers. Both the source sampling rate and receiver sampling rates are 50%. |
针对当前地震数据采集中面临的低效率、高成本问题,本文开展了地震数据高效采集方法理论研究,在压缩感知理论的基础上,对地震数据高效采集方法理论及其具体实施策略做出了相关探索研究.本文从地震波场的传播理论出发,研究并给出了地震数据具有稀疏性的数学物理依据,从而表明基于Nyquist采样定理的常规地震数据采集方法是以地震数据频带有限且频谱是稠密地分布在其频带范围内为基础的,不是最高效的采集方法.在稀疏性先验条件下,本文提出了改进的分段采样方法用于指导实际地震数据高效采集,即利用稀疏约束的随机采样方法改变常规规则密集测网中炮点和检波点(或二者之一)的布置方式,提出了三种高效采集测网设计方案(DsRg、RsDg和RsRg)及其对应采集数据的重建方案,从1)重建数据和常规采集地震数据的对比、2)高效采集地震数据、重建地震数据和常规规则密集地震数据的成像结果等两个方面的对比中证明了本文高效采集方案(包括数据重建方案)的可行性和有效性.相比常规规则密集采样,DsRg高效采集可以减少布置与移动检波器的工作量,RsDg高效采集可以减少布置与移动震源的工作量,而RsRg高效采集则可以同时减少布置检波点和炮点的时间.三种高效采集方法不仅可以提高采集效率,而且可以降低存储与传输地震数据的成本,从而可以大大降低勘探成本.
从DsRg、RsDg和RsRg的测网布置、数据重建方法以及模型试验结果可知,三种高效采集方法具有明显的优缺点:1)数据采集方面,DsRg、RsDg都是在一个方向上进行稀疏采集,而RsRg是在两个方向上同时进行稀疏采集,因而后者的复杂度较高,在测网设计时需要考虑实际探区状况;现有的震源激发和检波器布置技术水平的差异也会在一定程度上影响三种高效采集方法在提高采集效率上的作用;由于实际勘探中不可能在一个方向上无限稀疏,因而RsRg方法在实际应用中具有更高效的潜力;2)数据处理方面,根据地震波场的互易性原理,DsRg、RsDg采集数据重建处理在一定程度上具有一致性;RsRg数据重建需要在两个方向上进行,并且需要根据采样数据的采样比(炮域或道域)以及统计稀疏性(炮域或道域)来确定重建次序,计算复杂度较高.
| Abma R, Kabir N. 2006. 3D interpolation of irregular data with a POCS algorithm. Geophysics , 71 (6) : E91-E97. DOI:10.1190/1.2356088 | |
| Abma R. 2009. Issues in multi-dimensional interpolation.//International Exposition and 79th International Annual Meeting, SEG, Expanded Abstracts, 1152-1156. | |
| Allen S J, Brown P A. 1995. Isotherm analyses for single component and multi-component metal sorption onto lignite. Journal of Chemical Technology and Biotechnology , 62 (1) : 17-24. DOI:10.1002/(ISSN)1097-4660 | |
| Berkhout A J, Blacquière G, Verschuur E. 2008. From simultaneous shooting to blended acquisition.//78th International Annual Meeting, SEG, Expanded Abstracts, 2831-2838. | |
| Berkhout A J, Pao Y H. 1982. Seismic migration-imaging of acoustic energy by wave field extrapolation. Journal of Applied Mechanics , 49 (3) : 682-683. | |
| Bloom S D, Marscher A P. 1996. An analysis of the synchrotron self-compton model for the multi-wave band spectra of blazars. The Astrophysical Journal , 461 : 657. DOI:10.1086/177092 | |
| Blumensath T. 2012. Accelerated iterative hard thresholding. Signal Processing , 92 (3) : 752-756. DOI:10.1016/j.sigpro.2011.09.017 | |
| Burrus C S, Gopinath R A, Guo H T. 1998. Introduction to Wavelets and Wavelet Transforms. New Jersey:Prentice Hall. | |
| Candès E J, Donoho D L. 2004. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities. Communications on Pure and Applied Mathematics , 57 (2) : 219-266. DOI:10.1002/cpa.v57:2 | |
| Candès E J, Donoho D L. 2005a. Continuous curvelet transform:I. Resolution of the wavefront set. Applied and Computational Harmonic Analysis , 19 (2) : 162-197. DOI:10.1016/j.acha.2005.02.003 | |
| Candès E J, Donoho D L. 2005b. Continuous curvelet transform:Ⅱ. Discretization and frames. Applied and Computational Harmonic Analysis , 19 (2) : 198-222. DOI:10.1016/j.acha.2005.02.004 | |
| Candès E J, Romberg J, Tao T. 2006a. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory , 52 (2) : 489-509. DOI:10.1109/TIT.2005.862083 | |
| Candès E, Demanet L, Donoho D, et al. 2006b. Fast discrete curvelet transforms. Multiscale Modeling & Simulation , 5 (3) : 861-899. | |
| Chen S C, Cao J Z, Ma Z T. 2001. Prestack depth migration method based on quasi-linear born approximation. Chinese Journal of Geophysics (in Chinese) , 44 (5) : 704-710. | |
| Chen S C, Wang H C, Chen G X. 2012. The preliminary study on high efficient acquisition of geophysical data based on compressed sensing.//Proceedings of the 28th Annual Meeting of China Geophysical Society (in Chinese). Beijing:Chinese Geophysical Society. | |
| Chen S C, Chen G X, Wang H C. 2015. The preliminary study on high efficient acquisition of geophysical data with sparsity constraints. Geophysical Prospecting for Petroleum (in Chinese) , 54 (1) : 24-35. | |
| Chen S S, Donoho D L, Saunders M A. 1998. Atomic decomposition by basis pursuit. SIAM Journal on Scientific Computing , 20 (1) : 33-61. DOI:10.1137/S1064827596304010 | |
| Cordsen A, Galbraith M. 2002. Narrow-versus wide-azimuth land 3D seismic surveys. The Leading Edge , 21 (8) : 764-770. DOI:10.1190/1.1503181 | |
| Daubechies I, Defrise M, De Mol C. 2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics , 57 (11) : 1413-1457. DOI:10.1002/(ISSN)1097-0312 | |
| Daubechies I, Fornasier M, Loris I. 2008. Accelerated projected gradient method for linear inverse problems with sparsity constraints. Journal of Fourier Analysis and Applications , 14 (5-6) : 764-792. DOI:10.1007/s00041-008-9039-8 | |
| Do M N, Vetterli M. 2005. The contourlet transform:an efficient directional multiresolution image representation. IEEE Transactions on Image Processing , 14 (12) : 2091-2106. DOI:10.1109/TIP.2005.859376 | |
| Donoho D L, Johnstone J M. 1994. Ideal spatial adaptation by wavelet shrinkage. Biometrika , 81 (3) : 425-455. DOI:10.1093/biomet/81.3.425 | |
| Donoho D L, Huo X M. 2002. Beamlets and Multiscale Image Analysis. Berlin Heidelberg:Springer. | |
| Donoho D L. 2006. Compressed sensing. IEEE Transactions on Information Theory , 52 (4) : 1289-1306. DOI:10.1109/TIT.2006.871582 | |
| Du S T. Seismic Wave Dynamics:Theory and Method. (in Chinese) Dongying: China Petroleum University Press, 2009 . | |
| Dunbar D, Humphreys G. 2006. A spatial data structure for fast Poisson-disk sample generation. ACM Transactions on Graphics (TOG) , 25 (3) : 503-508. DOI:10.1145/1141911 | |
| Hennenfent G, Herrmann F J. 2006. Seismic denoising with nonuniformly sampled curvelets. Computing in Science & Engineering , 8 (3) : 16-25. | |
| Hennenfent G, Herrmann F J. 2008. Simply denoise:wavefield reconstruction via jittered undersampling. Geophysics, 73(3):V19-V28. | |
| Hennenfent G, Fenelon L, Herrmann F J. 2010. Nonequispaced curvelet transform for seismic data reconstruction:A sparsity-promoting approach. Geophysics , 75 (6) : WB203-WB210. DOI:10.1190/1.3494032 | |
| Herman M A, Strohmer T. 2009. High-resolution radar via compressed sensing. IEEE Transactions on Signal Processing , 57 (6) : 2275-2284. DOI:10.1109/TSP.2009.2014277 | |
| Herrmann F J, Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International , 173 (1) : 233-248. DOI:10.1111/gji.2008.173.issue-1 | |
| Herrmann F J. 2010. Randomized sampling and sparsity:Getting more information from fewer samples. Geophysics , 75 (6) : WB173-WB187. DOI:10.1190/1.3506147 | |
| Koh K, Kim S J, Boyd S P. 2007. An interior-point method for large-scale l1-regularized logistic regression. Journal of Machine Learning Research , 8 : 1519-1555. | |
| Le Pennec E, Mallat S. 2005. Sparse geometric image representations with bandelets. IEEE Transactions on Image Processing , 14 (4) : 423-438. DOI:10.1109/TIP.2005.843753 | |
| Lin T T Y, Herrmann F J. 2009. Unified compressive sensing framework for simultaneous acquisition with primary estimation.//International Exposition and 79th International Annual Meeting, SEG, Expanded Abstracts, 3113-3117. | |
| Lin T T Y, Lebed E, Erlangga Y A, et al. 2008. Interpolating solutions of the Helmholtz equation with compressed sensing.//SEG Technical Program Expanded Abstracts 2008, 2122-2126. | |
| Liu X W, Liu H, Liu B. 2004. A study on algorithm for reconstruction of de-alias uneven seismic data. Chinese Journal of Geophysics (in Chinese) , 47 (2) : 299-305. | |
| Lustig M, Donoho D, Pauly J M. 2007. Sparse MRI:The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine , 58 (6) : 1182-1195. DOI:10.1002/(ISSN)1522-2594 | |
| Ma J W. 2011. Sparsity-promoting seismic exploration.//Proceedings of the 27th Annual Meeting of China Geophysical Society (in Chinese). Changsha. | |
| Mallat S G. 1989. A theory for multiresolution signal decomposition:the wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence , 11 (7) : 674-693. DOI:10.1109/34.192463 | |
| Mamaghanian H, Khaled N, Atienza D, et al. 2011. Compressed sensing for real-time energy-efficient ECG compression on wireless body sensor nodes. IEEE Transactions on Biomedical Engineering , 58 (9) : 2456-2466. DOI:10.1109/TBME.2011.2156795 | |
| Marks R J. 1991. Introduction to Shannon Sampling and Interpolation Theory. New York:Springer-Verlag. | |
| Milton A, Trickett S, Burroughs L. 2011. Reducing acquisition costs with random sampling and multidimensional interpolation.//81st International Annual Meeting, SEG, Expanded Abstracts, 52-56. | |
| Mohan D, Singh K P. 2002. Single-and multi-component adsorption of cadmium and zinc using activated carbon derived from bagasse-an agricultural waste. Water Research , 36 (9) : 2304-2318. DOI:10.1016/S0043-1354(01)00447-X | |
| Moldoveanu N. 2010. Random sampling:A new strategy for marine acquisition.//Proceedings of the 2010 SEG Annual Meeting, Society of Exploration Geophysicists, 51-55. | |
| Mosher C, Kaplan S, Janiszewski F. 2012. Non-uniform optimal sampling for seismic survey design.//Proceedings of the 74th EAGE Conference & Exhibition. SPE, EAGE. | |
| Oppenheim A V, Schafer R W, Buck J R. 1989. Discrete-Time Signal Processing. Englewood Cliffs:Prentice-Hall. | |
| Park S C, Park M K, Kang M G. 2003. Super-resolution image reconstruction:a technical overview. IEEE Signal Processing Magazine , 20 (3) : 21-36. DOI:10.1109/MSP.2003.1203207 | |
| Regone C J. 2006. A modeling approach to wide-azimuth design for subsalt imaging. The Leading Edge , 25 (12) : 1467-1475. DOI:10.1190/1.2405331 | |
| Sirgue L, Barkved O I, Van Gestel J P, et al. 2009. 3D waveform inversion on Valhall wide-azimuth OBC.//Proceedings of the 71st EAGE Conference & Exhibition. SPE, EAGE. | |
| Starck J L, Murtagh F, Fadili J M. Sparse Image and Signal Processing:Wavelets, Curvelets, Morphological Diversity. Cambridge: Cambridge University Press, 2010 . | |
| Tang G, Shahidi R, Herrmann F J, et al. 2009. Higher dimensional blue-noise sampling schemes for curvelet-based seismic data recovery.//International Exposition and 79th International Annual Meeting, SEG, Expanded Abstracts, 191-195. | |
| Tang G. 2010. Seismic data reconstruction and denoising based on compressive sensing and sparse representation[Ph. D. thesis] (in Chinese). Beijing:Tsinghua University. | |
| ten Kroode F, Bergler S, Corsten C, et al. 2013. Broadband seismic data-The importance of low frequencies. Geophysics , 78 (2) : WA3-WA14. DOI:10.1190/geo2012-0294.1 | |
| Tropp J A, Gilbert A C. 2007. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory , 53 (12) : 4655-4666. DOI:10.1109/TIT.2007.909108 | |
| Verdú S. Multiuser Detection. Cambridge: Cambridge University Press, 1998 . | |
| Vermeer G. 2003. Responses to wide-azimuth acquisition special section. The Leading Edge , 22 (1) : 26-30. DOI:10.1190/1.1523756 | |
| VerWest B J, Lin D C. 2007. Modeling the impact of wide-azimuth acquisition on subsalt imaging. Geophysics , 72 (5) : SM241-SM250. DOI:10.1190/1.2736516 | |
| Wang D L, Tong Z F, Tang C, et al. 2010. An iterative curvelet thresholding algorithm for seismic random noise attenuation. Applied Geophysics , 7 (4) : 315-324. DOI:10.1007/s11770-010-0259-8 | |
| Wang W, Han B, Tang J P. 2013. Regularization method with sparsity constraints for seismic waveform inversion. Chinese Journal of Geophysics (in Chinese) , 56 (1) : 289-297. DOI:10.6038/cjg20130130 | |
| Wang Y F, Cao J J, Yang C C. 2011. Recovery of seismic wavefields based on compressive sensing by an l1-norm constrained trust region method and the piecewise random subsampling. Geophysical Journal International , 187 (1) : 199-213. DOI:10.1111/gji.2011.187.issue-1 | |
| Wright J, Ma Y, Mairal J, et al. 2010. Sparse representation for computer vision and pattern recognition. Proceedings of the IEEE , 98 (6) : 1031-1044. DOI:10.1109/JPROC.2010.2044470 | |
| Xu S, Zhang Y, Pham D, et al. 2005. Antileakage Fourier transform for seismic data regularization. Geophysics , 70 (4) : V87-V95. DOI:10.1190/1.1993713 | |
| Yang J C, Wright J, Huang T S, et al. 2010. Image super-resolution via sparse representation. IEEE Transactions on Image Processing , 19 (11) : 2861-2873. DOI:10.1109/TIP.2010.2050625 | |
| 陈生昌, 曹景忠, 马在田. 2001. 基于拟线性Born近似的叠前深度偏移方法. 地球物理学报 , 44 (5) : 704–710. | |
| 陈生昌, 王汉闯, 陈国新. 2012. 基于压缩感知的地球物理数据高效采集方法初步研究.//中国地球物理学会第二十八届年会论文集. 北京:中国地球物理学会. | |
| 陈生昌, 陈国新, 王汉闯. 2015. 稀疏性约束的地球物理数据高效采集方法初步研究. 石油物探 , 54 (1) : 24–35. | |
| 杜世通. 地震波动力学理论与方法. 东营: 中国石油大学出版社, 2009 . | |
| 刘喜武, 刘洪, 刘彬. 2004. 反假频非均匀地震数据重建方法研究. 地球物理学报 , 47 (2) : 299–305. | |
| 马坚伟. 2011. 稀疏促进地震勘探.//中国地球物理学会第二十七届年会论文集. 长沙. | |
| 唐刚. 2010. 基于压缩感知和稀疏表示的地震数据重建与去噪[博士论文]. 北京:清华大学. http://cdmd.cnki.com.cn/article/cdmd-10003-1011280421.htm | |
| 王薇, 韩波, 唐锦萍. 2013. 地震波形反演的稀疏约束正则化方法. 地球物理学报 , 56 (1) : 289–297. DOI:10.6038/cjg20130130 | |
 2016, Vol. 59
2016, Vol. 59


