2. EXPEC ARC, Saudi Aramco, Dhahran 31311, Saudi Arabia
2. EXPEC Advanced Research Center, Saudi Aramco, Dhahran 31311, Saudi Arabia
深度域偏移成像方法是油气勘探领域的一项关键技术,传统的偏移成像方法,如Kirchhoff偏移、单程波偏移等,存在一定局限性,无法满足复杂地区,复杂地表情况下的高精度成像要求.基于射线理论的Kirchhoff积分偏移法(Wiggins,1984;Keho and Beydoun,1988),求取的是波动方程高频近似解,对复杂构造中的高陡倾角地层不能很好地成像.基于单程波算子的波动方程偏移法,例如相移法(Gazdag,1978)、分步傅里叶法(Stoffa et al.,1990)、傅里叶有限差分法(Ristow and Rühl,1994)等,尽管有算法稳定、背景噪声小的优点,但在横向速度变化特别大的时候成像精度有限.在20世纪80年代,一些学者提出了逆时偏移成像方法及实现策略(Baysal et al.,1983;McMechan,1983;Whitmore,1983),但是受当时的计算能力限制,该方法并没有得到广泛应用.近年来,随着计算能力的飞速发展,逆时偏移以其能对高陡倾角成像,并能够处理地震数据中多种成分(反射波,绕射波,棱柱波等)的优点,在学术界和工业界都成为了研究热点.
在逆时偏移中,首先需要求解双程波动方程,构建震源波场和检波点波场,然后利用合适的成像条件生成成像结果.一般我们采用的是有限差分法来求解常密度声波方程,在时间空间域进行波场的正向和反向传播.最常用的成像条件是经典的互相关成像条件(Claerbout,1971),即震源波场和检波点波场在所有时间采样点上进行零延迟互相关后再进行叠加.这种成像方法在计算和存储能力满足需求的情况下比较容易实现,但其主要问题是成像结果中存在高振幅的低频噪声.这种低频噪声是由波动方程双向传播的特点所引起的,会严重干扰成像质量.为了避免在反射界面处产生强噪声,可以在波场模拟中进行针对性处理.Baysal等(1984)提出在波场模拟中采用无反射的双程波动方程,Loewenthal等(1987)提出对偏移速度进行充分光滑以降低反射波能量.此外,Zhang等(2009)提出采用滤波方法来消除低频噪声.根据低频噪声的产生原理,如果能在成像时分离不同方向的波场能量,则可以从本质上解决低频噪声问题.但常规的基于波场分离的逆时偏移成像方法,通常需要存储所有时刻的波场值并进行傅里叶变换,需要较大的存储量和计算量.Yoon和Marfurt(2006)利用Poynting矢量确定波场传播方向并据此来进行波场分离成像.Liu等(2011)提出了一种基于Hilbert变换的波场分离成像条件,可以有效去除高振幅的低频噪声.Fei等(2015)进一步指出,在偏移速度模型存在速度剧烈变化区域时,常规逆时偏移方法会产成成像假象.为此他们利用Hilbert变换构建了一个波场分离算子,来实现下行震源波场和上行检波点波场的互相关成像,并有效去除了成像假象,但他们只是探讨了成像过程中的上下行波场分离,针对的成像问题有一定局限性.
为此,本文首先分析了常规逆时偏移过程中噪声和假象的产生原理,然后在上下行波场分离成像条件的基础上,构建了基于Hilbert变换的全波场分离算子,推导了上左、上右、下左以及下右四个方向的波场分离算子、相应的互相关成像条件以及具体实现策略,最后针对Sigsbee 2B模型给出了16种波场分离成像条件对应的逆时偏移成像结果.数值计算结果表明本文方法不仅可以有效地压制常规逆时偏移成像方法的噪声和假象,还可以根据成像目标的地质情况获取最佳成像结果.
2 上下行波场分离及成像条件常规逆时偏移采用的是不进行波场分离的互相关成像条件(Claerbout,1971),其表达式为
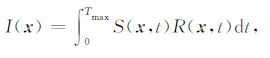
|
(1) |
这里, x 是地下某一点的空间位置, t 表示时间, Tmax 是最大波场传播时间,一般选择为地震数据的最大记录时间. S(x,t) 是正向传播的震源波场, R(x,t) 是反向传播的检波点波场.这两个波场可以通过求解双程波动方程获得,例如采用有限差分法求解常密度声波方程.为了避免存储整个正传或反传波场,逆时偏移可以采用以下数值步骤实现:
(1) 对于每一炮,正演震源波场,记录所有边界点的波场值和最后时刻的波场快照;(2) 反向传播检波点波场,同时根据存储的边界点波场值和最后时刻的波场快照按时间逆推震源波场;(3) 在每个时间采样点应用零延迟互相关成像条件,即对检波点波场和震源波场进行点乘,然后叠加所有时间采样点和所有炮的结果,获得偏移剖面.
逆时偏移采用双程波动方程模拟波场传播过程,可以准确地生成沿各个方向传播的波组成分.即使是在其他成像方法中难以处理的回折波或棱柱波,逆时偏移也可以对他们正确成像.但是常规互相关成像条件会在成像结果中生成强振幅的低频噪声,尤其当偏移速度中存在强反射界面时,噪声更为明显.为了提高成像精度,有必要改进常规成像条件.
假设地下介质存在水平反射层,当波场遇到该反射层时,由于双程波动方程的特点,入射波场会分为向下透射和向上反射两部分,可以用公式表示为
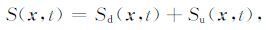
|
(2) |

|
(3) |
这里的下标 u和d 分别表示上行波和下行波,把公式(2)和(3)代入互相关成像条件(1)中,可将成像结果进一步表达为如下形式:

|
(4) |
Liu等(2011)指出正是最后两项, SdRd和SuRi, 生成了逆时偏移中强振幅的低频噪声.这两部分表示的是波场中沿相同方向传播的能量,不应该包括在互相关成像条件中.为此,他们提出应当在公式(4)中去掉最后两项.Fei等(2015)进一步指出,在偏移速度中存在速度变化特别剧烈的区域时,公式(4)中的第二项 SuRd 将产生假象并严重干扰成像质量,应该在互相关成像条件中去除,则公式(4)所示的成像条件可进一步表示为
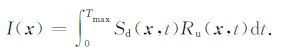
|
(5) |
对于公式(5)所示的波场分离成像条件,其实现难点在于如何快速有效地进行波场分离.以二维地震数据的逆时偏移为例,传统的波场分离方法是将震源与检波点波场全部存储,然后变换到频率波数域,采用公式(6)至公式(9)实现波场分离,获得上行波和下行波:

|
(6) |

|
(7) |
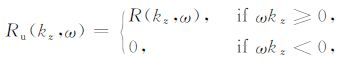
|
(8) |
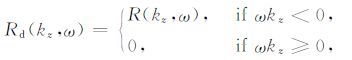
|
(9) |
这里的 S(kz,ω) 对应震源波场的二维傅里叶变换, R(kz,ω) 对应检波点波场的二维傅里叶变换.公式(6)至公式(9)所示的分离方法需要较大的数据存储量,在实际生产中存在一定问题.为此Fei等(2015)提出了一种利用Hilbert变换的高效波场分离算法.
对于一个给定的函数f(t),Hilbert变换具有如下性质:

|
(10) |
这里的 F 表示傅里叶变换算子, H 表示Hilbert变换算子,下标t表示变换作用的变量,sgn表示符号函数,定义为
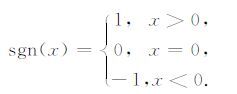
|
(11) |
可以构建波场分离算子U:

|
(12) |
该算子的傅里叶变换具有如下性质:
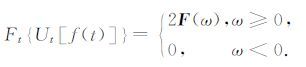
|
(13) |
该算子既可以作用于时间变量t也可以作用于空间坐标x或z,则公式(5)中的成像条件可以表示为(Fei et al.,2015)

|
(14) |
经推导可将公式(14)进一步表达为(Fei et al.,2015)
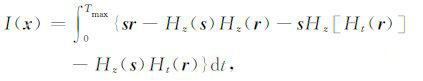
|
(15) |
这里的s代表震源波场,r代表检波点波场, r 满足 r=g*r0, 其中 g 是基于波动方程计算获得的格林函数, r0 表示实际地震记录,可证明 Ht(r)=g*Ht(r0),即Ht(r) 表示的是一个地震记录经过Hilbert变换之后正演模拟得到的波场.
3 全波场分离及成像条件在某些复杂情况下,仅使用上下行波的波场分离成像条件是不够的,需要进一步获取精细成像结果,例如在地下存在高陡倾角构造时,就需要将上下行波场进一步分离为左行与右行波场.
震源与检波点波场按照左上、左下、右上与右下四个方向分解后可以表示为
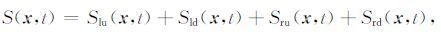
|
(16) |
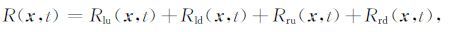
|
(17) |
这里的下标l和r分别表示左行波和右行波.把公式(16)和公式(17)代入互相关成像条件(1)中,将获得16个成像结果.可以根据地层倾角特点对16个成像结果进行选择性组合,以获取相对合理的成像结果,例如对位于震源和检波点下方左侧的垂直反射层成像时,相对合理的成像结果可能是
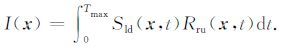
|
(18) |
以下推导全波场分离公式,首先定义一个新的算子V,其表达式为

|
(19) |
将该算子作用于空间变量 x, 可得
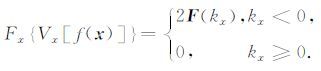
|
(20) |
则左右行波的波场分离算子可以表示为 UxUtS(x,t)和VxUtS(x,t). 可推导获得左下、左上、右下、右上四种类型波场成分表达式为
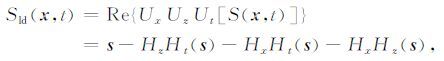
|
(21) |
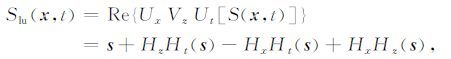
|
(22) |

|
(23) |
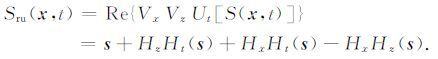
|
(24) |
实际计算时,只需在常规逆时偏移基础上额外计算一个Hilbert变换后的地震记录的正演波场,对其沿不同坐标方向进行Hilbert变换并加以组合,就可以获得四个方向的波场分离结果.整个计算过程不需要存储波场快照和进行傅里叶变换,具有很高的计算效率.
根据上述波场分离公式,可进一步推导相应的波场分离互相关成像条件,例如左下行震源波场和右上行检波点波场互相关成像条件为
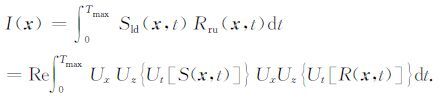
|
(25) |
值得注意的是由于算子 Ut 作用的震源波场或者检波点波场在频率域内对于负的 ω 均为0,我们只需在时间变量上对震源波场或者检波点波场作用一次算子 Ut, 则公式(25)可以简化为
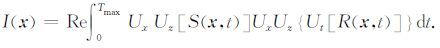
|
(26) |
将波场分离算子的定义公式(12)和(19)代入公式(26),可得左下行震源波场与右上行检波点波场互相关成像条件的最终表达式:

|
(27) |
在对波场进行左右行和上下行分离后,我们一共可以得到16种互相关成像结果,每一种成像公式的表达形式均与公式(25)类似.我们认为其中有四种成像结果是Sigsbee 2B模型相对合理的成像结果,第一种即为公式(27)所示,其余三种成像公式经推导具有如下表达式.
第二种是左下行震源波场和左上行检波点波场的互相关:
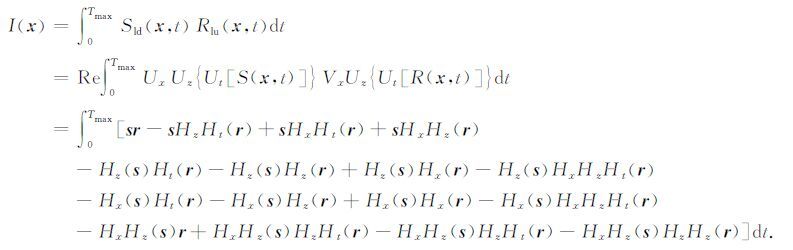
|
(28) |
第三种是右下行震源波场和右上行检波点波场的互相关:

|
(29) |
第四种是右下行震源波场和左上行检波点波场互相关:

|
(30) |
当炮点和检波点都在地表,地下只有水平反射层时,仅有下行震源波场和上行检波点波场的互相关是正确的成像结果.但如果地下反射层的倾角接近90°时,就应该采用左行震源波场与右行检波点波场的互相关成像结果,或者采用右行震源波场与左行检波点波场的互相关成像结果.我们需要针对待处理工区地质结构的特点,对各种成像结果进行选择性组合,以获取最佳成像效果.
4 数值算例我们采用一个简单模型来验证前文推导的波场分离公式的有效性.图 1是一个双层速度模型,该模型的水平方向有300个网格点,垂直方向有150个网格点,网格点间距为10 m.震源位置在地表水平坐标1500 m处.图 2是0.6 s时刻的震源波场快照.图 3a至图 3d是震源波场的四个方向分离结果,如图所示,波场的左下、左上、右下与右上四个不同方向的波场成分均得到了有效分离.

|
图 1 双层速度模型 Fig. 1 A two-layer velocity model |

|
图 2 0.6 s的震源波场快照 Fig. 2 The source wavefield snapshot at 0.6 s |

|
图 3 四个方向的波场分离结果:(a)左下;(b)左上;(c)右下;(d)右上 Fig. 3 Four directional wavefield after decomposition.(a)Left-downgoing;(b)Left-upgoing;(c)Right-downgoing;(d)Right-upgoing |
我们采用Sigsbee 2B数据来验证波场分离成像条件的有效性.如图 4a所示,该模型的水平方向有3201个网格点,垂直方向有1201个网格点,网格点间距为7.62 m.该数据有496炮,炮点间距是45.72 m,单炮最大道数为348道,炮点间距为45.72 m,检波点间距为22.86 m,炮点和检波点深度均为7.62 m,炮记录的时间长度为12 s,时间采样间隔为8 ms.我们采用自由表面多次波去除之后的数据进行逆时偏移.

|
图 4 (a)Sigsbee 2B 速度模型;(b)Sigsbee 2B偏移速度模型 Fig. 4 (a) Sigsbee 2B stratigraphic velocity model;(b)Sigsbee 2B migration velocity model |
图 4b是Sigsbee 2B数据对应的偏移速度模型,图 5a是采用常规互相关成像条件的逆时偏移结果,图 5b是图 5a经过Laplace滤波之后的结果.图 6a至图 6d分别是采用公式(27)至公式(30)所示的四种波场分离互相关成像条件获得的逆时偏移成像结果.图 6a至图 6d是Sigsbee 2B模型对应的四个相对合理的成像结果,但图 6b与图 6c的盐丘上部均存在一些噪声,这是由于盐丘上边界为倾斜边界,而图 6b与图 6c对应的成像公式中存在水平方向同向传播的震源与检波点波场,这两个同向传播波场的互相关导致了盐丘上部出现低频噪声.图 7a至图 7d分别是左上类型的震源波场与分离后的四种检波点波场采用互相关成像条件的逆时偏移结果.图 8a与图 8b分别是左下类型的震源波场与左下、右下两种检波点波场采用互相关成像条件的逆时偏移结果.图 9a至图 9d分别是右上类型的震源波场与分离后的四种检波点波场采用互相关成像条件的逆时偏移结果.图 10a与图 10b分别是右下类型的震源波场与左下、右下两种检波点波场采用互相关成像条件的逆时偏移结果.图 7至图 10所示的12种成像结果大都是偏移噪声和假象,主要是由同方向传播的震源与检波点波场互相关产生的,如 SldRld,SluRlu,SrdRrd,SruRru 等.

|
图 5 (a) Sigsbee 2B数据的常规逆时偏移剖面;(b)对图(a)所示的常规逆时偏移剖面进行Laplace滤波的结果 Fig. 5 (a) The conventional RTM result of Sigsbee 2B dataset;(b)Laplace filtering result of the conventional RTM image as shown in(a) |
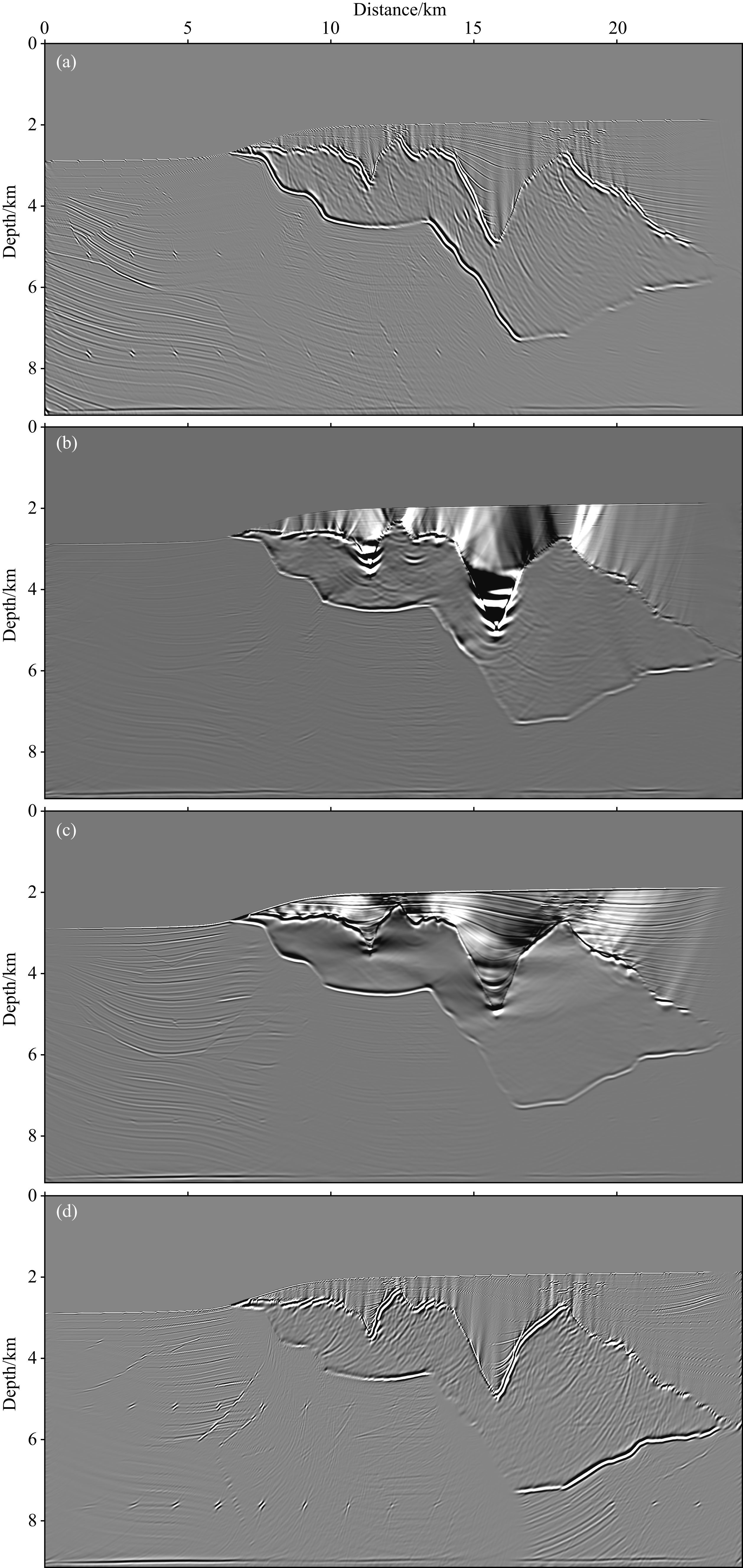
|
图 6 Sigsbee 2B模型对应的四种相对合理的成像结果 (a) SldRru; (b) SldRlu; (c) SrdRru; (d) SrdRlu. Fig. 6 Four relatively correct RTM images related with Sigsbee 2B model |

|
图 7 左上类型的震源波场与分离后的四个检波点波场进行互相关成像的结果 (a) SluRlu; (b) SluRld; (c) SluRru; (d) SluRrd. Fig. 7 The RTM images constructed by the cross-correlation of the left-upgoing type source wavefield with decomposed four receiver wavefields |
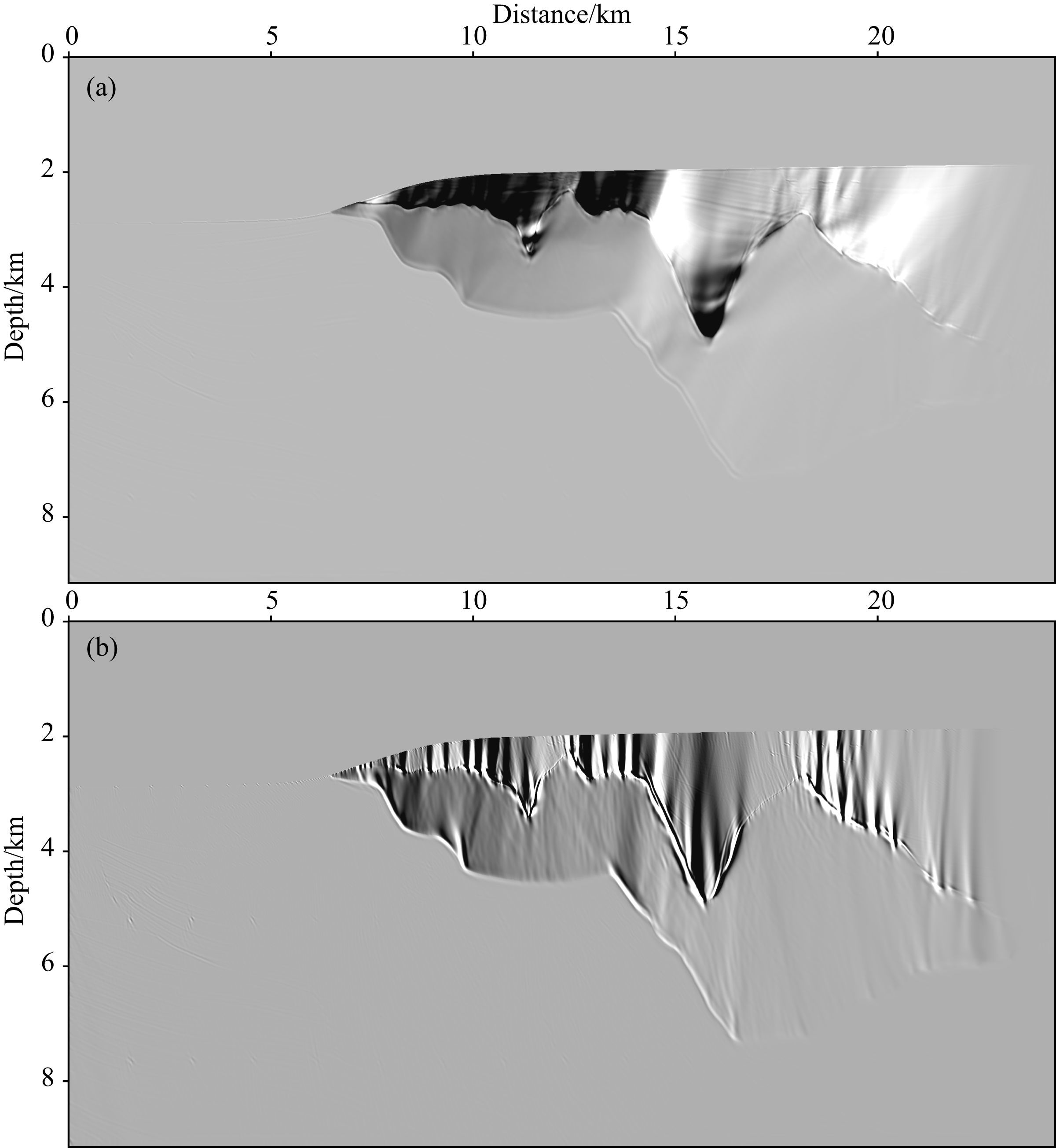
|
图 8 左下类型的震源波场与分离后的两个检波点波场进行互相关成像的结果.(a) SldRld; (b) SldRrd Fig. 8 The RTM images constructed by the cross-correlation of the left-downgoing type source wavefield with decomposed two receiver wavefields |

|
图 9 右上类型的震源波场与分离后的四个检波点波场进行互相关成像的结果 (a) SruRlu; (b) SruRld; (c) SruRru; (d) SruRrd. Fig. 9 The RTM images constructed by the cross-correlation of the right-upgoing type source wavefield with decomposed four receiver wavefields |

|
图 10 右下类型的震源波场与分离后的两个检波点波场进行互相关成像的结果 (a) SrdRld; (b) SrdRrd. Fig. 10 The RTM images constructed by the cross-correlation of the right-downgoing type source wavefield with decomposed two receiver wavefields |
逆时偏移是地震勘探领域一种重要的成像方法,它成像精度高并且适用于复杂地质构造成像,但常规逆时偏移结果存在低频噪声,而且在偏移速度梯度较大时还可能存在偏移假象.本文在上下行波场分离互相关成像条件的基础上,推导了基于Hilbert变换的全波场分离公式以及相应的互相关成像条件,并针对Sigsbee 2B模型给出了16种采用全波场分离互相关成像条件的偏移结果,可以有效地分离常规逆时偏移方法产生的噪声和假象.本文建立的全波场分离逆时偏移成像方法计算效率高,易于实现,在实际应用中可以利用本文方法根据目标地层的特点高效地获取最优成像结果,这对于逆时偏移的实际应用有一定意义.
| Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration. Geophysics , 48 (11) : 1514-1524. DOI:10.1190/1.1441434 | |
| Baysal E, Kosloff D D, Sherwood J W C. 1984. A two-way nonreflecting wave equation. Geophysics , 49 (2) : 132-141. DOI:10.1190/1.1441644 | |
| Claerbout J F. 1971. Toward a unified theory of reflector mapping. Geophysics , 36 (3) : 467-481. DOI:10.1190/1.1440185 | |
| Fei T W, Luo Y, Yang J R, et al. 2015. Removing false images in reverse time migration:The concept of de-primary. Geophysics , 80 (6) : S237-S244. DOI:10.1190/geo2015-0289.1 | |
| Gazdag J. 1978. Wave equation migration with the phase-shift method. Geophysics , 43 (7) : 1342-1351. DOI:10.1190/1.1440899 | |
| Keho T H, Beydoun W B. 1988. Paraxial ray Kirchhoff migration. Geophysics , 53 (12) : 1540-1546. DOI:10.1190/1.1442435 | |
| Liu F Q, Zhang G Q, Morton S A, et al. 2011. An effective imaging condition for reverse-time migration using wavefield decomposition. Geophysics , 76 (1) : S29-S39. DOI:10.1190/1.3533914 | |
| Loewenthal D, Stoffa P L, Faria E L. 1987. Suppressing the unwanted reflections of the full wave equation. Geophysics , 52 (7) : 1007-1012. DOI:10.1190/1.1442352 | |
| McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting , 31 (3) : 413-420. DOI:10.1111/gpr.1983.31.issue-3 | |
| Ristow D, Rühl T. 1994. Fourier finite-difference migration. Geophysics , 59 (12) : 1882-1893. DOI:10.1190/1.1443575 | |
| Stoffa P L, Fokkema J T, de Luna Freire R M, et al. 1990. Split-step Fourier migration. Geophysics , 55 (4) : 410-421. DOI:10.1190/1.1442850 | |
| Whitmore N D. 1983. Iterative depth migration by backward time propagation.//53rd Annual International Meeting. SEG Expanded Abstracts, 382-385. | |
| Wiggins J W. 1984. Kirchhoff integral extrapolation and migration of nonplanar data. Geophysics , 49 (8) : 1239-1248. DOI:10.1190/1.1441752 | |
| Yoon K, Marfurt K J. 2006. Reverse-time migration using the Poynting vector. Exploration Geophysics , 37 (1) : 102-107. DOI:10.1071/EG06102 | |
| Zhang Y, Sun J. 2009. Practical issues in reverse time migration:True amplitude gathers, noise removal and harmonic source encoding. First Break , 26 : 29-35. | |
 2016, Vol. 59
2016, Vol. 59

