2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266071
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
岩石的宏观物理性质是微观结构骨架、孔隙等各组成成分的综合效应,对于体积模量、剪切模量、速度等,这些弹性参数在地球物理勘探领域等实际工作中发挥着重要作用(刘向君等,2014).岩石物理是连接储层弹性参数与物性参数的桥梁,也是地球物理反演的基础(宗兆云等,2012a;印兴耀等,2015).随着计算机技术与成像技术的提高,数字岩石物理技术得到了迅速发展,根据岩石微观结构信息重建反映岩石真实孔隙空间的三维数字模型,以实际地质资料为约束,在计算机上运用数值计算方法研究孔隙结构、裂缝特征及其与岩石物理特性(如电阻率、弹性模量、速度与波场、渗透率和核磁共振)之间的关系(孙建孟等,2012;朱伟和单蕊,2014).基于数字岩心的物理性质研究是岩石物理的重要发展方向,特别是随着页岩气、致密油气等开发,发展数字岩心岩石物理方法对其具有重要的指导意义.相比于传统的岩石物理实验,数字岩石物理在岩石弹性、物性多尺度模拟方面有较大的优势,针对不同类型储层(如疏松砂岩、碳酸盐岩、致密砂岩、页岩气、页岩油等)岩样,利用数字化成像技术,通过岩心整体扫描建立多尺度岩石模型,明确不同类型储层岩石骨架及孔隙的多尺度特征并将其参数化,抽象出不同类型储层岩石数学模型,发展基于模型驱动的叠前地震反演方法,为地震反演提供理论指导(宗兆云等,2012b;宗兆云,2013).与传统的岩石物理实验相比,数字岩石物理实验操作简单,速度快而且成本低,对实验的条件要求低,同时避免了人为操作、实验环境及仪器的影响所带来的误差,节省大量人力物力.基于数字岩心的岩石物理数值模拟对岩心不具有破坏性,岩心可重复使用.为了建立多物理场属性的内在关系,可以在同一块数字岩心上进行不同物理场的模拟,如电阻率、弹性模量、速度与波场、渗透率等,并且可以测量传统岩石物理实验难以直接测量的物理量,如三相相对渗透率(孙建孟等,2012).此外传统的岩石物理实验对于低孔低渗等复杂油气储层,岩心驱替测试困难,因此对于裂缝发育的碳酸盐岩储层岩石物理参数的准确获得也具有重要意义(陈怀震等,2014a).基于数字岩心可以在微观上模拟岩石弹性模量随裂缝密度、裂缝发育方向的变化,同时可以模拟裂缝介质的波场特征,有助于裂缝的识别,建立各向异性岩石物理模型为AVAZ反演提供理论基础(陈怀震等,2014b).对于碳酸盐岩及页岩、油砂等难以取到代表性的岩心,取心费用高、成功率低,对于疏松岩心保存困难,岩石物理实验难以开展,无法定量研究微观参数对岩石宏观物理属性的影响,利用数字岩石物理实验可代替传统岩石物理实验弥补这些不足.除了上述优势,通过调整数字岩心的微观参数,利用数字岩石物理实验有利于认识储层参数对岩石物理属性的影响,由于数字岩心的微观结构直观可见,为直接计算几何特征参数提供了便利,数值模拟的边界条件灵活,可连续呈现物理场的变化过程(朱伟和单蕊,2014).中国的地层结构复杂,在三维数字岩心方面的研究起步较晚,为了缩小国际差距,数字岩石物理是发展趋势,地球物理工作者应该实施数字化智能化的战略.
在油气勘探与开发领域数字岩石物理主要在测井及油气开发渗流模拟领域得到研究及应用,屈乐(2014)基于低渗透储层建立三维数字岩心模型及电性模拟研究.数字岩石物理在地震勘探领域以弹性模拟为主,目前处于起步阶段,研究及应用范围有一定的局限性.Saenger等(2000)在标准交错网格基础上提出了旋转交错网格有限差分方法.Saenger等(2004)假设数字岩心模型孔隙中饱含高密度流体,计算等效弹性参数,这一研究为数字岩石物理实验在地震勘探方面的研究奠定了基础.Saenger等(2007)利用旋转交错网格有限差分方法研究岩石孔隙空间气、水分布对波传播的影响,模拟结果与实验测量结果接近,表明该方法的高精度性与鲁棒性.基于三维数字岩石物理,假设介质含有裂缝,利用旋转交错网格有限差分进行波场动力学模拟(Saenger and Shapiro, 2002).通过广义Maxwell型和旋转交错网格有限差分,对黏滞性孔隙流体进行数值模拟,得到纵横波速度(Saenger et al., 2011).Saxena和Mavko(2015)基于数字岩心研究双相介质中流体或固体替代下剪切模量和体积模量的计算方法,讨论了孔隙填充物性质对弹性模量的影响.对于孔隙联通性良好的多矿物岩石,Brown和Korringa(1975)扩展Gassmann流体替换方程用于弹性模量的计算,但是实际应用中很少采用此方程,Saxena等(2015)基于三维数字岩心提出了流体替换的新方法,该方法在计算岩石基质模量时,不依赖Gassmann流体替换中的Voigt-Reuss-Hill平均模量或Hashin-Shtrikman界限.除此之外,利用数字岩心开展准静态模拟,建立波速、衰减系数与孔隙流体黏滞度的关系,建立计算数字岩心(黏)弹性参数的新方法.
岩石弹性微观数值模拟方法主要有声格子、有限元以及旋转交错网格有限差分方法等(Andrä et al,2013a).一些学者应用有限元方法进行了材料的静力学模拟,计算了复合材料的等效弹性参数及岩石的弹性参数(Garboczi and Day, 1995; Bohn and Garboczi, 2003),但有限元方法运行速度慢,计算效率低.Del Valle-García和Sánchez-Sesma(2003)利用声格子方法模拟了声波在孔隙介质中的传播,但由于该方法的计算量较大,目前还只限于二维数值模拟研究.本文直接在三维数字岩心基础上利用有限差分方法来模拟波的传播过程,测量由数字岩石样本非均匀结构带来的峰值振幅的时间差,完成弹性模量的计算,验证了该方法的有效性与合理性,高阶有限差分方法占用内存相对较少,计算速度快,模拟结果合理,为数字岩石物理实验提供了一套新的研究思路.
2 方法原理三维标量波方程为
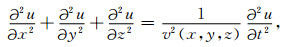
|
(1) |
其中,u(x, y, z, t)为波场,v(x, y, z)为介质速度.
在地震波模拟的模型区域对方程(1)进行离散,即网格化.令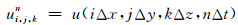
对方程(1)进行泰勒级数展开, 得到方程(2)和(3)为
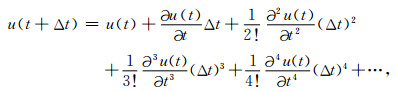
|
(2) |
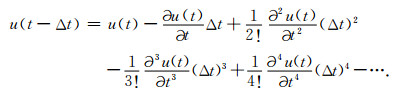
|
(3) |
相加式(2)和式(3)得:
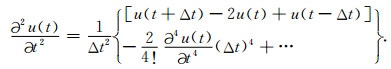
|
(4) |
化简式(4)可写为
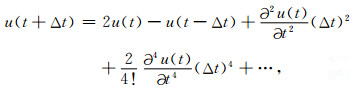
|
(5) |
取等号右端的前三项,得到关于时间的二阶差分格式为
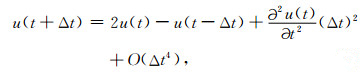
|
(6) |
式(6)在时间方向上的截断误差为O(Δt4),是二阶精度的差分格式.
关于x、y、z方向空间二阶偏导数的高阶差分格式推导过程是类似的,在此仅对X方向展开讨论.假设X方向上的截断误差为O(Δx2N),N是大于2的偶数.
将u(x+nΔx)和u(x-nΔx)进行泰勒级数展开,有
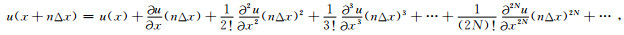
|
(7) |
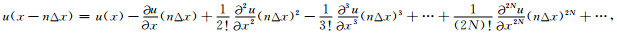
|
(8) |
相加式(7)和式(8),得:
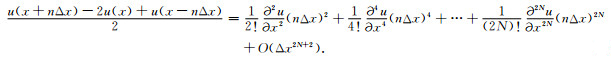
|
(9) |
将上述n个方程同时乘以ω1,ω2,…,ωn然后相加并化简整理,写成矩阵形式为
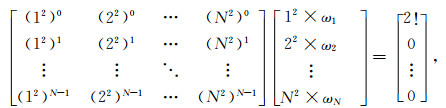
|
(10) |
其系数矩阵即为范德蒙矩阵.
令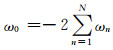
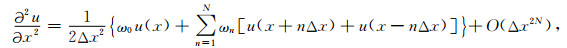
|
(11) |
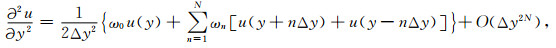
|
(12) |
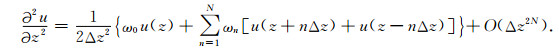
|
(13) |
根据前面的推导,截断误差为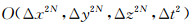
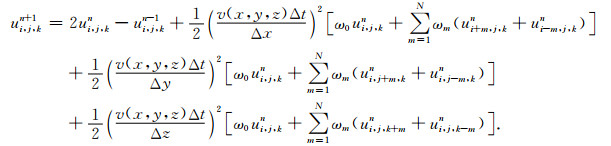
|
(14) |
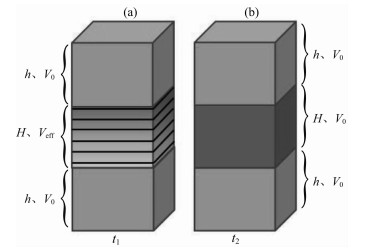
该方法的基本思想是利用有限差分来模拟波的传播过程,在孔隙尺度远远小于波长的情况下,研究非均质三维数字岩心样本的速度.为了计算岩石的有效弹性参数,将数字岩石样本、参考样本分别嵌入均匀弹性区域形成新模型和参考模型如图 1所示,假设该弹性区域和参考样本具有与数字岩石样本骨架颗粒相同的弹性性质.选择最佳匹配层(Perfectly Matched Layer,简称PML)吸收边界条件来消除边界效应.波源在模型顶部激发,纵波或横波在模型中传播,检波器在底部接收,测量由数字岩石样本非均匀结构带来的峰值振幅的时间差,利用时间差(相对于参考模型)估算等效速度,进而求取等效弹性模量.具体的计算公式为:
|
图 1 嵌入数字岩石样本的新模型(a)和参考模型(b) Fig. 1 New model of embedded digital rock samples (a) and reference model (b) |
|
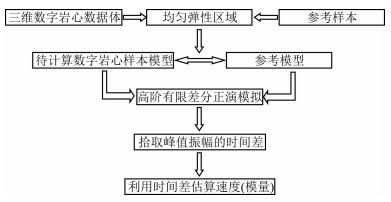
图 2 计算流程与方法框图 Fig. 2 Chart of computation process and the method |
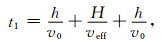
|
(15) |
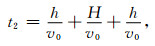
|
(16) |
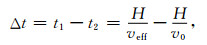
|
(17) |
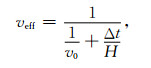
|
(18) |

|
(19) |
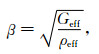
|
(20) |
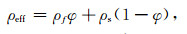
|
(21) |
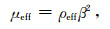
|
(22) |
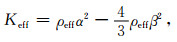
|
(23) |
其中h表示被嵌入均匀弹性区域的高度,H表示三维数字岩心样本的高度,V0表示均匀弹性区域的速度,Veff表示三维数字岩心样本的等效速度,t1表示波源激发平面波经过新模型的时间,t2表示波源激发平面波经过参考模型的时间,α、β分别表示估算得到的纵、横波速度,Keff、Geff分别表示三维数字岩心样本的等效体积模量、剪切模量,ρf、ρs、ρeff分别表示三维数字岩心样本的孔隙流体密度、骨架密度、等效密度,φ为三维数字岩心样本的孔隙度.利用得到的纵、横波速度根据公式(19)和(20)即可得到三维数字岩心样本的等效弹性模量,如公式(22)和(23)所示.
用于本文研究的理论模型是细层层状介质模型,三维数字岩心模型为Fontainebleau(枫丹白露)和Berea(贝雷)砂岩模型.以四块Fontainebleau砂岩及一块Berea砂岩的三维数字岩心样本为例,在三维数字岩心的基础上利用高阶有限差分计算岩石的体积模量和剪切模量.三维数字岩心的分辨率分别为5.68 μm/像素,5.345 μm/像素,岩心尺寸分别为200×200×200像素,400×400×400像素.Fontainebleau砂岩为研究提供了一种理想的三维数字岩心.首先,Fontainebleau砂岩的弹性模量实验数据充分,且岩石孔隙度的变化范围广,为对比实验结果和数值模拟结果提供了方便.其次,Fontainebleau砂岩均质性好,岩石骨架矿物成分单一,只有石英颗粒,而且该类砂岩孔隙结构简单,只存在粒间孔隙.在进行数字岩心数值模拟的研究中岩心的扫描,图像的获得是前提.刘学锋等(2013)对三维数字岩心建模做了大量研究.如何利用X射线CT建立三维数字岩心及扫描后的图像处理刘学峰(2010)做了详细介绍.除此之外,Andrä等(2013b)对不同岩石类型的数字岩心的成像做了大量研究.
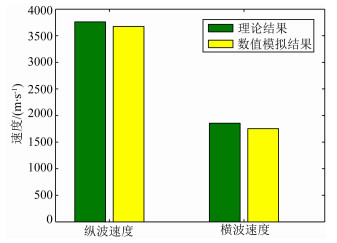
3 模型试算 3.1 细层层状介质-Backus平均该模型上部介质(绿色)纵波速度Vp(1)=5200 m·s-1,横波速度Vs(1)=2700 m·s-1,密度ρ1=2450 kg·m-3,厚度d1=0.75 m;下部介质(黄色)纵波速度Vp(2)=2900 m·s-1,横波速度Vs(2)=1400 m·s-1,密度ρ2=2340 kg·m-3,厚度d2=0.5 m.根据Backus平均计算公式可以得出理论垂向等效纵波速度为3761.0 m·s-1,理论垂向等效横波速度为1854.8 m·s-1;数值模拟结果分别为3675.3 m·s-1、1753.2 m·s-1,如图 4所示.误差分别为2.3%、5.3%.由此可见,数值模拟结果与理论计算结果的吻合程度较高.说明在三维数字岩心基础上,采用高阶有限差分方法计算三维数字岩心样本的速度是可行的,为模量计算打下了基础,验证了该方法的有效性.

|
图 3 细层层状介质模型 Fig. 3 Schematic model of thin-layered media |
|
图 4 数值模拟结果与理论计算结果比较 Fig. 4 Comparison of numerical simulation and theoretical results |
|
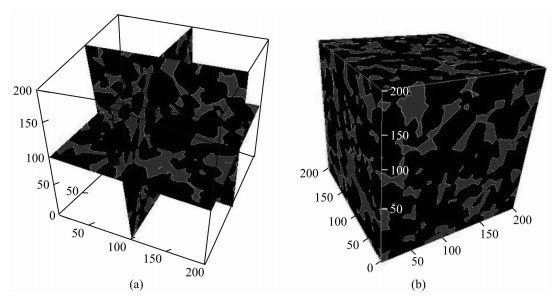
图 5 三维Fontainebleau模型 Fig. 5 The 3D model of Fontainebleau |
|
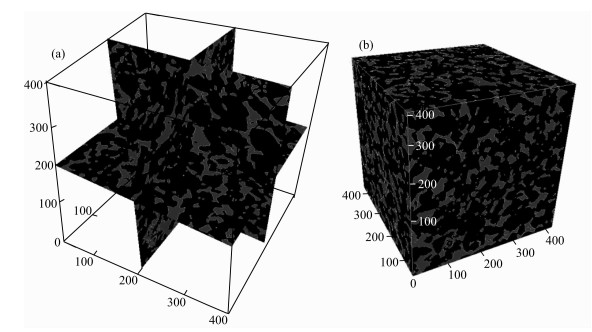
图 6 Berea模型 Fig. 6 The 3D model of Berea |
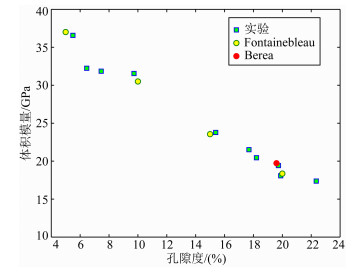
数值模拟中,设岩石骨架的体积模量K=37 GPa,剪切模量G=44 GPa,密度ρs=2.65 g·mm-3.孔隙中饱含流体水,体积模量K=1.02 GPa,剪切模量G=0 GPa,密度ρf=1.00 g·mm-3.砂岩孔隙度φ分别为5%、10%、15%和20%,Berea砂岩孔隙度φ=19.6%.Fontainebleau砂岩及Berea砂岩三维数字岩心的体积模量和剪切模量的模拟结果如图 7和图 8所示,图中绿色正方形数据点为实验结果

|
图 7 体积模量数值模拟结果 Fig. 7 Simulation results of bulk moduli |
|
图 8 剪切模量数值模拟结果 Fig. 8 Simulation results of shear moduli |
(Han et al., 1986),黄色圆形数据点表示Fontainebleau砂岩数值模拟结果,红色圆形数据点表示Berea砂岩数值模拟结果.岩石弹性模量的数值模拟结果与实验结果的吻合程度较高.说明在三维数字岩心基础上,采用高阶有限差分方法计算岩石的弹性模量是可行的,验证了该方法的有效性.
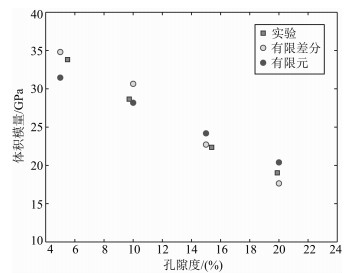
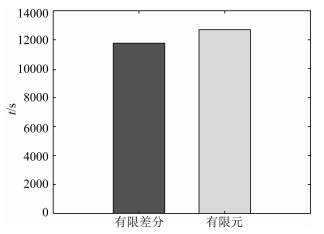
4 有限差分与有限元方法对比三维Fontainebleau砂岩岩心的分辨率为5.68 μm/像素,岩心尺寸为200×200×200像素.以孔隙度分别为5%、10%、15%和20%的三维Fontainebleau砂岩的数值模拟结果为例,从图 9和图 10有限元及有限差分的计算结果不难发现.孔隙度在10%左右的时候有限元的计算结果要好于有限差分,孔隙度为5%、15%和20%时有限差分的计算结果与实验结果更接近.利用有限差分法和有限元法分别对孔隙度为20%的三维Fontainebleau数字岩心进行数值模拟计算,计算时间分别是11757 s、12694 s,如图 11.从而说明了有限差分方法计算精度高,速度快,结果合理.
|
图 9 有限差分法与有限元法的体积模量计算比较 Fig. 9 Comparison between the finite element method and finite difference method in simulation results of bulk moduli |

|
图 10 有限差分法与有限元法的剪切模量计算比较 Fig. 10 Comparison between the finite element method and finite difference method in simulation results of shear moduli |
|
图 11 有限差分法与有限元法的计算效率比较 Fig. 11 Comparison between the finite element method and finite difference method in computational efficiency |
基于三维数字岩心,利用高阶有限差分方法对现有的岩石物理等效模型进行验证,计算岩石的体积模量和剪切模量,数值模拟结果与实验结果相符,验证了该方法的可行性与合理性.建立了模量与孔隙流体的关系,形成计算数字岩心弹性参数的新方法.与有限元计算方法相比有限差分计算速度快,精度较高,结果合理.基于三维数字岩心利用有限差分方法来模拟波传播过程计算岩石的等效模量应用前景广泛,为数字岩石物理的研究提供了一条新的途径,为地球物理勘探人员提供了一套可借鉴的研究思路.
| Andrä H, Combaret N, Dvorkin J, et al. 2013a. Digital rock physics benchmarks-Part Ⅱ:Computing effective properties. Computers & Geosciences , 50 : 33-43. | |
| Andrä H, Combaret N, Dvorkin J, et al. 2013b. Digital rock physics benchmarks-Part I:Imaging and segmentation. Computers & Geosciences , 50 : 25-32. | |
| Bohn R B, Garboczi E J. 2003. User manual for finite element and finite difference programs:A parallel version of NISTIR 6269. National Institute of Standards and Technology. | |
| Brown R J S, Korringa J. 1975. On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid. Geophysics , 40 (4) : 608-616. DOI:10.1190/1.1440551 | |
| Chen H Z, Yin X Y, Gao C G, et al. 2014b. AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory. Chinese J. Geophys. , 57 (3) : 968-978. DOI:10.6038/cjg20140326 | |
| Chen H Z, Yin X Y, Zhang J Q, et al. 2014a. Seismic inversion for. Chinese J. Geophys. , 57 (10) : 3431-3441. DOI:10.6038/cjg20141029 | |
| Del Valle-García R, Sánchez-Sesma F J. 2003. Rayleigh waves modeling using an elastic lattice model. Geophysical Research Letters , 30 (16) : 1866. DOI:10.1029/2003GL017600 | |
| Garboczi E J, Day A R. 1995. An algorithm for computing the effective linear elastic properties of heterogeneous materials:Three-dimensional results for composites with equal phase Poisson ratios. Journal of the Mechanics and Physics of Solids , 43 (9) : 1349-1362. DOI:10.1016/0022-5096(95)00050-S | |
| Han D H, Nur A, Morgan D. 1986. Effects of porosity and clay content on wave velocities in sandstones. Geophysics , 51 (11) : 2093-2107. DOI:10.1190/1.1442062 | |
| Liu X F. 2010. Numerical simulation of elastic and electrical properties of rock based on digital cores[Ph. D. thesis] (in Chinese). Qingdao:China University of Petroleum. | |
| Liu X F, Zhang W W, Sun J M. 2013. Methods of constructing 3-D digital cores:A review. Progress in Geophys. , 28 (6) : 3066-3072. DOI:10.6038/pg20130630 | |
| Liu X J, Zhu H L, Liang L X. 2014. Digital rock physics of sandstone based on micro-CT technology. Chinese J. Geophys. , 57 (4) : 1133-1140. DOI:10.6038/cjg20140411 | |
| Qu L. 2014. Modeling and application of three-dimensional digital core based on low permeability reservoir[Ph. D. thesis] (in Chinese). Xi'an:Northwest University. | |
| Saenger E H, Ciz R, Krüger O S, et al. 2007. Finite-difference modeling of wave propagation on microscale:A snapshot of the work in progress. Geophysics , 72 (5) : SM293-SM300. DOI:10.1190/1.2753552 | |
| Saenger E H, Enzmann F, Keehm Y, et al. 2011. Digital rock physics:Effect of fluid viscosity on effective elastic properties. Journal of Applied Geophysics , 74 (4) : 236-241. DOI:10.1016/j.jappgeo.2011.06.001 | |
| Saenger E H, Gold N, Shapiro S A. 2000. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion , 31 (1) : 77-92. DOI:10.1016/S0165-2125(99)00023-2 | |
| Saenger E H, Krüger O S, Shapiro S A. 2004. Numerical considerations of fluid effects on wave propagation:Influence of the tortuosity. Geophysical Research Letters , 31 (21) : L21613. | |
| Saenger E H, Shapiro S A. 2002. Effective velocities in fractured media:a numerical study using the rotated staggered finite-difference grid. Geophysical Prospecting , 50 (2) : 183-194. DOI:10.1046/j.1365-2478.2002.00309.x | |
| Saxena N, Mavko G. 2015. The embedded-bound method for estimating the change in rock moduli under pore fill and mineral phase substitution. Geophysics , 80 (3) : L1-L10. DOI:10.1190/geo2014-0448.1 | |
| Saxena N, Mavko G, Mukerji T. 2015. Fluid substitution in multimineralic rocks with large mineral stiffness contrast. Geophysics , 80 (3) : L11-L33. DOI:10.1190/geo2014-0309.1 | |
| Sun J M, Jiang L M, Liu X F, et al. 2012. Log application and prospect of digital core technology. Well Logging Technology , 36 (1) : 1-7. | |
| Yin X Y, Zong Z Y, Wu G C. 2015. Research on seismic fluid identification driven by rock physics. Science China Earth Sciences , 58 (2) : 159-171. DOI:10.1007/s11430-014-4992-3 | |
| Zhu W, Shan R. 2014. Progress of digital rock physics. Oil Geophysical Prospecting , 49 (6) : 1138-1146. | |
| Zong Z Y, Yin X Y, Wu G C. 2012a. Fluid identification method based on compressional and shear modulus direct inversion. Chinese J. Geophys. , 55 (1) : 284-292. DOI:10.6038/j.issn.0001-5733.2012.01.028 | |
| Zong Z Y, Yin X Y, Zhang F, et al. 2012b. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio. Chinese J. Geophys. , 55 (11) : 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 | |
| Zong Z Y. 2013. Methodologies of model driven inversion with Pre-stack seismic data[Ph. D. thesis] (in Chinese). Qingdao:China University of Petroleum. | |
| 陈怀震, 印兴耀, 张金强, 等. 2014a. 基于方位各向异性弹性阻抗的裂缝岩石物理参数反演方法研究. 地球物理学报 , 57 (10) : 3431–3441. DOI:10.6038/cjg20141029 | |
| 陈怀震, 印兴耀, 高成国, 等. 2014b. 基于各向异性岩石物理的缝隙流体因子AVAZ反演. 地球物理学报 , 57 (3) : 968–978. DOI:10.6038/cjg20140326 | |
| 刘学锋. 2010.基于数字岩心的岩石声电特性微观数值模拟研究[博士论文].青岛:中国石油大学. | |
| 刘学锋, 张伟伟, 孙建孟. 2013. 三维数字岩心建模方法综述. 地球物理学进展 , 28 (6) : 3066–3072. DOI:10.6038/pg20130630 | |
| 刘向君, 朱洪林, 梁利喜. 2014. 基于微CT技术的砂岩数字岩石物理实验. 地球物理学报 , 57 (4) : 1133–1140. DOI:10.6038/cjg20140411 | |
| 屈乐. 2014.基于低渗透储层的三维数字岩心建模及应用[博士论文].西安:西北大学. | |
| 孙建孟, 姜黎明, 刘学锋, 等. 2012. 数字岩心技术测井应用与展望. 测井技术 , 36 (1) : 1–7. | |
| 印兴耀, 宗兆云, 吴国忱. 2015. 岩石物理驱动下地震流体识别研究. 中国科学:地球科学 , 45 (1) : 8–21. | |
| 朱伟, 单蕊. 2014. 虚拟岩石物理研究进展. 石油地球物理勘探 , 49 (6) : 1138–1146. | |
| 宗兆云, 印兴耀, 吴国忱. 2012a. 基于叠前地震纵横波模量直接反演的流体检测方法. 地球物理学报 , 55 (1) : 284–292. DOI:10.6038/j.issn.0001-5733.2012.01.028 | |
| 宗兆云, 印兴耀, 张峰, 等. 2012b. 杨氏模量和泊松比反射系数近似方程及叠前地震反演. 地球物理学报 , 55 (11) : 3786–3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 | |
| 宗兆云. 2013.基于模型驱动的叠前地震反演方法研究[博士论文].青岛:中国石油大学(华东). | |
 2016, Vol. 59
2016, Vol. 59

