共成像点道集(Common-Imaging Gathers, CIGs)不仅反映偏移速度、正演算法和散射模型的准确性，还反映地下介质的各向异性、AVO和AVA等特征，是偏移技术从构造成像走向波阻抗反演的一个关键环节.受波场多传播路径的影响，叠前深度偏移方法产生的CIGs按照地表记录属性(如共方位角、共偏移距等)进行排序很容易出现偏移假象，降低CIGs的质量.而利用角度域成像条件得到的角度域共成像点道集(Angle-Domain Common-Imaging Gathers, ADCIGs)不受波场多传播路径的影响，是信噪比比较高的CIGs(Xu et al., 2001).

基于ADCIGs的速度分析方法和AVA分析方法已经存在丰富的理论和应用成果(Jin and Madariaga, 1993; Symes, 1993; Beydoun et al., 1993; Liu and Bleistein, 1995; Tura et al., 1998; Dong and Ponton, 1999; Chauris et al., 2002).角度域成像条件大致可以分为以下几种方法：局部平面波分解方法(Xie and Wu, 2002; Yan and Xie, 2009; Xu et al., 2011)；Poynting矢量方法(Yoon and Marfurt, 2006; Vyas et al., 2011a, 2011b; Dickens and Winbow, 2011; Yoon et al., 2011)；扩展成像道集转化方法(Sava and Fomel, 2003, 2006; Fomel, 2004).其中局部平面波分解方法和Poynting矢量方法通过计算波矢量方向将偏移结果投影到对应的ADCIGs上，属于直接方法.扩展成像道集转化方法先用扩展成像条件得到扩展成像道集，然后再用线性Radon变换将扩展成像道集转化为ADCIGs，属于间接方法.

局部平面波分解方法在频率空间域中对波场进行平面波分解并生成角度域成像道集，包括单程波方法和双程波方法.其中单程波方法在频率空间域中沿深度方向对波场进行外推并对波场做局部平面波分解，利用得到的局部平面波进行成像并提取ADCIGs(Xie and Wu, 2002; Soubaras, 2003; Yan and Xie, 2009).双程波方法通过记录所有时刻的正演波场，然后用Fourier变换将时间空间域的波场变换为频率空间域的波场，在频率空间域中实现局部平面波分解和角度域成像条件并提取ADCIGs(Xu et al., 2011).在双程波方法中，为了实现时间域的Fourier变换，需要记录所有时刻的震源波场和检波点波场并以时间为快维对波场重新排序.该重排序操作会增加大量的数据读写操作.

Poynting矢量方法在波场的正演过程中先用Poynting矢量计算波矢量方向，然后用波矢量方向判断波场的传播方向并实现角度域成像条件，生成ADCIGs.Poynting矢量是目前常用的波矢量计算方法，利用Poynting矢量可以快速得到波矢量方向并实现角度域成像条件(Yoon and Marfurt, 2006; Vyas et al., 2011a, 2011b; Dickens and Winbow, 2011; Yoon et al., 2011).但Poynting矢量得到的是波场的能流方向.当波场的波前存在交叉情况时，Poynting矢量无法区分沿不同方向传播的波前，得到的矢量方向实际上是所有波前叠加后的能流方向.因此，Poynting矢量方法在计算复杂波场的波矢量方向时具有一定的局限性.另外，Poynting矢量方法是一种抗噪能力比较差的波矢量方向计算方法.在计算检波点波场的波矢量方向时，Poynting矢量方法会因为地震数据中的噪音而得不到准确的波矢量方向.

扩展成像道集转化方法先用扩展成像条件得到局部偏移距道集或时延相关道集，然后再用线性Radon变换将该扩展成像道集转化为ADCIGs(Sava and Fomel, 2003, 2006; Fomel, 2004).在二维情况下，时延相关道集和局部偏移距道集都可以较为简单地转化为ADCIGs.但在三维情况下，时延相关道集是一个四维数据体(空间的x、y、z坐标和时延量τ)，在转化为五维的ADCIGs(空间的x、y、z坐标，入射角Φ和方位角φ)时会损失部分信息.而局部偏移距道集与ADCIGs之间的关系在三维情况下会变得很复杂，大大增加转化过程所需要的计算量，降低该方法的计算效率.另外，将扩展成像道集从局部偏移距域(或时延量)投影到角度域时还存在采样不足、采样不均匀等现象，这些现象都会降低ADCIGs的质量，影响正确的AVA特征.

在上述的几种方法中，局部平面波分解方法和Poynting矢量方法的物理意义更明确，得到的ADCIGs的物理含义更清楚.这两种方法均需要计算局部波场的传播方向.其中局部平面波分解方法得到的波矢量方向信息更丰富、更准确，但需要更多的计算量和数据读写操作；Poynting矢量方法利用Poynting矢量计算波矢量方向，计算效率高，但抗噪能力和适用范围不及局部平面波分解方法.高效、准确的波矢量方向计算方法和局部平面波分解方法是角度域成像条件两个最重要的研究内容，它们共同决定角度域成像条件的计算效率和ADCIGs的质量.任何一种不准确的波矢量方向计算方法或局部平面波分解方法均会在ADCIGs中产生偏移假象，影响ADCIGs的质量.签于上述原因，本文提出一种用波动方程的柯西条件构造柯西波场的方法，并以柯西波场为基础提出一种高效的波矢量方向计算方法和局部平面波分解方法，提出一种新的角度域成像方法.最后的数值实验证明本文提出的角度域成像方法可以得到高质量的ADCIGs，为下一步的波阻抗反演和AVA分析等研究工作提供了良好的基础.

考虑如下波动方程：

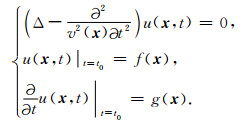
(1)

该方程为波动方程的纯初值问题，描述了声波介质在无外力情况下的波传播现象.由于方程(1)的解取决于方程在t₀时刻的Cauchy条件f(x)和g(x)，因此利用f(x)和g(x)可以得到u(x, t)在t₀时刻的传播方向.假设u(x, t)存在如下的形式表达式：

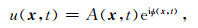
(2)

其中A和Φ分别表示u(x, t)的振幅函数和相位函数.沿时间方向对该形式表达式进行求导可得：

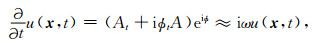
(3)

其中A_t和Φ_t分别表示A和Φ对时间的导数，ω表示波场的频率.在上式推导中，本文假设u(x, t)满足高频假设条件，因此有A_t«AΦ_t.根据波动方程的频散关系可以得到u(x, t)的频率和波数具有如下关系：

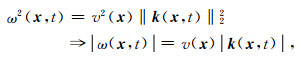
(4)

其中v(x)表示x处的声波速度，k表示波场的波数.结合(3)和(4)得到的结果，用u(x, t)和u_t(x, t)可以构造如下的复值波场c(x, t)：

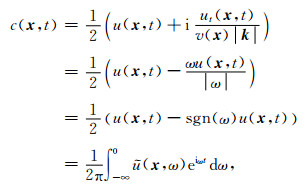
(5)

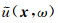
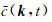
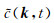
其中表示u(x, t)的时间域Fourier变换结果.从c(x, t)的表达式可知，c(x, t)只包含原波场u(x, t)中的负频率成分，即当ω>0时，c(x, t)=0.假设是c(x, t)的空间域Fourier变换结果，由于c(x, t)只包含原波场的负频率成分，因此可以根据的振幅谱得到准确的波矢量方向：当k_i>0时，波场沿x_i的正方向传播；当k_i < 0时，波场沿x_i的负方向传播.由于复值波场c(x, t)由波动方程的Cauchy条件计算得到，因此本文将c(x, t)称为柯西波场(Cauchy Wave Field, CWF).

方程(5)给出了CWF的构造方法.该方法包含了波数域的微分算子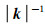，可以利用Fourier变换在波数域中实现该微分算子：

(6)

其中F_x和F_x^-1分别表示沿x方向的正、反Fourier变换.方程(6)即为本文构造CWF的方法.方程(6)可以得到任意时刻的CWF，因此可以在实现成像条件时根据方程(6)构造CWF并计算波矢量方向.由方程(6)可知，构造CWF时只需要计算一次正、反Fourier变换.由于成像条件沿时间方向的采样间隔远小于波场正演时的采样间隔，因此构造CWF所增加的计算量要远小于偏移中正演波场的计算量.

上面介绍的波矢量方向计算方法用波动方程的柯西条件构造一个只含原波场负频率成分的柯西波场c(x, t)，并用c(x, t)在空间域的Fourier变换结果计算波矢量方向.CWF的构造方法利用快速Fourier变换提高其计算效率，并保留了波场所有方向的波矢量信息，可以高效、准确地计算出波场的波矢量方向.

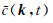
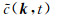
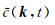
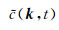
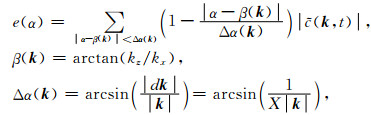
根据前面的分析可知，由方程(6)构造得到的CWF只包含原波场的负频率成分，c(x, t)的空间域Fourier变换结果给出了原波场的波矢量分布情况.因此，可以利用的振幅谱在时间波数域实现原波场的局部平面波分解.为了讨论方便，下面以二维波场的平面波分解为例，得到的结论可以直接推广到三维情况.由于的振幅谱反映了原波场的波矢量方向分布情况，因此可以对的振幅谱做如下的角度分解：

(7)

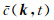
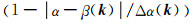
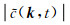
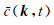
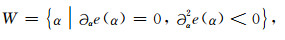
其中β(k)表示波数k对应的角度，Δα(k)表示波数k对应的角度分辨率，X表示波场孔径的大小(这里假设沿x方向和z方向的波场孔径相同)，e(α)表示的振幅谱在角度α方向上的能量.在e(α)的表达式中，加权系数表示β(k)的值越接近α，的权重越大.e(α)给出了的振幅谱在各个角度上的能量分布情况.e(α)的值越大，沿角度α传播的局部平面波的能量越强.根据测不准原理，e(α)同样存在角度分辨率的问题，因此本文用e(α)的极大值点作为有效的波传播方向，并用W表示这些极值点组成的集合：

(8)

集合W给出了波场u(x, t)包含的所有平面波传播角度的集合.

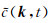
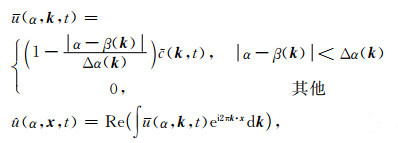
对于给定的传播角度α，本文用下面的公式提取在角度α方向上的投影，实现波场u(x, t)的平面波分解：

(9)

其中表示在角度α方向上的投影，表示u(α, k, t)的反Fourier变换结果，表示波场u(x, t)中沿角度α传播的平面波，其中β(k)和Δα(k)的定义由公式(7)式给出.

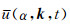
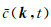
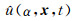
公式(9)即为本文在实现角度域成像条件时所采用的局部平面波分解方法.该方法最大的优点是计算复杂度小、计算成本低，保证实现角度域成像条件的计算效率.利用集合W和平面波分解方法(9)，可以将原波场u(x, t)分解为一系列沿不同角度传播的平面波之和：

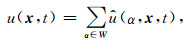
(10)

其中W和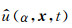的定义分别由(8)和(9)式给出.局部平面波是实现角域成像条件的基本单位，局部平面波的分解效率直接决定了实现角度域成像条件的计算效率.

波矢量方向的计算和波场的局部平面波分解是实现角度域成像条件的两个关键环节.这两个环节即决定实现角度域成像条件的计算效率，也决定最终生成的ADCIGs的质量.利用CWF本文可以高效地得到波矢量方向、实现波场的平面波分解，总波场则可以表示为这些平面波的叠加结果.将波场的平面波表达形式(10)代入到单炮叠前偏移公式可得

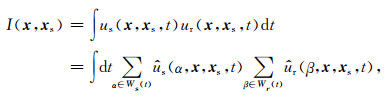
(11)

其中u_s(x, x_s, t)和u_r(x, x_s, t)分别表示第x_s炮的震源波场和检波点波场，I(x, x_s)表示第x_s炮的成像结果.由于总波场的波前并不满足平面波假设条件，因此，在成像过程中需要用局部空间窗对总波场进行分解，使得窗内的波场满足平面波假设条件，然后再在局部窗内实现成像条件，即

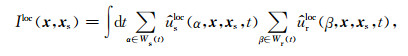
(12)

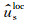
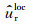
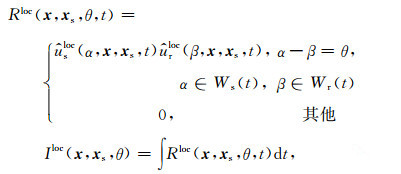
其中I^loc表示局部空间窗内的成像结果，和分别表示炮点和检波点端的局部平面波，W_s(t)和W_r(t)分别表示t时刻的震源波场和检波点波场在局部空间窗内包含的平面波传播角度的集合.用(12)式得到的I^loc是所有角度的平面波相关成像后的叠加结果，未对成像结果进行角度分选.为了得到ADCIGs需要对集合W_s(t)和W_r(t)内的所有角度进行循环，然后将不同角度平面波的相关成像结果投影到对应的ADCIGs上，即

(13)

其中θ表示入射波与反射波之间的张角，R^loc(x, x_s, θ, t)表示t时刻在张角θ上的成像结果，I^loc(x, x_s, θ)表示第x_s炮在局部窗内得到的ADCIGs.由于计算R^loc(x, x_s, θ, t)需要对W_s(t)和W_r(t)内的所有角度进行循环，因此波场越复杂、局部平面波的个数越多，R^loc(x, x_s, θ, t)的计算成本越高.

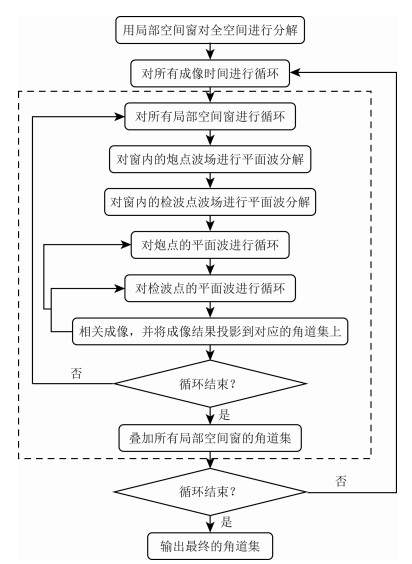
公式(13)给出了角度域成像条件的计算方法，利用该公式可以得到波场在任意局部空间窗内的ADCIGs，将所有局部空间窗内的成像结果叠加后即可得到全空间的ADCIGs.图 1展示了角度域成像条件的实现流程，在该实现流程中虚框内的计算过程是角度域成像条件与常规零延迟相关成像条件的主要区别.

图 1

Fig. 1

图 1 基于炮道集的角度域成像条件 Fig. 1 The angle domain imaging condition of shot domain migration

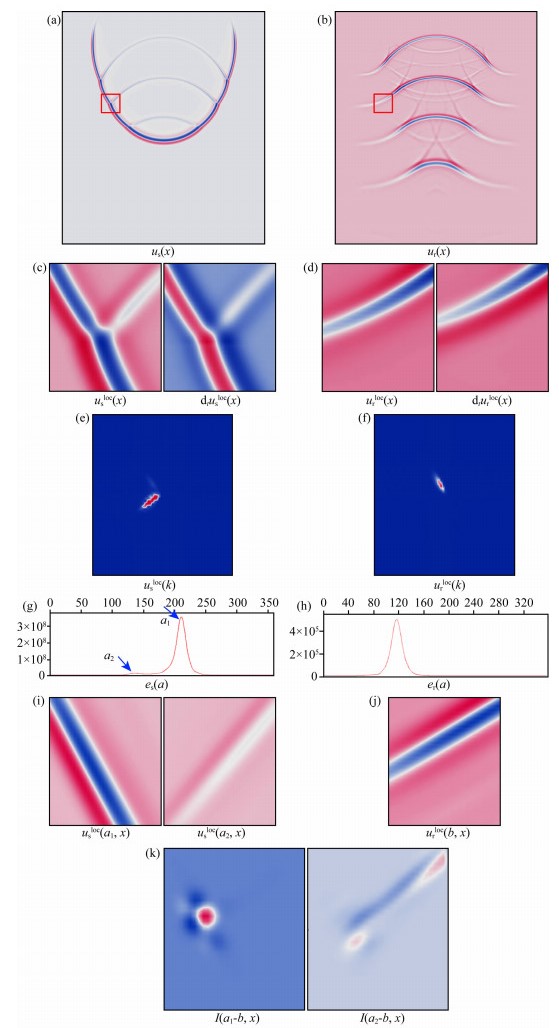
图 2用一个数值实验说明角度域成像条件的实现过程，该数值实验的速度模型为水平层状模型.图 2a和图 2b分别是某一时刻的震源波场和检波点波场.在角度域成像条件中，为了使波前满足平面波假设条件，需要用局部空间窗对全空间进行分解，使得波前在每个局部空间窗内都满足平面波假设条件.图 2c和图 2d分别是图 2a和图 2b所示的局部空间窗内的波场以及波场对时间的一阶导.根据CWF的构造方法(6)，本文可以用图 2c和图 2d所示的波场合成柯西波场c_s^loc(x, t)和c_r^loc(x, t).图 2e和图 2f分别是柯西波场c_s^loc(x, t)和c_r^loc(x, t)的空间域Fourier变换结果所对应的振幅谱，该振幅谱准确地给出了波场的传播方向.用图 2e和图 2f所示的振幅谱，可以根据公式(7)对振幅谱内的能量分布进行角度投影，图 2g和图 2h分别是图 2e和图 2f的角度投影结果.从图 2g和图 2h可知，e_s(α)包含两个极值点，表示震源波场包含两个平面波；e_r(α)只有一个极值点，表示检波点波场只包含一个平面波.利用图 2g和图 2h的结果，根据公式(9)可以得到炮点端和检波点端的平面波波场.图 2i和图 2j分别是根据图 2g和图 2h的角度投影结果得到的平面波分解结果，其中震源波场包含两个平面波，检波点波场包含一个平面波.利用图 2i和图 2j得到的平面波分解结果，根据公式(13)即可得到该局部空间窗内不同张角的成像结果.图 2k是用公式(13)得到的成像结果，其中I(α₁-b, x)表示入射波与反射波的相关结果，是偏移过程中的有效信号；I(α₂-b, x)表示反射波与反射波的相关结果，是常规RTM成像结果中的低频噪音.

图 2

Fig. 2

图 2 角度域成像条件实现流程示意图 (a、b)某一时刻炮点端和检波点端的波场快照；(c、d)该时刻图a、b红框内的波场以及波场对时间的一阶导数；(e、f)由图c、d构造得到的柯西波场所对应的振幅谱；(g、h)振幅谱e、f在角度域的能量分布函数，横坐标表示角度，单位°，纵坐标表示能量大小；(i、j)局部平面波分解结果；(k)局部平面波的成像结果. Fig. 2 The realization flow of angle domain imaging condition (a、b) Snapshots of source wave field and receiver wave field; (c、d) Local wave field and its derivative with respect to time in the red rectangles of figure 2a and 2b; (e、f) Spectrum of Cauchy Wave Field constructed from Cauchy condition shown in figure 2c and 2d; (g、h) Energy distribution function of Cauchy Wave Field in angle domain, the axises mean energy and angle respectively; (i、j) Local plane wave decomposition result; (k) Imaging result of local plane waves shown in figure 2i and 2j.

用本文提出的角度域成像条件分别计算水平层状模型和Marmousi模型的ADCIGs.这两个数值实验证明了本文提出的角度域成像方法可以准确地获得复杂模型的ADCIGs，是一种适用性比较强的成像方法.

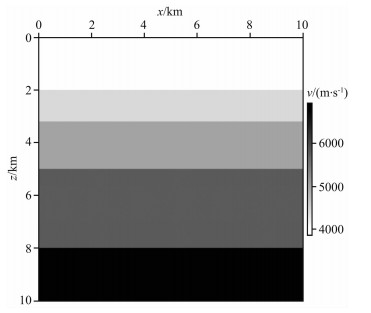
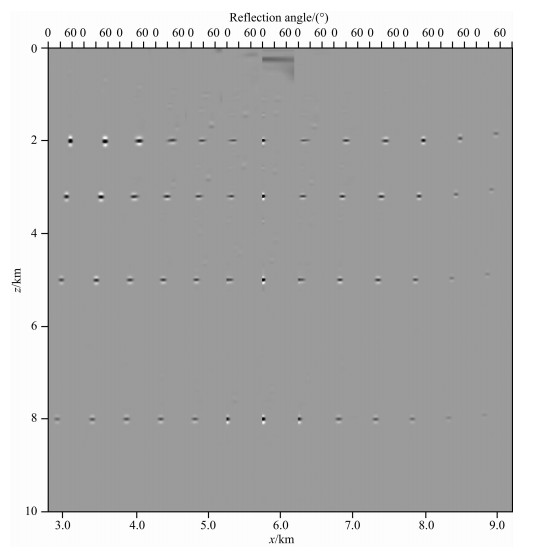
首先用一个水平层状模型测试本文提出的角度域成像方法.图 3展示了一个水平层状速度模型，该模型的观测系统如下：炮点间隔100 m，检波点间隔20 m；炮点范围从地表x=0 km到x=10 km；每一炮的接收排列均从地表x=0 km到x=10 km.图 4为x_s=6 km处的单炮数据得到的不同地表位置的ADCIGs，其中横坐标的快维表示ADCIGs对应的反射角，慢维表示ADCIGs对应的地表位置.在图 4中，位于炮点正下方的ADCIGs的能量集中在0°的位置，表示该炮对炮点正下方的照明能量主要集中在入射角为0°的位置.随着地表偏移距的增加，该炮对地下层位照明的入射角越来越大.图 4所示的ADCIGs准确地反映了该炮对地下层位的角度照明情况，为后续AVA分析和角度照明分析等研究工作提供了重要基础.

图 3

Fig. 3

图 3 水平层状速度模型 Fig. 3 The layer velocity model

图 4

Fig. 4

图 4 单炮数据的ADCIGs，炮点位置位于xs=6 km处 Fig. 4 The ADCIGs of single shot gather, the position of source is xs=6 km

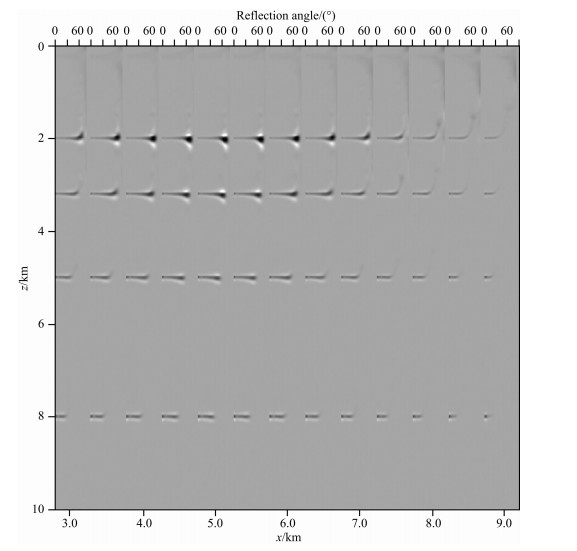
图 5展示了用所有炮数据生成的ADCIGs.在图 5中，浅层界面的角度照明比较均衡，除了边界处的ADCIGs受观测系统的影响外，其他地方的ADCIGs基本达到全角度照明.在生成的ADCIGs中，小角度的照明能量对应着地震波的反射现象，是成像中的有效能量；大角度的照明能量对应着地震波的全反射现象，是成像中的噪音部分，这部分能量会降低最后成像结果的分辨率.受地表观测孔径和速度模型的影响，模型深层界面的照明角度主要集中在小反射角范围内，数据对界面的照明情况基本表现为：界面的深度越深，有效照明角度的范围越小，照明角度的采样间隔越小.

图 5

Fig. 5

图 5 所有炮数据得到的ADCIGs Fig. 5 The ADCIGs generated by all shot gathers

图 6展示的是不同入射角范围的ADCIGs的叠加结果.图 6所示的偏移结果与地下构造的实际角度照明情况一致(如图 6(a—e)中第一个反射界面的照明情况所示)，进一步证明本文提出的角度域成像方法具有较高的角度分辨率，可以准确地得到地下界面的角度照明情况，生成高质量的ADCIGs.成像中的有效信号(入射波与反射波的相关结果)主要集中在ADCIGs的中、小入射角范围内，ADCIGs的大入射角的能量多为炮点的反射波、折射波与检波点的反射波相关后的结果，是成像中的低频噪音部分.因此，用ADCIGs的中、小入射角范围内的数据进行叠加即可得到最终的偏移结果.图 6f展示了入射角范围为0~50°的ADCIGs的叠加结果，该图即为最终的偏移结果.

图 6

Fig. 6

图 6 不同入射角范围的ADCIGs的叠加结果 (a)入射角为0°~10°；(b)入射角为10°~20°；(c)入射角为20°~30°；(d)入射角为30°~40°；(e)入射角为40°~50°；(f)入射角为0°~50°. Fig. 6 The stack results of ADCIGs with different incident angle (IA) (a) From 0 to 10 degree; (b) From 10 to 20 degree; (c) From 20 to 30 degree; (d) From 30 to 40 degree; (e) From 40 to 50 degree; (f) From 0 to 50 degree.

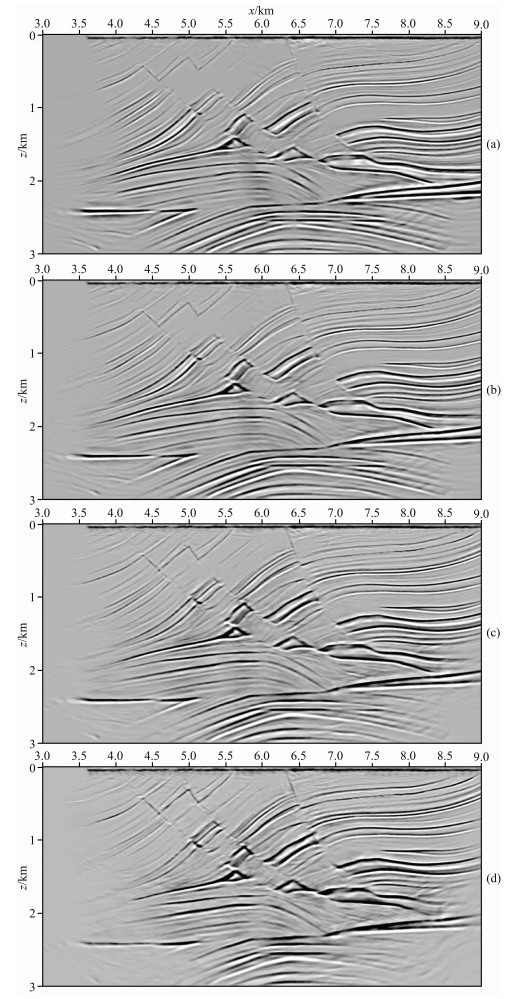
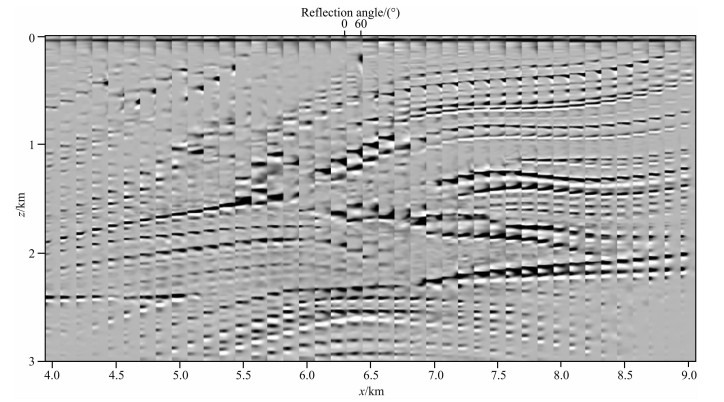
用本文的角度域成像方法计算Marmousi模型的ADCIGs.为了改善地下构造的角度照明情况，这里设计了如下观测系统：炮点间隔100 m，检波点间隔25 m；炮点范围从地表x=3.6 km到x=9.0 km；每一炮的接收排列均从地表x=3.0 km到x=9.0 km.根据前面分析得到的结论可知，ADCIGs的中、小入射角范围内的能量是成像中的有效信号成分，大入射角的能量是成像中的低频噪音成分.因此，在成像过程中本文只生成中、小入射角范围的ADCIGs.图 7(a—d)分别展示了入射角范围为0~10°、10~20°、20~30°和30~40°的ADCIGs的叠加结果.图 8是所有入射角(0~45°)的ADCIGs的叠加结果，图 9是不同地表位置的ADCIGs，ADCIGs的入射角范围为0~60°.图 7、图 8和图 9证明了本文提出的角度域成像条件可以准确地获得地下构造的角度照明情况，生成高质量的ADCIGs.

图 7

Fig. 7

图 7 不同入射角范围的ADCIGs的叠加结果 (a)入射角为0°~10°；(b)入射角为10°~20°；(c)入射角为20°~30°；(d)入射角为30°~40°. Fig. 7 The stack results of ADCIGs with different incident angle (IA) (a) From 0 to 10 degree; (b) From 10 to 20 degree; (c) From 20 to 30 degree; (d) From 30 to 40 degree.

图 8

Fig. 8

图 8 入射角为0°~45°的ADCIGs的叠加结果 Fig. 8 The stack result of ADCIGs with IA from 0 to 45 degree

图 9

Fig. 9

图 9 不同地表位置的ADCIGs(最大入射角为60°) Fig. 9 The ADCIGs of different place (the maximum incident angle is 60 degree)

波矢量方向计算和局部平面波分解是角度域成像条件的两个核心内容.本文提出一种利用波动方程的柯西条件构造柯西波场(CWF)的方法，并以CWF为基础实现波矢量方向计算和局部平面波分解，从而实现角度域成像条件并生成ADCIGs.CWF是根据波动方程的柯西条件构造的只含原波场负频率成分的复值波场，因此可以根据CWF在波数域的振幅谱计算波矢量方向.另外，本文还提出一种以CWF为基础的局部平面波快速分解方法.该方法根据CWF在角度域的能量分布情况设计相应的角度滤波器，并用该滤波器实现局部平面波的快速分解，保证实现角度域成像条件的计算效率.根据测不准原理，局部平面波的角度分辨率主要受局部空间窗的孔径和波前的曲率影响，而局部平面波的角度分辨率将决定生成的ADCIGs的角度分辨率.在本文提出的角度域成像方法中，CWF是最核心的内容，它是本文计算波矢量方向和实现局部平面波分解的基础.本文提出的CWF构造方法以快速Fourier变换为基础，具有较高的计算效率，保证了该方法的实用性.本文相关的数值实验证明本文提出的角度域成像条件可以生成高质量的ADCIGs.