2. 中国科学院大学, 北京 100049;
3. 宇航动力学国家重点实验室, 西安 710043
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. State Key Laboratory of Astronautic Dynamics, Xi'an 710043, China
对于低轨道航天器而言,大气密度产生的阻力摄动是影响卫星轨道的重要因素之一.大气密度预报模型的准确程度对低轨道航天器的精密定轨、轨道预报、变轨控制、寿命预测、飞船返回控制,及空间碎片的碰撞规避等方面均具有重要意义.计算表明,若大气密度模型存在10%的误差,神舟八号飞船轨道位置20天后的预报偏差将达800 km以上(刘舒莳,2014).随着中国载人航天工程的深入开展,航天操作越来越复杂,工程要求越来越高,这对大气密度预报精度也提出了更高要求.
从20世纪50年代后期开始,随着导弹和航天活动对各种高层大气模型的不断要求,发展了多种半经验的高层大气模型,形成了CIRA系列(Kallmann-Bijl et al., 1961)、Jacchia系列(Jacchia,1970)、DTM系列(Berger et al., 1998;Bruinsma et al., 2003)、MSIS系列(Hedin, 1987, 1991;Picone et al., 2002)等各种参考大气模型,为空间活动提供服务.由于高层大气的变化极其复杂,虽然几十年来大气模型在不断地改进和发展,但一般情况下,模型仍存在15%~30%左右的误差(Marcos et al., 1994;Rhoden et al., 2000).因此,如何进一步提高大气模型的预报精度成为模型研究者一直致力解决的问题.改进大气模型预报精度主要有两种方式:一是建立新模型,增加新的控制变量或采用新的拟合函数,如Bowman(2006;2008a, 2008b)采用新的太阳辐射指数和地磁指数建立了JB2006和JB2008模型、Lei等(2012)基于新自然正交函数分析法建立了400km高度大气密度变化特征模型;二是在原有模型的基础上进行修正,如美国空军空间指挥中心的HASDM计划(Storz and Bowman, 2005)、苗娟和刘四清(2001)开展的基于监测数据的大气密度模型实时修正.但无论哪种改进方法,其基础都是要获取大量准确的大气密度数据.
虽然当前已发射运行的卫星众多,但直接用于大气密度探测的还比较匮乏.除了国际公开的CHAMP、GRACE(A,B)热层密度数据外,目前公开渠道可获取的热层大气密度数据较少.在大量卫星两行轨道根数(TLEs)的基础上,Picone等(2006)提出了一种从TLEs数据快速得到大气密度的方法,Lean等(2006)将该方法应用于Starshine卫星,Emmert等(2004, 2008, 2009)及任廷领等(2014)使用该方法研究大气密度的长期变化.但从北美防控司令部(NORAD)公开的TLEs监测数据来看,数据点比较稀疏,每天约1~4个监测时间点,这在一定程度上制约了所提取密度的精度,而星载高精度GPS观测数据可以弥补这一缺点.本文以天宫一号上搭载的GPS观测数据为例,开展利用高精度GPS观测数据的大气密度反演,为后期载人轨道大气密度模型预报精度的改善提供数据基础,为今后获取高精度大气密度提供一种新方法.
2 基本原理和方法热层大气虽然很稀薄,但相对于高速运行的航天器而言,产生的阻力不可小视,阻力会使航天器动能减少,导致高度下降,轨道收缩,发生轨道衰变.
卫星在大气中运动,所受阻力F为
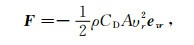
|
(1) |
其中,CD为阻力系数;A为卫星的迎风面积;υr=|υ-V|表示卫星相对于大气的速度大小;eυr表示υr方向上的单位向量.因此大气阻力产生的加速度为

|
(2) |
其中,B=CDA/m,为卫星的反弹道系数,m为卫星质量.组成该系数的三个量CD,A,m在卫星运行过程中都是变化的,尤其是阻力系数CD,它不仅与卫星的运行姿态、卫星表面的物理性质有关,还与大气组成成分等因素有关(Cook,1965),从而导致B非常难以确定.
大气阻力对卫星的影响主要表现在平均平动参数nM的变化上.卫星轨道在大气阻力的影响下逐渐衰减,使轨道半长轴a逐渐减小,平均平动nM逐渐增大.在消去地球的非球形引力摄动影响后,卫星的半长轴在大气阻力下的变化规律可用公式(3)表示(King-Hele,1987):
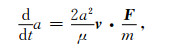
|
(3) |
其中,μ=GME,为万有引力常数与地球质量的乘积.
根据平均平动参数和半长轴的变化关系nM=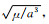
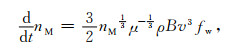
|
(4) |
其中,fw为无量纲参数,表示风因素的影响,可近似为
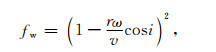
|
(5) |
其中,r为卫星的地心距,ω=7.292×10-5rad·s-1为地球自转角速度,i为卫星轨道倾角.与利用水平风场模型HWM-93的计算值相比,该近似所产生的误差小于3%(Hedin,1996),而且在对(5)式积分过程中,二者之间的偏差会减小,因此(5)式是对fw很好的近似.
对(4)式沿卫星轨道积分,即可得到有效密度ρGPS如下:
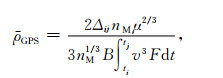
|
(6) |
其中,nM=(nM(ti)+nM(tj))/2,ΔijnM=nM(tj)-nM(ti),该有效密度值由GPS观测数据得到,完全不依赖于已有的经验大气模型.为了将有效密度和模型值进行对比,同样对经验大气模型进行处理,得到模型的有效密度ρM如下:
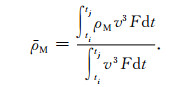
|
(7) |
从有效密度计算可以看出,ρGPS与积分的时间段相关,无法体现具体位置、具体时间点的变化.为求某一位置在某一时刻的密度ρ(r, t),首先引入一个经验大气模型.假设大气密度模型值与真实值之间的关系为ρ(r, t)=λρM(r, t),λ代入公式(4)并进行积分,则可得:
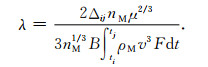
|
(8) |
得到λ后,即可得卫星相应位置上的大气密度.
3 大气密度反演过程与结果 3.1 平均平动nM的计算在利用卫星轨道参数反演大气密度过程中,平均平动nM是至关重要的参数,它消除了地球非球形引力和大气阻力的周期项摄动及其他摄动力的影响,反映了卫星轨道在大气阻力摄动影响下的长期变化.在没有人为进行轨道制动及其他特殊情况下,nM随时间递增,这就保证了公式(4)式两侧均为正值,从而确保所求的大气密度为正值.
需要注意的是,由星载高精度GPS观测数据通过初轨计算可以很容易地求出轨道的瞬时半长轴a,然后再求得瞬时平动n,但该值并不能用来替代nM.虽然二者相差很小,但表示的物理含义却大不相同.瞬时平动n包含了地球非球形引力和大气阻力的周期项摄动影响以及其他摄动力的影响,无法直接体现出大气阻力的影响,并且在积分区间内可能产生随时间减小的情况,因此需要把瞬时值n换算到平均平动nM,具体方法如下:
首先利用高精度GPS观测数据计算出惯性系下卫星的位置矢量r和速度矢量v,通过初轨计算得到轨道的瞬时六根数,包括倾角i,升交点赤经Ω,离心率e,近地点角距ω,平近点角M,瞬时平动n;其次再将六根数转换为可迭代计算的参数形式,转换过程不考虑大气模型的影响;最后采用公式(9),经过反复迭代,将轨道瞬时值转换为平均值:
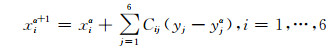
|
(9) |
其中,y表示卫星态函数y(r, v);x表示所求的6个轨道根数;Cij=Z-1,Z满足矩阵(10);f表示SGP4模型.
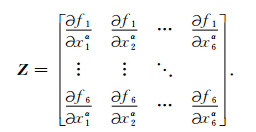
|
(10) |
将收敛精度设置为10-10,即可利用迭代法由态函数y(r, v)求出卫星的平均轨道根数.以北美防空联合司令部给出的Explore 8卫星为例,选取2000年历元为1.19565055时刻,将该时刻的轨道数据代入SGP4模型中,可得态矢量,然后将该态矢量用上述方法进行迭代,可得平均轨道根数,具体参数见表 1,由表可知,采用迭代法计算所得的6个轨道根数与NORAD公布结果一致,满足本文的精度需求,本文用此方法来计算平均轨道根数.
|
|
表 1 NORAD所给轨道参数与迭代法得到参数误差比较 Table 1 Comparison of errors between iteration method and orbit parameters from NORAD |
除了平均平动nM之外,在利用上述方法反演大气密度的过程中,反弹道系数B(B=CDA/m)是另一个非常重要的参数,它的精度决定着所求大气密度的精度.CD和A是随卫星的运动变化的,CD不仅与卫星的运行姿态和表面的物理性质有关,还受大气组成及状态的影响.因此很难确定,但是可以通过计算求出一段时间内的平均值,该值可近似认为是真实值.
Bowman等(2002)通过计算31年的卫星数据,将所得反弹道系数进行平均,得到一个非常精确的观测值.但是该方法需要一个高精度的经验大气模型,而实际上,大气密度随时间在变化,阻力系数CD也会随近地点高度的变化而变化,这就使所得B值偏离真实值.在本文中,采用Emmert等(2006)的公式,并使用另一种计算方式求解B值.
假设B的真实值在所研究的时间范围内保持不变,且近地点高度相似的两颗卫星B值的修正量一致.如果存在一颗参考卫星,其反弹道系数BsT已知,经验大气模型对应的BM可由(11)求得,那么待求卫星的反弹道系数BxT可由方程(12)计算得到:
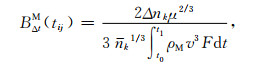
|
(11) |

|
(12) |
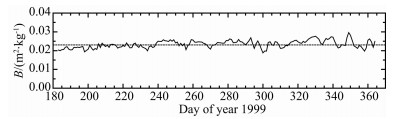
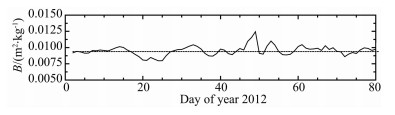
本文选择Starshine I为参考卫星,该卫星是开展高层大气阻力对低轨道目标拖曳影响的教学卫星,属于低轨卫星.由于Starshine I卫星外形为球形,运行过程中具有确定的面值比,其阻力系数由Bowman等(2002)通过分析卫星轨道的衰减给出,所以该卫星具有确定的反弹道系数BsT,可作为参考卫星.通过(11)式得到同时间段内的BxM、BsM后,即可由(12)式计算得到该时间内的BxT值.以Explorer 8卫星为例,选取时间段1999年7月1日至1999年12月31日,计算得到Explorer 8卫星1999年的BxT值随时间变化(见图 1),对其求平均可得B为0.02301 m2·kg-1,该值与Emmert等(2006)计算的结果(0.02315)偏差仅为-0.6%,因此该方法所得B值满足精度要求.同理,本文应用此方法计算得到2012年天宫一号的反弹道系数的变化(见图 2),得到此段时间内的平均值为0.00939 m2·kg-1.
|
图 1 1999年Explore 8反弹道系数变化 Fig. 1 Variation of B value for Explorer 8 in 1999 |
|
图 2 2012年天宫一号反弹道系数变化 Fig. 2 Variation of B value for Tiangong-1 in 2012 |
天宫一号是我国第一个目标飞行器和空间实验室,于2011年9月29日发射,分别于2011年11月3日、2012年6月18日、2013年6月13日与神舟八号、神舟九号和神舟十号成功对接.在飞行任务期间,经过多次姿态和轨道调控.图 3给出了天宫一号在2012年轨道高度的变化情况,可以看到在任务过程中进行了4次调轨.在密度反演过程中,为避免轨道高度突然变化所导致的密度反演异常情况,需选择一段轨道相对平稳的时间段.本文选择2012年1—3月自主飞行时间段,开展高精度GPS观测数据反演大气密度研究,其中平均平动nM采用本文计算方法获得,反弹道系数B值采用3.2节中计算得到的0.00939 m2·kg-1.

|
图 3 2012年天宫一号轨道变化 Fig. 3 Variation of Tiangong-1 orbit in 2012 |
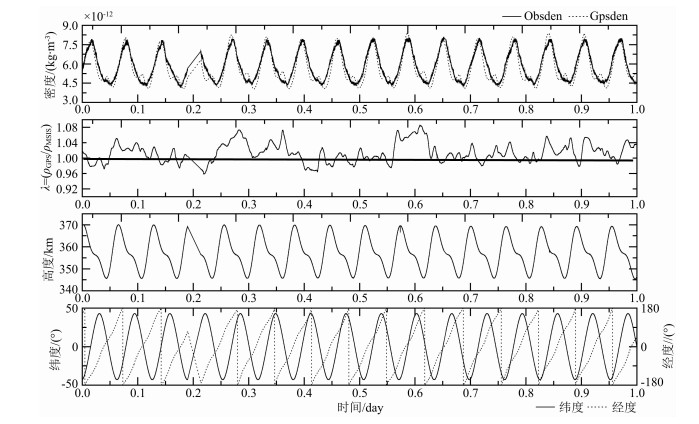
天宫一号搭载有大气密度探测器,天宫一号飞行姿态的变化,使探测器的探测效果受到影响,在三轴稳定对地期间,数据观测质量最好.为了进行反演结果与探测结果比对,本文选择2012年1月1—12日和2月23日—3月4日两个三轴稳定时间段,采用文中的密度反演方法,利用天宫一号的高精度GPS观测数据反演大气密度.图 4、图 5分别给出了2012年1月1日、2月24日的反演结果,包括反演密度和探测值的比较,反演密度/模型密度,卫星高度、纬度和经度的变化,数据时间间隔为2s.图 4中,由于2012年1月1日09:56:02—11:37:00GPS观测数据的缺失,密度值、λ(ρGPS/ρMSIS)、高度、经度、纬度出现了跳跃.

|
图 4 2012年1月1日GSP观测数据反演得到的大气密度与天宫一号密度测量值比较 Fig. 4 Comparisons between GPS-derived density and observed density on 1 January in 2012 |
|
图 5 2012年2月24日GPS观测数据反演得到的大气密度与天宫一号密度测量值比较 Fig. 5 Comparisons between GPS-derived density and observed density on 24 February in 2012 |
从图 4、图 5中的对比结果可以看到,基于GPS观测数据反演的大气密度(Gpsden表示)与探测结果(Obsden表示)均符合很好,通过误差计算,1月1日、2月24日的反演密度与探测值之间的均方差分别为8.6%和8.4%,远小于大气模型的平均误差.自主运行期间,受大气密度拖曳的影响,1月1日天宫一号高度处于357~380 km范围内,2月24日天宫一号高度下降至345~370 km.通过图 4、图 5中λ的变化,可以看到基于GPS观测数据反演的大气密度与模型计算结果的比值在1上下波动,这也从另一个方面验证了反演结果的合理性.λ > 1时,说明天宫一号所在位置的当地密度要高于模型计算值,λ < 1则反之.
4 结论与讨论无论研究大气密度的变化规律,还是提高大气模型的预报精度,其基础首先是要有大量准确的密度数据.在目前大气密度直接探测数据相对匮乏的情况下,利用星载高精度GPS观测数据反演大气密度,可以为今后获取高精度大气密度数据提供一种新途径.本文以天宫一号为例,开展利用高精度GPS观测数据反演大气密度研究,结论如下:
(1)利用GPS观测数据反演大气密度过程中,平运动nM是至关重要的参数,本文利用迭代法得到高精度的平均轨道根数,其中倾角i、升交点赤经Ω、离心率e、近地点角距ω、平近点角M与NORAD公布数据一致,平均平运动nM的误差 < 10-7.
(2)基于近地点高度相似的两颗卫星其B值修正量一致的假设,以Starshine I作为参考卫星,计算得到1999年7—12月Explorer 8的反弹道系数与Emmert等的结果一致,天宫一号2012年1—3月的反弹道系数为0.00939 m2·kg-1.
(3)通过2012年1月1日、2月24日的反演大气密度与观测结果的比较,可以看到,利用天宫一号的GPS观测数据反演得到的大气密度与观测值符合很好,反演密度与观测值之间的均方差分别为8.6%和8.4%,说明利用GPS观测数据反演大气密度是有效、可行的,可成为今后获取高精度大气密度的一种新途径.
本文仅以天宫一号为例开展了大气密度反演验证.下一步,将针对多颗卫星的GPS观测数据,评估和分析不同太阳活动和地磁条件下的大气密度反演结果.
致谢感谢审稿专家对本文提出的宝贵建议.
| Berger C, Biancale R, Ill M, et al. 1998. Improvement of the empirical thermospheric model DTM:DTM94-a comparative review of various temporal variations and prospects in space geodesy applications. J. Geod. , 72 (3) : 161-178. DOI:10.1007/s001900050158 | |
| Bowman B R. 2002. True satellite ballistic coefficient determination for HASDM.//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. California, Monterey:AIAA, AAS. | |
| Bowman B R. 2006. A new empirical thermospheric density model JB2006 using new solar indices.//AIAA/AAS Astrodynamics Specialist Conference and Exhibit 21-24 August 2006. Keystone, Colorado:AIAA, AAS. | |
| Bowman B R, Tobiska W K, Marcos F A, et al. 2008. The JB2006 empirical thermospheric density model. J. Atmos. Solar-Terr. Phys. , 70 (5) : 774-793. DOI:10.1016/j.jastp.2007.10.002 | |
| Bowman B R. 2008. A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices.//AIAA/AAS Astrodynamics Specialist Conference 18-21 August 2008. Honolulu, Hawaii:AIAA/AAS. | |
| Bruinsma S, Thuillier G, Barlier F. 2003. The DTM-2000 empirical thermosphere model with new data assimilation and constraints at lower boundary:Accuracy and properties. J. Atmos. Solar-Terr. Phys. , 65 (9) : 1053-1070. DOI:10.1016/S1364-6826(03)00137-8 | |
| Cook G E. 1965. Satellite drag coefficients. Planet. Space Sci. , 13 (10) : 926-964. | |
| Emmert J T, Picone J M, Lean J L, et al. 2004. Global change in the thermosphere:Compelling evidence of a secular decrease in density. J. Geophys. Res. , 109 (A2) : A02301. DOI:10.1029/2003JA010176 | |
| Emmert J T, Meier R R, Picone J M, et al. 2006. Thermospheric density 2002-2004:TIMED/GUVI dayside limb observations and satellite drag. J. Geophys. Res. , 111 (A10) : A10S16. DOI:10.1029/2005JA011495 | |
| Emmert J T, Picone J M, Meier R R. 2008. Thermospheric global average density trends, 1967-2007, derived from orbits of 5000 near-Earth objects. Geophys. Res. Lett. , 35 (5) : L05101. DOI:10.1029/2007GL032809 | |
| Emmert J T. 2009. A long-term data set of globally averaged thermospheric total mass density. J. Geophys. Res. , 114 (A6) : A06315. DOI:10.1029/2009JA014102 | |
| Hedin A E. 1987. MSIS-86 thermospheric model. J. Geophys. Res. , 92 (A5) : 4649-4662. DOI:10.1029/JA092iA05p04649 | |
| Hedin A E. 1991. Extension of the MSIS thermosphere model into the middle and lower atmosphere. J. Geophys. Res. , 96 (A2) : 1159-1172. DOI:10.1029/90JA02125 | |
| Hedin A E, Fleming E L, Manson A H, et al. 1996. Empirical wind model for the upper, middle and lower atmosphere. J. Atmos. Terr. Phys. , 58 (13) : 1421-1447. DOI:10.1016/0021-9169(95)00122-0 | |
| Jacchia L G. 1970. New static models of the thermosphere and exosphere with empirical temperature profiles. Technical Report 313, Cambridge, MA:Smithsonian Astrophysical Observatory . | |
| Kallmann-Bijl H, Boyd R L F, Lagow H, et al. 1961. CIRA 1961:COSPAR international reference atmosphere 1961. Amsterdam:North-Holland Publishing Company . | |
| King-Hele D. 1987. Satellite Orbits in an Atmosphere:Theory and Application. Glasgow:Blackie and Son Ltd., 291 . | |
| Lean J L, Picone J M, Emmert J T, et al. 2006. Thermospheric densities derived from spacecraft orbits:Application to the Starshine satellites. J. Geophys. Res. , 111 (A4) : A04301. DOI:10.1029/2005JA011399 | |
| Lei J H, Matsuo T, Dou X K, et al. 2012. Annual and semiannual variations of thermospheric density:EOF analysis of CHAMP and GRACE data. J. Geophys. Res. , 117 (A1) : A01310. DOI:10.1029/2011Ja017324 | |
| Liu S H, 2014. The investigation of thermospheric density change during geomagnetic storm and model correction (in Chinese).[Ph.D.thesis] Beijing:University of Chinese Academy Sciences. | |
| Marcos F A, Bass J N, Baker C R, et al. 1994. Neutral density models for aerospace applications.//32nd Aerospace Sciences Meeting and Exhibit. Reno, NY:AIAA. | |
| Miao J, Liu S Q, Li Z T, et al. 2001. Atmospheric density calibration using the real-time satellite observation. Chinese J. Space Sci. , 31 (4) : 459-466. | |
| Picone J M, Hedin A E, Drob D P, et al. 2002. NRLMSISE-00 empirical model of the atmosphere:Statistical comparisons and scientific issues. J. Geophys. Res. , 107 (A12) : SIA 15-SIA 15-16. DOI:10.1029/2002JA009430 | |
| Picone J M, Emmert J T, Lean J L. 2005. Thermospheric densities derived from spacecraft orbits:Accurate processing of two-line element sets. J. Geophys. Res. , 110 (A3) : A03301. DOI:10.1029/2004JA010585 | |
| Ren T L, Miao J, Liu S Q, et al. 2014. Research on thermospheric densities derived from two-line element sets. Chinese J. Space Sci. , 34 (4) : 426-433. | |
| Rhoden E A, Forbes J M, Marcos F A. 2000. The influence of geomagnetic and solar variabilities on lower thermosphere density. J. Atmos. Solar-Terr. Phys. , 62 (1) : 999-1013. | |
| Storz M F, Bowman B R, Branson M J I, et al. 2005. High accuracy satellite drag model (HASDM). Adv. Space Res. , 36 (12) : 2497-2505. DOI:10.1016/j.asr.2004.02.020 | |
| 刘舒莳. 2014.暴时热层大气密度时空分布规律研究及模式修正.[博士论文]北京:中国科学院大学. | |
| 苗娟, 刘四清, 李志涛, 等. 2001. 基于实时观测数据的大气密度模式修正. 空间科学学报 , 31 (4) : 459–466. | |
| 任廷领, 苗娟, 刘四清, 等. 2014. 利用卫星两行轨道根数反演热层密度. 空间科学学报 , 34 (4) : 426–433. | |
 2016, Vol. 59
2016, Vol. 59


