2. 中国科学院大学, 北京 100049;
3. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. CAS Center for Excellence in Tibetan Plateau Earth Sciences, Beijing 100101, China
This study is based on the synthetic seismograms computed by both analytical solutions and semi-analytical solutions. The analytical solutions used in previous studies are obtained through asymptotic analysis, while the semi-analytical solutions are computed by numerical integration. The semi-analytical solutions are of higher accuracy and therefore regarded as "true solutions". Synthetic seismograms from the analytical solutions are compared to true solutions to validate whether the analytical solutions are applicable to certain cases or not. Accuracy is crucial to the comparison. Yet the high oscillation of solutions in frequency-wavenumber domain brings out a great challenge. We developed a brand-new numerical method called Steepest Descent Integration Method(SDIM). The new method is inspired by the Method of Steepest Descent(SDM)in asymptotic analysis that is specially designed for highly oscillatory integral and is the very method used to obtain the analytical solutions. Replacing approximate integration path and approximate integrand in SDM with accurate ones, SDIM breaks the restraints of small borehole and far field and can compute seismograms at arbitrary offset and arbitrary source frequency with extremely high accuracy efficiently. We calculate the seismograms by both SDIM and SDM for a large offset(1000 m, significantly large compared to borehole radius of 0.1 m)and varied source frequency(0.1~1000 Hz). The assumption of small-borehole is violated in high frequency cases, while far-field assumption fails when the frequency is low. The same experiment is conducted for all three basic borehole sources.
The works presented in the paper can be categorized into two parts, namely the new SDIM and comparison of seismograms. The study of SDIM shows that:(1)The solutions of borehole sources problem in frequency-wavenumber domain are highly oscillatory. The oscillation depends on source frequency and offsets. High frequency sources result in severe oscillation, so as large offsets.(2)The oscillation is attributed to Hankel functions in the solutions whose exponential part account for most of it. Hence, exponential functions are used in the derivation of SDIM instead of Hankel functions, making the work much easier.(3)The only difference between SDIM and SDM is the accuracy of the steepest descent path and the integrand. SDIM uses the accurate path and integrand, while SDM uses approximate ones. In addition, four numerical examples are presented in the paper. Each is designed specifically. They demonstrate that:(1)Results from SDIM are identical to ones from SDM when small-borehole assumption and far-field assumption are satisfied, which supports the validity of SDIM.(2)When small-borehole assumption is violated, the SDM results differ much from the SDIM ones that are considered as true results. It infers that the influence from borehole might not be ignored even for far-field wave field.(3)When far-field assumption fails, the results from SDM are inaccurate as well, which means the absolute value of the offset cannot guarantee far-field. The ratio of the offset to the characteristic wave length matters.(4)The same phenomenon occurs in the wave field of all the three basic borehole sources.
Obtaining accurate far-field seismograms is the key problem of borehole sources research. Yet it is challenging because of highly oscillatory integral involved. By taking advantage of the special form of analytical solutions, we developed a brand-new method for computing highly oscillatory wavenumber integration. It completely avoids the oscillation and results in numerical integration of a fully smooth function, leading to synthetic seismograms with high precision. It also allows us to compute P, S and surface waves separately, reducing their mutual interference. Numerical experiments demonstrate that the results from SDM are considerably different from ones from SDIM, in both amplitude and phase when the small-borehole assumption or the far-field assumption fails. Therefore, the SDM has its constraint and SDIM is a better alternative if accurate wave-field information is needed.
井中震源是指具有圆柱形结构的震源,常用于人工震源的地震探测和勘探中,例如深地震测深、地震勘探和采矿地球物理等领域.常见的井中震源包括炸药震源,井下的空气枪、水枪、射孔枪、以及钻头震源等(Chen et al.,1990).钻井的存在给井中震源问题带来了较为复杂的边界条件,使得井中震源波场体现出与常规震源不同的特性(Lee and Balch,1982; Meredith et al.,1993).
以震源类型划分,井中震源可以大致分为三种:即径向应力源、轴向应力源和旋转应力源,其他震源可以由这三种震源的组合而成.采矿地球物理中的炸药震源可以简化为径向应力源(Blair,2007,2010),随钻地震勘探中的钻头震源可以简化成轴向应力源和旋转应力源的组合(Rector and Hardage,1992).以研究区域划分,井中震源的波场可以分为井内波场和井外波场.井内波场作为声波测井的主要研究区域,前人已经对其有大量而详实的研究(Tsang and Rader,1979; Cheng and Toksöz,1981; Tubman et al.,1984; Cheng,1994; 沈建国和张海澜,2000);而井外波场的研究还相对较少(Heelan,1953; Lee and Balch,1982; Meredith,1991; 刘银斌等,1993a,b; 张钋等,1995; Blair,2007).但是随着采矿地球物理和随钻地震的发展,井外波场研 究的重要性日益明显(Rector and Marion,1991; Rector and Hardage,1992; Haldorsen et al.,1995; Poletto,2005; Vasconcelos and Snieder,2008; 陆斌等,2009; 王鹏等,2009;黄伟传等2010;吴何珍等,2010).
井中震源的波场研究方法主要分为数值模拟方法(Cheng,1994; Dong and Toksöz,1995)和解析法(Heelan,1953; Tsang and Rader,1979; Lee,1986; Meredith et al.,1993; De Hoop et al.,1994; Blair,2007)两类.而井外波场问题的计算区域(如炮检距为1000m)和研究对象(如钻井半径为0.1m)的尺度相差很大,因此在使用数值模拟方法时,如果要求网格尺寸逼近钻井半径,波场模拟效果较好,但计算量会过大;如果网格尺寸过大则不能很好地研究井中震源的地震波场特征(王鹏等,2009).所以,解析法成为目前研究井外波场的主要手段.
Heelan(1953)在远场近似下得到了有限长度 的三种基本井中震源的远场解析解.Jordan(1962)和Abo-Zena(1977)使用不同的方法也获得了井中震源的远场解析解.Lee和Balch(1982)考虑了钻井中流体的存在,得到含液井的远场解析解.刘银斌等(1993a,b)将多个震源的解叠加起来,得到了井中震源阵列的远场解析解.上述研究均基于两个假设条件:(1)井孔半径远小于特征波长;(2)炮检距大于特征波长.本文中我们分别称之为“小井孔”和“远场”假设.Meredith(1991)和Blair(2007)使用离散波数法对频率波数域的解进行数值积分,得到了精确的远场波场,并分别应用于井间地震和采矿地球物理的研究.离散波数法通过增加等间距的虚拟震源,将积分转化为求和,是计算波数域积分的常用方法(Bouchon and Aki,1977; Bouchon,1978,2003).但是波数域积分中极点(pole)和支线(branch cut)所代表的丰富物理意义也随之消失(Lapwood,1949).为了保留波数域积分的优势,井内波场的研究通常采用实轴积分法(Tsang and Rader,1979; 沈建国和张海澜,2000).但是当研究井外波场时,由于炮检距一般远大于钻孔半径,实轴积分的积分函数会出现高频振荡的现象,严重影响数值积分的精度和计算量,不适用于井外波场的计算.
为了克服波数域实轴积分中出现的高频振荡现象,本文提出一种基于最速下降路径的数值积分方法,并通过比较数值积分和解析解之间的误差,探讨远场解析解的适用性条件.
2 井中震源波场解析解 2.1 频率波数域的解析解假设在各向同性弹性全空间中存在一个无限长的圆柱形空洞(半径为a),用来模拟钻井或者炮眼.井内的震源通过圆柱形的边界对井外空间产生的影响,通常可以用井壁两侧位移或者应力的连续性来传递.本文中我们考虑井中为真空,井壁为自由边界 条件的情况,因此只需考虑应力源对井外空间的作用.
为了便于边界条件的描述,我们采用柱坐标系,并将柱坐标系的z轴与圆柱形空洞的对称轴重合(图 1a).在柱坐标系下,边界上的应力可以用σrr,σrθ,σrz三个分量来表示,它们分别对应于径向、旋转和轴向应力源(图 1b).
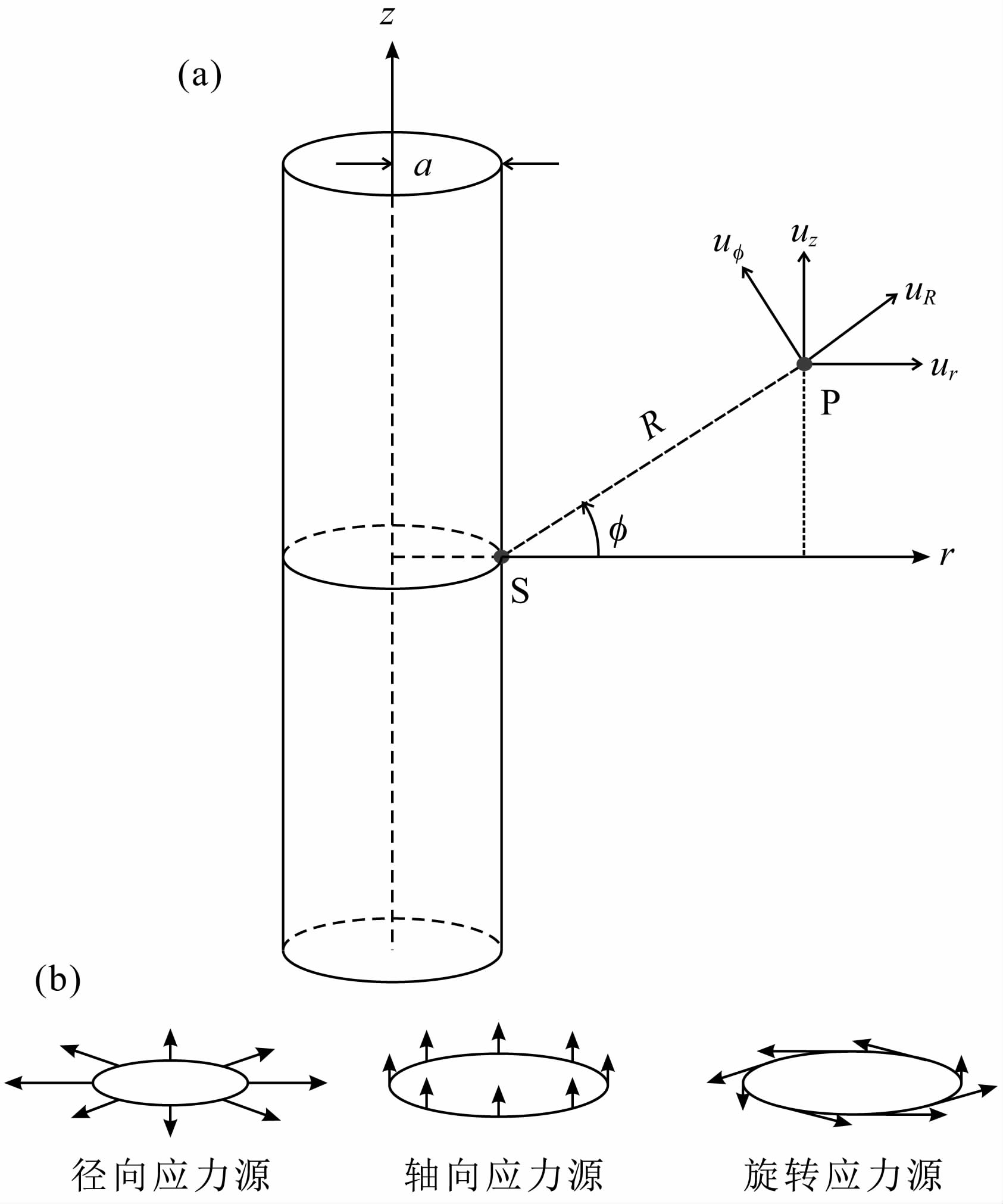 |
图 1 井中震源示意图 (a)震源结构.震源S呈轴对称状分布于半径为a的井壁上,检波器位于P(r,z)点.(b)三种基本的井中震源. Fig. 1 Diagram of downhole seismic sources (a)Source geometry. The source S is distributed axisymmetrically around the borehole wall of radius a. The receiver is placed at point P(r,z).(b)Three basic types of downhole seismic sources. |
柱坐标系下的平衡方程(忽略体力项)为
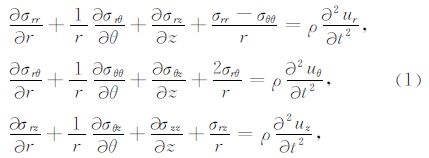
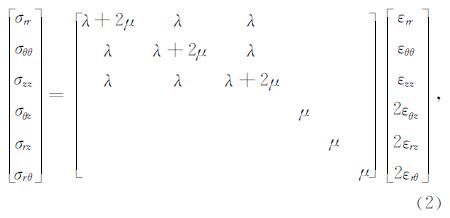
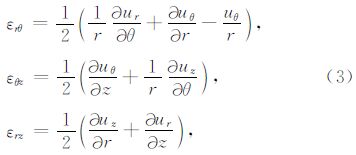
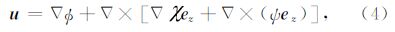

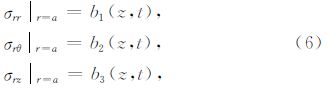
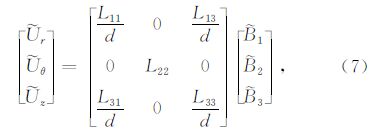
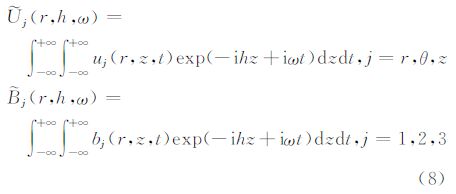
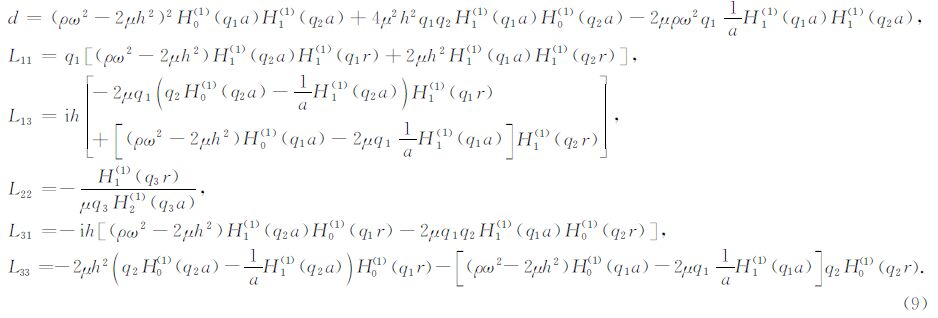
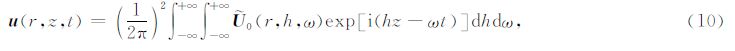
前人关于井中震源的解析解研究中,尽管采用的具体方法不尽相同,但最终都会得到与(9)式等价的解(Heelan,1953; Abo-Zena,1977; Lee and Balch,1982; Meredith,1991; 刘银斌等,1993a,b; Blair,2007).而对(10)式中双重积分的计算方法则主要分为两类.一类是在远场的假设下,解析地计算两个积分,得到远场解析解(Heelan,1953; Abo-Zena,1977; Lee and Balch,1982);另一类是采用数值积分法计算,得到半解析解(Meredith,1991; Blair,2007).
2.2 近似条件下的远场解析解建立远场解析解需要两个基本假设条件.首先是“小井孔”假设,即钻井半径远小于特征波长.这时qa=2π$\frac{a}{\lambda }\ll 1$,故Hankel函数有如下近似表达式:
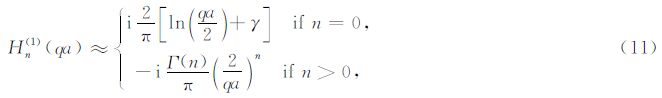

当r大于特征波长,即“远场”假设成立时,可以采用最速下降法(Aki and Richards,2002)计算关于Hn(1)(qr)的波数域积分,从而得到频率域的解析解:
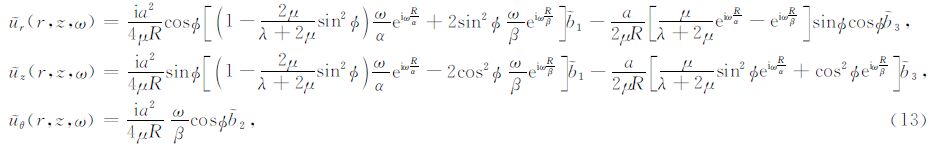
假设三种应力源的形式都是δ(z)G(t),其中G(t)是震源时间函数.那么对(13)式作反Fourier 变换,可以得到这三类震源在物理空间域的解.
(1)径向应力源:
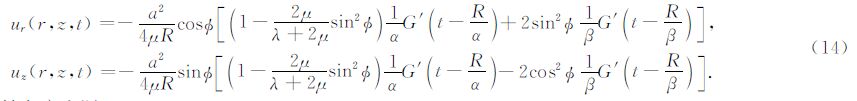
(2)轴向应力源:
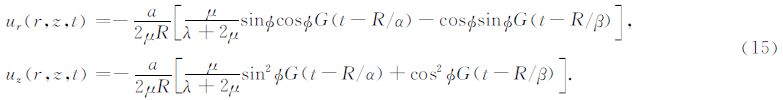
(3)旋转应力源:
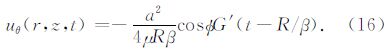
在径向和轴向应力源的位移表示为P波和SV波的组合.为了分离P和SV的贡献,我们引入坐标系(R,φ,θ),其中
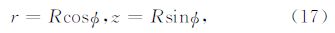
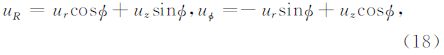
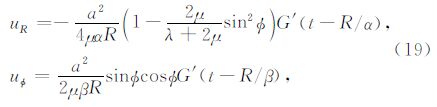
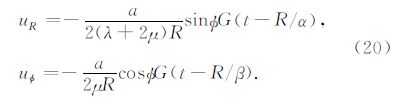
考虑到本文中φ的定义与前人使用的φL的关系φ=φL-π/2,上述公式与前人的结果一致(Heelan,1953; Lee and Balch,1982).从(19)、(20)式中可以看出,两种震源激发的SV波能量都比P波 能量大,并且能量差会随着两种波速差的增大而增大(图 2).
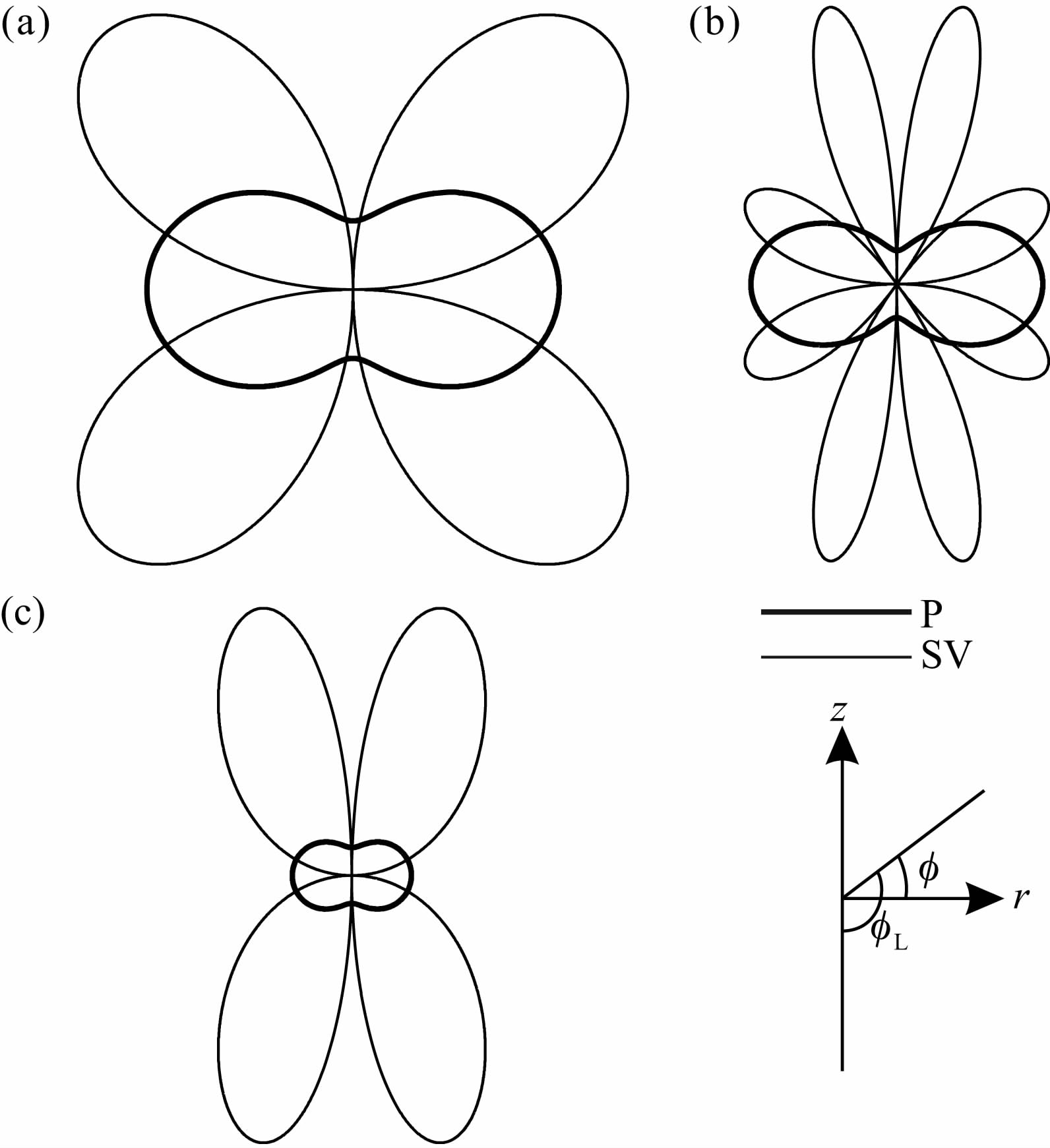 |
图 2 井中震源的远场辐射图样 (修改自Lee and Balch,1982;参数相同) 震源分别是(a)施加在裸眼井井壁上的径向压力源,(b)施加在充 液井井壁上的径向压力源,和(c)位于充液井对称轴上的单极声波源. Fig. 2 Far-field radiation patterns for downhole seismic sources(modified after Lee and Balch,1982; same parameters are used) The sources are respectively(a)a radial stress source applied on an empty borehole,(b)a radial stress source applied on a fluid-filled borehole,and (c)a monopole acoustic source placed at the center of a fluid-filled borehole. |
为了计算最速下降路径积分,我们首先求解最速下降路径的解析表达式,然后采用数值积分方法,沿着最速下降路径计算频率波数域解的积分.
理想情况下,计算F(h)的最速下降积分路径应遵循如下步骤:
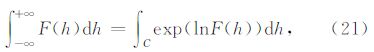
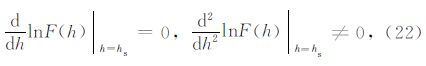
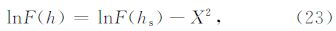
实际情况下遇到的函数往往形式较为复杂,解析地计算F(h)的最速下降路径比较困难.如果积 分函数可以写成G(h)F(h)的形式,其中F(h)可以解析地计算最速下降路径,且G(h)是一个变化平缓的函数,则使用F(h)的最速下降路径代替G(h)F(h)的最速下 降路径也可以得到很好的结果(图 3d).从(7)、(9)式中可以看出,${\tilde{U}}$(h,ω)由Hankel 函数组成,而Hankel函数的振荡性由exp(iz)贡 献.我们记去除振荡性后的Hankel函数为 $\hat{H}_{n}^{\left(1 \right)}$(z),则有
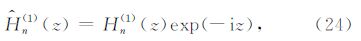
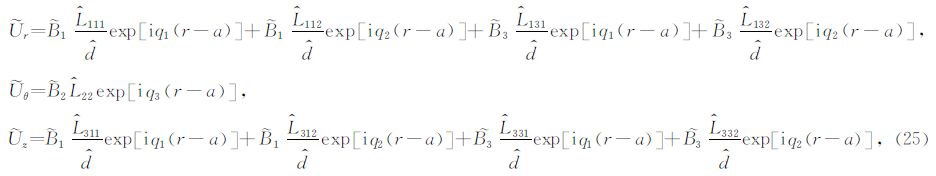
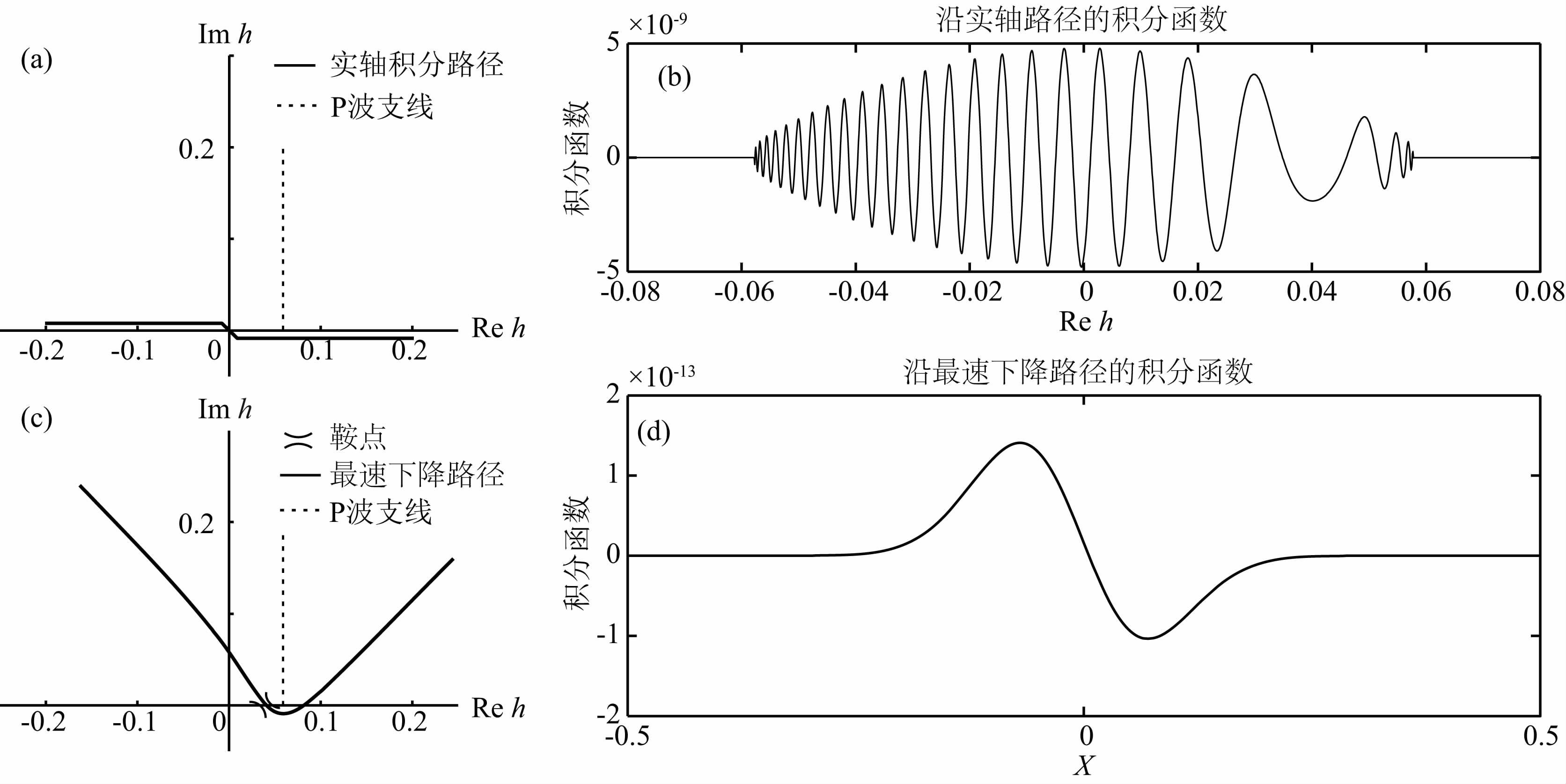 |
图 3 最速下降积分和实轴积分的对比 图(a)(c)分别是实轴积分和最速下降积分在复波数平面内的积分路径,图(b)(d)则是两个路径上的积分函数.波数h的单位是m-1. Fig. 3 Comparison of Steepest Descent Integration Method and Real-axis Integration Method Panels(a)(c)show two different integration paths for Real-axis Integration Method and Steepest Descent Integration Method in complex wavenumber plane,while(b)(d)are the corresponding integr and s along the paths. |
记
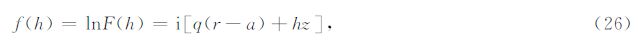
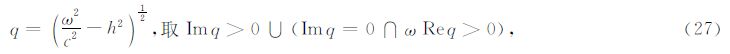
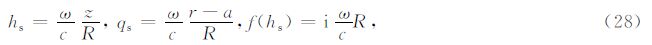
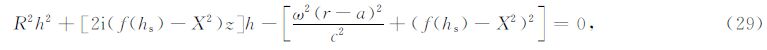
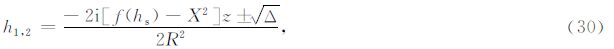

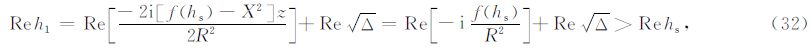
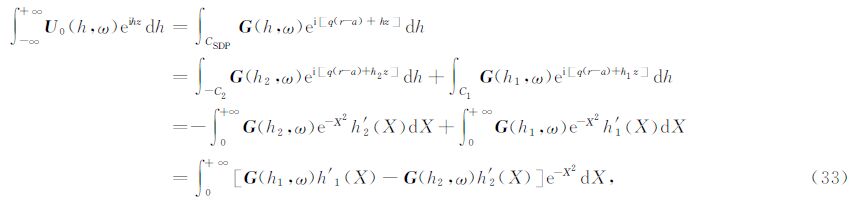
我们首先验证最速下降积分法在计算远场波场 时的适用性,采用如下参数模型:井孔半径为0.1 m,检波器放置在距离钻井1000 m处;井外地层为常见的Pierre页岩,其P波波速为2074 m·s-1,S波为 869 m·s-1,密度为2250 kg·m-3(Meredith,1991); 震源为径向应力震源,震源时间函数是主频为30 Hz的Ricker子波(图 4a).该主频的震源在这种地层中的特征波长λm约为346 m,既远大于井孔半径2 m,又远小于1000 m,同时满足“小井孔”和“远场”假设,近似条件下的解析解可以准确地得到位移解.
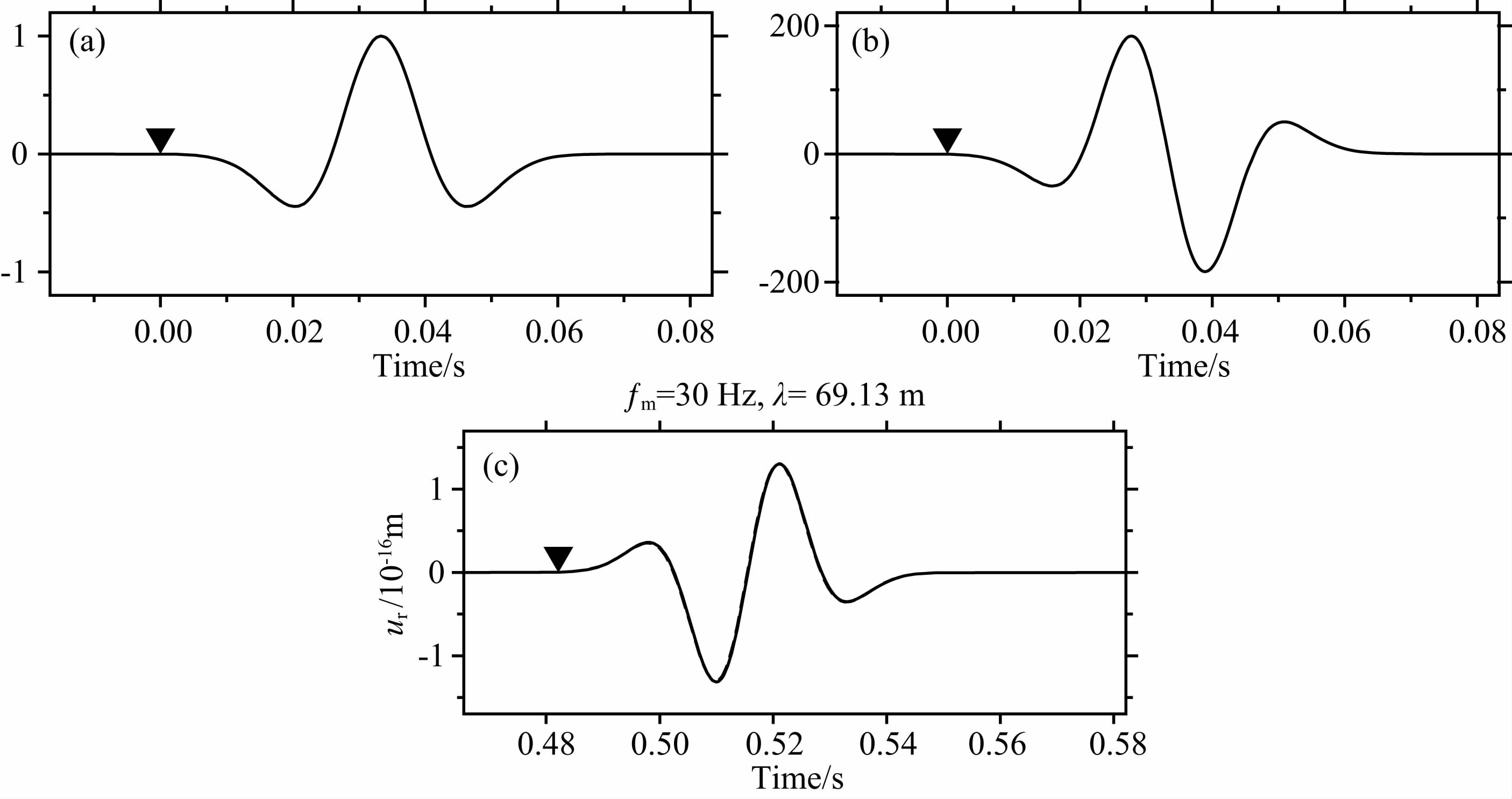 |
图 4 径向应力源激发波场的半解析解和解析解对比 (a)震源时间函数(Ricker子波);(b)解析解远场波形(Ricker子波的导数);(c)实线表示最速下降积分得到ur的半解析解,虚线为解析解.倒三角形为P波的到时. Fig. 4 Comparison of the semi-analytical solution and the analytical solution of wave field excited by a radial stress source (a)Source time function(Ricker wavelet);(b)Far-field waveform of analytical solution(derivative of Ricker wavelet);(c)Solid line denotes the semi-analytical solution of ur obtained by Steepest Descent Integration Method and dashed line is the analytical solution. The inverted triangle denotes the theoretical arrival time of P waves. |
从径向应力源的远场解析解(14)式可知,远场的波形正比于Ricker子波的导数(图 4b).图 4c是地震记录的径向分量,其中实线代表半解析解,虚线代表解析解,倒三角形标注了P波的理论到时.数值试验结果表明,用最速下降路径积分得到的数值解与近似条件下的解析解吻合很好(图 4c).由于在本例条件下,解析解对位移刻画较为准确,所以这一结果进一步验证了最速下降积分法的正确性.
4.2 径向应力震源 4.2.1 高频情况径向应力震源通常用来模拟炮眼中的爆炸震源,典型的炮眼半径约为0.1 m.为了避免震源激发时地面的剧烈振荡破坏检波器和近井的井壁面波的影响,检波器一般放置在离井一段距离之外,放置在r=1000 m,z=0 m处,其他参数也同4.1节.
我们首先检验“小井孔”假设失效时的情况.在井孔绝对半径不变的情况下,通过减小特征波长同样可以使“小井孔”假设失效.在地层速度不变的前提下,提高震源的主频可以减小特征波长.计算结果如图 5所示.该模型中,“小井孔”的条件为特征波场λ»a=0.1 m,图 5a中可以看出,该假设条件完全满足时,两者之间差异很小.当震源主频逐渐增加时,子波波长逐渐减小,图 5b和图 5c的假设条件接近失效,两者之间的差异增加,但波形差异仍然较小.当子波波长进一步减小时,“小井孔”假设失效(图 5d-5f),虽然数值解和近似条件下的解析解的P波到时一直保持在理论到时0.4821 s处,但两者在振幅和相位方面的差异开始凸显.其中,半解析解的振幅略高于解析解的振幅,最大振动的到时相对滞后.
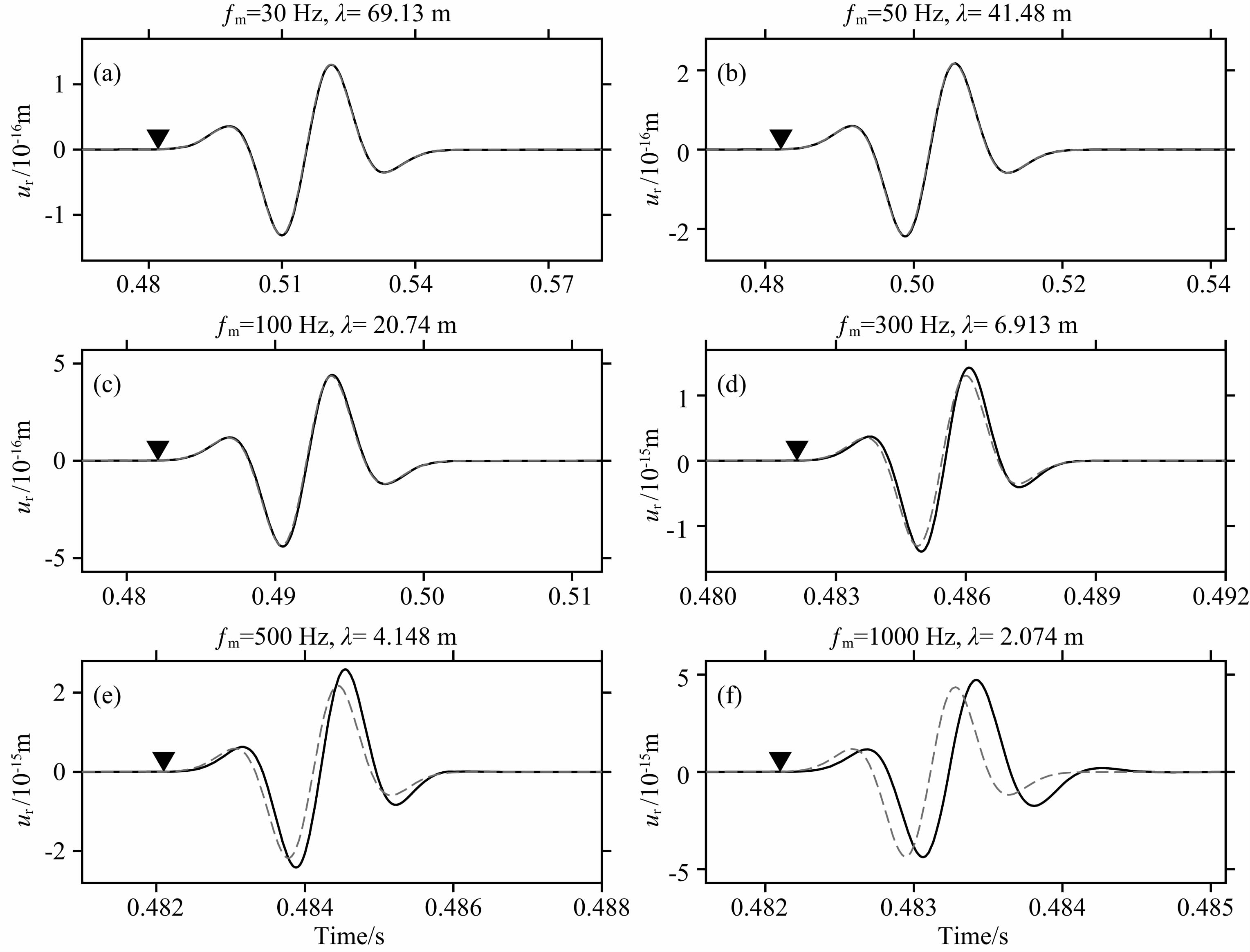 |
图 5 高频情况下径向应力源激发波场的半解析解(实线)和近似条件下的解析解(虚线)对比 图(a-f)分别是Ricker子波主频为30,50,100,300,500,1000 Hz时,位于r=1000 m,z=0 m处的检波器记录的径向分量.倒三角形为P波理论到时. Fig. 5 Comparison of the semi-analytical solution(solid line) and the analytical solution(dashed line) of wave field excited by a radial stress source for high frequency Panels(a-f)are radial components of seismograms recorded by the receiver placed at r=1000 m,z=0 m with the peak frequency of Ricker wavelet being 30,50,100,300,500,1000 Hz respectively. The inverted triangle denotes the theoretical arrival time of P waves. |
解析解将波场对圆柱形井壁这一特殊的边界条件的复杂响应简化为一个尺度因子a2(见式(14)).满足“小井孔”假设时,由于井孔半径远小于特征波长,钻井对远场波场影响不大,解析解的简化较为合理.而当“小井孔”假设失效时,井孔对波场的作用开始体现,即使在远场的地震记录上也会有响应.
除了振幅和相位相对的差异外,两者的绝对振幅都会随着频率的变大而迅速地增加.这是因为两者的位移都大致正比于Ricker子波的导数.
4.2.2 低频情况当震源频率变低时,特征波长会随之增加.虽然这时“小井孔”假设不会受到影响,但是有可能会导致“远场”假设失效.低频情况下的计算结果如图 6 所示.该模型中“远场”假设的条件是λ«r=1000 m. 从图 6a中可以看出,该假设完全满足,两者差异很小.但是当震源主频逐渐到5 Hz时,“远场”假设接近失效,两者差异已经开始体现(图 6b).随着震源主频的进一步增加,两者之间的差异越来越明显(图 6c-6f).在低频情况下,半解析解和解析解同样出现了振幅和相位上的偏差.数值解的振幅大于解析解,并且比高频情况下更加明显(图 6d-6f).与高频情况不同的是,低频情况下数值解的波形与解析解也有比较明显的差别,逐渐从Ricker子波的导数变成了Ricker子波.
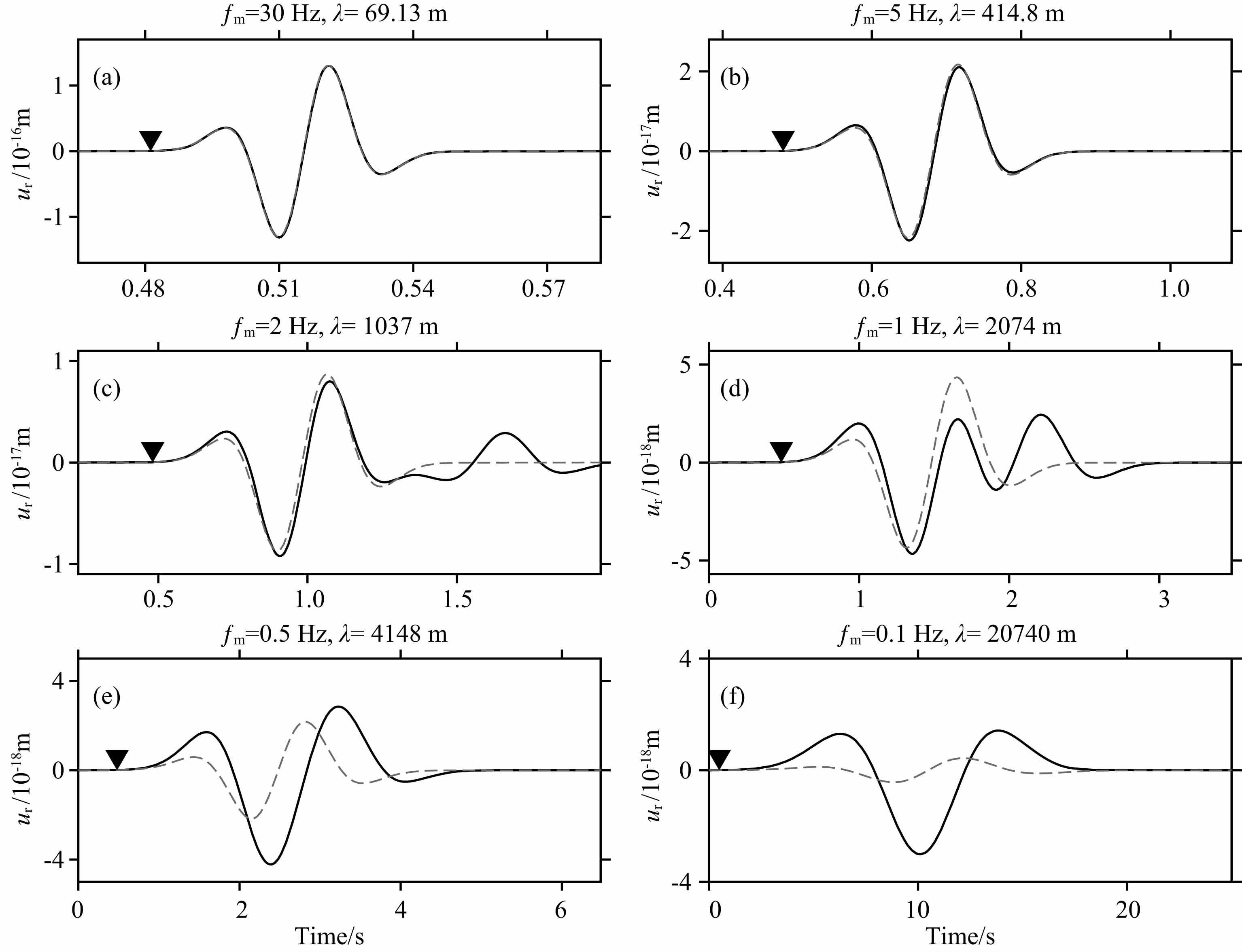 |
图 6 低频情况下径向应力源激发波场的半解析解(实线)和解析解(虚线)的对比 图(a-f)分别是Ricker子波主频为30,5,2,1,0.5,0.1 Hz时检波器记录的径向分量.倒三角形为P波理论到时. Fig. 6 Comparison of the semi-analytical solution(solid line) and the analytical solution(dashed line) of wave field excited by a radial stress source for low frequency Panels(a-f)are radial components of seismograms recorded by the receiver placed at r=1000 m,z=0 m with the peak frequency of Ricker wavelet being 30,5,2,1,0.5,0.1 Hz respectively. The inverted triangle denotes the theoretical arrival time of P waves. |
一般情况下,远场是指炮检距的尺度远大于震源尺度;而在井中震源问题中,“远场”假设比较的是炮检距的尺度和特征波长的尺度.所以虽然本例中 炮检距(1000 m)远大于震源的尺度(0.1 m),但是并不一定满足“远场”假设.如图 6c-6f中,特征波长大 于或等于炮检距时,解析解与数值解出现明显的差异.
4.3 轴向应力震源轴向应力震源会用来模拟一些附着在井壁上的振荡器震源、随钻震源,或者与径向震源来共同模拟一些较为复杂的震源.计算结果如图 7所示.因为轴向震源在检波器处的位移场只有垂向分量,所以图中对比的是解析解和数值解的垂向分量.轴向震源的远场波形是Ricker子波(图 7),因此两者绝对振幅都无明显变化.当满足“小井孔”假设和“远场”假设时,两者差异很小(图 7a),而当“远场”假设失效(图 7b)或“小井孔”假设失效(图 7c)时,两者之间会有较为明显的差异.
 |
图 7 轴向应力源激发波场的半解析解(实线)和解析解(虚线)的对比 图(a-c)分别是Ricker子波主频为30,0.5,500 Hz时检波器的垂向分量.倒三角形是SV波的理论到时. Fig. 7 Comparison of the semi-analytical solution(solid line) and the analytical solution(dashed line) of wave field excited by a axial stress source Panels(a)-(c)are vertical components of seismograms with the peak frequency of Ricker wavelet being 30,0.5,500 Hz respectively. The inverted triangle denotes the theoretical arrival time of SV waves. |
旋转应力震源可能由钻头旋转产生,也有可能 由钻缆与井壁的摩擦产生.通常情况下旋转应力源 的强度较小,产生的地震波能量也较弱.计算结果如图 8所示.与前两种震源产生P-SV波不同,旋转应力震源只产生SH波,所以图 8中比较的是位移的横向分量.由于旋转震源远场波形是Ricker子波的导数,所以两者的绝对振幅与频率呈现正相关.在“远场”假设(图 8b)或“小井孔”假设(图 8c)失效时,两者同样会出现明显的差异.
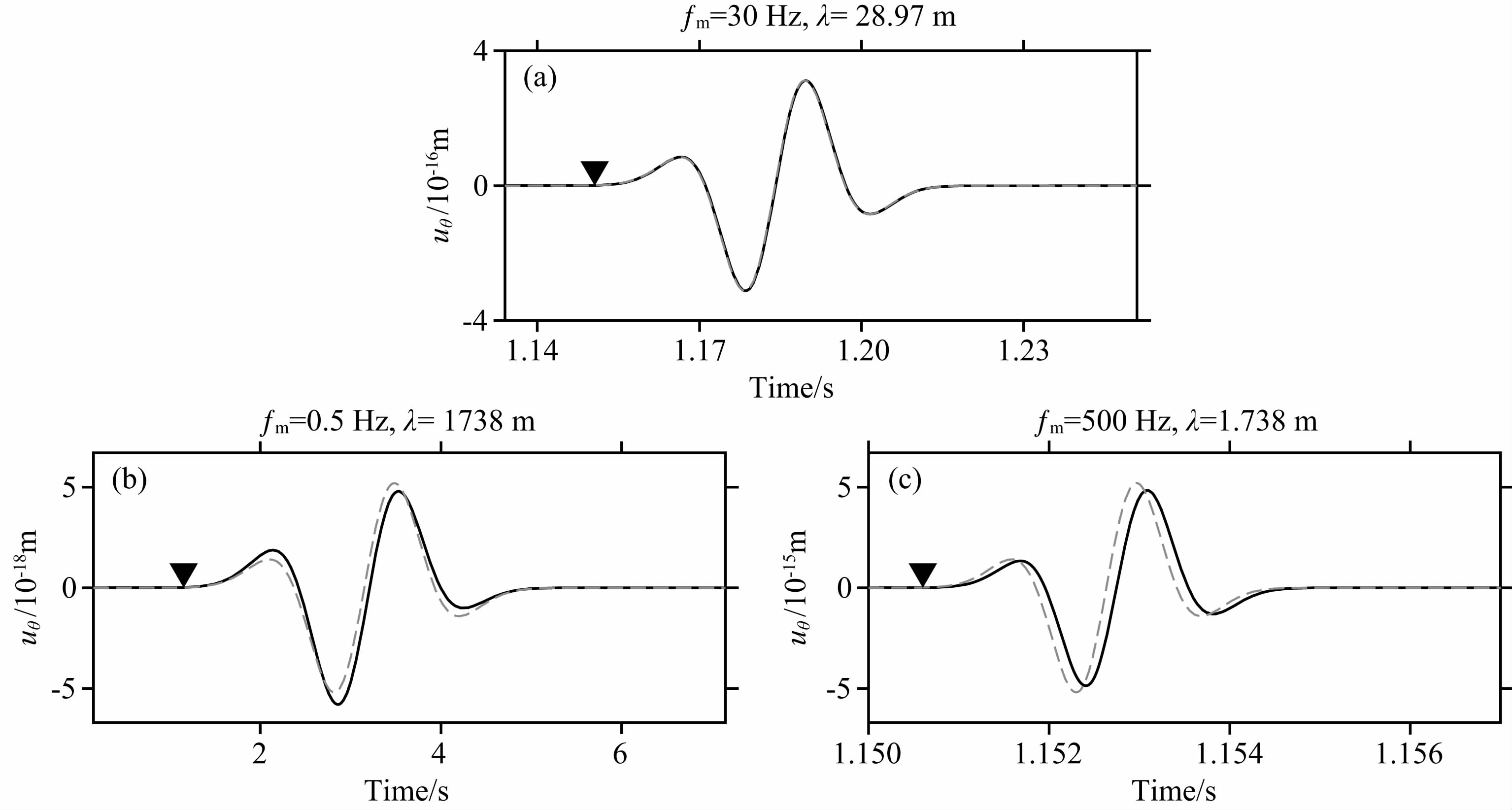 |
图 8 旋转应力源激发波场半解析解(实线)和解析解(虚线)的对比 图(a-c)分别是Ricker子波主频为30,0.5,500 Hz时检波器的横向分量.倒三角形是SH波的理论到时. Fig. 8 Comparison of the semi-analytical solution(solid line) and the analytical solution(dashed line)of wave field excited by a torsional stress source Panels(a-c)are transverse components of seismograms with the peak frequency of Ricker wavelet being 30,0.5,500 Hz respectively. The inverted triangle denotes the theoretical arrival time of SH waves. |
本文采用沿最速下降路径的数值积分计算了井中震源的远场波场.由于沿该路径的积分函数不存在任何振荡,因此获得了高精度的数值积分.最速下降积分在计算时可以将P波和SV波分离,避免了波形之间的互相干扰.该方法保留了对波数域极点和支线进行分析的可能性,可以解析地得到面波,折射波出现的位置和波形.模型试验表明,当“小井孔”和“远场”假设不满足时,近似条件下解析解的振幅和波形相对于半解析解都会有明显的偏差,使用半解析解能获得更准确的波场信息.
附录A 井中震源的频率波数域解柱坐标系下的波动方程为
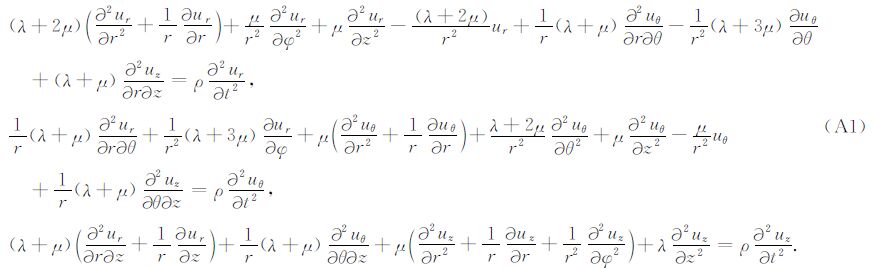
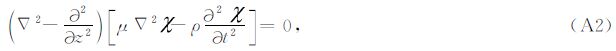
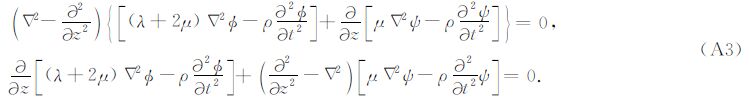
在柱坐标系下,通常用柱面波分解代替平面波分解来求解波动方程.柱面波可以表示为Hn(1)(qr)e-iωt,其中Hn(1)(z)是Bessel函数的一种,也叫做第一类Hankel函数,q是径向波数.在前人的研究工作中(Abo-Zena,1977; Blair,2007),有些研究者采用修正Bessel函数,但是<e-iωt和Hn(1)(z)的组合可以更直观描述向外传播的柱面波.设
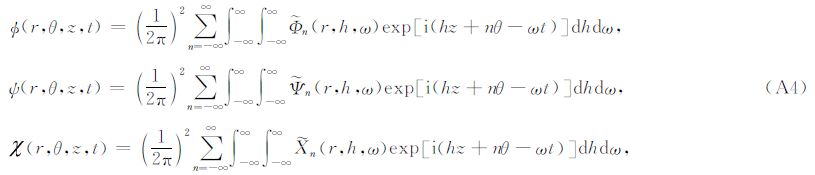
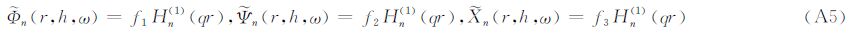
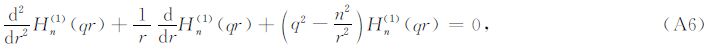
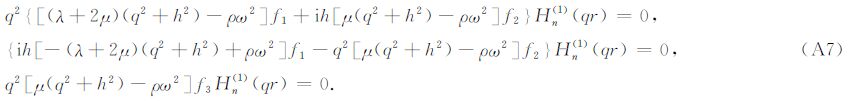
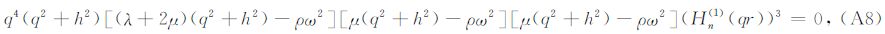
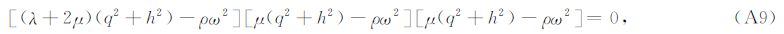




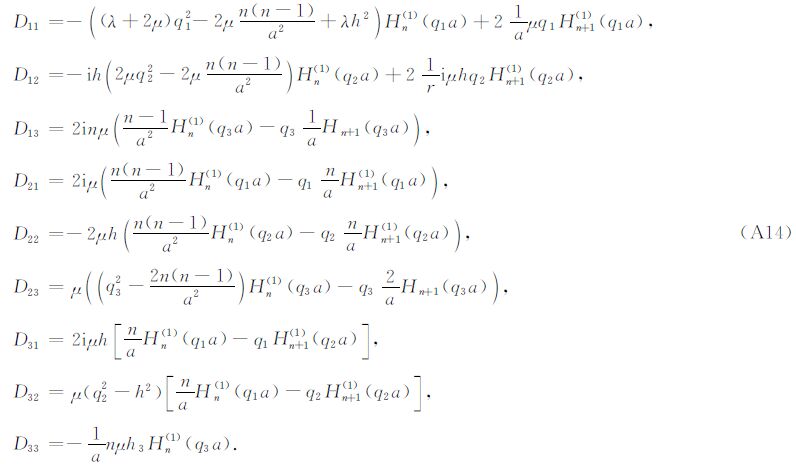
轴对称情况对应于n=0的情况.这时Dij的表达式退化成



| [1] | Abo-Zena A M. 1977. Radiation from a finite cylindrical explosive source. Geophysics, 42(7):1384-1393, doi:10.1190/1.1440799. |
| [2] | Aki K, Richards P G. 2002. Quantitative seismology. Sausalito, California:University Science Books. |
| [3] | Blair D P. 2007. A comparison of Heelan and exact solutions for seismic radiation from a short cylindrical charge. Geophysics, 72(2):E33-E41, doi:10.1190/1.2424543. |
| [4] | Blair D P. 2010. Seismic radiation from an explosive column. Geophysics, 75(1):E55-E65, doi:10.1190/1.3294860. |
| [5] | Bouchon M, Aki K. 1977. Discrete wave-number representation of seismic-source wave fields. Bull. Seismol. Soc. Am., 67(2):259-277. |
| [6] | Bouchon M. 1978. The importance of the surface or interface Pwave in near-earthquake studies. Bull. Seismol. Soc. Am., 68(5):1293-1311. |
| [7] | Bouchon M. 2003. A review of the discrete wavenumber method. Pure Appl. Geophys., 160(3-4):445-465, doi:10.1007/PL00012545. |
| [8] | Chen S T, Eriksen E A, Miller M A. 1990. Experimental studies on downhole seismic sources. Geophysics, 55(12):1645-1651, doi:10.1190/1.1442818. |
| [9] | Cheng C H, Toksöz M N. 1981. Elastic wave propagation in a fluid-filled borehole and synthetic acoustic Logs. Geophysics, 46(7):1042-1053, doi:10.1190/1.1441242. |
| [10] | Cheng N Y. 1994. Borehole wave propagation in isotropic and anisotropic media:three-dimensional finite difference approach. Massachusetts:Massachusetts Institute of Technology. |
| [11] | De Hoop A T, De Hon B P, Kurkjian A L. 1994. Calculation of transient tube-wave signals in cross-borehole acoustics. J. Acoust. Soc. Am., 95(4):1773-1789, doi:10.1121/1.408697. |
| [12] | Dong W J, Toksöz M N. 1995. Borehole seismic-source radiation-pattern in transversely isotropic media. Geophysics, 60(1):29-42, doi:10.1190/1.1443759. |
| [13] | Haldorsen J B U, Miller D E, Walsh J J. 1995. Walk-away VSP using drill noise as a source. Geophysics, 60(4):978-997, doi:10.1190/1.1443863. |
| [14] | Heelan P A. 1953. Radiation from a cylindrical source of finite length. Geophysics, 18(3):685-696, doi:10.1190/1.1437923. |
| [15] | Huang W C, Ge H K, Wang B S, et al. 2010. Deconvolution interferometry and its application to seismic while drilling data processing. Progress in Geophysics (in Chinese), 25(3):951-956, doi:10.3969/j.issn.1004-2903.2010.03.032. |
| [16] | Jordan D W. 1962. The stress wave from a finite, cylindrical explosive source. J. Math. Mech., 11(4):503-551. |
| [17] | Lapwood E R. 1949. The disturbance due to a line source in a semi-infinite elastic medium. Philos. Trans. Roy. Soc. Lond. A Math. Phys. Sci., 242(841):63-100, doi:10.1098/rsta.1949.0005. |
| [18] | Lee M W, Balch A H. 1982. Theoretical seismic-wave radiation from a fluid-filled borehole. Geophysics, 47(9):1308-1314, doi:10.1190/1.1441391. |
| [19] | Lee M W. 1986. Low-frequency radiation from point sources in a fluid-filled borehole. Geophysics, 51(9):1801-1807, doi:10.1190/1.1442226. |
| [20] | Liu Y B, Li Y M, Wu R S, et al. 1993a. Far-field radiation pattern of dowhole source and array source. OGP (in Chinese), 28(4):379-388. |
| [21] | Liu Y B, Li Y M, Wu R S, et al. 1993b. Radiative energies from downhole source and array source. OGP (in Chinese), 28(4):389-395. |
| [22] | Lu B, Ge H K, Wu H Z, et al. 2009. SWD data preprocessing using wavelet transform of correlation domain. Chinese Journal Geophysics (in Chinese), 52(9):2349-2356, doi:10.3969/j.issn.0001-5733.2009.09.020 |
| [23] | Meredith J A. 1991. Numerical and analytical modelling of downhole seismic sources, the near and far field Massachusetts:Massachusetts Institute of Technology. |
| [24] | Meredith J A, Toksöz M N, Cheng C H. 1993. Secondary shear waves from source boreholes. Geophys. Prospect., 41(3):287-312, doi:10.1111/j.1365-2478.1993.tb00571.x. |
| [25] | Poletto F. 2005. Energy balance of a drill-bit seismic source, part 1:Rotary energy and radiation properties. Geophysics, 70(2):T13-T28, doi:10.1190/1.1897038. |
| [26] | Rector J W, Marion B P. 1991. The use of drill-bit energy as a downhole seismic source. Geophysics, 56(5):628-634, doi:10.1190/1.1443079. |
| [27] | Rector J W, Hardage B A. 1992. Radiation pattern and seismic waves generated by a working roller-cone drill bit. Geophysics, 57(10):1319-1333, doi:10.1190/1.1443199. |
| [28] | Shen J G, Zhang H L. 2000. Numerical study on 3D acoustic field generated by eccentric sources in borehole. Chinese Journal Geophysics (in Chinese), 43(2):279-286. |
| [29] | Tsang L, Rader D. 1979. Numerical evaluation of the transient acoustic waveform due to a point source in a fluid-filled borehole. Geophysics, 44(10):1706-1720, doi:10.1190/1.1440932. |
| [30] | Tubman K M, Cheng C H, Toksöz M N. 1984. Synthetic full waveform acoustic logs in cased boreholes. Geophysics, 49(7):1051-1059, doi:10.1190/1.1441720. |
| [31] | Vasconcelos I, Snieder R. 2008. Interferometry by deconvolution:Part 2-Theory for elastic waves and application to drill-bit seismic imaging. Geophysics, 73(3):S129-S141, doi:10.1190/1.2904985. |
| [32] | Wang P, Ge H K, Lu B, et al. 2009. Numerical simulation on SWD seismic wave propagation and data processing.Petroleum Drilling Techniques (in Chinese), 37(2):5-9. |
| [33] | Wu H Z, Ge H K, Yang D H, et al. 2010. A research of cepstrum analysis of drill string vibration and extracting the bit source signals. Chinese Journal Geophysics (in Chinese), 53(8):1968-1975, doi:10.3969/j.issn.0001-5733.2010.08.023. |
| [34] | Zhang B, Li Y M, Liu Y B. 1995. The calculation of cross-well seismic in isotropic porous layered media. Acta Geophysica Sinica (in Chinese), 38(4):507-518. |
| [35] | 黄伟传,葛洪魁,王宝善等.2010.反褶积干涉成像及其在随钻地震数据处理中的应用.地球物理学进展,25(3):951-956,doi:10.3969/j.issn.1004-2903.2010.03.032. |
| [36] | 刘银斌,李幼铭,吴如山等.1993a.井下震源和阵列震源的远场辐射花样.石油地球物理勘探,28(4):379-388. |
| [37] | 刘银斌,李幼铭,吴如山等.1993b.井下震源和阵列震源的辐射能量.石油地球物理勘探,28(4):389-395. |
| [38] | 陆斌,葛洪魁,吴何珍等.2009.利用相关域小波变换进行SWD 资料预处理.地球物理学报,52(9):2349-2356,doi:10.3969/j.issn.0001-5733.2009.09.020. |
| [39] | 沈建国,张海澜.2000.井内偏心声源激发的三维声场的数值研究.地球物理学报,43(2):279-286. |
| [40] | 王鹏,葛洪魁,陆斌等.2009.随钻地震波场传播与数据处理方法的数值实验.石油钻探技术,37(2):5-9. |
| [41] | 吴何珍,葛洪魁,杨顶辉等.2010.钻柱振动倒谱分析及其钻头源信号提取方法研究.地球物理学报,53(8):1968-1975,doi:10.3969/j.issn.0001-5733.2010.08.023. |
| [42] | 张钋,李幼铭,刘银斌.1995.层状各向同性多孔介质中井间地震的数值计算.地球物理学报,38(4):507-518. |
 2015, Vol. 58
2015, Vol. 58


