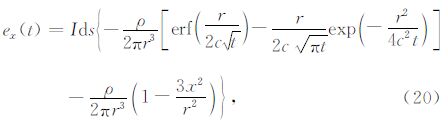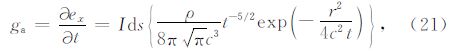2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 北京工业大学, 北京 100124
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. Beijing University of Technology, Beijing 100124, China
The fundamental of system identification using the m sequence is the Wiener-Hopf function,which reveals the relation between auto-correlation of input signal AR,identified system g and cross-correlation between input and output signal CR that is the convolution of AR and g. Because of the complicated effect of the sidelobes of AR,even if the main lobe of AR could be regarded as a delta function,g cannot yet be read out directly from CR with high precision. From the Wiener-Hopf function,it can be recognized that the effect of the sidelobes comes into the CR through the convolution process. This means that the AR could be regarded as a filter,and therefore,a deconvolution could be performed to extract g from CR by inverting the effect of the convolution with AR. For this purpose,CR,AR and g are primarily discretized and reformed individually into vectors and matrixes,and the convolution process is consequently reformed into vector=matrix×vector,where the left vector is CR,matrix is AR and right vector is g. The AR matrix could be regarded as a linear operator. Therefore the least square procedure could be introduced for the g vector estimation. Through several iterations and smoothing,g could be extracted with high precision.
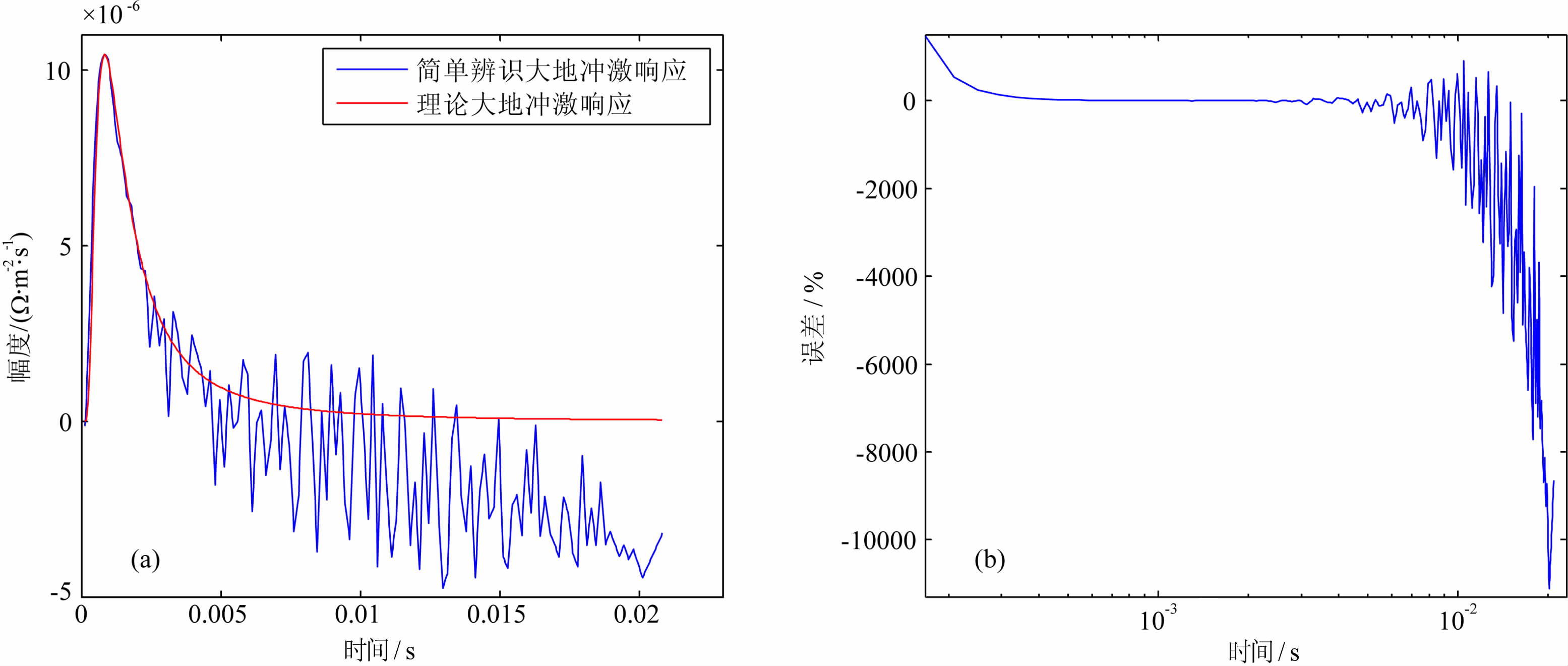
To check the effectiveness of this method,a numerical simulation is performed. A grounded line source on a homogeneous half-space is computed as the model,and the transmitting waveforms are coded by the m sequence. The result shows that the relative identification error is smaller than 2% in the time interval from 0 to 10 tpeak,where tpeak is the arrival time of the peak of the earth impulse response. On contrary the relative identification error with the traditional method in the same interval is much worse,and the biggest relative error is more than 538%. In another numerical simulation,it is proved that this method can provide identification result with high quality even if the choice of m sequence parameters is considered not fully enough from the perspective of some existing theories. Furthermore,we organized a field test in 2014 and compared the identified earth impulse response with that of other EM methods. The comparison shows that the identified result is matched well with other EM methods.
The sidelobes can be regarded as a disturbing factor in identification,and its effect comes into cross-correlation through the convolution process. The new algorithm proposed in this paper realized the high precision identification of earth impulse response by deconvolution. Numerical simulation shows that the relative identification error using this method is smaller than 2% in the main section of the earth impulse response. This method is also applied to field data processing already,and the identified earth impulse response is in good agreement with that of other EM methods. All these tests prove that this method is an applicable method in the future EM surveys.
勘探地球物理电磁方法往往通过对大地电磁响应的观测、数据处理以及反演等流程,建立地下电性结构模型,以实现对地下目标体的识别.对于所研究对象,其电磁感应过程从整体上可以看作为一个线性、时不变过程,将系统辨识的相关理论与方法引入到电磁法精细勘探中,成为目前研究的热点.
伪随机二进制序列(Pseudo R and om Binary Sequence,PRBS)中的m序列(Maximal Length Sequence)是一种常见的系统辨识输入信号(珀尼克和费尔阁,2007).最早将m序列引入地球物理中的是加拿大多伦多大学的Duncan、Edwards和Holladay等人(Duncan,1978; Duncan et al.,1980; Edwards and Holladay,1991),其利用m序列的特性对大地系统的电磁冲激响应进行观测,并将之转换至频域进行处理.2000年后,由爱丁堡大学的Ziolkowski、Hobbs和Wright等人开发的MTEM系统(Multi-Transient Electromagnetic)逐渐兴起并获得成功(Wright,2003; Wright et al.,2006; Ziolkowski et al.,2007),该系统自第二代产品开始使用m序列作为发射波形,数据通过相关处理获得大地冲激响应后利用拟地震方法进行解释.在国内,何继善于1982年提出了αpk序列伪随机信号电法,并于21世纪初对系统进行了进一步完善(何继善,2010).罗延钟及其团队也于20世纪80年代展开伪随机信号宽带激电仪系统的研制工作,并于近期提出“第二方案”算法,以提升对大地系统的辨识精度(罗延钟,2015).21世纪初,赵碧如研发了多种用于电阻率法和激电法的伪随机信号发射机和接收机(赵碧如等,2006).2008年汤井田、罗维斌完成了基于逆重复m序列伪随机电磁法的相关研究,提出了在频域辨识大地系统传输函数的方法(汤井田和罗维斌,2008; 罗维斌等,2012).2013年以来,中国科学院地质与地球物理研究所开展以m序列为发射波形的时间域电法勘探系统研发.
尽管国内外对基于m序列发射波形的EM方法研究方兴未艾,然而,如何能够在时域高精度地辨识出大地系统的电磁冲激响应依然是一个研究难点.本文在基本相关辨识方法的基础上,进一步考虑发射自相关旁瓣的影响,提出一种数学方法实现大地冲激响应的高精度辨识.在此基础上,本文对实际观测中的m序列码型参数选择展开研究,提出选择m序列主要参数的方法.最后,利用本文提出的方法对野外实测数据进行辨识处理,通过与其他方法结果进行对比,验证本文提出方法的可靠性.
2 基本相关辨识方法与旁瓣效应问题利用m序列进行系统辨识的基本原理基于Wiener-Hopf方程,对于如图 1所示的一个线性时不变系统,表达式可为
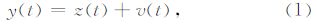
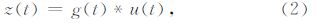
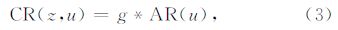
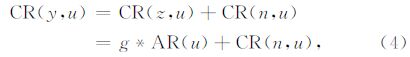
 |
图 1 典型线性系统数据流程图 Fig. 1 Data flow chart of a typical linear system |
m序列能够较好地满足上述要求,因此成为一种常见的系统辨识输入信号.利用m序列对电法发射电流波形进行编码,并按照系统辨识方法提取大地冲激响应,其信号流程如图 2.假设观测到的实际发射源电流波形为Tx(t)(后称“实际发射电流观测波形”),大地冲激响应为g(t),在观测点观测到的大地响应为Rx(t).Tx(t)和Rx(t)可被表述为
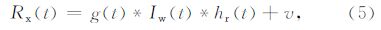
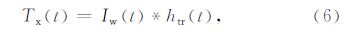
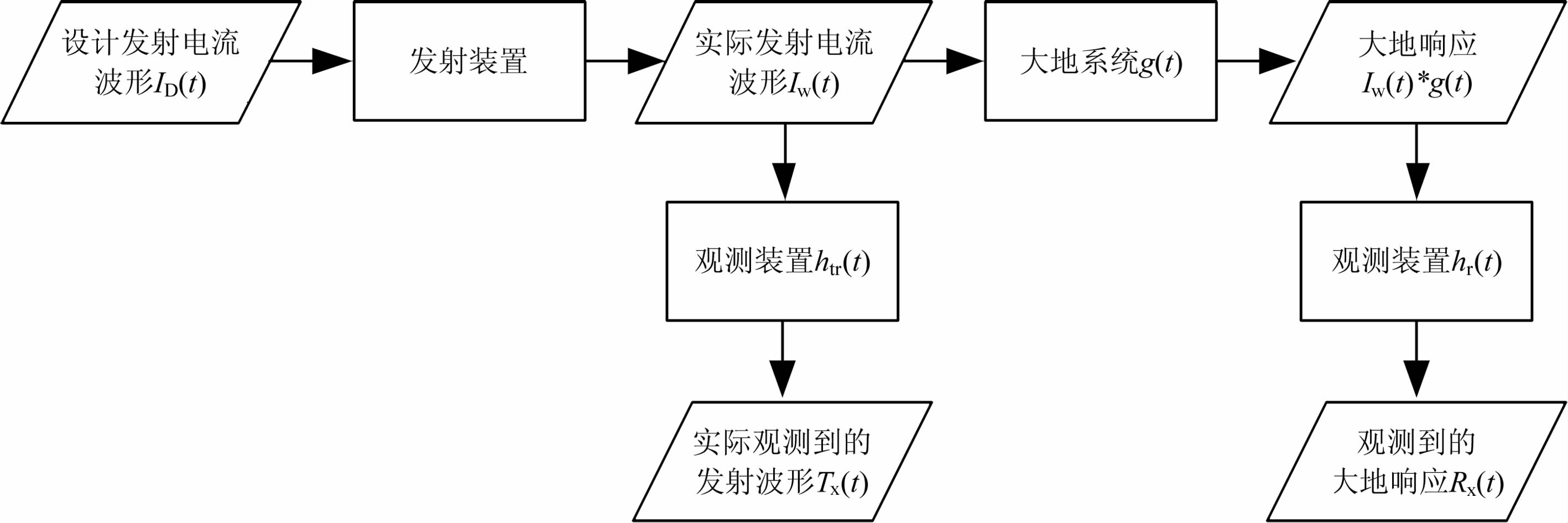 |
图 2 辨识系统信号流程图 Fig. 2 Flow chart of signal identification system |
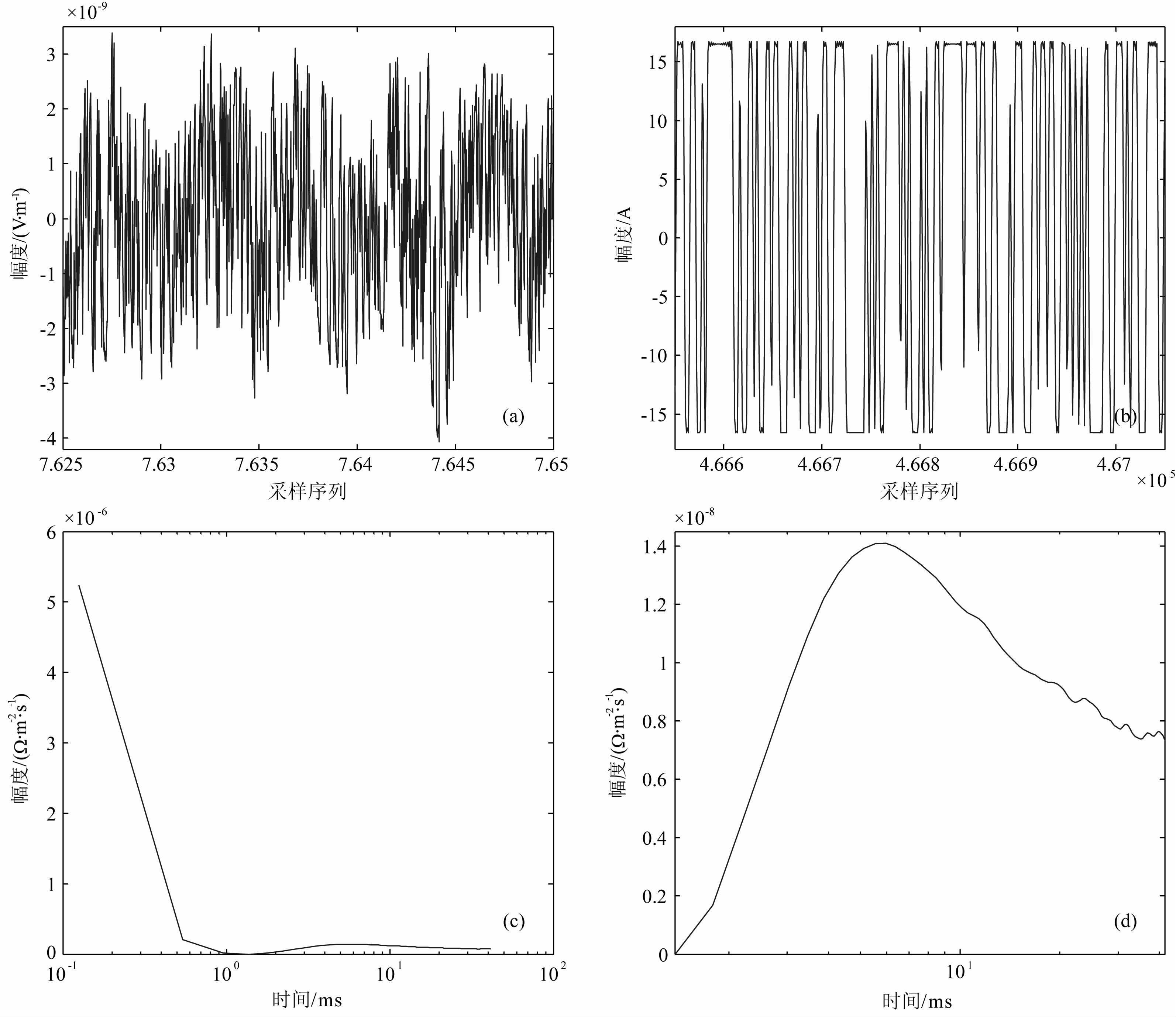
在实际工作中,一次独立的发射过程主要包含三个参数:阶数n、码元宽度ts以及循环发射次数Ncyc,即循环发射Ncyc次参数为n和ts的m序列.在发射过程中,一方面由于发射系统的外部阻抗环境(尤其对于电性源)对于发射波形中不同频率成分的阻抗特性不一致,导致不同频率成分与地下的耦合 特性不同;另一方面,不同的发射时间和地点,系统外部阻抗环境也不同.因此,对每一次独立发射过程,均需要对实际发射电流波形Iw(t)与大地响应Iw(t)*g(t)进行完整观测,并将两者观测数据Tx(t)与Rx(t)整体应用于数据处理中(Wright et al.,2002; Ziolkowski et al.,2006).
然而,与常见m序列自相关函数(隐含周期性条件)不同,有限次循环m序列的整体自相关为非周期函数(如图 3),其包含若干幅度不同的类δ(t)函数尖峰,同时在各尖峰两侧存在具有震荡特性的旁瓣.在实际工作中,由于大地对发射电流的畸变作用以及受接收机htr(t)特性的影响,发射自相关旁瓣的震荡将更为复杂.由公式(4)可见,收发互相关是大地冲激响应g(t)与发射自相关的卷积,故自相关旁瓣的影响也会随着卷积过程进入收发互相关,从而导致无法按照基本相关辨识方法直接从收发互相关中高精度地提取出大地冲激响应.
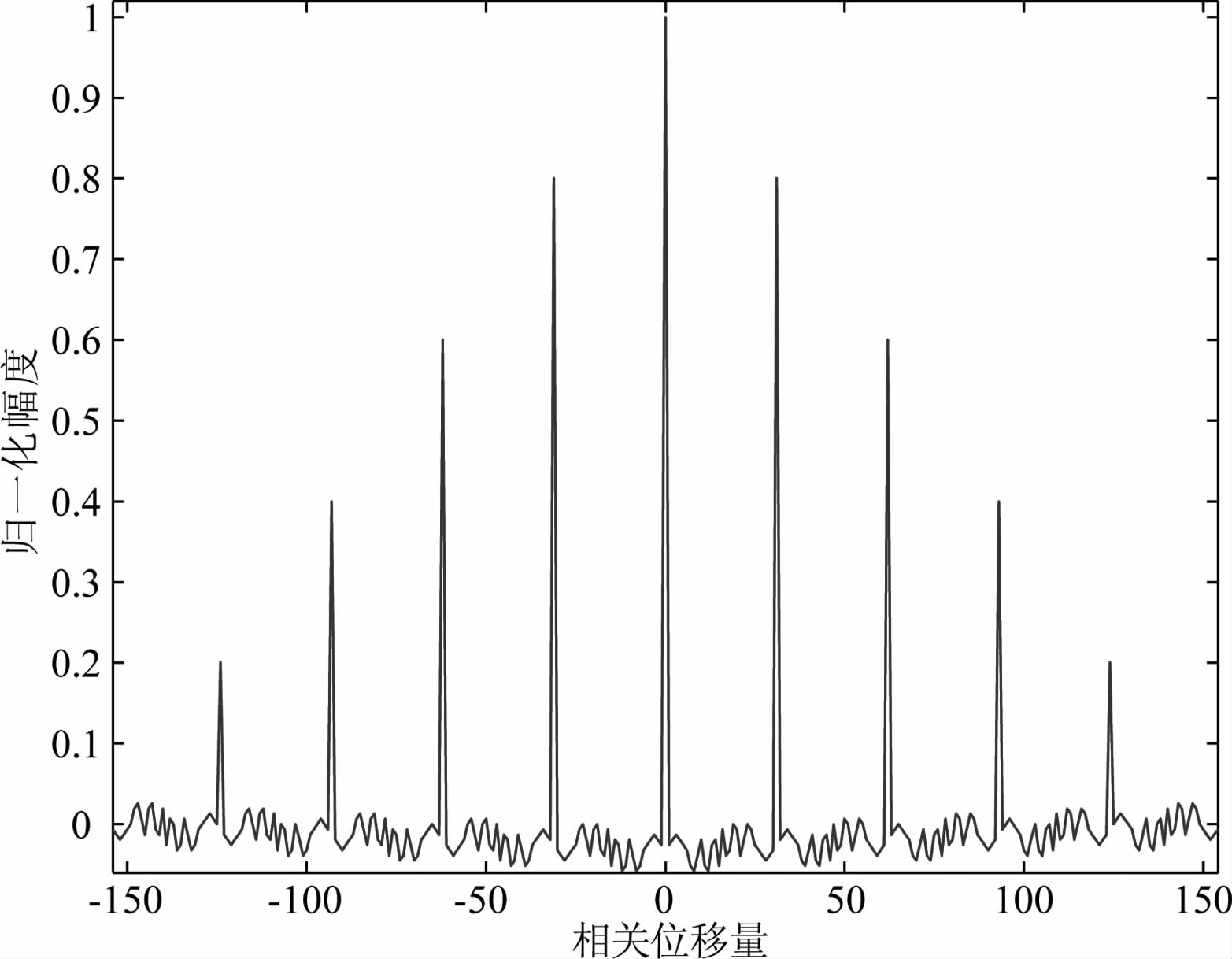 |
图 3 连续循环5个周期m序列的整体自相关 Fig. 3 Auto-correlation of an m sequence including 5 continuous cycles |
作为一种基于系统辨识的方法,本文并未使用术语“系统响应”描述使用接收机观测实际发射电流波形的过程.在早期MTEM研究(项目THERMIE project OG/0305/92/NL-UK)中使用术语“系统响应”源自Strack的著作((Strack,1992)),认为大地冲激响应是输入信号,而由实际发射波形与数据采集设备整体引起的对大地冲激响应观测的失真总效果是系统.此系统可被看作一个滤波器,其响应即“系统响应”.由于要求上述滤波器中仅包含收发系统的特性,在早期Duncan的研究中将之称作“零大地异常滤波器”.可见,使用术语“系统响应”,即认为对大地冲激响应的提取过程是对输入信号的重构.而本文所讨论的方法认为大地为待辨识系统,实际发射电流观测波形Tv(t)是对辨识输入信号Iw(t)的观测.因此,尽管实现“系统响应”观测和“实际发射电流波形”观测的方法类似,但其体现的大地冲激响应提取逻辑并不相同.
对于公式(5),基于Wiener-Hopf方程计算Rx(t)与Tx(t)的互相关,得到:
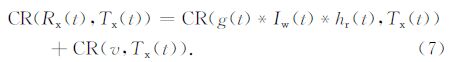
根据互相关的性质,因为Tx(t)为实信号,有:
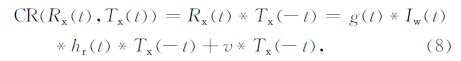
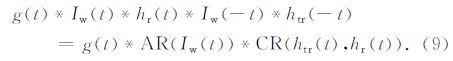
由公式(9)可见,收发互相关中除了大地冲激响应外,实际还包含了:(1)实际发射波形Iw(t)的自相关;(2)用于记录发射波形的接收机与用于观测大地响应的接收机系统响应之间的互相关.其中,htr(t)和hr(t)可以在实验室中观测得到,但Iw(t)无法独立获得.在实际操作中,一种简便的方法是使用实际观测到的发射波形自相关AR(Tx(t))来替代AR(Tw(t))*CR(htr(t),hr(t)),即:
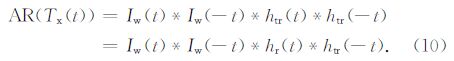
将公式(10)带入公式(9),则有:
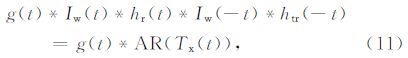
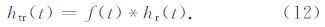
根据公式(12),可在相关计算前使用关系函数f(t)对响应Rx(t)进行处理,得到公式为
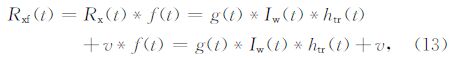
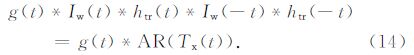
基于公式(12)得到公式(14)的形式与公式(11)相同,以此为基础,公式(8)可改写为
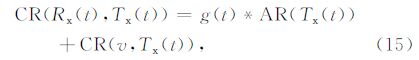
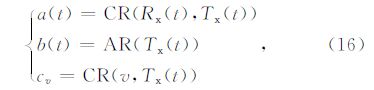
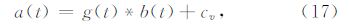
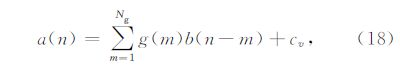
将公式(18)矩阵化,可得:

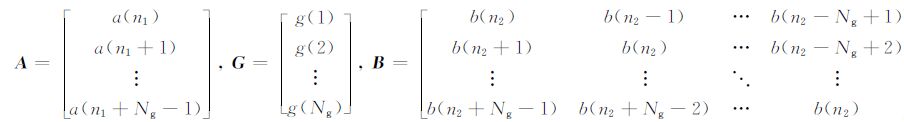
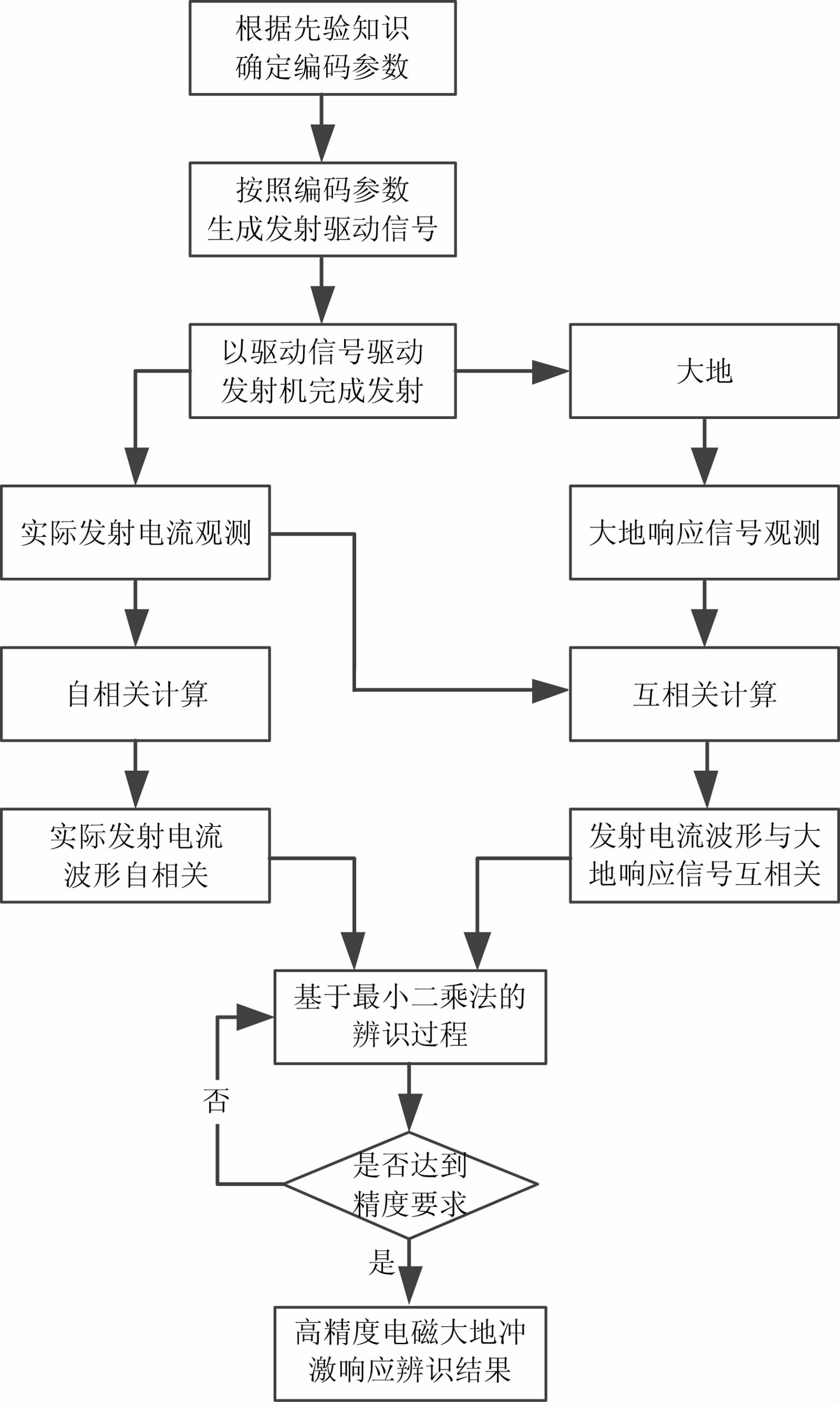 |
图 4 基于自相关旁瓣去除的大地 Fig. 4 Block diagram of the identification method for earth impulse response based on cancellation of auto-correlation sidelobes |
假设使用m序列对电性源EM方法发射波形进行编码,发射电极间距1000 m,发射电流10 A.在发射电极轴向延长线上布设观测点(X轴向),观测点距收发电极中心1000 m.观测电场X分量,观测电极间距为单位长度,其他计算参数如表 1.
参考文献
|
 2015,Vol. 58
2015,Vol. 58