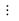2. 中国地质大学(武汉)湖北省地球内部多尺度成像重点实验室, 武汉 430074
2. Hubei Subsurface Multi-scale Imaging Key Laboratory, China University of Geosciences, Wuhan 430074, China
1 引言
浅地表不仅与人类活动息息相关,而且直接支撑着人类生存和发展的需要.人类在上面行走、耕种、钻孔、开挖(再开挖)、充填(再充填)、建筑、取水、注水、排污、注气、采矿以满足其日益提高的物质要求.人类已经认识到当最后一滴石油从地下取出的时候,人类还是需要清洁的水;当不断在地球表面“装修”的时候,还是需要同浅地表和谐共存.随着中国经济的高速发展和城市化进程的加快,浅地表大约100 m厚的物质以不同方式改变原本的状态.利用地球物理参数精确确定这个状态对于建立可靠的水文模型,建设坚固的工程设施,从事对地球资源的精确勘探和有责任开采,以及最终改善人类的生存环境和社会的可持续发展至关重要.
浅地表最关键地震参数是横波速度.Imai和Tonouchi(1982)曾在一个堤岸冲击层、洪积层以及第三纪沉积层中研究纵波和横波速度,证明了横波速度与N值的相关性.N值是土壤机理和基础工程的地层硬度指数.横波速度也是评估浅层界面动力学特征的一个重要参数(Yilmaz et al., 2006),并为地震划区提供依据.又如,通用建筑准则(Uniform Building Code,简称UBC)和欧盟规范(Eurocode8,简称EC8)均利用了VS30(地表到地下30 m的平均横波速度),根据地震工程用地类型设计的不同目的,对场地进行分类.在石油勘探方面,浅地表的地层具有滤波器的作用,模糊深部反射的信息.因此,获得精确的浅地表速度对消除这种模糊效应是十分重要的.过去40多年,浅层SH折射波法是环境与工程地球物理界常用的确定浅地表的横波速度的方法.但该法存在两个致命弱点: 1)地层略有倾斜时波型转换不可避免,此时由折射波确定的速度是转换波(P波)的速度(Xia et al., 2002a),而横波速度则无法确定;2)在有低速层存在的情况下,折射波不存在.同时,由于SH折射波法仅利用初至波到达时的信息,产生的横波速度的分辨率和精度都较低,已不能满足对浅地表介质精细刻划的要求.
反演地震形成的面波(瑞雷波和/或勒夫波)预测地壳和上地幔的横波速度方法早在20世纪60年代就被提出(Dorman and Ewing, 1962;Lee and Solomon, 1979),并有系统的研究和讨论(Aki and Richards, 1980).利用勒夫波和瑞雷波的群速度对我国的地壳厚度进行研究也始于20世纪60年代(宋仲和和谭承业,1965),以及后来的关于反演勒夫波频散曲线确定地球内部构造的研究(石耀霖和金文,1995).陈运泰(1974a,1974b)在对多层各向同性弹性介质中的地震波的研究中导出了勒夫波的频散方程以及点源辐射下的勒夫波的位移谱表达式及其各项的物理意义,并提出可以将勒夫波用于震源深度、震源机制和地壳及上地幔的研究中.
反演高频面波获取浅地表横波速度的研究始于20世纪80年代.迄今为止,此项技术的研究重点是瑞雷波.Song等(1989)尝试了利用规则排列的多道采集系统来估计浅地表横波速度的方法.20世纪90年代初,美国堪萨斯大学开展了利用面波多道分析方法(Multichannel Analysis of Surface Waves,MASW)确定浅地表横波速度的系统研究.此项高频面波技术受到浅地表地球物理界的极大关注.一个层状地球模型的瑞雷波的相速度取决于频率和四组模型参数(P波速度、SV波速度、层密度、层厚度).对雅克比(Jacobian)矩阵的分析可知影响高频(大于1 Hz)瑞雷波相速度的主要因素是横波速度(Xia et al., 1999),因此反演高频瑞雷波相速度可估计浅地表横波速度.Xia等(2002b)研究结果表明瑞雷波多道分析方法可得到较可靠的横波速度(与直接钻井测量值相比,差异小于15%).横波速度模型的精度可以通过多阶模式数据的联合反演获得提高(Xia et al., 2000,2003; Beaty et al., 2002;Song et al., 2007;Luo et al., 2007;鲁来玉等,2006;凡友华等,2007).该方法已被用于解决一系列浅地表地球物理和地质问题(Yilmaz et al., 2006;杨成林,1993;Miller et al., 1999;Beaty and Schimitt, 2003;Ivanov et al., 2006b).相对于钻井而言,它是一种非侵入性、无损、高效、低成本,具有较高精度的地球物理方法.在城市化高速发展的中国,它的应用范围广阔,发展潜力巨大.
近20年来,大量有关瑞雷波的研究问世.如:层状介质中面波的能量分布(张碧星等, 1997,1998),P-SV波展平变换的精确求解(黄慧和陈晓非,2008),讨论瑞雷波反演(石耀霖和金文,1995;Xia et al., 1999;陈祥和孙进忠,2006),瑞雷波的数值模拟研究(Xu et al., 2007;周竹生等,2007;熊章强等,2008;赵海波和王秀明等,2008;Zeng et al., 2011a;高静怀等,2012),时间-空间域中的全波场反演(Zeng et al., 2011b)和在频率-速度域的频散能量反演(Ryden and Park, 2006),浅地表品质因子Q(Xia et al., 2002c),SH折射波调查中的误区(Xia et al., 2002a),岩洞的探测和面波的绕射(Xia et al., 2004,2007a;赵成刚等,2008),折射波和瑞雷波的联合反演(Ivanov et al., 2006b),连续地球模型横波速度估计(Xia et al., 2006a),利用群速度估计浅地表横波速度(Luo et al., 2011;鲁来玉等,2014; 余大新等,2014),地形对瑞雷波/勒夫波传播的影响(刘国利和刘殿魁,1994;周红和陈晓非,2007;Zeng et al., 2012),波场数据的采集的研究(关小平等,1993;Tian et al., 2003;Lin et al., 2004;Xia et al., 2006a,2006b;Xu et al., 2006,2009),关于微动中面波的研究和应用(徐佩芬等, 2012,2013;王小龙等,2013;周晓华等,2014),以及面波和其他地球物理资料联合反演(郭震等,2015).
对高频勒夫波的研究远落后于瑞雷波.一个层状地球模型的勒夫波的相速度取决于频率和三组模型参数(SH波速度、层密度、层厚度),而与P波速度无关(Aki and Richard, 1980).就理论而言,较少的参数可使求得的横波速度更可靠.然而在浅层地球物理学界,人们对浅地表勒夫波的关注明显少于瑞雷波(Steeples,2005),这主要是因为瑞雷波数据比SH波数据更易获得.随着数字地震仪和检波器的灵敏度提高,采集高质量的SH波数据已不再是想象的那么困难了(Xia et al., 2012).近些年关于高频勒夫波研究已出现在一些文献中.如:多孔分层半空间中由于流体黏度而造成衰减的勒夫波频散方程(Wang and Zhang, 1998),属性呈线性变化的非均匀流体饱和多孔半空间中的勒夫波的频散方程(Ke et al., 2006),反演勒夫波改进横波速度估计结果(Safani et al., 2006),联合反演瑞雷波和勒夫波(Misiek et al., 1997),用勒夫波的反演数据测量海洋沉积物的声波特性的变化(Winsborrow et al., 2003),以及模拟高频勒夫波(Luo et al., 2010).高频勒夫波的模拟为研究时间-空间域中勒夫波的反演开拓了道路.Eslick等(2008)根据他们的波场实例,认为最薄层厚度为1 m的浅地表低速层的存在是可记录5~50 Hz频率范围内的实用勒夫波数据所必需的条件.对高频勒夫波的分析可为浅地表地球物理研究提供横波参数.由此,它理应获得与瑞雷波分析相同的关注.Xia等人(2012)提出的勒夫波多道分析方法(Multichannel Analysis of Love Waves,MALW)就是利用SH波的数据对勒夫波进行分析从而获得浅地表精细横波速度模型.浅层SH波的数据含有强大的高频勒夫波能量,通过反演高频勒夫波可以获得浅地表横波参数.
在利用高频面波确定浅地表精确的横波速度的研究领域中,浅地表地球物理学家面临着一批正在研究和亟待解决的关键问题.对高频勒夫波进行类似瑞雷波的系统的研究还没有开始.在瑞雷波勘探中,模式的误判——如“模式接吻”(Xia et al., 2006b;Zhang and Chan, 2003)和泄漏波的存在而引发反演的横波速度变大的问题(Gao et al., 2014)已 引起广泛的关注.需要寻找解决高速夹层(Calderón-Macías and Luke, 2007)和低速夹层模型(Lu et al., 2007;Liang et al., 2008)反演问题的有效方法.如何提高反演横波速度模型的水平分辨率是一个从MASW方法问世的时候就提出的问题(Xia et al., 2005).倾斜叠加(Xia et al., 2007b)和高分辨率拉东变换(Luo et al., 2008)为生成频散能量图提供了新的方法.高分辨率拉东变换(Luo et al., 2008)进行模式分离对提高反演横波速度模型的水平分辨率极具潜力,是一个值得深入研究的方向.被动源面波层析成像(Shapiro et al., 2005;Chevrot and Zhao, 2007)和评估反演的模型(Xia et al., 2005,2008,2010)也是目前的研究热点.最近浅地表地球物理学家开始研究利用三维高频面波数据的有效途径.
近年来,中国地质大学(武汉)浅地表地球物理团队针对上述问题的研究取得了一系列成果,使我们对高频面波的认识更加完整并可推动该方法在环境和工程领域的进一步应用.这篇综述论文将介绍 在泄漏波、虚震源法、勒夫波多道分析方法(MALW)、 瑞雷波和勒夫波的勘探深度同波长的关系和时间域勒夫波反演方面的进展.因篇幅有限,关于速度倒转类型(高速地层位于低速地层之上)的地球模型的频散曲线计算方法和对该类地球模型敏感度的研究成果将另文介绍.
2 泄漏模式面波引起的模式误判泄漏模式面波通常存在于未固结的浅地表沉积物中.从理论上讲,它仅存在于泊松比大于0.26的介质中.Roth和Holliger(2000)的研究表明在高泊松比介质中,在近炮检距记录中会出现一种非几何波.该非几何波的波速大约是表层介质S波速度的2倍.这个结论提供了确定浅地表S波速度的快速有效方法.通过求解瑞雷波方程和数值模拟实验,我们分析了均匀半空间介质中的瑞雷波相速度,证明了这种存在于近炮检距记录中的非几何波实际上是一类泄漏模式波,非几何波与泄漏模式面波的理论相速度值(表 1)之间的差距几乎可以忽略(Gao et al., 2014).泄漏波的速度(表 1中复数根的实部)约为均匀半空间S波速度的1.9倍.泄漏波在f-v域中的能量通常出现在低频段,且往往与该段的瑞雷波能量重合并延伸(Gao et al., 2014).因此,我们很容易将泄漏波能量误认为瑞雷波能量,从而导致错误的反演结果.
|
|
表 1 频散方程随着不同泊松比所得到的根(VS 表示S波速度) Table 1 Roots of Rayleigh equation vary with different Poisson′s ratios(VS st and s for S-wave velocity) |
为了获得浅地表介质S波速度,我们在美国怀俄明州进行了一次面波勘探.在炮集记录中(图 1a)同时包含较强的瑞雷波信号及泄漏波信号(非几何 波,图 1a 中圈内).在该炮集对应的频散能量图(图 1b)中 的低频段内,存在着速度为500 m·s-1至800 m·s-1 的额外的能量团.该能量团正是由于泄漏波的存在而造成.如果我们误将泄漏波能量当作瑞雷波能量,则会获得一个错误的较真实模型而言具有更高S波速度的反演结果.
 | 图 1 怀俄明地区实测数据 (a)在怀俄明地区采集的地震数据,红色线框表示泄露波(非几何波);(b)由(a)中的炮集记录提取的频散能量图.红色线框范围内表示 由于泄露波的存在引起的能量团.绿色圆点和三角分别表示 用反演结果正演所获得的基阶和一阶高阶的相速度值.黄色三角表示用反演结果正演所获得的泄露波相速度值. Fig.1 Raw data in Wyoming (a)Raw data acquired from Wyoming,signals in the red circle are leaky waves(non-geometric wave);(b)A dispersive image of raw field data(a). The red circle represents for the leaky-wave energy. The green solid dots and triangles represent the theoretical fundamental mode and first higher mode of Rayleigh wave,respectively. The yellow triangles represent leaky surface wave. |
通过反演多道高频瑞雷波的相速度可以得到近地表的S波速度.采用类似共深度点滚动排列的方式采集面波数据,我们将反演得到的S波速度按一定的顺序排列可以得到横波速度剖面,但是这就要求进行大量的数据采集工作.地震干涉法(虚源法)是地球物理发展中的一个重大进展,丰富了地震波 传播规律的认识和研究.地震干涉法(Snieder,2004)的基本思想就是利用互相关方法提取任意两个检波器之间的脉冲响应.这个脉冲响应可以认为是在其中一个检波器处放置了一个虚震源,而在另一个进行接收.在油气勘探中,地震干涉法可以消除近地表复杂地质条件的影响,直接利用新构建的地震记录获得更高精度的地下地质构造成像(Bakulin and Calvert, 2004,2006).虚震源法通过互相关技术获得两道之间的经验格林函数.在瑞雷波主动源勘探方面,地震干涉法应用的比较少.我们提出了一种虚震源瑞雷波勘探方法,其基本思想就是利用人工源得到的地震炮集记录,通过各道与其中一道进行互相关得到对应的虚源炮集记录.
我们通过直接推导互相关函数证明了和的相关不等于相关的和.瑞雷波在非均匀介质中具有多阶性.由于高基阶瑞雷波具有一定的相关性,直接利用两道的地震记录进行互相关计算得到的结果并非是地下介质的经验格林函数,而是基阶瑞雷波格林函数,高阶瑞雷波格林函数,以及高基阶瑞雷波相关函数之和.要获得真正的面波格林函数,必须先对瑞雷波进行高基阶分离,再分别对单一阶态(模式)的瑞雷波信号进行互相关处理获得单一阶态的格林函数,再通过求和来获得瑞雷波格林函数.
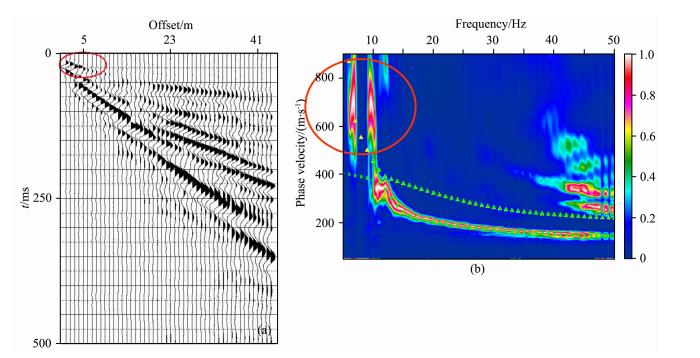
高分辨率线性拉东变换(Luo et al., 2008,2009)是保幅、保角并且快速高效的方法,为各模式波的分离和重构提供了基础.从图 2a和2b中可以看到,未经分离的原始炮集记录的互相关函数存在很大的差别.在互相关运算之前,先利用高分辨率线性拉东变换进行模式分离,再将各阶模式瑞雷波通过高分辨率线性拉东变换的逆变换重构成对应模式的炮集记录,然后对重构以后的地震记录进行互相关操作,就可以避免虚假信息的出现.我们提取了经过高分辨率线性拉东分离以后的炮集记录的第3道和第13道,第13道和第23道,第23道和第33道之间的互相关函数进行对比,结果如图 2c所示.可以明显看到,三个互相关结果基本吻合.我们还提取了不同震源情况下的第3道和第13道的互相关函数进行对比,其结果如图 2d所示.与图 2a和2b相比,互相关结果得到了明显的改善,三个互相关结果基本吻合.这也证明了利用高分辨率线性拉东变换进行模式分离以后提取瑞雷波格林函数的有效性.
 | 图 2 互相关函数结果对比图 (a)表示直接利用原始炮集记录对同一震源所得的三个不同位置(第3道和第13道,第13道和第23道,第23道和第33道)的检波器对的互相关结果;(b)表示直接利用原始炮集记录对不同震源所得炮集记录的相同位置检波器对的互相关结果;(c)表示利用分离以后的结果对同一震源所得的三个不 同位置的检波器对的互相关结果;(d)表示利用分离以后的结果对不同震源所得的相同位置检波器对的互相关结果. Fig. 2 Comparisons of cross-correlation results (a)Cross-correlation results of three pairs of receivers in original shot gather obtained by the same source(Trace 3 and Trace 13,Trace 13 and Trace 23,Trace 23 and Trace 33);(b)Cross-correlation results of the same pair of receivers in original shot gathers obtained by the different sources;(c)Cross-correlation results of three pairs of receivers in reconstructed shot gather obtained by the same source(Trace 3 and Trace 13,Trace 13 and Trace 23,Trace 23 and Trace 33);(d)Cross-correlation results of the same pair of receivers in reconstructed shot gathers obtained by the different source. |
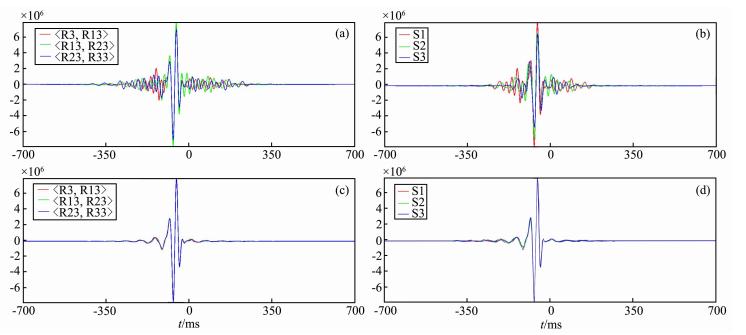
为了验证虚震源瑞雷波勘探方法的可行性,我们将原始炮集记录的第一道作为虚震源所在位置,其他地震道和第一道进行互相关,将所得结果和在第一道处放置一个真实震源进行对比.从图 3a可以看到,虚源法得到的炮集记录和真实震源炮集记录吻合较好.我们分别提取了虚源炮集记录(图 3b)和真实震源(图 3c)得到的炮集记录的频散曲线,分别和理论相速度进行对比,两者吻合较好,而真实震源记录由于炮检距较小,在低频范围内吻合不是很好.数值模拟实验证明了虚源法瑞雷波勘探的可行性.利用虚震源瑞雷波法来获得横波速度剖面可极大地减少野外资料采集的成本.
 | 图 3 虚震源得到的炮集和频散能量图 (a)虚源炮集记录和真实震源炮集记录之间的对比;(b)虚源炮集记录提取得到的频散曲线和理论相速度之间的对比; (c)真实震源炮集记录提取得到的频散曲线和理论相速度之间的对比.绿色圆点表示理论相速度. Fig. 3 The shot gather and the dispersion images obtained by virtual source method (a)Comparison between the virtual source shot gather and real source shot gather;(b)Comparison between the dispersion image obtained by virtual source shot gather and the theoretical phase velocities;(c)Comparison between the dispersion image obtained by real source shot gather and the theoretical phase velocity. The green dots represent for the theoretical phase velocities. |
勒夫波是一系列SH波(水平方向S波)相互干涉后的结果.层状地球模型中勒夫波的相速度是一个包含频率和三组模型特性参数(SH波速度、密度、层厚度)的函数.由于勒夫波的频散性与纵波速度无关(Aki and Richards, 1980),这一特性可减少反演的横波速度模型的非唯一程度.对于一个层状地球模型,勒夫波除了与纵波速度无关外,还具有以下的特点:高频率相速度的渐近线趋于第一层的横波速度,低频率的相速度的渐近线趋于半空间的横波速度.Xia等(2012)提出的勒夫波多道分析方法(MALW)就是利用SH波的数据对勒夫波进行分析从而获得浅地表精细横波速度模型.
由于勒夫波的频散性与纵波速度无关,在实际应用中,勒夫波相比瑞雷波其能量图像通常更清晰,并且具有更高的分辨率,从而可以更容易地拾取精确的勒夫波相速度.在中国地质大学(武汉)校园内,我们做了一个对比试验.地震仪记录了48道道间距为1 m,最小偏移距为2 m的高频面波数据.记录勒夫波的检波器是4.5 Hz水平检波器,记录震动方向垂直于测线,震源是5 kg重锤敲击嵌入地表的1 m长的木桩两头,木桩放置方向垂直于测线(图 4a);记录瑞雷波的检波器是2 Hz垂直检波器,震源是5 kg重锤敲击30 cm见方的树脂板(图 4b).原始记录中勒夫波(图 4a)的连续性和线性性都比瑞雷波的(图 4b)好.在频率-速度域中,勒夫波频散能量(图 4c)比瑞雷波的(图 4d)更清晰,并具有更高的分辨率,同时频带更宽.
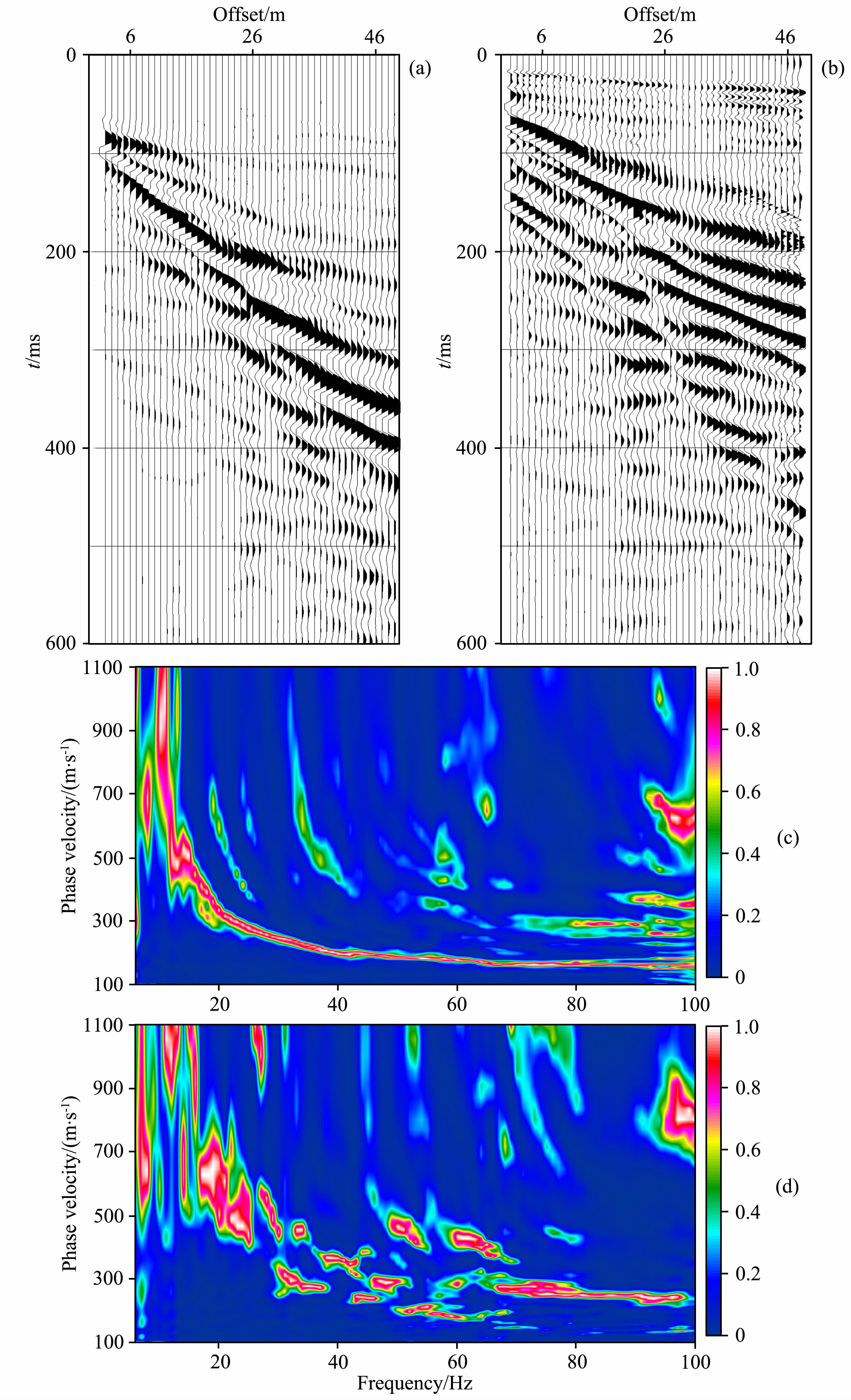 | 图 4 中国地质大学(武汉)校园内沿同一测线采集的数据 (a)高频勒夫波数据;(b)高频瑞雷波数据;(c)勒夫波频散能量图;(d)瑞雷波频散能量图. Fig. 4 Shot gathers and dispersion images obtained in China University of Geosciences campus (a)High-frequency Love wave shot gather;(b)Higher-frequency Rayleigh wave shot gather; (c)Dispersion image of Love wave;(d)Dispersion image of Rayleigh wave. |
勒夫波频散曲线较瑞雷波的简单.用一个浅地表常见的两层模型(软土层覆盖在基岩上)来说明这 个特性.这个模型的第一层的参数: VS=150 m·s-1,VP=300 m·s-1,ρ=1500 kg·cm-3,层厚度10 m; 半空间的参数: VS=450 m·s-1,VP=900 m·s-1,ρ=2000 kg·cm-3.瑞雷波基阶相速度同一阶高阶相速度在6 Hz处几乎相同(图 5a).依目前频散能 量图分辨能力,在频散能量图上很难区分瑞雷波基阶相速度(313 m·s-1)和一阶高阶相速度(326 m·s-1). 这种现象称为“模式接吻”(Xia et al., 2006b).“模式接吻”是瑞雷波多道分析方法中一个容易引起模式误判的异常现象,它导致反演的横波速度比真实值高.然而在勒夫波能量的图像中“模式接吻”现象的出现比瑞雷波的少(图 5b).
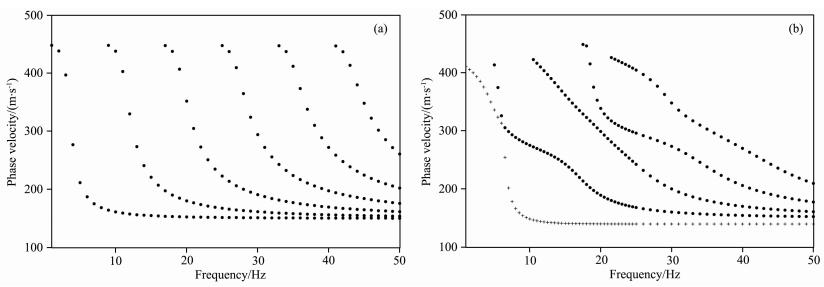 | 图 5 一个基岩上覆软土层模型的瑞雷波和勒夫波频散曲线 (a)勒夫波频散曲线;(b)瑞雷波频散曲线.在瑞雷波频散曲线图上,6 Hz处基阶相速度(“+”表示)几乎同一阶高阶相速度(“实心圆点”表示)一样.此现象称为“模式接吻”. Fig. 5 Rayleigh-wave and Love-wave dispersion curves of a two-layer model with a soft-soil layer overlaying a bedrock (a)Love-wave dispersion curves;(b)Rayleigh-wave dispersion curves.In the dispersion image,at the 6 Hz,the fundamental mode phase velocity is almost same with the first higher mode phase velocity,which is the “mode kissing” phenomenon. |
勒夫波频散曲线与纵波速度无关使得勒夫波的反演比瑞雷波的更容易、对初值的要求更低和反演也更稳定.图 6a是一个在美国华盛顿州采集的SH折射波的数据(只需初至波到达时).尽管没有完整记录勒夫波,但其能量图很清晰并具有很高的分辨率(图 6b).按Xia等(1999)确定瑞雷波初始模型的公式,确定初始模型(图 6c).仅2次迭代,均方根差从45 m·s-1 降到5 m·s-1.折射波法和钻井的结果均支持反演所得的模型.
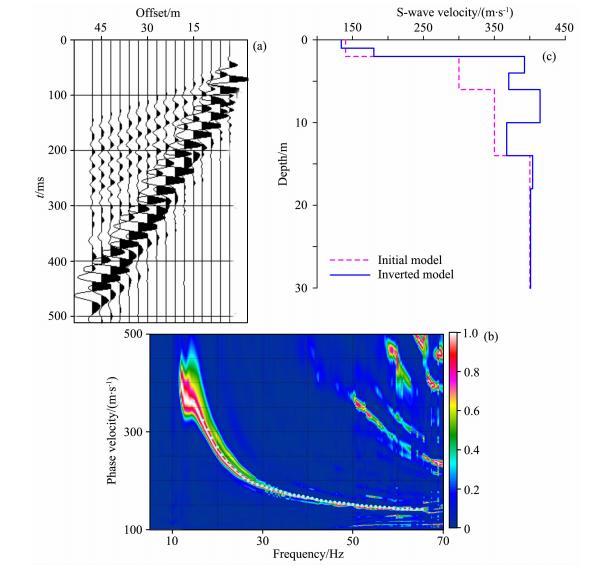 | 图 6 华盛顿州采集的SH折射波的数据 (a)原始炮集记录;(b)频散能量图;(c)根据Xia等(1999)确定瑞雷波初始模型的公式,确定初始模型(红虚线). 仅2次迭代,均方根差从45 m·s-1降到5 m·s-1,获得反演模型(实线). Fig. 6 The SH-wave data obtained from Washington (a)The raw shot gather;(b)The dispersion image;(c)The initial model according to the formula proposed by Xia et al.(1999) (red dotted line). RMS error decrease to 5 m·s-1 from 45 m·s-1 after 2 iterations,then get the inversion model(solid line). |
雅克比矩阵的归一化行向量反映了某一波长分量的面波对勘探到不同深度的灵敏度,这里将归一化行向量的最小值降低到0.001时所对应的深度定义为某一波长分量的最大勘探深度(Xia et al., 2003).
我们针对Xia等(1999)的六层模型(表 2)讨论瑞雷波和勒夫波的探测深度.图 7和图 8分别表示瑞雷波和勒夫波的基阶和一阶高阶模式波对某一特 定波长在不同深度的灵敏度.对于基阶模式波,8.76 m 波长的基阶模式瑞雷波可穿透至12.8 m(图 7a),而相同波长的基阶模式勒夫波的勘探深度仅为9.6 m(图 8a).波长12.31 m的基阶模式瑞雷波的勘探深度为17 m(图 7a),而12.31 m波长的基阶模式勒夫 波的勘探深度仅为12.8 m(图 8a).灵敏性分析表明,相同波长的基阶模式瑞雷波比勒夫波探测深度深.
|
|
表 2 一个六层模型的参数(计算勒夫波时,不计 VP) Table 2 Parameters of six-layer earth models(For Love waves,P-wave velocities are ignored) |
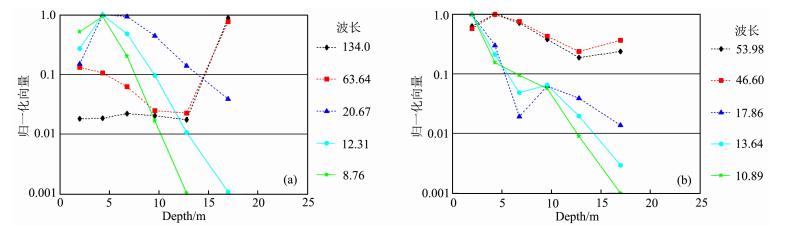 | 图 7 瑞雷波的某一特定波长成分在不同深度的灵敏度 (a)基阶;(b)一阶高阶. Fig. 7 The sensitivities at different depth of Rayleigh-wave data for a certain wavelength (a)The fundamental mode;(b)The first higher mode. |
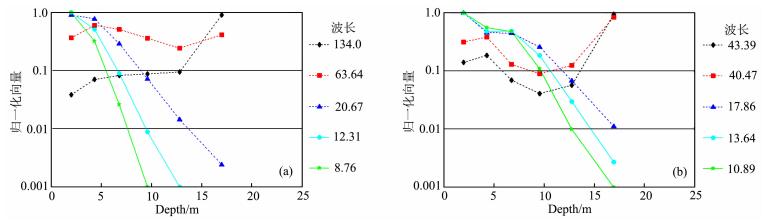 | 图 8 勒夫波的某一特定波长在不同深度的灵敏度 (b)基阶;(b)一阶高阶. Fig. 8 The sensitivities at different depth of Love-wave data for a certain wavelength (a)The fundamental mode;(b)The first higher mode. |
为了进一步定量分析基阶模式瑞雷波与勒夫波勘探深度的差异,我们选取了五个波长分量进行灵敏性探究.根据瑞雷波和勒夫波相关的雅克比矩阵的归一化行向量,确定每一波长分量对应的最大勘探深度(表 3).研究结果表明对于给定波长的基阶模式瑞雷波的勘探深度是基阶模式勒夫波的1.3~1.4倍(Yin et al., 2014).
|
|
表 3 不同波长时瑞雷波和勒夫波的不同探测深度 Table 3 Different penetrating depth of Rayleigh wave and Love wave with the different wavelength |
对于瑞雷波探测深度的研究表明,相同波长时高阶模式瑞雷波比基阶模式瑞雷波探测深度深(Xia et al., 2003).对于勒夫波,波长为12.31 m的基阶模式波的最大勘探深度为12.8 m(图 8a).波长为10.89 m的一阶高阶模式波可探测到17 m的深度(图 8b).然而波长为8.12 m的二阶高阶模式波即可穿透至17 m的深度.基于勒夫波雅克比矩阵的行向量分析,证明高阶模式勒夫波比基阶模式勒夫波穿透深度深,这同瑞雷波的特点一致.由于高阶模式的瑞雷波和勒夫波主要受横波速度的影响(Kennett and Clarke, 1983),相同波长的高阶模式瑞雷波和勒夫波可勘探到相同深度.
6 勒夫波波形反演勒夫波多道分析方法(MALW)(Xia et al., 2012)通过反演勒夫波频散曲线获得地下S波速度信息.由于频散曲线的正演是基于水平层状地球模型进行的(Schwab and Knopoff, 1970),这导致勒夫波多道分析方法只适用于水平层状模型或波速缓变的介质模型.我们提出直接对勒夫波波形进行反演,通过基于波动方程的数值模拟技术(Luo et al., 2010)及合适的最优化算法直接拟合勒夫波波形,从而获得地下介质S波速度分布情况.该方法不需要水平层状模型假设,适用于任意二维弹性介质模型.
地震波全波形反演中有两个比较关键的问题:地震子波的拾取及最优化算法的选择.由于很难从面波信号中恢复精度较高的子波信号,我们采用反卷积算法去除了子波对波形反演的影响.选取炮集记录中的第一道(最小炮检距道)作为参考道,将其余道地震波信号与该参考道地震波信号进行反卷积(在频率域中相除),反卷积后的波形中则去除了子波对波形的影响.将反卷积后的实测波形与反卷积后的模拟波形在二范数下的差异定义为目标函数,并采用共轭梯度算法(Gilbert and Nocedal, 1992)作为最优化算法进行反演.共轭梯度算法是一类局部线性化算法,该方法较为稳定且收敛速度较快,但它的成功依赖于初始模型的选择.通过勒夫波多道分析方法,我们往往可以建立一个与真实模型较为接近的初始模型,从而为波形反演的成功提供了前提条件.将地下介质模型按照勒夫波分辨能力剖分成大小随深度的增加而增大的若干个块体(本文中 选择的块体大小由浅至深依次为1 m×1 m、 1 m×1.5 m、 1.5 m×1.5 m、1.5 m×2 m、2 m×2 m、2 m×3 m和3 m×3 m(前一个数值代表深度方向,后一个数值代表水平方向),通过更新每个块体的S波速度来寻找目标函数值靠近初始模型的极小值,从而获得地下S波速度的分布.
以一个含垂直断层的两层模型为例来验证该方法的可行性.该模型的震源为30 Hz主频30 ms延迟的雷克子波,20道检波器呈线状排列,最小偏移距为6 m,道间距为1 m.断层位于第8道检波器正下方,表层地层的厚度在断层位置从5 m减小至2 m.断层面上、下方地层的S波速度分别为 200 m·s-1和400 m·s-1,密度均为2000 kg·m-3. 通过二维有限差分数值模拟技术(Luo et al., 2010)获得了该模型的实测地震波形记录.由于密度对勒夫波波形影响较小,我们在反演过程中将密度值设为真值.建立了一个六层层状模型作为初始模型(图 9a),其每层的S波速度从200 m·s-1(表层)随深度的增加而逐渐增大到400 m·s-1(半空间),层厚(m)分别为(1,1,1.5,1.5,2,无穷大).从图 9c中可以看出,初始模型对应的反卷积后的波形与反卷积后的实测波形之间差异较大.对该实测波形进行波形反演,经过100次反演迭代后(图 9b),反演结果清晰地显示出了断层的位置及其深度,断层面上、下方地层的平均S波速度分别为198 m·s-1和388 m·s-1,与真实模型之间的误差很小,且反演结果对应的反卷积后的模拟波形和实测波形基本一致(图 9c).为了更好地模拟实际工作情况,我们对实测数据加入了10%的高斯白噪声,并利用相同的方法对加入噪声后的实测波形进行反演,其结果如图 9d所示.从反演结果中,仍可以清晰地看到断层的位置及其深度的变化,上下地层的S波速度也与真值较为接近.这些数值模拟实验结果证明了该勒夫波波形反演方法的正确性及可行性.
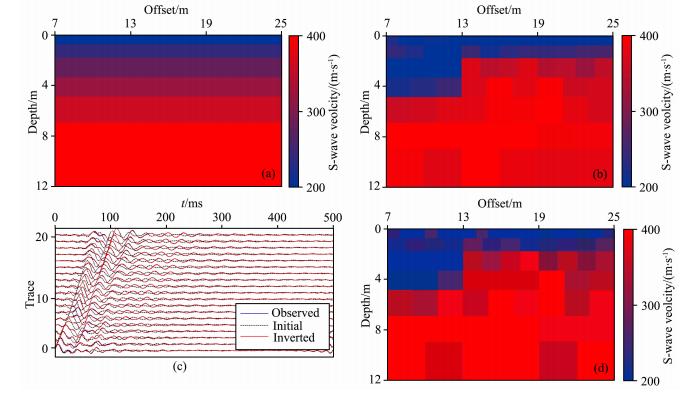 | 图 9 勒夫波全波形反演 (a)初始六层层状模型;(b)无噪声数据经100次迭代后的反演结果;(c)无噪声实测数据,初始模型及反演结果对应的反卷积后的波形;(d)添加10%高斯白噪声的实测数据经100次迭代后的反演结果. Fig. 9 Full waveform inversion of Love wave (a)The initial six-layer model;(b)The inversion result after 100 iterations;(c)Waveform of deconvolved observed data without noise, initial model and inversion result;(d)The inversion result after 100 iterations for observed shot gather with 10% Gauss white noise. |
本文介绍了中国地质大学(武汉)浅地表地球物理团队近年来在研究高频面波的传播理论和应用中取得的部分成果,对面波勘探中会遇到的问题和存在的不足进行了研究和补充.
(1)浅地表应用面波多道分析方法(MASW)时,在高泊松比地区会采集到非几何波,它的存在可能导致分析瑞雷波数据过程中的模式误判.我们需要对这类波格外注意.对原始数据进行例如切除等预处理可以有效地避免这类模式误判的发生.
(2)现行的高频面波滚动采集方式费时费力.我们的研究表明对瑞雷波进行高基阶分离,并将单一阶态(模式)的瑞雷波格林函数求和可以获得真正的瑞雷波格林函数.这一结果为虚源瑞雷波勘探奠定了理论基础,同时,数值模拟实验也证明了虚源瑞雷波法的可行性.虚震源瑞雷波法的潜在优势是可极大地减少野外资料采集的成本.
(3)现行的高频面波方法(MASW)仅利用了瑞雷波信息.我们的研究表明勒夫波多道分析方法(MALW)中由勒夫波数据生成的能量图像通常比瑞雷波的更清晰且具有更高的分辨率,从而提高了频散曲线的拾取精度,提高了反演结果的可靠性.勒夫波的频散曲线比瑞雷波的简单,从而使得勒夫波反演更稳定.较瑞雷波而言,基阶勒夫波勘探深度较 浅,但相同阶数的高阶瑞雷波和勒夫波勘探深度接近.
(4)基于频散曲线反演的高频面波方法仅适用于横向缓变的地球模型.我们提出了时间域勒夫波反演,按照勒夫波分辨率从浅到深降低的特点,将地球模型剖分成从浅到深逐渐变大的块体,并利用反卷积消除地震子波对勒夫波波形的影响.该方法无需水平层状假设,适用于任意二维介质模型,具有极大的潜力.
| [1] | AkiK, Richards P G. 1980. Quantitative Seismology. San Francisco:W. H. Freeman and Company. |
| [2] | Bakulin A, Calvert R. 2004. Virtual source:new method for imaging and 4D below complex overburden.//Proceeding of the 74th Annual International Meeting, SEG, Expanded Abstracts, 2477-2480. |
| [3] | Bakulin A, Calvert R. 2006. The virtual source method:theory and case study. Geophysics, 71(4):SI139-SI150. |
| [4] | Beaty K S, Schmitt D R, Sacchi M. 2002. Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure. Geophysical Journal International, 151(2):622-631. |
| [5] | Beaty K S, Schmitt D R. 2003. Repeatability of multimode Rayleigh-wave dispersion studies. Geophysics, 68(3):782-790. |
| [6] | Calderón-Macías C, Luke B. 2007. Addressing non-uniqueness in inversion of Rayleigh-wave data for shallow profiles containing stiff layers. Geophysics, 72(1):U1-U10. |
| [7] | Chen X, Sun J Z. 2006. An improved equivalent homogenous half-space method and reverse fitting analysis of Rayleigh wave dispersion curve. Chinese Journal of Geophysics (in Chinese), 49(2):569-576. |
| [8] | Chen Y T. 1974a. Seismic waves in multilayered elastic half-space(I). Chinese Journal of Geophysics(Acta Geophysica Sinica)(in Chinese), 17(1):20-43. |
| [9] | Chen Y T. 1974b. Seismic waves in multilayered elastic half-space(II). Chinese Journal of Geophysics(Acta Geophysica Sinica)(in Chinese), 17(3):173-185. |
| [10] | Chevrot S, Zhao L. 2007. Multiscale finite-frequency Rayleigh wave tomography of the Kaapvaal craton. Geophysical Journal International, 169(1):201-215. |
| [11] | Dorman J, Ewing M. 1962. Numerical inversion of seismic surface wave dispersion data and Crust-Mantle structure in the New York-Pennsylvania area. Journal of Geophysical Research, 67(13):5227-5241. |
| [12] | Eslick R, Tsoflias G, Steeples D. 2008. Field investigation of Love waves in near-surface seismology. Geophysics, 73(3):G1-G6. |
| [13] | Fan Y H, Chen X F, Liu X F, et al. 2007. Approximate decomposition of the dispersion equation at high frequencies and the number of multimodes for Rayleigh waves. Chinese Journal of Geophysics(in Chinese), 50(1):233-239. |
| [14] | Gao J H, He Y Y, Ma Y C. 2012. Comparison of the Rayleigh wave in elastic and viscoelastic media. Chinese Journal of Geophysics(in Chinese), 55(1):207-218, doi:10.6038/j.issn.0001-5733.2012.01.020. |
| [15] | Gao L L, Xia J H, Pan Y D. 2014. Misidentification caused by leaky surface wave in high-frequency surfacewave method. Geophysical Journal International, 199(3):1452-1462. |
| [16] | Gilbert J C, Nocedal J. 1992. Global convergence properties of conjugate gradient methods for optimization. SIAM Journal on Optimization, 2(1):21-42. |
| [17] | Guan X P, Huang J Z, Zhou H Q. 1993. Probe the interpretation theory of steady-state Rayleigh wave method in engineering exploration. Chinese Journal of Geophysics(Acta Geophysica Sinica)(in Chinese), 36(1):96-105. |
| [18] | Guo Z, Chen Y S, Yin W W. 2015. Three-dimensional crustal model of Shanxi graben from 3D joint inversion of ambient noise surface wave and Bouguer gravity anomalies. Chinese Journal of Geophysics(in Chinese), 58(3):821-831, doi:10.6038/cjg20150312. |
| [19] | Huang H, Chen X F. 2008. Exact solution of earth-flattening transformation for P-SV waves:Taking surface wave as an example. Acta Seismologica Sinica(in Chinese), 30(2):105-113. |
| [20] | Imai T, Tonouchi K. 1982. Correlation of N-value with S-wave Velocity and shear modulus.//Proceedings of the Second European Symposium on Penetration Testing, 67-72. |
| [21] | Ivanov J, Miller R D, Lacombe P, et al. 2006a. Delineating a shallow fault zone and dipping bedrock strata using multichannal analysis of surface waves with a land streamer. Geophysics, 71(5):A39-A42. |
| [22] | Ivanov J, Miller R D, Xia J H, et al. 2006b. Joint analysis of refractions with surface waves:An inverse solution to the refraction-traveltime problem. Geophysics, 71(6):R131-R138. |
| [23] | Ke L L, Wang Y S, Zhang Z M. 2006. Love waves in an inhomogeneous fluid saturated porous layered half-space with linearly varying properties. Soil Dynamics and Earthquake Engineering, 26(6-7):574-581. |
| [24] | Kennett B L N, Clarke T J. 1983. Seismic waves in a stratified half-space-IV:P-SV wave decoupling and surface wave dispersion. Geophysical Journal International,72(3):633-645. |
| [25] | Lee W B, Solomon S C. 1979. Simultaneous inversion of surface-wave phase velocity and attenuation:Rayleigh and Love waves over continental and oceanic paths. Bulletin of the Seismological Society of America, 69(1):65-96. |
| [26] | Liang Q, Chen C, Zeng C, et al. 2008. Inversion stability analysis of multimode Rayleigh-wave dispersion curves using low-velocity-layer models. Near Surface Geophysics, 6(3):157-165. |
| [27] | Lin C P, Chang C C, Chang T S. 2004. The use of MASW method in the assessment of soil liquefaction potential. Soil Dynamics and Earthquake Engineering, 24(9-10):689-698. |
| [28] | Liu G L, Liu D K. 1994. Dispersion of Love waves in ridge or canyon topography of inhomogeneous medium with a homogeneous layer. Chinese Journal of Geophysics(Acta Geophysica Sinica)(in Chinese), 37(1):461-466. |
| [29] | Lu L Y, Wang C H, Zhang B X. 2007. Inversion of multimode Rayleigh waves in the presence of a low-velocity layer:numerical and laboratory study. Geophysical Journal International, 168(3):1235-1246. |
| [30] | Lu L Y, Zhang B X, Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes. Chinese Journal of Geophysics(in Chinese), 49(4):1082-1091. |
| [31] | Lu L Y, He Z Q, Ding Z F, et al. 2014. Azimuth anisotropy and velocity heterogeneity of Yunnan area based on seismic ambient noise. Chinese Journal of Geophysics(in Chinese), 57(3):822-836, doi:10.6038/cjg20140312. |
| [32] | Luo Y H, Xia J H, Liu J P, et al. 2007. Joint inversion of high-frequency surface waves with fundamental and higher modes. Journal of Applied Geophysics, 62(4):375-384. |
| [33] | Luo Y H, Xia J H, Miller R D, et al. 2008. Rayleigh-wave dispersive energy imaging using ahigh-resolution linear Radon transform. Pure and Applied Geophysics, 165(5):903-922. |
| [34] | Luo Y H, Xia J H, Miller R D, et al. 2009. Rayleigh-wave mode separation by high-resolution linear Radon transform. Geophysical Journal International, 179(1):254-264. |
| [35] | Luo Y H, Xia J H, Xu Y X, et al. 2010. Finite-difference modeling and dispersion analysis of high-frequency Love waves for near-surface applications. Pure and Applied Geophysics, 167(12):1525-1536. |
| [36] | Luo Y H, Xia J H, Xu Y X, et al. 2011. Analysis of group-velocity dispersion of high-frequency Rayleigh waves for near-surface applications. Journal of Applied Geophysics, 74(2-3):157-165. |
| [37] | Miller R D, Xia J H, Park C B, et al. 1999. Multichannel analysis of surface waves to map bedrock. The Leading Edge, 18(12):1392-1396. |
| [38] | Misiek R, Liebig A, Gyulai A, et al. 1997. A joint inversion algorithm to process geoelectric and surface wave seismic data.Part II:application. Geophysical Prospecting, 45(1):65-85. |
| [39] | Roth M, Holliger K. 2000. The non-geometric ˉP S wave in high-resolution seismic data:observations and modeling. Geophysical Journal International, 140(1):F5-F11. |
| [40] | Ryden N, Park C B. 2006. Fast simulated annealing inversion of surface waves on pavement using phase-velocity spectra. Geophysics, 71(4):R49-R58. |
| [41] | Safani J, O'Neill A, Matsuoka T. 2006. Love wave modelling and inversion for low velocity layer cases.//Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems(SAGEEP).Seattle, WA, 1181-1190. |
| [42] | Schwab F A, Knopoff L. 1970. Surface-wave dispersion computations. Bulletin of Seismological Society of America, 60(2):321-344. |
| [43] | Shapiro N M, Campillo M, Stehly L, et al. 2005. High-resolution surface-wave tomography from ambient seismic noise. Science, 307(5715):1615-1618. |
| [44] | Shi Y L, Jin W. 1995. Genetic algorithmsinversion of lithospheric structure from surface wave dispersion. Chinese Journal of Geophysics(Acta Geophysica Sinica)(in Chinese), 38(2):189-198. |
| [45] | Snieder R. 2004. Extracting the Green's function from the correlation of coda waves:A derivation based on stationary phase. Phys. Rev. E., 69(4):046610. |
| [46] | Song X H, Gu H M, Liu J P, et al. 2007. Estimation of shallow subsurface shear-wave velocity by inverting fundamental and higher-mode Rayleigh waves. Soil Dynamics and Earthquake Engineering, 27(7):599-607. |
| [47] | Song Y Y, Castagna J P, Black R A, et al. 1989. Sensitivity of near-surface shear-wave velocity determination from Rayleigh and Love waves. Technical Program with Biographies, the 59th Annual Meeting of the Society of Exploration Geophysicists, Dallas, Texas. 509-512. |
| [48] | Song Z H, Tan C Y. 1965. Ascertaining thickness of the crust of China using speed of Rayleigh wave and Love surface wave group. Chinese Journal of Geophysics(Acta Geophysica Sinica)(in Chinese), 14(1):33-44. |
| [49] | Steeples D W. 2005. Near-surface geophysics:75 years of progress. The Leading Edge, 24(s1):S82-S85. |
| [50] | Tian G, Steeples D W, Xia J H, et al. 2003. Useful resorting in surface-wave method with the autojuggie. Geophysics, 68(6):1906-1908. |
| [51] | Wang X L, Ma S L, Guo Z, et al. 2013. S-wave velocity of the crust in Three Gorges Reservoir and the adjacent region inverted from seismic ambient noise tomography. Chinese Journal of Geophysics(in Chinese), 56(12):4113-4124, doi:10.6038/cjg20131216. |
| [52] | Wang Y S, Zhang Z M. 1998. Propagation of Love waves in a transversely isotropic fluid-saturated porous layered half-space. J. Acoust. Soc. Am., 103(2):695-701. |
| [53] | Winsborrow G, Huwsa D G, Muyzert E. 2003. Acquisition and inversion of Love wave data to measure the lateral variability of geo-acoustic properties of marine sediments. Journal of Applied Geophysics, 54(1-2):71-84. |
| [54] | Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh wave. Geophysics, 64(3):691-700. |
| [55] | Xia J H, Miller R D, Park C B. 2000. Advantage of calculating shear-wave velocity from surface waves with higher modes. Technical Program with Biographies, the 70th Annual Meeting of the Society of Exploration Geophysicists, Calgary, Canada, 1295-1298. |
| [56] | Xia J H, Miller R D, Park C B, et al. 2002a. A pitfall in shallow shear-wave refraction surveying. Journal of Applied Geophysics, 51(1):1-9. |
| [57] | Xia J H, Miller R D, Park C B, et al. 2002b. Comparing shear-wave velocity profiles inverted from multichannel surface wave with borehole measurements. Soil Dynamics and Earthquake Engineering, 22(3):181-190. |
| [58] | Xia J H, Miller R D, Park C B, et al. 2002c. Determining Q of near-surface materials from Rayleigh waves.Journal of Applied Geophysics,51(2-4):121-129. |
| [59] | Xia J H, Miller R D, Park C B, et al. 2003. Inversion of high frequency surface waves with fundamental and higher modes. Journal of Applied Geophysics, 52(1):45-57. |
| [60] | Xia J, Chen C, Li P H, et al. 2004. Delineation of a collapse feature in a noisy environment using a multichannel surface wave technique. Géotechnique, 54(1):17-27. |
| [61] | Xia J, Chen C, Tian G, et al. 2005. Resolution of high-frequency Rayleigh-wave data. Journal of Environmental and Engineering Geophysics, 10(2):99-110. |
| [62] | Xia J H, Xu Y X, Miller R D, et al. 2006a. Estimation of elastic moduli in a compressible Gibson half-space by inverting Rayleigh-wave phase velocity. Surveys in Geophysics, 27(1):1-17. |
| [63] | Xia J H, Xu Y X, Chen C, et al. 2006b. Simple equations guide high-frequency surface-wave investigation techniques. Soil Dynamics and Earthquake Engineering, 26(5):395-403. |
| [64] | Xia J H, Nyquist J E, Xu Y X, et al. 2007a. Feasibility of detecting near-surface feature with Rayleigh-wave diffraction. Journal of Applied Geophysics, 62(3):244-253. |
| [65] | Xia J H, Xu Y X, Miller R D. 2007b. Generating an image of dispersive energy by frequency decomposition and slant stacking. Pure and Applied Geophysics, 164(5):941-956. |
| [66] | Xia J H, Miller R D, Xu Y X. 2008. Data-resolution matrix and model-resolution matrix for Rayleigh-wave inversion using a damped least-squares method. Pure and Applied Geophysics, 165(7):1227-1248. |
| [67] | Xia J H, Xu Y X, Miller R D, et al. 2010. A trade-off solution between model resolution and covariance in surface-wave inversion. Pure and Applied Geophysics, 167(12):1537-1547. |
| [68] | Xia J H, Xu Y X, Luo Y H, et al. 2012. Advantages of using multichannel analysis of Love waves(MALW) to estimate near-surface shear-wave velocity. Surveys in Geophysics, 33(5):841-860. |
| [69] | Xiong Z Q, Zhang D Z, Qin Z, et al. 2008. Boundary conditions and case analysis of numerical modeling of Rayleigh wave. Journal of Central South University(Science and Technology)(in Chinese), 39(4):824-830. |
| [70] | Xu P F, Shi W, Ling S Q, et al. 2012. Mapping spherically weathered "Boulders" using 2D microtremor profiling method:a case study along subway line 7 in Shenzhen. Chinese Journal of Geophysics(in Chinese), 55(6):2120-2128,doi:10.6038/j.issn.0001-5733.2012.06.034. |
| [71] | Xu P F, Li S H, Ling S Q, et al. 2013. Application of SPAC method to estimate the crustal S-wave velocity structure. Chinese Journal of Geophysics(in Chinese), 56(11):3846-3854,doi:10.6038/cjg20131126. |
| [72] | Xu Y X, Xia J H, Miller R D. 2006. Quantitative estimation of minimum offset for multichannel surface-wave survey with actively exciting source. Journal of Applied Geophysics, 59(2):117-125. |
| [73] | Xu Y X, Xia J H, Miller R D. 2007. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach. Geophysics, 72(5):SM147-SM153. |
| [74] | Xu Y X, Xia J H, Miller R D. 2009. Approximation to cutoffs of higher modes of Rayleigh waves for a layered earth model. Pure and Applied Geophysics, 166(3):339-351. |
| [75] | Yang C L. 1993. Rayleigh Wave Exploration(in Chinese). Beijing:Geological Publishing House. |
| [76] | Yilmaz , Eser M, Berilgen M. 2006. A case study of seismic zonation in municipal areas. The Leading Edge, 25(3):319-330. |
| [77] | Yin X F, Xia J H, Shen C, et al. 2014. Comparative analysis on penetrating depth of high-frequency Rayleigh and Love waves. Journal of Applied Geophysics, 111:86-94. |
| [78] | Yu D X, Li Y H, Wu Q J, et al. 2014. S-wave velocity structure of the northeastern Tibetan Plateau from joint inversion of Rayleigh wave phase and group velocities. Chinese Journal of Geophysics(in Chinese), 57(3):800-811, doi:10.6038/cjg20140310. |
| [79] | Zeng C, Xia J H, Miller R D, et al. 2011a. Application of the multiaxial perfectly matched layer(M-PML) to near-surface seismic modeling with Rayleigh waves. Geophysics, 76(3):T43-T52. |
| [80] | Zeng C, Xia J H, Miller R D, et al. 2011b. Feasibility of waveform inversion of Rayleigh waves for shallow shear-wave velocity using a genetic algorithm. Journal of Applied Geophysics, 75(4):648-685. |
| [81] | Zeng C, Xia J H, Miller R D, et al. 2012. An improved vacuum formulation for 2D finite-difference modeling of Rayleigh waves including surface topography and internal discontinuities. Geophysics, 77(1):T1-T9. |
| [82] | Zhang B X, Yu M, Xiong W, et al. 1997. Study of acoustic wave and surface waves in stratified media. Acta Acustica(in Chinese),22(3):230-241. |
| [83] | Zhang B X, Lan C Q, Yu M, et al. 1998. Energy distribution of surface waves in stratified media. Acta Acustica(in Chinese), 23(2):97-106. |
| [84] | Zhang S X, Chan L S. 2003. Possible effects of misidentified mode number on Rayleigh wave inversion. Journal of Applied Geophysics, 53(1):17-29. |
| [85] | Zhao C G, Wang L, Li W H. 2008. Scattering of plane Rayleigh waves by circular-arc alluvial valleys with saturated soil deposits and water layer. Chinese Journal of Geophysics(in Chinese), 51(5):1567-1573. |
| [86] | 陈祥, 孙进忠. 2006. 改进的等效半空间法及瑞雷波频散曲线反演. 地球物理学报, 49(2): 569-576. |
| [87] | 陈运泰. 1974a. 多层弹性半空间中的地震波(一). 地球物理学报, 17(1): 20-43. |
| [88] | 陈运泰. 1974b. 多层弹性半空间中的地震波(二). 地球物理学报, 17(3): 173-185. |
| [89] | 凡友华, 陈晓非, 刘雪峰等. 2007. Rayleigh波的频散方程高频近似分解和多模式激发数目. 地球物理学报, 50(1): 233-239. |
| [90] | 高静怀, 何洋洋, 马逸尘. 2012. 黏弹性与弹性介质中Rayleigh面波特性对比研究. 地球物理学报, 55(1): 207-218, doi: 10.6038/j.issn.0001-5733.2012.01.020. |
| [91] | 关小平, 黄嘉正, 周鸿秋. 1993. 工程勘察中稳态瑞利面波法解释理论的探讨. 地球物理学报, 36(1): 96-105. |
| [92] | 郭震, 陈永顺, 殷伟伟. 2015. 背景噪声面波与布格重力异常联合反演: 山西断陷带三维地壳结构. 地球物理学报, 58(3): 821-831, doi: 10.6038/cjg20150312. |
| [93] | 黄慧, 陈晓非. 2008. P-SV波展平变换的精确求解——以地震面波为例. 地震学报, 30(2): 105-113. |
| [94] | 刘国利, 刘殿魁. 1994. 单覆盖层起伏非均匀地形中的勒夫波. 地球物理学报,37(增刊1): 461-466. |
| [95] | 鲁来玉, 张碧星, 汪承灏. 2006. 基于瑞利波高阶模式反演的实验研究. 地球物理学报, 49(4): 1082-1091. |
| [96] | 鲁来玉, 何正勤, 丁志峰等. 2014. 基于背景噪声研究云南地区面波速度非均匀性和方位各向异性. 地球物理学报, 57(3): 822-836, doi: 10.6038/cjg20140312. |
| [97] | 石耀霖, 金文. 1995. 面波频散反演地球内部构造的遗传算法. 地球物理学报, 38(2): 189-198. |
| [98] | 宋仲和, 谭承业. 1965.用瑞雷和乐夫面波群速度确定我国地壳厚度. 地球物理学报, 14(1): 33-44. |
| [99] | 王小龙, 马胜利, 郭志等. 2013. 利用地震背景噪声成像技术反演三峡库区及邻近地区地壳剪切波速度结构. 地球物理学报, 56(12): 4113-4124, doi: 10.6038/cjg20131216. |
| [100] | 熊章强, 张大洲, 秦臻等. 2008. 瑞雷波数值模拟中的边界条件及模拟实例分析. 中南大学学报 (自然科学版), 39(4): 824-830. |
| [101] | 徐佩芬, 侍文, 凌苏群等. 2012. 二维微动剖面探测“孤石”: 以深圳地铁7号线为例. 地球物理学报, 55(6): 2120-2128,doi: 10.6038/j.issn.0001-5733.2012.06.034. |
| [102] | 徐佩芬, 李世豪, 凌甦群等. 2013. 利用SPAC法估算地壳S波速度结构. 地球物理学报, 56(11): 3846-3854,doi: 10.6038/cjg20131126. |
| [103] | 杨成林. 1993. 瑞雷波勘探. 北京: 地质出版社. |
| [104] | 余大新, 李永华, 吴庆举等. 2014. 利用Rayleigh波相速度和群速度联合反演青藏高原东北缘S波速度结构. 地球物理学报, 57(3): 800-811, doi: 10.6038/cjg20140310. |
| [105] | 张碧星, 喻明, 熊伟等. 1997. 层状介质中的声波场及面波研究. 声学学报, 22(3): 230-241. |
| [106] | 张碧星, 兰从庆, 喻明等. 1998. 分层介质中面波的能量分布. 声学学报, 23(2): 97-106. |
| [107] | 赵成刚, 王磊, 李伟华. 2008. 具有饱和土沉积层的充水河谷对平面瑞雷波的散射. 地球物理学报, 51(5): 1567-1573. |
| [108] | 赵海波, 王秀明. 2008. 利用时间分解的交错网格差分法模拟两相流体饱和孔隙介质中的声波传播. 中国科学(G辑:物理学力学天文学), 38(7): 785-804. |
| [109] | 周红, 陈晓非. 2007. 凹陷地形对Rayleigh面波传播影响的研究. 地球物理学报, 50(4): 1182-1189. |
| [110] | 周晓华, 林君, 张怀柱等. 2014. 微动中多模式面波频散曲线的映射式提取方法. 地球物理学报, 57(8): 2631-2643, doi: 10.6038/cjg20140822. |
| [111] | 周竹生, 刘喜亮, 熊孝雨. 2007. 弹性介质中瑞雷面波有限差分法正演模拟. 地球物理学报, 50(2): 567-573. |
 2015, Vol. 58
2015, Vol. 58