2015年4月25日,尼泊尔发生了MS8.1大地震,自1950年Mw8.7察隅地震以后成为尼泊尔近70年来受到影响最大的地震(Mittal and Kumar, 2015).该地震震中位于尼泊尔博克拉城市,地理坐 标:(28.147°N,84.708°E),震源深度15 km(http://earthquake.usgs.gov/). 地震造成东南向发展的破裂带长度100多千米,且震中距首都加德满都仅70多千米,造成尼泊尔大量人员伤亡(截止2015年5月15日,已超过8千人死亡(http://world.people.com.cn/))、众多建筑物倒塌.大地震释放巨大能量且震源浅,破坏性大,不仅引起强烈的地面震动,大量水电大坝、高速公路/道路受到了结构性损坏,还触发了珠穆朗玛峰发生雪崩.同时,我国西藏自治区日喀则等地区也有明显的震感,吉隆县、定日县和聂拉木县相继发生了3.6、5.9和5.3级地震(http:// www.cea.gov.cn/).5月12日在尼泊尔主震MS8.1 的西南部又发生了MS7.5级余震.此次尼泊尔地震不但给当地人民带来巨大灾害,而且对我国日喀则一些地区造成了损失.
尼泊尔位于印度板块与欧亚板块的主要碰撞带上,地形起伏非常明显,紧邻世界上最高山峰——珠穆朗玛,且被喜马拉雅弧贯穿.受印度板块与欧亚板块陆陆俯冲碰撞和推挤,历史上沿该带发生过多次大地震,例如,1897年Mw8.1 Shillong地震,1950年Mw8.7察隅地震(Mittal and Kumar, 2015),2005年Mw7.6 Kashmir地震(Shah,2013)及2011年Mw6.9 Sikkim地震(Prajapati et al., 2013).图 1给出了自1976年尼泊尔及其邻近区域历史大地震和断层分布情况.可以看出,长期以来在这种陆-陆俯冲挤压过程中,位于喜马拉雅和青藏高原南部的转换带上大地震不断发生.GPS数据显示印度板块以大约50 mm/yr的速度俯冲于欧亚板块,在喜马拉雅弧汇聚速度则达到20 mm/yr,应力异常集中,形成喜马拉雅地震带(邓起东等,2014).此次尼泊尔MS8.1地震位于该地震带上,是由于欧亚板块与印度板块持续的南北向俯冲挤压逆冲造成的.
在地质构造上,尼泊尔位于喜马拉雅山中段南麓,跨越恒河平原和德赖平原,且该区域处于拆离断层带,分布有喜马拉雅主前锋冲断裂(MFT)和主边冲断裂(MBT)和主中冲断裂(MCT)区域及深部主喜马拉雅逆冲断层(MHT)(许志琴等,2013),而这些断裂带是目前最为活跃的地震带(Wang et al., 2014; Yin,2010).自新生代以来,MFT断层最为活跃,且在其附近逆冲地震不断发生.然而,此次MS8.1地震在地表上显示发生在MBT断裂带附近,但震源深度在15 km且为低角度,向深部延伸则很有可能发生在MHT上.
地震的发生会引发一系列物理场变化,其中力学场的变化包括反映地球弹性的同震(Co-seismic)位移、应力的变化和反映地球黏弹性响应的震后(Post-seismic)位移、应力变化等.而地震发生时产生的同震位移、应力变化,对于地震危险性评估、了解震源断层的运动方式、破裂过程和地震触发等问题的研究中有重要的意义.本文采用PREM分层模型,应用全球有效体力等效方法计算了不同断层模型下尼泊尔MS8.1大地震同震位移、应力变化,同时给出了周围区域位移和应力计算结果,以期估计大地震后尼泊尔地区地震危险性和分析该地震对我国西南地区的应力环境的影响.
2 计算方法与断层模型1958年Steketee(1958)将位错理论引入地震学,推导了走滑断层的位移格林函数,计算震源位错造成的地表同震形变.随后很多学者对位错理论和同震变形进行了研究,给出了半无限空间弹性均匀 介质地壳模型(Chinnery, 1961,1963; Press,1965; Okada,1985)、 半无限空间成层介质的地球模型(Okubo,1992; Wang,2003)、球型成层弹性地球模型(Ben-Menahem and Singh, 1968; McGinley,1969; Saito,1974; Sun,1992)和球型成层黏弹性 地球模型(Rudle,1982; Sabadini et al., 1995; Wang,1999)及侧向非均匀性的三维地球模型(Fu and Sun, 2007,2008; Fu et al., 2010),这些研究促进了人们对地震破裂过程和同震形变的认识.特别是,1985年Okada(1985)弹性半无限空间均匀介质模型已成为位错理论经典表达式.Wang等(2003,2006)进一步发展了半无限空间和层状弹性/黏弹性介质的模型,编写了EDGRN/EDCMP计算程序,可以计算同震与震后位移、应变和重力变化等.Okada和汪荣江的工作在计算震后变形研究中得到了广泛应用.
然而,半无限空间地壳模型和分层地壳模型不能考虑地球曲率的影响,特别是对于大地震发震断层大、影响区域空间尺度大,平面假设已不再适用,在同震-震后计算中地球曲率的影响是不可忽略的. 同时,在计算得到位移计算应变(应力)时,球体模型和平面模型又不尽相同.Ben-Menahem等(1969)、Ben-Menahem和Israel(1970)通过均质无自重球形模型计算,得出地球的曲率影响在震源矩20°以内可忽略不计,而对于一个震级8.5的浅源地震在一定的纬度上最大有30%的误差.Amelung和Wolf(1994)通过对比考虑重力增量球形模型和无重力平面模型,得出地球曲率产生的误差可以和重力增量影响相弥补.Pollitz(1996)应用自由震荡方法对层状地球模型(忽略自重)计算了不同震源深度壳内不同形状震源的近场同震位移和应变,认为在震中矩 100 km以内地球曲率的影响一般小于2%.Antonioli 等(1998)通过比较层状黏弹结构球形和平面模型的震后位移场变化,得出地球曲率影响在近场可忽略不计,而在远场却有显著的差别,对于走滑地震可达到20%.Nostro等(1999,2001)比较了平面模型(Bonafede84黏弹模型和Okada85弹性模型)和球形模型(Piersanti95带自重黏弹模型)同震和震后剪切变形,对于走滑断层地球曲率引起的同震位移显著差异出现在3倍断层长度内,而震后位移差别将更大一些;这些差别与断层形状、震后时间和震源距离有关,且可以超过10倍.Sun和Okubo(2002)认为地球曲率和分层对同震垂直位移的影响不可忽略,在假设地球自重的影响小于地球曲率影响的情况下,随着震源深度的增加地球曲率的影响也增大,且引张震源的曲率效应比剪切震源的大.石耀霖和朱守彪(2006)指出在从位移计算应变和应力时,必须使用球坐标,使用平面直角坐标会带来系统误差,在大位移和高纬度时,这种误差不能忽视.
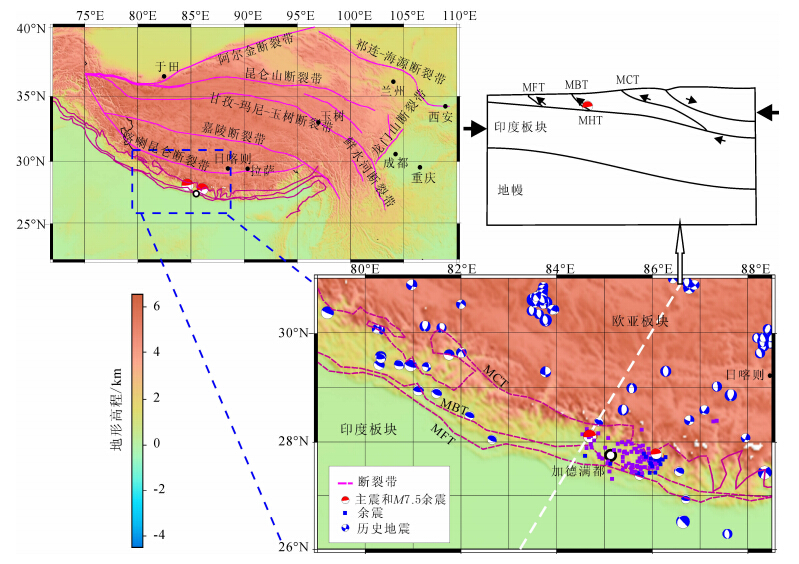 |
图 1 尼泊尔及其邻近区域地形高程和历史地震分布 图中余震截止2015年5月13日(http://earthquake.usgs.gov/),紫色方块为MS8.1地震震后余震分布,蓝色方块为MS7.5地震震后余震分布; MCT(Main Central Thrust fault)为主中冲断裂; MBT(Main Boundary Thrust fault)为主边冲断裂; MFT(Main Frontier Thrust fault)为主前锋冲断裂; MHT(Main Himalaya Thrust)为主喜马拉雅逆冲断裂带.历史地震为1976-01-01—2015-05-01的震级>6.5的地震(http://www.globalcmt.org).Fig. 1 The elevation and historical earthquake distribution in Nepal and its adjacent area Aftershocks in the figure as April 27,2015,from(http://earthquake.usgs.gov/); the purple square represent aftershocks of MS8.1 and the blue square st and for aftershocks of MS7.5; MCT: the Main Central Thrust fault; MBT: the Main Boundary Thrust fault; MFT: Main Frontier Thrust fault;MHT: Main Himalaya Thrust fault. |
据上述分析,本文应用有限元方法,建立全球分层模型来分析.网格划分上采用自适应技术,自动将断层处网格加密,周围逐渐增大;并且据计算地球动力学实验室开发的等效体力代替位错源,避免常规有限元方法处理不连续面时遇到的困难(张贝等,2015).图 2给出了计算时全球计算网格,共858566个节点和734508单元,并在断层处做网格加密处理,大小约为15 km.
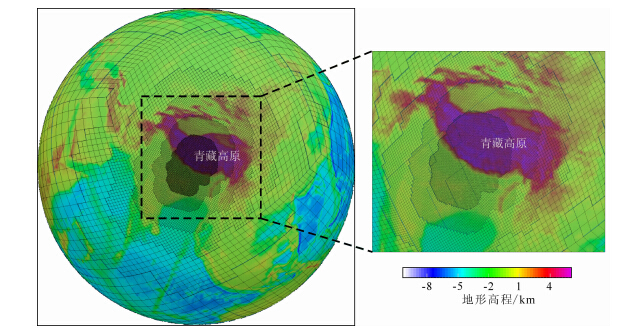 |
图 2 全球模拟计算模型及网格Fig. 2 The computational model and grids |
断层滑动模型选取目前已公布的模型:(1)USGS 的121个子断层模型(http://earthquake.usgs.gov),发震断层参数:走向295°,倾角10°,滑动110°;(2)中国地震局地球物理所利用全球地震台网(GSN)记录的长周期数字地震资料,采用单一机制的有限断层模型反演得出的MS8.1发震断层:(走向301°,倾角11°,滑动130°),(http://www.cea-jgp.ac.cn),见图 3.可以看出,除了断层滑动面走向 略不同外,两者断层滑动面的最大滑移量也有所不 同,中国地震局(CEA)给出最大相对滑移量为2.1 m,USGS给出为4 m. 同时,两者的滑动面大小也不同, 前者滑动面积约7.0×1010m2,后者滑动面积约3.6×1010m2.
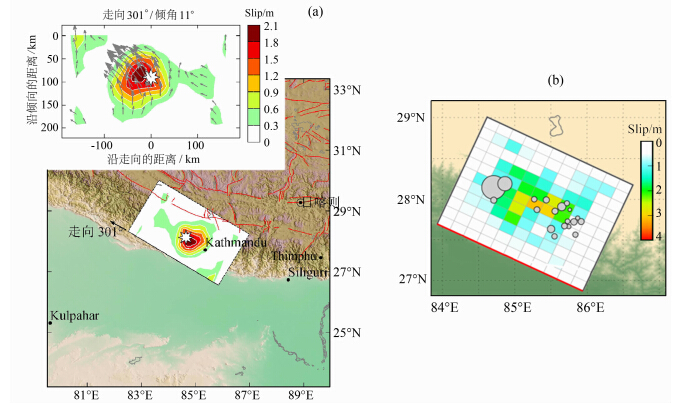 |
图 3 尼泊尔MS8.1断层滑动模型 (a)中国地震局地球物理所给出的滑动模型(http://www.cea-jgp.ac.cn);(b)美国USGS给出的断层滑动模型(http://earthquake.usgs.gov).Fig. 3 The slip model of MS8.1 earthquake (a)The slip model from Institute of Geophysics,China seismological(http://www.cea-jgp.ac.cn); (b)The slip model from USGS(http://earthquake.usgs.gov). |
图 4给出了尼泊尔MS8.1大地震的地表同震位移计算结果,由于尼泊尔MS8.1地震断裂向东南方向扩展,断层面上相对较大的水平位移主要发生在地震断层的东南部,特别是尼泊尔首都加德满都及其东南附近,是破坏严重的地方.地震造成南北方向上的水平位移较大、且比较集中在首都加德满都,CEA模型计算得出断层上盘向南最大位移有1.2 m,USGS模型为3.5 m;而断层下盘向北位移约0.2 m. 同震东西方向水平位移相对较小,上盘相对下盘滑动大一些,CEA模型计算得出上盘由北往南先向西0.2 m,然后向东最大有0.5 m位移;USGS模型为上盘则先向西0.2 m,然后向东1.4 m;下盘分别向西约0.2 m,这与断层滑动模型有紧密的关联.在垂直方向上同震位移也相对较小,两模型均表现出上盘向上移动0.4 m,而下盘向下移动0.1 m,体现了在倾角较小的情况同震水平位移大,而垂直位移较小.再次表明,尼泊尔MS8.1地震是一个低角度的逆冲地震.
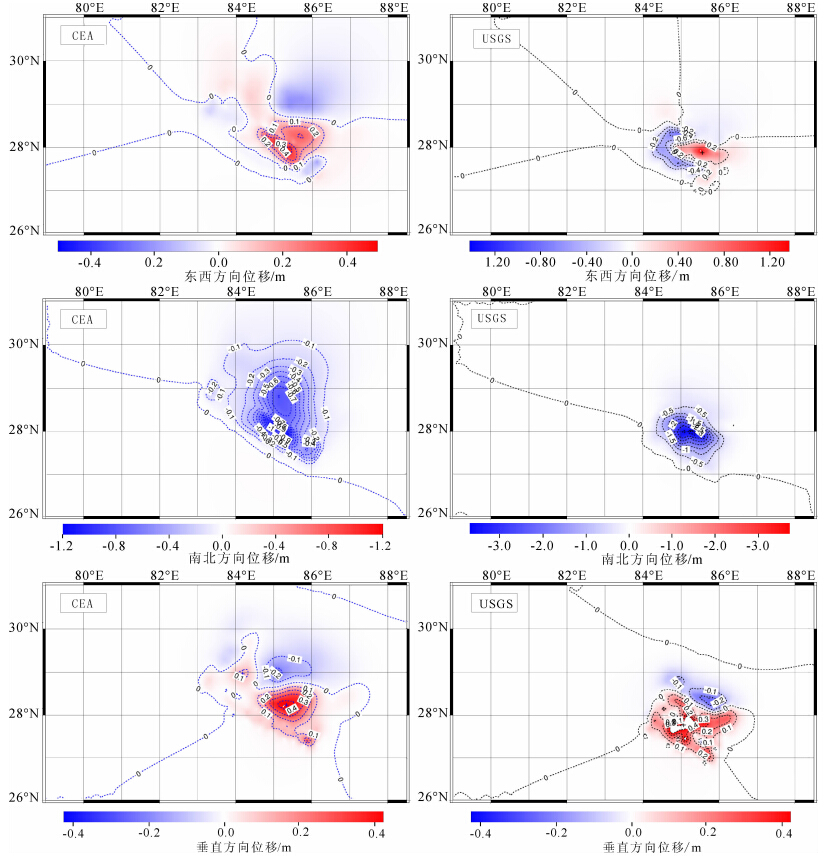 |
图 4 尼泊尔MS8.1地震发生产生的地表同震位移 东西向以东为正,南北向以北为正,垂向上以上为正.Fig. 4 The surface co-seismic displacement caused by the MS8.1 earthquake with positive in East,North and Upward |
图 5给出了两种断层滑动模型下,尼泊尔MS8.1 地震的地表同震水平位移矢量图,可以看出两个模型均显示了MS8.1地震是一个比较典型的逆冲地震(上盘向上滑移,下盘向下俯冲).此次地震倾角较小,上盘水平位移量大,特别是USGS模型计算结果显示在首都加德满都附近水平滑移量接近4 m.CEA模型同震位移量级在0.1 m以上的区域主要集中在(27.7°N—30.0°N,83.5°E—87°E)及附近,且比较集中.USGS模型同震位移量级在0.1 m以上的区域主要集中在(27.5°N—29.3°N,84.1°E—86.6°E)及附近.
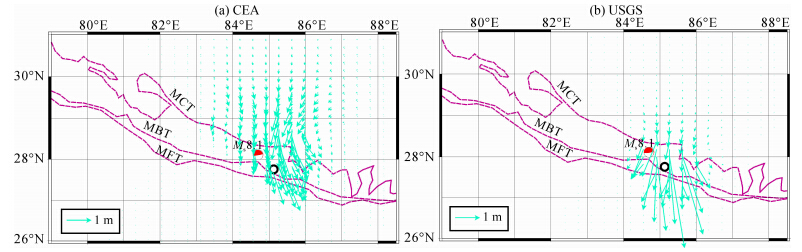 |
图 5 MS8.1地震引起的地表水平位移矢量图Fig. 5 The vector map of surface co-seismic horizontal displacement caused by the MS8.1 earthquake |
在背景应力场绝对值不清楚的情况下,研究者广泛采用库仑应力变化(ΔCFS)来判断地震触发和地震危险性(石耀霖和曹建玲,2010),其表达式为 ΔCFS=Δτ+μ(Δσn+Δp),(1) 式中Δσn是法向正应力变化,Δτ是沿断层面剪应力沿滑动方向的变化,μ为断层面内摩擦系数,Δp为孔隙压力变化.本文中应力正负遵循弹性力学定义.公式(1)表明了当断层面上的剪应力和孔隙压力增加、法向压应力减小时,库仑破裂应力为正,说明应力调整增加了断层面滑动的危险性,相反,则阻碍了断层破裂滑动.
据CEA、USGS给出的震源机制及公式(1),可计算得出尼泊尔及其邻近地区15 km深度处库仑应力变化,见图 6,其中(a)表示接收断层与CEA给出的主震错动相同时(走向301°,倾角11°,滑动角130°)计算得出的库仑应力变化;(b)表示接收断层与USGS给出的主震错动相同时(走向295°,倾角10°,滑动110°)计算得出的库仑应力变化.可以看出:(1)两种不同断层滑动模型下,MS8.1地震在震区应力场变化均达到MPa量级,大部分地区库仑应力变化为正,特别是断层滑动面处,地震危险性依然较大;(2)余震及5月12号MS7.5地震均落在库仑应力变化为正的区域.
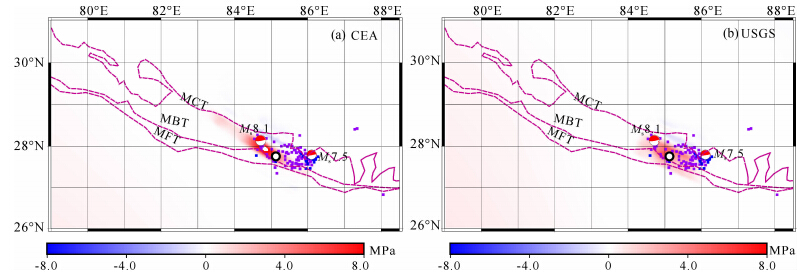 |
图 6 尼泊尔MS8.1地震引起近场库仑应力变化图 (a)接收断层与CEA给出的主震错动相同时(走向301°,倾角11°,滑动角130°)计算得出的库仑应力变化;(b)接收断层与USGS给出的主震错动相同时(走向295°,倾角10°,滑动角110°)计算得出的库仑应力变化.Fig. 6 The Coulomb failure stress of near field caused by the MS8.1 earthquake (a)The ΔCFS of far field caused by the MS8.1 earthquake using the CEA slip model;(b)The ΔCFS of far field caused by the MS8.1 earthquake using the USGS slip model. |
为了进一步探讨尼泊尔MS8.1地震对我国西部地区应力场的影响,图 7给出了MS8.1地震造成的同震应力场变化.因垂直方向应力变化很小,在此仅绘出水平应力变化图.可以看出,采用CEA和USGS两个断层滑动模型计算得出的远场应力场相差不大,两个模型均显示:MS8.1地震对我国青藏高原有较大的影响,特别是西藏南部地区.随着发震逆掩断层活动造成垂直于断层的正应力释放,垂直于断层的压应力显著降低.图中震中以北我国西藏地区的南北向正应力σ θθ增加显著(弹性力学定义张应力为正,正应力增加即表示压应力减小).南北向正应力增加1kPa的区域可涉及到雅鲁藏布江地区、拉萨块体和羌塘地块;甘孜、玉树、海源、阿拉善地区的应力变化量级在0.1 kPa量级.地震在西藏地区造成的东西向正应力σφφ变化较为复杂,在震中东北(包括日喀则、拉萨)和西北的广大区域也造成正应力增加(压应力减小),但震中正北有一些地方正应力减小(压应力增加).水平剪应力σθφ变化在震中东北为负、西北为正.
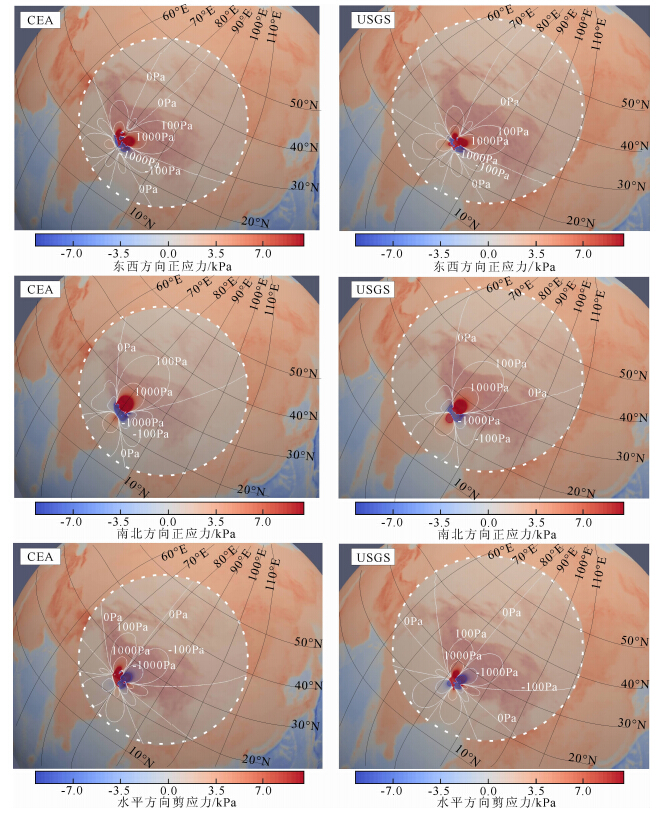 |
图 7 尼泊尔MS8.1地震引起的我国西部地区水平地应力变化 从上向下分别为东西向水平正应力σφφ,南北向水平正应力σθθ和水平σθφ变化; 左边一列为CEA错断模型计算结果,右边一列为USGS错断模型计算结果.图中圆形区域半径2000 km.Fig. 7 Horizontal stress changes in western China caused by the MS8.1 earthquake From top to bottom: E-W normal stress σφφ,N-S normal stress σθθ, and horizontal shear stress σθφ.The white circle shows the far field boundary of radius 2000 km. |
这种应力变化意味着,对于震中东北高原内部近东西走向的右旋走滑断层,原有法向压应力减小,剪应力增大,因此发震危险增大.对藏南南北向走向的正断层,法向张应力增大,因而地震危险性也增大.
据公式(1)可知,更精细的分析需要对不同性质的断层根据其不同走向、倾角计算特定断层上不同部位的库仑应力变化.图 8(a—b)表示接收断层分别与CEA确定的主震错动相同(走向301°,倾角11°,滑动130°)的断层和与USGS确定的主震错动相同(走向295°,倾角10°,滑动110°)的断层计算的库仑应力变化.可以看出大部分区域(除去雅鲁藏布江等区域)的库仑应力变化为负,是相对安全.然而,大量的地质学家对青藏高原西南部研究取得许多重要进展并形成了共识:在雅鲁藏布江缝合带之南、喜马拉雅北坡的藏南地区存在着一系列接近南北向构造,而最常见的是正断层及其组合的地堑和裂谷(尹安,2006;Hodges,2000).当接受断层为近南北走向高倾角正断层时,库仑应力变化为正.图 8(c—d)显示了CEA模型采用两种不同正断层(走向NE20°和走向NW20°,倾角均为70°,滑动角均为270°)上的库仑应力变化图,MS8.1地震的发生将会增加这些正断层破裂的危险性.
 |
图 8 尼泊尔MS8.1地震引起的我国西部地区库仑应力变化 (a)接收断层为CEA(走向301°,倾角11°,滑动角130°)计算得出的库仑应力变化;(b)接收断层为USGS(走向295°,倾角10°,滑 动角110°)计算得出的库仑应力变化;(c)接收断层为(走向20°,倾角均为70°,滑动角270°)计算得出的库仑应力变化;(d)接收断层 为(走向160°,倾角均为70°,滑动角270°)计算得出的库仑应力变化; 背景地图显示为地形高程.Fig. 8 The Coulomb failure stress of western parts of China caused by the MS8.1 earthquake (a)The ΔCFS of far field caused by the MS8.1 earthquake using the CEA slip model;(b)The ΔCFS of far field caused by the MS8.1 earthquake using the USGS slip model;(c)The ΔCFS of far field caused by the MS8.1 earthquake based on the fault(strike angle 20°,dip angle 70°,slip angle 270°);(d)The ΔCFS of far field caused by the MS8.1 earthquake based on the fault(strike angle 160°, dip angle 70°,slip angle 270°); the background denote the elevation. |
尼泊尔MS8.1地震后,我国西藏日喀则地区相继发生5.9级、5.3级地震(http://www.cea.gov.cn/).日喀则5.9级地震断层节面Ⅰ:走向351°和走向41°,倾角-101°,节面Ⅱ:走向185°和走向44°,倾角-63°,是由近南北向的正断层系活动引发的(http://www.cea-igp.ac.cn/).徐锡伟等(http://news.sciencenet.cn)认为日喀则地区的地震是藏南拆离系与控制近南北向拉张断陷盆地的正断层型地震,是由MS8.1地震触发而发生的.由图 8(c—d)可以看出,当接受断层为近南北向断层时,日喀则和拉萨地区均落在库仑应力增加的区域,库仑应力变化应力值量级在几个kPa.
4 结论与讨论自55 Ma前印度板块与欧亚板块碰撞挤压从未终止,印度板块岩石圈地幔往北俯冲于喜马拉雅 山之下,导致了青藏高原不断抬升,造成了一系列的 大地震在喜马拉雅造山带发生(Molnar and Tapponnier, 1975). 2015年尼泊尔MS8.1地震处于喜马拉雅南部,是两个板块之间的挤压逆冲造成的.
基于弹性位错理论和分层地壳模型的等效体力代替位错源全球有限元同震计算模型,利用USGS和CEA断层滑动模型,计算了尼泊尔MS8.1地震引起的同震位移场、应力场以及库仑应力变化,以及对周边区域的应力调整.计算结果获得以下认识:
(1)尼泊尔MS8.1地震是一个比较典型的低角度逆冲地震,地震造成的同震位移主要集中在水平面上,且集中在首都加德满都周围区域.USGS滑动模型的同震水平滑移量最大约为4 m,CEA滑动模型的同震水平滑移量最大约为2 m;相比地震造成东西向和垂直方向的位移,南北方向上的水平位移较大,表现为断层上盘向南移动;CEA模型计算得出断层上盘向南移动最大有1.2 m,USGS模型为3.47 m;
(2)尼泊尔地区处于欧亚板块与印度板块碰撞挤压断裂带上,构造断层较为发育.MS8.1地震发震断层很可能属于MHT断裂带.地震造成尼泊尔地区库仑应力变化为正,地震危险性依然较大;余震及5月12号MS7.5地震均落在库仑应力变化为正的区域.
(3)尼泊尔MS8.1地震对我国西藏地区有一定的影响,据MS8.1地震发震断层计算得出雅鲁藏布江地区和拉萨块体的应力变化为数kPa,甚至可达10 kPa,日喀则和拉萨地区均落在库仑应力变化增加的区域.应该密切关注拉萨、日喀则区域被诱发地震的可能性.
(4)文章采用全球分层介质模型,消除了地球曲率和均质的影响.但采用的线弹性本构,探讨震后较短时间内对地震活动性的影响,未考虑黏弹效应.此外,模型主要采用地震位错分布,断层形态、摩擦系数等参数,有着较大的不确定性,在计算的震前构造应力场时较为简单,且没有考虑动态应力触发,流体作用等影响,今后将继续深入研究.
| [1] | Amelung F, Wolf D. 1994. Viscoelastic perturbations of the Earth: significance of the incremental gravitational force in models of glacial isostasy. ,Geophys. J. Int. 117(3): 864-879. |
| [2] | Antonioli A, Piersanti A, Spada G. 1998. Stress diffusion following large strike-slip earthquakes: a comparison between spherical and flat-earth models., Geophys. J. Int. 133(1): 85-90. |
| [3] | Ben-Menahem A, Singh S J. 1968. Eigenvector expansions of Green's dyads with applications to geophysical theory. , Geophys. J. Int.16(4): 417-452. |
| [4] | Ben-Menahem A, Singh S J, Solomon F. 1969. Static deformation of a spherical earth model by internal dislocations. Bull. ,Seism. Soc. Am. 59(2): 813-853. |
| [5] | Ben-Menahem A, Israel M. 1970. Effects of major seismic events on the rotation of the Earth. ,Geophys. J. Int. 19(4): 367-393. |
| [6] | Chinnery M A. 1961. The deformation of the ground around surface faults. Bull. ,Seism. Soc. Am. 51(3): 355-372. |
| [7] | Chinnery M A. 1963. The stress changes that accompany strike-slip faulting. Bull., Seism. Soc. Am.53(5): 921-932. |
| [8] | Deng Q D, Cheng S P, Ma J, et al. 2014. Seismic activities and earthquake potential in the Tibetan Plateau. Chinese J. Geophys. (in Chinese), 57(7): 2025-2042, doi:10.6038/cjg20140701. |
| [9] | Fu G Y, Sun W K. 2007. Effects of lateral inhomogeneity in a spherical Earth on gravity Earth tides. J. ,Geophys. Res. 112(B6): B06409. |
| [10] | Fu G Y, Sun W K. 2008. Surface coseismic gravity changes caused by dislocations in a 3-D heterogeneous earth. , Geophys. J. Int.172(2): 479-503. |
| [11] | Fu G Y, Sun W K, Fukuda Y, et al. 2010. Coseismic displacements caused by point dislocations in a three-dimensional heterogeneous, spherical earth model. ,Geophys. J. Int. 183(2): 706-726. |
| [12] | Hodges K V. 2000. Tectonics of the Himalaya and southern Tibet from two perspectives. Geological Society of America Bulletin, 112(3): 324-350. |
| [13] | Mittal H, Kumar A. 2015. Stochastic finite-fault modeling of Mw5.4 earthquake along Uttarakhand-Nepal border. Nat. Hazards, 75(2): 1145-1166. |
| [14] | McGinley J R. 1969. A comparison of observed permanent tilts and strains due to earthquakes with those calculated from displacement dislocations in elastic earth models[Ph.D. thesis]. Pasadena, California: California Institute of Technology. |
| [15] | Molnar P, Tapponnier P. 1975. Cenozoic tectonics of Asia: effects of a continental collision. Science, 189(4201): 419-462. |
| [16] | Nostro C, Piersanti A, Andrea A, et al. 1999. Spherical versus flat models of coseismic and postseismic deformations. J. Geophys. Res., 106(B6): 13115-13134. |
| [17] | Nostro C, Piersanti A, Cocco M. 2001. Normal fault interaction caused by coseismic and postseismic stress changes. J. Geophys. Res., 106(B9): 19391-19410. |
| [18] | Okada Y. 1985. Surface deformation due to shear and tensile faults in a half-space. Bull. , Seism. Soc. Am.75(4): 1135-1154. |
| [19] | Okubo S. 1992. Gravity and potential changes due to shear and tensile faults in a half-space. J. , Geophys. Res.97(B5): 7137-7144. |
| [20] | Pollitz F F. 1996. Coseismic deformation from earthquake faulting on a layered spherical Earth. , Geophys. J. Int.125(1): 1-14. |
| [21] | Prajapati S K, Kumar A, Chopra S, et al. 2013. Intensity map of Mw6.9 2011 Sikkim-Nepal border earthquake and its relationships with PGA: distance and magnitude. Nat. Hazards, 69(3): 1781-1801. |
| [22] | Press, F. 1965. Displacements, strains and tilts at teleseismic distances. J., Geophys. Res.70(10): 2395-2412. |
| [23] | Rudle J B. 1982. Viscoelastic-gravitational deformation by a rectangular thrust fault in a layered Earth. J. ,Geophys. Res. 87(B9): 7787-7796. |
| [24] | Sabadini R, Piersanti A, Spada G. 1995. Toroidal/poloidal partitioning of global post-seismic deformation., Geophys. Res. Lett.22(8): 985-988. |
| [25] | Saito M. 1974. Some problems of static deformation of the earth. J. Phys.Earth, 22(1): 123-140. |
| [26] | Shah A A. 2013. Two great historical earthquake ruptures revealed in Nepal. Current Science, 104(8): 994. |
| [27] | Shi Y L, Cao J L. 2010. Some aspects in static stress change calculation——Case study on Wenchuan earthquake. Chinese J. Geophys. (in Chinese), 53(1): 102-110, doi:10.3969/j.issn.0001-5733.2010.01.011. |
| [28] | Shi Y L, Zhu S B. 2006. Discussion on method of calculating strain with GPS displacement data. Journal of Geodesy and Geodynamics (in Chinese), 26(1): 1-8. |
| [29] | Steketee J A. 1958. On Volterra's dislocations in a semi-infinite elastic medium. Can. J., Phys. 36(2): 192-205. |
| [30] | Sun W. 1992. Potential and gravity changes caused by dislocations in spherically symmetric Earth models. Bull. Earthquake Res. Inst. Univ. Tokyo, 67(2): 89-238. |
| [31] | Sun W K, Okubo S. 2002. Effects of earth's spherical curvature and radial heterogeneity in dislocation studies—for a point dislocation. Geophys. , Res. Lett.29(12): 1605. |
| [32] | Wang C S, Dai J G, Zhao X X, et al. 2014. Outward-growth of the Tibetan Plateau during the Cenozoic: A review. Tectonophysics, 621: 1-43. |
| [33] | Wang H. 1999. Surface vertical displacements, potential perturbations and gravity change of viscoelastic earth model induced by internal point dislocations. Geophys. J., Int.137(2): 429-440. |
| [34] | Wang R J, Martin F L, Martín L, et al. 2003. Computation of deformation induced by earthquakes in a multi-layered elastic crust-FORTRAN programs EDGRN/EDCMP. Comput. , Geosci.29(2): 195-207. |
| [35] | Wang R J, Lorenzo-Martín F, Rotha F. 2006. PSGRN/PSCMP—a new code for calculating co- and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Comput., Geosci.32(4): 527-541. |
| [36] | Xu Z Q, Wang Q, Zeng L S, et al. 2013. Three-dimensional extrusion model of the Great Himalaya slice. Geology in China (in Chinese), 40(3): 671-680. |
| [37] | Yin A. 2006. Cenozoic tectonic evolution of the Himalayan orogen as constrained by along-strike variation of structural geometry, exhumation history, and foreland sedimentation. Earth Science Frontiers (in Chinese), 13(5): 416-515. |
| [38] | Yin A. 2010. Cenozoic tectonic evolution of Asia: A preliminary synthesis. Tectonophysics, 488(1-4): 293-325. |
| [39] | Zhang B, Zhang H, Shi Y L. 2015. Equivalent-bodyforce approach on modeling elastic dislocation problem using finite element method. Chinese J. Geophys. (in Chinese),58(5):1666-1674,doi:10.6038/cjg20150518. |
| [40] | 邓起东, 程绍平, 马冀等. 2014. 青藏高原地震活动特征及当前地震活动形势. 地球物理学报, 57(7): 2025-2042, doi:10.6038/cjg20140701. |
| [41] | 石耀霖, 朱守彪. 2006. 用 GPS 位移资料计算应变方法的讨论. 大地测量和地球动力学, 26(1): 1-8. |
| [42] | 石耀霖, 曹建玲. 2010. 库仑应力计算及应用过程中若干问题的讨论——以汶川地震为例. 地球物理学报, 53(1): 102-110, doi:10.3969/j.issn.0001-5733.2010.01.011. |
| [43] | 孙文科. 2012. 地震位错理论. 北京: 科学出版社, 28-38. |
| [44] | 许志琴, 王勤, 曾令森等. 2013. 高喜马拉雅的三维挤出模式. 中国地质, 40(3): 671-680. |
| [45] | 尹安. 2006. 喜马拉雅造山带新生代构造演化: 沿走向变化的构造几何形态、剥露历史和前陆沉积的约束. 地学前缘, 13(5): 416-515. |
| [46] | 张贝,张怀,石耀霖. 2015. 有限元模拟弹性位错的等效体力方法.地球物理学报,58(5):1666-1674,doi:10.6038/cjg20150518. |
 2015, Vol. 58
2015, Vol. 58


