2. 中国石化石油物探技术研究院, 南京 210014
2. Sinopec Geophysical Research Institute, Nanjing 210014, China
As the SNR of passive retrieved data reconstructed by the conventional method is low, the quality of imaging is influenced seriously. Based on conventional methods, we propose a multidomain iterative denoising reconstruction method, which is based on the Curvelet threshold iterative denoising and multilevel median filter. As to the two cases mentioned above, and considering the matching degree of passive virtual wavelets and active wavelets, we suggest two time-domain interpolation methods using active and passive seismic data. They are the energy matching interpolation in the common source domain and least square matching interpolation in the common receiver domain. When the two kinds of wavelets match well, we adopt the energy matching method to calculate the interpolation factors. When the two kinds of wavelets do not match well, we adopt the least square matching interpolation and linear interpolation methods to calculate matching factors. Using the above reconstruction and interpolation methods, we analyze three cases and compare the results before and after pre-stack depth migration.
For the ideal case, we adopt 1000 random noise sources, which are distributed uniformly both in axial and lateral directions. The recording time is 1200 s. After reconstruction, we conduct pre-stack depth migration with active and passive source data. The results show that in the ideal case, there is a large amount of effective reflection information. In the imaging results, the imaging result of passive-source seismic data is very close to that of active-source data. The complex structures and reservoirs are displayed clearly. For the case with inadequate passive sources, we adopt 400 locally distributed noise sources. We estimate the source region by comparing the causal and un-causal parts of reconstruction results. Then we conduct interpolation and migration. We can see from the results that the deep detailed information is clearer after interpolation. For the case of sparse data in active-source seismic exploration, we use a few noise sources located at depth. From the interpolation results, we can see that the active-source data and passive-source data match well after matching. The imaging results show that the complex structures and deep information become clearer after interpolation.
The numerical results show that effective use of active- and passive-source data can greatly improve the quality of imaging. The multidomain iterative denoising reconstruction method can suppress noises effectively. By adjusting the threshold value and filter windows, we can extract effective signals gradually. In the interpolation processing of active- and passive-source data, energy matching interpolation in the common source domain and least square matching interpolation in the common receiver domain can obtain good results in different cases. In the area with a few passive sources, we can estimate the source region from the causal and un-causal part of data. Adding a few active data in the quiet area can compensate the imaging results effectively. In the sparse shot active seismic exploration, the use of passive data can add some detailed information.
在地震勘探中,地表接收的地震记录往往同时包含主动源和被动源数据.由于被动源信号微弱,且杂乱无章,人们往往将其视为噪声而消除.被动震源位于地下一定深度位置,它的透射波同样按照地震波的传播规律通过地下介质而被接收,同样包含丰富的地下信息,如果能被充分地利用,必定能为主动源勘探提供有效的补充.而且在实际工作中,由于环境、成本和效率等原因,往往会得到较稀疏的主动炮记录,或丢失某些主动炮记录.信息的不足会较大地影响偏移成像的效果,这时,我们考虑如何能有效利用被动源信息,来增加成像结果的信息量和准确度.而且,在被动源勘探中,如果遇到被动震源活跃度不是很高的地区,要想接收到足够多的震源信息,就需要很长的接收时间.这时,我们考虑到适当地加入少量主动源信息来提高被动源的成像效果.
对地下被动源数据的重构一般采用地震干涉法(Draganov et al., 2007;Snieder et al., 2009;Xu et al., 2012).在地表接收透射波地震记录,将其进行自相关运算后合成的地震记录相当于地表的自激自收模拟记录(Claerbout,1968).在勘探地球物理领域,从互相关信息中恢复波场的研究是通过地震数据的广义相关方法建立的(Schuster and Rickett, 2001).应用地震干涉技术对未知震源的地震数据进行成像已展开研究,对地表地震数据进行偏移,已经取得过很好的效果(Sheng,2001).随后,人们用积分理论和互易定理论证了地震波干涉法对不同的非衰减的介质和不同的震源均成立(Wapenaar,2003;Wapenaar et al., 2004).相关型互易方程被认为是各种相关型重建数据方法的数学基础(Wapenaar,2004).人们也对经过互相关处理后的道集记录进行Kirchhoff偏移成像,并将结果与主动源地震记录的叠加偏移剖面进行对比,得出对地下噪声源地震记 录做互相关运算可以获得有用信息的结论(Schuster et al., 2004;Bakulin and Calvert, 2006). 用数值模拟的方法已经讨论过两种被动震源情况下的数据重构方法,并在声波介质和弹性介质中都取得了较好的效果(Draganov et al., 2006).在国内,利用背景噪声进行地震成像的方法提出较晚(齐诚等,2007).近几年,国际上新的重构方法也被不断提出,主要有多维反褶积方法(Wapenaar et al., 2008),稀疏反演法(Groenestijn and Verschuur, 2010),RPSI(Receiver-Pair Seismic Interferometry,检波对地震干涉法)方法(Ruigrok and Vidal, 2013).对被动源直接进行偏移成像的方法也已被提出(Artman et al., 2004),其利用互相关的成像条件,在重构之前对数据进行偏移,但实质上与重构之后的偏移是等价的.同时适用于主动源混合采集和被动源采集数据的一种成像方法已经有人提出(Berkhout and Verschuur, 2011).但是,单纯利用被动数据的成像效果往往不太理想,与主动源相比,信息的缺失较为严重.而且在勘探中,主动和被动数据匹配方法研究很少,将匹配后的数据应用于成像过程来相互补充也鲜有研究.
本文研究了两种情况下被动源和主动源联合数据的成像效果.一种是被动源勘探中,在被动源活跃度不是很高的区域,用少量主动源信息来控制和补充被动源的成像效果;另一种是在炮点稀疏的主动源勘探中,用被动源信息来补充主动源数据.基于互相关重构原理,本文提出了结合多域迭代去噪算法的被动源重构方法.提出了共炮点域能量匹配插值和共检波点域最小平方匹配插值来对主动源和被动源数据进行插值,最后进行PSPI(phase shift plus interpolation,相移加插值)叠前深度偏移成像. 2 方法原理 2.1 常规互相关法被动源数据重构
根据震源特征的不同,可以将被动源分为两种(Draganov et al., 2006):一种是瞬态震源,另一种是噪声震源.对这两种被动源数据的重构原理是相同的,只是实际处理上稍有区别.对于瞬态震源,可以分别截取出包含震源信息的数据段,然后分别对每一段数据做相关运算,最后将所有的相关结果相加.对于噪声震源,可以连续接收被动源记录,然后对接收到的记录直接做互相关运算.实际勘探中,数据存储在很多分文件中,分别相关后再叠加也能得到正确的结果,但从时间域相关运算原理上看,分段相关对幅度是有影响的,且分文件越多,影响越大.我们建议先对分文件尽可能多的进行连接,然后进行相关和叠加处理.
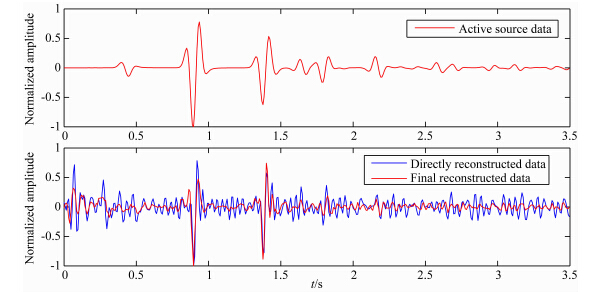
本文模拟背景噪声的情况,采用的被动源都为噪声震源,且噪声震源随机分布在地下,震源的信息未知.地表布设有两个检波器,用xA和xB表示.它们连续接收地下的透射波记录,分别表示为T(xA,t)和T(xB,t).利用透射记录重构地震反射响应的时间域表达式为
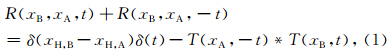
Wapenaar曾用互易定理严格推导了声波介质 提取格林函数的精确表达式(Wapenaar and Fokkema, 2006),对于噪声震源情况,基于远场近似给出了格林函数近似表达式.对透射记录的互相关得到的重构记录的振幅信息与格林函数本身是有误差的(Ramirez and Weglein, 2009),但是重构的走时和相位都是准确的.Zheng(2010),Zheng等(2011)等通过构造互相关核函数提取了真振幅格林函数,并在平面和球面震源分布情况进行了成功的应用,但该方法构造互相关核函数时,需要知道震源的精确位置,因此对于背景噪声情况的重构还不能成功应用.
本文采用噪声震源作为被动源,数量较多,并假设其在地下一定深度内随机分布.故其位置未知,得到的是很多震源信息相互叠加的复杂原始记录,这种情况很难做波场分离和震源定位.对于这种情况,目前适用的常规重构方式都是基于互相关算法.本文将提出一种结合多域迭代去噪算法的重构方法.下文的插值处理和偏移成像主要利用了重构记录走时和相位的准确性,而不考虑其振幅的精确值,因为通过匹配插值,可以让重构记录的振幅值尽量接近主动震源记录的振幅值. 2.2 多域迭代去噪技术被动源数据重构
利用以上常规的方法得到的被动源重构数据往往含有严重的噪声干扰,这些噪声一方面来自透射记录本身,另一方面来自相关运算的过程.这些噪声的强度有的甚至强于有效信号,而且在频率域与有效信号重叠,导致常规的去噪方法很难取得很好的效果.这些噪声会影响后续处理过程,也会影响最后的偏移成像效果.于是,基于以上重构原理,我们提出了结合多域迭代去噪技术的被动源数据重构方法.
多域迭代去噪的思路曾被应用于混合炮分离的研究(Doulgeris et al., 2010;Tan et al., 2012;韩立国等,2013).基于前人的研究,我们提出了适用于被动源信号提取的新的组合方法来构成多域迭代去噪算法,并将其加入到被动源数据重构过程中.分别在共炮点道集和共检波点道集进行Curvelet阈值迭代去噪和二维多级中值滤波.在Curvelet域中,有效信息的系数和随机噪声的系数仅有较小的重叠.Curvelet阈值迭代去噪算法的基本思想是将压制地震随机噪声的问题转换为L1范数最优化反演问题.它的基本流程是把要处理的数据变换到Curvelet域中,设定适当的阈值进行限制,最后将处理后的数据变换到时空域.对于中值滤波而言,较小的滤波长度可以更好地保护有效信号,但会降低其去噪效果;较大的滤波长度可以提高去噪效果,但是会破坏更多的有效信息.所以在每一次应用中值滤波时,都要根据噪声水平调整中值滤波窗口.在第一次处理结束后,计算差剖面,当差剖面中仍含有很多有效信号时,需对差剖面进行第二次迭代处理,将提取的有效信息加入到上次得到的结果中.再对第二次迭代结果求取差剖面,根据有效信号残留量判断是否需要进行下次迭代.从迭代过程可见,通过调节阈值、滤波窗口及迭代次数,能在很大程度上从原始记录中提取出有效信号.
我们采用的多域迭代去噪算法如下:
(1)对接收到的被动数据做相关运算,得到一系列的单炮记录,用 R 0表示. P i 表示第i次迭代去噪后的结果.初始值i=0,P 0=0;
(2)i=i+1;
(3)计算差剖面 M i= R 0- P i-1;
(4)当 M i 中有效信号高于预期值时,进行第5步.反之,进行第8步;
(5)将 M i 在共炮点域依次进行Curvelet阈值迭代去噪和中值滤波处理,每次调整阈值和滤波窗口,得到 M ′ i ;
(6)将 M ′ i 变换到共检波点域,并依次进行Curvelet阈值迭代去噪和中值滤波处理,每次调整阈值和滤波窗口,得到 M ″ i ;
(7)将 M ″ i 变换到共炮点域,计算Pi=Pi-1+ M ″ i,回到第2步;
(8)将 P i 的因果部分和非因果部分的时间反转进行加和,得到最后的重构结果.
为了对比重构的效果,我们在一个模型上测试了以上的迭代去噪重构算法.采用如图 1a所示的速度模型,网格间距为10 m×10 m.检波器布设在地表 0~10000 m范围内,间距50m,1000个噪声震源随机分布于地下2000~3900 m深度范围内.噪声震源的横向分布越广,就越接近理论上关于震源包围检波器的假设,纵向分布越广,越能有效压制重构可能产生的鬼波等的虚假同相轴.图 1b为采用的噪声震源函数,可见震源都为互不相关的杂乱信号,且延续时间各不相同.接收1200 s的被动源记录后,首先按常规方法,直接相关重构,并将因果与非因果部分加和,得到记录如图 2a所示,记录中噪声非常严重,且有很多明显的极值点.图 2b为采用上述迭代去噪重构算法得到的记录,可见其信噪比大大提高,有效信号被成功地提取.为了进行对比,同时模拟了地表激发的主动震源记录,如图 2c所示.对比发现,除直达波外,其他有效波都被成功地重构出来.由于多次波的能量较弱,其在重构记录中较不明显,这对于后续的处理来说是有利的.图 3为抽取图 2记录的相同道得到的波形图,进一步说明了重 构记录的到时和相位是正确的,但是振幅是不准确的.
 | 图 1 速度模型和被动震源信息 (a)速度模型和震源分布;(b)噪声震源信号.Fig. 1 Velocity model and the information of passive sources (a)Velocity model and the source distribution;(b)Noise sources used in modeling experiments. |
 | 图 2 两种重构方法得到的地震记录对比图 (a)常规重构的结果;(b)迭代去噪重构结果;(c)主动源正演记录. Fig. 2 The comparison of seismic recordings using two different reconstruction methods (a)Conventional reconstructed recording;(b)The reconstructed result using iterative denoising method;(c)Forward recording of active source. |
 | 图 3 去噪前后某道的波形对比图Fig. 3 The waveform comparison before and after denoising |
在进行了迭代去噪重构之后,可以得到有效信 息明显的重构记录,这时可以根据有效信息的能量来对主动源数据进行插值,以得到主动源与被动源的联合数据.如果插值进行的不合适,会造成联合数据中主动或被动数据的有效信息所占比重被人为压制,不仅达不到数据补充的效果,还会损害原有的有效信息.本文在时间域对主动和被动数据进行插值.为了保证被动源数据的低频优势,我们尽量不改变其频率特性,尽量减少对其波形的调整.因此,下文根据两种记录震源子波的匹配程度分两种情况进行插值方法讨论.当震源子波匹配程度较好时,只在共炮点域进行能量匹配插值;当震源子波匹配不太好时,在共检波点域进行能量和相位的匹配插值.
(1)主动震源子波与被动重构数据虚拟子波匹配较好时的情况
当重构记录的同相轴信息简单时,可以提取一条同相轴,由其能量来确定增益系数,再用线性插值的方法求取插值系数;当重构记录的同相轴信息复杂时,可以用最小平方的方法来匹配有效能量,再求插值系数.
由于被动源数据是非常灵活的,即只要有检波器阵列的地方,就可以得到以某一个检波器为炮点时的重构记录,因此可以利用这个优点去主动匹配主动源记录.设主动源记录和被动源记录分别用矩阵 A和P 表示,当j为定值,i和t 取定义内所有值时,矩阵 A j(i,t)和P j(i,t)分别表示主动和被动记录的第j炮的数据,i代表检波器位置,t为采样时间.假设由于某种因素的限制,只有j和j+3位置处的主动源数据,用 A j(i,t)和A j+3(i,t)表示,经过 处理发现数据信息是不足的,此时可以考虑用被动 源数据来补充主动源数据,例如以j+1和j+2为炮点位置加入被动数据信息.首先,在j和j+3位置处分别重构出虚拟单炮记录,用 P j(i,t)和P j+3(i,t)表示.经过迭代去噪处理后,噪声已经在一定程度上被压制.
当同相轴信息较简单时,分别提取被动源记录虚拟炮点位置附近的若干道数据,提取这些道有效信息段的最大值并取平均,得到的数值分别用pj和pj+3表示.由于重构记录的浅部是错误的异常信息,故此处的信息提取必须避开浅部,从有效信息开始的时窗内取值.对于主动源记录进行同样的操作,得到rj和rj+3.利用线性插值的方法计算增益系数为
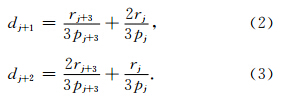
当重构记录的同相轴信息较复杂时,应首先设定一个阈值,将被动源记录中振幅绝对值大于阈值的振幅保留,其他位置充零,分别得到矩阵 P ′ j(i,t)和P ′ j+3(i,t).在主动源重构过程中,保留被动源处 理中的非零地震道,其他位置充零,得到矩阵 A ′ j(i,t)和A ′ j+3(i,t).用最小平方法分别求解(4)(5)式得到系数
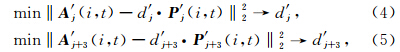
如果j+1和j+2位置处的被动源重构数据用 P j+1(i,t)和P j+2(i,t)表示,那么d′ j+1 P j+1(i,t)和d′ j+2 P j+2(i,t)可作为插值数据加入到主动源数据系列中去.在插值处理前,如果重构记录能量分布不均匀,应先对其做能量的归一化处理,这样插值后的结果能体现更多的被动源信息.
(2)主动震源子波与被动重构数据虚拟子波匹配不太好时的情况
由于本文的插值是将主动源单炮记录或者被动源重构单炮记录加入到多炮记录序列中去,因此,相当于在共检波点道集进行缺失道插值.当主动源震源子波与被动源重构数据虚拟震源子波匹配不太好时,我们不仅要匹配二者的振幅,还要调整记录的相位.采用的思路如下:首先确定期望通过插值达到的总炮数,即插值后共检波点道集的道数.然后根据(4)和(5)式进行主动源数据和被动源数据的单道匹配,此时公式中的d′ j和d′ j+3不再是能量系数,而是匹配算子,是一个列向量.再利用线性插值算法可以得到第j+1道和j+2道的匹配算子.匹配算子与被动源数据进行褶积运算即可得到需要的被动源数 据.最后将匹配道插入到主动源共检波点道集的缺 失处,变换回共炮点道集即得最后的插值结果.
为了说明插值的效果,我们在Marmousi模型上进行了测试.采用如图 4所示的模型.模型长10420 m,深3010 m,网格间距为10 m×10 m,最大速度为5500 m·s-1,最小速度为1500 m·s-1.
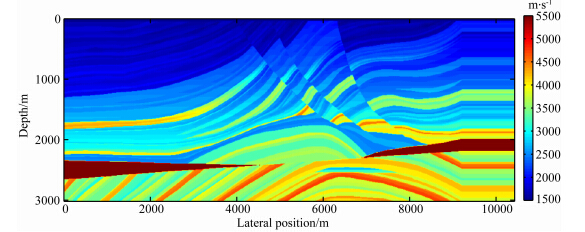 | 图 4 Marmousi模型Fig. 4 Marmousi velocity model |
模拟主动源数据时,炮间距为800 m,检波器布设在地表 0~10420 m的范围内,间距为20 m.模拟被动源数据时,让1000个噪声震源随机分布在x方向0~10420 m,z方向1000~3000 m的矩形区域内,检波器布设在地表 0~10420 m的范围内,间距为20 m.接收的噪声记录长度为1200 s.进行迭代去噪被动源数据重构得到要利用的被动源记录.现在要插值得到炮间距为400 m的联合数据.在共检波点道集,这就成为一个缺失道插值问题,均匀缺失信息50%.待插值的一个主动源共检波点道集数据如图 5a所示.用以上的方法对被动源数据进行匹配,并插值到主动源记录中,得到的结果如图 5b所示.可见缺失道信息得到了补充,很多细节信息得到了保留,记录的同相轴连续,说明我们的方法可以将能量和相位都匹配得很好.插值前后的差剖面如图 5c所示,由于被动源记录中不可避免地存在噪声,因此在差剖面中直达波以上可以看到一些噪声信息,但是这些噪声很微弱,叠加后基本不会对成像结果造成影响.将所有的共检波点道集数据进行匹配 插值,再变换回共炮点道集,就得到了炮间距为400 m 的主动源和被动源联合数据.变换回共炮点域的联合数据将在下文成像的讨论中展示.
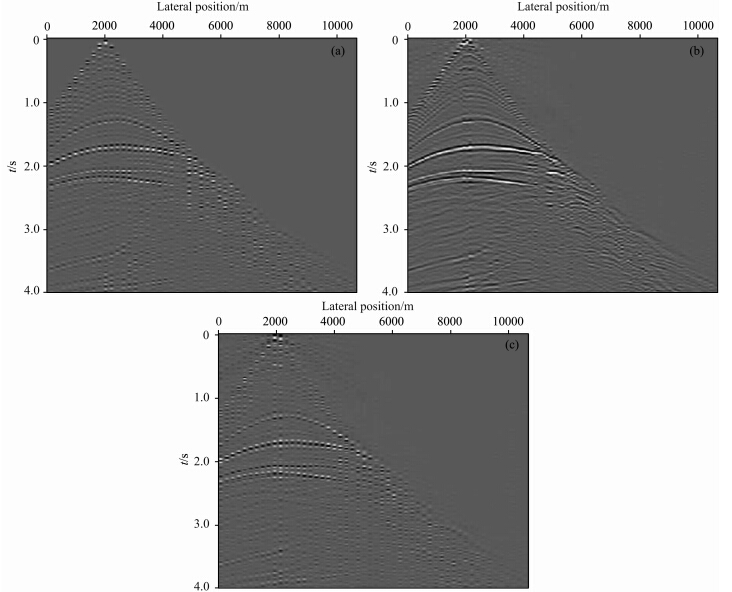 | 图 5 用被动源数据对主动源数据插值效果对比 (a)共检波点域的缺失炮主动源数据;(b)用被动源数据匹配插值后的共检波点域联合地震数据;(c)插值前后的差剖面. Fig. 5 The interpolation of active data using passive data (a)The missing shot active data in common detector domain;(b)The combined seismic data in common detector domain after matching interpolation using passive data;(c)The difference profile before and after interpolation. |
被动源数据的相关重构在理论上假设被动震源包围着检波器,当地表为自由表面时,相当于一个镜面,所以只需震源在地下区域包围检波器.但在实际情况中很难有包围的情况.当震源数量较多,震源在地下横向分布比较广泛,且震源横向间隔较小,在纵向一定深度内随机分布,总体分布均匀的时候,我们认为是一种理想的情况,能得到很好的重构效果.这里我们称符合条件的区域为被动震源非常活跃区,该区适合进行单纯的被动源勘探.
采用如图 4所示的Marmousi模型.模拟理想情况时,让1000个噪声震源随机分布在x方向0~10420 m,z方向1000~3000 m的矩形区域内,检波器布设在地表 0~10420 m的范围内,间距为20 m.接收较长时间的被动源记录,本次试验的噪声记录长度为1200 s.在这样理想的参数配置下,能重构出含有丰富有效信息的被动源记录.本文采用了PSPI叠前深度偏移方法进行偏移成像,结果如图 6a所示.在重构得到的单炮记录中虽然也有很多噪声,但即使不经过预处理,而是直接进行偏移成像,也能得到较好的效果.这是因为在理想情况下,被动源重构数据的反射信息较强且准确,而且偏移过程有多炮结果的累加过程,所以在偏移结果中噪声很大程度上被压制.作为对比,以与虚拟震源相同的震源位置和间隔模拟主动源记录,并进行PSPI叠前深度偏移,结果如图 6b所示.可见,在理想情况下,被动源的偏移效果能够很接近主动源数据的偏移效果,只是在浅部的偏移效果弱于主动源,因为被动源数据多为来自地下的较低频信息,且对浅部的重构较不准确.
 | 图 6 理想情况下主动和被动数据的深度偏移结果 (a)被动源数据叠前深度偏移结果;(b)主动源数据叠前深度偏移结果. Fig. 6 The depth migration results of active and passive data in an ideal situation (a)The pre-stack depth migration result using passive data;(b)The pre-stack depth migration result using active data. |
在实际情况中,往往和理想情况差别较大,比如震源数量不会很多,且横向分布不会无限广.下面讨 论震源数量为400,且只分布在地下某一区块的情况. 这时,单纯的被动源数据已经很难准确对地下进行 成像,在这种情况下进行被动源勘探时,可以加入少量的主动源信息来帮助成像,下面讨论这种情况下主动源对被动源数据的补充效果.
采用图 4的模型,震源只分布在一个有限区域内,这更接近实际的情况.震源水平范围为2000~4500 m,深度范围为1500~2800 m,如图 7f所示.检波器布设和接收时间同上.在实际中,需要对原始数据做预处理来保证后续数据处理的质量.这里我们对接收到的原始数据做高频噪声切除和能量归一化处理,然后用迭代去噪重构方法对被动源数据进行重构和有效信息提取.在用主动源信息对被动源信息进行补充之前,需要知道地下被动源分布的大致区域,以便在被动源较平静区较多地增加主动源信息以补充勘探效果.
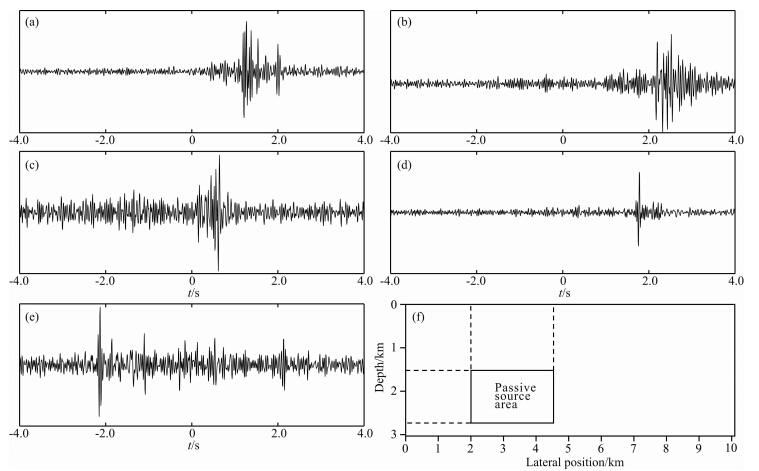 | 图 7 不同检波器记录互相关结果 (a)检波器C与D的互相关结果;(b)检波器C与E的互相关结果;(c)检波器B与C的互相关结果;(d)检波器B与A的互相关结果;(e)检波器F与B的互相关结果;(f)被动震源实际分布图.Fig. 7 Cross-correlation of recordings from different receivers (a)Cross-correlation of receiver C and D;(b)Cross-correlation of receiver C and E;(c)Cross-correlation of receiver B and C;(d)Cross-correlation of receiver B and A;(e)Cross-correlation of receiver F and B;(f)The actual distribution area of passive sources. |
根据重构记录因果与非因果部分的关系可以大致判断震源的分布区域.Stehly等(2006)研究了重构记录因果和非因果部分的非对称性与噪声震源能量通量的关系,本文参考这个关系来判断地下被动震源的大致分布区域,判断方法如下:在地表均匀选取几个检波器,对任意两个检波器记录的噪声记录做互相关运算,则此时一个检波器为虚拟震源,另一个检波器为虚拟检波器.若得到的互相关结果中,因果部分的能量强于非因果部分,那么说明虚拟震源一侧的地下震源密度大于虚拟检波器所在一侧的震源密度.将选取的检波器两两进行互相关运算,根据以上规律便可以判断地下震源的大致分布区域.其中,检波器的选取个数根据精度要求而定,适当地增加数量,可以提高震源区域确定的准确度.针对本次试验的判断过程如下:
在接收完毕后,共得到522道地震记录,检波器 间距为20 m.现在分别选取2000m,4000m,6000m,8000m,10000 m 位置处的5个检波器作为判断标准,分别称为检波器A,B,C,D,E.首先选择靠近中间位置的检波器C分别与检波器D和E做互相关运算,都是以C为虚拟炮点位置,得到的相关结果如图 7a和7b所示.可见,两个相关结果都指示虚拟震源一侧,即检波器C一侧的震源密度较大.将检波器B分别与检波器C和A做互相关运算,都以B作为虚拟震源位置,得到的相关结果如图 7c和7d所示.结果显示检波器B左侧和A右侧区域的震源密度较高.作为验证,选取3000 m位置的检波器(记为F)与检波器B做互相关运算,以F作为虚拟炮点位置,得到结果如图 7e所示.结果显示虚拟检波器B一侧的震源密度稍大,此时因果与非因果的能量差别不大,说明B和F很可能都位于震源区以上,判断结果显示B侧震源密度较大的原因是B一侧地质构造复杂,地震波发生复杂的反射和绕射,很多位置作为二次震源产生的能量被B接收,导致这样的判断结果.综上所述,判断结果是本次试验的地 下被动源大致分布在水平位置2000~4000 m范围之内,与实际布设震源区域(2000~4500 m)大致相符,这个结论能够用于指导主动源信息补充区域的选取.
本次试验可判断出震源位于左侧地下.模型右侧为被动源相对平静区,在5300~7300 m范围内加入主动源信息,由于主动源是辅助勘探,此处只加入11%的主动源数据,对应实际中少量放炮以补充被动源数据的情况.然后用主动源数据对被动源数据进行共炮点域能量匹配插值,得到的结果中的连续三炮如图 8所示.可见经过能量最小平方插值之后,主动源和被动源能量能达到较好的匹配,这保证了在成像过程中两种信息的比例协调.
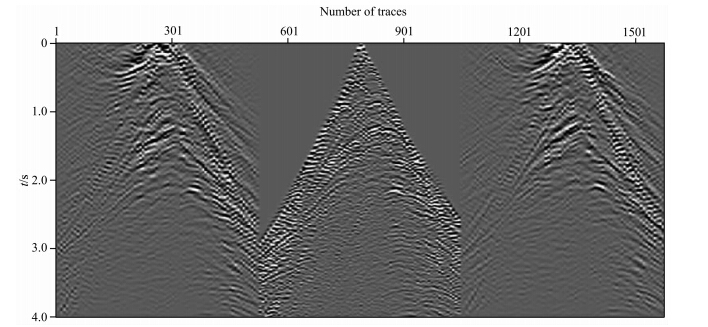 | 图 8 用主动源数据对被动源数据进行共炮点域能量匹配插值的结果Fig. 8 The energy matching interpolation result of passive data in common source domain using active data |
如果做纯被动源勘探,对被动源重构数据进行PSPI叠前深度偏移,得到结果如图 9a所示,可见此时偏移结果已经不能清楚地反映地下构造,在中间位置下方的一系列断层构造处的分辨率也很低.用加入了主动源数据的联合地震数据做PSPI叠前深度偏移成像,得到偏移结果如图 9b所示.可见利用联合数据的偏移结果,中间的断层部分和深部的构造都更加明显,分辨率有所提高,一些细节信息得到增强.整体成像效果明显好于纯被动源的情况.11%的主动源信息对应较小的实际工作量,而得到的效果能明显增强,所以在被动源勘探中,主动源信息对被动源的补充很有意义.
 | 图 9 被动数据中加入少量主动数据前后的偏移结果对比 (a)纯被动源数据的叠前深度偏移结果;(b)加入11%主动源信息的叠前深度偏移结果. Fig. 9 The comparison of migration results with and without active information (a)The pre-stack depth migration result using only passive data;(b)The pre-stack depth migration result after adding 11% active information. |
在某些地区,被动源的活动可能较微弱,此时进行被动源勘探将达不到较好的效果,还应进行主动源勘探.在得到的主动源数据中仍然会含有背景噪声的信息.在通常的处理中,我们会将其作为噪声消除,这里,我们把它看作能补充主动源的有效信息进行提取.在试验中,采用少量的、且分布在深部的噪声震源来模拟此时的背景噪声情况.
在野外采集中,由于某些原因,可能只得到炮间距较大的一组数据,单纯用这些数据进行成像是不够的,此时考虑用被动源信息来补充主动源数据.被动源数据的优点是它可以在任意检波器处重构出以该检波器为炮点的虚拟记录,这就为加密主动源数据带来可能.我们仍在Marmousi模型上进行试验. 震源数量为300,随机分布在水平0~10420 m,深度 2200~3000 m范围内,检波器布设在地表 0~10420 m的范围内,间距为20 m.假设主动源的炮间距为800 m,信息量是不足的.被动源的优势就是只要有足够密的检波器,就可以将数据加密到很密,但是如果加入的被动源比重太大,将会反过来压制主动源的有效信息,所以二者的比重要在实际中调节.提取出被动源数据,然后进行迭代去噪重构.在共检波点域进行最小二乘匹配插值处理,将原来的主动源数据用被动源信息加密一倍,得到的联合数据变换到共炮点域,其中的连续三炮如图 10所示.可见,经过共检波点域最小二乘插值后,被动源的有效信息与主动源较接近.首先对炮间距为800 m的主动源数据进行PSPI叠前深度偏移,得到的结果如图 11a所示,可见由于主动源信息的不足,偏移结果变差,中间部分的复杂构造信息得不到反映.用被动源插值后的联合数据进行PSPI叠前深度偏移,结果如图 11b所示.可见成像效果得到增强,尤其在中间断层及深部向斜构造处,信息得到明显的增强,连续性也变得更好.
 | 图 10 用被动源数据对主动源数据进行共检波点域匹配插值结果Fig. 10 The matching interpolation result of active data in common detector domain using passive seismic data |
 | 图 11 主动数据中加入被动数据前后的叠前深度偏移结果对比 (a)较稀疏炮间距的主动源数据的偏移结果;(b)被动源加密一倍的联合数据的偏移结果.Fig. 11 The comparison of pre-stack depth migration results with and without passive information (a)The migration result using active data with sparse shot intervals;(b)The migration result using combined seismic data with equal passive information. |
被动源信息来自于地下的一定深度位置处,包含着丰富的地下构造信息.通常在勘探中,由于其能量较弱,往往将其视为噪声而消除.本文通过试验证明,有效地利用主动源和被动源联合数据,能够很大程度上提高成像质量.
常规的被动源重构记录中含有大量的强噪声,结合多域迭代去噪算法的重构方法能够有效的压制噪声,提取有效信号.通过调整阈值和滤波窗口,并进行迭代,可以从差剖面中不断提取有效信号.在主动源与被动源数据的插值处理中,共炮点域能量匹配插值和共检波点域最小平方匹配插值针对不同的情况都能取得较好的效果.得到的联合数据在叠前深度偏移中取得了很好的补充效果.
在被动源活跃度不是很高的地区进行被动源勘探时,可从因果与非因果重构结果中大致判断震源的分布区域,在较平静区加入少量主动源数据能够有效地控制和补充被动源的成像结果.在稀疏炮点的主动源勘探中,有效利用被动源数据,能够补充成像中的一些细节信息,得到更好的成像结果.
| [1] | Artman B, Draganov D, Wapenaar K, et al. 2004. Direct Migration of passive seismic data.//66th EAGE Conference and Exhibition Extended Abstracts, Z-99. |
| [2] | Bakulin A, Calvert R. 2006. The virtual source method: Theory and case study. Geophysics, 71(4): SI139-SI150. |
| [3] | Berkhout A J, Verschuur D J. 2011. A scientific framework for active and passive seismic imaging, with applications to blended data and micro-earthquake responses. Geophysical Journal International, 184(2): 777-792, doi: 10.1111/j.1365-246X.2010.04855.x. |
| [4] | Claerbout J F. 1968. Synthesis of a layered medium from its acoustic transmission response. Geophysics, 33(2): 264-269. |
| [5] | Doulgeris P, Mahdad A, Blacquiere G. 2010. Separation of blended impulsive sources using an iterative approach.//72nd EAGE Conference and Exhibition Extended Abstracts, B004. |
| [6] | Draganov D, Wapenaar K, Thorbecke J. 2006. Seismic interferometry: Reconstructing the earth's reflection response. Geophysics, 71(4): SI61-SI70. |
| [7] | Draganov D, Wapenaar K, Mulder W, et al. 2007. Retrieval of reflections from seismic background-noise measurements. Geophysical Research Letters, 34: L04305, doi: 10.1029/2006GL028735. |
| [8] | Ferguson R J, Margrave G F. 2005. Planned seismic imaging using explicit one-way operators. Geophysics, 70(5): S101-S109. |
| [9] | Groenestijn G V, Verschuur D J. 2010. Estimation of primaries by sparse inversion from passive seismic data. Geophysics, 75(4): SA61-SA69. |
| [10] | Han L G, Tan C Q, Lü Q T, et al. 2013. Separation of multi-source blended seismic acquisition data by iterative denoising. Chinese J. Geophys. (in Chinese), 56(7): 2402-2412, doi: 10.6038/cjg20130726. |
| [11] | Qi C, Chen Q F, Chen Y. 2007. A new method for seismic imaging from ambient seismic noise. Progress in Geophysics (in Chinese), 22(3): 771-777. |
| [12] | Ramirez A C, Weglein A B. 2009. Greens theorem as a comprehensive framework for data reconstruction, regularization, wavefield separation, seismic interferometry, and wavelet estimation: A tutorial. Geophysics, 74(6): W35-W62, doi: 10.1190/1.3237118. |
| [13] | Ruigrok E N, Vidal C A. 2013. Body-wave Receiver-pair Seismic Interferometry.//75th EAGE Conference and Exhibition Extended Abstracts, Th-P15-02. |
| [14] | Schuster G T, Rickett J. 2001. Daylight imaging in V(x, y, z) media.//Stanford Exploration Project, Report SEP-105, 209-227. |
| [15] | Schuster G T, Yu J, Sheng J, et al. 2004. Interferometric/ daylight seismic imaging. Geophysics Journal International, 157(2): 838-852. |
| [16] | Sheng J. 2001. Migrating multiples and primaries in CDP data by cross-correlation migration.//71st SEG Annual meeting Expanded Abstracts, 1297-1300. |
| [17] | Snieder R, Miyazawa M, Slob E, et al. 2009. A comparison of strategies for seismic interferometry. Surveys in Geophysics, 30(4-5): 503-523, doi: 10.1007/s10712-009-9069-z. |
| [18] | Stehly L, Campillo M, Shapiro N M. 2006. A study of the seismic noise from its long-range correlation properties. Journal of Geophysical Research, 111(B10306): 1-12, doi: 10.1029/2005JB004237. |
| [19] | Tan C Q, Han L G, Zhang Y H, et al. 2012. Separation of blended data by iterative denoising.//74th EAGE Conference and Exhibition Extended Abstracts, A045. |
| [20] | Thorbecke J W, Draganov D. 2011. Finite-difference modeling experiments for seismic interferometry. Geophysics, 76(6): H1-H18, doi: 10.1190/GEO2010-0039.1. |
| [21] | Wapenaar K. 2003. Synthesis of an inhomogeneous medium from its acoustic transmission response. Geophysics, 68(5): 1756-1759. |
| [22] | Wapenaar K. 2004. Retrieving the elastodynamic Green's function of an arbitrary inhomogeneous medium by cross correlations. Physical Review Letters, 93: 1-4, 254301, doi: 10.1103/PhysRevLett.93.254301. |
| [23] | Wapenaar K, Thorbecke J, Draganov D. 2004. Relations between reflection and transmission responses of 3-D inhomogeneous media. Geophysical Journal International, 156(2): 179-194. |
| [24] | Wapenaar K, Fokkema J. 2006. Green's function representations for seismic interferometry. Geophysics, 71(4): SI33-SI46, doi: 10.1190/1.2213955. |
| [25] | Wapenaar K, Neut J, Ruigrok E. 2008. Passive seismic interferometry by multidimensional deconvolution. Geophysics, 73(6): 51-56. |
| [26] | Xu Z, Juhlin C, Gudmundsson O, et al. 2012. Reconstruction of subsurface structure from ambient seismic noise: an example from Ketzin, Germany. Geophysical Journal International, 189(2): 1085-1102. |
| [27] | Zheng Y C. 2010. Retrieving the exact Green's function by wavefield crosscorrelation. J. Acoust. Soc. Am., 127(3): EL93-EL98. |
| [28] | Zheng Y C, He Y F, Fehler M C. 2011. Crosscorrelation kernels in acoustic Green's function retrieval by wavefield correlation for point sources on a plane and a sphere. Geophysical Journal International, 184(2): 853-859." |
| [29] | 韩立国, 谭尘青, 吕庆田等. 2013. 基于迭代去噪的多源地震混合采集数据分离. 地球物理学报, 56(7): 2402-2412, doi: 10.6038/cjg20130726. |
| [30] | 齐诚, 陈棋福, 陈颙. 2007. 利用背景噪声进行地震成像的新方法. 地球物理学进展, 22(3): 771-777. |
 2015, Vol. 58
2015, Vol. 58


