2015, Vol. 58
This paper focuses on studying the numerical dispersion and stability of wave motion with triangle-based finite element algorithm. Considering two kinds of commonly used grid structures (denoted by I mesh structure and II mesh structure, respectively), according to the assemble principle of structural stiffness matrix and plane wave theory, we obtain dispersion functions under the assumption that computational area is uniform and without borders. The stability conditions are obtained in the condition of second order middle difference, to provide reference for the selection of time step. In order to fully understand the characteristics of numerical dispersion in triangular meshes, we analysed quantitatively the effect of spatial sampling interval, the propagation direction of seismic wave, the ratio of vertical to horizontal (mesh shape) on numerical dispersion. To obtain optimal mesh generation, the influences of mesh shape are studied mainly. In a practical simulation, we should consider the numerical calculation accuracy. Therefore, the maximum dispersion errors of the two kinds of grid structures are analyzed comparatively. Finally, we verify our conclusions by wave-field simulations. The authors hope that the study in this paper can provide some useful suggestions for the division of triangular mesh and parameter setting.
From the theoretical analyses and numerical experiments, the following results can be gained: (1) The numerical phase velocity varies significantly with the propagation direction, and this variation is periodic, the period of the numerical dispersion is π except regular triangle mesh, the period of which is π/3, because the mesh structure is invariant under π/3 rotation. (2) When the ratio of vertical to horizontal is equal to 1, the maximum dispersion error and minimum dispersion error of I mesh structure appear in the direction of θ=0° and θ=45°, respectively; and the maximum dispersion error and minimum dispersion error of II mesh structure appear in the direction of θ=90°and θ=0°, respectively. (3) In terms of I mesh structure, the dispersion error in horizontal direction has nothing to do with the ratio of vertical to horizontal, which is also the maximum dispersion error, in other words, by reducing the ratio of vertical to horizontal to suppress the numerical dispersion is not an effective method. (4) In terms of II mesh structure, the maximum dispersion error can be suppressed effectively by reducing the ratio of vertical to horizontal as long as it does not appear obtuse triangle mesh; it is worth pointing out that regular triangle mesh almost removes the directional dependence of the phase velocity, which means the numerical anisotropy is the weakest. (5) In the case of no visible numerical dispersion, the number of sampling point in the wavelength corresponding to peak frequency of source wavelet of II mesh structure is less than that of I mesh structure, and this can help improve the calculation efficiency and reduce the occupation of memory. (6) The stability factor of II mesh structure is also larger than that of I mesh structure.
The dispersion characteristics analysed in the above can provide some theoretical guidances for mesh generation. The arrangements of elements should be chosen with care; unreasonable meshes will reduce the precision of numerical simulation, and even lead to erroneous results. The best arrangement of triangles appears to be hexagonal, which has the further benefit that it almost removes the directional dependence of the phase velocity, which can be useful in maintaining wave front definition.
波动方程正演模拟对认识地震波传播规律和指导地震资料解释等具有重要意义，有限差分法(FDM)和有限元法(FEM)是地震波正演模拟非常重要的两种方法.有限差分法因其方法简单、精度高而得到广泛的应用，但其缺点是不能准确模拟具有复杂几何形态的物性界面，采用规则网格模拟横向变速剧烈或地形起伏较大的介质时会导致阶梯状的界面，从而引起数值散射等问题(薛东川等，2007；薛昭等，2014)，干扰对有效反射波的识别，对研究复杂介质下地震波传播特征以及偏移成像已经是捉襟见肘.有限元法因具有能够适应剧烈的物性变化、自然地满足自由边界条件等优点而受到地球物理学家们的青睐(汪文帅等，2013；吴子泉和宋文杰，2013；王若等，2014；刘有山等，2014；鲁杏等，2014)，特别是三角单元(任意四边形单元)能够对任意复杂的边界进行有效的剖分，因而能够准确模拟起伏地形、复杂构造和复杂介质条件下的地震波场(Ke et al., 2001；薛东川和王尚旭，2008a；刘有山等，2013).针对有限元法计算量大以及内存占用高的缺点，一般采用对角的集中质量矩阵代替一致质量矩阵，避免在时间递推过程中的求逆运算，根据结构刚度矩阵的特点(稀疏、对称)，只需存储结构刚度矩阵下三角部分的非零元素即可，同时在时间递推过程中结构刚度矩阵的零元素不参与运算(郭建，1991；Saad，2000；刘有山等，2013)，通过这些措施可以极大地提高有限元法的计算效率以及减少对内存的占用.
稳定性和数值频散是波动方程数值解固有的两个重要问题(吴国忱和王华忠，2005；孙成禹等，2010).在地震波数值模拟中，有限元法(有限差分法)对连续介质进行了空间离散，因此会引起误差，导致模拟的波的相速度(数值相速度)随频率发生变化的伪波动，即所谓的数值频散，数值频散不仅没有实际意义，而且还会影响到对真实波动现象的认识(贺茜君等，2014).因此，进行波动方程的数值模拟时，非常有必要厘清影响数值频散的因素，这对提高数值模拟的精度非常重要.在波动方程有限元数值解的频散问题上，Mullen和Belytschko(1982)最早对该问题进行了研究，考虑了不同形状的单元网格以及质量矩阵对数值频散的影响，最终得出的结论是矩形网格单元的计算精度高于三角网格单元，等边三角网格单元为三角网格单元中的最佳网格单元；Abboud和Pinsky(1992)对三维声波方程有限元数值解的频散特性做了研究，得到最佳离散网格的方法；Lee和Cangellaris(1992)对波动方程有限元数值解的离散误差做了详细分析，影响离散误差的主要因素有：节点密度、网格尺寸、入射波的传播方向、单元类型以及边界条件等；Liu等(1994)研究了不规则网格中波动的数值频散特性，得到了当使用不恰当的单元时会导致集中质量矩阵的相速度大于介质真实速度的结论；Christon(1999)研究了质量矩阵对波动数值频散的影响，并采用集中质量矩阵与一致质量矩阵的线性组合来压制数值频散；Mulder(1999)分析了一维情况下谱元法的数值频散特性，得出了谱元法的频散特性要优于常规有限元法的结论；Yue和Guddati(2005)通过构造新的质量矩阵与刚度矩阵的方法，改进了4节点低阶有限元法波动的数值频散特性；De Basabe和Sen(2007)对高阶四边形谱元法的数值频散特性以及稳定性条件进行了分析；Seriani和Oliveira(2008)证明了弹性波谱元法对压制数值频散也具有较好的效果；Liu等(2012)和李琳等(2014)对三角谱元法的数值频散以及稳定性条件做了分析；Hu等(1999)、De Basabe等(2008)、Ainsworth等(2006)以及贺茜君等(2014)对间断有限元法的数值频散性质做了研究.在国内，薛东川和王尚旭(2008b)研究了两种质量矩阵(一致质量矩阵和集 中质量矩阵)对数值频散的影响，并采用二者的线性组合来提高空间采样效率，得到速度为2500~4000 m·s-1 时的最优组合系；印兴耀等(2014)对矩形网格中的波动数值频散以及假频现象做了分析，认为震源子波主频对应的波长内采样点数目应不少20才能使频散误差不高于0.5%.
本文在理论以及数值算例上研究了波动在线性三角网格中的数值频散特性以及稳定性，为三角网格有限元法正演模拟的网格剖分以及参数设置提供一定的理论指导. 2 三角网格有限元法声波方程数值模拟的基本原理以及频散函数的推导 2.1 三角网格有限元法声波方程数值模拟的基本原理
波动方程经有限元法离散后，得到如下的有限元方程组为(杜世通，1982)
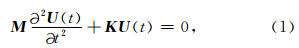
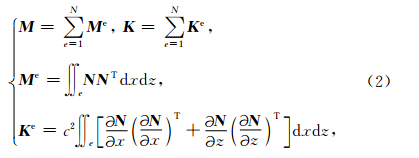
其中，Me和Ke分别为单元的质量矩阵和刚度矩阵，N为结构中单元的个数，c代表单元内介质的声波速度，N为形函数矩阵，∑代表单元质量(刚度)矩阵组装为结构质量(刚度)矩阵的法则.
三角单元的三个顶点按逆时针顺序分别记为1、2、3(如图 1所示)，则形函数为(徐世浙，1994)
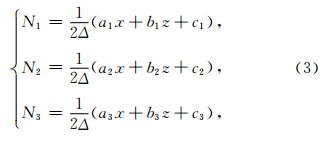
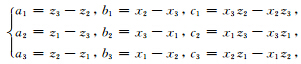
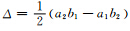是三角单元的面积.将(3)式代入(2)式中，可求得三角单元的一致质量矩阵Me和刚度矩阵Ke分别为
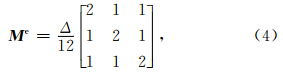
将单元的质量均匀地分配到3个节点上，得到对角的单元集中质量矩阵Mle为(王勖成，2003)
 |
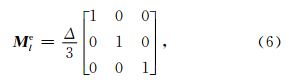
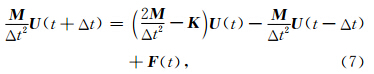
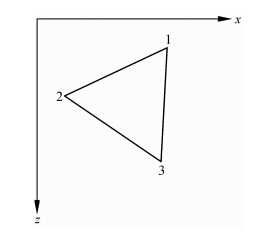图 1 三角形单元Fig. 1 Triangular element |
显然，当时间域采用显示差分格式后，在时间的递推过程中需要对结构质量矩阵M进行求逆，这不仅需要占用大量的内存以及计算耗时，而且引入数值计算误差的可能性也增大.因此，一般将单元的质量均匀地分配到节点上，得到对角的集中质量矩阵(组装后的结构质量矩阵也是对角的)，从而避免求解大型稀疏方程组. 2.2 频散函数的推导
采用三角网格单元均匀地离散模型时，具有多种剖分方式.本文考虑两种常用的剖分方式，分别如图 2a和图 2b所示.图 2a中的三角网格单元是在矩形单元上添加对角线形成的，图 2b则是在两条平行线之间以等腰三角网格单元进行剖分，底边与X轴方向平行.为了便于叙述，将图 2a和图 2b所示的网格结构分别记为Ⅰ类和Ⅱ类三角网格结构.两种网格结构在X轴、Z轴方向上的采样间隔分别为Δx和Δz，单元网格纵横比：γ=Δz/Δx.
 |
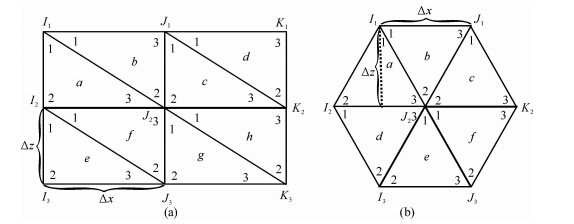图 2 共点单元网格结构(带下标的大写字母为结构节点编号，小写字母为单元编号，阿拉伯数字为单元内节点编号) (a)Ⅰ类三角网格结构;(b)Ⅱ类三角网格结构. Fig. 2 Arrangement of common-point element(capital letters with subscript are numbers of the node; small letters are the numbers of elements; Arabic figures are the code of nodes in an element) (a)Triangular mesh arrangement Ⅰ;(b)Triangular mesh arrangement Ⅱ. |
在该类结构中，有两种类型的三角单元(相同类型单元具有相同的刚度矩阵)：其一是矩形对角线上方的三角单元，如单元b、d、f、h，另一类是对角线下方的三角单元，如单元a、c、e、g.将单元的节点坐标代入(5)式，得到a类单元的刚度矩阵Kae以及b类单元的刚度矩阵Kbe分别为
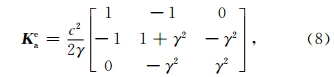
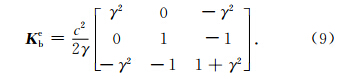
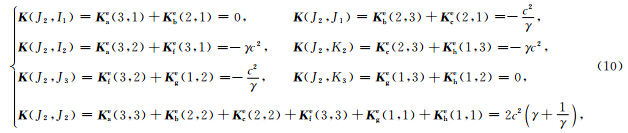
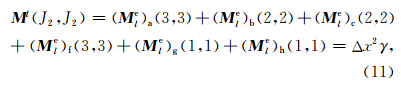
设节点J2的坐标为(mΔx，nΔz)，则该点处的位移值um，n可以表示为(孙成禹，2007)
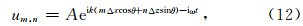
将(1)式进行第J2行的运算，得到节点J2的位移与相关节点位移的关系为
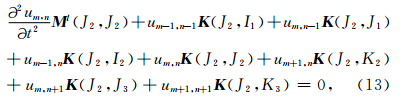
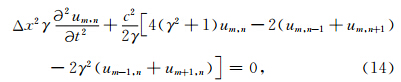
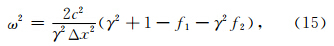
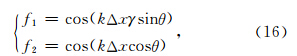
该类结构中，也有两种类型的三角单元：其一是底边所对应的顶点在底边之上的单元，如单元a、c、e；另一类是底边所对应的顶点在底边之下的单元，如单元b、d、f.仍将单元的节点坐标代入(5)式，得到a类单元的刚度矩阵Kae以及b类单元的刚度矩阵Kbe分别为
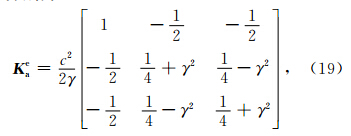
结构刚度矩阵K第J2 行需要叠加计算的元素为(其余元素均为零)
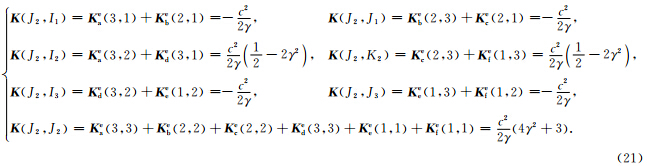
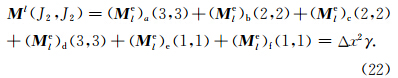
当(1)式进行第J2行的运算后，得到
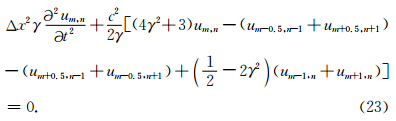
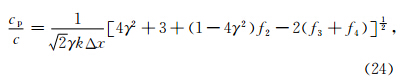
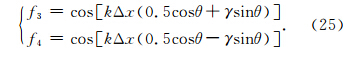
注意到，cp/c值可以衡量数值频散误差的大小，如果cp/c=1，即相速度等于介质的真实速度，则不存在数值频散；如果cp/c值远大于或小于1，数值频散误差也越大.在数值模拟中，需要根据介质速度以及震源主频选择合适的空间采样间隔使得cp/c的值接近1，以保证数值模拟的精度.在本节中，我们将研究波传播方向θ、单元网格纵横比γ以及空间采样间隔Δx等因素对数值频散的影响，以期获得三角网格剖分下的数值频散规律.此外，为防止出现假频现象，要求每个波长内空间采样点不应少于2个(Nyquist频率)，即kΔx ≤ π(孙成禹等，2009；Liu and Sen，2009). 3.1 Ⅰ类三角网格结构数值频散特性分析
首先研究波传播方向以及单元网格纵横比对数值频散的影响.假定kΔx=π/2，图 3和图 4分别显示了数值频散与波传播方向θ和单元网格纵横比γ的关系.对比分析图 3与图 4，可以得到如下结论：
(1)数值频散在传播方向上发生周期性的变化，当γ=1时，周期为π/2，且以kπ/2+π/4(k=0，1，2，3…)为对称轴，这是因为网格结构进行90°旋转后就不会发生变化；当γ≠1时，周期变为π，对称轴为kπ+π/2(k=0，1，2，3…)，因为此时网格结构需旋转180°才能保持不变.
 |
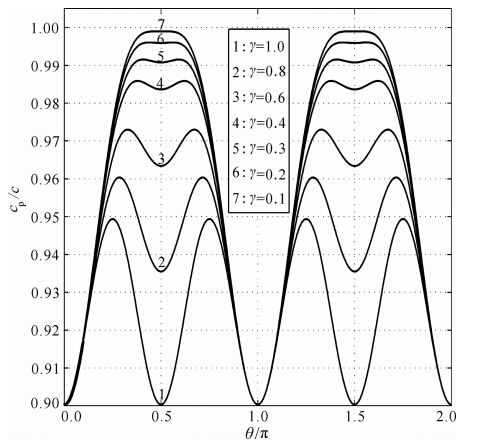图 3 γ取不同值时，cp/c随θ变化关系(kΔx=π/2)Fig. 3 The variation of cp/c with θ for different values of γ(kΔx=π/2) |
(2)当波在水平方向附近传播时(θ较小)，数值频散受单元网格纵横比γ的影响较小，如图 4中的1、2以及3号线条；特别地，当波沿水平方向传播时(θ=0°)，数值频散不受单元网格纵横比的影响，且此时频散误差最大，如图 4中的1号线条.
 |
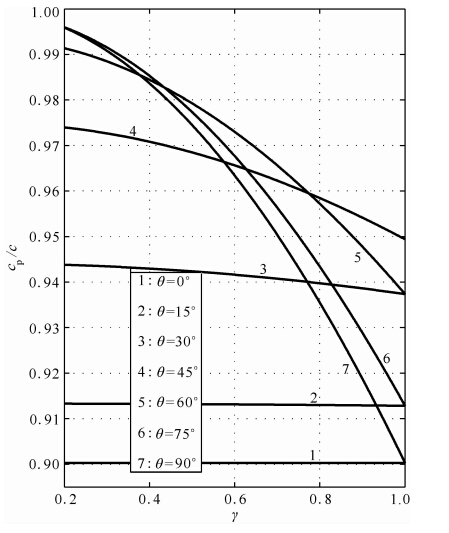图 4 θ取不同值时，cp/c随γ变化关系(kΔx=π/2)Fig. 4 The variation of cp/c with γ for different values of θ(kΔx=π/2) |
(3)当γ的值小于或等于某一常数时(将该常数记为γ1，从图中可见该常数约为0.3)，数值频散误差随着θ的增加而减小，如图 3中的5、6以及7号线条；当γ大于γ1时，随着θ的增加，频散误差先减小，后增加，如图 3中的1、2、3以及4号线条.
(4)当单元网格纵横比γ=1时，水平方向和垂直方向上的频散误差达到最大，π/4方向上的频散误差最小.
(5)在单元网格纵横比减小的过程中，数值相速度的变化因传播方向的不同而差异较大，水平方向及其附近的数值相速度不受或基本不受单元网格纵横比的影响，而竖直方向附近的数值相速度受单元网格纵横比的影响较大，因此，减小单元网格纵横比并不能达到有效压制最大频散误差的目的.
图 5给出了在不同传播方向上，cp/c与kΔx之间的关系(γ=1)，可见：当kΔx的值较小时，不仅数值频散误差小，而且数值频散受波传播方向的影响也较小；随着kΔx的增大，cp/c值逐渐远离1，且不同方向上的频散曲线分离程度也在增大.
 |
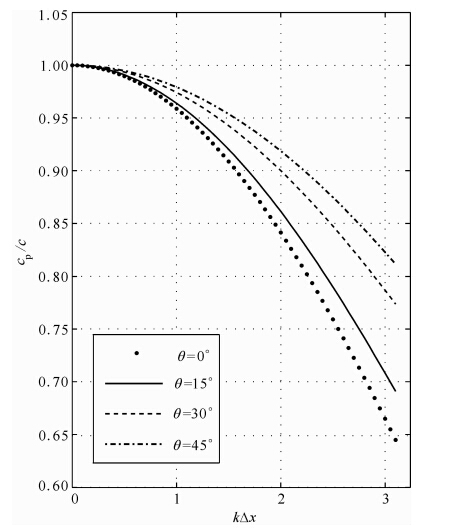图 5 对于不同的θ，cp/c随kΔx变化关系(γ=1)Fig. 5 The variation of cp/c with kΔx for different values of θ(γ=1) |
在kΔx=π/2的条件下，运用(24)式得到数值频散与θ以及γ的关系分别如图 6和图 7所示.在该类网格结构下，当γ的值取得较小时，会使得数值相速度变得非常大，因此γ的最小值取为0.2.分析发现：
 |
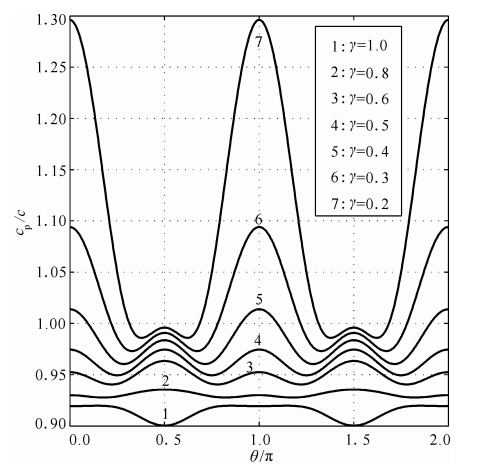图 6 γ取不同值时，cp/c随θ变化关系(kΔx=π/2)Fig. 6 The variation of cp/c with θ for different values of γ(kΔx=π/2) |
(1)当单元网格纵横比γ小于0.5时(对应的三角单元为钝角三角形)，出现数值相速度有可能大于介质真实速度的现象(如图 6中5、6以及7号线条)，与集中质量矩阵下的数值相速度小于介质的真实速度相矛盾，当γ≥0.5(对应的三角单元为非钝角三角形)时，则不会出现集中质量矩阵下的数值相速度大于介质的真实速度的现象；因此，当采用三角网格单元离散模型时，不要出现过锐或过钝的三角网格单元，否则会对数值模拟精度产生不良影响.
(2)图 7出现了所有曲线相交于同一点的现象，此时单元网格纵横比为0.866，三角网格单元为等边三角形，也就是说正三角网格单元的数值各向异性(频散随波传播方向的变化)效应最弱.
 |
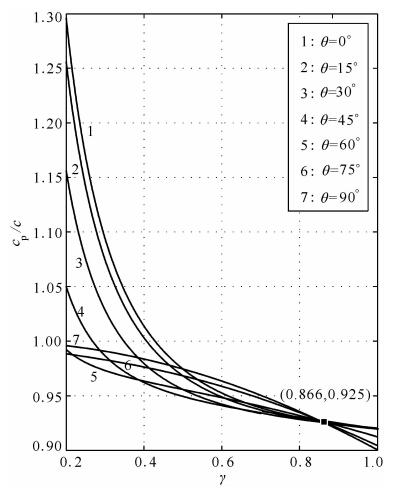图 7 θ取不同值时，cp/c随γ变化关系(kΔx=π/2)Fig. 7 The variation of cp/c with γ for different values of θ(kΔx=π/2) |
(3)在保证单元为非过锐或过钝三角形的前提下，减小单元网格纵横比可以有效地压制各个传播方向上的数值频散.
图 8给出了钝角三角网格单元下(γ=0.4)不同传播方向上的数值频散曲线，可见，在水平方向附近出现了数值相速度大于介质真实速度的现象(1、2号线条).
3.3 两种网格结构的最大频散误差比较 为了比较两种网格结构压制数值频散的效率，本文还研究了两种网格结构在不同纵横比下的最大 频散误差(如图 9所示).实心圆点为Ⅰ类网格结构的最大频散误差随空间采样间隔的变化规律(θ=0°，γ=1；Ⅰ类网格结构的最大频散误差出现在θ=0°传播方向上，且不受纵横比的影响)，实线条为Ⅱ类网格结构在γ=1时的最大频散误差随空间采样间隔的变化规律(θ=90°)，点划线为Ⅱ类网格结构在γ=0.866时的最大频散误差随空间采样间隔的变化规律(θ=30°)，双划线为Ⅱ类网格结构在γ=0.5时的最大频散误差随空间采样间隔的变化规律(θ=45°).对比分析易知，减小单元网格纵横比对压制Ⅰ类网格结构的最大频散误差没有任何效果，对压制Ⅱ类网格结构的最大频散误差具有较为明显的效果，Ⅰ类网格结构的最大频散误差与Ⅱ类网格结构在γ=1时的最大频散误差相等(空间采样间隔相同的情况下).如果认为当最大频散误差Rmax=
在得到(14)式和(23)式之后可以很容易分析两种网格结构的稳定性条件.假设在求解(1)式时，节点位移对时间的二阶偏导数通过二阶中心差分格式进行求解，公式为
由(12)式得到
为了求出Q值，需要求出F(kΔx，γ，θ)的最小值.易知，F(kΔx，γ，θ)也是关于θ的周期对称函数，因此只需要研究F(kΔx，γ，θ)在第一个半周期内的变化规律即可.在γ=1的情况下，两种网格结构的F函数随kΔx(此处不考虑Nyquist频率)的变化规律分别如图 10a与10b所示.可见，Ⅰ类网格结构稳定性因子的临界值Q(θ=45°)为0.70，随着θ的增加，稳定性条件的限制变得更加严格，当波沿水平方向传播时，得到的稳定性条件与俞康胤(1982)提出的稳定性条件相一致；Ⅱ类网格结构稳定性因子的临界值Q(θ=0°)为0.86，随着θ的增加，稳定性条件反而变得宽松.
不同单元网格纵横比下的Q值如表 1所示.从表 1中可以看出，随着γ的减小，两种网格结构稳定性条件的限制变得更加严格，在非过钝或过锐的三角单元以及相同的纵横比下，Ⅱ类网格结构比Ⅰ类网格结构具有更为宽松的稳定性条件.
下面，我们通过数值试验来验证以上结果的正确性.在进行数值试验之前，作者觉得有必要简单介绍一下结构刚度矩阵K的紧凑存储.以Ⅰ类网格结构为例，说明K的紧凑存储法：从(10)式中可以看到，结构刚度矩阵K第J2 行需要计算的元素只有7个，其他元素均为零，再考虑K的对称性，因此只需要存储该行的第I1、J1、I2以及J2列的元素即可，即紧凑存储法.此外在时间推演过程中，涉及到结构刚度矩阵与结构位移列向量的乘法，结构刚度矩阵K每一行的零元素对矩阵乘法没有任何贡献，因此只需要K每一行的非零元素与对应的节点位移相乘即可.通过以上算法，不仅最大限度地减少对内存的占用，而且还可以将计算效率提高几十倍，甚至上百倍.
5.1 数值频散特性的验证 在该数值试验中，选取波速c=2.3 km·s-1的均匀介质模型，震源为主频是40 Hz的雷克子波，加载在模型的中心，时间采样间隔Δt=0.7 ms，单元网格的横向采样间隔Δx=6 m.图 11给出了在不同纵横比下两种网格结构的波场快照(T=0.275 s).Ⅰ类网格结构下的波场快照如图 11a(γ=1)和图 11b(γ=0.3)所示，可以直观地看到，当单元网格纵横比γ=1时，数值频散在水平方向上最强，随着θ的增大而逐渐减弱，在θ=45°方向上的频散误差最小；把单元网格纵横比减小到0.3，此时只有当传播方向θ≥45°时，才无可见的数值频散.Ⅱ类网格结构下的波场快照分别如图 11c(γ=1)、11d(γ=0.866)、11e(γ=0.5)以及11f(γ=0.3)所示.对比分析不同纵横比下的波场快照可以发现，在保证单元为非钝角三角形的前提下，减小单元网格纵横比可以有效地减弱数值频散，如图 11c、11d和11e的变化，且正三角网格单元下的数值频散几乎不受波传播方向的影响(图 11d)；当单元网格为钝角三角形时，在水平方向及其附近出现了数值相速度大于介质真实速度的现象(图 11f).
为了比较在消除可见数值频散情况下两种网格结构的空间采样效率，我们分别将Ⅰ类网格结构(γ=1)、Ⅱ类网格结构(γ=1和γ=0.866)进行网格加密.作者通过大量的数值模拟试验得到了在消除 可见数值频散条件下上述三种网格单元的横向采样间隔分别为：3.2 m、3.2 m以及3.7 m，在T=0.275 s 时刻的波场快照如图 12所示.在消除可见数值频散情况下，Ⅰ类网格结构(γ=1)与Ⅱ类网格结构(γ=1)的单元面积均为 5.12 m2，而在Ⅱ类网格结构(γ=0.866)下，单元面积为5.93 m2，空间采样效率提高了15.8%.因此，采用三角网格对同一模型进行剖分时，在确保无可见数值频散前提下，等边三角单元所需网格数最少，这有利于提高计算效率和减少对内存的占用.
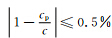时，可以忽略数值频散的影响，则Ⅰ类网格结构以及Ⅱ类网格结构在γ=1时的空间采样间隔Δx需要满足条件：kΔx≤0.348，即震源峰值频率对应的波长内应至少配置19个网格节点(指横向采样间隔，下同)，Ⅱ类网格结构在γ=0.866以及γ=0.5时需要在震源峰值频率对应的波长内分别至少配置17个与14个网格节点.
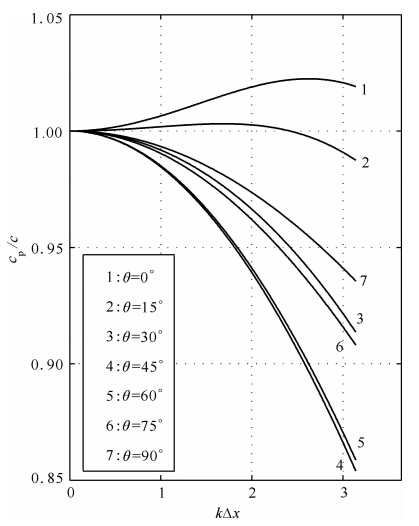
图 8 对于不同的θ，cp/c随kΔx变化关系(γ=0.4)Fig. 8 The variation of cp/c with kΔx for different values of θ(γ=0.4)
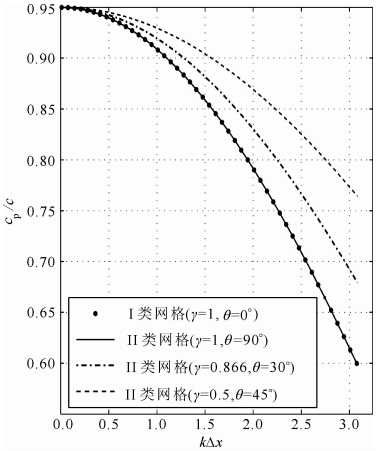
图 9 最大频散误差比较Fig. 9 Comparison of maximum dispersive errors
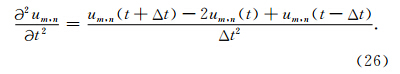
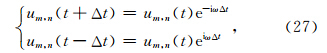
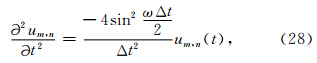
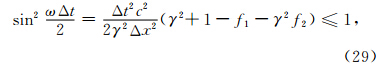
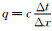，并代入(29)式可以得到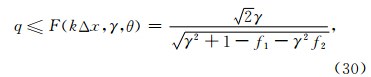
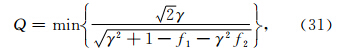
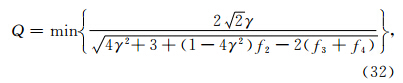
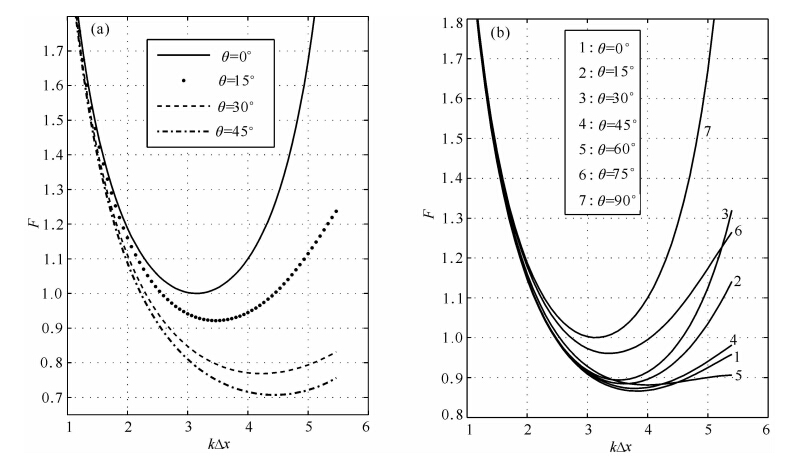
图 10 稳定性因子分析
(a)Ⅰ类网格结构，γ=1;(b)Ⅱ类网格结构，γ=1. Fig. 10 The computed stability condition
(a)Grid structure Ⅰ，γ=1;(b)Grid structure Ⅱ，γ=1.
表 1 不同网格纵横比γ下的Q值Table 1 The values of Q for different γ
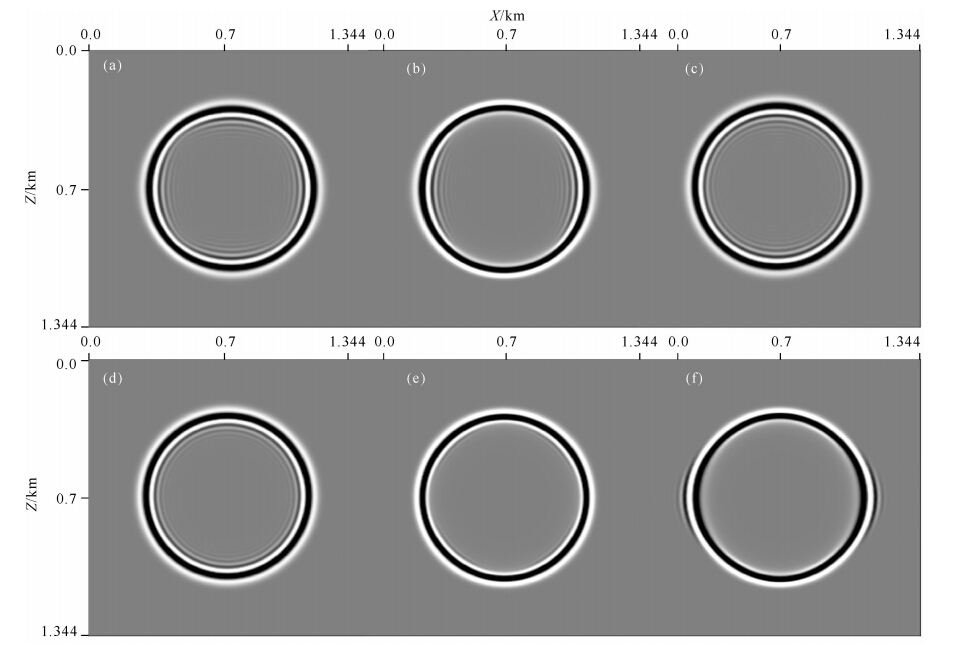
图 11 不同条件下的数值频散现象(T=0.275 s)
(a)Ⅰ类网格结构，γ=1;(b)Ⅰ类网格结构，γ=0.3;(c)Ⅱ类网格结构，γ=1;(d)Ⅱ类网格结构，γ=0.866;
(e)Ⅱ类网格结构，γ=0.5;(f)Ⅱ类网格结构，γ=0.3. Fig. 11 The numerical dispersion phenomena under different conditions
(a)Grid structure Ⅰ，γ=1;(b)Grid structure Ⅰ，γ=0.3;(c)Grid structure Ⅱ，γ=1;
(d)Grid structure Ⅱ，γ=0.866;(e)Grid structure Ⅱ，γ=0.5;(f)Grid structure Ⅱ，γ=0.3.
图 12 无可见数值频散条件下的波场快照(T=0.275 s)
(a)Ⅰ类网格结构，γ=1;(b)Ⅱ类网格结构，γ=1;(c)Ⅱ类网格结构，γ=0.866. Fig. 12 Snapshots in the condition of no visible numerical dispersion(T=0.275 s)
(a)Grid structure Ⅰ，γ=1;(b)grid structure Ⅱ，γ=1;(c)Grid structure Ⅱ，γ=0.866.
在本算例中，我们选取凹陷速度模型以及Ⅰ类 网格结构(γ=1)进行数值模拟.模型大小为2.4 km×2.4 km，网格剖分示意图如图 13所示(为清楚起见，网格密度减少为原来的1/25)，从上到下，每层的速 度依次为 2.5 km·s-1、3.0 km·s-1、3.5 km·s-1、 3.8 km·s-1(加粗线条为界面)，横向采样间隔Δx=4 m，网格数为600×600.震源采用主频为34 Hz的雷克子波，位于(x=1200 m，z=1000 m)处，时间采样间隔Δt=0.7 ms.图 14给出了不同时刻的波场快照，并无可见的数值频散，说明本文数值频散分析结论仍然适用于复杂介质中的声波.此外，入射波、透射波、反射波以及凹陷断点处产生的绕射波清晰可见，由于采用了三角网格单元拟合倾斜界面，因此避免了阶梯状界面产生的非物理绕射波.
 |
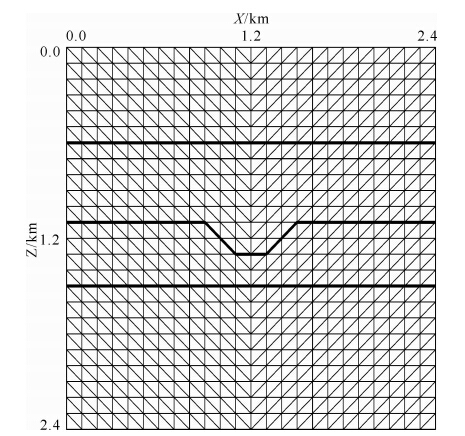图 13 凹陷速度模型三角形网格剖分示意图 Fig. 13 Depressed velocity model divided by triangular meshes |
 |
图 14 不同时刻的波场快照 (a)0.24 s波场快照;(b)0.3 s波场快照;(c)0.36 s波场快照;(d)0.42 s波场快照. Fig. 14 Snapshots at different time instant (a)0.24 s;(b)0.3 s;(c)0.36 s;(d)0.42 s. |
数值频散和稳定性是波动方程数值模拟必须讨论的两个重要问题.本文针对三角网格有限元法波动数值模拟，从理论和数值算例角度，深入细致地研究了其数值频散特性，并得到相应的稳定性条件，通过归纳总结可以得到如下结论：
(1)两种网格结构的数值相速度均受到波传播方向的影响，且具有周期性，能使网格结构旋转后保持不变的角度即为相应的周期，但在空间采样间隔足够小以及正三角网格单元下，数值相速度受波传播方向的影响较小.
(2)在单元网格纵横比为1的条件下，Ⅰ类网格结构的最大频散误差出现在θ=0°以及θ=90°的方向上，最小频散误差出现在θ=45°的方向上，而Ⅱ类网格结构的最大频散误差出现在θ=90°方向上，最小频散误差出现在θ=0°方向上.
(3)减小单元网格纵横比，Ⅰ类网格结构能够压制垂直方向及其附近的数值频散，对压制水平方向及其附近的数值频散没有作用或效果不明显；而对Ⅱ类网格结构而言，只要不出现过钝或过锐的三角网格单元，减小单元网格纵横比可以有效地减弱所有传播方向上的频散误差，特别地，当单元网格纵横比为0.866时(等边三角形)，数值频散基本不受波传播方向的影响，也就是说其数值各向异性效应最弱，这可以保持波前面的清晰度.
(4)在无可见数值频散情况下，Ⅱ类网格结构的空间采样效率比Ⅰ类网格结构高，这有利于提高计算效率和减少对内存的占用；在地震波数值模拟中，可以根据两种网格结构的数值频散特点选择单元网格的类型，例如对纵向需要进行高采样率，而横向采样间隔要求不高的数值模拟而言，选Ⅰ类网格结构较为合理.
(5)在非过钝或过锐的三角网格单元以及相同的纵横比下，Ⅱ类网格结构比Ⅰ类网格结构具有更宽松的稳定性条件.
致 谢 本文的完善得益于两位匿名审稿专家提出的宝贵修改意见，作者在此表示衷心感谢！感谢《地球物理学报》编辑部的老师对文章编辑加工!| [1] | Abboud N N, Pinsky P M. 1992. Finite element dispersion analysis for the three-dimensional second-order scalar wave equation. Int. J. Numer. Methods Eng., 35(6): 1183-1218. |
| [2] | Ainsworth M, Monk P, Muniz W. 2006. Dispersive and dissipative properties of discontinuous Galerkin finite element methods for the second-order wave equation. J. Sci. Comput., 27(1-3): 5-40. |
| [3] | Christon M A. 1999. The influence of the mass matrix on the dispersive nature of the semi-discrete, second-order wave equation. Comput. Methods Appl. Mech. Eng., 173(1): 147-166. |
| [4] | Du S T. 1982. Finite element numerical solution of wave propagation in non-homogeneous medium with variable velocities. Journal of East China Petroleum Institute (in Chinese), 6(2): 1-20. |
| [5] | De Basabe J D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations. Geophysics, 72(6): T81-T95. |
| [6] | De Basabe J D, Sen M K, Wheeler M F. 2008. The interior penalty discontinuous Galerkin method for elastic wave propagation: grid dispersion. Geophys. J. Int., 175(1): 83-93. |
| [7] | Guo J. 1991. A kind of fast finite element algorithm. Geophysical Prospecting for Petroleum (in Chinese), 30(2): 36-43. |
| [8] | Hu F Q, Hussaini M Y, Rasetarinera P. 1999. An analysis of the discontinuous Galerkin method for wave propagation problems. J. Comput. Phys., 151(2): 921-946. |
| [9] | He X J, Yang D H, Wu H. 2014. Numerical dispersion and wave-field simulation of the Runge-Kutta discontinuous Galerkin method. Chinese J. Geophys. (in Chinese), 57(3): 906-917,doi:10.6038/cjg20140320. |
| [10] | Ke B, Zhao B, Cai J, et al. 2001. 2-D finite element acoustic wave modeling including rugged topography. 71th Annual International Meeting, SEG, Expanded Abstracts, 1199-1202. |
| [11] | Lee R, Cangellaris A C. 1992. A study of discretization error in the finite element approximation of wave solutions. IEEE Trans. Antennas Propag., 40(5): 542-549. |
| [12] | Liu J B, Sharan S K, Yao L. 1994. Wave motion and its dispersive properties in a finite element model with distortional elements. Comput. Struct., 52(2): 205-214. |
| [13] | Liu Y, Sen M K. 2009. A new time-space domain high-order finite-difference method for the acoustic wave equation. J. Comput. Phys., 228(23): 8779-8806. |
| [14] | Liu T, Wei X, De Basabe J D, et al. 2012. Grid dispersion and stability of the spectral element method with triangular elements. 82th Annual International Meeting, SEG, Expanded Abstracts, 1-5. |
| [15] | Liu Y S, Teng J W, Liu S L, et al. 2013. Explicit finite element method with triangle meshes stored by sparse format and its perfectly matched layers absorbing boundary condition. Chinese J. Geophys. (in Chinese), 56(9): 3085-3099,doi:10.6038/cjg20130921. |
| [16] | Liu Y S, Teng J W, Xu T, et al. 2014. Numerical modeling of seismic wavefield with the SEM based on Triangles. Progress in Geophysics (in Chinese), 29(4): 1715-1726,doi:10.6038/pg20140430. |
| [17] | Lu X, Zhang S Y, Cui X W. 2014. Finite element method for 2.5D resistivity forward modeling based on anomaly electric field. Progress in Geophysics (in Chinese), 29(6): 2718-2722,doi:10.6038/pg20140637. |
| [18] | Li L, Liu T, Hu T Y. 2014. Spectral element method with triangular mesh and its application in seismic modeling. Chinese J. Geophys. (in Chinese), 57(4): 1224-1234,doi:10.6038/cjg20140419. |
| [19] | Mullen R, Belytschko T. 1982. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation. Int. J. Numer. Methods Eng., 18(1): 11-29. |
| [20] | Mulder W A. 1999. Spurious modes in finite-element discretizations of the wave equation may not be all that bad. Appl. Numer. Math., 1999, 30(4): 425-445. |
| [21] | Saad Y. 2000. Iterative Methods for Sparse Linear Systems. Philadelphia: SIAM. |
| [22] | Sun C Y. 2007. Theory and Methods of Seismic Waves. Dongying: China University of Petroleum Press (in Chinese): 31-37. |
| [23] | Sun C Y, Gong T J, Zhang Y L, et al. 2009. Analysis on dispersion and alias in finite-difference solution of wave equation. Oil Geophysical Prospecting (in Chinese), 44(1): 43-48. |
| [24] | Sun C Y, Xiao Y F, Yin X Y, et al. 2010. Study on the stability of finite difference solution of visco-elastic wave equations. Acta Seismologica Sinica (in Chinese), 32(2): 147-156. |
| [25] | Seriani G,Oliveira S P. 2008. Dispersion analysis of spectral element methods for elastic wave propagation. Wave Motion, 45(6): 729-744. |
| [26] | Wang M C. 2003. Finite Element Method. Beijing: Tsinghua University press (in Chinese): 472-475. |
| [27] | Wu G C, Wang H Z. 2005. Analysis of numerical dispersion in wave-field simulation. Progress in Geophysics (in Chinese), 20(1): 58-65. |
| [28] | Wang W S, Zhang H, Li X F. 2013. Review on application of the discontinuous Galerkin method for modeling of the seismic wavefield. Progress in Geophysics (in Chinese), 28(1): 171-179,doi:10.6038/pg20130118. |
| [29] | Wu Z Q, Song W J. 2013. Resistivity transverse section method and its application in quantified explanation of oblique faults. Progress in Geophysics (in Chinese), 28(5): 2748-2752,doi:10.6038/pg20130559. |
| [30] | Wang R, Wang M Y, Di Q Y, et al. 2014. 3D1C CSAMT modeling using finite element method. Progress in Geophysics (in Chinese), 29(2): 839-845,doi:10.6038/pg20140249. |
| [31] | Xu S Z. 1994. Finite Element Method for Geophysics. Beijing: Science Press (in Chinese): 39-42. |
| [32] | Xue D C, Wang S X, Jiao S J. 2007. Wave equation finite element modeling including rugged topography and complicated medium. Progress in Geophysics (in Chinese), 22(2): 522-529. |
| [33] | Xue D C, Wang S X. 2008a. Wave-equation finite element prestack reverse-time migration. Oil Geophysical Prospecting (in Chinese), 43(1): 17-21. |
| [34] | Xue D C, Wang S X. 2008b. Using combined mass matrix to suppress numerical dispersion. Oil Geophysical Prospecting (in Chinese), 43(3): 318-320. |
| [35] | Xue Z, Dong L G, Li X B, et al. 2014. Discontinuous Galerkin finite-element method for elastic wave modeling including surface topography. Chinese J. Geophys. (in Chinese), 57(4): 1209-1223,doi:10.6038/cjg20140418. |
| [36] | Yu K Y. 1982. Numerical analysis in the construction of synthetic seismograms by the finite element method. Journal of East China Petroleum Institute (in Chinese), 6(4): 11-27. |
| [37] | Yue B, Guddati M N. 2005. Dispersion-reducing finite elements for transient acoustics. J. Acoust. Soc. Am., 118(4): 2132-2141. |
| [38] | Yin X Y, Zhou J K, Wu G C, et al. 2014. Dispersion analysis for the finite element algorithm in acoustic wave equation numerical simulation. Acta Seismologica Sinica (in Chinese), 36(5): 944-955. |
| [39] | 杜世通. 1982. 变速不均匀介质中波动方程的有限元法数值解.华东石油学院学报, 6(2): 1-20. |
| [40] | 郭建. 1991. 一种有限元快速算法. 石油物探, 30(2): 36-43. |
| [41] | 贺茜君, 杨顶辉, 吴昊. 2014. 间断有限元方法的数值频散分析及其波场模拟. 地球物理学报, 57(3): 906-917,doi:10.6038/cjg20140320. |
| [42] | 刘有山, 滕吉文, 刘少林等. 2013. 稀疏存储的显式有限元三角网格地震波数值模拟及其PML吸收边界条件. 地球物理学报, 56(9): 3085-3099,doi:10.6038/cjg20130921. |
| [43] | 刘有山, 滕吉文, 徐涛等 . 2014. 三角网格谱元法地震波场数值模拟. 地球物理学进展, 29(4): 1715-1726,doi:10.6038/pg20140430. |
| [44] | 鲁杏, 张胜业, 崔先文. 2014. 基于异常场的2.5维电阻率有限元正演模拟. 地球物理学进展, 29(6): 2718-2722,doi:10.6038/pg20140637. |
| [45] | 李琳, 刘韬, 胡天跃. 2014. 三角谱元法及其在地震正演模拟中的应用. 地球物理学报, 57(4): 1224-1234,doi:10.6038/cjg20140419. |
| [46] | 孙成禹. 2007. 地震波理论与方法. 山东东营: 中国石油大学出版社: 31-37. |
| [47] | 孙成禹, 宫同举, 张玉亮等. 2009. 波动方程有限差分法中的频散与假频分析. 石油地球物理勘探, 44(1): 43-48. |
| [48] | 孙成禹, 肖云飞, 印兴耀等. 2010. 黏弹介质波动方程有限差分解的稳定性研究. 地震学报, 32(2): 147-156. |
| [49] | 王勖成. 2003. 有限单元法. 北京: 清华大学出版社: 472-475. |
| [50] | 吴国忱, 王华忠. 2005. 波场模拟中的数值频散分析与校正策略. 地球物理学进展, 20(1): 58-65. |
| [51] | 汪文帅, 张怀, 李小凡. 2013. 间断的Galerkin方法在地震波场数值模拟中的应用概述. 地球物理学进展, 28(1): 171-179,doi:10.6038/pg20130118. |
| [52] | 吴子泉, 宋文杰. 2013. 电阻率横向剖面法对倾斜断层的定量化研究及解释. 地球物理学进展, 28(5): 2748-2752,doi:10.6038/pg20130559. |
| [53] | 王若, 王妙月, 底青云等. 2014. CSAMT三维单分量有限元正演. 地球物理学进展, 29(2): 839-845,doi:10.6038/pg20140249. |
| [54] | 徐世浙. 1994. 地球物理中的有限元法. 北京: 科技出版社: 39-42. |
| [55] | 薛东川, 王尚旭, 焦淑静. 2007. 起伏地表复杂介质波动方程有限元数值模拟方法.地球物理学进展, 22(2):522-529. |
| [56] | 薛东川, 王尚旭. 2008a. 波动方程有限元叠前逆时偏移.石油地球物理勘探, 43(1): 17-21. |
| [57] | 薛东川, 王尚旭. 2008b. 利用组合质量矩阵压制数值频散. 石油地球物理勘探, 43(3): 318-320. |
| [58] | 薛昭, 董良国, 李晓波等. 2014. 起伏地表弹性波传播的间断Galerkin有限元数值模拟方法. 地球物理学报, 57(4): 1209-1223,doi:10.6038/cjg20140418. |
| [59] | 俞康胤. 1982. 合成地震记录制作中的有限元法数值分析. 华东石油学院学报, 6(4): 11-27. |
| [60] | 印兴耀, 周建科, 吴国忱等. 2014. 有限元算法在声波方程数值模拟中的频散分析. 地震学报, 36(5): 944-955. |