2. 中国石油大学胜利学院, 东营 257097;
3. 中国科学院大学, 北京 100049
2. Shengli College, China University of Petroleum, Dongying 257097, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着地震勘探的不断深入,所面临的问题越来越复杂,因此迫切需要建立准确的近地表速度模型.近地表速度不准确,会直接影响地震资料静校正、叠前偏移和叠加成像等多个勘探环节,进而影响最终的勘探成果.目前速度求取的方法主要有三种:叠加速度分析、偏移速度分析和层析成像速度分析(Woodward et al., 2008).这三种方法的准确性依次升高,难度依次增大,所需要的数学手段和工具也依次增多.对于近地表速度建模问题,叠加速度分析和偏移速度分析由于覆盖次数不足和缺少近地表反 射,一般很难取得近地表的有效速度信息;而层析成像速度分析则越来越受到人们的重视(He et al., 2013).
地震层析成像的研究始于20世纪70年代,最初以井间速度结构为研究对象(Bios et al., 1972);Dines和Lytle(1979)利用地震射线进行地下速度成像,并首先将层析成像一词用于论文标题.80年代,地震层析成像在地震勘探领域得到发展,第54届地球物理年会(SEG)设置了地震层析成像研究的 专题;这一阶段以Daily(1984)、Somerstein等(1984)、Bishop等(1985)、Dyer和Worthington(1988)等人的研究为代表,用数值模拟的形式研究人工地震层析成像的理论、方法和技术.90年代以来,地震层析成像方法在资源勘探、工程勘察、环境保护、岩体结构研究等许多领域得到应用(杨文采和李幼铭,1993).地震层析成像从不同的角度可以进行不同的分类(成谷等,2002),这些分类之间存在交叉.(1)根据数据类型,可分为透射层析、反射层析、折射层析等.(2)根据地震属性,可分为走时层析和波形层析.(3)根据理论基础,可分为以射线理论为基础的射线层析和以波动理论为基础的绕射层析.
本文的初至波走时层析成像是指利用地震初至波走时和其传播的射线路径来反演地下介质速度的技术,它基于射线理论.地震勘探中的初至波是指从炮点出发,经过介质首先到达接收点的地震波,可能是直达波、折射波、回转波或者它们的组合.这些波主要在近地表传播,其走时包含了近地表的速度信息;并且初至波易获得、能量强、可追踪性好,因此利用初至波走时层析成像对近地表速度进行精细分析最为有利(景月红,2009).国内外的专家学者在这方面做了许多有意义的工作:McMechan等(1987)利用井间层析成像解决复杂地表问题;White(1991)通过阻尼最小二乘解同时求取近地表地层的速度和厚度;Zhang和Toksoz(1998)提出了正则化非线性折射波走时层析成像方法;常旭等(1999)对层析成像中非线性反演问题解的可靠性进行研究,讨论了ART(Algebraic Reconstruction Technique,代数重建法)、SVD(Singular Value Decomposition,奇异值分解法)、LSQR(Least Square QR,最小二乘QR分解法)三种方法的稳定性及其反演效果;李录明等(2000)把近地表模型离散成矩形单元,利用阻尼最小QR分解求解大型稀疏矩阵;张建中(2004)用双线性函数表示近地表速度单元,采用LSQR解非线性最优化问题;韩晓丽等(2008)采用非显式射线追踪方式在全偏移距内进行反演,提高了表层模型的精度;卢回忆等(2013)将医学成像领域研究的MSFM(Multi-stencils Fast Marching Methods,多模板快速推进法)算法应用于地震层析反演中的走时计算,改善了标准FMM方法存在的对角方向误差大的缺陷,对复杂地表模型具有很强的适应能力.
层析成像的理论基础是Radon变换,而在地震勘探中,观测方式的限制决定了地震层析成像解的非唯一性(投影角度不全);数据和射线的不均匀覆盖决定了地震层析方程组是一个混定问题(成谷,2004).因此初至波走时层析成像在本质上是一个不适定问题,必需使用正则化方法并辅之以适当的最优化技巧.正则化是层析成像反演研究的一个重点:Clapp等(2004)用正则化方法将地质信息引入层析成像反演算法提高了成像精度;Fomel(2007)采用 正则化方法在层析成像中对模型进行平滑处理;刘玉柱等(2007)通过正则化手段将先验信息引入初至波层析成像方程,代替传统的外部约束模式;王薇等(2013)使用非线性稀疏约束正则化方法,并采用对偶方法求解稀疏约束泛函的极小点,对不连续介质模型的边缘具有良好的识别能力.这些研究都取得了一定的效果.
本文研究近地表速度建模的初至波走时层析成像方法,并针对该反演问题的不适定性,从数值优化的角度介绍了初至波走时层析成像的反演原理,建立了Tikhonov正则化层析成像反演模型并提出求解极小化问题的加权修正步长的梯度下降算法. 2 走时层析成像基本原理
层析成像的理论基础是Radon变换:u(ρ,θ)=∫Lf(x,y)ds,其中f(x,y)称为图像函数,u(ρ,θ)称为投影函数,θ为入射方向,ρ为观测点位置.1917年数学家Radon证明:已知所有入射角θ的投影函数u(ρ,θ)可以唯一地恢复图像函数f(x,y).在地震走时层析成像中,图像函数是地下介质的慢度分布,投影函数是走时,积分路径是射线路径.可以理解为:沿射线路径传播的地震波走时里累加了该路径上模型的慢度信息,当多道射线沿不同路径传经同一模型时,就可以提供足够的信息重建该慢度模型,而慢度的倒数就是我们要求的速度.这是一个典型的地球物理反问题,下面对其进行详细介绍.
首先对模型参数化,目前地震层析成像中多采用网格化方法.如图 1所示,将地层模型离散化为n个慢度单元,任意的第j个单元具有一个未知的常慢度sj.用dij表示第i条射线在第j个单元的射线路径长度.这样,走时积分可简化为慢度加权求和,加权值是该单元内的射线路径长度:

 | 图 1 地层离散化示意图Fig. 1 Schematic drawing of earth discretization |
地震勘探中的射线追踪指的是根据地震波的传播规律确定波在实际地层中传播的射线路径.它的理论基础在于:在高频近似条件下,地震波场的主能量沿射线轨迹传播.射线追踪方法的种类很多,传统的是基于初值问题的试射法和基于边值问题的弯曲法.20世纪80年代末以来,出现了大量新型算法,这些方法的主要特点在于不再局限于地震波的射线路径描述,而是直接从Huygens原理或Fermat原理出发,采用等价的波前描述地震波场的特征(张钋等,2000).
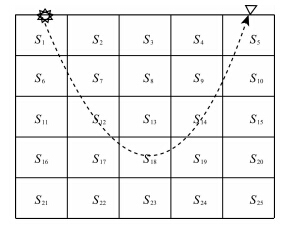
针对近地表速度建模的初至波走时层析成像,我们采用先进的最小走时射线路径追踪方法.它的理论基础是Fermat原理以及图论中的最短路径问题(郭继茹等,2008).其基本思路是:在划分的网格单元边界设置节点,每个节点只能与它所在的网格单元内的节点相连,节点之间的走时为它们的欧氏距离与平均慢度之积.一条射线路径由多个相互连接的节点组成,射线沿该路径传播的走时为节点间走时之和.如图 2所示,首先由一个震源点出发,计算出其到相连节点的射线路径和走时;然后把相连节点作为次级震源,计算新震源到它们的相连节点的射线路径和走时;将新计算出的走时加上震源到相应的次级震源的走时作为震源点到该网格节点的走时,并记录下相应的射线路径;以此类推.震源到任意节点可能有无数条路径,根据Fermat原理,选取走时最小的路径作为射线路径.
 | 图 2 从某一震源出发的射线追踪路径图Fig. 2 The roadmap of ray tracing from one origin |
由地震记录拾取走时,对估计的慢度模型进行射线追踪得到射线路径,就可以构建走时方程,然后用它求解速度.如前所述,层析成像需要大量的射线,因此有大量形如方程(1)的方程.为了将这一信息用更清晰的方式表达,可以将所有的走时方程重新写成一个矩阵变量的形式,得到:
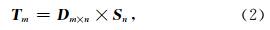
这样就将地震走时层析成像问题转化为了求解线性方程组的问题,我们在此基础上讨论它的数值解法. 2.3 层析反演模型
尽管问题可以简单地表述为 T = D × S,但求解并不简单.在了解算法的细节和具体步骤之前,先要指出我们所面对的两组数据——观测数据 To和模型数据 T m.它们可以分别写作:

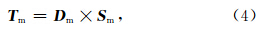
这些数据中,真正所知的只有 To.因此我们要做一定的假设,否则由于未知量太多反演注定会失败.这里要做的假设就是射线追踪所提供的路径足够准确,可以认为两个距离矩阵近似相等,从而得到:
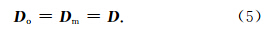
为了计算So的值,或者一个在误差范围内逼近它的值,提出以下算法:
(1)估计一个 Sm的初始值,对该模型进行射线追踪得到 D ;
(2)计算一个临时的Tm= D × S m;
(3)有了Tm和观测到的T o,可以计算走时之差ΔT = To- Tm;
(4)之后,可以用T o=D× S o减去Tm= D× S m得到T o- Tm= D×(S o- S m),ΔT=D ×Δ S ;
(5)解ΔT= D×Δ S 得到Δ S,然后计算 So= Sm+ΔS ;
(6)再令Sm= S o,这里“=”表示赋值.
重新迭代步骤(2)—(6),直到 S m和So的差很小甚至为零.这时就得到了真实慢度的最精确的值.
无论从计算角度还是从对整个算法的重要性上,最关键的步骤都是求解方程组的步骤 5.在地震初至波走时层析成像中,观测方式不能满足Radon变换对观测系统的布局要求(投影角度不全),这决定了解的非唯一性;数据和射线的不均匀覆盖,使得某些模型参数位于超定空间,某些模型参数位于欠定空间甚至是零空间,这决定了问题是混定的.混定问题一般使用阻尼最小二乘解(王彦飞,2007),解的形式为Sest=[DTD+ε2 I ]-1DTT,其中ε是阻尼因子.但距离矩阵D的每行代表一条射线,每列代表一个网格单元,是一个大型矩阵;并且每条射线穿过的网格单元数比总网格单元数要少得多,也就是说每一行只有少量不为零的元素,因此D是一个大型稀疏矩阵.对于这类矩阵的乘法和求逆是非常困难的,不能直接按照公式求解.了解了问题的本质,我们有针对性的采用线性方程组迭代解的形式,并在建立方程组的过程中,添加适当的正则化算子. 3 反演模型正则化
如前所述,初至波走时层析成像问题是一个不适定问题,需要使用正则化方法.所谓正则化,就是用一族与原不适定问题相“邻近”的适定问题的解去逼近原问题的解(王彦飞,2007).这里正则化的作用主要有两个方面:(1)对欠定分量和零空间分量进行约束.这两种分量的不确定性强,迭代中收敛速度慢,对结果影响很大.我们可以使用先验信息或者超定分量来进行约束;(2)对射线不均匀覆盖和数据的不确定性进行阻尼.Wang和Braile(1995)指出:如果忽略不均匀覆盖问题,得出的模型校正量会正比于射线的覆盖程度.也就是说,覆盖程度高的网格校正过量,覆盖程度低的网格校正不足,没有覆盖到的网格校正量为零.为了解决这个问题,需要根据网格覆盖程度对网格参数加以不同的权重进行阻尼.而数据的不确定性来自于噪声,可根据数据的准确程度施加不同的权重进行阻尼. 3.1 Tikhonov正则化
Tikhonov正则化的基本思想(王彦飞等,2011)是给定观测数据 T(带噪声的观测数据),构建一个正则算子R(α,T),使得当α→0并且噪声水平趋于0时,R(α,T)→S*,其中S*为真实的地层慢度值.根据该思想,我们建立正则化模型如下:
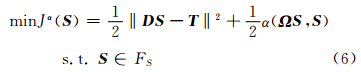
容易算得,函数Jα(S)的梯度为
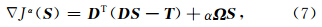
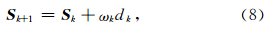
有关正则化参数α选取策略的讨论一直伴随着不适定问题的研究过程,为了得到迭代正则化算法的收敛性结果,需要对正则化参数加上很强的限制条件.目前正则化参数的选择有先验和后验两种取法.先验法需要预先对原始数据的误差水平δ做出估计,后验法可以直接应用带噪声的原始数据做估计,但需要求解相应的偏差方程和多次解线性方程组(王彦飞,2007).由于层析计算量很大,解偏差方程和多次解线性方程组会导致很大的CPU时间.因此本文采用先验的正则参数选取方法:即正则参数α=O(δ2).这样的选取,能够保证(6)式定义的是一个正则算子(肖庭延等,2003). 3.2 选取规范化算子Ω
最简单的选取方式就是令Ω 为恒等算子,该算子显然满足正定性.但这种选取过于保守.为此,注意到公式(2)是下述连续问题
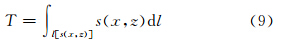

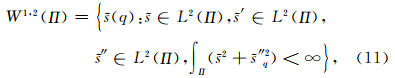
其中q=(x,z)∈Π,L2(Π)为包含Π的平方可积空间.因而可以构建基于在W1,2(Π)上规范的算子,即‖s(x,z)‖ .对Ω(s)= ‖s(q)‖
.对Ω(s)= ‖s(q)‖ 求梯度并离散化后得到的算子记为Ω,记h为相同的离散格点间距,则Ω 的形式如下(肖庭延等,2003):
求梯度并离散化后得到的算子记为Ω,记h为相同的离散格点间距,则Ω 的形式如下(肖庭延等,2003):
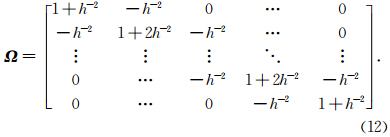
3.3 步长因子ωk的选取
通常搜索步长的方法是采用柯西步长,即利用下面的公式计算ωk(袁亚湘,1993):

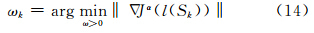
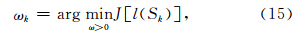
在实际计算中,公式(14)和(15)可以交互使用.为了充分利用上述两个步长的信息,本文提出下面的加权组合公式
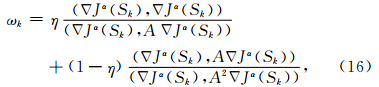
易见,公式(16)是对柯西公式的改进方式.当η=1时,(16)就退化为传统的柯西公式.公式(16)说明我们可以在一个修改的方向上搜索不同的下降步长,一方面满足梯度的模随着迭代递减,另一方面使得目标函数充分下降,因而能够达到快速收敛(Wang et al., 2012).王彦飞(2007)证明了梯度迭代方法对应着某种正则化,因而为应用该方法求解层析反演问题提供了理论依据.
在实际计算中,注意到 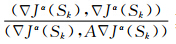 ≥
≥ 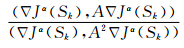 ,为了迭代步长不至于跳跃太大,加权系数η可以取个折中:即η<1-η,因此,η<0.5.本文中,我们取η=0.3. 3.4 层析成像迭代正则化算法
,为了迭代步长不至于跳跃太大,加权系数η可以取个折中:即η<1-η,因此,η<0.5.本文中,我们取η=0.3. 3.4 层析成像迭代正则化算法
基于上述准备工作,可以给出基于初至波走时层析的速度更新算法如下:
(1)输入初始慢度模型S0 ∈ FS,停机参数ε>0,正则参数α>0,0<η<1,规范化算子 Ω,最大迭代次数kmax,令k∶ =1.
(2)计算梯度 Δ Jα(Sk),若(ΔJα(Sk),Δ Jα(Sk))≤ε 或k>kmax,则停止迭代;令dk=- ΔJα(Sk).
(3)按公式(16)计算步长因子ωk,更新慢度向量Sk+1=Sk+ωkdk,且使得Sk+1∈FS.令k:=k+1,转到第2步. 4 数值试验
为了检验新算法的正确性及稳定性,我们设计了水平层状、地堑和起伏界面加断层三组理论模型进行试算. 4.1 模型一:水平层状模型
图 3为水平层状速度模型,模型参数设置如下: 横向2000 m,纵向700 m,速度从上到下依次为600 m·s-1,1200 m·s-1,2000 m·s-1.双边放炮,每炮40道,道间距50 m,炮间距100 m,共放20炮.图 4为初始速度模型,由真实模型做随机扰动生成,这与近地表实际地震数据的速度谱资料联系更紧密.从图中可以看出,该速度模型距离真实值相距甚远.图 5为共轭梯度法迭代6次的反演结果,图 6为新算法迭代3次的反演结果,可见,我们提出的层析成像正则化方法在初始模型很差的条件下也能迅速收敛,获得较好的反演结果.迭代继续进行,反演模型会发生轻微扰动,但没有明显改善,说明该方法能够快速稳定收敛.新算法在内存占用以及运算速度上也优于原始共轭梯度法,相同反演条件下,原始共 轭梯度法内存占用是新算法的2倍多,所需时间是新算法的1.82倍.
 | 图 3 模型一:水平层状模型Fig. 3 Model one: the horizontal layered model |
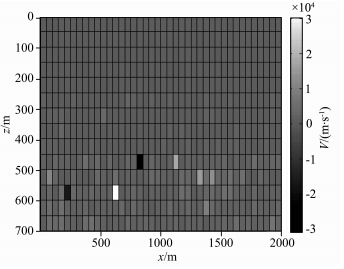 | 图 4 模型一的初始速度模型Fig. 4 The initial velocity model of model one |
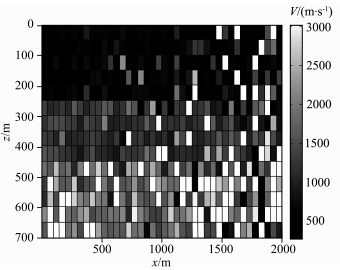 | 图 5 原始共轭梯度法得到的模型一的速度模型Fig. 5 The velocity model of model one recovered by the CG algorithm |
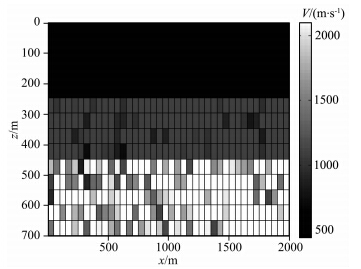 | 图 6 新算法得到的模型一的速度模型Fig. 6 The velocity model of model one recovered by the new algorithm |
图 7为理论速度模型,模型参数设置如下:横向 2000 m,纵向700 m,速度从上到下依次为1000 m·s-1,3000 m·s-1,1000 m·s-1.双边放炮,每炮40道,道间距50 m,炮间距100 m,共放20炮.图 8为初始速度模型,由真实模型做随机扰动生成.同样从图中可以看出,该初始速度模型距离真实值相距甚远.图 9为原始共轭梯度法迭代6次的反演结果,图 10为新算法迭代3次的反演结果,可见,我们提出的层析成像正则化方法在初始模型很差的条件下也能迅速收敛,获得比较好的反演结果.迭代继续进行,反演模型会发生轻微扰动,但没有明显改善,说明该方法能够稳定收敛.
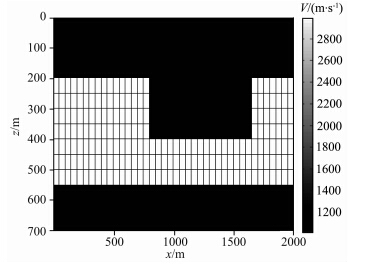 | 图 7 模型二:地堑速度模型Fig. 7 Model two: the graben velocity model |
 | 图 8 模型二的初始速度模型Fig. 8 The initial velocity model of model two |
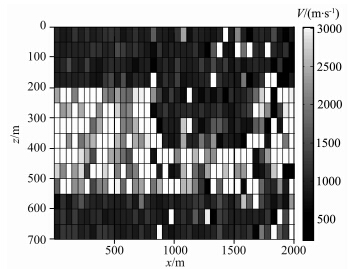 | 图 9 原始共轭梯度法得到的模型二的速度模型Fig. 9 The velocity model of model two recovered by the CG algorithm |
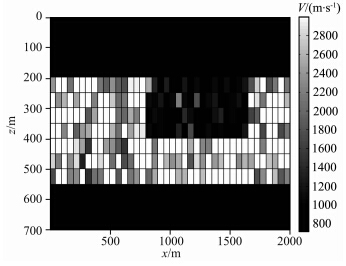 | 图 10 新算法得到的模型二的速度模型Fig. 10 The velocity model of model two recovered by the new algorithm |
图 11为理论速度模型,模型参数设置如下:横向 2000 m,纵向800 m,速度从上到下依次为1000 m·s-1,2000 m·s-1,3000 m·s-1.图 12为初始速度模型,由真实模型做随机扰动生成.从该图看出,初速速度模型与真实模型相去甚远.图 13为原始共轭梯度法迭代6次的反演结果,图 14为新算法迭代3次的反演结果,同样可见,我们提出的层析成像正则化方法在初始模型很差的条件下也能迅速收敛,获得比较好的反演结果.迭代继续进行,反演模型会发生轻微扰动,但没有明显改善,说明该方法能够稳定收敛.
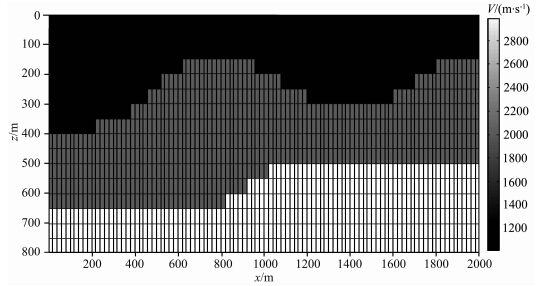 | 图 11 模型三:起伏界面+断层模型Fig. 11 Model three: the irregular interface and fault velocity model |
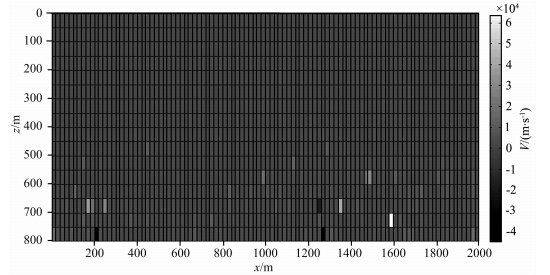 | 图 12 模型三的初始速度模型Fig. 12 The initial velocity model of model three |
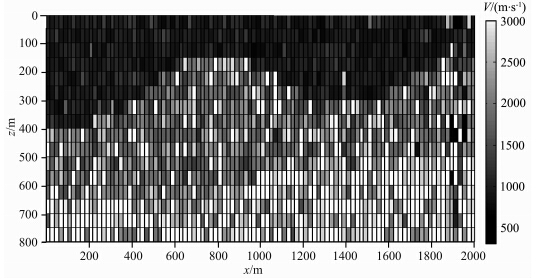 | 图 13 原始共轭梯度法得到的模型三的速度模型Fig. 13 The velocity model of model three recovered by the CG algorithm |
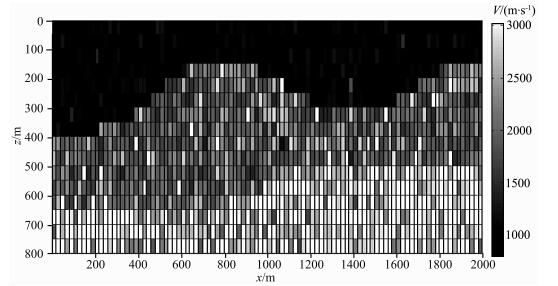 | 图 14 新算法得到的模型三的速度模型Fig. 14 The velocity model of model three recovered by the new algorithm |
在本文的试验中,我们选取初始速度模型为真实模型做随机扰动生成,因为这与近地表实际地震数据的速度谱资料联系更紧密.从算法本身角度讲,本文的算法对于任意的在可行集范围内的初始速度模型都收敛,比如可以取初始速度模型为均匀模型,但收敛的速度非常慢.如果初始模型比我们期望反演的速度要快,并且有一个随深度增加的垂向梯度,我们以几乎任意速度模型开始反演都会收敛于正确的解.这是由于在反演初始时使用了强正则化.如果初始速度模型速度太小,算法会陷入误差函数的局部极小解,从而给出一个不真实的结果.在迭代初始,这个反演方案会在很浅的深度处制造一个强折射物.一旦放置了折射物,即使做强正则化,射线也无法穿过折射物从而正确地更新速度模型. 5 结论
本文研究近地表速度建模的初至波走时层析成像方法.首先给出该方法的基本原理,包括模型参数化、射线追踪和走时方程、反演模型的建立.在此基础上,进一步从数值优化的角度入手,建立了初至波走时层析成像的Tikhonov正则化反演模型,并提出一种层析成像的梯度优化算法.通过数值试验,验证了该方法具有以下特点:
(1)针对近地表速度建模问题,使用网格法对模型进行参数化,并采用最小走时射线路径追踪方法进行正演模拟,该算法可以适用于速度剧烈变化的任意复杂构造模型,震源与检波器可以任意进行集合排列,所需的计算时间与模型的复杂程度无关,三维计算易于实现(Chang et al., 2002).
(2)针对问题的不适定性,引入正则化方法,使解能够稳定收敛.
(3)该方法可以从速度模型的可行域中迭代找到一个最优解.
现如今,由于地震观测数据大多是在三维空间介质中形成的,因此下一步的工作是将算法在三维空间中实现,使其更具有实际意义.
致谢十分感谢两位审稿人和编辑提出的宝贵意见,使得论文内容更加充实.| [1] | Bios P, Porte M L, Lavergne M, et al. 1972. Well-to-well seismic measurements. Geophysics, 37(3):471-480. |
| [2] | Bishop T N, Bube K P, Cutler R T, et al. 1985. Tomographic determination of velocity and depth in laterally varying media. Geophysics, 50(6):903-923. |
| [3] | Chang X, Lu M X, Liu Y K. 1999. Error analysis and appraisals for three general solutions in seismic tomography. Chinese Journal of Geophysics (in Chinese), 42(5):695-701. |
| [4] | Chang X, Liu Y K, Wang H, et al. 2002. 3-D tomographic static correction. Geophysics, 67(4):1275-1285. |
| [5] | Cheng G, Ma Z T, Geng J H, et al. 2002. A review on the growth of seismic tomography. Progress in Exploration Geophysics (in Chinese), 25(3):6-12. |
| [6] | Cheng G. 2004. Theory and applications of seismic reflection traveltime tomography [Ph. D. thesis] (in Chinese). Shanhai:Tongji University. |
| [7] | Clapp R G, Biondi B, Claerbout J F. 2004. Incorporating geologic information into reflection tomography. Geophysics, 69(2):533-546. |
| [8] | Daily W D. 1984. Underground oil-shale retort monitoring using geotomography. Geophysics, 49(10):1701-1711. |
| [9] | Dines K A, Lytle R J. 1979. Computerized geophysical tomography. Proc. IEEE, 67(7):1065-1073. |
| [10] | Dyer B C, Worthington M H. 1988. Seismic reflection tomography:a case study. First Break, 6:354-366. |
| [11] | Fomel S. 2007. Shaping regularization in geophysical estimation problems. Geophysics, 72(2):R29-R36. |
| [12] | Guo J R, Feng X, Wang J X, et al. 2008. Study of shortest path method of ray tracing algorithm. Journal of Jilin University (Earth Science Edition) (in Chinese), 38(S1):72-75. |
| [13] | Han X L, Yang C C, Ma S H, et al. 2008. Static of tomographic inversion by first breaks in complex areas. Progress in Geophysics (in Chinese), 23(2):475-483. |
| [14] | He L, Zhang W, Zhang J. 2013. 3D wave-ray traveltime tomography for near surface imaging. 83rd SEG Annual Conference, Houston, Texas, 1749-1753. |
| [15] | Jing Y H. 2009. Seismic first break travel-time tomography and its application in near-surface velocity model building[Ph. D. thesis] (in Chinese). Xi'an:Chang'an University. |
| [16] | Li L M, Luo S X, Zhao B. 2000. Tomographic inversion of first break in surface model. Oil Geophysical Prospecting (in Chinese), 35(5):559-564. |
| [17] | Liu Y Z, Dong L G, Xia J J. 2007. Regularization methods for first-arrival travel time tomography. Oil Geophysical Prospecting (in Chinese), 42(6):682-698. |
| [18] | Lu H Y, LiuY K, Chang X. 2013. MSFM based travel times calculation in complex near surface model. Chinese Journal of Geophysics (in Chinese), 56(9):3100-3108, doi:10.6038/cjg20130922 |
| [19] | McMechan G A, Harris J M, Anderson L M. 1987. Cross-hole tomography for strongly variable media with applications to scale model data. Bulletin of the Seismological Society of America, 77(6):1945-1960. |
| [20] | Somerstein S F, Berg M, Chang D, et al. 1984. Radio-frequency geotomography for remotely probing the interior of operating mini and commercial-sized oil-shale retorts. Geophysics, 49(9):1288-1300. |
| [21] | Wang B, Braile L W. 1995. Effective approaches to handling non-uniform data coverage problem for wide-aperture refraction/reflection profiling. The 65th Ann. International Meeting, SEG, Expanded abstracts, 659-662. |
| [22] | Wang W, Han B, Tang J P. 2013. Regularization method with sparsity constraints for seismic waveform inversion. Chinese Journal of Geophysics (in Chinese), 56(1):289-297, doi:10.6038/cjg20130130 |
| [23] | Wang Y F. 2007. Computational Methods for Inverse Problems and Their Applications (in Chinese). Beijing:Higher Education Press. |
| [24] | Wang Y F, Yagola A G, Yang C C. 2012. Optimization and Regularization for Computational Inverse Problems and Applications. Berlin:Springer. |
| [25] | Wang Y F, Stepanova I E, Titarenko V N, et al. 2011. Inverse Problems in Geophysics and Solution Methods (in Chinese). Beijing:Higher Education Press. |
| [26] | White D J. 1991. Two-dimensional seismic refraction tomography. Geophysical Journal, 72(2):223-245. |
| [27] | Woodward M J, Nichols D, Zdraveva O, et al. 2008. A decade of tomography. Geophysics, 73(5):VE5-VE11. |
| [28] | Xiao T Y, Yu S G, Wang Y F. 2003. Numerical Methods for the Solution of Inverse Problems (in Chinese). Beijing:Science Press. |
| [29] | Yang W C, Li Y M. 1993. Applied Seismic Tomography (in Chinese). Beijing:Geological Publishing House, |
| [30] | Yuan Y X. 1993. Numerical Methods for Nonlinear Programming (in Chinese). Shanghai:Shanghai Science and Technology Publisher. |
| [31] | Zhang J, Toksoz M N. 1998. Nonlinear refraction traveltime tomography. Geophysics, 63(5):1726-1737. |
| [32] | Zhang J Z. 2004. First break tomography for near-surface layers in seismic exploration. Journal of Xiamen University (Natural Science) (in Chinese), 43(1):63-66, doi:10.3321/j.issn:0438-0479.2004.01.016. |
| [33] | Zhang P, Liu H, Li Y M. 2000. The situation and progress of ray tracing method research. Progress in Geophysics (in Chinese), 15(1):36-45, doi:10.3969/j.issn.1004-2903.2000.01.002. |
| [34] | 常旭, 卢孟夏, 刘伊克. 1999. 地震层析成像反演中3种广义解的误差分析与评价. 地球物理学报, 42(5): 695-701. |
| [35] | 成谷, 马在田, 耿建华等. 2002. 地震层析成像发展回顾. 勘探地球物理进展, 25(3): 6-12. |
| [36] | 成谷. 2004. 地震反射走时层析理论与应用研究[博士论文]. 上海: 同济大学海洋与地球科学学院. |
| [37] | 郭继茹, 冯晅, 王俊祥等. 2008. 最佳路径射线追踪算法研究. 吉林大学学报(地球科学版), 38(增刊): 72-75. |
| [38] | 韩晓丽, 杨长春, 麻三怀等. 2008. 复杂山区初至波层析反演静校正. 地球物理学进展, 23(2): 475-483. |
| [39] | 景月红. 2009. 地震初至波走时层析成像与近地表速度建模[硕士论文]. 西安: 长安大学地球探测与信息技术学院. |
| [40] | 李录明, 罗省贤, 赵波. 2000. 初至波表层模型层析反演. 石油地球物理勘探, 35(5): 559-564. |
| [41] | 刘玉柱, 董良国, 夏建军. 2007. 初至波走时层析成像中的正则化方法. 石油地球物理勘探, 42(6): 682-698. |
| [42] | 卢回忆, 刘伊克, 常旭. 2013. 基于MSFM的复杂近地表模型走时计算. 地球物理学报, 56(9): 3100-3108, doi: 10.6038/cjg20130922. |
| [43] | 王薇, 韩波, 唐锦萍. 2013. 地震波形反演的稀疏约束正则化方法. 地球物理学报, 56(1): 289-297, doi: 10.6038/cjg20130130. |
| [44] | 王彦飞. 2007. 反演问题的计算方法及其应用. 北京: 高等教育出版社. |
| [45] | 王彦飞, 斯捷潘诺娃 I E, 提塔连科 V N等. 2011. 地球物理数值反演问题. 北京: 高等教育出版社. |
| [46] | 肖庭延, 于慎根, 王彦飞. 2003. 反问题的数值解法. 北京: 科学出版社. |
| [47] | 杨文采, 李幼铭. 1993. 应用地震层析成像. 北京: 地质出版社. |
| [48] | 袁亚湘. 1993. 非线性规划数值方法. 上海: 上海科技出版社. |
| [49] | 张建中. 2004. 近地表介质地震初至波层析成像. 厦门大学学报, 43(1): 63-66, doi: 10.3321/j.issn:0438-0479.2004.01.016. |
| [50] | 张钋, 刘洪, 李幼铭. 2000. 射线追踪方法的发展现状. 地球物理学进展, 15(1): 36-45, doi: 10.3969/j.issn.1004-2903.2000.01.002. |
 2015, Vol. 58
2015, Vol. 58


