地球物理学报  2015, Vol. 58 Issue (4): 1305-1316   PDF    
引用本文
刘玉柱, 王光银, 杨积忠, 董良国. 2015. 基于Born敏感核函数的VTI介质多参数全波形反演. 地球物理学报, 58(4): 1305-1316, doi: 10.6038/cjg20150418   
LIU Yu-Zhu, WANG Guang-Yin, YANG Ji-Zhong, DONG Liang-Guo. 2015. Multi-parameter full-waveform inversion for VTI media based on Born sensitivity kernels. Chinese J. Geophysics, 58(4): 1305-1316, doi: 10.6038/cjg20150418   
基于Born敏感核函数的VTI介质多参数全波形反演
刘玉柱1, 王光银1,2, 杨积忠1, 董良国1    
1. 海洋地质国家重点实验室, 同济大学, 上海 200092;
2. 中国石油川庆钻探工程有限公司地球物理勘探公司, 成都 610213
投稿时间:2014-06-27    最后修改时间: 2014-12-13 .
基金项目：国家自然科学基金(41274116;41474034)与海洋地质国家重点实验室自主课题(MGG2013001)共同资助.
作者简介：刘玉柱,男,博士,1979年生,副教授、博士生导师,主要从事地震波正反演理论、方法与应用研究. E-mail:liuyuzhu@tongji.edu.cn
摘要：本文基于VTI介质拟声波方程,利用散射积分原理,在Born近似下导出了速度与各向异性参数的敏感核函数,同时结合作者前期研究提出的矩阵分解算法实现了一种新的VTI介质多参数全波形反演方法.矩阵分解算法通过对核函数-向量乘进行具有明确物理含义的向量-标量乘分解累加运算实现目标函数一阶方向或二阶方向的直接求取,从而避免了庞大核函数矩阵与Hessian矩阵的存储,该方法同时可以大大降低常规全波形反演在计算二阶方向时的庞大计算量.为了克服不同参数对波场影响程度的不同,本文利用作者前期在VTI介质射线走时层析成像研究中提出的分步反演策略实现了多参数联合全波形反演.理论模型实验表明,本文提出的基于Born敏感核函数的各向异性矩阵分解全波形反演方法可以获得较好的多参数反演结果.
关键词： 全波形反演     各向异性     拟声波方程     敏感核函数     矩阵分解     多参数    
Multi-parameter full-waveform inversion for VTI media based on Born sensitivity kernels
LIU Yu-Zhu1, WANG Guang-Yin1,2, YANG Ji-Zhong1, DONG Liang-Guo1    
1. State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092, China;
2. CNPC CDEC Sichuan Geophysical Company, Chengdu 610213, China
Abstract: Anisotropic full waveform inversion (FWI) is being widely studied. However, it remains a problem for FWI to reveal all the anisotropic parameters simultaneously because of their coupling. Parameterization and inversion strategy are important solutions to such a problem. In this study, we propose a new VTI FWI method based on a pseudo-acoustic wave equation. This method uses a matrix decomposition algorithm to explicitly construct the gradient of the objective function instead of the traditional adjoint-state method. Meanwhile, a triple-round strategy is tested effective to implement the joint inversion of all the three parameters.In FWI, the least-squares objective function is usually used, and the increment Δm=(Δv,Δε,Δδ) around a starting model m0=(v0,ε0,δ0) can be expressed as the product of a direction vector p and a step length t under local optimization theory. The direction vector p equals the product of the transposed kernels K and the wavefield residual. Based on frequency-domain pseudo-acoustic wave equations in VTI media, we derive the corresponding sensitivity kernels for the three parameters v,ε,δ. However, the kernels are too huge to store in memory. Therefore, we use a matrix decomposition algorithm, instead of the adjoint-state method, to calculate p and t by accumulation of single vector-scalar products. By this way, the huge kernel matrix K is not necessarily stored in memory beforehand. In order to obtain VTI parameters simultaneously, we analyze the sensitivities and find that v has the most dominant influence on the wavefield, δ is the weakest, and ε is in the middle. Therefore, we use a triple-round strategy to reveal the three parameters. In the first round, we invert simultaneously for (v1,ε1,δ1) according to an initial model (v0,ε0,δ0). In the second round, we use (v1,ε0,δ0) as the initial model and invert simultaneously for (v2,ε2,δ2). In the third round, we use v2,ε2,δ0 as the initial model and invert simultaneously for (v3,ε3,δ3). By this way, both the strong and weak parameters can be successfully constructed.In order to test the inversion capability of this method, we design a 2D VTI homogenous model with three anomalies inside. In this experiment we only invert for v and ε simultaneously, with δ being fixed as the true model because δ has a very weak influence on data. The dimension of this model is 4 km×4 km, with the discretized interval 10 m×10 m. In total 52 shots are uniformly distributed along the shot side, and 60 receivers are uniformly laid along the other three sides away from the shot side. Inversion is accomplished in the frequency domain. The starting frequency is 2 Hz, and the end frequency is 11.5 Hz, with frequency interval 0.5 Hz. The starting model of v is homogeneous without anomalies. The starting model of ε is a highly smoothed version of the true ε model. Finally, both v and ε are well revealed, while the resolution of obtained ε is not as high as v because of its natural weaker influence on the wavefield. We propose a new FWI scheme for VTI media based on Born kernels derived from a pseudo-acoustic wave equation. A matrix decomposition algorithm is employed to calculate the directions and step length through accumulation, while without need to store the huge Fréchet kernel or the approximate Hessian beforehand. To reveal all the anisotropic parameters, we use a triple-round strategy to overcome the different influences of different parameters on the wavefield. Numerical experiment proves the effectiveness of this method and shows its potential to construct all the parameters in complex anisotropic media.
Key words: Full-waveform inversion     Anisotropy     Pseudo-acoustic wave equation     Sensitivity kernel     Matrix decomposition     Multiple parameters    
1 引言

2 0世纪80年代提出的全波形反演(FWI，Full-waveform inversion)旨在利用最优化理论使得观测数据与模拟数据之间的距离最小以实现模型的更新.Tarantola(1984)在时间域通过激发点正传波场和接收点反传残差波场的互相关求取目标函数的梯度，建立了基于2-范数目标泛函的伴随状态法全波形反演框架.Pratt等(1996)在Tarantola时间域全波形反演框架的基础上提出了频率域全波形反演方法.频率域全波形反演仅需要观测数据中的几个有限离散频率成分就可以建立高精度的参数模型，推动了波形反演向实际应用的发展.Sirgue等(2010)将全波形反演应用于挪威北海的Valhall油田，获得的速度模型不仅提高了成像质量，偏移剖面还呈现出了从未出现过的地质特征.这表明，全波形反演在工业运用中能取得相当惊人的成绩.

最初的全波形反演并没有考虑各向异性.Berryman(1979)指出，在短偏移距数据中，横波的各向异性比纵波明显；基于地震勘探现阶段常用的地表观测系统，全波形反演需要低频和长偏移距数据来更新模型中的长波长成分；如果不考虑各向异性，长偏移距数据和短偏移距数据不能同时被很好地匹配.Barnes等(2008)也指出，随着长偏移距和宽方位采集的增加，各向异性对数据的影响越来越明显.Plessix(2009)指出，处理过程中考虑各向异性可以大幅提高FWI的反演精度.Barnes等(2008)指出，在VTI介质全波形反演中，多个参数同步反演有助于不同参数间的相互约束.然而，由于包含多种参数，且不同参数对波场的影响程度不同，各向异性全波形反演要比各向同性情况困难得多.Gholami等(2010)指出，即使利用四周观测系统，全波形反演也很难将vS0、vP0、ε、δ等参数同时反演出来.因此，很多学者对参数化方法、反演策略、初始模型的构建等进行了研究.例如，Plessix和Cao(2011)通过对VTI介质纵波层析中Hessian矩阵做特征值分析后指出，v0、vh、vnmo是较为合适的参数化方法，但存在一定的模糊性；Watanabe等(1996)在全波形反演中先做各向同性假设下的单参数速度反演，再在此基础上实现各向异性多参数反演；Koren等(2008)为了能够在成像道集上利用剩余速度分析更新各向异性介质中的背景速度，提出首先用长偏移距数据反演ε，再用短偏移距数据反演δ的策略；Plessix和Rynja(2010)指出，各向异性全波形反演对速度初始模型的精度要求低于对各向异性参数初始模型的要求，只有当各向异性参数初始模型能够相当准确地描述地震波的运动学特征时，它们才有可能被准确地反演出来.

可见，对VTI介质，目前还没有一套统一的多参数反演策略或联合反演方法.杨积忠等(2014)在研究变密度声波方程全波形反演方法时提出了一种同时反演速度与密度的两步法反演策略.刘玉柱等(2014b)将该策略应用于VTI介质地震走时层析成像中，并将两步法发展为三步法，成功反演得到了描述纵波各向异性的3个Thomsen参数.刘玉柱等(2014a)提出了一种基于Born敏感核函数的矩阵分解全波形反演方法，该方法通过对核函数-向量乘进行具有明确物理含义的向量-标量乘分解累加运算实现目标函数梯度的直接求取，而无需存储庞大的核函数矩阵或Hessian矩阵.该方法同时可以大大降低常规全波形反演方法在计算二阶方向时的庞大计算量，而且可以考虑二阶方向中不同参数间的相互耦合，无需策略即可以将多参数同时反演出来(Yang et al., 2014).在矩阵分解全波形反演方法中，核函数的推导与计算是关键.因此，本文基于VTI介质拟声波方程，利用散射积分原理导出了速度与所有各向异性参数的敏感核函数，并结合刘玉柱等(2014a)提出的矩阵分解算法与杨积忠等(2014)、刘玉柱等(2014b)提出的分步反演策略实现了VTI介质多参数全波形反演.

2 全波形反演方法

根据最优化理论，频率域全波形反演的目标函数可以建立为如下L2范数的形式

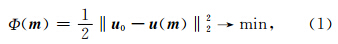
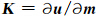其中，m代表模型向量，u0为观测数据向量，u为满足某个波动方程的理论合成数据向量.通常采用局部最优化方法求解上述反问题，即把模型的增量表示为Δm=t·p，其中t为正实数的步长，p是与模型维度相同的方向向量.方向的表达与计算是最优化反演方法中的关键，通常采用如下两种方向(姚姚，2002):

其中，p1是目标函数的负梯度方向，即最速下降方向；p2是牛顿方向.由于该两种方向与目标函数的一阶近似或二阶近似有关，因此本文借鉴刘玉柱等(2014a)将其称为一阶方向或二阶方向. 为反映模型参数扰动对波场影响程度的Fréchet核函数，也称为敏感核函数.Δu=u0－u表示波场残差.上标T表示复矩阵的共轭转置. H 是目标函数对模型参数向量的二阶偏导数构成的Hessian矩阵， H a= KT K为近似Hessian矩阵.利用近似Hessian矩阵构造的牛顿方向称为高斯牛顿方向.为了获得步长，可以在假设方向已知的情况下构建一关于步长t的新的目标函数E(t)=Φ(m +t p)，并对该目标函数进行一阶或二阶近似即可以得到(姚姚，2002)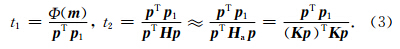

由于利用公式(2)、(3)直接求取方向与步长需要计算并存储Fréchet核函数或Hessian矩阵，无论计算量还是存储量都比较大，因此目前广泛采用伴随状态法间接计算目标函数的梯度(Tromp et al., 2005)，然后再利用其计算方向与步长.根据伴随状态法，目标函数的梯度总可以表达为正传波场与反传残差波场的互相关，因此可以避免核函数的计算与存储，但该方法直接应用于计算目标函数的二阶方向比较困难.

刘玉柱等(2014a)在研究声介质全波形反演方 法时提出了一种基于Born敏感核函数(Woodward，1992)计算目标函数一阶方向与二阶方向的矩阵分解算法.该矩阵分解算法的核心思想是对公式(2)、(3)中的核函数-向量乘运算分解为具有明确物理含义的向量-标量乘累加运算，这样就避免了庞大的核函数矩阵或者Hessian矩阵的存储，同时大大降低 了常规全波形反演算法在计算二阶方向时的计算量.假设m是由n个元素构成的模型向量，u是由m个元素构成的数据向量，则 K是由m×n个元素构成的 核函数矩阵.矩阵分解计算一阶方向的实现方式如下：

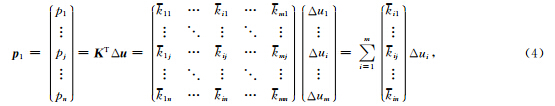
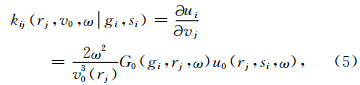
其中，kij表示第i个数据元素对第j个网格参数的敏感性，例如对于声介质(Woodward，1992)，

其中，gi代表第i个观测数据所对应的检波点的位置，si代表第i个观测数据所对应的炮点的位置，rj表示空间第j个网格的位置，v0是扰动前的介质速度，ω为角频率，G0(g，r，ω)是无扰动介质中r点产生的g点处的格林函数，u0(r，s，ω)是由s点产生的r点处的无扰动波场.因此，(4)式最右端求和运算中的每一个列向量代表一个炮检对所对应的核函数的共轭.这样，同一时刻只需临时存储一个炮检对所对应的核函数，然后通过累加运算即可实现方向p1的计算，而无需事先存储庞大的核函数矩阵 K.

同样地，t2中 Kp 的计算可以直接通过如下方法求取，

式中，矩阵 K的每一行为某个单一炮检对所对应的核函数.同样，同一时刻只需临时存储一个炮检对所 对应的核函数，而无需事先存储庞大的核函数矩阵 K.

Hessian对角元素被广泛用于一阶方向的预条件(Choi and Shin， 2007)，刘玉柱等(2014a)同时也 给出了如下计算Hessian对角元素的矩阵分解算法：

同样，注意(7)式最右端求和运算中的每一个对角阵的对角元素都是关于一个炮检对所对应的核函数的运算.

二阶方向涉及Hessian矩阵求逆计算，难于直接实现，但采用内部最优化方法，利用2次核函数-向量乘运算仍可以实现二阶方向的迭代计算，而且内部迭代过程中无需额外的正演计算，可以大大提高二阶方向的计算效率.由于本文只采用一阶方向，因此二阶方向的实现这里不予赘述，具体实现可以参考Liu等(2014).

方向得到后利用公式(3)可以方便地实现步长的计算.

3 VTI介质敏感核函数的推导

由第2节介绍可知，矩阵分解全波形反演方法的核心在于推导出各个参数所对应的敏感核函数.二维VTI介质时间-空间域拟声波方程(Duveneck et al., 2008)的频率-空间域表达形式为

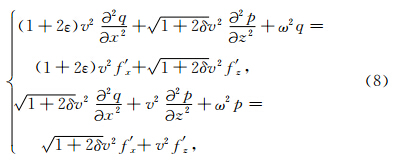
其中，v、ε、δ为VTI介质的声学Thomsen参数表征，ω为角频率.q、p代表波场的两个分量，且只具备数学含义，并无物理意义.fx、fz分别表示x、z方向的体力源，.

将微小扰动后的速度表达为

那么扰动后的波场可以表达为

其中，q0、p0为参考模型(v0，ε，δ)下的波场，qs、ps为参考模型v0存在扰动量vs时产生的扰动波场.

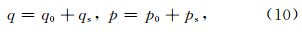
将(9)、(10)式代入(8)式，并假设v0>>vs，则得到：

考虑到q0、p0、v0同样满足公式(8)，即

则(11)式可以改写为

进而结合(8)式得

根据散射积分原理，设格林函数Gq、Gp为满足方程

的解，其中(x′，z′)表示脉冲源位置.根据表示定理(Aki and Richards， 2002)，方程(14)的解为

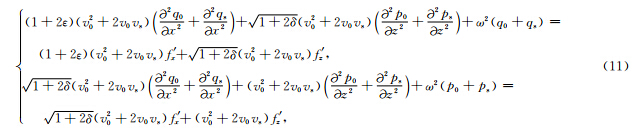
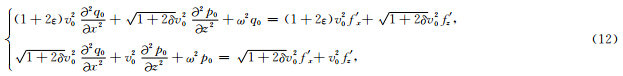
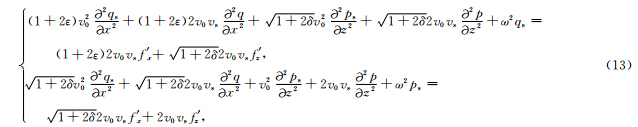
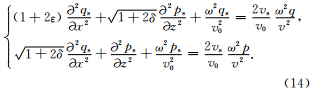
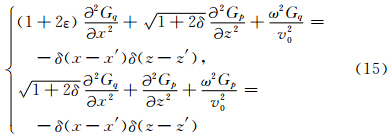
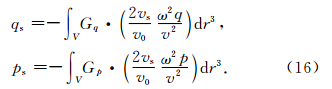
Woodward(1992)根据频率域声波方程导出了声波散射场us与速度扰动vs之间的非线性关系

为了导出它们之间的线性关系，Woodward利用Born近似提出了弱散射条件假设，即当v0>>vs时，u0>>us，因此(17)式可以重写为

并根据此关系给出了Born波路径k的定义(5).

仿照Woodward对声波Born波路径的定义与推导，假设VTI介质满足Born近似假设条件，即当v0>>vs时，q0>>qs，p0>>ps.那么，根据(16)式，速度扰动引起的波场扰动满足线性关系

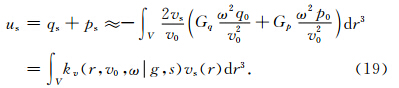
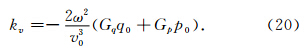
这样，就可以得到VTI介质中速度所对应的Born波路径，即速度敏感核函数

从式(20)可以看出，VTI介质速度核函数表达式与Woodward给出的声波各向同性介质中的速度核函数表达式基本一致，都是由激发点的正传波场与接收点的格林函数相作用得到.

同理，仿照上述推导过程也可以得到各向异性参数ε、δ核函数表达式，

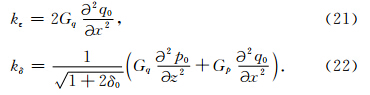
从式(21)可以看出，ε的核函数只受q分量的影响，由激发点的理论合成q分量在x方向的二阶导数与接收点的格林函数相作用组成，而根据(22)式，δ的核函数则由接收点处的q、p格林函数与激发点处的理论合成q、p分量的二阶偏导数的交叉作用组成.需要强调的是，式(20)—(22)与Wang等(2012)利用伴随状态法导出的目标函数梯度表达式的核函数退化形式是一致的.

将核函数表达式(20)—(22)代入公式(4)、(6)或(7)即可实现VTI介质矩阵分解全波形反演中一阶方向及其相应步长的计算，进而实现模型的迭代更新.

4 数值试验与反演策略

为了验证本文推导的核函数的正确性以及提出的VTI介质矩阵分解全波形反演方法的有效性，本文设计了复杂程度不同的两个理论模型.简单理论模型如图 1所示，模型包含201×201个网格，网格大小为10 m×10 m.16炮平均分布于4边，起始激发点位于(50，50)m处，炮间隔500 m，其余三边接收.接收点间距400 m，每炮15个接收点.速度模型 背景值为3600 m·s-1，中心异常值为3960 m·s-1. ε背景值为0.13，中心异常值为0.2.δ背景值为0.05，中心异常值为0.1.模型的最外层为各向同性介质，即激发点与接收点均在各向同性介质中，以降低理论合成波场中的“横波”干扰.反演在频率域完成，起始频率为2 Hz，频率间隔0.5 Hz，终止频率11.5 Hz.

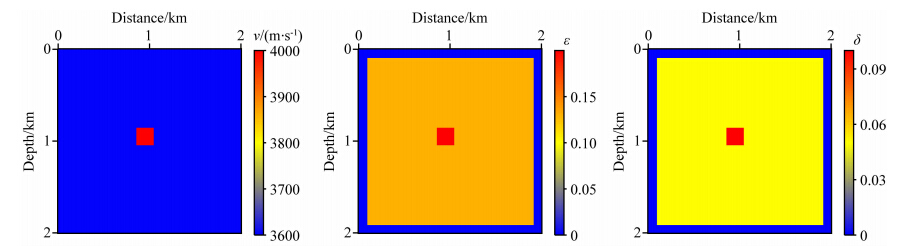图 1 简单理论模型Fig. 1 Simple true models

为了考察全波形反演对不同参数的反演能力及寻找一个合适的反演策略，本文做了5组实验(表 1)，实验结果分别如图 2—9所示.图 2是S1、S2实验结果，图 3是S1、S2实验结果在X=1000 m处的垂直速度剖面对比.从图 2、图 3可以看出，编号S1实验结果比S2实验结果反演精度略高，这表明VTI介质中δ对FWI的反演结果影响较小.结合射线层析中δ对射线走时的不敏感性(刘玉柱等，2014b)，本文认为在VTI FWI中δ对目标函数的影响也不明显.因此，在下面的实验中只反演v、ε两个参数.同时，为了克服强弱参数对波场影响程度的不同，本文借鉴杨积忠等(2014)在变密度声波方程全波形反演研究中及刘玉柱等(2014b)在VTI介质走时层析成像研究中提出的两步法反演策略，即首先基于初始模型v0、ε0进行双参数联和反演得到v1、ε1；考虑到在v0不够准确的情况下ε1的反演精度很低，甚至劣于ε0，但v1的精度应该优于v0，因此在第二步反演中将v1、ε0作为初始模型继续进行双参数联和反演得到v2、ε2.在v1比较准确的情况下ε2的反演精度会比较好，v2的反演精度也会得到提高，因此将v2、ε2作为最终的反演结果.如果进行三参数反演，该两步法策略可以方便地扩展到三步法(刘玉柱等，2014b).

表 1 理论模型试验方案Table 1 Parameters for simple model experiments

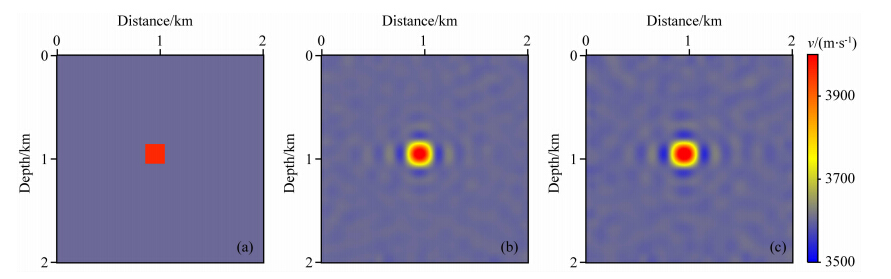图 2 真实速度模型(a)、S1单参数反演结果(b)与S2单参数反演结果(c)Fig. 2 True velocity(a)，results of S1 experiment(b) and S2 experiment(c)

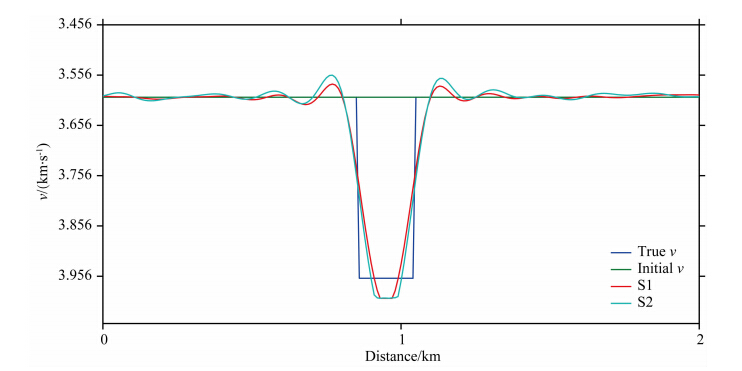图 3 S1和S2速度反演结果在X=1000 m处的垂直剖面对比Fig. 3 Velocity sections of results of experiments S1 and S2 at X=1000 m

J1实验中，δ固定为真实值，均匀背景速度、均匀背景ε作为初始模型，采用两步法策略同步反演v和ε.图 4为J1实验速度反演结果，图 5为J1实验 速度反演结果在X=1000 m处的垂直剖面对比.可 以看出，第二步的速度反演精度比第一步有了一定的改善.图 6为J1实验ε反演结果，图 7为J1实验ε反演结果在X=1000 m处的垂直剖面对比.可以看出，第二步的ε反演分辨率低于第一步，但第二步的ε反演精度比第一步高很多.图 7同时表明，不采用任何反演策略，在初始速度模型不够准确的情况下，双参数同步反演无法得到准确的各向异性参数.原因在于速度比各向异性参数对地震数据的影响更大，也就是说在反演过程中哪怕只有一小部分数据残差被投影到各向异性参数上，都可能造成其较大的修正量.

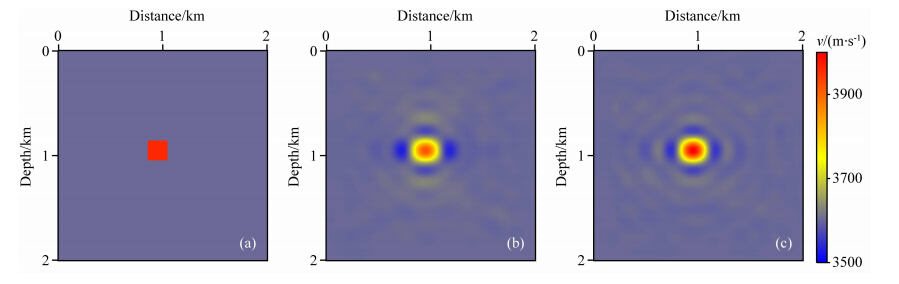图 4 真实速度模型(a)、第一步速度反演结果(b)与第二步速度反演结果(c)Fig. 4 True velocity(a) and revealed velocities after the first round(b) and the second round(c)

图 5 两步法速度反演结果在X=1000 m处的垂直剖面对比Fig. 5 Sections of velocity results of experiments S1 and S2 at X=1000musing double-round strategy

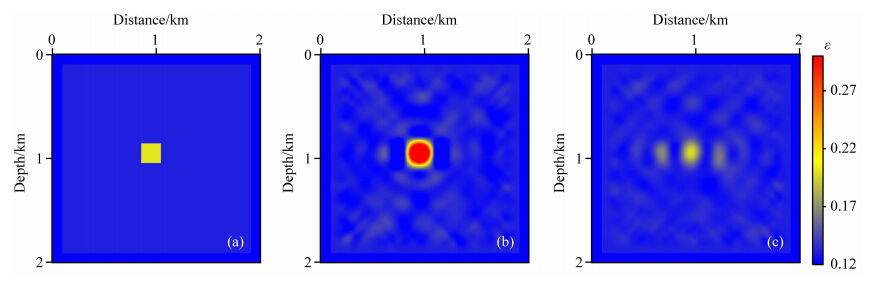图 6 真实ε模型(a)、第一步ε反演结果(b)与第二步ε反演结果(c)Fig. 6 True ε(a) and revealed ε after the first round(b) and the second round(c)

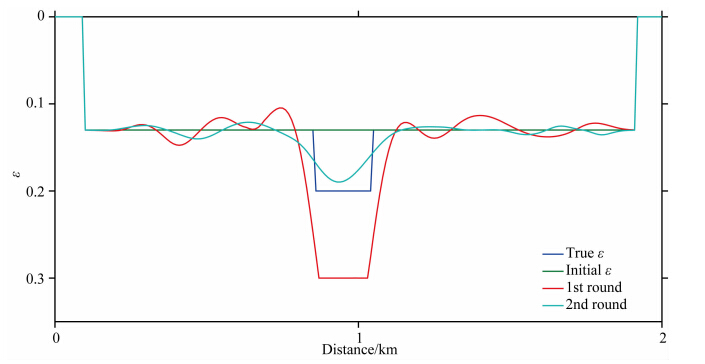图 7 两步法ε反演结果在X=1000 m处的垂直剖面对比Fig. 7 Sections of ε results of experiments S1 and S2 at X=1000musing double-round strategy

图 8为编号J2、J3速度反演结果.从J2实验结果可以看出，当各向异性参数离真实模型都较远时，即使δ对波场影响不大，也会影响速度反演精度.编号J3实验结果表明，当所有各向异性参数初始模型都包含准确的背景值时，可以反演得到一个满意的速度模型.参考S2实验结论(ε比较准确时，δ对反演结果的影响不大)，J2实验说明ε对波形的影响大 于δ对波形的影响；参考J3实验结果，说明δ对波形的影响只是略低于ε.参考刘玉柱等(2014b)在VTI介质走时层析研究中得出的结论，本文认为各向异性参数，尤其是δ参数，在走时层析和全波形反演中都表现出不敏感，因此全波形反演不需要精确的各向异性参数初始值.但正如Plessix和Rynja(2010)指出，所有各向异性参数对波场影响的总效应是不容忽略的，因此仍需要通过其他地球物理手段或者经验公式设定包括δ在内的所有各向异性参数一个合理的初始模型，使其不至于偏离真实模型太远.

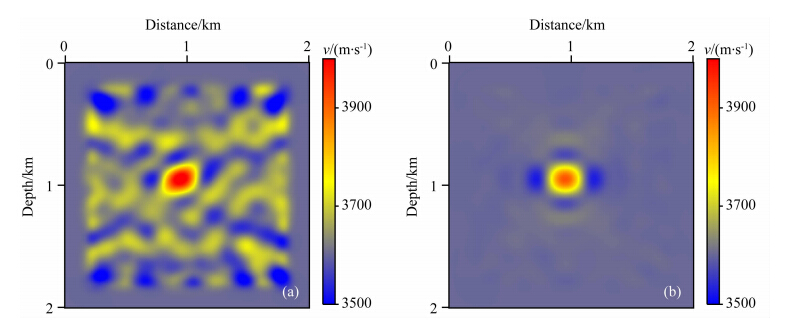图 8 编号J2第一步速度反演结果(a)与编号J3第一步速度反演结果(b)Fig. 8 Obtained velocities of experiments J2(a) and J3(b)through the first round

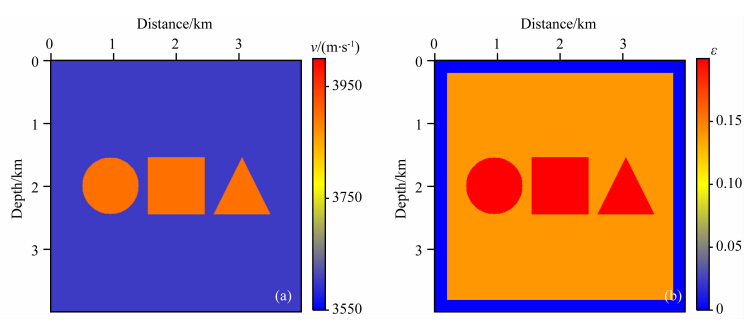图 9 复杂理论模型的真实速度模型(a)与真实ε模型(b)Fig. 9 Complex synthetic models of true velocity(a) and true ε(b)

另一方面，核函数本身反映了参数对波场的影响程度，反过来该影响程度又可以说明反演中该参数对初始模型的依赖性，即核函数越大说明该参数对初始模型的依赖性越小(刘玉柱等，2014b).因此，通过对比公式(20)—(22)(在反演速度时，通常采用慢度参数化方式)不难发现，速度的核函数远远大于ε，而ε略大于δ，即理论上速度对初始模型的依赖性远远小于ε，而ε对初始模型的依赖性又略小于δ.

为了进一步测试本文提出方法及选取的策略的有效性，设计了图 9所示复杂理论模型.该模型包含400×400个网格，网格大小为10 m×10 m.52炮平均分布于4边，起始激发点位于(50，50)m处，炮间隔300 m，其余三边接收，接收点间距200 m，每炮60个接收点.速度模型背景值为3600 m·s-1，中心异常值为3900 m·s-1.ε模型背景值为0.14，中心异常值为0.2.模型最外层为各向同性介质.反演在频率域完成，起始频率为2 Hz，频率间隔0.5 Hz，终止频率11.5 Hz.速度初始模型为均匀背景速度，ε初始模型由真实模型平滑得到，如图 10所示.图 11为最终的两步法双参数全波形反演结果.可以看出，基于均匀背景速度与平滑的ε模型，利用本文方法得到了较好的速度与ε反演结果，但ε的反演分辨率低于速度.为了进一步分析反演精度，提取了深度2000 m处的反演剖面，如图 12、图 13所示.可以发现，速度反演精度比较高，ε反演精度稍低.ε的反演分辨率与反演精度都低于速度是由ε物理上对波场的相对不敏感造成的.

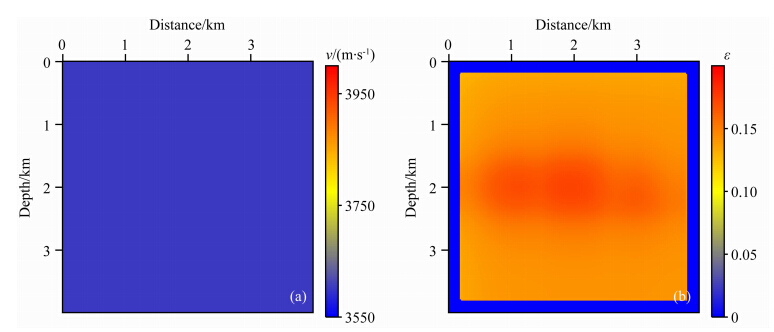图 10 初始速度(a)与初始ε模型(b)Fig. 10 Initial models of velocity(a) and ε(b)

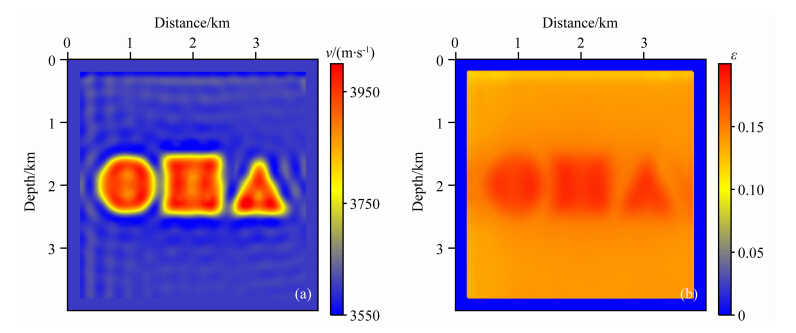图 11 速度反演结果(a)与ε反演结果(b)Fig. 11 Final revealed results of velocity(a) and ε(b)

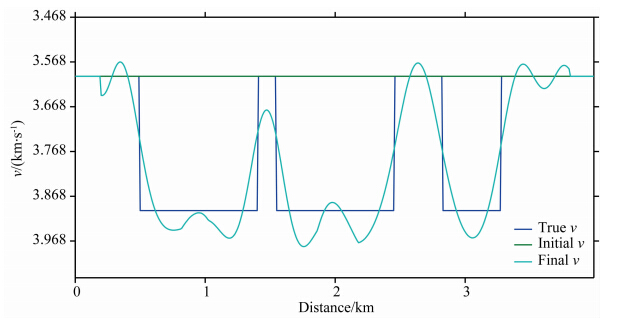图 12 复杂模型全波形反演Z=2000 m处的速度横向剖面图Fig. 12 Horizontal sections of velocities at Z=2000mof complex-model test

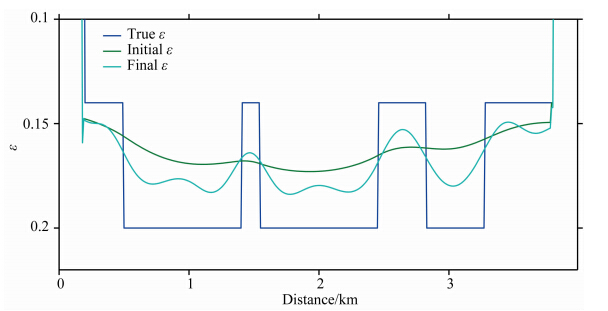图 13 复杂模型全波形反演Z=2000 m处的ε横向剖面图Fig. 13 Horizontal sections of ε at Z=2000mof complex-model test
5 结论

基于Born敏感核函数的VTI介质矩阵分解全波形反演方法，无需存储Fréchet核函数和Hessian矩阵即可实现方向及其相应步长的高效、灵活计算.Fréchet核函数的推导与计算是矩阵分解全波形反演方法的关键.本文基于一种VTI介质拟声波方程导出了速度与各向异性参数的敏感核函数.同时，利用前期提出的分步反演策略实现了VTI介质全波形反演中多参数的联和反演.理论模型试验验证了本文导出的敏感核函数的正确性以及VTI介质矩阵分解全波形反演方法与策略的有效性.由于数值实验表明δ参数对走时和波形均不敏感，本文只进行了v、ε双参数反演，但反演过程中仍需要一定的先验信息以构造各向异性参数的初始模型或为反演提供约束.

需要注意的是本文并未实现考虑参数耦合的二阶方向的计算，但该二阶方向无疑对多参数联合反演具有重要影响，相关工作正在进行中，并将另文发表.

参考文献
[1] Aki K, Richards P G. 2002. Quantitative Seismology, 2nd Edition. Sausalito:University Science Books.
[2] Barnes C, Charara M, Tsuchiya T. 2008. Feasibility study for an anisotropic full waveform inversion of cross-well seismic data. Geophysical Prospecting, 56(6):897-906.
[3] Berryman J G. 1979. Long-wave elastic anisotropy in transversely isotropic media. Geophysics, 44(5):896-917.
[4] Choi Y, Shin C. 2007. Frequency-domain elastic full-waveform inversion using the new pseudo-Hessian matrix:elastic Marmousi-2 synthetic test. SEG Conference & Exhibition, 1908-1912.
[5] Duveneck E, Milcik P, Bakker P M, et al. 2008. Acoustic VTI wave equations and their application for anisotropic reverse-time migration. SEG Conference & Exhibition, 2186-2190.
[6] Gholami Y, Ribodetti A, Brossier R, et al. 2010. Sensitivity analysis of full waveform inversion in VTI media. EAGE Conference & Exhibition.
[7] Koren Z, Ravve I, Gonzalez G, et al. 2008. Anisotropic local tomography. Geophysics, 73(5):VE75-VE92.
[8] Liu Y Z, Xie C, Yang J Z. 2014a. Gaussian beam first-arrival waveform inversion based on Born wavepath. Chinese Journal of Geophysics (in Chinese), 57(9):2900-2909, doi:10.6038/cjg20140915.
[9] Liu Y Z, Wang G Y, Dong L G, et al. 2014b. Joint inversion of VTI parameters using nonlinear traveltime tomography. Chinese Journal of Geophysics (in Chinese), 57(10):3402-3410, doi:10.6038/cjg20141026.
[10] Liu Y Z, Yang J Z, Chi B X, et al. 2014.An alternative realization of Gauss-Newton for frequency-domain acoustic waveform inversion.AGU, NS33B-04.
[11] Plessix R E. 2009. Three-dimensional frequency-domain full-waveform inversion with an iterative solver. Geophysics, 74(6):WCC149-WCC157.
[12] Plessix R E, Cao Q. 2011. A parametrization study for surface seismic full waveform inversion in an acoustic vertical transversely isotropic medium. Geophysical Journal International, 185(1):539-556.
[13] Plessix R E, Rynja H. 2010. VTI full waveform inversion:a parameterization study with a narrow azimuth streamer data example. SEG Conference & Exhibition, 962-966.
[14] Pratt R G, Song Z M, Williamson P, et al. 1996. Two-dimensional velocity models from wide-angle seismic data by wavefield inversion. Geophysical Journal International, 124(2):323-340.
[15] Sirgue L, Barkved O I, Dellinger J, et al. 2010. Full waveform inversion:The next leap forward in imaging at Valhall. First Break, 28(4):65-70.
[16] Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8):1259-1266.
[17] Tromp J, Tape C, Liu Q Y. 2005. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels. Geophysical Journal International, 160(1):195-216.
[18] Wang C, Yingst D, Bloor R, et al. 2012. VTI waveform inversion with practical strategies:application to 3D real data. EAGE Conference & Exhibition, 1-6.
[19] Watanabe T, Hirai T, Sassa K. 1996. Seismic traveltime tomography in anisotropic heterogeneous media. Journal of Applied Geophysics, 35(2-3):133-143.
[20] Woodward M J. 1992. Wave-equation tomography. Geophysics, 57(1):15-26.
[21] Yang J Z, Liu Y Z, Dong L G. 2014. Truncated Gauss-Newton implementation for multi-parameter full waveform inversion. AGU, NS43A-3849.
[22] Yang J Z, Liu Y Z, Dong L G. 2014. A multi-parameter full waveform inversion strategy for acoustic media with variable density. Chinese Journal of Geophysics (in Chinese), 57(2):628-643, doi:10.6038/cjg20140226.
[23] Yao Y. 2002. Basic Theory and Applications of Geophysical Inversion (in Chinese). Beijing:China University of Geosciences Press.
[24] 刘玉柱, 谢春, 杨积忠. 2014a. 基于Born波路径的高斯束初至波波形反演. 地球物理学报, 57(9): 2900-2909, doi: 10.6038/cjg20140915.
[25] 刘玉柱, 王光银, 董良国等. 2014b. VTI介质多参数联合走时层析成像方法. 地球物理学报, 57(10): 3402-3410, doi: 10.6038/cjg20141026.
[26] 杨积忠, 刘玉柱, 董良国. 2014. 变密度声波方程多参数全波形反演策略. 地球物理学报, 57(2): 628-643, doi: 10.6038/cjg20140226.
[27] 姚姚. 2002. 地球物理反演基本理论与应用方法. 北京: 中国地质大学出版社.