2. 同济大学结构工程与防灾研究所, 上海 200092;
3. 同济大学上海防灾救灾研究所, 上海 200092
2. Institute of Structural Engineering and Disaster Reduction, Tongji University, Shanghai 200092, China;
3. Institute of Disaster Prevention and Relief, Tongji University, Shanghai 200092, China
反应谱理论是抗震设计的重要理论之一,包含下列几个基本假定:(1)结构的地震反应是弹性的,可以采用叠加原理进行振型组合;(2)现有反应谱是在结构的所有支承处的地震动完全相同,基础与土壤无相互作用的假定下求得的,因而也只适用于这一条件.另外现在给出的不少反应谱并不是一次地震动作用下的反应谱,而是所谓标准反应谱或平均反应谱,他们都是不同地震反应谱的包线,或者是不区分某些有影响因素的结果;(3)结构物最不利的地震反应为其最大反应,与其他动力反应参数,如达到最大值附近的次数或概率无关(胡聿贤,2006).
反应谱是一系列具有单位质量、相同阻尼、不同频率的单自由度体系在输入地震动时程作用下的反应的最大值.其本质是对设计地震力的规定,设计反应谱并不反映某一具体的地震动时程特性,而是在总体上把握地震动的工程特性.反应谱理论是一种拟静力反应计算理论,因此在应用上存在一定局限性,主要表现在:(1)反应谱理论只能反应结构的最大弹性地震反应,不能反映结构在实际地震反应中可能出现的非弹性特性;(2)反应谱无法反映结构低周疲劳特性的影响,不能反映结构在实际地震动作用过程中结构性能随时间的变化,无法进行结构在罕遇地震作用下的倒塌分析;(3)计算经验表明,反应谱的计算主要决定于地震动加速度记录中最强烈的一段(谢礼立和马玉宏,2003).
利用反应谱理论进行结构抗震设计,是将动力设计的问题简化为静力设计的问题;根据叠加原理还可得出复杂结构对输入地震动反应的最大值,但其仅考虑了地震动工程特性中的振幅、频谱两个特性,没有考虑地震动持时特性的影响.地震动持时对结构破坏的重要影响是不容忽视的.1966年美国Parkfield地震记录加速峰值为0.15 g,1972年美国Stonecanyon地震记录加速度峰值为0.169 g,但这些记录点周围的地震破坏却相对较轻;究其原因,发现这两条地震记录的持续时间都较短,强震段只有几秒.1962年墨西哥地震中某记录加速度峰值为0.105 g,由于地震动持续时间较长,致使当地及周围地震破坏相对严重.Shen和Wu(2007)在研究钢结构地震反应分析模型时认为,结构的累积破坏效应十分重要.研究了七个典型砌体结构模型在约500条强震记录作用下的反应之后,Bommer等(2004)认为,应该改进砌体结构的抗震评估方法,分析中需要考虑地震动持时的影响.强震动持时与结构的累积破坏、结构的非线性变形的低周疲劳效应关系密切(杜修力和刘勇生,1992).盛明强和罗奇峰(2008)按场地类别和强震持时将Northridge地震记录和ChiChi 地震记录的峰值进行规一化处理,分别用3种恢复力模型,对单自由度体系进行弹塑性时程分析,发现平均滞回耗能值强烈地依赖于场地条件、强震持时和阻尼比等因素.
弹塑性时程分析考虑了结构构件的弹塑性性能,结构的刚度不断地变化,通过输入地震动作用下结构反应的逐步计算,可以得到结构各质点的位移,速度和加速度时程反应.这种方法虽然考虑了地震动的持时特性,但计算繁琐,耗时颇长,所得结果的精度取决于模型单元的划分精度、材料的本构关系以及地震波的选择.并且弹塑性时程分析因其要进行相当巨大数据量的处理,对硬件要求很高.由于弹塑性时程分析方法的计算复杂性,目前只用于核电站、大型水坝、大型桥梁、高层建筑等重要工程项目.另外,采用结构动力分析方法进行抗震分析时,输入地震动时程非常关键.无论采用修正的天然地震波记录,还是取自场地地震安全性评估中的人造地震波,据此所做的抗震设计,严格地说它只反应所选择的地震动时程作用下结构抗震的可靠性.
反应谱法不能反映地震动的持时对结构地震反应的影响;而动力分析方法,虽然能反映地震动振幅、频谱、持时的影响,但即便用一组地震动时程进行抗震分析,据此抗震设计的结构,也可能经受不了另一些地震动的作用.为试图研究与解决上述问题,(张晓哲和罗奇峰,1999;张晓哲,2000;罗奇峰和张晓哲,2002;Luo and Li, 2004)提出并给出地震波的时-频反应谱.本文首先介绍时-频反应谱,在计算分析唐山地震天津波SN方向(记录台站为天津人民医院)、集集地震波SN方向(记录台站为南投Hsinjie中学)和汶川地震波EW方向(记录台站为卧龙)时-频反应谱的基础上(以下简称上述几条波为天津波SN、集集波SN和汶川波EW),提出归一化时-频反应谱概念,计算并分析了这三条典型地震波的归一化时-频反应谱.
2 时-频反应谱的提出加速度反应谱的计算公式为
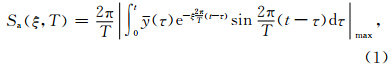
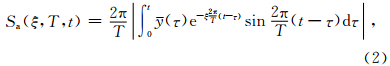
从定义可知,时-频反应谱是地震动三要素振幅、频谱和持时三者构成的空间三维谱,它同时反映了结构体系的地震反应随地震动周期和持续时间的变化.
张晓哲(2000)计算分析了美国El Centro地震记录的时-频反应谱,Luo和Li(2004)以及李仕栋(2004)提出了时-频反应谱标准化的概念,计算了美国El Centro等典型地震波地震记录的标准化时-频反应谱;采用推覆分析获得一榀六层框架模型的回复力曲线,并将该结构简化成单自由度弹塑性模型,提出结构损伤曲线的概念,将地震反应时程分析结果与时-频反应谱特性进行比较,研究结构破坏的机理,说明引入时-频反应谱的必要性.郭梦秋等(2004)计算了2001年云南施甸地区5.9级地震两个测点加速度记录的三个方向分量的时-频反应谱.黄俊杰(2004)对比了阻尼对时-频反应谱的影响,提出弹塑性时-频反应谱的概念和计算方法,计算了宁河波的弹塑性时-频反应谱,分析了屈服位移对弹塑性时-频反应谱的影响.车伟(2009)、Che和Luo(2010)利用汶川主震和集集地震某一台站的平动记录,分别合成了所在台站的地震转动分量,并计算了转动分量的时-频反应谱,也分析了结构转动破坏的损伤曲线,用时-频反应谱讨论结构破坏机理.邱志刚和罗奇峰(2014)根据 V2时-频反应谱定义“累计动能曲线”,然后结合结构振型质量参与系数,提出了地震动“潜在破坏能(PDE)”的概念,通过PDE定量地预测Northridge地震的三条近断层脉冲型地震记录和三条非脉冲型地震记录对12层RC框架结构的潜在破坏性.
3 几条典型地震波的时-频反应谱本文计算了天津波SN方向、集集波SN方向和汶川波EW方向的时-频反应谱,见图 1.由于集集波和汶川波持时较长,分别截取集集波SN地震动幅值较大的0~40 s的部分和汶川波EW地震动幅值较大的20~90 s的部分作为有效地震动持时.从图中可以看出三个地震波的时-频反应谱形状差异很大:天津波SN时-频反应谱成一喇叭状,拥有一个独立峰,沿时间轴连续,持时的尾部沿周期方向仍有一定宽度,显得底部宽阔厚实;集集波SN时-频反应谱成锯齿状,沿时间轴拥有数个大小不等排列紧凑的峰,但持时尾部沿周期方向分布较窄,成狭窄带状;汶川波EW时-频反应谱沿着持时方向排列着三个相互独立的峰,且峰的高度沿持时逐渐降低.
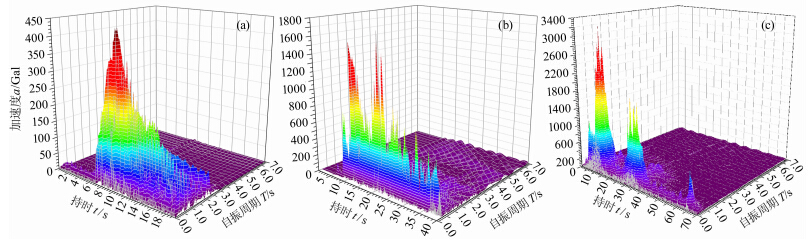 | 图 1 时-频反应谱(天津波SN、集集波SN、汶川波EW)Fig. 1 Time-frequency response spectrum(Tianjin NS,ChiChi NS and Wenchuan EW seismic waves) |
从图 1可以看出,由于不同地震波时-频反应峰值不同,坐标轴比例差异很大,为了让结果具有可比性,本文采用归一化处理方法.具体的归一法方法是:对不同地震波的时-频反应谱,除以其最大反应值,将所得结果称为归一化时-频反应谱,将这一计算称为时-频反应谱的归一化.为分析方便,本文绘出归一化时-频反应谱的等高线图,天津波SN、集集波SN和汶川波EW的归一化时-频反应谱及相应等高线图见图 2—图 4.
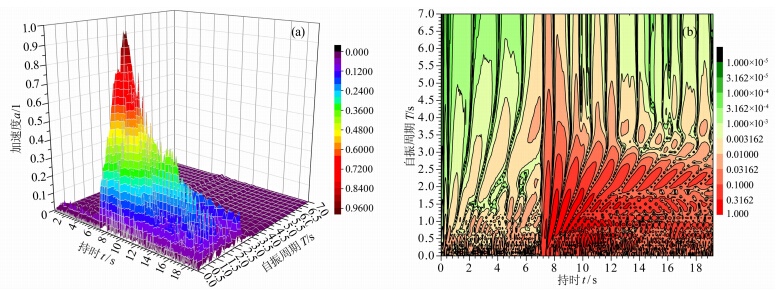 | 图 2 天津波SN归一化时-频反应谱 (a)三维图;(b)等高线图.Fig. 2 Normalized time-frequency response spectrum of Tianjin NS seismic waves (a)3D map;(b)Contour map. |
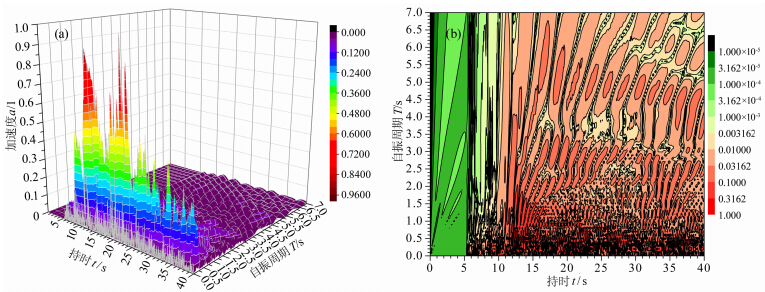 | 图 3 集集波SN归一化时-频反应谱 (a)三维图;(b)等高线图.Fig. 3 Normalized time-frequency response spectrum of ChiChi NS seismic waves (a)3D map;(b)Contour map. |
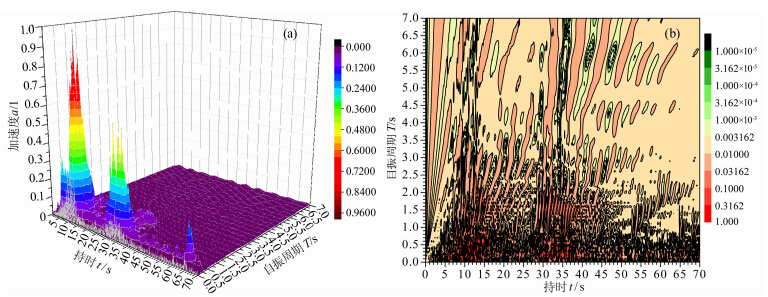 | 图 4 汶川波EW归一化时-频反应谱 (a)三维图;(b)等高线图.Fig. 4 Normalized time-frequency response spectrum of Wenchuan EW seismic waves (a)3D map;(b)Contour map. |
从图 2中可以看出虽然天津波SN持时只有19.19 s,但其归一化时-频反应谱峰值区域(颜色深红的部分)覆盖面积较大,基本覆盖了持时7.0~19.19 s自振周期0~2.7 s的区域.天津波SN时-频反应谱峰值区域有数个大小相近的一级二级峰脊几乎平行排列且排列紧凑.可以想象,持时7.0 s以前自振周期在各个范围的结构反应都很小,但从持时7.0 s开始结构自振周期在0~1.9 s之间的结构将连续遭遇时-频反应谱一级峰脊的冲击,对于强度中等的地震动输入,即使不发生倒塌破坏也极易发生塑性变形导致自振周期增加.自振周期发生改变的结构,在持时方向上仍将遭遇连续的二级和三级峰脊的冲击而发生严重破坏,最后一个很小的冲击都可能最终导致结构发生整体垮塌.
从图 3中可以看出截取的集集波SN持时仍长达40.0 s,但其时-频反应谱峰值区域覆盖面积却很狭窄(颜色深红的部分),除了持时12.0~16.0 s之间二级峰脊区域达到了自振周期1.9 s以外,基本覆盖了持时6.0~40.0 s和自振周期0~0.8 s的带状区域.可以想象,在遭受中等强度地震动输入时,对于自振周期0~0.8 s的结构,也可能进入塑性发生累积破坏;而对于自振周期在0.8~7.0 s的结构,则只会遭遇二级及以下峰脊,结构即使发生轻微破坏,也不会因进入后面很小的峰值区域而发生累积破坏.
从图 4中可以看出截取的汶川波EW持时长达70.0 s,其时-频反应谱峰值区域分为三个部分:持时8.0~16.0 s自振周期0~0.8 s之间的区域;持时29.0~38.0 s自振周期0~0.7 s之间的区域和持时64.5~65.5 s自振周期0~0.3 s之间的区域(颜色深红的部分).可以想象,在遭受中等强度地震动输入时,对于自振周期0~0.7 s的结构,有可 能进入塑性发生累积破坏;而对于自振周期在0.7~7.0 s 的结构,则只会遭遇三级及以下峰脊,结构不会发生破坏或仅可能发生轻微破坏.
5 12层框架结构的弹塑性时程分析反应谱理论不能反映结构在实际地震反应中可能出现的非弹性特性,也无法反映在实际地震作用过程中结构性能随时间的变化.在罕遇地震下,结构进入塑性阶段,地震动的持时特性显得愈发重要.Luo和Li(2004)、李仕栋(2004)将结构在地震力作用下从弹性阶段到破坏阶段自振周期的变化曲线定义为结构的损伤曲线.邱志刚和罗奇峰(2013)利用结构损伤曲线对某十层RC框架结构在地震动时频特性截然不同的两条地震波作用下的损伤机制进行了对比分析.
本文选取图 3集集波SN,并将峰值加速度调整为500 Gal(相当于8度罕遇水平),对12层钢筋混凝土框架结构进行弹塑性时程分析.计算模型为12层RC框架结构,柱脚假设理想固结于地面,首层高4.2 m,其余层高3.2 m,结构平面呈正方形,纵横向皆为三跨,边跨跨距5.8 m,中跨跨距3.4 m.柱截 面尺寸为550×550 mm,梁截面尺寸为300×600 mm,楼板板厚120 mm并考虑平面内刚度无限大.均采用C30混凝土,抗压强度fc=30.0 MPa,质量密度ρ=2.4 t/m3,弹性模量E0=30.0 GPa,泊松比υ=0.2,剪切模量G=12.5 GPa.配筋采用HRB335,抗拉强度fy=300.0 MPa,质量密度ρ=77.0 t/m3,弹性模量E0=200.0 GPa.
结构顶层角点的加速度时程曲线见图 5,从图中可以看到该点最大加速度反应发生在12.1 s,为-5.26 m·s-2,但此时结构并没有发生倒塌破坏.而在13.2 s,结构的加速度反应为-3.68 m·s-2,仅为最大加速度反应的70%,结构却发生严重破坏最终倒塌.这也说明了当结构反应进入塑性阶段,用反应最大值进行抗震设计存在一定局限性.
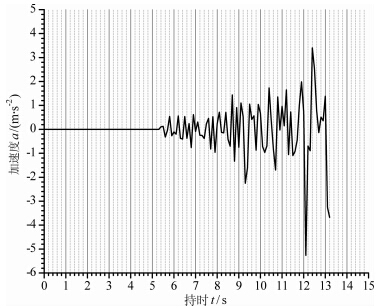 | 图 5 结构顶层角点加速度时程Fig. 5 Acceleration time history of structure-top corner |
为获得结构损伤曲线,本文采用文献(邱志刚和罗奇峰,2013)中的方法,根据不同时刻结构框架梁柱端点塑性铰的发展情况,修改相应位置处结构的等效部分固定弹簧刚度,进而获得不同时刻结构的 自振周期变化曲线.结构分别在时刻7.5、9.0、12.0 s和13.2 s的塑性铰发展情况见图 6.粉色代表铰屈服;深蓝色代表铰能力水平为直接使用;浅蓝色代表铰能力水平为生命安全;黄色(绿色)代表铰能力水平为防止倒塌,铰开始失去承载力.
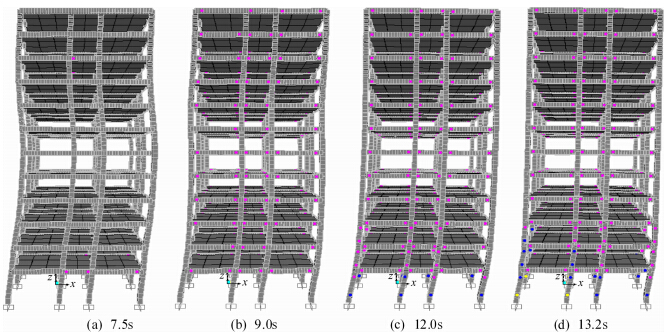 | 图 6 结构模型的塑性铰发展Fig. 6 Development of structure plastic hinge |
将计算得到的结构损伤曲线与集集波SN归一化时-频反应谱等高线图绘于图 7.可以看到,结构 自振周期在7.3 s至10.1 s之间跳跃较大,从1.41 s增加到了2.21 s,而结构损伤曲线此时却处于归一化时-频反应谱峰值较小的区域.这说明大震时结构延性耗能构件在地震持时开始阶段的较小地震动往复作用下就会进入塑性以增加结构的耗能能力,在地 震动反应峰值区域,结构的自振周期已经不同于弹性阶段的自振周期.
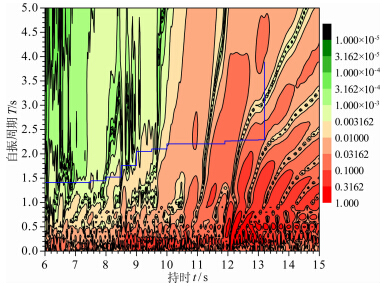 | 图 7 结构损伤曲线Fig. 7 Structural damage curve |
在12.1 s附近结构损伤曲线第一次到达归一化时-频反应谱峰值区域,结构自振周期有小幅上扬但增加不大.当结构损伤曲线到达13.2 s附近的第二个峰值区域时,结构自振周期阶跃到3.89 s,并在一个峰值较小的区域结构发生倒塌破坏.上述分析表明,通过结构损伤曲线与地震动的归一化时-频反应谱的对比可以分析结构破坏机理.
6 结论地震动持时对结构造成的累积破坏作用不容忽视,时-频反应谱是地震动振幅、频谱和持时三要素构成的空间三维谱,它同时反映地震动幅值在周期和持续时间上的变化.
本文在时-频反应谱的基础上,提出归一化时-频反应谱,并计算了我国三条典型地震记录的归一化时-频反应谱.通过分析对比可知,不同地震记录的时-频反应谱的幅值在时间和周期两个轴上的分布差别很大,具有不同时-频反应谱的地震波可能对结构地震响应产生不同影响.因此,对不同的结构应选取“适合”该类结构的地震记录进行抗震设计,否则结果将不太可靠.
对12层钢筋混凝土框架结构进行的弹塑性分析表明,强震作用下结构的自振周期会发生阶跃性增大,通过结构地震反应、结构损伤曲线与输入地震动的归一化时-频反应谱对比,结构最大反应并不一定是造成结构倒塌的直接原因,用结构弹性阶段反应最大值进行抗震设计的反应谱理论存在一定局限性.研究结果表明,归一化时-频反应谱能有效用来分析地震动工程特性与结构破坏机理,值得深入研究.
| [1] | Bommer J J, Magenes G, Hancock J, et al. 2004. The influence of strong-motion duration on the seismic response of masonry structures. Bulletin of Earthquake Engineering, 2(1):1-26. |
| [2] | Che W. 2009. Study on Seimic Input Parameters for Long-Span Bridge (in Chinese)[Ph. D. thesis]. Shanghai:Tongji University. |
| [3] | Che W, Luo Q F. 2010. Time-frequency response spectrum of rotational ground motion and its application. Earthquake Science, 23(1):71-77. |
| [4] | Du X L, Liu Y S. 1992. Influence of strong motion duration on accumulated seismic damage of RC structures. Earthquake Engineering and Engineering Vibration (in Chinese), 12(3):65-70. |
| [5] | Guo M Q, Wang B, Cui J W. 2004. Temporal-frequency response spectra analysis of observed strong ground motion data for Shidian Ms5.9 earthquake. Journal of Seismological Research (in Chinese), 27(3):237-240. |
| [6] | Hu Y X. 2006. Earthquake Engineering (in Chinese). Beijing:Seismological Press. |
| [7] | Huang J J. 2006. Elastoplastic time-frequency response spectrum and time-frequency response spectrum analysis method in structural dynamic analysis (in Chinese). Shanghai:Tongji University. |
| [8] | Li S D. 2004. Preliminary study on time-frequency response spectrum analysis method of seismic waves (in Chinese)[Master's thesis]. Shanghai:Tongji University. |
| [9] | Luo Q F, Zhang X Z. 2002. Temproal-frequency response spectrum analysis method of strong ground motion.//Proceedings of the 9th Science Conference of Seismological Society of China (in Chinese). Beijing:Seismological Press. |
| [10] | Luo Q F, Li S D. 2004. Time-frequency response spectrum analysis of seismic wave.//Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver B. C., Canada. |
| [11] | Qiu Z G, Luo Q F. 2013. Application of normalized time-frequency response spectrum and structural damage curve. Journal of Southeast University (Natural Science) (in Chinese), 43(1):165-168. |
| [12] | Qiu Z G, Luo Q F. 2014. Potential damage energy analysis for pulse-like ground motions. China Civil Engineering Journal (in Chinese), 47(12):56-63. |
| [13] | Safak E, Franke A. 1995. Structural response to 3D simulated earthquake motions sciences valley. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 32(6):2820-2839. |
| [14] | Shen Z Y, Wu A H. 2007. Seismic analysis of steel structures considering damage cumulation. Frontiers of Architecture and Civil Engineering in China, 1(1):1-11. |
| [15] | Sheng M Q, Luo Q F. 2008. Comparison of hysteretic energy spectra in Northridge and Chichi earthquake. Journal of Tongji University (Natural Science) (in Chinese), 36(10):1314-1319. |
| [16] | Xie L L, Ma Y H. 2003. The development process of the modern earthquake resistant design theory. Recent Developments in World Seismology (in Chinese), 27(10):1-8. |
| [17] | Zhang X Z, Luo Q F. 1999. Temproal-frequency response spectrum analysis of earthquake acceleration. Structural Engineers (in Chinese), Supplement. |
| [18] | Zhang X Z. 2000. Preliminary Study on Time-frequency Response Spectrum Analysis Method of Seismic Waves in Anti-seismic Theory of Structures (in Chinese)[Master's thesis]. Shanghai:Tongji University. |
| [19] | 车伟.2009. 大跨度桥梁结构地震动输入参数的若干问题研究[博士论文]. 上海: 同济大学. |
| [20] | 杜修力, 刘勇生. 1992. 强震持时对钢筋混凝土结构地震累积破坏的影响. 地震工程与工程振动, 12(3): 65-70. |
| [21] | 郭梦秋, 王彬, 崔建文. 2004. 施甸5. 9级地震强震观测资料的时-频反应谱分析. 地震研究, 27(3): 237-240. |
| [22] | 胡聿贤. 2006. 地震工程学. 北京: 地震出版社. |
| [23] | 黄俊杰. 2006. 弹塑性时频反应谱和动力分析的时频反应谱法[硕士论文]. 上海: 同济大学. |
| [24] | 李仕栋. 2004. 地震波时频反应谱分析方法的初步研究[硕士论文]. 上海: 同济大学. |
| [25] | 罗奇峰, 张晓哲. 2002. 强震地面运动的时-频反应谱的分析方法. //中国地震学会第九次学术大会论文摘要集. 北京: 地震出版社. |
| [26] | 邱志刚, 罗奇峰. 2013. 归一化时-频反应谱与结构损伤曲线的应用. 东南大学学报(自然科学版), 43(1): 165-168. |
| [27] | 邱志刚, 罗奇峰. 2014. 脉冲型地震动的潜在破坏能分析. 土木工程学报, 47(12):56-63. |
| [28] | 盛明强, 罗奇峰. 2008. Northridge与ChiChi地震滞回耗能谱的比较. 同济大学学报(自然科学版), 36(10): 1314-1319. |
| [29] | 谢礼立, 马玉宏. 2003. 现代抗震设计理论的发展过程. 国际地震动态, 27(10): 1-8. |
| [30] | 张晓哲, 罗奇峰. 1999. 地震加速度时-频反应谱分析. 结构工程师, 增刊. |
| [31] | 张晓哲. 2000. 结构抗震理论中地震波时-频反应谱分析方法的初步研究[硕士论文]. 上海: 同济大学. |
 2015, Vol. 58
2015, Vol. 58

