地球物理学报  2015, Vol. 58 Issue (4): 1135-1144   PDF    
引用本文
詹金刚, 王勇, 史红岭, 柴华, 朱传东. 2015. 应用平滑先验信息方法移除GRACE数据中相关误差. 地球物理学报, 58(4): 1135-1144, doi: 10.6038/cjg20150404   
ZHAN Jin-Gang, WANG Yong, SHI Hong-Ling, CHAI Hua, ZHU Chuan-Dong. 2015. Removing correlative errors in GRACE data by the smoothness priors method. Chinese J. Geophysics, 58(4): 1135-1144, doi: 10.6038/cjg20150404   
应用平滑先验信息方法移除GRACE数据中相关误差
詹金刚1, 王勇1, 史红岭1, 柴华1, 朱传东1,2    
1. 中国科学院测量与地球物理研究所 大地测量与地球动力学国家重点实验室, 武汉 430077;
2. 中国科学院大学, 北京 100049
投稿时间:2014-04-28    最后修改时间: 2015-03-05 .
基金项目：国家自然科学基金项目(41321063,41274084,40974044,41174064,41374086),中国科学院国家外专局国际合作创新研究团队计划(KZZD-EW-TZ-05),大地测量与地球动力学国家重点实验室项目(SKLGED2013-6-1-Z)资助.
作者简介：詹金刚,男,1972年生,副研究员,主要从事卫星重力数据处理及应用.E-mail:zjg@whigg.ac.cn
通讯作者：王勇,男,1964年生,研究员,主要从事地球重力场解释及应用研究.E-mail:yang@whigg.ac.cn
摘要：由于GRACE卫星数据解算的时变重力场模型中高阶位系数存在误差,这些误差在重力异常图中表现为南北向的条带噪声,在应用GRACE时变重力场数据时必须进行滤波.本文在空间域引入了一种有效消除GRACE时变重力场条带噪声的平滑先验信息方法,并将其与目前常用的高斯滤波和去相关误差等滤波方法分别应用于合成的质量变化趋势数字模型,检测不同滤波方法消除条带噪声的能力及其对真实信号的影响.滤波结果显示,与目前常用的高斯滤波和去相关误差滤波器相比,本文滤波方法在有效移除条带噪声的同时,具有有效信号幅度衰减小、有效信号形变小以及保存了更多的短波长细节信息等优势;此外,统计结果显示,本文滤波结果在信号最大值、最小值以及残差均方根等方面均与模拟真实信号最为接近.相比300 km高斯平滑和组合滤波结果,有效信号振幅的极小值和极大值分别提高了约18%和6%,残差均方根分别降低了25%和33%.说明本文滤波方法移除GRACE相关误差的同时,在保留有效信号方面具有明显的优势.
关键词： GRACE时变重力场     平滑先验信息方法     相关误差    
Removing correlative errors in GRACE data by the smoothness priors method
ZHAN Jin-Gang1, WANG Yong1, SHI Hong-Ling1, CHAI Hua1, ZHU Chuan-Dong1,2    
1. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China
Abstract: The errors, which are present in short wavelength components of time-variable gravity solutions produced by the Gravity Recovery and Climate Experiment (GRACE) satellite, manifest themselves in maps of gravity change as long, linear features generally trending in north-south (i.e., stripes). Thus, filtering is needed to remove them before using the GRACE time-variable gravity solutions. Here, we introduce a smoothness priors method to remove such stripe errors with application to a synthetic mass change model and show significant effects. The method used in this paper is based on the smoothness priors approach and operates like a time-varying finite impulse response high-pass filter. In this paper, the correlative errors in maps of GRACE mass variation are regard as the high frequency signals varying with longitude reserved when the data is filtered, then we subtract them from the original data to get the filtering result. In order to examine the effect of the filter, we generate a model consisting of two parts:'true' geophysical signals and stripe noise. First, following the approaches of Duan et al., we construct a numerical model of mass change trend composed of the NOAH GLDAS model between the latitudes of ±60°, a surface mass change rate corresponding to the gravity variation of a PGR model based on the RF3L20 ice model over Canada and the GRACE mass variation trend over the Arctic and Antarctic areas (90°S—60°S, 60°N—90°N). We use this numerical model as the 'true' geophysical signal of mass change. In addition, we also need a north-south 'stripe' model similar to that in GRACE data to test the effect of the filter and its signal distortion. The stripe model is constructed using the difference between the GRACE monthly time-variable gravity solutions and the filtered field. Its amplitude is reduced to be comparable with that of the numerical mass change trend model. The filtered field is computed using the algorithms of Swenson and Wahr and an isotropic Gaussian filter of radii 300 km. Finally, we apply the smoothness priors method (SPM) to the model to test the effect of the filter. As a comparison, we use the filter of correlated errors (for A=30, K=10), the Gaussian filter of smoothing radius 300 km, the combination of above two methods, as well as the SPM filter to the synthetic model, respectively. To conform with the processing of GRACE data, we transform the mass change of the synthetic model into Stokes coefficients when applying the correlated error filter and Gaussian smoothing, then transform them back to mass change.Compared with other filtered results above mentioned, the result of SPM shows a better signal-to-noise ratio, though a few of slight stripes appearing in the Pacific Northwest. We find that our result has the advantages of less reducing the signal magnitudes, preserving more details of short wavelength components and less signal distortion. For example, the magnitude of the signals at high latitudes such as the positive signals in the Antarctic and southern Chile are not obviously reduced. Some short wavelength components such as the positive signal in middle America and the negative signal in the Jan Mayen Island are also preserved in the filtered result. The positive signal in eastern Brazil is also not distorted compared with the other results.The grid statistic results show that the minimum value and maximum value of the results using the method of Gaussian filtering and the combination method of Gaussian filtering and correlative errors filter are -6.78 cm, 11.06 cm, -6.53 cm and 11.10 cm, respectively. Compared with the 'true' values of -11.45 cm and 13.15 cm, this result shows that the magnitudes of the negative signal are sharply reduced when using the two kinds of filters. Their RMS values are also reduced from 1.448 cm to 1.231 cm and 1.196 cm, respectively. All these statistic data indicate that we have applied a stronger filter on the synthetic field. Compared with the results of the three methods above mentioned, the grid statistics of SPM approach shows a better result. Its minimum value, maximum value and the RMS of the grid statistics are -8.81 cm, 11.88 cm and 1.371 cm, respectively, which are most close to the true values among the filtered results.The smoothness priors method operates like a time-varying finite impulse response high-pass filter, and shows remarkable effect in removing the GRACE stripe noise. The advantage of this filter is that it has less reduction in magnitude of signals and preserves more details of short wavelength components in the filtered field. Another advantage of it is that the filter is flexible in use.
Key words: GRACE time variable gravity     Smoothness priors method     Correlated errors    

1 引言

地球重力场变化反映了地球表层及内部物质分布及运动状态.研究地球的物理环境及其变化等重要信息，可为人类认识和利用自然资源、减轻环境灾害等问题提供重要的依据. 近十年来，随着卫星重力测量技术的成熟发展，为人们研究全球重力场变化和全球环境随时间变化信息提供了契机.尤其是GRACE卫星重力获得的全球重力场随时间变化信息，为定量探测和研究地球物理环境乃至全球环境变化信息(海平面与环流变化、冰川消融、陆地水量变化、强地震及极端气候等)提供了独特的、不可替代的观测资料.

由每月的GRACE重力卫星资料可以解算得到每个月的重力场模型，利用多个月的重力场模型数据减去其均值就可以得到相应时期的重力场变化信息.由于目前解算的GRACE月重力场模型中高阶位系数仍存在着较大的误差，这些误差在重力异常图中表现为严重的南北向条带噪声(如图 1所示)，给地球物理信号的识别带来一定的困难，因此必须进行滤波提高信噪比.起初，由于GRACE卫星重力资料解算得到的时变重力场的精度较差以及资料积累的周期较短，人们主要利用GRACE资料验证和研究地表质量迁移在大尺度上的季节变化信息(Chambers et al., 2010; Velicogna et al., 2012;Wahr et al., 1998，2004;Wouters et al., 2011;钟敏等，2009; 胡小工等，2006;汪汉胜等，2007;彭鹏等，2013).随着利用GRACE资料恢复重力场方法的改进和滤波技术的进一步提高，目前由一个月的GRACE重力卫星资料反演大地水准面的精度在400 km尺度上已达到1~2 cm(鄂栋臣等，2009；许厚泽等，2012；李琼等，2013；冯伟等，2012；周新等，2011；詹金刚等，2011；Wang et al., 2012).随着观测资料的积累，越来越多的学者把研究的重点放在局部地区时变重力场的变化，探讨其变化的可能原因及机制.这就需要在GRACE数据后处理中寻求更为合适有效的滤波技术，在有效滤去条带噪声的同时提高信噪比，防止因滤波方法不当导致的局部地区信号形变，减少对短波长细节特征信息的损失.

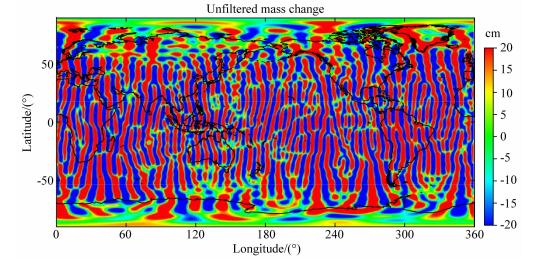图 1 GRACE时变重力场变化(等效水柱高) Fig.1 GRACE time-variable gravity field(Equivalent Water Column)

目前，针对消除GRACE条带误差的常用处理方法按照其滤波思想主要分为两类：一类是通过引入滤波因子降低模型高阶次位系数的权重，从而达到减少条带噪声的目的.这类滤波方法的典型代表是高斯滤波器(Jekeli，1981).起初，Wahr 等(1998)注意到在计算大地水准面异常时，系数中的误差会随着模型阶l的递增而被放大2l+1倍，进而采取引入高斯核函数的方法降低模型高阶位系数的权重以达到滤波的效果.随后，许多学者依此思想提出了诸如最优滤波、扇形滤波及非对称高斯滤波等方法(Sasgen et al., 2006;Chen et al., 2006;Klees et al., 2008; Kusche，2007; Zhang et al., 2009; Han et al., 2005;Guo et al., 2010).这类方法的核心思想是通过降低模型高阶次位系数的权重以减少短波长分量中误差的影响，从而达到降低条带噪声的效果，其实质是以牺牲模型的空间分辨率为代价换取空间结果的平滑效果.其缺点是滤波半径越大，模型的空间分辨率损失也越大，相应的一些短波长信息丢失越多.

另一类滤波方法是去相关误差滤波.Swenson和Wahr(2006)注意到，由GRACE时变重力场计算得到的重力异常图中条带噪声在空间上具有一定的相关性，从而推断条带误差空间上的相关性是由模型中某些位系数间的相关性引起的，进而通过滑动窗多项式拟合这些系数间的相关误差并将其扣除，从而达到滤波的目的.Chambers(2006)和Chen等(2007)根据自己的研究区域和目的采取了不同阶的多项式拟合方法消除相关误差而没有采用滑动窗技术.Duan等(2009)在Swenson的基础上提出了更为精细的去相关误差滤波技术，主要区别是根据模型中球谐系数误差的分布特点采用了更为复杂的窗宽选取技术.詹金刚等(2011)也提出了相关误差的改进方法.这类滤波方法的核心思想是利用多项式拟合某些球谐系数间的相关误差并将其扣除，缺点是该方法在赤道附近区域滤波效果不甚理想，并且在高纬度地区可能会导致一些短波长信息的形变和丢失.此外，也有一些学者利用基于协方差矩阵的正交函数分析(EOF)技术和球面小波滤波方法来消除条带噪声并取得不错的效果(Wouters and Schrama， 2007;Schmidt et al., 2006).但是这些方法的实现过程过于复杂，从而限制了这些方法的进一步应用.

GRACE相关误差在空间上表现为南北向的条带噪声，这些条带噪声随经度变化呈现一定的周期特性.本文根据条带噪声在空间上具有周期性这一特性，利用时变高通滤波器将其进行分离并移除，从而实现滤波的目的，该方法对于分离具有周期特性的高频噪声效果特别显著.最后，我们将此滤波方法与高斯滤波器、去相关误差滤波器以及高斯滤波与去相关误差滤波相结合的组合滤波技术进行比较，将各滤波器分别应用于同一个合成数字模型，比较不同滤波器的滤波效果及其对有效信号的形变.滤波结果显示本文滤波方法不仅具有良好的去条带误差效果，而且在保留有效信号，特别是短波长细节信息方面具有明显的优势，统计结果表明本文滤波方法在最大值、最小值以及残差均方根等方面均显示与模拟真实信号统计结果最为接近. 2 理论方法

对于任意时间序列 z，可表示为：

其中，n为采样点个数. z 可看作由近似稳态的周期分量和低频的非周期性的趋势项两部分组成：

其中， z stat表示近似稳态的高频周期分量， z trend表示低频的非周期性的趋势分量.低频非周期成分可由(3)式拟合

其中， H ∈Rn×m叫做观测矩阵， θ ∈Rm为回归参数，m是回归参数的个数，ε为观测误差.接下来的工作是如何按照一定的推估准则来估计回归参数，常用的方法是利用最小二乘准则来估计这些回归参数，这里采用更为一般的正则化最小二乘准则方法求解回归参数的估计值

其中，λ是正则化参数， D d为第d次导数操作的离散逼近.很显然，方程(4)是在普通最小二乘方法的基础上增加了一个条件，属于条件极值问题.极值条件的目的是使方程(4)的解在满足‖ Hθ － z ‖取得极小值的同时，使得‖ D d(Hθ)‖取值也尽可能小.这样就可以在推估线性项 Hθ 的过程中，加入一些已知的先验信息.方程(4)的解可表示为

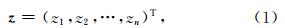
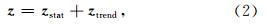
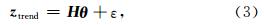
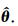
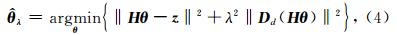
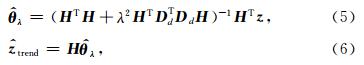
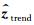其中，为低频非周期分量的估计值.观测矩阵 H 的选择可以包含时间序列 z 的一些已知信息，例如使用一些高斯型函数或三角函数，这里选取单位阵 I 作为观测矩阵，即 H = I ∈Rn×n，详细参见Karjalainen(1997).方程(4)中正则化部分可以理解为求解正则化矩阵 D d零空间里的解，二阶差分矩阵的零空间包含了所有的一阶曲线，因此，D 2是用来估计低频非周期项的一个不错的选择(Tarvainen et al., 2002; Karjalainen，1997).二阶差分矩阵 D 2∈R(n－2)×n形式如下：

有了这些特殊选择后，该方法称为平滑先验信息方法(Gersch，1991).

这样，高频周期噪声可以表示为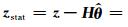=(I －(I +λ2 D2 T D 2)－1)z .对于高频周期噪声来讲，滤波器 L = I －(I +λ2 D2 T D 2)－1 相当于一个时变高通滤波器，实现高频噪声与低频非周期项的分离. 3 平滑参数的选择

正如Tarvainen等(2002)所讲，该滤波器的最大优点是其频率响应的调整仅依赖于一个平滑参数λ，使用起来非常简单.选取不同的平滑参数可以得到不同性能的滤波器，分别对不同的滤波器进行傅里叶变化，并取其3 dB截止频率，可以得到不同平滑参数对应的截止频率变化示意图.图 2给出了不同平滑参数对应的截止频率变化曲线，例如，λ=1，2，4，10，20，50，300时，对应的截止频率分别是0.189、 0.132、 0.093、 0.059、 0.041、 0.025 Hz和0.011 Hz(对应1 Hz采样频率).

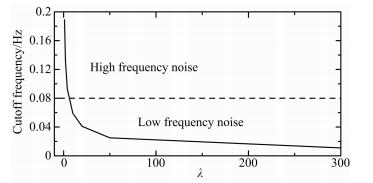图 2 平滑参数与截止频率变化关系曲线(3 dB截止频率) Fig. 2 The relationship between the cutoff frequency and smoothing parameter(λ)

如果从图 1中沿纬度带比如沿赤道方向任意截取一剖面，可以发现质量异常中噪声信号随经度的变化呈显著的周期特性.如图 3所示，真实的地球物理信号完全被高频的周期噪声所淹没，其归一化功率谱如图 4所示，归一化功率谱的能量主要集中在频率大于0.08 Hz的频率段.因此，如果认为频率大于0.08 Hz的信号主要为高频噪声并将其从质量异常变化信号中移除，那么就应该设计一个截止频率为0.08 Hz的滤波器.这样，频率大于0.08 Hz的高频信号就会被分离出来，从而留下有用信号.根据图 2曲线，平滑参数λ的取值约为6.平滑参数的选择可以根据个人不同的滤波目的和滤波效果做适当的调整，平滑参数取值越大，滤波结果就越平滑.图 3中蓝线为质量异常变化剖面的滤波结果，从图中可以明显看出，滤波之后高频噪声显著下降.

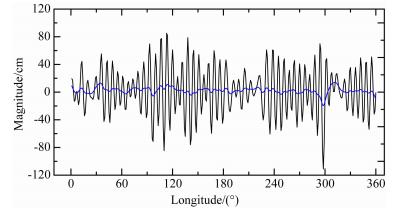图 3 质量异常沿赤道剖面变化(黑线)及其滤波后的低频分量(蓝线) Fig. 3 The mass variation along the profile of equator(black line) and the low frequency aperiodic component(blue line)

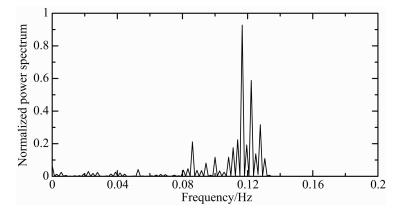图 4 沿赤道剖面质量异常变化的归一化功率谱 Fig. 4 The normalized power spectrum of mass variation along the profile of equator

按照这种准则，本文根据条带噪声空间分布的频率特性，将全球质量异常变化简单地分为几个区 域分别进行滤波，即平滑因子λ在90°S—50°S、50°S—30°S 以及30°S—0°区域的取值分别为30、10和6.因条带噪声在北半球具有类似的特征，因而平滑因子λ在北半球地区的取值与南半球的取值方法类似. 4 滤波结果与信号评估

Swenson和Wahr(2006)指出，去相关误差滤波方法会对高纬度地区的信号产生一定的影响，特别是一些短波长信号有可能会被移除.因为全球质量异常变化趋势在两极高纬度地区具有足够明显的信号，便于比较不同滤波方法对高纬度地区信号的影响.因此，本文采用全球质量异常变化趋势数字模型作为滤波对象.按照Duan等(2009)所述方法，在纬度为±60°范围内，全球质量异常变化趋势数字模型数据主要由2003年1月至2010年12月间土壤湿度模型GLDAS资料获得(Rodell et al., 2004)，在两极的高纬度地区，数字模型数据主要由GRACE时变重力场以及RF3L20冰后回弹模型资料计算得到(汪汉胜等，2009).模拟的全球质量异常变化趋势如图 5a所示，在本文中作为输入的真实地球物理信号.

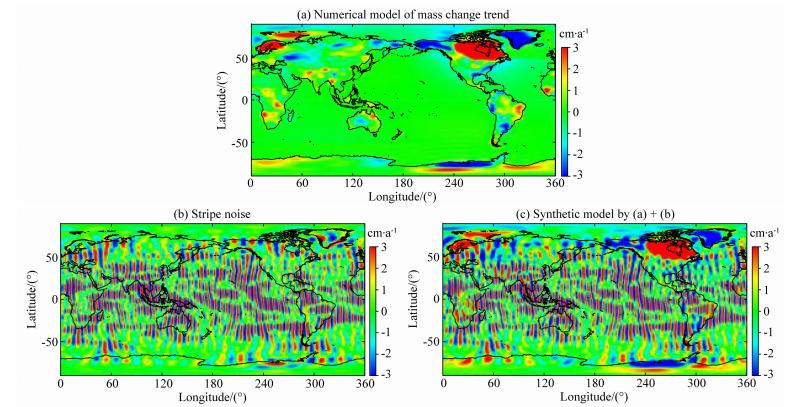图 5 质量变化模拟模型：(a)质量变化趋势模型;(b)条带误差模型;(c)合成模型(a)+(b) Fig. 5(a)The numerical model of mass change trend;(b)The stripe noise model;(c)Synthetic model by(a)add(b)

此外，我们还需要模拟GRACE时变重力场中南北向的条带噪声，以检测滤波器消除条带噪声的能力及其对有效信号的影响.由于模拟真实信号为质量异常变化趋势，因此，条带噪声模型的变化幅度也应该和GRACE质量异常变化趋势中条带噪声的幅度变化相一致.本文条带噪声模型由GRACE月时变重力场模型系数减去模型滤波之后的系数并进行适当缩放得到，滤波方法采用300 km高斯平滑和去相关误差滤波相结合的组合滤波技术.首先，由每个月的GRACE时变重力场模型在不经过任何滤波的情况下直接计算得到月质量异常变化，再由月质量异常变化时间序列采用最小二乘拟合技术得到质量异常年变化趋势.对比月质量异常变化与质量异常年变化趋势的量级可以发现，月质量异常中条带噪声变化的量级约为后者的10倍，为使两者条带变化的幅度相一致，本文在解算时将月条带噪声的振幅缩小了1/5.模拟的条带噪声模型如图 5b所示，图 5c为合成的全球质量变化趋势图，即由图 5a加上图 5b得到.本文以此数字模型作为滤波对象，比较不同滤波方法间的差异.

实际上，目前对于GRACE时变重力场数据滤波效果的评判，并没有一个公认的准则.虽然信号的均方根在一定程度上可以反映滤波器移除条带噪声的能力，但是并不能揭示滤波器对真实信号的影响或者真实信号有多大程度保留下来.这里，我们将不同滤波方法直接应用于一个合成的全球质量变化模型中，以此检验不同滤波方法对有效信号的直接影响.以滤波结果中有效信号的保留程度、有效信号的形变情况以及滤波结果及其与真实信号残差的均方根等统计结果作为滤波效果的评价准则.

作为对比，本文将去相关误差滤波方法、300 km 高斯平滑滤波技术、去相关误差滤波和300 km高斯平滑技术相结合的组合滤波方法以及本文滤波方法四种滤波技术分别应用于合成的质量异常变化数字模型，比较不同滤波结果之间的差异.滤波结果如图 6所示.

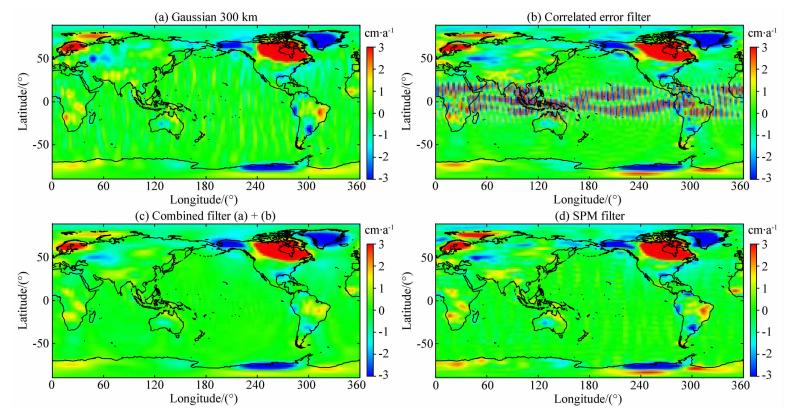图 6 不同滤波方法结果比较
(a)300 km高斯平滑；(b)去相关误差滤波；(c)去相关误差滤波及300 km高斯平滑相结合组合滤波；(d)SPM滤波. Fig. 6 Results by applying different filters on the synthetic model
(a)The Gaussian filter with a smoothing radius of 300 km;(b)The correlated error filter; (c)A 300 km Gaussian smoothing after the correlated error filter;(d)The SPM filter.

图 6a为300 km高斯平滑结果.从图中可以看出，除太平洋地区仍具有较为严重的条带噪声外，陆地上大部分地球物理信号已逐渐显露出来.与模拟真实信号相比，在高纬度地区有效信号的振幅大大削弱，如俄罗斯远东地区的2个负信号、南极地区以及智力南部地区正信号的振幅经滤波之后明显减小.在中纬度地区如非洲北部和我国青藏高原南部等地区，一些短波长信号的形态发生改变，甚至存在信号分裂现象.此外，高纬度地区一些短波长信号在滤波之后消失，如北美洲中部地区的一个正信号以及扬马延岛地区的负信号在滤波结果中被移除.这主要是因为高斯滤波器消除条带噪声的核心思想是通过降低GRACE时变重力场中高阶次位系数的权重来实现，这种方法实际上极大地降低了模型的空间分辨率.

图 6b为去相关误差滤波结果.从图中可以看出，条带噪声在中高纬度区域得到极大的压制，而在赤道附近区域滤波效果不明显.滤波结果与真实模拟信号相比，中高纬度地区一些短波长信号的幅度明显减小，而且在格陵兰地区信号存在明显的泄露.此外，我们发现滤波结果中扬马延岛地区的一个小的负信号被移除，并且出现了幅度为正的假信号等.

图 6c为去相关误差滤波和300 km高斯平滑组合滤波结果.从图中可以看出，该方法滤波结果与模拟数字模型相比，条带噪声显著降低，信噪比得到很大提高.缺点是该组合滤波方法与高斯滤波和去相关误差滤波方法类似，具有在高纬度地区信号的振幅明显减弱，一些短波长信息在滤波之后消失，在中纬度地区一些短波长信号出现分裂和形变等现象，例如巴西中部地区存在明显的正信号分裂和形变.

图 6d为本文平滑先验信息空间滤波结果.从图中滤波结果可以明显看出，除太平洋西北部区域具有轻微的条带噪声外，其他地区的条带噪声均得到有效移除并具有较好的信噪比.与上面三种滤波结果相比，本文滤波结果具有有效信号幅度衰减小、较小的信号形变以及保留更多的短波长信号细节信息等优点.例如，滤波结果中有效信号的振幅在诸如南极地区以及智利南部等高纬度地区并没有明显的衰减；一些短波长信息如北美洲中部地区的正信号及扬马延岛地区的负信号在滤波结果中得以保留；在巴西以及非洲中部地区的正信号没有出现明显的信号形变和分裂等现象.

表 1是不同滤波方法得到的质量异常变化结果以及模拟的全球质量异常变化格网统计结果.从表 1中可以看出，模拟真实信号的振幅最小值和最大值分别为-11.45 cm和13.15 cm，格网均方根为1.448 cm.去相关误差滤波结果显示，有效信号振幅的最小值和最大值分别为-11.53 cm和11.69 cm，接近于模拟真实信号的振幅.但是，其格网统计结果的均方根为1.727 cm，远大于真实模拟信号的均方根，这说明在滤波结果中仍存在严重的条带噪声.

表 1 质量变化趋势模拟信号及其经不同滤波 方法后的格网统计结果(单位: cm) Table 1 The grid statistics results of the numerical mass change trend model and the filtered mass change results by applying different filter on a synthetic mass change model(Unit: cm)

模型经300 km高斯平滑滤波后，有效信号振幅的最小值和最大值分别减小为-6.78 cm和11.06 cm，分别占实际信号的59.2%和84.1%.其格网统计结果显示均方根减小为1.231 cm，占实际信号均方根的 85.0%.而组合滤波方法统计结果显示，有效信号振幅的最小值和最大值分别减小为-6.53 cm和11.10 cm，分别占实际信号振幅的57.0%和84.4%，格网均方根减小到1.196 cm，占实际信号均方根的82.6%.这些统计数据表明在滤波时使用了较强的滤波器，导致有效信号的振幅显著削弱，降低了有效信号的空间差异性.

模型经本文平滑先验信息滤波后，有效信号振 幅的最小值和最大值分别为-8.81 cm和11.88 cm，分别占真实信号振幅的76.9%和90.3%，振幅极小值和极大值较300 km高斯平滑及组合滤波技术分别提高了约18%和6%.滤波后有效信号的格网均方根为1.371 cm，占实际信号格网均方根的94.6%，较高斯滤波和组合滤波结果分别提高了9.4%和12%.

表 2是不同滤波方法得到的质量异常变化结果与模拟的真实全球质量异常变化之差的残差格网统计结果.从表 2中可以看出，相比其他三种滤波残差结果，本文滤波结果得到的残差值，其最小值、最大值以及残差的格网均方根分别为-3.40 cm、4.79 cm和0.417 cm，均为相应残差统计结果中的最小值.上述统计结果表明本文平滑先验信息滤波方法结果更接近模拟的实际信号.

表 2 不同滤波结果与模拟的无噪声全球质量 异常变化之差的格网统计结果(单位: cm) Table 2 The grid statistics results of the difference between the different filtering results and the numerical mass change trend model(Unit:cm)
5 结论

本文引入了一种在空间域移除GRACE时变重力场条带误差的滤波方法，并详细介绍了其滤波原理及平滑参数的选择.该方法主要用于分离具有周期特性的高频噪声信号特别有效，因而对于具有非周期特性的有效信号滤波效果甚微.本文正是利用该滤波器的这一特性，根据GRACE时变重力场条带误差在空间上沿纬度线方向恰好具有显著周期性的特点，将该滤波方法应用于GRACE时变重力场数据后处理，并取得了较为理想的滤波效果.

为验证本文滤波方法在处理GRACE数据中的滤波效果及其对有效信号的形变，我们将高斯平滑滤波、去相关误差滤波、高斯平滑与去相关误差滤波相结合的组合滤波技术以及本文空间滤波方法，分别应用于合成数字模型，以检验各滤波方法消除条带误差的能力及其对有效信号的影响.

滤波结果表明300 km高斯滤波以及组合滤波技术表现出过强的滤波效应，导致有效信号的幅度大大降低，其中，有效信号的极小值和极大值分别减少约40%和16%；其次，这两种滤波方法还会导致高纬度地区某些短波长信息的丢失以及中纬度地区某些短波长信号的分裂.这主要是因为高斯滤波器的实质是通过牺牲模型的空间分辨率来换取空间平滑的效果.

去相关误差滤波方法在高纬度地区去相关误差效果明显，信号的幅度衰减较小，但是对短波长信息可能会产生一定的影响，如扬马延岛地区的负信号变成了正信号；其次，该方法在赤道区域去相关误差效果不甚理想，表现为条带现象依然严重.使用该滤波方法的前提是需要知道哪些系数间具有相关误差，而目前对于赤道附近区域产生条带噪声的认识显然还不十分清楚.

相比上述三种滤波结果，本文滤波结果更为合理.表现为去条带噪声效果显著，滤波后有效信号幅值的衰减显著降低，滤波结果中保存了更多的短波长细节信息.如北美洲中部地区的正信号及扬马延岛地区的负信号在滤波结果中得以保留，巴西以及非洲中部地区的正信号没有出现明显的信号形变和分裂现象.这主要是因为平滑先验信息滤波方法主要用于分离具有周期特性的高频信号，而对于不具有周期特性的真实信号影响甚微.该滤波方法的另一个优点就是其使用非常简单，滤波器的频率响应仅需调整一个滤波参数.

参考文献
[1] Chambers D P. 2006. Evaluation of new GRACE time-variable gravity data over the ocean. Geophysical Research Letters, 33:L17603, doi:10.1029/2006GL027296.
[2] Chambers D P, Wahr J, Tamisiea M E, et al. 2010. Ocean mass from GRACE and glacial isostatic adjustment. Journal of Geophysical Research:Solid Earth (1978—2012), 115(B11).
[3] Chen J L, Wilson C R, Seo K W. 2006. Optimized smoothing of Gravity Recovery and Climate Experiment (GRACE) time-variable gravity observations. Journal of Geophysical Research:Solid Earth (1978—2012), 111(B6), doi:10.1029/2005JB004064.
[4] Chen J L, Wilson C R, Tapley B D, et al. 2007. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophysical Research Letters, 34(13):L13302, doi:10.1029/2007GL030356.
[5] Duan X J, Guo J Y, Shum C K, et al. 2009. On the postprocessing removal of correlated errors in GRACE temporal gravity field solutions. Journal of Geodesy, 83(11):1095-1106.
[6] E D C, Yang Y D, Chao D B. 2009. The sea level change from the Antarctic ice sheet based on GRACE. Chinese J. Geophys. (in Chinese), 52(9):2222-2228, doi:10.3969/j.issn.0001-5733.2009.09.005.
[7] Feng W, Lemoine J M, Zhong M, et al. 2012. Terrestrial water storage changes in the Amazon basin measured by GRACE during 2002-2010. Chinese J. Geophys. (in Chinese), 55(3):814-821, doi:10.6038/j.issn.0001-5733.2012.03.011.
[8] Gersch W. 1991. Smoothness priors.//New Directions in Time Series Analysis, Part II. New York:Springer-Verlag, 113-146.
[9] Guo J Y, Duan X J, Shum C K. 2010. Non-isotropic Gaussian smoothing and leakage reduction for determining mass changes over land and ocean using GRACE data. Geophysical Journal International, 181(1):290-302.
[10] Han S C, Shum C K, Jekeli C, et al. 2005. Non-isotropic filtering of GRACE temporal gravity for geophysical signal enhancement. Geophysical Journal International, 163(1):18-25.
[11] Hsu H Z, Lu Y, Zhong M, et al. 2012. Satellite gravity and its application to monitoring geophysical environmental change. Sci. Sin. Terrae (in Chinese), 42(6):843-853.
[12] Hu X G, Chen J L, Zhou Y H, et al. 2006. The seasonal change of water storage measured by GRACE in the Yangtze River Basin. Science in China Ser. D Earth Sciences (in Chinese), 36(3):225-232.
[13] Jekeli C. 1981. Alternative methods to smooth the Earth's gravity field. Technical Report No 327, Geodetic Science. Ohio:Ohio State University.
[14] Karjalainen P A. 1997. Regularization and Bayesian methods for evoked potential estimation[Ph. D. thesis]. Kuopio:University of Kuopio.
[15] Klees R, Revtova E A, Gunter B C, et al. 2008. The design of an optimal filter for monthly GRACE gravity models. Geophysical Journal International, 175(2):417-432.
[16] Kusche J. 2007. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. Journal of Geodesy, 81(11):733-749.
[17] Li Q, Luo Z C, Zhong B, et al. 2013. Terrestrial water storage changes of the 2010 southwest China drought detected by GRACE temporal gravity field. Chinese J. Geophys. (in Chinese), 56(6):1843-1849, doi:10.6038/cjg20130606.
[18] Peng P, Zhu Y Z, Zhong M, et al. 2013. Annual sea level fingerprint caused by global water mass transport. Chinese J. Geophys. (in Chinese), 56(3):824-833, doi:10.6038/cjg20130311.
[19] Rodell M, Houser P R, Jambor U, et al. 2004. The global land data assimilation system. Bull. Amer. Meteor. Soc., 85(3):381-394.
[20] Sasgen I, Martinec Z, Fleming K. 2006. Wiener optimal filtering of GRACE data. Studia Geophysica et Geodaetica, 50(4):499-508.
[21] Schmidt M, Han S-C, Kusche J, et al. 2006. Regional high-resolution spatiotemporal gravity modeling from GRACE data using spherical wavelets. Geophysical Research Letters, 33(8):L08403.
[22] Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data. Geophysical Research Letters, 33(8):L08402.
[23] Tarvainen M P, Ranta-aho P O, Karjalainen P A. 2002. An advanced detrending method with application to HRV analysis. IEEE Transactions on Biomedical Engineering, 49(2):172-175.
[24] Velicogna I, Tong J, Zhang T, et al. 2012. Increasing subsurface water storage in discontinuous permafrost areas of the Lena River basin, Eurasia, detected from GRACE. Geophysical Research Letters, 39(9):L09403.
[25] Wahr J, Molenaar M, Bryan F. 1998. Time variability of the Earth's gravity field:Hydrological and oceanic effects and their possible detection using GRACE. Journal of Geophysical Research, 103(B12):30205-30229.
[26] Wahr J, Swenson S, Zlotnicki V, et al. 2004. Time-variable gravity from GRACE:First results. Geophysical Research Letters, 31(11), doi:10.1029/2004GL019779.
[27] Wang H S, Jia L L, Steffen H, et al. 2012. Increased water storage in North America and Scandinavia from GRACE gravity data. Nature Geoscience, 6(1):38-42.
[28] Wang H S, Wang Z Y, Yuan X D, et al. 2007. Water storage changes in Three Gorges water systems area inferred from GRACE time-variable gravity data. Chinese J. Geophys. (in Chinese), 50(3):730-736, doi:10.3321/j.issn:0001-5733.2007.03.011.
[29] Wang H S, Wu P, Van der Wal W, et al. 2009. Glacial isostatic adjustment model constrained by geodetic measurements and relative sea level. Chinese J. Geophys. (in Chinese), 52(10):2450-2460, doi:10.3969/j.issn.0001-5733.2009.10.004.
[30] Wouters B, Schrama E J O. 2007. Improved accuracy of GRACE gravity solutions through empirical orthogonal function filtering of spherical harmonics. Geophysical Research Letters, 34(23):L23711.
[31] Wouters B, Riva R E M, Lavallée D A, et al. 2011. Seasonal variations in sea level induced by continental water mass:First results from GRACE. Geophysical Research Letters, 38(3), doi:10.1029/2010GL046128.
[32] Zhan J G, Wang Y. 2011. Detect water storage variation of Longtan Reservoir with GRACE data. Chinese J. Geophys. (in Chinese), 54(5):1187-1192, doi:10.3969/j.issn.0001-5733.2011.05.007.
[33] Zhan J G, Wang Y, Hao X G. 2011. Improved method for removal of correlated errors in GRACE data. Acta Geodaetica et Cartographica Sinica (in Chinese), 40(4):442-446.
[34] Zhang Z Z, Chao B F, Lu Y, et al. 2009. An effective filtering for GRACE time-variable gravity:Fan filter. Geophysical Research Letters, 36(17), doi:10.1029/2009GL039459.
[35] Zhong M, Duan J B, Xu H Z, et al. 2009. Trend of China land water storage redistribution at medi- and large-spatial scales in recent five years by satellite gravity observations. Chinese Sci. Bull., 54(5):816-821, doi:10.1007/s11434-008-0556-2.
[36] Zhou X, Sun W K, Fu G Y. 2011. Gravity satellite GRACE detects coseismic gravity changes caused by 2010 Chile Mw8.8 earthquake. Chinese J. Geophys. (in Chinese), 54(7):1745-1749, doi:10.3969/j.issn.0001-5733.2011.07.007.
[37] 鄂栋臣, 杨元德, 晁定波. 2009. 基于GRACE资料研究南极冰盖消减对海平面的影响. 地球物理学报, 52(9): 2222-2228, doi: 10.3969/j.issn.0001-5733.2009.09.005.
[38] 冯伟, Lemoine J M, 钟敏等. 2012. 利用重力卫星GRACE监测亚马逊流域2002—2010年的陆地水变化. 地球物理学报, 55(3): 814-821, doi: 10.6038/j.issn.0001-5733.2012.03.011.
[39] 胡小工, 陈剑利, 周永宏等. 2006. 利用GRACE空间重力测量监测长江流域水储量的季节性变化. 中国科学: D辑,36(3): 225-232.
[40] 许厚泽, 陆洋, 钟敏等. 2012. 卫星重力测量及其在地球物理环境变化监测中的应用. 中国科学(D辑: 地球科学), 42(6): 843-853.
[41] 李琼, 罗志才, 钟波等. 2013. 利用GRACE时变重力场探测2010年中国西南干旱陆地水储量变化. 地球物理学报, 56(6): 1843-1849, doi: 10.6038/cjg20130606.
[42] 彭鹏, 朱耀仲, 钟敏等. 2013. 全球水质量迁移对海平面空间模式周年变化的影响. 地球物理学报, 56(3): 824-833, doi: 10.6038/cjg20130311.
[43] 汪汉胜, 王志勇, 袁旭东等. 2007. 基于GRACE时变重力场的三峡水库补给水系水储量变化. 地球物理学报, 50(3): 730-736, doi: 10.3321/j.issn:0001-5733.2007.03.011.
[44] 汪汉胜, Wu P, Van der Wal W等. 2009. 大地测量观测和相对海平面联合约束的冰川均衡调整模型. 地球物理学报, 52(10): 2450-2460, doi: 10.3969/j.issn.0001-5733.2009.10.004.
[45] 詹金刚, 王勇. 2011. 卫星重力捕捉龙滩水库储水量变化. 地球物理学报, 54(5): 1187-1192, doi: 10.3969/j.issn.0001-5733.2011.05.007.
[46] 詹金刚, 王勇, 郝晓光. 2011. GRACE时变重力位系数误差的改进去相关算法. 测绘学报, 40(4): 442-446.
[47] 钟敏, 段建宾, 许厚泽等. 2009. 利用卫星重力观测研究近5年中国陆地水量中长空间尺度的变化趋势. 科学通报, 54(9): 1290-1294.
[48] 周新, 孙文科, 付广裕. 2011. 重力卫星GRACE检测出2010年智利Mw8.8地震的同震重力变化. 地球物理学报, 54(7): 1745-1749, doi: 10.3969/j.issn.0001-5733.2011.07.007.