2. 武汉大学测绘遥感信息工程国家重点实验室, 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
For the ground tilt records with high noise level and finite amplitude, the ensemble empirical mode decomposition (EEMD) is applied as a dyadic filter bank to enhance the signal-to-noise ratio. The estimation of the center frequencies and quality factors is based on the autoregressive (AR) method proposed by Chao and Gilbert. Moreover, it is widely accepted that the observed results have hardly meaning if the corresponding errors are not given. So the bootstrap method is jointly applied to estimate the errors of observations.
Using the three effective data processing approaches, almost all of the spheroidal oscillation modes (0S5 to 0S38) and toroidal oscillation modes (0T4 to 0T35) with their frequencies lower than 4.7 mHz and 15 harmonic modes (including one first-order mode, six two-order modes and eight three-order modes) excited by the earthquake were observed. Parts or all of the spectral splittings of five low-order spheroidal triplets (0S2,2S1,0S3, 0S4 and 1S2) with their frequencies lower than 1 mHz were also detected. The corresponding accuracy estimates for all of the observation results are provided. Moreover, we analyze the spectral coupling of some spheroidal oscillation and toroidal oscillation. The results show that the spectral coupling has significant impact on relevant parameters of the Earth's free oscillation. The results can help us better understanding some geodynamical processes to induce the real coupling effect.
We emphasize that it does not mean VTP cannot record the spectra splitting of intrasonic elastic normal modes despite we cannot extract these signals using the direct FFT analysis. Some effective methods can distinguish the weak signals from the mixed strong background noises. In addition, the ground tilt responding to the Earth free oscillations can indirectly reflect the coseismic displacement, which can be used to constrain focal mechanism of the earthquake. All of the observational results with high accuracy can help us to restrain the 3D Earth model.
受地震特别是大地震激发,地球会产生无数自由振荡模态.这些模态与地球内部相关物理参数(如密度、黏度、分层结构等)有关.通过观测地球自由振荡模态可反过来约束地球内部相关物理参数.因为地球是一个有限体,它仅在一定的离散频率处才能产生共振,也即驻波.理论研究表明(Ness et al., 1961; Alterman et al., 1974),地球自由振荡由无数本征球型振荡nSlm和环型振荡nTlm构成:(1)球型振荡nSlm,其质点位移既有径向分量,也有水平分量,其效果是这种振荡能够引起水平向和垂直向惯性力,同时引起地球内部物质密度的变化,从而能够引起重力位势的变化,所以重力仪、应变仪、倾斜仪、 地震仪甚至GPS阵列观测等均可记录到这种振荡信号(Van Camp,1999; Alsop et al., 1961; Braitenberg et al., 2006; Dziewonski and Gillbert, 1972; Yuta and Kosuke, 2012); 球型振荡存在于整个地球内部;(2)环型振荡nTlm,其质点只在以地球为同心的球面上移动,位移无径向分量,地球介质只会产生剪切形变,无体积变化,地球的重力场不会受到扰动,所以在理想的SNREI(spherical non-rotation elastic isotropy)情形,重力仪记录不到这种振荡信号;但实际上,由于地球的椭球性、自转科里奥利力的作用以及3D各向异性结构的影响,本来只有水平位移的环型振荡会产生垂直分量上的运动,所以重力仪也能记录到一些大地震(如2004年苏门答腊大地震等)激发的环型振荡(Rosat et al., 2005);环型振荡在液核中不存在.
早在20世纪70年代,国际上已开始利用倾斜仪观测记录探测地球自由振荡信号.但囿于台站自身幅值的限制,地倾斜观测记录多限于低频自由振 荡的探测,前人(Bolt and Currie, 1975; Braitenberg et al., 2006; Ferreira et al., 2006)利用地倾斜观测记录仅检测4.0 mHz以下的基频振荡信号;倾斜仪在超低频段(1 mHz以下)的噪声水平较高,且观测精度远低于超导重力仪,超低频自由振荡信号极易受观测噪声的干扰,因此很难检测到其谱峰分裂现象.然而,这并不代表利用倾斜仪探测不到超低频简正模的分裂现象,它们只是被掩盖在较强的背景噪声中,如果采用合适的方法来提高目标信号的信噪比(SNR),例如本文采用的EEMD(ensemble empirical mode decomposition)方法(Wu and Huang, 2009),则它们仍可能被观测到.
VPT是我国自行研制的一种小型台式高精度宽频带倾斜仪,它以铅垂线为基准,通过一个固定摆测量地壳相对于铅垂线的偏移,以此来间接测量地倾斜,主要应用于研究地壳垂直方向的相对运动和固体潮汐的动态变化(肖峻等,2004).张纳莉等(2011)利用张家口台VPT在2011日本Mw9.0级地震之后的NS分量观测记录,采用通用的功率谱密度估计方法,仅检测到了该地震激发的基频球型振型(0S2—0S35)、少量的环型振型(0T2—0T7)以及7个谐频振型.本文将基于该地震后珞珈山台VPT不同长度的连续地倾斜观测数据,进行范围更广的低频球型振荡和环型振荡的检测. 2 观测数据和方法
由于地倾斜变化一般非常小,倾斜仪实际输出电压与倾斜角之间基本上呈线性关系(肖峻等,2004;Sun et al., 2012);对VP型垂直摆倾斜仪观测数据进行标定,只会影响绝对振幅,不会影响模态的频率及模态之间的相对振幅.因此,是否进行标定,对本研究来说不会造成影响,直接利用VPT电压输出值来检测球型振荡和环型振荡是可行的.本文利用2011年日本Mw9.0级地震后珞珈山台站VPT在EW和NS两个分量上的电压观测数据(采样间隔为1 min)检测地球自由振荡信号.
本文主要采用了3种数据处理方法,即EEMD方法(Wu和Huang,2009)、AR(autoregressive)方法(Chao and Gilbert, 1980)和bootstrap法(Efron and Tibshirani, 1986).
EEMD是Wu and Huang(2009)基于噪声辅 助数据分析(NADA)理论,对EMD(empirical mode decomposition)方法(Huang et al., 1998)做出的进一步改进方法,其目的是减弱或消除模态混叠效应(mode mixing effect)及端点效应(end effect),使分解得到的IMF(本征模态函数)具有更集中的频率信息,有助于提取数据中的真实信号.本文,我们将EEMD方法应用于数据分析主要有两个作用:(1)将目标序列分解到不同频段的IMF,完成对潮汐信号的改正工作;(2)将EEMD方法作为一种矢量滤波器,将低频自由振荡信号分解为处于不同狭窄频段内的信号,以期能减弱目标频段上的噪声水平,从而提高多线态的分裂信号被探测到的可能性.主要处理思路为:首先利用EEMD 对目标序列进行分解,得到相应的 IMF;然后根据各 IMF 所对应的频率不同,筛选出我们感兴趣的目标频段所对应的 IMF;将所选 IMF(或其中几个的线性组合)作为新的序列,进行后续分析.EEMD方法在探测弱信号中的有效性和优越性参见Shen和Ding(2014).
基于Prony法(Prony,1795)的经典AR模型估计理论,可以在时间域估计出一个序列中所含信号的复频率信号,其核心思想是:将离散目标时间序列表示为一系列衰减余弦函数叠加的负指数形式,通过差分和傅里叶变换等步骤,将所有的谐波信号 分到不同的狭窄频率段上,以提高目标信号的SNR.AR方法的详细步骤可参阅Chao和Gilbert(1980).
PREM(地球初步参考模型,Dziewonski and Anderson(1981))是1D球对称模型,其建立除了采用大量地震波数据以及天文大地测量相关观测约束(如地球总质量、转动惯量等)之外,还利用了约1000个地球自由振荡模态的简并频率及约500个模态的品质因子,但它与真实3D地球模型并不相符(Häfner and Widmer-Schnidrig, 2013).近10年 基于高精度观测数据的研究表明(Park et al., 2005; Roult et al., 2010; Häfner and Widmer-Schnidrig, 2013),PREM 模型理论值与实际观测值之间存在显著差异;仅根据观测值与其对应的理论模型值之间的差异,难以说明探测结果的优劣.因此在给出频率估值的同时,需要同时给出合理的精度评估,以表明观测结果的可信度;否则,频率估值难以令人信服.本文参照Häfner和Widmer-Schnidrig(2013)的方法,采用一种从统计分析角度出发的bootstrap法给出观测结果的频率精度评估.关于bootstrap法的基本思想,可参见Efron和Tibshirani(1986). 3 数据处理
就探测地震激发的地球自由振荡信号而言,观测资料的预处理主要包括重力潮汐改正和大气改正.对于大气重力效应,环境气压变化(季节性变化)引起的地表应力变化是日月起潮力的1/10,且珞珈山台VPT处于山体内部,气压荷载对山洞中的潮汐观测影响很小;建立潮汐观测残差与气压资料的实测模型或全球气压模型实施观测资料的气压改正,难以描述和解决“洞室效应”问题.考虑到洞室气压效应对利用地倾斜记录检测自由振荡信号影响很小(Ferreira et al., 2006),本文未做气压改正.因此,本文数据预处理主要包括潮汐改正.应用珞珈山台VPT不同长度的两个分量观测记录进行低频地球自由振荡的检测,主要包括以下3个步骤.
步骤1:利用EEMD将VPT分钟观测序列分解成12个IMF,从中提取重力潮汐信号;然后从观测序列中扣除潮汐信号得到残差序列,完成对分钟数据的潮汐改正.为详细了解各IMF的频率信息,我们以EW分量观测序列的分解结果为例,对每个IMF作傅里叶变换得到各自的振幅谱(图 1).可以看到,按照分解的顺序IMF的能量分别集中在由高到低分布的频段上;针对IMF6+IMF7和IMF8+IMF9两个组合的振幅谱,两个谱峰对应周期分别为12.3 h和23.7 h,分别对应了半日波和日波波群;剩余的3个IMF给出了原始观测的长周期项.图 2给出了应用EEMD扣除半日波、日波和长周期项后的残差序列.需要指出,EEMD处理并不能完全剔除观测序列中的非线性潮汐信号,更好的方式是采用国际通用的调和分析方法,但限于该仪器未作标定,更细致的数据处理有待将来完成.
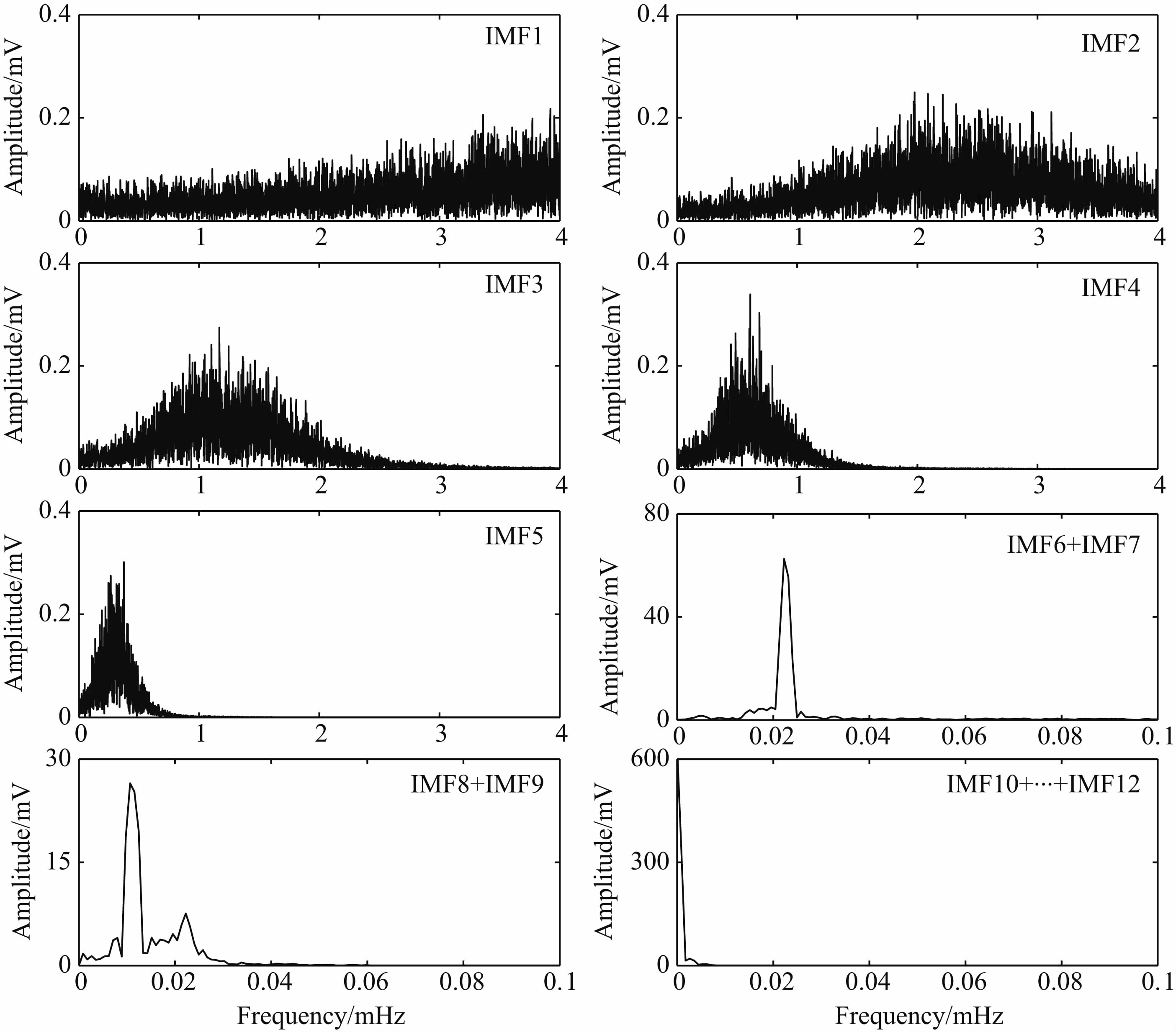 |
图 1 珞珈山台VPT在EW分量的观测序列经EEMD处理得到的IMFs和其不同组合对应的振幅谱Fig. 1 The amplitude spectra of the IMFs of the EW-component data segment of the VPT apparent tilt series after EEMD at the Luojianshan station |
 |
图 2 应用EEMD扣除半日波、日波和长周期项后的残差序列Fig. 2 The residual series after removing semidiurnal waves,diurnal waves and long period signals using EEMD |
步骤2:将EEMD作为一个滤波器,提取含有目标信号的IMF作为最终的残差序列.针对自由振荡的检测,考虑到对应于不同振型的频率和品质因子不同,以及不同IMF所携带的噪声水平不同,需要合理选择一个或几个 IMF作为最佳组合序列.
步骤3:获取目标频段的功率谱;利用AR方法估计目标信号的相关参数(主要包括频率、衰减因子、品质因子、振幅和相位),并结合bootstrap法进行频率精度评估.对于同一振型,VPT两个分量可能得到不同的频率估值和误差,因此我们参考Shen和Ding(2014)的方法,采用加权过程得到该简并频率的加权估值,即
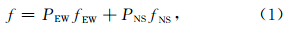
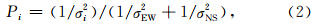
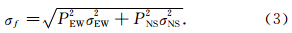
这里需要指出,任何观测值(或基于观测值确定的值),如果没有精度评估,则结果几乎没有意义.这也是本文需要对每个频率观测值给出精度评估的原因. 4 地球自由振荡的检测
大地震激发的地球自由振荡信号可持续数天至数月,但随着时间的推移而不断衰减,因此理想起始时间和数据长度的选取是能否有效探测到更多的地球自由振荡信号的前提(Masters and Widmer-Schnidrig, 1995).
选取数据的起始时间一般至少选取地震发生几十分钟后的整点时刻,但为了获得完整的自由振荡驻波模态,需要将数据起始时间推迟几个小时(Masters and Widmer-Schnidrig, 1995;Shen and Ding, 2014),因为很多驻波需要地震后的几个小时才能形成,这是由于地震波传播速度有限(纵波传播速度大约1.5~11.3 km·s-1,横波传播速度大约3.2~7.3 km·s-1(Dziewonski and Anderson, 1981))所致;有时,为了分离不同信号的混叠效应,需要将所选取数据的起始时间推迟几十个小时开始(Shen and Ding, 2014).
数据长度越长的观测序列携带的背景噪声也越多;而某些模态之间的频率间隔太小,要清晰将这些模态分辨出来,要求数据长度(丁浩和申文斌,2013)
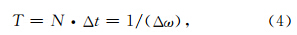
Munechika等(1993)的研究表明,对于观测到的自由振荡信号,如果其信噪比SNR>3,则认为检测结果是可信的,这里SNR=Smax/Snoise,其中Smax为该目标信号的谱峰振幅值,Snoise为该频段上的背景噪声振幅谱平均值.本文在目标信号的两侧选取 两个频率窄带,减少目标信号对噪声水平的影响,计算这两个频段对应振幅谱的 平均值作为近似Snoise值.
此外,检核观测值是否正确的标准如下:(1)与PREM模型理论值进行比对,实测频率与理论频率不应该偏离太远;(2)给出观测结果的精度评估,以考察观测结果的可信度,这是评价观测结果的重要指标;(3)不同数据源、不同处理方法得到的结果的相互比对.其中,第(3)点最为重要,若不同学者利用不同数据源和处理方法得到相同的结果(在一定精度范围内),也就证实了观测结果的正确性,进而为 精化地球模型(如国际上正在实施的 REM(reference Earth model)构建计划)提供约束. 4.1 0S2、2S1、0S3、0S4和1S2的谱峰分裂
综合考虑上述多种因素,我们选择在小于1 mHz频段背景噪声更低的EW分量观测序列,从震后整点时刻开始,选取不同数据长度和IMF组合,检测到0S2、2S1、0S3、0S4和1S2的谱峰分裂(图 3).表 1给出了珞珈山台VPT观测到的日本地震激发的0S2、2S1、0S3、0S4和1S2谱峰分裂的检测结果.从表 1可知,本文检测到的5个多线态分裂谱峰的平均信噪比均大于3,说明检测结果可信.
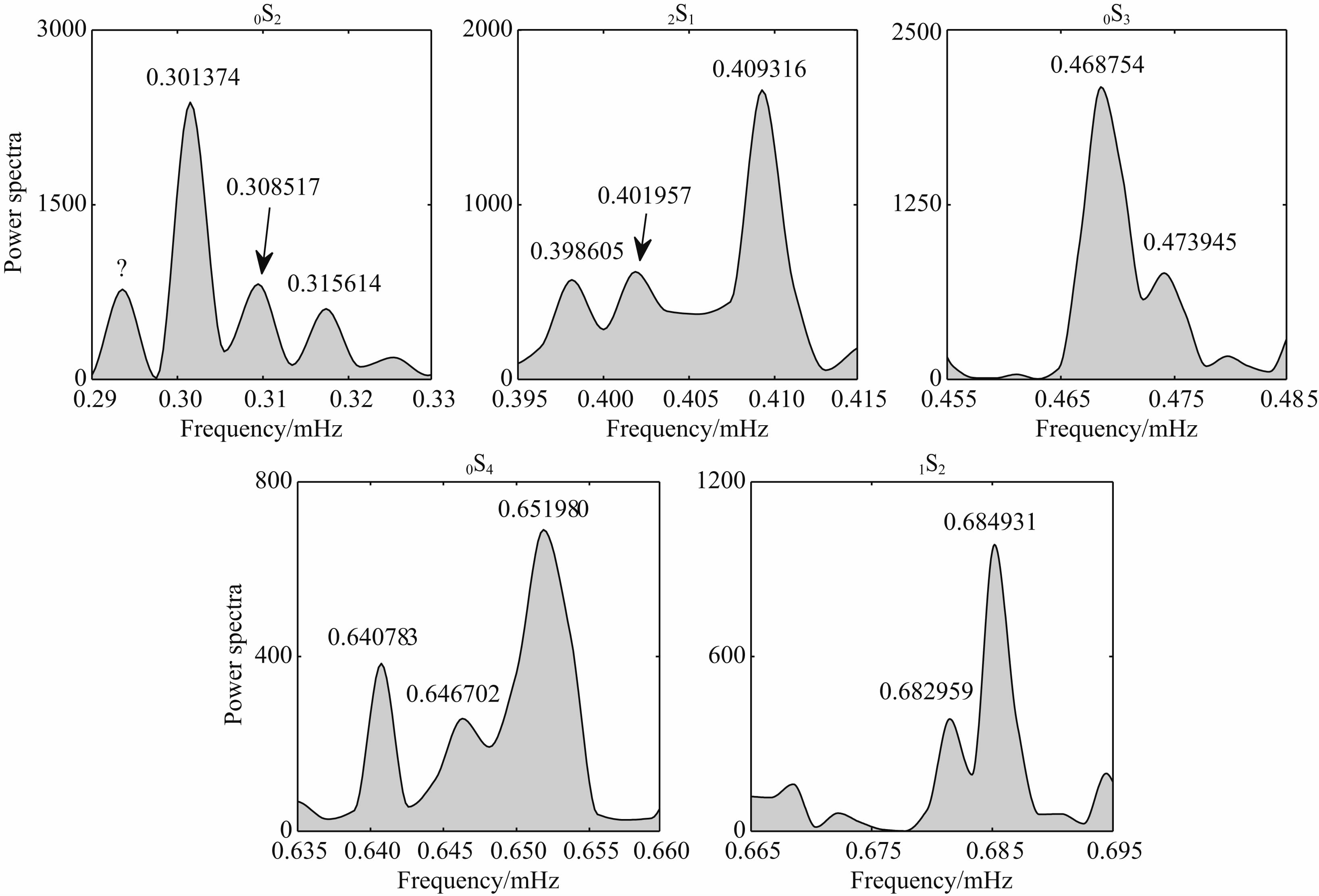 |
图 3 0S2、2S1、0S3、0S4和1S2的谱峰分裂Fig. 3 Spectral splitting of 0S2,2S1,0S3,0S4 and 1S2 |
| 表 1 0S2、2S1、0S3、0S4和1S2谱线分裂的观测结果Table 1 The observed results of the spectral splitting of 0S2,2S1,0S3,0S4 and 1S2 |
从图 3可以看出,除2S1,其他所有4个多线态均没有检测到完整的分裂谱峰,一方面可能是由于频率分辨率不足而导致各个信号耦合在一起(如0S4);另一方面可能由于仪器观测精度不够,目标单线态信号受背景噪声中的干扰严重(如0S2、0S3和1S2).2S1虽然检测到完整的3个分裂谱峰,但受噪声干扰,与 PREM 模型频率、Shen和Ding(2014)基于超导重力数据探测的结果相差较大;0S2检测到的3个分裂谱峰m=-2、m=0和m=+1的Q值(分别为170.38、65.53和190.38)均远小于 PREM模型理论值(分别为494.58、509.29和517.01),本文认为这主要是由于数据长度不够和EEMD分解导致谐频信号能量损失造成的(1S2的检测结果类似).
对于0S4,看似检测到m=-4、m=0和m=+4三个单线态信号,但根据对应的理论频率可知,m=±4的谱峰的跨度大于对应的理论频率宽度,也即m=±4的观测结果极可能是由于分辨率不足导致不同单线态自耦合的结果而并非m=±4的实际结 果.根据0S4的PREM模型的理论频率可知,对应的9个分裂谱峰之间的最小频率间隔为0.001015 mHz,因此至少需要274小时的数据长度才能将9个单线态清晰地分辨出来.
对于0S3,其检测结果信噪比最高,m=0的单线态与Shen和Ding(2014)、Roult等(2010)的探测结果都非常接近;但在分辨率足够的情况下,m=+2和m=+3两个单线态仍然耦合在一起,可能是受噪声干扰造成的.
对于1S2,虽然我们未检测到m=0的单线态,但较好地检测到了两个单线态m=+1和m=+2,而Widmer-Schnidrig和Laske(2007)利用单线态剥离(SS)法(Gilbert,1971)研究了1S2的分裂,其中m=+1和m=+2的单线态几乎是重叠的;Roult等(2010)基于地震波数据的探测结果中,1S2的m=+1的单线态难以识别.
目前研究表明,实测谱峰分裂宽度Wobs与基于PREM模型的理论谱峰分裂宽度Wmod之差ΔW在通常情况下远小于Wmod,即分裂宽度之比R(R=Wobs/Wmod)应该在1附近(Dahlen,1968; Giardini et al., 1988; Ritzwoller et al., 1986;Roult et al., 2010);而当分裂宽度之比R大于1.5时,则认为目标多线态信号是异常分裂(Widmer et al., 1992).从表 2可以看出,0S2、2S1、0S3、0S4和1S2的分裂宽度之比R分别为0.772、0.879、0.793、1.118和0.907,均在1附近,因此它们均为正常分裂模态,表明地球自转和椭率是引起0S2、2S1、0S3、0S4和1S2谱峰分裂的主要原因(Giardini et al., 1988).
| 表 2 本文基频球型振型的观测结果与PREM模型理论值和其他三组观测值的比较Table 2 The comparison between observed results in this paper and three groups of former observations or theoretical predictions on spheroidal normal modes |
对于0S4以上的自由振荡信号,目前多数研究均是关注其简并态,其全部分裂通常很难确定.前人(Bolt and Currie, 1975; Braitenberg et al., 2006; Ferreira et al., 2006)利用地倾斜观测记录检测自由振荡仅关注4 mHz以下的频段,主要原因是更高频段的自由振荡信号衰减较快(对应的品质因子相对较小),目标信号极易淹没于背景噪声中.
利用傅里叶变换(加汉宁窗)得到珞珈山台VPT两个分量序列在0.7~4.7 mHz频段内的功率谱,根据数据长度选取不同(均从震后整点时刻开始),将其分为0.7~2.7 mHz和2.7~4.7 mHz两个频段.图 4和图 5分别给出了EW和NS两个分量的功率谱分布,图中垂直虚线为PREM-re模型理论值的位置(后同).从图 4和图 5可以看出,利用VPT观测数据检测到0S5~0S38的全部基频振型以及15个谐频振型(其中包括:1个1级谐频、6个2级谐频、8个3级谐频);虽然部分检测结果信噪比较低,但仍大于3,证明检测结果可靠.此外,我们的检测结果均给出了精度评估,相关探测结果列于表 2和表 3.
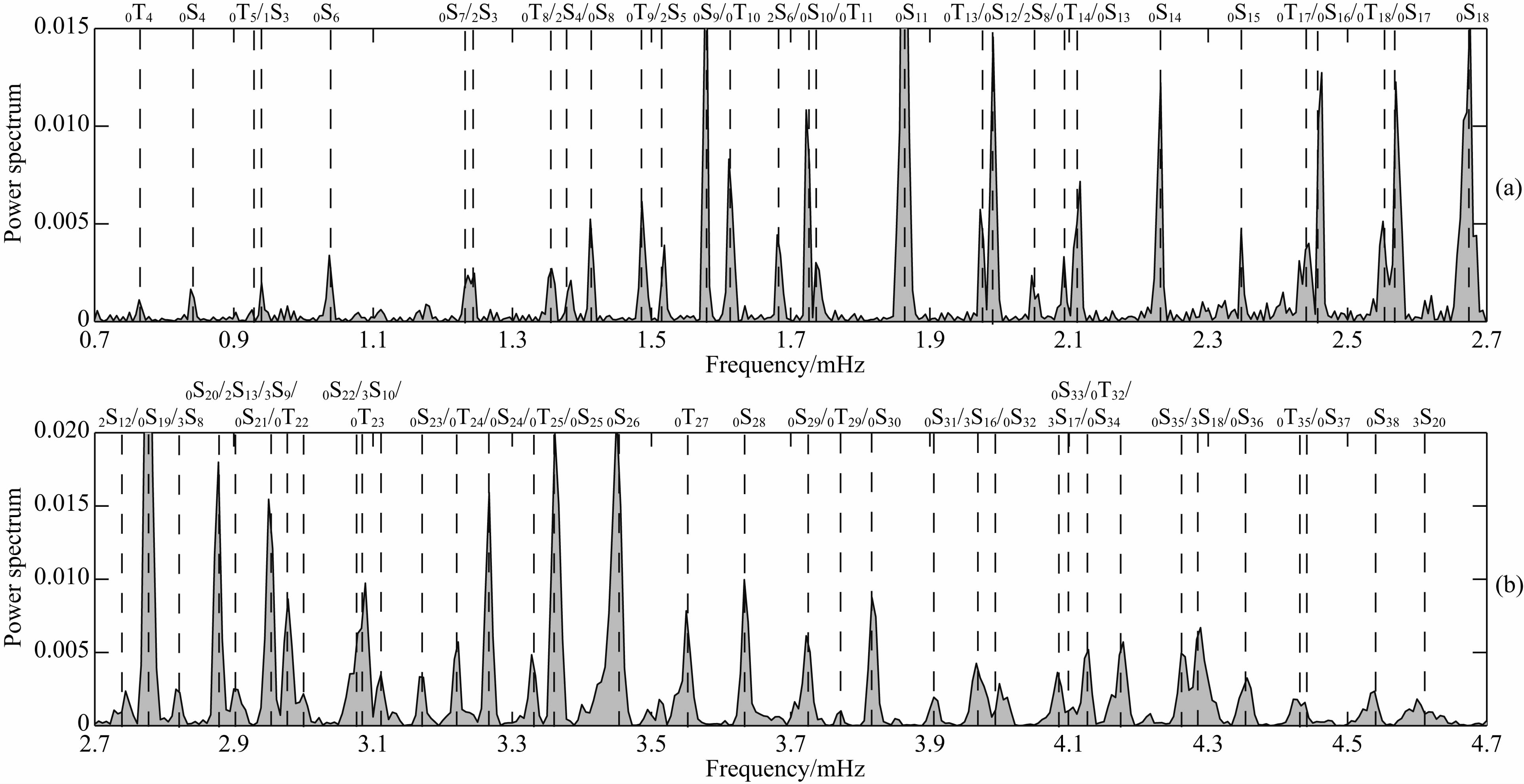 |
图 4 EW分量不同频段的自由振荡功率谱 (a)0.7~2.7 mHz频段自由振荡功率谱,数据长度为60小时;(b)2.7~4.7 mHz频段自由振荡功率谱,数据长度为50小时.Fig. 4 Power spectra of Earth′s free oscillations modes of different frequency b and s of EW-component (a)Power spectra from 0.7 to 2.7 mHz,the data length is 60 hours;(b)Power spectra from 2.7 to 4.7 mHz,the data length is 50 hours. |
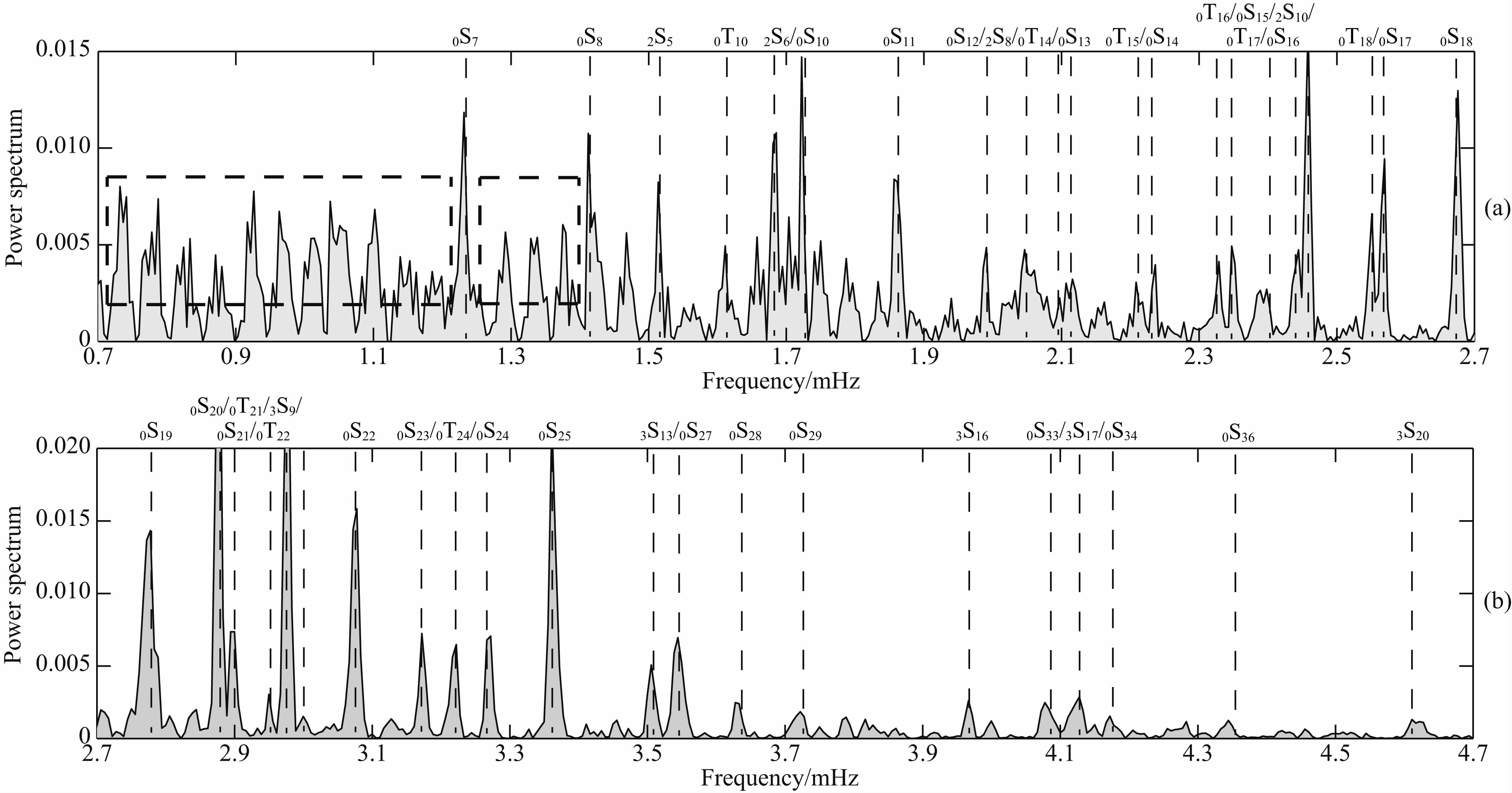 |
图 5 NS分量不同频段的自由振荡功率谱 (a)0.7~2.7mHz频段自由振荡功率谱,数据长度为60小时;(b)2.7~4.7 mHz频段自由振荡功率谱,数据长度为50小时.矩形虚线框标出了某些干扰周期信号.Fig. 5 Power spectra of Earth′s free oscillations modes of different frequency b and s of NS-component (a)Power spectra from 0.7 to 2.7 mHz,the data length is 60 hours;(b)Power spectra from 2.7 to 4.7 mHz,the data length is 50 hours. Dashed rectangular box marked some disturbed periodic signal. |
| 表 3 本文谐频振型的观测结果Table 3 The observed results of harmonic normal modes in this paper |
对于同一简正模,EW和NS分量的振幅响应不同(信噪比不同).在小于2.4 mHz频段,NS分量自由振荡信号的信噪比较低,基本被噪声淹没,这表明在NS向上台站周边存在长期的低频噪声累积,严重干扰到低频自由振荡信号的检测,这也为台站的选址提供参考;在大于4.3 mHz频段,自由振荡信号逐渐变得很模糊,主要包括两个原因:(1)随着频率的增加,模态的振幅衰减加速;(2)由于在此频段的基频振荡随着角次l的增高其振荡效果逐渐向表层发展,地球介质的横向不均匀性或各向异性逐渐变得明显(Alsop et al., 1961).
此外,从理论上来说,最佳数据长度应该是1.1Q/f(Dahlen,1982;Shen and Ding, 2014),因此,在0.73~4.63 mHz频段内,检测2S3的最佳数据长度约102小时,而84%振型的理想检测数据长度小于50小时,这表明本研究所选的两个数据长度大致满足检测球型振荡所需数据长度1.1Q个周期的要求. 4.3 环型振荡0Tl的检测
理论上,环型振荡通常只出现在水平向记录中,因此许多学者选择具有水平分量的观测仪器(如地震仪、应变仪、倾斜仪等)来检测环型振荡(Alsop et al., 1961; Braitenberg et al., 2006; Dziewonski and Gillbert, 1972; Ferreira et al., 2006).然而,由于球型振荡也有水平位移,也会出现在水平记录中;与地震仪、应变仪记录不同,垂向位移和水平位移均会被记录在地倾斜记录中.因此,若将地面倾斜位移分解成垂直位移和水平位移以期分别检测球型振荡和环型振荡,这种方式并不能简单地将两种振型的振荡信号分别开.
从图 4和图 5可以看出,结合VPT两个分量检测结果,本文检测到了0T4—0T35除0T6、0T7、0T12、0T19、0T20、0T26、0T28、0T30、0T31、0T33、0T34的全部环型振型;由于台站幅频特性的限制,大部分环型振荡信号的信噪比较低,且与相邻近的球型振荡产生了不同程度的耦合现象,但VPT依然能较好地分辨出来.这表明在未进行矢量分解的情况下,我们依然能够检测到4.6 mHz以下大部分基频环型振荡信 号.环型振荡信号的检测结果(包括精度评估)见表 4.
| 表 4 本文环型振型的观测结果与PREM模型理论值和其他三组观测值的比较Table 4 The comparison between observed results in this paper and three groups of former observations or theoretical predictions on toroidal normal modes |
在NS分量,本文与张纳莉等(2011)均只检测到少量的低频环型振荡信号;而在EW分量,环型振荡信号的数量和信噪比均优于NS向.我们认为这主要是由于2011日本Mw9.0地震激发的环型自由振荡引起的地表水平位移量在EW向和NS向存在较大差异.殷海涛等(2013)的研究表明,该地震引起中国地区的同震位移量在EW向远大于NS向.这说明若利用全球分布的地倾斜观测资料分析 地球环型简正模,可用于研究和约束地震的震源机制. 4.4 自由振荡的耦合效应
自由振荡信号极为复杂,耦合效应既可发生于同一种振荡类型之间(如:S-S或T-T),也可以发生于不同种振荡类型之间(如:S-T或T-S).对于VPT观测记录,在1 mHz以下,我们主要关注同一振型不同单线态之间的耦合效应,在4.1节我们已有相关阐述.在1 mHz以上,我们主要关注不同振型之间的耦合效应.
邱泽华等(2007)利用钻孔应变仪观测到环型振荡0T11—0T21与球型振荡0S10—0S20由于耦合作用近乎重合,这主要是由于他们选取数据的频率分辨率不足,我们称之为“虚假耦合效应”;而本文则能够分辨出其中大部分振型.少数简并模态频率间隔太小,难以分辨,如0S18—0T19和0S19—0T20,Braitenberg等(2006)和Ferreira等(2006)利用地倾斜观测资料均未能将它们分辨出来.
我们以0S11、0T12两个振型为例,分别选取不同长度的EW分量观测数据得到它们的振幅谱(图 6).表 5给出了0S11、0T12的检测结果.可以看出,根据0S11、0T12的PREM模型的理论频率可知,这两个振型之间的频率间隔为0.0045 mHz,因此至少需要61.73小时的数据长度才能将两个信号清晰地分辨出来.然而检测结果表明,在分辨率足够的情况下,仍无法将它们分辨出,说明0S11和0T12的耦合主要与地球结构的横向不均匀性及各向异性、地球自转、地球椭率、震源机制等因素有关(Backus and Gilbert, 1961; Geller and Stein, 1977; Smith and Masters, 1989),我们称之为“真实耦合效应”.
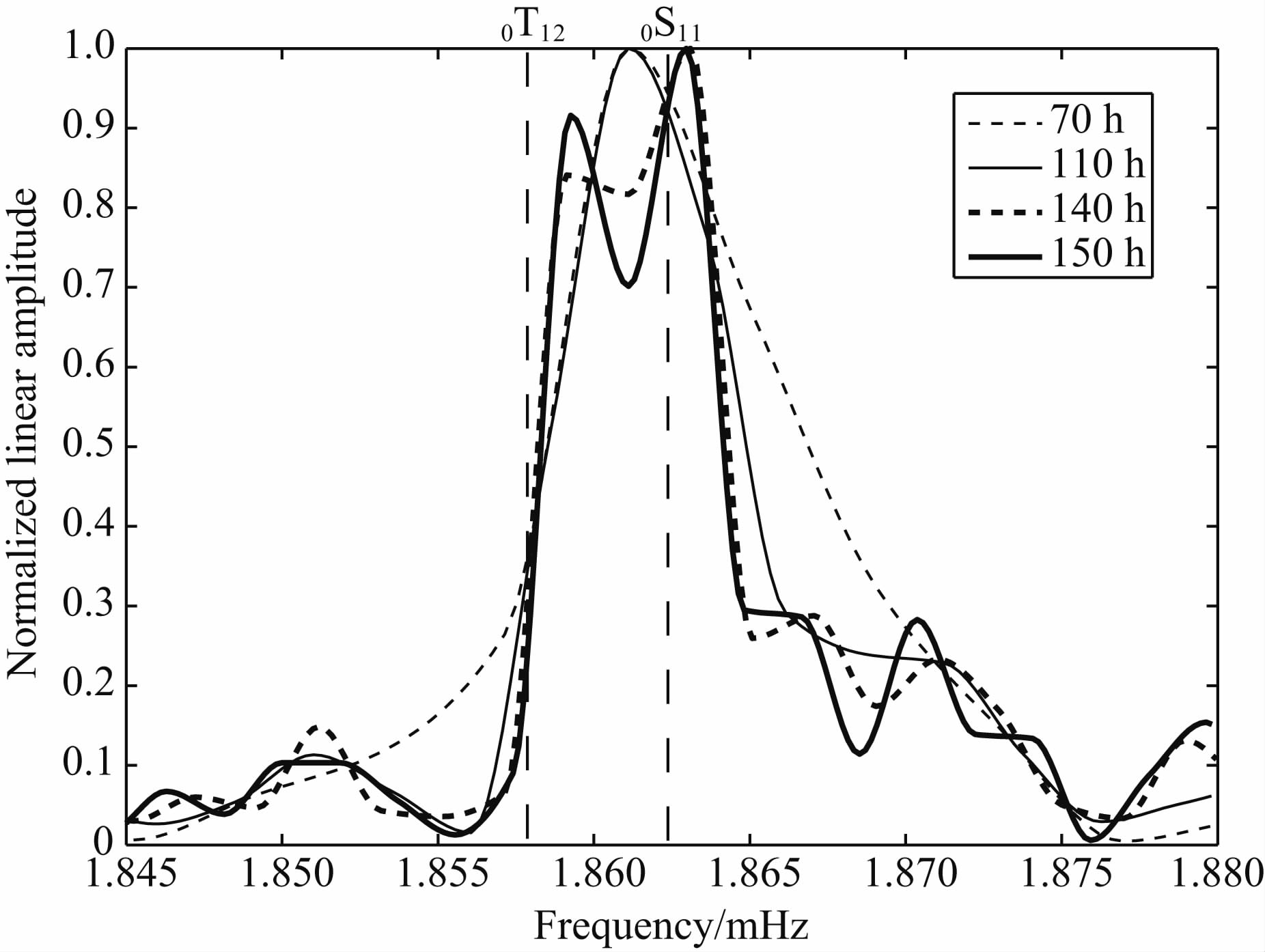 |
图 6 不同长度观测序列检测到的0S11和0T12的振幅 谱,对每个所选序列的结果中最大振幅都作了归一化, 以便于比较Fig. 6 The amplitude spectra of 0S11 and 0T12 using observations with different lengths,the maximum of the amplitude of the two normal modes obtained from each of the chosen records is normalized to 1 |
采用AR方法估计0S11、0T12的相关参数(表 5),结果表明耦合效应将显著影响地球自由振荡信号的频率、相位、振幅和品质因子,这也证实了Deuss和Woodhouse(2001,2004)的观点.
| 表 5 0S11和0T12的理论频率、观测频率、振幅、相位、品质因子Table 5 The model predicted frequencies,observed frequencies,amplitude,phase and Q of 0S11 and 0T12 |
本文利用珞珈山台VP型垂直摆倾斜仪观测资料有效地检测到了2011年日本Mw9.0级大地震激发的低频地球球型自由振荡和环型自由振荡模态并给出了精度评估,其中球型振荡检测到了0S2—0S38的全部基频振型和15个谐频振型,环型振荡检测到了0T4至0T35之间21个基频振型.研究结果表明,珞珈山站VP型垂直摆倾斜仪运行状态十分稳定,对低频自由振荡信号具有良好的观测能力,但对高频自由振荡信号的观测能力较差.
对于幅值有限、噪声水平较高的地倾斜观测记录,本文应用EEMD方法将观测序列分解成一组本征模态函数(IMF),过滤观测记录中的潮汐信号;并通过合理组合不同IMF,提高目标模态的SNR,首次利用地倾斜观测数据检测到了0S2、2S1、0S3、0S4和1S2的部分或全部谱峰分裂现象.
VP型垂直摆倾斜仪对自由振荡信号的响应较快,高频段部分信噪比较差,这表明高频信号衰减较快(对应的品质因子相对较小);而低频自由振荡信号的信噪比较高,能量衰减较慢(对应的品质因子相对较大).研究表明,对自由振荡信号的检测需要选取合适的数据长度:数据长度长,分辨率高,但信噪比变弱;另一方面,较长的数据段将使品质因子小的振荡信号迅速衰减,有利于提取出由于耦合效应而原本混合在一起的品质因子较大的信号.因此,如何取舍,视具体情况而定(Shen and Ding, 2014).
VP型垂直摆倾斜仪EW和NS向的环型振荡观测情况,间接反映地震在该两个方向的同震位移量,可用于约束地震的震源机制.
此外,耦合效应将显著影响自由振荡信号的频率、相位、振幅和品质因子,可用于约束地球内部结构和震源模型. 致谢 感谢两位匿名审稿人提出的有价值的评论及修改建议,致使本文更加完善.
| [1] | Alsop L E, Sutton G H, Ewing M. 1961. Free oscillations of the earth observed on strain and pendulum seismographs. J. Geophys. Res., 66(2): 631-641. |
| [2] | Alterman Z S, Eyal Y, Merzer A M. 1974. On free oscillations of the earth. Geophysical Surveys, 1(4): 409-428. |
| [3] | Backus G, Gilbert F. 1961. The rotational splitting of the free oscillations of the Earth. Proceedings of the National Academy of Sciences of the United States of America, 47: 362-371. |
| [4] | Bolt B A, Currie R G. 1975. Maximum entropy estimates of Earth torsional eigenperiods from 1960 Trieste data. Geophys. J. Int., 40(1): 107-114. |
| [5] | Braitenberg C, Romeo G, Taccetti Q, et al. 2006. The very-broad-band long-base tiltmeters of Grotta Gigante (Trieste, Italy): Secular term tilting and the great Sumatra-Andaman islands earthquake of December 26, 2004. Journal of Geodynamics, 41(1-3): 164-174. |
| [6] | Chao B F, Gilbert F. 1980. Autoregressive estimation of complex eigenfrequencies in low frequency seismic spectra. Geophys. J. Int., 63(3): 641-657. |
| [7] | Dahlen F A. 1968. The normal modes of a rotating, elliptical earth. Geophys. J. Int., 16(4): 329-367. |
| [8] | Dahlen F A. 1982. The effect of data windows on the estimation of free oscillation parameters. Geophys. J. Int., 69(2): 537-549. |
| [9] | Deuss A, Woodhouse H J. 2001. Theoretical free-oscillation spectra: the importance of wide band coupling. Geophys. J. Int., 146(3): 833-842, doi: 10.1046/j.1365-246X.2001.00502.x. |
| [10] | Deuss A, Woodhouse H J. 2004. Iteration method to determine the eigenvalues and eigenvectors of a target multiplet including full mode coupling. Geophys. J. Int., 159(1): 326-332. |
| [11] | Ding H, Shen W B. 2013. Comparative study of the MSE technique and SHS method used for detection nS1 mode triplet. Chinese J. Geophys. (in Chinese), 56(10): 3313-3323, doi: 10.6038/cjg20131008. |
| [12] | Dziewonski A M, Gillbert F. 1972. Observations of normal modes from 84 recordings of the Alaskan earthquake of 1964 March 28. Geophys. J. Int., 27(4): 393-446. |
| [13] | Dziewonski A M, Anderson D L. 1981. Preliminary reference earth model. Phys. Earth Planet. Int., 25(4): 297-356. |
| [14] | Efron B, Tibshirani R. 1986. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statist. Sci., 1(1): 54-77, doi: 10.1214/ss/1177013815. |
| [15] | Ferreira A M G, d'Oreye N F, Woodhouse J H, et al. 2006. Comparison of fluid tiltmeter data with long-period seismograms: Surface waves and earth's free oscillations. J. Geophys. Res., 111(B11): B11307, doi: 10.1029/2006JB004311. |
| [16] | Geller R J, Stein S. 1977. Split free oscillation amplitudes for the 1960 Chilean and 1964 Alaskan Earthquakes. Bulletin of the Seismological Society of America, 67(3): 651-660. |
| [17] | Giardini D, Li X D, Woodhouse J H. 1988. Splitting functions of long-period normal modes of the earth. J. Geophys. Res., 93(B11): 13716-13742. |
| [18] | Gilbert F. 1971. The diagonal sum rule and averaged eigenfrequencies. Geophysical Journal of the Royal Astronomical Society, 23(1): 119-123, doi: 10.1111/j.1365-246X.1971.tb01806.x. |
| [19] | Häfner R, Widmer-Schnidrig R. 2013. Signature of 3-D density structure in spectra of the spheroidal free oscillation 0S2. Geophys. J. Int., 192(1): 285-294, doi: 10.1093/gji/ggs013. |
| [20] | Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Roy. Soc. Lond., A454: 903-995. |
| [21] | Lei X E, Xu H Z, Sun H P. 2005. Detection of spheriodal free oscillation excited by Peru 8.2 Ms earthquake with five international superconducting gravimeter data. Sci. China Ser. D-Earth Sci., 48(1): 123-133. |
| [22] | Masters G, Widmer-Schnidrig R. 1995. Free oscillations: frequencies and attenuations. //Ahrens T J ed. Global Earth Physics: A Handbook of Physical Constants. Washington, DC: AGU, Reference Shelf Series 1, 104. |
| [23] | Munechika C K, Warminck J S, Salvaggio C, et al. 1993. Resolution enhancement of multispectral image data to improve classification accuracy. Photogrammetric Engineering and Remote Sensing, 59(1): 67-72. |
| [24] | Ness N R, Harrison C T, Slichter L B. 1961. Observations of the free oscillations of the earth. J. Geophys. Res., 66(2): 621-629. |
| [25] | Park J, Song T R A, Tromp J, et al. 2005. Earth's Free Oscillations Excited by the 26 December 2004 Sumatra-Andaman Earthquake. Science, 308: 1139-1144, doi: 10.1126/science.1112305. |
| [26] | Pekeris C L, Alterman Z, Jarosch H. 1961. Comparison theoretical with observed values of the periods of free oscillation of the earth. Geophysics, 47(1): 91-98. |
| [27] | Prony R. 1795. Essai experimental et analytique sur les lois de la dilatabilite des fluids elastiques et sur celles della force expansive de la vapeur de l'eau et de la vapeur de l'alkool, a differentes temperatures. J. Ec. Polytech. Paris,1(2):24-76. |
| [28] | Qiu Z H, Ma J, Chi S L, et al. 2007. Earth's free torsional oscillations of the great Sumatra earthquake observed with borehole shear strainmeter. Chinese J. Geophys. (in Chinese), 50(3): 797-805. |
| [29] | Ritzwoller M, Masters G, Gilbert F. 1986. Observations of anomalous splitting and their interpretation in terms of aspherical structure. J. Geophys. Res., 91(B10): 10203-10228. |
| [30] | Rosat S, Sato T, Imanishi Y, et al. 2005. High-resolution analysis of the gravest seismic normal modes after the 2004 Mw=9 Sumatra earthquake using superconducting gravimeter data. Geophys. Res. Lett., 32(13): L13304, dot: 10.1029/2005GL023128. |
| [31] | Roult G, Roch J, Clévédé E. 2010. Observation of split modes from the 26th December 2004 Sumatra-Andaman mega-event. Phys. Earth Planet. Int. 179(1-2): 45-59. |
| [32] | Shen W B, Ding H. 2014. Observation of spheroidal normal mode multiplets below 1 mHz using ensemble empirical mode decomposition. Geophys. J. Int., 196(3): 1631-1642. |
| [33] | Smith M F, Masters G. 1989. The effect of Coriolis coupling of free oscillation multiplets on the determination of aspherical earth structure. Geophys. Res. Lett., 16(3): 263-266. |
| [34] | Sun L, Li M, Wei G, et al. 2012. Response of tilt and strain meters in Hubei province to the 2011 Mw9.0 Japan earthquake. Geodesy and Geodynamics, 2(4): 46-52. |
| [35] | Van Camp M. 1999. Measuring Seismic normal modes with the GWR C021 Superconducting gravimeter. Phys. Earth Planet. Int., 116(1-4): 81-92. |
| [36] | Widmer R, Masters G, Gilbert F. 1992. Observably split multiplets-data analysis and interpretation in terms of large-scale aspherical structure. Geophys. J. Int., 111(3): 559-576. |
| [37] | Widmer-Schnidrig R, Laske G. 2007. Theory and observations-normal modes and surface wave measurements. //Schubert G ed. Treatise on Geophysics. Amsterdam: Elsevier, 3, 67-125. |
| [38] | Wu Z H, Huang N E. 2009. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv. Adapt. Data Anal., 1(1), doi: 10.1142/S1793536909000047. |
| [39] | Xiao J, Mo Y M, Hu G Q. 2004. High precision vertical pendulum tiltmeter for measuring earth tide. Geomatics and Information Science of Wuhan University (in Chinese), 29(11): 973-976. |
| [40] | Yin H T, Gan W J, Huang B, et al. 2013. Study on the effects of Japan M9.0 huge earthquake on the crustal movement of Shandong area. Chinese J. Geophys. (in Chinese), 56(5): 1497-1505, doi: 10.6038/cjg20130508. |
| [41] | Yuta M, Kosuke H. 2012. Observation of Earth's free oscillation by dense GPS array: After the 2011 Tohoku megathrust earthquake. Scientific Reports, 931, doi: 10.1038/srep00931. |
| [42] | Zadar M B, Caputo M. 1968. Spectral, bispectral analysis and Q of the free oscillations of the earth. Supplemento al Nuovo Cimento, 1(6): 67-81. |
| [43] | Zhang N L, Li X S, Cheng N, et al. 2011. Free oscillation of Japan 9.0 magnitude earthquake extracted by broadband clinometer. Journal of Disaster Prevention and Reduction (in Chinese), 27(3): 32-36. |
| [44] | 丁浩, 申文斌. 2013. 探测一阶模态三重分裂的MSE技术和SHS方法的比较研究. 地球物理学报, 56(10): 3313-3323, doi: 10.6038/cjg20131008. |
| [45] | 邱泽华, 马瑾, 池顺良等. 2007. 钻孔差应变仪观测的苏门答腊大地震激发的地球环型自由振荡. 地球物理学报, 50(3): 797-805. |
| [46] | 肖峻, 莫易敏, 胡国庆. 2004. 基于固体潮观测的高精度垂直摆倾斜仪. 武汉大学学报(信息科学版), 29(11): 973-976. |
| [47] | 殷海涛, 甘卫军, 黄蓓等. 2013. 日本M9.0级巨震对山东地区地壳活动的影响研究. 地球物理学报, 56(5): 1497-1505, doi: 10.6038/cjg20130508. |
| [48] | 张纳莉, 李细顺, 成娜等. 2011. 利用宽频带倾斜仪观测资料检测日本9.0级大地震激发的地球自由振荡. 防灾减灾学报, 27(3): 32-36. |
 2015, Vol. 58
2015, Vol. 58


