地球物理学报  2015, Vol. 58 Issue (3): 767-779   PDF    
引用本文
郑伟, 许厚泽, 钟敏, 员美娟. 2015. 基于下一代三向车轮双星编队改善地球重力场空间分辨率研究. 地球物理学报, 58(3): 767-779, doi: 10.6038/cjg20150307   
ZHENG Wei, HSU Hou-Tse, ZHONG Min, YUN Mei-Juan. 2015. A study on the improvement in spatial resolution of the Earth's gravitational field by the next-generation ACR-Cartwheel-A/B twin-satellite formation. Chinese J. Geophysics, 58(3): 767-779, doi: 10.6038/cjg20150307   
基于下一代三向车轮双星编队改善地球重力场空间分辨率研究
郑伟1, 许厚泽1, 钟敏1, 员美娟2    
1. 中国科学院测量与地球物理研究所 大地测量与地球动力学国家重点实验室, 武汉 430077;
2. 武汉科技大学理学院, 武汉 430081
投稿时间:2014-03-07    最后修改时间: 2014-07-01 .
基金项目：中国科学院知识创新工程重要方向青年人才项目(KZCX2-EW-QN114), 国家自然科学基金青年项目(41004006, 41202094)、国家自然科学基金重点项目(41131067)和国家自然科学基金面上项目(11173049), 国家留学人员科技活动项目择优资助基金(2011), 中国科学院卢嘉锡青年人才和青年创新促进会基金(2013), 国家民用空间基础设施项目子课题(2014),武汉大学地球空间环境与大地测量教育部重点实验室测绘基础研究基金(11-01-02), 中国测绘科学研究院地理空间信息工程国家测绘地理信息局重点实验室开放基金(201322), 西安测绘研究所地理信息工程国家重点实验室开放基金(SKLGIE2013-M-1-5), 中国科学院测量与地球物理研究所重要方向项目(Y309451045)和大地测量与地球动力学国家重点实验室自主项目(Y309491050)联合资助.
作者简介：郑伟, 男, 1977年生, 博士, 副研究员, 主要从事基于卫星重力测量反演地球、月球和火星重力场的理论和方法等方面的研究. E-mail: wzheng@asch.whigg.ac.cn
摘要：由于当前GRACE(Gravity Recovery and Climate Experiment)串行式编队存在"南北向条带误差"等缺陷,因此本文基于星间速度插值法开展了利用下一代三向车轮双星编队ACR(Along-Cross-Radial)-Cartwheel提高地球重力场空间分辨率的可行性研究论证. 第一,采用GRACE卫星轨道参数和关键载荷精度,利用三向车轮双星编队ACR-Cartwheel-A/B反演了120阶地球重力场.结果表明:基于ACR-Cartwheel-A/B双星编队反演地球重力场的模拟精度较德国波茨坦地学研究中心(GFZ)公布的EIGEN-GRACE02S地球重力场模型的实测精度平均提高2.6倍,从而检验了基于下一代三向车轮双星编队ACR-Cartwheel-A/B反演地球重力场精度优于当前GRACE串行式双星编队的可行性. 第二,通过星间速度插值法,采用卫星轨道参数(初始轨道高度350 km、平均星间距离100 km、初始轨道倾角89°、初始轨道离心率0.0046)、卫星关键载荷精度指标(星间速度10-7 m·s-1、轨道位置10-3 m、轨道速度10-6 m·s-1、非保守力10-11 m·s-2)、观测时间30天和采样间隔10 s,基于经向车轮双星编队Lo-AR(Longitudinal-Along-Radial)-Cartwheel-A/B、纬向车轮双星编队La-AR(Latitudinal-Along-Radial)-Cartwheel-A/B和三向车轮双星编队ACR-Cartwheel-A/B,分别反演了120阶地球重力场;在120阶处,累计大地水准面精度分别为5.115×10-4 m、4.923×10-4m和3.488×10-4 m. 结果表明:(1)由于La-AR-Cartwheel-A/B编队的轨道稳定性优于Lo-AR-Cartwheel-A/B编队,因此基于La-AR-Cartwheel-A/B编队反演重力场精度高于Lo-AR-Cartwheel-A/B编队;(2)由于ACR-Cartwheel-A/B编队可以同时获得轨向、垂向和径向的重力场信息,卫星观测数据具有各向同性优点,因此ACR-Cartwheel-A/B编队是建立下一代高精度和高空间分辨地球重力场模型的优化选择.
关键词： 三向车轮编队     经向和纬向车轮编队     轨向、垂向和径向观测值     空间分辨率     轨道根数    
A study on the improvement in spatial resolution of the Earth's gravitational field by the next-generation ACR-Cartwheel-A/B twin-satellite formation
ZHENG Wei1, HSU Hou-Tse1, ZHONG Min1, YUN Mei-Juan2    
1. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
2. College of Science, Wuhan University of Science and Technology, Wuhan 430081, China
Abstract: Because the design defects (e.g., the orbital altitude could not be substantially decreased, the measurement accuracy of space-borne instrumentations is unable to be sufficiently improved, and the isotropic gravity information is incapable of being simultaneously acquired, etc.) of the present twin Gravity Recovery and Climate Experiment (GRACE) satellites have resulted in poor spatial resolution of the Earth's gravitational field, this study aims to carry out the feasibility demonstrations regarding the next-generation ACR(Along-Cross-Radial)-Cartwheel twin-satellite formation for improving the spatial resolution of the Earth's gravitational field by the intersatellite range-rate interpolation method. The research on improving the accuracy of the Earth's gravitational field by the Radial-Cartwheel and Inclined-Cartwheel twin-satellite formation has been developed using the short-arc integral approach. The disadvantage of the short-arc integral approach is that the accuracy of the Earth's long-wavelength gravitational field is apt to be decreased owing to a shorter orbital arc of about 30 minutes. The different methods of satellite gravity recovery have different sensitivities to the signal spectrum of gravity field. Unlike previous recovery methods, we perform the exploratory investigations on optimizing spatial resolution by the future ACR-Cartwheel-A/B twin-satellites formation based on the six-point intersatellite range-rate interpolation method.
Firstly, the Earth's gravitational field from ACR-Cartwheel-A/B complete up to degree and order 120 is precisely recovered using the satellite orbital parameters and the measurement precision of key payloads from the twin GRACE satellites. The research results show that the accuracy of the Earth's gravitational field determination from the next-generation ACR-Cartwheel twin-satellite formation is averagely improved by 2.6 times than that from the EIGEN-GRACE02S model released by the German GeoForschungsZentrum Potsdam (GFZ), which sufficiently verifies that the next-generation ACR-Cartwheel twin-satellite formation is obviously better than the current GRACE collinear formation. Secondly, the Earth's gravitational field complete up to degree and order 120 is accurately measured based on the satellite orbital parameters (e.g., orbital altitude of 350 km, intersatellite range of 100 km, orbital inclination of 89° and orbital eccentricity of 0.0046), the measurement precision of key payloads (e.g., 10-7 m·s-1 in intersatellite range-rate, 10-3 m in orbital position, 10-6 m·s-1 in orbital velocity and 10-11 m·s-2 in non-conservative force), an observation time of 30 days and a sampling interval of 10 s by the Lo-AR(Longitudinal-Along-Radial)-Cartwheel-A/B, La-AR(Latitudinal-Along-Radial)-Cartwheel-A/B and ACR-Cartwheel-A/B twin-satellite formations using the intersatellite range-rate interpolation method, and the cumulative geoid height errors are 5.115×10-4 m, 4.923×10-4 m and 3.488×10-4 m, respectively. Since the orbital stability of the La-AR-Cartwheel-A/B formation is superior to the Lo-AR-Cartwheel-A/B formation, the accuracy of satellite gravity recovery from the La-AR-Cartwheel-A/B formation is higher than that from the Lo-AR-Cartwheel-A/B formation. Because the ACR-Cartwheel-A/B twin-satellite formation can synchronously obtain gravity information in the along-track, cross-track and radial-track directions, satellite observation data are provided with some strongpoints consisting of homogeneity, isotropy, and so on. On all accounts, the next-generation ACR-Cartwheel twin-satellite formation will prospectively play a significant role in producing the Earth gravity field model with higher accuracy and resolution.
Key words: ACR-Cartwheel formation     Lo-AR-Cartwheel and La-AR-Cartwheel formations     Along-cross-radial-track observations     Spatial resolution     Orbital element    
 1 引言

自2002年3月17日美德联合研制的GRACE重力双星成功发射以来，已在地球总体形状随时间变化、地球各圈层物质的分布和变化、全球海洋质量的分布与变化、极地冰川的增大和缩小、以及地下蓄水总量信息特性等领域做出了突出贡献. 但GRACE卫星重力计划的固有缺陷限制了地球重力 场时空分辨率的进一步提高，主要不足之处包括：(1)“南北向条带误差(Striping)”效应. 由于GRACE-A/B双星被设计为“串行式(collinear)” 编队系统，因此仅能感测轨向(along-track)卫星观测数据，而无法同时获得垂向(cross-track)和径向(radial-track)地球重力场信息. 由于获得的卫星观测信号和误差非各向同性(anisotropic)，而且GRACE串行式轨道设计对经向重力场变化异常敏感，因此导致了削弱地球时变重力场精度的“南北向条带误差”效应(Swenson and Wahr， 2006; Klees et al., 2008).(2)“混频(Aliasing)”效应. GRACE双星被设计为非重复轨道，约30天的卫星轨道在地面的投影轨迹可完全覆盖地球，因此基于GRACE卫星观测数据最大程度仅能获得时间分辨率为1个月的时变重力场模型. 因为时间变化周期小于30天的海潮和大气潮等高频误差无法从地球时变重力场月模型中精确扣除，所以导致了限制地球时变重力场精度的“混频”效应(Han et al., 2004; Ray and Luthcke， 2006; Moore and King， 2008; Seo et al., 2008; Gruber et al., 2009).

对于“南北向条带误差”效应而言，可通过增加垂向和径向的卫星观测数据得以缓解；对于“混频”效应而言，可通过提高地球重力场的时空分辨率得以削弱. 因此，为了最大程度减弱“南北向条带误差”和“混频”效应对地球时变重力场精度的负面影响，寻求最优的下一代重力卫星编队飞行模式是当前国内外众多科研机构的研究热点(Bender et al., 2003; Rummel，2003; Sneeuw et al., 2005; Sharifi et al., 2007; 郑伟等，2010a/b，2012a)：(1)串行式双星编队有美国宇航局喷气推进实验室(NASA-JPL)等提出的GRACE Follow-On卫星重力计划(Stephens et al., 2006; Flechtner et al., 2009; Zheng et al., 2009b; 郑伟等， 2010c，2012b，2014; Loomis et al., 2012)、 欧空局的意大利泰利斯阿莱尼亚空间公司(Italy-TAS)等提出的NGGM(Next-Generation Gravimetry Mission)卫星重力计划(Anselmi et al., 2010; Silvestrin et al., 2012; Cesare and Sechi， 2013)等；(2)钟摆式双星编队有欧空局的法国空间研究中心(ESA-CNES)和德国慕尼黑工业大学(Germany-TUM)等提出的E.MOTION(Earth System Mass Transport Mission)卫星重力计划(Gruber，2010; Gruber et al., 2012; Panet et al., 2013)等；(3)串行-钟摆组合三星编队有德国波恩大学(Bonn-IGG)等提出的GRACE-Pendulum-3S卫星重力计划(Elsaka et al., 2009)；(4)串行式三星编队有中国科学院测量与地球物理研究所(CAS-WHIGG)等提出的GRACE-3S卫星重力计划(Zheng et al., 2009a)；(5)转轮式四星编队有美国宇航局喷气推进实验室(NASA-JPL)等提出的FSCF(Four-Satellite Cartwheel Formation)卫星重力计划(Wiese et al., 2009; 郑伟等，2013)等；(6)不同轨道倾角组合四星编队(Bender et al., 2008; Zheng et al., 2008; Wiese et al., 2012).

Massonnet(1998)首次将卫星转轮式编队模式应用于被动雷达干涉测量；Sneeuw和Schaub(2004)提出了基于卫星转轮式编队系统精密探测地球重力场的新思想；Wiese 等(2009)和郑伟等(2013)基于下一代转轮式四星编队系统精确快速反演了地球重力场；Sneeuw和Schaub(2005)开展了利用转轮式六星编队系统提高地球重力场精度的可行性研究. 如表 1所示，下一代车轮式双星编队Cartwheel-A/B预期采用近圆轨道、近极轨道和低 地球轨道设计，通过高轨道的GNSS星座(美国GPS、俄罗斯GLONASS、欧洲Galileo、 中国Compass等)精密跟踪低轨Cartwheel-A/B双星(定轨精度优于10-2 m)，利用激光干涉测距仪高精度感测星间速度(10-7~10-9 m·s-1)，基于非保守力补偿系统(Drag-free)精确消除作用于双星的非保守力(10-11~10-13 m·s-2). 相对于当前GRACE串行式双星编队系统，下一代车轮式双星编队系统Cartwheel-A/B的优点如下：第一，采用车轮式轨道设计，可同时获得轨向(along-track)、垂向(cross-track)和径向(radial-track)的卫星观测信号，有利于获得各向均匀的卫星观测数据信号和误差，以及提高地球重力场的空间分辨率. 第二，通过获得各向同性的地球重力场信息，有利于削弱地球时变重力场模型的“南北向条带误差”效应. 第三，采用激光干涉测距仪大幅度提高星间速度的测量精度(1~3个数量级)，旨在进一步降低卫星观测误差对地球重力场反演精度的负面影响；通过非保守力补偿系统消除非保守力(大气阻力、太阳光压、地球辐射压、轨道高度和姿态控制力等)对卫星寿命的负面影响，旨在进一步降低卫星轨道高度(300~400 km)，从而抑制地球重力场信号的衰减效应. 第四，相对于转轮式四星和六星编队飞行模式，转轮式双星编队系统Cartwheel-A/B不仅研制技术难度较小和测控精度要求较低，而且研究费用较低廉.

表 1 当前GRACE和将来Cartwheel-A/B双星编队系统对比 Table 1 A comparison of satellite formations between present GRACE and future Cartwheel-A/B

目前国内外科研机构通常采用动力学法、能量守恒法、卫星加速度法等反演地球重力场. 动力学法的优点是不依赖于任何先验地球重力场模型，理论框架严密，各种地球重力场参数求解精度较高；缺点是整体解算过程较复杂，需要高性能的并行计算机支持，而且随着轨道弧长增加，解算模型误差将迅速增大(周旭华，2005; 张兴福，2007). 能量守恒法的优点是避免了数值微分、数值积分等计算，直接利用地球扰动位和引力位系数的线性关系建立卫星运动观测方程，而且观测方程物理含义明确，易于地球重力场的敏感度分析，通常采用PC计算机可完成高阶地球重力场的快速求解；缺点是对卫星速度的测量精度要求较高(程芦颖和许厚泽，2006; 郑伟等，2006). 卫星加速度法的优点是观测方程形式简单、在保证求解精度的前提下计算量较小；缺点是采用的数值微分算法在一定程度上损失了地球低频重力场的精度(沈云中等，2005; 郑伟等，2011). Elsaka(2010)通过短弧法围绕径向和倾斜车轮式双星编队开展了改善地球时变重力场模型时空分辨率的论证研究. 相对于传统动力学法，短弧法的优点是计算量较小和计算过程简单；缺点是由于采用了较短的轨道弧长(约30 min)，因此地球长波重力场解算精度较低(Mayer-Gürr，2006). 由于不同卫星重力反演方法对地球重力场频谱的敏感度不同，因此不同于上述卫星重力反演法，我们通过6点星间速度插值法开展了基于双向车轮式和三向车轮式双星编队飞行模式进一步提高下一代地球重力场空间分辨率的探索性研究. 2 星间速度插值卫星重力反演法

6点星间速度插值观测方程表示如下(Zheng et al., 2012)：

其中，

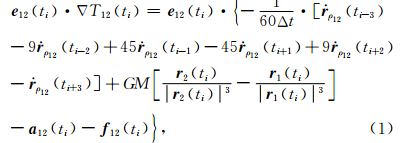
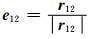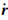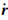ρ · 12表示激光干涉测距系统的星间速度；表示第一颗卫星指向第二颗卫星的单位矢量，r 12= r 2－ r 1表示双星的轨道位置矢量差，r 1和r 2分别表示双星的轨道位置矢量；12=2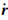－1表示双星的轨道速度矢量差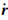，1和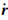2分别表 示双星的轨道速度矢量. GM表示地球质量M和万有引力常数G的乘积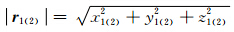；分别表示双星的地心半径，x1(2)，y1(2)，z1(2)表示轨 道位置矢量 r 1(2)的3个分量；Δt表示采样间隔. a 12= a 2－ a 1表示作用于双星的保守力差(如日月引力，地球固体潮、海潮、大气潮、极潮汐力，相对论效应等)(Kim，2000; 张捍卫等，2004; Petit and Luzum， 2010)，f 12= f 2－ f 1表示作用于双星的非保守力差(如大气阻力、太阳光压、地球辐射压、轨道高度和姿态控制力等)(Roesset，2003). T(r，θ，λ)表示地球扰动位，有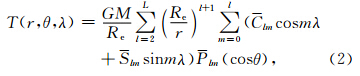

其中，r，θ，λ分别表示地心半径、地心余纬度和地心经度，Re表示地球平均半径；Plm(cosθ)表示规格化的缔合Legendre函数，l表示阶数，m表示次数；Clm和Slm表示待估的地球引力位系数.

地球引力位系数精度公式表示如下:

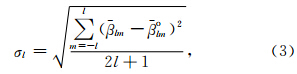
其中，βlm=(Clm，Slm)表示待估的地球引力位系数，βlmo表示参考地球重力场模型EGM2008的引力位系数.

累积大地水准面误差公式表示如下

3 原理 3.1 双向车轮双星编队

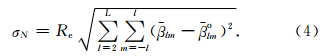
双向车轮双星编队系统的相对椭圆运动的长半轴和短半轴之比为ρmax ∶ ρmin=2 ∶ 1，可同时获得轨向和径向的卫星观测数据. 双向车轮双星编队系统的长短半轴比例可通过轨道离心率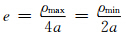(a表示卫星到地心的距离)设定，一颗卫星的远地点和另一颗卫星的近地点的间距等于双星的径向最大距离ρmin，而轨向最大距离ρmax为径向最大距离ρmin的2倍(Schaub and Junkins， 2003). 依据双星径向距离最大值出现的方向，双向车轮双星编队系统包括经向车轮双星编队(图 1)和纬向车轮双星编队(图 2). 在图 1—3中，O-XYZ表示地心惯性坐标系，X轴指向平春分点的方向，Z轴指向地球自转轴 的方向，Y轴和X轴、Z轴呈右手螺旋关系. o-xyz 表示卫星轨道坐标系，x轴指向卫星运动方向(along-track)，y轴指向垂直于轨道面方向(cross- track)，z轴由地心指向外(radial-track).

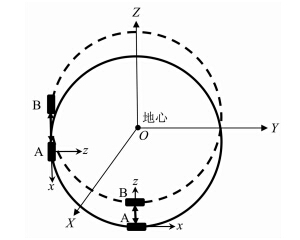图 1 经向车轮双星编队Lo-AR-Cartwheel-A/B测量原理Fig. 1(Measurement principle of the twin Lo-AR-Cartwheel-A/B satellites formation

图 2 纬向车轮双星编队 La-AR-Cartwheel-A/B测量原理Fig. 2 Measurement principle of the twin La-AR-Cartwheel-A/B satellites formation

双向车轮双星编队的初始运动状态表示如下(Elsaka，2010)：

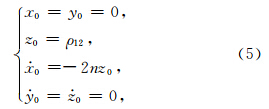
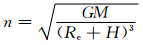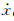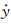其中，表示平均轨道角速度，H表示卫星轨道高度，(x0，y0，z0)和(0，0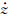，0)表示初始运动的位置和速度，ρ12表示星间距离.

双向车轮双星编队的相对运动方程表示如下：

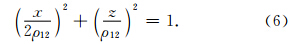
3.2 三向车轮双星编队

如图 3所示，三向车轮双星编队系统可同时获 得轨向、垂向和径向的卫星观测数据. 三向车轮双星编队的初始运动状态表示如下(Elsaka，2010)：

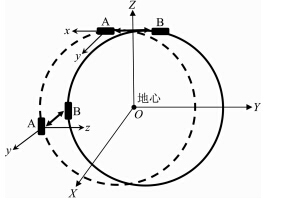图 3 三向车轮双星编队 ACR-Cartwheel-A/B测量原理Fig. 3 Measurement principle of the twin ACR-Cartwheel-A/B satellites formation

三向车轮双星编队的相对运动方程表示如下：

4 结果 4.1 Cartwheel-A/B双星编队观测值的色噪声模拟

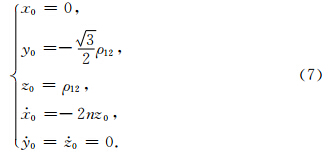
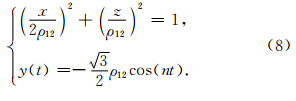
本文首先利用9阶Runge-Kutta线性单步法结合12阶Adams-Cowell线性多步法数值积分公式模拟了Cartwheel-A/B双星的轨道位置和轨道速度(刘林，1992)，开普勒轨道根数如表 2所示，参考 地球重力场模型EGM2008截断至120阶.

表 2 车轮双星编队Cartwheel-A/B的开普勒轨道根数 Table 2 Keplerian orbital elements of the twin Cartwheel-A/B satellites formation

基于Gauss-Markov模型，卫星观测值的色噪声表示如下(沈云中，2000):

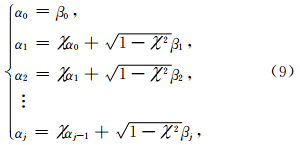
其中，表示色噪声相关系数；βj(j=1，2，…)表示正态分布的随机白噪声(=0)，j表示观测点的个数；αj(j=1，2，…)表示具有相关性的色噪声(0< <1).

本文基于Gauss-Markov色噪声模型，利用相关系数(激光干涉测距仪的星间速度0.85，GPS接收机的轨道位置和轨道速度0.95，星载加速度计的非保守力0.90)和采样间隔10 s模拟了星间速度、轨道位置、轨道速度和非保守力的色噪声，其中星间速度，以及轨道位置、轨道速度和非保守力在X轴方向的色噪声如图 4所示，统计结果如表 3所示.

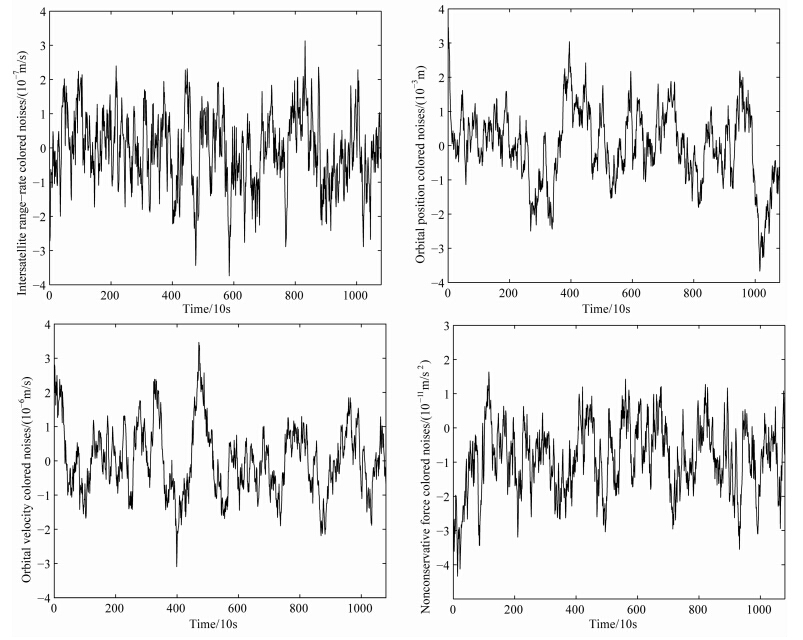图 4 星间速度、轨道位置、轨道速度和非保守力的色噪声模拟Fig. 4 Colored noises of intersatellite range-rate，orbital position，orbital velocity and non-conservative force

表 3 Cartwheel-A/B卫星观测值色噪声统计结果 Table 3 Statistical results of colored noise from Cartwheel-A/B satellite observations
4.2 卫星重力反演 4.2.1 Cartwheel-A/B双星编队可行性检验

如图 5所示，星号线表示德国波茨坦地学研究中心(GFZ)公布的120阶EIGEN-GRACE02S地球重力场模型的实测精度，在120阶处反演累计大地水准面精度为1.893×10-1 m；实线表示基于星间速 度插值法，利用GRACE卫星关键载荷精度(星间速度10-6 m·s-1、轨道位置10-2 m、轨道速度10-5 m·s-1和非保守力10-10 m·s-2)、GRACE卫星轨道参数(轨道高度500 km、星间距离220 km、轨道倾角89°和轨道离心率0.001)、观测时间30天和采样间隔10 s，反演120阶ACR-Cartwheel-A/B地球重力场 的模拟精度，在120阶处累计大地水准面精度为1.329×10-1 m；在各阶处的累计大地水准面精度统计结果如表 4所示. 研究结果表明：基于相同的卫星关键载荷精度和卫星轨道参数，利用ACR-Cartwheel-A/B双星编队反演地球重力场精度(实线)较采用GRACE卫星编队反演地球重力场精度(星号线)平均提高2.6倍，主要原因分析如下：

表 4 基于GRACE和ACR-Cartwheel-A/B双星编队反演累计大地水准面精度统计 Table 4 Statistical results of cumulative geoid height errors from GRACE and ACR-Cartwheel-A/B

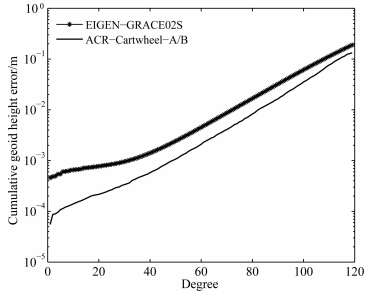图 5 基于GRACE和ACR-Cartwheel-A/B双星编队反演累计大地水准面精度对比Fig. 5 comparison of cumulative geoid height errors between GRACE and ACR-Cartwheel-A/B twin-satellite formations

第一，当前GRACE双星编队采用串行跟踪模式仅能感测轨向重力场信号，但无法获得垂向和径 向的重力场信号，因此必将导致由于垂向和径向信 号缺失而引起的地球静态和时变重力场反演精度下降，以及地球时变重力场信号在南北向的条带误差效应.

第二，下一代ACR-Cartwheel-A/B双星编队采用三向车轮跟踪模式可同时获得轨向、垂向和径向的地球重力场信号：(1)由于ACR-Cartwheel-A/B增加了垂向和径向重力场信号，因此进一步提高了地球重力场反演精度；(2)由于ACR-Cartwheel-A/B观测误差更加各向同性，因此有利于减弱地球时变重力场信号在南北向的条带误差影响. 因此，ACR-Cartwheel-A/B双星编队是进一步提高下一代地球重力场模型空间分辨率的优选途径. 4.2.2 基于双向和三向车轮编队反演重力场精度对比

如图 6所示，虚线、实线和十字线表示基于星间速度插值法，采用卫星轨道参数(表 2)、卫星关键载荷精度指标(表 3)、观测时间30天和采样间隔10 s，分别反演120阶Lo-AR-Cartwheel-A/B、La-AR-Cartwheel-A/B和ACR-Cartwheel-A/B地球重力场的模拟精度，在120阶处累计大地水准面精度为5.115×10-4 m、4.923×10-4m和3.488×10-4 m；在各阶处的累计大地水准面精度统计结果如表 5所示. 研究结果表明：

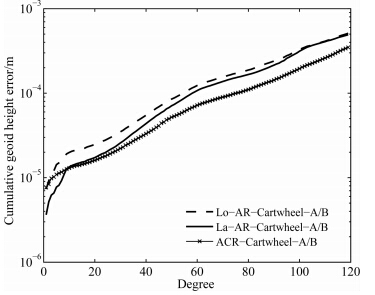图 6 基于经向车轮、纬向车轮和三向车轮双星编队反演累计大地水准面精度Fig. 6 comparison of cumulative geoid height errors based on Lo-AR-Cartwheel-A/B，La-AR-Cartwheel-A/B and ACR-Cartwheel-A/B twin-satellite formations

表 5 基于不同类型的车轮双星编队反演累计大地水准面精度统计 Table 5 Statistics of cumulative geoid height errors from different types of Cartwheel satellite formations

第一，基于纬向车轮双星编队La-AR-Cartwheel-A/B反演累计大地水准面精度较基于经向车轮双星编队Lo-AR-Cartwheel-A/B反演精度平均提高约20%. 具体原因分析如下：图 7和图 8分别表示经向车轮双星编队Lo-AR-Cartwheel-A/B和纬向车轮双星编队La-AR-Cartwheel-A/B在1个月内的星间距离变化趋势. 表 6表示双向和三向车轮双星编队在第1天和第30天的星间距离波动，其中波峰值(最大值)表示轨向星间距离，波谷值(最小值)表示径向星间距离. 在第1天内，两种双向车轮 双星编队的轨向和径向星间距离均保持平稳波动； 相对于第1天的轨向和径向星间距离，在第30天内，两种双向车轮双星编队的径向星间距离仍保 持平稳波动，但经向车轮双星编队Lo-AR-Cartwheel-A/B 的轨向星间距离漂移量(2.9 km)大于纬向车轮双星编队La-AR-Cartwheel-A/B的轨向星间距离漂移量(1.8 km). 由于经向车轮双星编队Lo-AR-Cartwheel-A/B的最大轨向星间距离位于赤道处，受地球椭球项J2的影响较大，因此随着时间推移，轨向星间距离的漂移将逐渐加剧. 综上所述，由于纬向车轮双星编队La-AR-Cartwheel-A/B的轨 道稳定性优于经向车轮双星编队Lo-AR-Cartwheel-A/B的，因此，基于纬向车轮双星编队La-AR-Cartwheel-A/B反演地球重力场精度高于基于经向车轮双星编队Lo-AR-Cartwheel-A/B反演重力场精度.

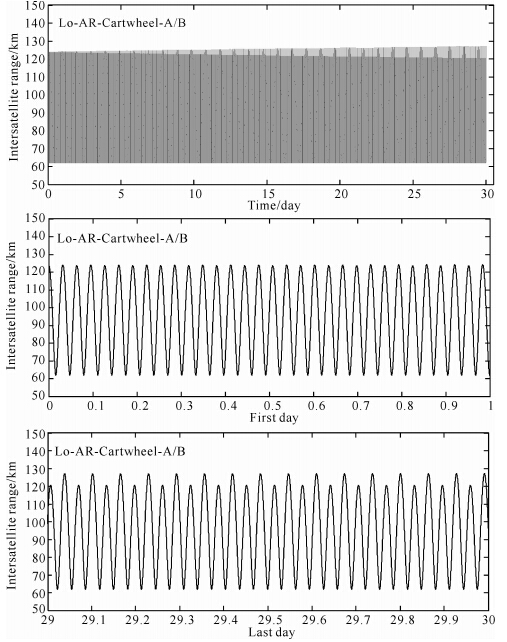图 7 经向车轮双星编队Lo-AR-Cartwheel-A/B的星间距离Fig. 7 Intersatellite range of the Lo-AR-Cartwheel-A/B satellite formation

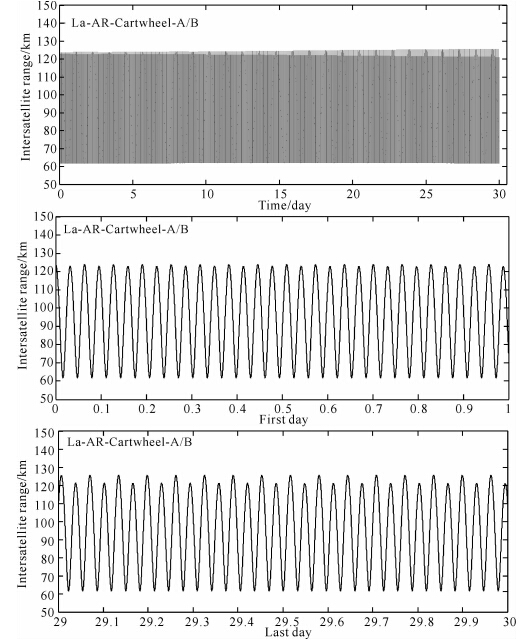图 8 纬向车轮双星编队La-AR-Cartwheel-A/B的星间距离Fig. 8 Intersatellite range of the La-AR-Cartwheel-A/B satellite formation

表 6 双向和三向车轮双星编队的第1天和第30天的星间距离 Table 6 A comparison of intersatellite ranges from Lo-AR-Cartwheel-A/B，La-AR-Cartwheel-A/B and ACR-Cartwheel-A/B twin-satellite formations in the first and thirtieth days

第二，在地球重力场长波段，基于纬向车轮双星编队反演累计大地水准面精度明显优于经向车轮双星编队. 但随着球函数阶数的增加，基于两种双向车轮双星编队反演重力场精度的差别逐渐缩小. 主要原因分析如下：由于GRACE卫星采用串行式双星编队模式，因此仅能获得轨向卫星观测数据；同时，GRACE卫星系统采用卫星跟踪卫星高低/低低观测模式敏感于地球重力场中长波信号. 因此，轨向卫星观测数据对地球中长波重力场反演精度贡献较大. 由于经向车轮双星编队Lo-AR-Cartwheel-A/B的轨向星间距离漂移程度较严重，因此基于经向车轮双星编队反演的地球中长波重力场精度明显低于纬向车轮双星编队. 但随着阶数的逐渐增加，轨向卫星观测数据对地球中长波重力场反演精度的优势将逐渐减弱，因此分别基于经向和纬向车轮双星编队反演地球重力场精度的能力将逐渐趋于一致.

第三，利用三向车轮双星编队ACR-Cartwheel-A/B反演地球重力场的精度较分别利用经向车轮双星编队Lo-AR-Cartwheel-A/B和纬向车轮双星编队La-AR-Cartwheel-A/B反演地球重力场的精度平均提高60%和35%. 这是因为经向车轮双星编队Lo-AR-Cartwheel-A/B和纬向车轮双星编队La-AR-Cartwheel-A/B仅能获得轨向和径向的卫星观测数据，由于缺乏垂向卫星观测数据，因此地球重力场信号和误差的均匀性较差，最终导致了地球重力场精度的损失. 由于三向车轮双星编队ACR-Cartwheel-A/B可以同时获得轨向、垂向和径向的地球重力场信息，卫星观测数据具有各向同性的优点，因此地球重力场反演精度得以较大程度提升.

综上所述，三向车轮双星编队ACR-Cartwheel-A/B是建立下一代高精度和高空间分辨地球重力场模型的优化选择. 5 结论

由于当前GRACE双星计划的设计缺陷(如无法降低卫星轨道高度、无法提高关键载荷精度、无法获得各向同性重力信息等)较大程度降低了地球重力场的时空分辨率，因此本文利用星间速度插值法开展了基于下一代三向车轮双星编队优化地球重力场空间分辨率的论证研究. 具体结论如下：

(1)基于GRACE卫星轨道参数和关键载荷精度，利用三向车轮双星编队ACR-Cartwheel-A/B反演了120阶地球重力场，并验证了基于下一代三向车轮双星编队ACR-Cartwheel-A/B解算重力场精度高于当前GRACE串行编队的可行性.

(2)采用卫星轨道参数(轨道高度350 km、星间距离100 km、轨道倾角89°、轨道离心率0.0046)和卫星 关键载荷精度(星间速度10-7 m·s-1、轨道位置10-3 m、轨道速度10-6 m·s-1、非保守力10-11 m·s-2)，分别反 演了120阶Lo-AR-Cartwheel-A/B、La-AR-Cartwheel-A/B和ACR-Cartwheel-A/B地球重力场精度. 结果表明：①基于纬向车轮双星编队La-AR-Cartwheel-A/B 反演地球重力场精度高于基于经向车轮双星编队Lo-AR-Cartwheel-A/B反演重力场精度；②随着阶数逐渐增加，轨向卫星观测数据对地球中长波重力场反演精度的优势将逐渐减弱，因此分别基于经向和纬向车轮双星编 队反演地球重力场精度的能力将逐渐趋于一致；③三向车轮双星编队ACR-Cartwheel-A/B 是反演下一代高精度和高空间分辨地球重力场的优选途径. 致谢 感谢匿名评审专家. 感谢美国宇航局(NASA)、欧空局(ESA)等科研机构提供了下一代卫星重力编队的相关信息.

参考文献
[1] Anselmi A, Cesare S, Cavaglia R. 2010. Assessment of a next generation mission for monitoring the variations of Earth's gravity. ESA Contract 22643/09/NL/AF, Final Report, Issue 2, 22 Dec.
[2] Bender P L, Nerem R S, Wahr J M. 2003. Possible future use of laser gravity gradiometers. Space Science Reviews, 108(1-2): 385-392.
[3] Bender P L, Wiese D N, Nerem R S. 2008. A possible dual-GRACE mission with 90 degree and 63 degree inclination orbits. //Pro-123 Design Considerations for A Dedicated Gravity 97 Proceedings of the Third International Symposium on Formation Flying, Missions and Technologies. ESA/ESTEC, Noordwijk, 1-6.
[4] Cesare S, Sechi G. 2013. Next generation gravity mission. //D'Errico M ed. Distributed Space Missions for Earth System Monitoring. Space Technology Library Volume 31, 575-598.
[5] Cheng L Y, Xu H Z. 2006. The rotation of the gravity potential on the Earth's gravity field recovery. Chinese J. Geophys. (in Chinese), 49(1): 93-98.
[6] Elsaka B, Ilk K H, Kusche J. 2009. Simulated multiple formation flights for future gravity field recovery. //Poster in European Geosciences Union (EGU), General Assembly, Vienna, Austria.
[7] Elsaka B. 2010. Simulated satellite formation flights for detecting the temporal variations of the Earth's gravity field [Ph. D. thesis]. Bonn: University of Bonn.
[8] Flechtner F, Neumayer K H, Doll B, et al. 2009. GRAF-A GRACE follow-on mission feasibility study. Geophysical Research Abstracts, Vol. 11, EGU, 8516.
[9] Gruber Th, Peters Th, Zenner L. 2009. The role of the atmosphere for satellite gravity field missions. //Sideris M G ed. Observing Our Changing Earth. International Association of Geodesy Symposia Volume 133, 105-112.
[10] Gruber Th. 2010. E. motion—A proposal for a future satellite mission for the determination of the time-variable Earth gravity field. GRACE Science Team Meeting, Potsdam, 11.
[11] Gruber Th, Panet I, Johannessen J, et al. 2012. Earth system mass transport mission (e. motion): technological and mission configuration challenges. //International Symposium on Gravity, Geoid and Height Systems, GGHS2012, Venice, 9-12.
[12] Han S C, Jekeli C, Shum C K. 2004. Time-variable aliasing effects of ocean tides, atmosphere, and continental water mass on monthly mean GRACE gravity field. Journal of Geophysical Research, 109(B4), doi: 10.1029/2003JB002501.
[13] Kim J. 2000. Simulation study of a low-low satellite-to-satellite tracking mission [Ph. D. thesis]. Austin: University of Texas.
[14] Klees R, Revtova E A, Gunter B C, et al. 2008. The design of an optimal filter for monthly GRACE gravity models. Geophysical Journal International, 175(2): 417-432.
[15] Liu L. 1992. Orbital Mechanics of Artificial Earth Satellites (in Chinese). Beijing: Higher Education Press, 1-619.
[16] Loomis B D, Nerem R S, Luthcke S B. 2012. Simulation study of a follow-on gravity mission to GRACE. Journal of Geodesy, 86(5): 319-335.
[17] Massonnet D. 1998. Roue interfrometrique. French patent no 339920D17306RS.
[18] Mayer-Gürr T. 2006. Gravitationsfeldbestimmung aus der Analyse kurzer Bahnbogen am Beispiel der Satellitenmissionen CHAMP und GRACE [Ph. D. thesis]. Bonn: University of Bonn.
[19] Moore P, King M A. 2008. Antarctic ice mass balance estimates from GRACE: tidal aliasing effects. Journal of Geophysical Research, 113(F2), doi: 10.1029/2007JF000871.
[20] Panet I, Flury J, Biancale R, et al. 2013. Earth system mass transport mission (e. motion): a concept for future Earth gravity field measurements from space. Surveys in Geophysics, 34: 141-163.
[21] Petit G, Luzum B. 2010. IERS Conventions (2010). IERS Technical Note 36, Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main, Germany.
[22] Ray R D, Luthcke S B. 2006. Tide model errors and GRACE gravimetry: towards a more realistic assessment. Geophysical Journal International, 167(3): 1055-1059.
[23] Roesset P J. 2003. A simulation study of the use of accelerometer data in the GRACE mission [Ph. D. thesis]. Austin: University of Texas, 1-253.
[24] Rummel R. 2003. How to climb the gravity wall. Space Science Reviews, 108(1-2): 1-14.
[25] Schaub H, Junkins J L. 2003. Analytical Mechanics of Space Systems. Reston, VA : AIAA Education Series.
[26] Seo K W, Wilson C R., Chen J L, et al. 2008. GRACE's spatial aliasing error. Geophysical Journal International, 172(1): 41-48.
[27] Sharifi M A, Sneeuw N, Keller W. 2007. Gravity recovery capability of four generic satellite formations. //Kilicoglu A, forsberg R eds. Gravity Field of the Earth. General Command of Mapping, ISSN 1300-5790, Special issue 18, 211-216.
[28] Shen Y Z. 2000. Study of recovering gravitational potential model from the ephemerides of CHAMP [Ph. D. thesis](in Chinese). Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 1-111.
[29] Shen Y Z, Xu H Z, Wu B. 2005. Simulation of recovery of the geopotential model based on intersatellite acceleration data in the low-low satellite to satellite tracking gravity mission. Chinese J. Geophys. (in Chinese), 48(4): 807-811.
[30] Silvestrin P, Aguirre M, Massotti L, et al. 2012. The future of the satellite gravimetry after the GOCE mission. //Kenyon S, Pacino M C, Marti U, eds. Geodesy for Planet Earth. International Association of Geodesy Symposia Volume 136, 223-230.
[31] Sneeuw N, Schaub H. 2004. Satellite clusters for future gravity field missions. //IAG International Symposium, Gravity, Geoid, and Space Missions, Porto, Portugal.
[32] Sneeuw N, Flury J, Rummel R. 2005. Science requirements on future missions and simulated mission scenarios. Earth Moon Planets, 94(1-2): 113-142.
[33] Sneeuw N, Schaub H. 2005. Satellite clusters for future gravity field missions. //Jekeli C, Ba-stos L, Fernandes J, eds. Gravity, Geoid and Space Missions. International Association of Geodesy Symposia Vol. 129. Berlin Heidelberg: Springer, 12-17.
[34] Stephens M, Craig R, Leitch J, et al. 2006. Demonstration of an interferometric laser ranging system for a follow-on gravity mission to GRACE. // Proceedings of IEEE International Conference on Geoscience and Remote Sensing Symposium. Denver, CO: IEEE, 1115-1118.
[35] Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data. Geophysical Research Letters, 33(8): L08402, doi: 10.1029/2005GL025285.
[36] Wiese D N, Folkner W M, Nerem R S. 2009. Alternative mission architectures for a gravity recovery satellite Mission. Journal of Geodesy, 83(6): 569-581.
[37] Wiese D N, Nerem R S, Lemoine F G. 2012. Design considerations for a dedicated gravity recovery satellite mission consisting of two pairs of satellites. Journal of Geodesy, 86(2): 81-98.
[38] Zhang H W, Xu H Z, Wang A S. 2004. Tidal wave formulas of solid tide on the temporal changes of gravitational field. Acta Geodaetica et Cartographica Sinica (in Chinese), 33(4): 299-302.
[39] Zhang X F. 2007. The Earth's field model recovery on the basis of satellite-to-satellite tracking missions (in Chinese)[Ph. D. thesis]. Shanghai: Tongji University, 1-120.
[40] Zheng W, Shao C G, Luo J, et al. 2006. Numerical simulation of Earth's gravitational field recovery from SST based on the energy conservation principle. Chinese J. Geophys. (in Chinese), 49(3): 712-717.
[41] Zheng W, Shao C G, Luo J, et al. 2008. Improving the accuracy of GRACE Earth's gravitational field using the combination of different inclinations. Progress in Natural Science, 18(5): 555-561.
[42] Zheng W, Xu H Z, Zhong M, et al. 2009a. Physical explanation of influence of twin and three satellite formation mode on the accuracy of Earth's gravitational field. Chinese Physics Letters, 26(2): 029101-1-029101-4.
[43] Zheng W, Xu H Z, Zhong M, et al. 2009b. Accurate and rapid error estimation on global gravitational field from current GRACE and future GRACE Follow-On missions. Chinese Physics B, 18(8): 3597-3604.
[44] Zheng W, Xu H Z, Zhong M, et al. 2010a. Research progress in international gravity satellites and future satellite gravity measurement program in China. Science of Surveying and Mapping (in Chinese), 35(1): 5-9.
[45] Zheng W, Xu H Z, Zhong M, et al. 2010b. Research on optimal selection of orbital parameters in the Improved-GRA
[1] Zheng W, Xu H Z, Zhong M, et al. 2010b. Research on optimal selection of orbital parameters in the Improved-GRACE satellite gravity measurement mission. Journal of Geodesy and Geodynamics (in Chinese), 30(2): 43-48.
[2] Zheng W, HSU H T, Zhong M, et al. 2010c. Efficient and rapid estimation of the accuracy of future GRACE Follow-On Earth′s gravitational field using the analytic method. Chinese J. Geophys. (in Chinese), 53(4): 796-806, doi: 10.3969/j.issn.0001-5733.2010.04.004.
[3] Zheng W, Xu H Z, Zhong M, et al. 2011. Accurate and fast measurement of GRACE Earth′s gravitational field using the intersatellite range-acceleration method. Progress in Geophysics (in Chinese), 26(2): 416-423, doi: 10.3969/j.issn.1004-2903.2011.02.003.
[4] Zheng W, Hsu H T, Zhong M, et al. 2012. Precise recovery of the Earth′s gravitational field with GRACE: Intersatellite Range-Rate Interpolation Approach. IEEE Geoscience and Remote Sensing Letters, 9(3): 422-426.
[5] Zheng W, Xu H Z, Zhong M, et al. 2012a. Progress in international next-generation satellite gravity measurement missions. Journal of Geodesy and Geodynamics (in Chinese), 32(3): 152-159.
[6] Zheng W, Hsu H T, Zhong M, et al. 2012b. Impacts of interpolation formula, correlation coefficient and sampling interval on the accuracy of GRACE Follow-On intersatellite range-acceleration. Chinese J. Geophys. (in Chinese), 55(3): 822-832, doi: 10.6038/j.issn.0001-5733.2012.03.012.
[7] Zheng W, Hsu H T, Zhong M, et al. 2013. Precise and rapid recovery of the Earth′s gravitational field by the next-generation four-satellite cartwheel formation system. Chinese J. Geophys. (in Chinese), 56(9): 2928-2935, doi: 10.6038/cjg20130907.
[8] Zheng W, Hsu H T, Zhong M, et al. 2014. Precise and rapid recovery of the Earth′s gravity field from the next-generation GRACE Follow-On mission using the residual intersatellite range-rate method. Chinese J. Geophys. (in Chinese), 57(1): 31-41, doi: 10.6038/cjg20140104.
[9] Zhou X H. 2005. Research on satellite gravity and its application (in Chinese) ［Ph. D. thesis］. Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 1-138.
[46] 程芦颖, 许厚泽. 2006. 地球重力场恢复中的位旋转效应. 地球物理学报, 49(1): 93-98.
[47] 刘林. 1992. 人造地球卫星轨道力学. 北京: 高等教育出版社, 1-619.
[48] 沈云中. 2000. 应用CHAMP卫星星历精化地球重力场模型的研究[博士论文]. 武汉: 中国科学院测量与地球物理研究所, 1-111.
[49] 沈云中, 许厚泽, 吴斌. 2005. 星间加速度解算模式的模拟与分析. 地球物理学报, 48(4): 807-811.
[50] 张捍卫, 许厚泽, 王爱生. 2004. 固体潮对地球重力场时变特征影响的潮波公式. 测绘学报, 33(4): 299-302.
[51] 张兴福. 2007. 应用低轨卫星跟踪数据反演地球重力场模型[博士论文]. 上海: 同济大学, 1-120.
[52] 郑伟, 邵成刚, 罗俊等. 2006. 基于卫-卫跟踪观测技术利用能量守恒法恢复地球重力场的数值模拟研究. 地球物理学报, 49(3): 712-717.
[53] 郑伟, 许厚泽, 钟敏等. 2010a. 国际重力卫星研究进展和我国将来卫星重力测量计划. 测绘科学, 35(1): 5-9.
[54] 郑伟, 许厚泽, 钟敏等. 2010b. Improved-GRACE卫星重力轨道参数优化研究. 大地测量与地球动力学, 30(2): 43-48.
[55] 郑伟, 许厚泽, 钟敏等. 2010c. 利用解析法有效快速估计将来GRACE Follow-On地球重力场的精度. 地球物理学报, 53(4): 796-806, doi: 10.3969/j.issn.0001-5733.2010.04.004.
[56] 郑伟, 许厚泽, 钟敏等. 2011. 基于星间加速度法精确和快速确定GRACE地球重力场. 地球物理学进展, 26(2): 416-423, doi: 10.3969/j.issn.1004-2903.2011.02.003.
[57] 郑伟, 许厚泽, 钟敏等. 2012a. 国际下一代卫星重力测量计划研究进展. 大地测量与地球动力学, 32(3): 152-159.
[58] 郑伟, 许厚泽, 钟敏等. 2012b. 插值公式、相关系数和采样间隔对GRACE Follow-On星间加速度精度的影响. 地球物理学报, 55(3): 822-832, doi: 10.6038/j.issn.0001-5733.2012.03.012.
[59] 郑伟, 许厚泽, 钟敏等. 2013. 基于下一代四星转轮式编队系统精确和快速反演FSCF地球重力场. 地球物理学报, 56(9): 2928-2935, doi: 10.6038/cjg20130907.
[60] 郑伟, 许厚泽, 钟敏等. 2014. 基于残余星间速度法精确和快速反演下一代GRACE Follow-On地球重力场. 地球物理学报, 57(1): 31-41, doi: 10.6038/cjg20140104.
[61] 周旭华. 2005. 卫星重力及其应用研究[博士论文]. 武汉: 中国科学院测量与地球物理研究所, 1-138.