2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
Numerical experiments reveal:(1) for a generally-chosen relaxation factor, the levels of the multi-grid decrease as the complexity of the model increases, and, accordingly, the method becomes less practical; (2) for complex models, the relaxation factor obtained by local mode analysis increases the levels and reduces the number of iterations for each single frequency. The bi-conjugate-gradient-stabilized method based on multi-grid precondition obtains its efficiency and precision by using one multi-grid cycle for the approximate inversion of the preconditioner. To obtain reasonably fast convergence of the multi-grid method for complex model, local model analysis is applied in the relaxation factor selection. Compared with a generally-chosen relaxation factor, the relaxation factor obtained by local mode analysis increases the levels and guarantees the convergence and practicality of the multi-grid method.These conclusions are of great significance for application of the multi-grid-precondition-based iterative algorithm.
全波形反演是近些年来地震勘探领域比较热门的研究课题,它表现出来的巨大潜力激起了越来越多研究者的兴趣.全波形反演方法是利用叠前地震波场的运动学和动力学信息重建地下速度、密度等物性参数,具有定量揭示复杂地质背景下构造与岩性细节信息的优势,它可在时间域或频率域实现(Tarantola,1984;Pratt,1990;Pratt et al., 1990;Pratt et al., 1998).频率域全波形反演方法因其灵活性和成本优势备受青睐,其核心是频率域波动方程正演,它适合多炮计算,便于模拟衰减效应,可灵活选择频率成分进行反演和层析成像(Virieux and Operto, 2009).
关于频率域波动方程正演方法,Jo等(1996)提出了频率域常密度标量波动方程的最优9点差分格式,相比于经典的5点格式,将最小波长内所需剖分网格点数减小到4;Štekl和Pratt(1998)将Jo等的最优9点格式推广到了变密度声波方程及黏弹介质中的波动方程;考虑到Jo等的最优9点差分格式只适应于横向网格间距和纵向网格间距相等的情况,Chen(2012)又发展了可以适应任意横纵网格间距的平均导数优化格式.
对于频率域波动方程经有限差分离散得到的大型线性方程组的求解,可采用直接解法或迭代解法,二者各有优缺点.直接解法的阻抗矩阵LU分解结果可以重复利用,多炮正演效率高(Marfurt,1984),然而对于大规模的问题,由于受存储和计算量的限制,LU分解直接解法一般不再适用,而是采用迭代方法.Riyanti等(2006)提出了一种重要的迭代方法——基于多重网格预条件的双共轭梯度稳定化方法,它采用一个频率域的强阻尼波动方程算子作为双共轭梯度稳定算法的预条件算子,多重网格算法用来求解预条件方程,二者结合可以提高计算效率,并节约内存.多重网格算法是20世纪60年代,前苏联数学家为提高隐式差分的求解速度提出来的,70年代中期Br and t又对其进行了深入的研究和发展(马召贵等,2010).其基本思想是将误差中的低频成分,通过网格变换到粗网格上进行快速迭代消除,克服了一般迭代算法对于低频误差消除较慢的缺点,具体操作中包含松弛迭代,网格变换,直接求解和修正四个主要部分.本文重点讨论了多重网格预条件求解过程中的松弛因子选择方法.研究结果表明,(1)对于一般选取的松弛因子,随模型复杂性的增加,所能计算的重数逐渐下降,方法的实用性也随之下降;(2)对于复杂模型,采用局部模式分析方法(Briggs et al., 2000)选取松弛因子,定量分析了平均导数优化格式中网格间距、频率和速度对于收敛情况的影响,并应用于SEG/EAGE Overthrust模型和Marmousi模型的正演计算,提高了所能计算的重数,保证了多重网格方法的收敛性和实用性. 2 平均导数优化格式与双共轭梯度稳定化迭代方法
二维频率域声波方程为
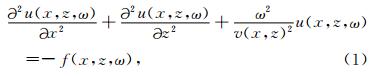
Chen(2012)提出的平均导数优化格式在保证了将一个波长内所需的剖分网格点数减少到4的同时,又可以适应任意横纵网格间距,二维情况下其具体形式如下:
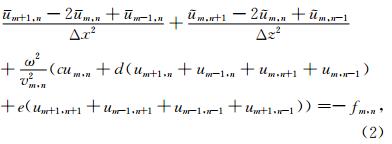
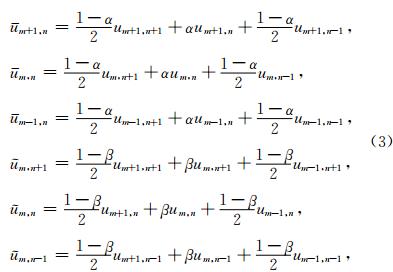
式(3)中e=(1-c-4d)/4,权系数α,β,c,d可通过最小二乘法求解式(4)中数值频散误差E的最小值获得,即
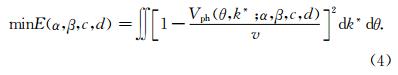
表 1给出了当Δx≥Δz时由最小二乘求得的最优权系数(Chen,2012),根据对称性,当Δx≤Δz时c,d值不变,只需对调α,β值即可.
|
|
表 1 Δx≥Δz时权系数α,β,c,d的最优取值 Table 1 Optimization coefficients for α,β,c and d when Δx≥Δz |
式(1)经平均导数优化格式离散后得到如下线性方程组:

双共轭梯度稳定化迭代方法(BI-CGSTAB)是 一种求解大型不定矩阵的常用方法(Van der Vorst,1992),它以初始猜测值 u 0进行迭代更新 u i,直到残差‖ s - Bu i‖足够小,其收敛速度依赖于预条件矩阵,在式(5)中引入预条件矩阵 M 后,可以得到下面的方程:

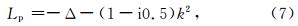
预条件方程采用一次多重网格循环是考虑到以下两点:第一,预条件矩阵 M 包含O(n2)个元素,而一次多重网格循环同样需要O(n2)次操作,求解时具有最优的计算复杂度(Plessix,2007);第二,对于椭圆类方程,如泊松方程、扩散方程等正定问题和复波数Helmholtz方程(强阻尼声波方程),多重网格算法具有较好的应用效果(Kim et al., 2002),但是直接应用于无阻尼声波方程等不定问题时,算法不收敛.
多重网格算法是将细网格上的数值求解与粗网格上的数值求解相结合,细网格用来估计解中的高频震荡部分,粗网格用来估计解中的低频光滑部分.本文采用的是最常用的V循环多重网格算法(Briggs et al., 2000),下面以一个三重网格的V循环为例进行说明:
(1)以 u 0h为初值,在细网格上对 M h u h= v h做k次松弛迭代,得到近似值 u (k)h及残差量
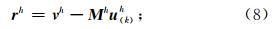
(2)通过限制算子 Ih 2h将残差量转移到网格间距扩大一倍的第二层网格上,其中 M 2h是在第二层网格上直接通过平均导数格式离散算子Lp获得的,之后以误差 e 02h=0为初值,对残差等式
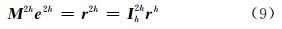
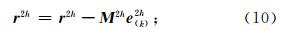
(3)通过限制算子 I 4h2h 将残差量转移到网格间距继续扩大一倍的第三层网格上,其中 M 4h是在第三层网格上直接通过平均导数格式离散算子Lp获得的,再采用LU分解直接解法求解
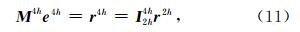
得到误差 e 4h;
(4)使用 e 4h对 e (k)2h做修正;
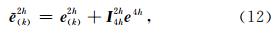
I 4h2h为插值算子,然后再以新的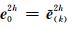 为初值,对式(9)的残差等式做m次迭代得到结果
为初值,对式(9)的残差等式做m次迭代得到结果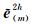 ;
;
(5)继续修正到细网格上得到预条件方程的近似解
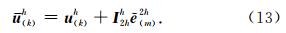
为了说明不直接采用多重网格算法求解声波方程而是将其应用于预条件方程的原因,我们将通过数值实验对比多重网格算法在两类方程上的实际应用效果.以一维均匀介质中的简谐波为例,实验中波传播速度3000 m·s-1,频率10 Hz,离散点数为257,点间距为10 m,计算中采用了一次V循环,并将LU直接解法结果与其进行了对比,如图 1.
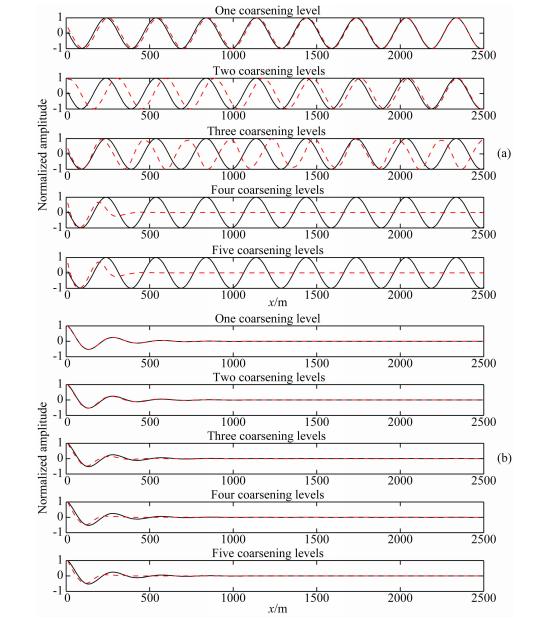 | 图 1 直接求解和一次V循环求解结果 (a)无阻尼声波方程,即L=-Δ-k2;(b)强阻尼声波方程,即Lp=-Δ-(1-i0.5)k2. 图中黑实线为直接解法获得的精确解,红虚线为一次V循环得到的近似解. Fig.1 Solutions of direct solver and one multigrid V-cycle (a)Pure acoustic case,L=-Δ-k2;(b)Heavily damped viscoacoustic case,Lp=-Δ-(1-i0.5)k2. The black line corresponds to the exact solution obtained with a direct solver, and the dotted red line corresponds to the solutions obtained after one multigrid V-cycle. |
数值实验结果(如图 1)显示,多重网格算法在无阻尼声波方程求解时,计算结果在网格层数达到 三层以上已完全偏离真实解,这是由于阻抗矩阵的不定性(正负特征值均存在),粗网格上的解不是近似等于真实解的光滑部分,而对于强阻尼声波方程,能量在一个波长以外几乎完全衰减,一次的多重网格V循环就可以近似达到其真实解. 4 多重网格预条件的松弛因子选取
在多重网格预条件的迭代求解过程中,网格变换的前后都要进行松弛迭代,目的是快速消除相应网格上误差的高频分量,其作用效果直接影响到多重网格算法对于预条件方程的求解结果.为此,在通过数值实验验证基于多重网格预条件的双共轭梯度稳定化算法(简称为多重网格预条件迭代法)的同时,我们进一步讨论了多重网格预条件过程中松弛因子的选取方法.
在这些数值实验中,我们采用了平均导数优化格式,震源子波为30 Hz主频的雷克子波,频率计算范围为0~80 Hz.对于任意给定的频率,网格间距的选取都保证了单位波长内的网格点数不少于4.一次的多重网格V循环算法用来求解预条件方程,计算中采用最大重数,即最粗网格上点数不能被2整除为止,松弛算子是加权雅克比迭代法,限制算子 为全 加权,插值算子为线性插值.BICGSTAB迭代的终止条件采用传统的归一化残差范数 ‖ s - Bu ‖/‖ s ‖. 此外,为了模拟无限介质,我们在每个方向上增加了15个点的PML边界层. 4.1 椭圆型方程松弛因子
4/5是多重网格算法中加权雅克比松弛算子的常用松弛因子,它是从椭圆型偏微分方程出发推导出的最适松弛因子,对于椭圆型方程有着较好的应用效果(Briggs et al., 2000).直接将其应用到预条件方程求解中也同样起到一定的作用.
在均匀模型计算中,取模型为nz×nx=97×97的网格,波速为3000 m·s-1,Δx=Δz=10 m,震源位于PML吸收层以下第10层的中间位置,接收点置于地表,道间距为10 m,如图 2a.分别利用直接法和多重网格预条件迭代法计算了单炮记录,并抽出x=480 m处的一道与解析解进行比较,由图 2b可见两种结果与解析解都具有较好的一致性.为了进一步研究多重网格预条件迭代法的实用性,又计算了相对复杂的SEG/EAGE Overthrust模型和Marmousi模型,其迭代结果均显示低频时收敛较慢,并且随着模型复杂度增加收敛较慢的低频点数也越来越多(如图 3),这与理论上随着频率的增大,矩阵 BM -1的条件数也增大,进而迭代次数也随之增大相矛盾,并且在Marmousi模型的计算中还发现网格重数达到三重以上,个别频点的迭代结果出现不收敛.其原因可能是在模型比较复杂时,椭圆型偏微分方程的最适松弛因子不完全适用于预条件方程的求解,为此,我们采用了局部模式分析方法对于复杂模型的松弛因子进行了分析与选取.
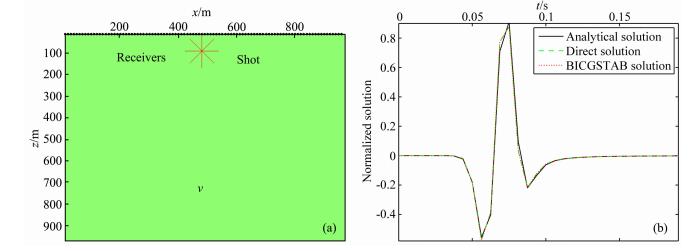 | 图 2 均匀模型 (a)观测系统布设图;(b)直接解法和多重网格预条件BICGSTAB迭代解法的单道地震记录与解析解对比图. Fig. 2 Homogeneous model (a)The acquisition geometry of homogeneous model;(b)Comparison of single trace obtained by direct solver, BICGSTAB iteration and analytical solution. |
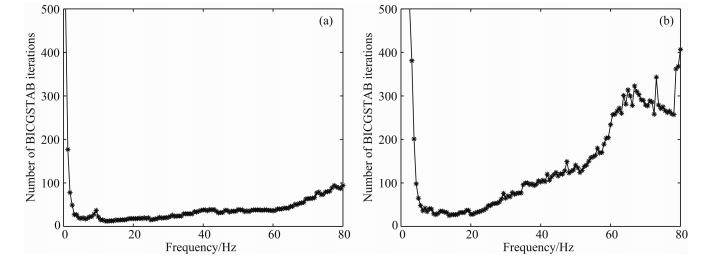 | 图 3 松弛因子为4/5时迭代次数与频率关系 (a)均匀模型;(b)SEG/EAGE Overthrust模型. Fig. 3 The relationship between number of BICGSTAB iterations and frequency when relaxation factor equals 4/5 (a)Homogeneous model;(b)SEG/EAGE Overthrust model. |
局部模式分析法(Briggs et al., 2000)首先假设松弛迭代是一个局部过程,每一个未知量使用其周围临近点的信息来升级,它要求在内部网格节点进行迭代时边界条件可以被忽略,而强阻尼声波方程在一个波长以外能量几乎完全衰减,所以满足这一要求.在松弛迭代过程中,m次松弛误差和m+1次松弛误差满足
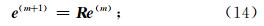
其次还要假设误差由傅里叶模式组成,重点是讨论松弛算子对于这些模式的影响.傅里叶模式在第j个网格节点上的分量可以表示为

松弛算子使用的加权雅克比迭代法的迭代矩阵为
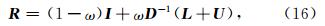
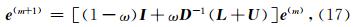
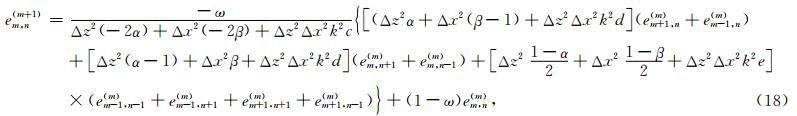
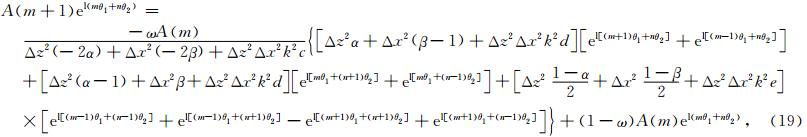

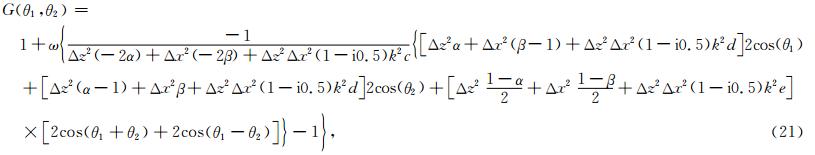
令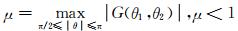 可保证迭代收敛.
可保证迭代收敛.
以Δx/Δz=1为例,当取频率为80 Hz,速度为1500 m·s-1时,根据平均导数优化格式的网格间距选取要求Δx=Δz=(1500/80)/4≈4 m,图 4给出了该情况下μ与松弛因子ω的关系.当选取μ最小值对应的松弛因子时,发现π附近,即对应于误差中高频成分的振幅因子要高于内部低频成分,如图 4b,这对于松弛算子迭代消除误差中高频成分是不利的.因此,我们在对松弛因子ω的选取中既要考虑使得μ较小,还要保证π附近的高频成分能够最大程度地在一次迭代中消除,综合考虑ω=0.53的效果较好,如图 4a.
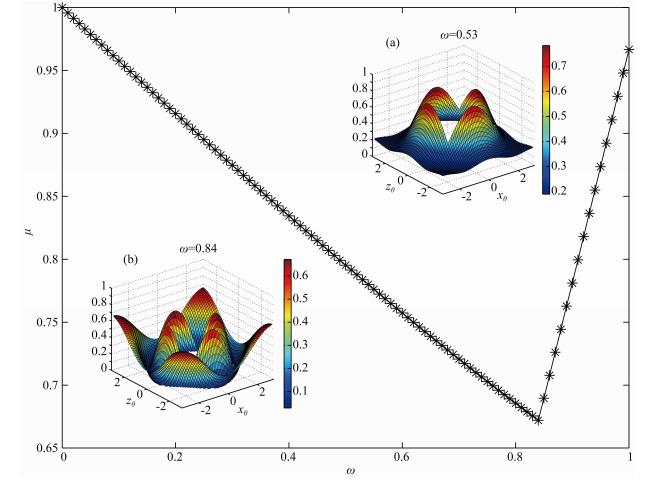 | 图 4 μ与松弛因子(ω)关系.内图为松弛因子ω=0.84(b)和0.53(a)时 G(θ1,θ2) 在π/2≤ θ1,θ2 ≤π区域内分布表面图 Fig. 4 The relationship between μ and relaxation factor(ω). The inset shows a surface of G(θ1,θ2) over the region π/2≤ θ1,θ2 ≤π when relaxation factor ω=0.84(b) and 0.53(a) |
此外,我们定量分析了平均导数优化格式中频率、速度和网格间距对于收敛情况的影响,如图 5.当控制其他条件不变时,μ随波场频率增加而呈现指数上升(如图 5a),即频率越高,松弛算子在一次迭代中对误差组分的作用效果就越弱,可通过增加松弛迭代次数来进行弥补;而μ与模型速度之间则呈现出负相关(如图 5b),即随速度增加,松弛算子作用越明显.然而在复杂模型中,各网格点上的速度值均不相同,关系也就变得较为复杂.综合这两种因素的作用效果,可以给出松弛因子的选择原则,要同时保证速度最低值和波场频率最高值对应的松弛因子,满足μ<1和π附近的高频成分能够最大程度地在一次迭代中消除这两点.由于局部模式分析法得出的规律是基于单个网格节点,没有将整个速度模型考虑在内,因此选取的松弛因子只能保证算法 收敛,不一定能保证收敛速度最快.在网格剖分 Δx≠Δz时,μ-w曲线趋势不变,但随二者的比值整体向上移动,意味着松弛算子作用效果逐渐减弱,其主要原因是松弛迭代中纵横方向网格间距不等导致的误差消除效果不一致,大网格间距方向上的松弛算子作用效果明显较弱(如图 5c内),进而影响到整个松弛迭代的收敛速度.
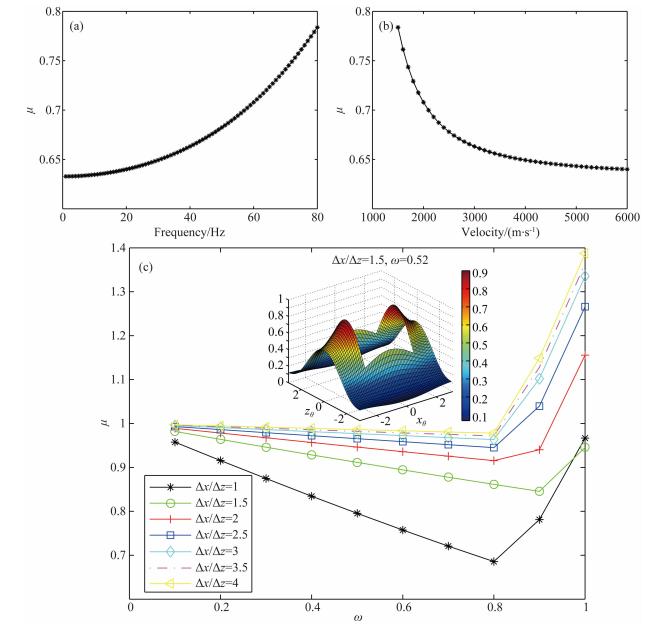 | 图 5 μ与频率(a)、模型速度(b)和Δx/Δz(c)关系.内图为Δx/Δz=1.5时 G(θ1,θ2) 在π/2≤ θ1,θ2 ≤π区域内分布表面图 Fig. 5 The relationship between relaxation factor and frequency(a),model velocity(b),Δx/Δz(c). The inset shows a surface of G(θ1,θ2) over the region π/2≤ θ1,θ2 ≤π when Δx/Δz=1.5 |
为了检验局部模式分析法选取的松弛因子的实际应用效果,本文分别正演计算了SEG/EAGE Overthrust模型(nz×nx=187×801)和Marmousi模型(nz×nx=750×737),模型剖分网格间距分别为Δx=Δz=(2500/80)/4≈8 m和Δx=Δz=(1500/80)/4≈4 m,震源位置(x,z)分别位于(3200 m,72 m)和(1472 m,76 m),接收点均置于地表,道间 距分别为8 m和4 m,如图 6a和7a.对比LU分解直接解法和多重网格预条件迭代解法的计算结果(如图 6和7),可以看出两个模型的迭代计算结果与直接求解结果都具有较好的一致性,为了更细致地分析两种算法的差异,分别对两种算法的单频波场和单炮记录随机抽取了3道进行对比,如图 6g、6h、7g、7h,结果显示两种算法得到的结果差别极小,量级均在误差允许范围内.此外,图 6b的迭代次数-频率关系曲线与图 3b相比较可以发现,原先低频部分迭代收敛较慢的现象已经得到了改善;而图 7b的迭代次数-频率关系曲线则表明,Marmousi模型在0~80 Hz频率范围内的所有频点均已收敛,克服了之前V循环采用3重以上个别频点出现迭代不收敛的现象,并将V循环网格重数扩充至5重,即极限网格重数.从而说明了局部模式分析法选取的松弛因子在应用于复杂模型的计算时,能够既减少了单个频点上的迭代次数,又提高了所能计算的重数,保证了多重网方法的收敛性和实用性.
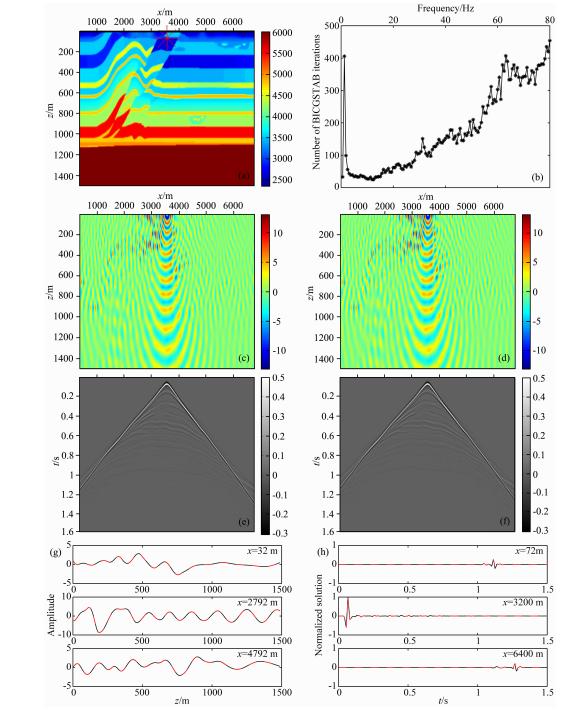 | 图 6 SEG/EAGE Overthrust模型直接求解和多重网格预条件迭代求解结果 (a)观测系统布设图;(b)迭代次数与频率关系(采用局部模式分析方法选取松弛因子);(c)30 Hz单频波场直接求解结果;(d)30 Hz单频波 场多重网格预条件迭代求解结果;(e)单炮记录直接求解结果;(f)单炮记录多重网格预条件迭代求解结果;(g)频率域结果c、d对比图;(h)时间 域结果e、f对比图.图中黑实线为直接解法结果,红虚线为多重网格预条件迭代法求解结果. Fig. 6 SEG/EAGE Overthrust model using the direct solver and the BICGSTAB iterative based on multi-grid precondition (a)The acquisition geometry of SEG/EAGE Overthrust model;(b)The relationship between number of BICGSTAB iterations and frequency(the relaxation factor obtained by local mode analysis);(c)The real part of the wavefield at 30 Hz obtained by direct solver;(d)The real part of the wavefield at 30 Hz obtained by iterative solver;(e)The seismogram obtained by direct solver;(f)The seismogram obtained by iterative solver;(g)Comparison between the frequency-domain results from(c) and (d);(h)Comparison between the time-domain results from(e) and (f). The black line corresponds to the solution obtained with a direct solver, and the dotted red line corresponds to the solutions obtained BICGSTAB iteration. |
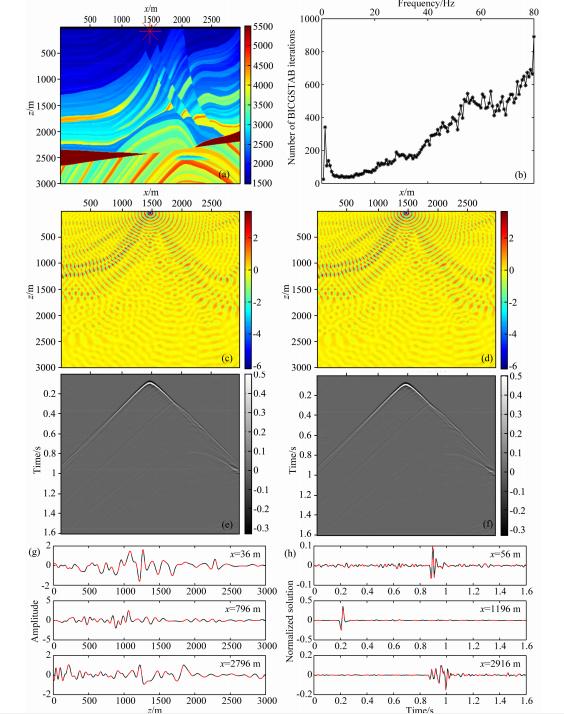 | 图 7 Marmousi模型直接求解和多重网格预条件迭代求解结果 (a)观测系统布设图;(b)迭代次数与频率关系(采用局部模式分析方法选取松弛因子);(c)30 Hz单频波场直接求解结果;(d)30 Hz单频波场 多重网格预条件迭代求解结果;(e)单炮记录直接求解结果;(f)单炮记录多重网格预条件迭代求解结果;(g)频率域结果(c、d)对比图;(h)时 间域结果(e、f)对比图.图中黑实线为直接解法结果,红虚线为多重网格预条件迭代法求解结果. Fig. 7 Marmousi model using the direct solver and the BICGSTAB iterative based on multi-grid precondition (a)The acquisition geometry of Marmousi model;(b)The relationship between number of BICGSTAB iterations and frequency(the relaxation factor obtained by local mode analysis);(c)The real part of the wavefield at 30 Hz obtained by direct solver;(d)The real part of the wavefield at 30 Hz obtained by iterative solver;(e)The seismogram obtained by direct solver;(f)The seismogram obtained by iterative solver;(g)Comparison between the frequency-domain results from(c) and (d);(h)Comparison between the time-domain results from(e) and (f). The black line corresponds to the solution obtained with a direct solver, and the dotted red line corresponds to the solutions obtained BICGSTAB iteration. |
本文研究了平均导数格式下的基于多重网格预条件的双共轭梯度稳定化方法,此算法在外层使用预条件的双共轭梯度稳定算法,并采用一个频率域的强阻尼波动方程算子作为预条件算子,而内层则利用一次V循环的多重网格算法来求解预条件方程,可以兼顾最优的计算复杂度和较高的精度,而对于复杂模型计算时采用椭圆型偏微分方程松弛因子所造成的收敛速度慢、甚至不收敛现象进行了说明,并引入了局部模式分析方法来选取松弛因子,定量分析了平均导数优化格式中网格间距、频率和速度对于收敛情况的影响.最终将所选取的松弛因子应 用于SEG/EAGE Overthrust模型和Marmousi模型的正演计算,与直接法求解的结果对比显示出较好的一致性,从而说明了局部模式分析法选取的松弛因子既减少了单个频点上的迭代次数,又提高了所能计算的重数,保证了多重网格方法的收敛性和实用性.
| [1] | Briggs W L, Van Emden H, McCormick S F. 2000. A Multigrid Tutorial Second Edition. Philadelphia, PA: Society for Industrial and Applied Mathematics. |
| [2] | Chen J B. 2012. An average-derivative optimal scheme for frequency-domain scalar wave equation. Geophysics, 77(6): T201-T210. |
| [3] | Erlangga Y A. 2008. Advances in iterative methods and preconditioners for the Helmholtz equation. Arch. Comput. Methods Eng., 15(1): 37-66. |
| [4] | Jo C H, Shin C, Suh J H. 1996. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics, 61(2): 529-537. |
| [5] | Kim S, Kim S. 2002. Multigrid simulation for high-frequency solutions of the Helmholtz problem in heterogeneous media. Society of Industrial and Applied Mathematics (SIAM) Journal on Scientific Computing, 24(2): 684-701. |
| [6] | Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. |
| [7] | Ma Z G, Wang S X, Song J Y. 2010. Multigrid iterative algorithm in frequency domain wave equation forward modeling. OilGeophysical Prospecting (in Chinese), 45(1): 1-5. |
| [8] | Plessix R E. 2007. A Helmholtz iterative solver for 3D seismic-imaging problems. Geophysics, 72(5): SM185-SM194. |
| [9] | Pratt R G. 1990. Frequency-domain elastic wave modeling by finite differences: A tool for cross-hole seismic imaging. Geophysics, 55(5): 626-632. |
| [10] | Pratt R G, Worthington M H. 1990. Inverse theory applied to multi-source cross-hole tomography, Part 1: Acoustic wave equation method. Geophysical Prospecting, 38(3): 287-310. |
| [11] | Pratt R G, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysics, 133: 341-362. |
| [12] | Riyanti C D, Erlangga Y A, Plessix R E, et al. 2006. A new iterative solver for the time-harmonic wave equation. Geophysics, 71(5): E57-E63. |
| [13] | Štekl I, Pratt R G. 1998. Accurate viscoelastic modeling by frequency-domain finite differences using rotated operators. Geophysics, 63(5): 1779-1794. |
| [14] | Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. |
| [15] | Van der Vorst H A. 1992. Bi-CGSTAB: A fast and smoothly converging variant of bi-CG for the solution of nonsymmetric linear systems. Society of Industrial and Applied Mathematics (SIAM) Journal on Scientific and Statistical Computing, 13(2): 631-644. |
| [16] | Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6): WCC1-WCC26. |
| [17] | 马召贵, 王尚旭, 宋建勇. 2010. 频率域波动方程正演中的多网格迭代算法. 石油地球物理勘探, 45(1): 1-5. |
 2015, Vol. 58
2015, Vol. 58

