A 1 km long grounded current line is laid out 7500 m away from observing sites. Current emitted is 1 A; source frequency is set to 10 Hz. Totally 200 sites are distributed along 10 profiles; line spacing is 100 m, while station separation is 50 m. On each observing site, Ex, Ey and Hy will be measured, from which five different possible parameter combinations, complex Ex, amplitude of Ex, Ex plus Ey, Ex plus Hy, and impedance element Zxy computed from Ex and Hy, are input into the inversion. 8 bodies of different conductivity are embedded into half space. The 3D model is divided into 30×30×20 grids; cell dimensions is 50 m×50 m×50 m in the model center, and doubles in the outside 5 border layers. All inversions start from a homogeneous half space, and terminate after 120 iterations. Numerical results show that (1) with a single Ex component as inversion data, the shallow 3D bodies can be definitely obtained; (2) as an important parameter reflecting EM induction effect, the phase of Ex is more sensitive to conductive abnormal; as a result, its incorporation into the inversion enhances the deep abnormal resolution, so complex Ex is prior to Ex amplitude; (3) when combined by Ey component, not only the indistinct boundary in y-direction of the model inversed from only Ex is sharpened, but also the deep structure is revealed; (4) but if Hy is bound to Ex in inversion, the results are almost the same as that from Ex; at this point, Hy does not add more information to the inversion; (5) on contrast, if Hy is used to normalize Ex, getting impedance Zxy as inversion input, both deep and shallow bodies can be delineated. Numerical results show that in controlled source EM method, it is best to observe Ex and Hy, and use the derived parameter Zxy as inversion parameter; and if the magnetic field Hy is not available, the complement of Ey is a appropriate choice to compensate the loss of magnetic tensor; as the last resort, complex Ex, or both amplitude and phase, should be observed. If only the amplitude is available, there exist very large uncertainties in deep structure. Our results coincide with the application in CSAMT method where Zxy is often used as inversion parameter, yet which is not confirmed by 3D modeling.
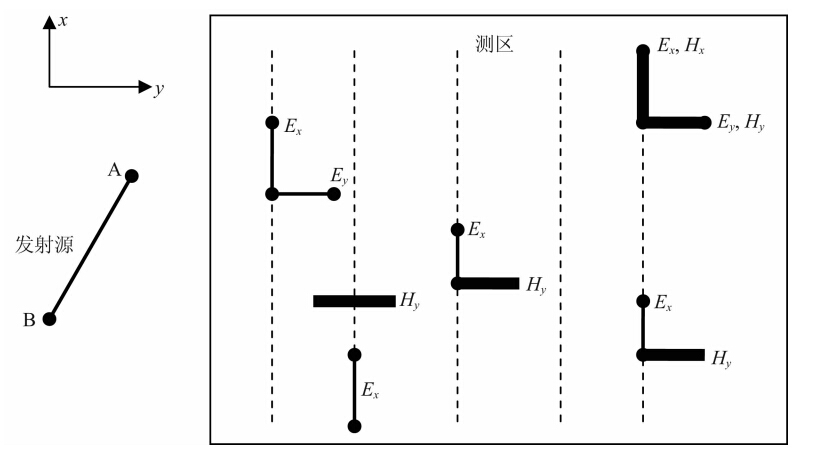
本文就地面标量可控源电磁测深工作装置中观测参数及其组合对勘探效果的影响进行讨论.对可控源频率电磁测深,目前常采用标量观测方案,在离发射源足够远区,观测与源平行的电场Ex分量,间隔测量正交的磁场Hy以便计算阻抗视电阻率和相位(Goldstein and Strangway, 1975).因为远区观测,可控源的电磁场近似平面电磁波,对应的阻抗视电阻率可以采用天然大地电磁测深的思路反演(Zonge and Hughes, 1988;汤井田和何继善,2005;底青云和王若,2008).何继善针对可控源音频大地电磁测深装置的不足,提出了广域电磁法观测方式(何继善,2010).在该工作方案中,每次测量一种参数类型,如E-EZ装置(表示接地导线发射,在工区只观测垂直电场分量).本文在上述思路的基础上,讨论如图 1所示的更为一般的电磁勘探可能工作装置:布设有限长导线作为发射源,在其周围空间任意位置观测电场或磁场的某个分量或其组合.其中,源可以相对测区任意布置,观测可以在源周围任意位置进行,可以观测电场(端点线)、磁场(粗实线)及其可能的组合.
由于可控源激发的电场和磁场是矢量,其各个分量组合方式有多种,如Ex,Ex+Hy,Ex+Ey,Ex+Ey+Hx+Hy等等,并且可以由它们导出其他参数及其组合,如阻抗Zxy,Zyx,Zxy+Zyx等.如何从这些可能的观测参数组合中,在尽可能保证最佳勘探效果的前提下,确定出最小的观测参数集合,是三维电磁勘探提高观测效果,节约野外工作量等亟待解决的实际问题.
实际上,某种地球物理勘探方法效果,涉及到如下可能的四个方面因素:(1)观测系统,(2)数据处理和反演手段,(3)数据干扰和背景地质干扰等地下地质构造和结构,以及(4)勘探对象的性质,如电导率差异、异常规模和形状等.虽然本文提出的最小观测参数集合的选择只是上述因素中有关观测系统方面的一个问题,但该问题的解决实际涉及的是上述所有因素,是一个系统问题.
 | 图 1 地面可控源可能的观测布置,实框为测量区域Fig. 1 Layout of a possible CSEmsurvey |
全面讨论并回答上述问题的一个较好思路是借助地震勘探中关于观测系统设计的理念(Vermeer,2008).在那里,最佳观测系统设计通常是通过模型数值模拟方法完成,即根据给定的模型,设计可能的工作装置,对由实际地质情况抽象得到的地质地球物理模型进行正确的数值模拟,确定出最佳的观测方案.针对电法勘探,实际上Stummer等(2004)已经提出利用试验设计方法,就尽可能获得地下信息如何设计电阻率测量数据集方案进行过探讨.
本文基于上述思路,通过三维可控源电磁勘探数值模拟技术进行最佳数据类型选择的讨论.涉及到的观测参数主要针对当前广泛使用的标量可控源音频大地电磁测深方式进行(何继善,1990).数值模拟的数据类型除常规的阻抗Zxy外,还包括导出该参数的电场Ex、磁场Hy及电场振幅|Ex|和很可能成为三维电磁勘探主要观测参数组合的水平正交电场分量Ex和Ey.为了便于对比,在本次研究中,除数据类型外,其他计算参数都一样,并且保持固定.数值模拟的手段主要包括:理论模型的电磁响应计 算采用考虑场源辐射影响的三维电磁模拟技术,借助三维交错网格有限差分方法实现数值计算(Alumbaugh et al., 1996; Commer and Newman, 2004,2008); 反演采用有限内存拟牛顿方法(L-BFGS)(NocedaLand Wright, 1990;Newman and Boggs, 2004;Avdeev and Avddeva, 2009; 刘云鹤和殷长春,2013).三维电阻率模型为嵌入8个异常体的均匀半空间.采用单个源激发,计算了模型地面投影区的电场、磁场,进而求出对应的阻抗,然后对这些数据分别进行反演,对比不同数据的反演效果.反演从均匀半空间背景模型开始,迭代120次.数据观测误差采用一个常数,其值为观测数据最大绝对值的5%.因此,反演结束时,其拟合误差远大于1.由于本文工作不强调反演方法的本身效果,只是横向比较不同参数类型数据的反演效果,故在讨论中,只选择频率为10 Hz的单个频率对应的数据进行讨论.
2 正演理论 2.1 基本公式基于电场的频率域可控源三维电磁场计算,可从二次异常电场 e s满足的Helmholtz方程
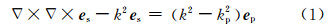
一旦计算得到剖分单元边界上中心点的异常二次电场,则对应总电场为





三维模拟的精度验证采用图 2中的模型(邓居智等,2011).一个电阻率为 10 Ωm的三维低阻六面体异常位于100 Ωm的均匀半空间中,异常体大小为 200 m×200 m×100 m,顶面埋深 100 m.取 异常体中心在地表的投影点为坐标原点.以(0,-300,0)为中心布设100 m长的水平接地导线源,沿x方向极化.
计算区域采用不均匀网格剖分,网格个数为 46×46×33(含 10 层空气层),异常体范围内三个方向网格大小均为20 m.图 2c到图 2f给出了积分方程 技术结果(IE)(邓居智等,2011)和三维交错网格有 限差分模拟(FD)得到的异常电场和磁场沿剖面变化情况.从图可见,本文反演中采用的交错网格有限差分方法计算的结果和积分方程计算得到的异常电场和磁场的基本一致.两种方法计算差异主要出现在异常体上方,就实部而言,相对误差小于5%左右;异常场虚部存在最大约20%的相对差异.
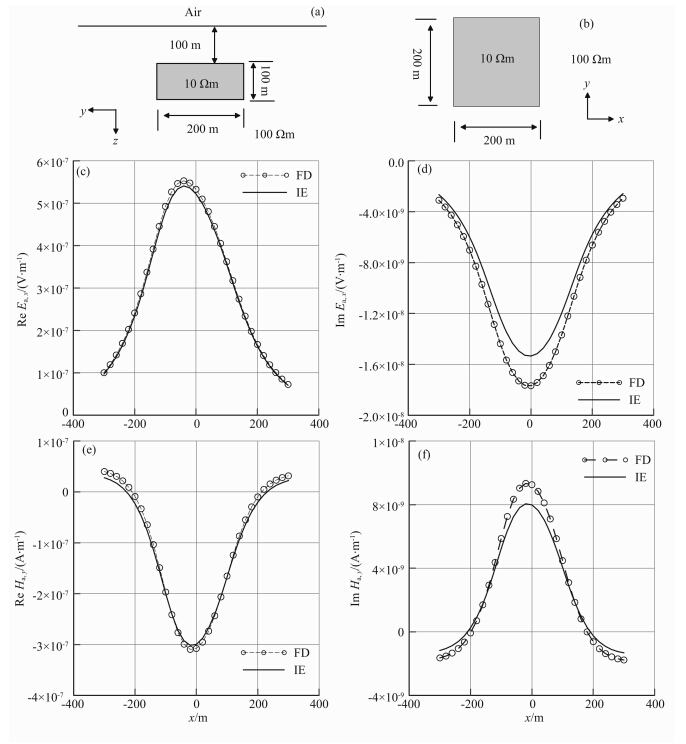 |
图 2 均匀半空间中低阻棱柱体三维异常模型及异常电磁场Ea,x,Ha,y沿剖面变化情况 (a)模型沿y方向正视图;(b)沿z方向模型俯视图;(c),(d)异常电场Ex的实部虚部;(e),(f)异常磁场Hy的实部和虚部.Fig. 2 Layered modeLto validate 3D CSFEmcode. xoz and xoy palnes of modeLis shown in(a) and (b); (c)—(f)are the secondary fields of Ex and Hy along profile through 3D body in x direction |
待反演的地面可控源电磁探测数据可以是磁场、电场、或者两者的组合,或运算得到的导出参数,如阻抗,视电阻率或者对应的振幅、相位等.记这些数据为矢量d.定义 F(m)为将模型矢量M
映射成数据矢量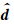 的正演算子,则三维电磁数据反演
的正演算子,则三维电磁数据反演
通过求解目标函数
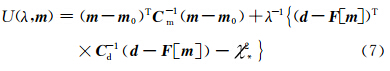
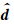 与观测数据d拟合最佳时,满足某种限制的模型参数M.在上式中,C d是数据方差矩阵; C m是模型方差函数,用来限定模型变量的幅值和光滑度,m0为参考模型;正则化参数λ平衡数据偏差和模型约束在求解中的权重.
与观测数据d拟合最佳时,满足某种限制的模型参数M.在上式中,C d是数据方差矩阵; C m是模型方差函数,用来限定模型变量的幅值和光滑度,m0为参考模型;正则化参数λ平衡数据偏差和模型约束在求解中的权重.(7)式优化问题Egbert和Kelbert(2012)从数值计算角度做了系统分析.通常采用基于梯度类的直接反演方法,比较成功的方法有高斯-牛顿方法(Mackie and Madden, 1993;林昌洪等,2012),非 线性共轭梯度算法(Newman and Alumbaugh, 1997,2000;Newman et al., 2010;翁爱华等,2012)和有限内存拟牛顿方法(L-BFGS)(刘云鹤和殷长春,2013).本文利用非线性共轭梯度算法中梯度算子计算原理,将其移植到有限内存拟牛顿反演方法中,实现有限内存拟牛顿方法的可控源电磁勘探数据反演.具体算法步骤如下:
给定初始模型M0、初始对称正定矩阵H0;
循环
计算梯度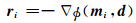 ,当Ri 满足迭代终止准则,输出最终解mi;
,当Ri 满足迭代终止准则,输出最终解mi;
近似计算Hessian矩阵Hi;
获得修正梯度方向ui=HiRi,在此方向搜索最佳步长αi;
如果步长αi小于阈值,减小正则化因子λ;
如果λ小于阀值,输出最终解mi,反演终止;
更新模型:mi+1=mi+αiui.
在上述有限内存拟牛顿反演方法中,Hessian矩阵Hi 的近似计算将利用前面已经完成的m次迭代结果,从而提高计算精度和效率. m的取值为3~20即可满足精度要求(NocedaL and Wright, 1999). 迭代过程中,梯度矢量通过数据灵敏度矩阵表达,从而实现不同数据对模型参数修正量的控制(翁爱华等,2012);正则化因子的确定采用最佳步长控制的自适应方法实现(Egbert and Kelbert, 2012);模型修正量最佳步长采用逆向追踪法进行计算(刘云鹤,2013).
4 结果分析和讨论理论模型及装置参数如图 3所示.背景模型为均匀半空间,电阻率为100 Ωm.于其中交错放置8个异常体,4个电阻率为500 Ωm高阻体(红色)和4 个电阻率为10 Ωm低阻体(蓝色).发射源长度1000 m,工作频率f=10 Hz.测区(浅绿色区域)由10条测 线组成,测线距离100 m,长度950 m,测点距离50 m,共有200个测点参与反演计算.观测参数分别为Ex,Ey和Hy.
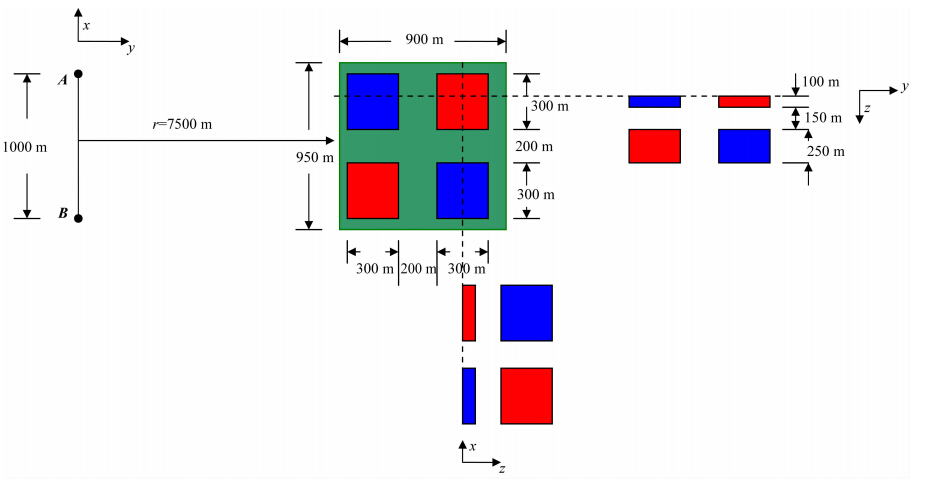 | 图 3 三维反演模型及工作装置示意图Fig. 3 CSFEmsurvey on a 3D modeLinvolving eight abnormals |
在测区范围内,三维模型剖分成20×20×15个网格单元,平面内单元大小均为50 m×50 m.在深度方向,剖分单元网格厚度均为50 m.数值模拟时,对模型镶边5个网格,因此模型网格总数为18000个.反演从100 Ωm均匀半空间开始,反演的正则化参数初始值为1,迭代进行120次.理论数据的误差取其数据最大值的5%.因此,反演终止时rms不等于1.为了比较不同数据类型的反演效果,分别绘制了包含过局部异常体中心的反演电阻率的三个水平切片,对应深度分别为25 m,75 m和375 m.
4.1 Ex复分量可控源电磁勘探中,观测电磁场包含振幅和相位信息,对应于场的实部和虚部,并且虚部往往和感应效应密切相关,能反映介质的导电特性(Kaufman and Keller, 1983).因此,对Ex分量在反演中同时考虑实部和虚部数据,考察电场感应效应的电磁勘探效果,结果如图 4所示.从图 4a和图 4b可见,浅部异常体,无论高阻还是低阻,反演结果都较为清晰地刻画出异常的形态,反演得到的电阻率值也较为接近模型真值.图 4c的深部电阻率异常中心位置和形态也基本反映理论模型;高阻体只是反演出大致轮廓,电阻率数值最大约150 Ωm,离真值较远;但对于低阻异常,形态较为完整清晰.从图 4的异常分布还可以看出,反演得到的电阻率异常在x方向边界较为清晰;而在y方向,在异常体边缘存在次异常,分析认为这可能因为反演只采用了Ex分量,而缺少y方向的测量信息.图 4d给出了迭代过程中拟合差变化,可以看到,随着迭代进行,拟合差持续减小,反演过程稳定收敛.
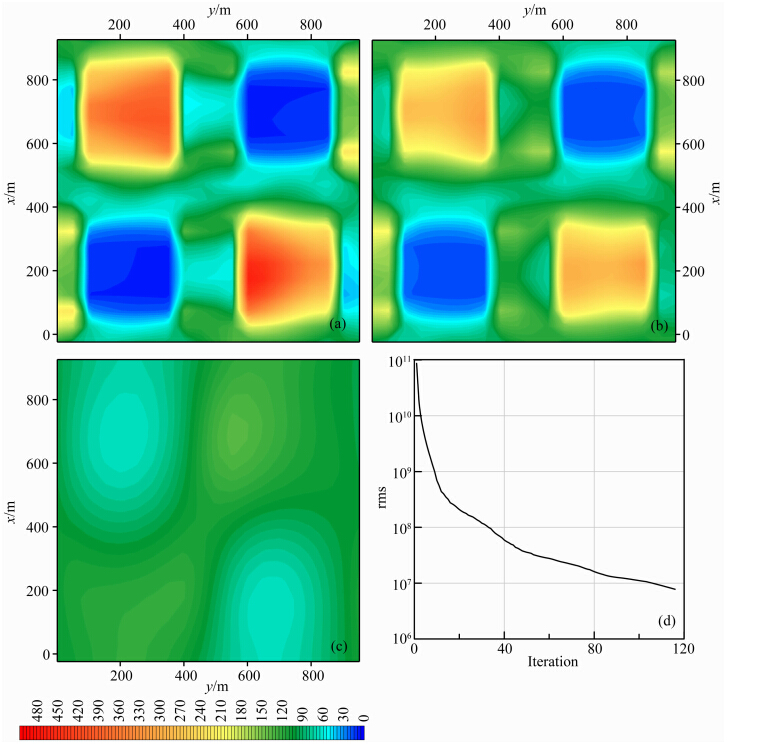 | 图 4 基于复电场数据的三维反演结果:(a)深度25 m切片;(b)深度75 m切片; (c)深度375 m切片;(d)拟合误差变化曲线Fig. 4 3D modeLinversed fromcomplex Ex component. HorizontaLslices are cut through depth z=25 m(a),75 m(b), and 375 m(c); while(d)is the rms curve |
可控源观测到的电磁场的虚部相对实部往往较小,特别是在高阻地区,由于感应效应较弱,虚部相对实部可能小很多.当受到噪音干扰,相位观测误差更大,甚至无法使用.此时,电场的振幅信息可靠性较大.针对这种实际可能性,基于电场Ex振幅进行反演,考察其勘探效果,结果如图 5所示.
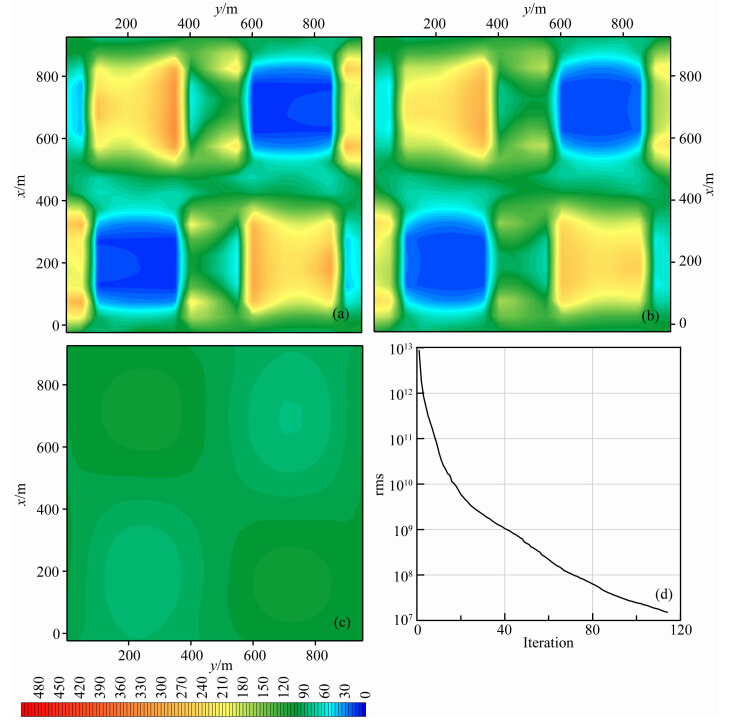 | 图 5 基于电场振幅数据的三维反演结果:(a)深度25 m切片;(b)深度75 m切片;(c)深度375 m切片;(d)拟合误差变化曲线Fig. 5 3D modeLinversed fromEx amplitude. HorizontaLslices(a),(b), and (c) are at depth 25m,75m, and 375mrespectively,while(d)is the rms curve |
从图 5可见,反演确定了浅部的异常分布规律;但深部异常体只恢复出基本轮廓,且无论高阻还是低阻异常体,反演电阻率均与真值相差甚远.同时,从图 5a和图 5b可见,除了实际的异常外,在异常体边缘还出现更加明显假异常,其形态复杂,且和主异常有较大伴生关系;高阻异常产生局部低阻假异常,低阻主异常伴生局部高阻次异常.比较图 4可以看到,由于缺少了相位信息,这种局部的次级异常更加明显和复杂,并且同图 4一样,这种次级异常主要发生在y方向,在x方向相对微弱.一种可能的解释是,只测量Ex分量时,缺少y方向数据信息,导致在y方向信息不足,反演不惟一.总体来说,只观测振幅,浅部效果不好,深部异常没有反映.由于振幅数据淹没感应信息,反演效果没有包含相位信息的复场量好.因此,野外工作中应该尽可能精确地获得电场和磁场的相位和振幅.
4.3 正交电场Ex+Ey在图 4和图 5的反演结果中,y方向都存在次级假异常,推测是由于缺少该方向信息.因此,如果增加观测Ey分量,可能能压制y方向假异常.图 6 展示了在测区所有测点上同时记录Ex和Ey分量反演得到的结果,尽管目前可控源观测中尚没有同时大规模观测正交的电场Ex和Ey分量.
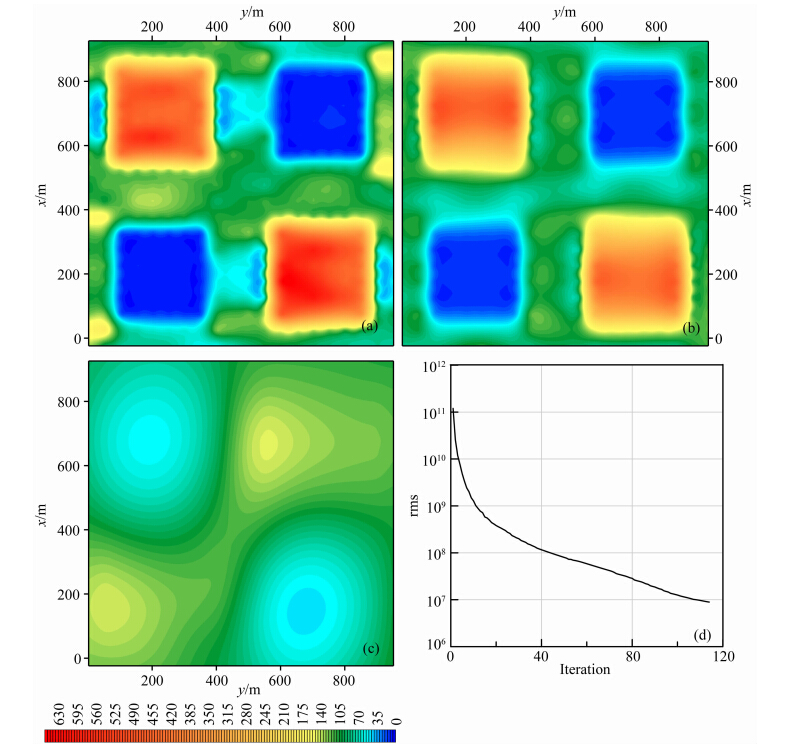 | 图 6 基于正交电场数据的三维反演结果:(a)深度25m切片;(b)深度75m切片; (c)深度375m切片;(d)拟合误差变化曲线Fig. 6 3D modeLinversed fromthe combination of complex Ex and Ey. Resistivity slices shown are at depth 25 m(a),75 m(b) and 375 m(c); while rms curve displayed in(d) |
从图可见,正如所料,在浅部,反演得到的异常体在形态和数值上都与理论模型吻合;并且无论是x方向还是y方向,相对图 4和图 5,异常体边界附近的次级异常都得到有效的压制.在深部,由于增加了Ey信息,异常体的形态更加完整,电阻率值更加接近理论值.在这个意义上,野外若同时观测水平电场的正交分量,对提高可控源电磁勘探效果和探测能力,比只观测Ex分量将有较大的提高.图 6d的拟合差曲线表明反演过程稳定收敛,迭代120次后,rms仍然呈下降趋势.基于此,继续迭代,反演结果还能得到进一步改善.
4.4 电场Ex和磁场Hy在标量可控源野外观测过程中,一般连续较密测量电场Ex分量,间隔测量正交的水平磁场Hy,以便计算阻抗或阻抗视电阻率.但在这里每个测点上同时观测Ex和Hy并直接作为观测数据进行反演,其120次迭代的反演结果如图 7所示.由图可见,反演的表层异常与理论模型一致;在深部,低阻异常体有较明显反映,但高阻异常体反映微弱.对比前面三种数据类型的反演结果,该数据类型的反演 效果基本与单独观测Ex分量相当,比同时观测Ex+Ey的效果差.
从(4)式可见,HMy实际是由Ex+Ez插值得到,而Ez在地表附近很小,故Hy实际主要由Ex贡献.因此,在一定程度上,可以说Hy是和Ex相关的,故增加Hy形成的数据组合所提供的感应信息并不比Ex有实质性增加.同时,磁场对电阻率变化没有电场灵敏,故在反演数据中增加磁场信息,会弱化电场对异常的灵敏度,导致深部高阻异常分辨率相对只 有电场数据的反演结果差.纵观已有的结果,Ex+ Hy数据比Ex+Ey效果差,比Ex的效果浅部好,深部差.图 7d的拟合差变化曲线显示该数据类型的反演能稳 定收敛,在120次迭代后仍存在近似线性的收敛速度.
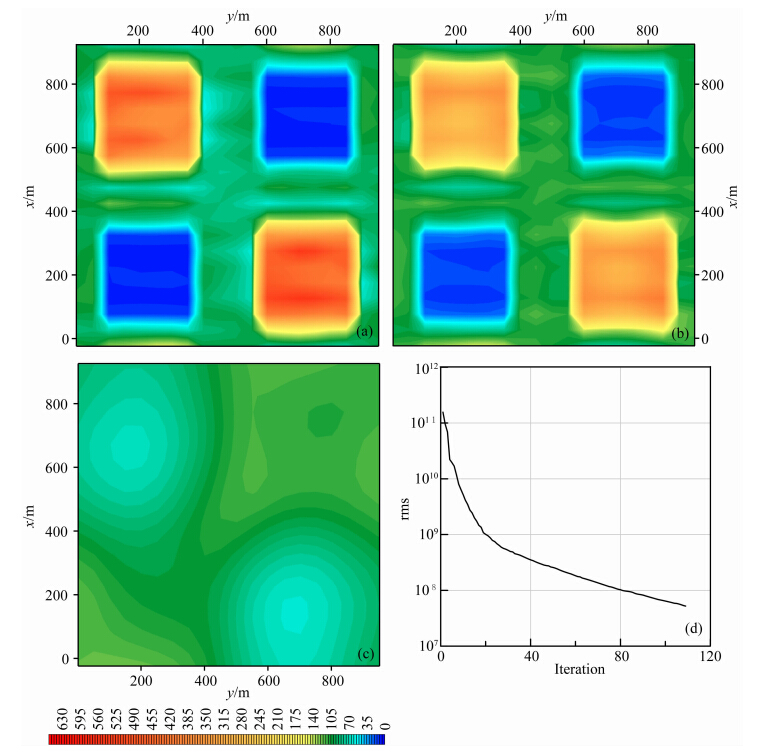 | 图 7 基于电场和磁场数据的三维反演结果:(a)深度25 m切片;(b)深度75 m切片; (c)深度375 m切片;(d)拟合误差变化曲线Fig. 7 3D modeLinversed fromthe combination of complex Ex and Hy. HorizontaLslices are cut at depth z=25 m(a),75 m(b), and 375 m(c),while(d)is the rms curve |
数据类型为阻抗Zxy的数据由图 7的电场Ex和磁场Hy计算得到,因此该数据也是观测位置的函数.图 8给出了基于复阻抗元素Zxy的反演结果.从图 8a和图 8b可见,浅部高阻和低阻异常形态和边界都较为清楚;并且在异常边界上,假异常明显消失.在深部,反演得到的高阻异常体和低阻异常体形态也较为完整,较为准确刻画出理论模型的异常分布.比较前面的各种数据类型,很明显,阻抗数据反演效果最好.从图 8d中反演迭代的rms减小趋势看,目标函数仍然保持较大的衰减速度,因此随着进一步的迭代,拟合的效果会更好.
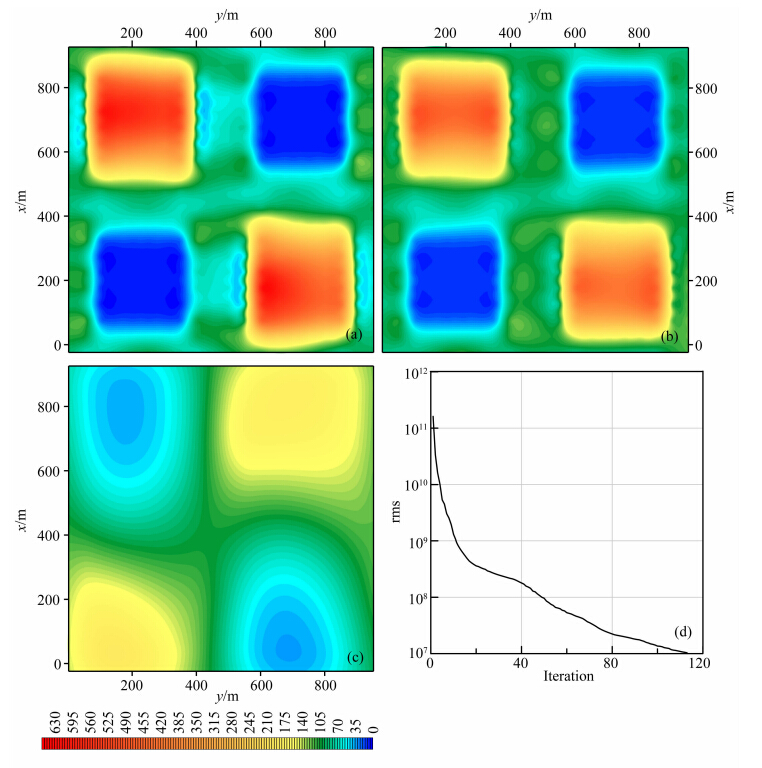 | 图 8 基于阻抗Zxy数据的三维反演结果:(a)深度25 m切片;(b)深度75 m切片; (c)深度375 m切片;(d)拟合误差变化曲线Fig. 8 HorizontaLresistivity slices at different depth in the modeLinversed fromZxy component. (a)z=25 m;(b)z=75 m;(c)z=375 m;(d)rms curve |
在理论上,阻抗数据是由电场和磁场导出的新数据类型,其本身并不能比同时观测电场Ex和磁场Hy提供更多的信息,但反演的结果却具有明显的优势.分析认为,可能有如下几个方面的原因:(1)在反演理论中,数据归一化的作用是让所有的数据在反演中具有同样的重要性,而阻抗实际是用磁场归一化的电场数据,因此,更能突出电场的感应效应;(2)从电磁理论本身看,电磁场本身的虚部对感应敏感,但数值比实部小很多.因此,在利用实部和虚部同时反演时,Ex虚部的优势并不明显;但阻抗的虚部和实部相差不大,从而感应效应在反演中的作用会得到加强;(3)从数据本身大小看,阻抗比电场和磁场高4~5个甚至更大的数量级,因此,阻抗数据的抗干扰能力比幅度小很多的电磁场强,其受误差的影响相对小,反演效果相应提高.
5 结论论文针对可控源电磁测深勘探方法,以目前广泛应用的标量可控源音频大地电磁测深为对象,通过理论模型数值模拟,研究不同数据类型的勘探效果.在数值模拟过程中,可控源产生的频率域电磁场利用三维交错网格有限差分技术进行计算,反演借助有限内存拟牛顿方法实现.研究的可控源电磁观测数据类型包括复电场Ex及其振幅|Ex|、Ex+Ey、Ex+Hy以及由其导出的阻抗分量Zxy.
通过对迭代120次得到的反演结果分析,得到如下的结论:
(1)相位信息在反演中非常重要,因为相位信息直接和电磁感应效应相关,增加相位信息,将较大提高可控源的探测效果;
(2)相对观测单分量电场,观测正交的电场,其反演分辨率和对假异常的克服能力有较明显提升;
(3)观测电场和磁场,并直接基于它们进行反演,勘探效果与对应单分量电场基本一样,仅仅增加正交的磁场数据并不能提高勘探效果;
(4)利用观测数据导出的阻抗进行反演,反演的效果最好,从而其勘探效果最佳.
总之,目前标量可控源音频电磁测深中,不同数据类型的勘探效果按照如下的顺序逐渐变差:Zxy,Ex+Ey,Ex+Hy,Ex,|Ex|.因此,对于可控源观测,在野外观测方案中,最好同时观测正交的水平电场和磁场,而在数据的反演解释时,采用由其导出的阻抗数据进行反演.
正如引言中指出的,地面电磁可以观测的分量及其组合有几十种之多,而本文只是针对其中少数几种参数进行讨论.希望本文的工作对类似问题的研究能起到抛砖引玉之作用.
致谢 感谢审稿人提出的建设性建议和启示,对于论文的完善受益匪浅.| [1] | Alumbaugh D L, Newman G A, Prevost L, et al. 1996. Three-dimensional wide band electromagnetic modeling on massively parallel computers. Radio Science, 31(1): 1-23. |
| [2] | Avdeev D, Avddeva A. 2009. 3D magnetotelluric inversion using a limited-memory quasi-Newton optimization. Geophysics, 74(3): F45-F57. |
| [3] | Chave A D. 1983. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion. Geophysics, 48(12): 1671-1686. |
| [4] | Commer M, Newman G A. 2004. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics, 69(5): 1192-1202. |
| [5] | Commer M, Newman G A. 2008. New advances in three-dimensional controlled-source electromagnetic inversion. Geophysical Journal International, 172(2): 513-535. |
| [6] | Das U C. 1995. A reformalism for computing frequency- and time-domain EM responses of a buried, finite-loop.// Extended Abstracts, 1995 SEG Annual Meeting. Houston: SEG, 811-814. |
| [7] | Deng J Z, Tan H D, Chen H, et al. 2011. CSAMT 3D modeling using staggered-grid finite difference method. Progress in Geophysics (in Chinese), 26(6): 2026-2032, doi: 10.3969/j.issn.1004-2903.2011.06.017. |
| [8] | Di Q Y, Wang R. 2008. Controlled Source Audio-Frequency Magnetotellurics (in Chinese). Beijing: Science Press. |
| [9] | Egbert G D, Kelbert A. 2012. Computational recipes for electromagnetic inverse problems. Geophysical Journal International, 189(1): 251-267. |
| [10] | Goldman M. 1990. Non-conventional Methods in Geoelectrical Prospecting. New York: Ellis Horwood Ltd Publisher. |
| [11] | Goldstein M A, Strangway D W. 1975. Audio-frequency magnetotellurics with a grounded electric dipole source. Geophysics, 40(4): 669-683. |
| [12] | He J S. 1990. Controlled Source Audio-Frequency Magnetotellurics (in Chinese). Changsha: Central South University of Technology Press. |
| [13] | He J S. 2010. Wide field electromagnetic sounding methods. Journal of Central South University (Science and Technology) (in Chinese), 41(3): 1065-1072. |
| [14] | Kaufman A A, Keller G V. 1983. Frequency and transient soundings. Amsterdam: Elsevier Science Publishers. |
| [15] | Lin C H, Tan H D, Shu Q, et al. 2012. Three-dimensional conjugate gradient inversion of CSAMT data. Chinese Journal of Geophysics (in Chinese), 55(11): 3829-3838, doi: 10.6038-.issn.00015733.2012.11.030. |
| [16] | Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data. Journal of Chinese Geophysics (in Chinese), 56(12): 4278-4287, doi: 10.6038/cjg20131230. |
| [17] | Liu Y H. 2013. Three-dimensional frequency-domain airborne electromagnetic modeling and inversion in anisotropic media (in Chinese). Post Doctorial Report. Changchun: Jilin University. |
| [18] | Mackie R L, Madden T R. 1993. Three-dimensional magnetotelluric inversion using conjugate gradients. Geophysical Journal International, 115(1): 215-229. |
| [19] | Newman G A, Alumbaugh D L. 1997. Three-dimensional massively parallel electromagnetic inversion-Ⅰ. Theory. Geophysical Journal International, 128(2): 345-354. |
| [20] | Newman G A, Alumbaugh D L. 2000. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophysical Journal International, 140(2): 410-424. |
| [21] | Newman G A, Boggs P T. 2004. Solution accelerators for large-scale three-dimensional electromagnetic inverse problems. Inverse Problems, 20(6): 151-170. |
| [22] | Newman G A, Commer M, Carazzone J J. 2010. Imaging CSEM data in the presence of electrical anisotropy. Geophysics, 75(2): F51-F61. |
| [23] | Nocedal J, Wright S J. 1990. Numerical Optimization. Berlin: Springer. |
| [24] | Shen J S. 2003. Modeling of 3-D electromagnetic responses in frequency domain by using staggered grid finite difference method. Chinese Journal of Geophysics (in Chinese), 46(2): 281-288, doi: 10.3321/j.issn:0001-5733.2003.02.024. |
| [25] | Stummer P, Maurer H, Green A G. 2004. Experimental design: electrical resistivity data sets that provide optimum subsurface information. Geophysics, 69(1): 120-139. |
| [26] | Tang J T, He J S. 2005. Controlled Source Audio-Frequency Magnetotellurics and Applications (in Chinese). Changsha: Central South University Press. |
| [27] | Vermeer G J O. 2008. 3-D Seismic Survey Design. Tulsa: SEG. |
| [28] | Wannamaker P E, Hohmann G W, SanFilipo W A. 1984. Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations. Geophysics, 49(1): 60-74. |
| [29] | Ward S H, Hohmann G W. 1988. Electromagnetic theory for geophysical applications. // Nabighian M N ed. Electromagnetic Methods in Applied Geophysics. Tulsa: SEG, 116-120. |
| [30] | Weng A H, Wang X Q. 2003. Utilizing direct integration to enhance calculation accuracy of 1D electromagnetic response for current dipole source. Northwestern Seismological Journal (in Chinese), 25(3): 193-197. |
| [31] | Weng A H, Liu Y H, Jia D Y, et al. 2012. Three-dimensional controlled source electromagnetic inversion using non-linear conjugate gradients. Chinese Journal of Geophysics (in Chinese), 55(10): 3506-3515, doi: 10.6038/j.issn.0001-5733.2012.10.034. |
| [32] | Weng A H, Liu Y H, Jia D Y, et al. 2013. Compute Green's function from discontinuity of tangential electrical fields inside source contained boundary. Journal of Jilin University (Earth Science Edition) (in Chinese), 43(2): 603-609. |
| [33] | Weng A H, Liu Y H, Yin C C, et al. 2014. Singularity-free Green's function for EM sources embedded in a stratified medium. Applied Geophysics, In printing. |
| [34] | Zonge K L, Hughes L J. 1988. Controlled source audio-frequency magnetotellurics. // Nabighian M N ed. Electromagnetic Methods in Applied Geophysics. Tulsa: SEG, 713-809. |
| [35] | 邓居智, 谭捍东, 陈辉等. 2011. CSAMT三维交错采样有限差分数值模拟. 地球物理学进展, 26(6): 2026-2032, doi: 10.3969/j.issn.1004-2903.2011.06.017. |
| [36] | 底青云, 王若. 2008. 可控源音频大地电磁数据正反演及方法应用. 北京: 科学出版社. |
| [37] | 何继善. 1990. 可控源音频大地电磁法. 长沙: 中南工业大学出版社. |
| [38] | 何继善. 2010. 广域电磁测深法研究. 中南大学学报(自然科学版), 41(3): 1065-1072. |
| [39] | 林昌洪, 谭捍东, 舒晴等. 2012. 可控源音频大地电磁三维共轭梯度反演研究. 地球物理学报, 55(11): 3829-3838, doi: 10.6038-.issn.00015733.2012.11.030. |
| [40] | 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究. 地球物理学报, 56(12): 4278-4287, doi: 10.6038/cjg20131230. |
| [41] | 刘云鹤. 2013. 三维各向异性介质中频率域航空电磁正反演研究. 博士后研究工作报告. 长春: 吉林大学. |
| [42] | 沈金松. 2003. 用交错网格有限差分法计算三维频率域电磁响应. 地球物理学报, 46(2): 281-288, doi: 10.3321/j.issn:0001-5733.2003.02.024. |
| [43] | 汤井田, 何继善. 2005. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社. |
| [44] | 翁爱华, 王雪秋. 2003. 利用数值积分提高一维模型电偶源电磁测深响应计算精度. 西北地震学报, 25(3): 193-197. |
| [45] | 翁爱华, 刘云鹤, 贾定宇等. 2012. 地面可控源频率测深三维非线性共轭梯度反演. 地球物理学报, 55(10): 3506-3515, doi: 10.6038/j.issn.0001-5733.2012.10.034. |
| [46] | 翁爱华, 刘云鹤, 贾定宇等. 2013. 基于电场不连续边界条件的层状介质电磁格林函数计算. 吉林大学学报(地球科学版), 43(2): 603-609. |
 2015, Vol. 58
2015, Vol. 58

