2015, Vol. 58
2. 广州海洋地质调查局, 广州 510075
2. Guangzhou Marine Geological Survey, Guangzhou 510075, China
On the basis of the traditional stochastic inversion, a new method of stochastic inversion is proposed, i.e. the fast stochastic inversion based on fast Fourier transform-moving average (FFT-MA) spectrum simulation. This method is used to conduct geostatistical simulation in the frequency domain, and the gradual deformation updating method (GDM) can be used to accelerate the simulation convergence through continuous modification of the reservoir model until it matches the real seismic data.
FFT-MA simulation is a spectrum simulation method which can perform fast simulation in the frequency domain by Fourier transform. Compared with the sequential Gaussian simulation algorithm, the FFT-MA spectrum simulation can greatly improve the computational efficiency while has better simulation result. The conditioned FFT-MA spectrum simulation method can reconstruct the data which satisfy the specified covariance structure and grid size as well as the known well data. The GDM can get a series Gauss white noises realization which having the same mean and variance distribution. By changing the Gauss white noise, the FFT-MA disturbance simulation results will have all or part of the continuous modification. The synthetic seismic data can be obtained from the simulation results by forward modeling. Fast optimized stochastic inversion results will be obtained while the synthetic seismic data match well with the real seismic data. Compared with the conventional stochastic inversion, the fast stochastic inversion method can get high-resolution inversion result. Moreover, it can enhance the computational performance and reduce the memory consumption,and also accelerate the convergence process of the inversion. The model tests show that the proposed stochastic inversion method can obtain higher resolution of inversion results than the deterministic inversion method and match the model well. The analysis of the real data also shows that the high-resolution inversion result of the stochastic inversion method can have better exhibit thin interbedded reservoirs.
The fast stochastic inversion method can get higher resolution of inversion result than deterministic inversion method and has faster computational efficiency than conventional stochastic inversion. The proposed method can be used in the identification of thin reservoirs. The proposed method is not affected by the sequential factors; therefore it can be parallel computed in the future research which will further improve the computational efficiency.
地震反演的实质是将地震观测数据转化为储层参数，用反演的储层参数信息进行地下目的储层的预测，从而为油田的勘探开发提供技术支持(Bosch，2010；Doyen，2007).其中，确定性反演和随机反演是地震反演的两大类别(杨晓春等，2001；Sams和Saussus，2010).与确定性反演方法相比，以地质统计学为基础、以测井资料为条件数据的随机反演方法能够模拟地震频带以外的信息，具有比常规确定 性反演更高的分辨率(Francis，2005；Moyen和Doyen，2009；Helgesen，2000；Sancevero，2005；Sams和Saussus，2008)，因此，受到了国内外地球物理学家的广泛关注与研究.
在国外，Bortoli等(1992)首先提出了基于序贯高斯模拟和单道匹配最优原则的随机反演方法，该方法能够在横、纵向变差以及井位置处测井资料的约束下，有效地融入地震频带以外的测井信息，提高反演解的分辨率.Haas和Dubrule(1994)发展了单道模拟的随机反演方法，捕获了超出地震带宽的频率信息.单道模拟方法虽然可以获得高分辨率的反演结果，但是计算效率低，限制了其在实际资料中的应用.Debeye(1996)、Sams(1999)和Contreras(2005)等通过引入模拟退火和马尔科夫链蒙特卡洛(MCMC)技术，用点扰动的方式取代了单道反复模拟，扩展了随机反演算法.Srivastava和Sen(2010)提出了基于分形初始模型的随机反演方法，该方法能够反演出纵横波阻抗等多个参数数据体.以上方法仍然没有解决计算耗时的问题.在国内，近年来，地球物理学家也在随机反演方面做了很多研究.黄捍东等(2009)研究了以测井、地质信息作为约束条件的非线性随机反演方法.张世鑫等(2010)针对目的储层薄互层发育的特点，运用随机反演方法成功实现了储层的精细预测.Huang等(2012)研究指出随机反演在薄储层地震反演中具有更大的优势，并对随机反演中关键参数的优选及其效果进行了分析.杨锴等(2012)将测井、井间地震与地面地震数据同时用于介质参数的随机反演，大大降低了模拟出的介质参数的不确定性，提高了反演精度.
尽管高分辨率的随机反演工作在实际资料应用中已取得了一定的进展，但仍普遍存在计算耗时的问题.鉴于此，本文针对常规随机反演计算效率低，占用内存大的问题，用傅里叶滑动平均(Fast Fourier Transform-Moving Average，FFT-MA)模拟方法进 行频率域的快速模拟(Pardo-Igúzquiza，1993；Ravalec和Noetinger，2000；Oliver，1995)，并利用逐步变形 算法(Gradual Deformation Method，GDM)(Hu，2000; Hu和Ravalec，2004；Ravalec和Noetinger，2002)确保反演解的快速收敛，构建了基于FFT-MA谱模拟的快速随机反演方法.模型试算与实例分析表明，与常规随机反演相比，该方法能够在保证高分辨反演结果的情况下，确保反演解的快速收敛，大大提高随机反演的计算效率.
2 方法原理 2.1 FFT-MA非条件谱模拟方法FFT-MA方法可进行快速的地质统计模拟，计算效率高，且不受网格大小限制，是一种非条件模拟方法.其基本公式为
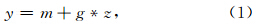
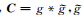，是g的共轭，*为卷积符号，z表示满足模拟网格大小的随机高斯白噪.该方法实现的关键之一是协方差矩阵 C 的构建，其中一维协方差矩阵 C(h)和变差函数之间满足 C(h)=σ2-γ(h)，σ2为模拟的方差，γ(h)为变差函数，h为空间距离.
2.2 条件化处理由于FFT-MA谱模拟是一种非条件模拟，不能满足硬数据(已知井数据).为解决该问题，本文采用克里金条件化方法(Francis， 2006a，2006b)对其进行了条件化处理:
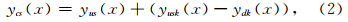
图 1是FFT-MA谱模拟条件化处理的示意图，首先求取硬数据点处数值(蓝色圆圈)的克里金得到待条件化点处的克里金值ydk(x)(红色圆圈)，然后再求取硬数据点处的非条件模拟值(橙色三角)的克里金得到待条件化点处的克里金值yusk(x)(绿色三角)，yusk(x)与ydk(x)的差值再加上待条件化点处的非条件模拟值yus(x)，就可以得到待条件化点处的条件化模拟值ycs(x).
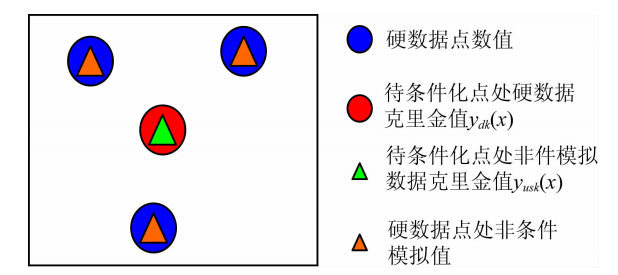 | 图 1 条件化处理示意图Fig. 1 Sketch map of conditional process |
从式(1)中可以看出，FFT-MA谱模拟的关键问题是高斯白噪z的更新，传统的随机反演通常采用反复模拟的方式来寻找最优结果，不但计算效率低，而且不能保证每次的模拟结果都比上一次更接近实际地震记录.因此，需要寻找一种合适的优化算法来改善反演解的收敛问题.
本文在FFT-MA算法扰动模拟的基础上，通过引入GDM不断更新模拟结果，使每次的模拟结果都比上一次结果更逼近实际地震数据，从而加快反演的求解速度.
GDM算法的核心思想是将一个高斯白噪的局部或整体加入另一个高斯白噪的对应部分，其结果仍是一个高斯白噪.具体可以表示为：
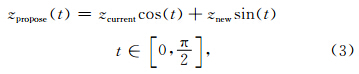
需要指出的是，高斯白噪z的存在使FFT-MA算法具有随机性，但由于协方差结构 C 不改变，所以这种扰动不会影响数据的空间变差结构.
3 算法测试与分析 3.1 FFT-MA谱模拟与序贯高斯模拟的对比为验证FFT-MA谱模拟的计算效率，本文基于相同的硬数据和变差，分别进行了条件化FFT-MA谱模拟和序贯高斯模拟，其结果如图 2所示.条件化FFT-MA谱模拟比序贯高斯模拟的分辨率高.图 3是二者的计算效率对比，可以看出，FFT-MA谱模拟的时间从154.84 s降至11.20 s，速度提高了14倍.因此，与序贯高斯模拟相比，频率域的FFT-MA谱模拟方法不但分辨率高，而且能够有效解决计算耗时、耗内存的问题.
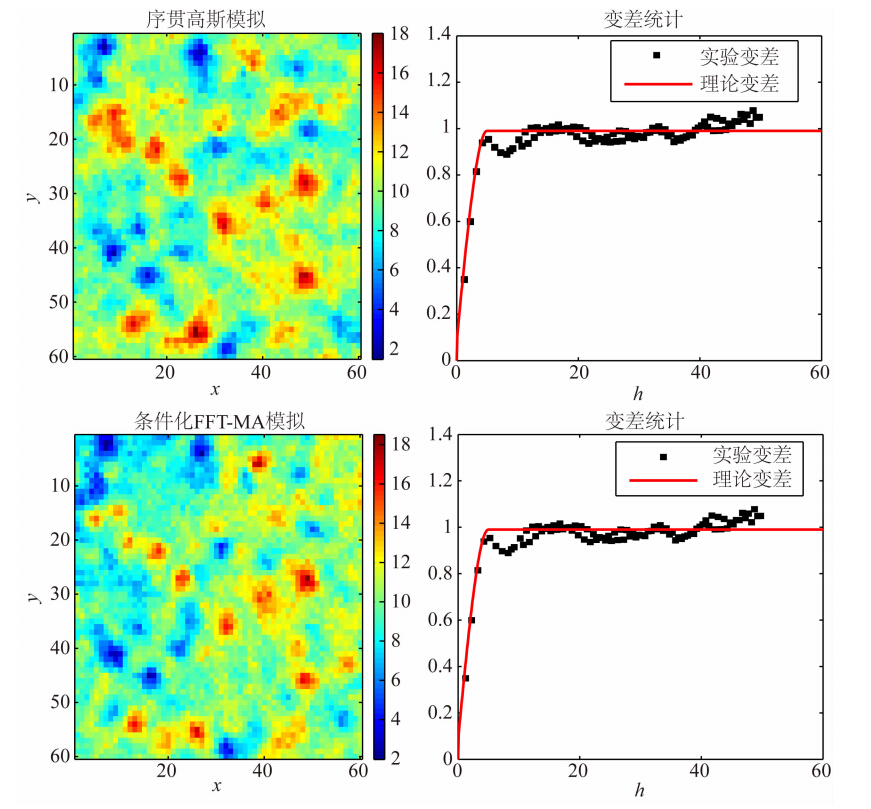 | 图 2 条件化FFT-MA谱模拟与序贯高斯模拟的结果对比图Fig. 2 Simulation results comparison of conditional FFT-MA spectrum simulation with sequential Gauss simulation |
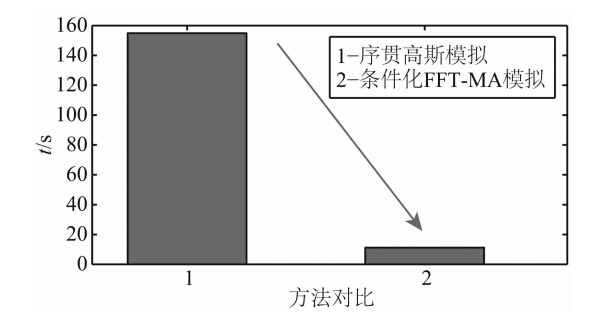 | 图 3 条件化FFT-MA谱模拟与序贯高斯模拟的计算效率对比图 Fig. 3 Computational efficiency comparison of conditional FFT-MA spectrum simulation with sequential Gauss simulation |
由方程(1)可知，FFT-MA谱模拟的最终结果受协方差C和高斯白噪z的影响，其中模拟的随机性来自于加入的随机高斯白噪z.图 4是一个50点的模拟，采用球状变差模型，变程值为10，在更新第25点的z值时，模拟结果在相关长度10以内均发生了扰动.图 5和图 6分别是网格大小均为80×60时的点和线扰动的情况，图 5是对位置(30，5)的点扰动，图 6是对第11列的线扰动，从图 5和图 6最右边的两者残差图可以看出，在相关半径内，模拟结果均发生了扰动.
模拟分析结果表明，局部(一个点或者一条线)高斯白噪z值的扰动，会引起FFT-MA谱模拟结果的局部扰动.正由于FFT-MA谱模拟的这种特性，在对实际地震数据进行模拟时，通过对z值在某道位置的扰动，可以产生相应道位置处的模拟波阻抗 的扰动，因此，可以对实际地震数据按道进行模拟，实现模拟模型的连续修改，最终达到与实际地震记录的匹配.
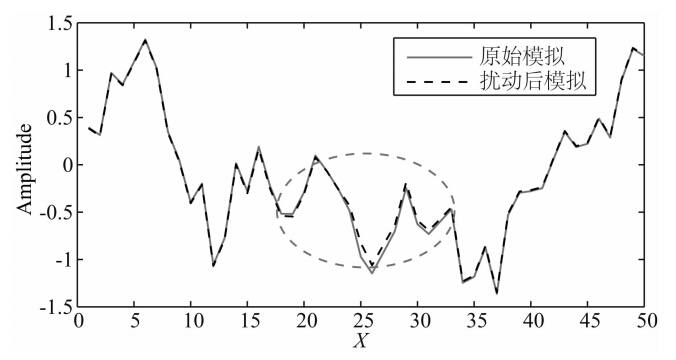 | 图 4 点(25)扰动前后模拟结果对比图Fig. 4 Comparison of simulation results before and after point(25)disturbance |
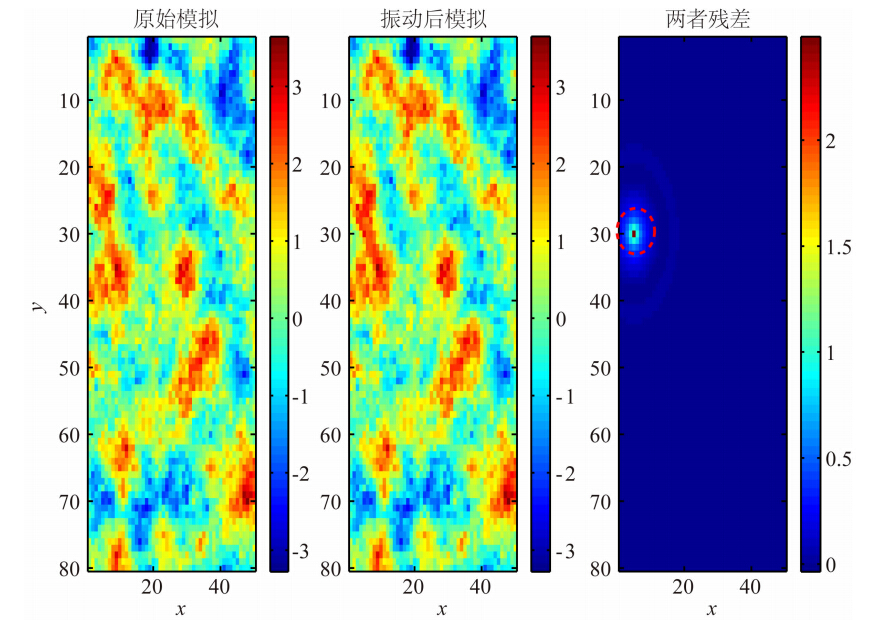 | 图 5 点(30，5)扰动前后模拟结果对比图Fig. 5 Comparison of simulation results before and after point(30，5)disturbance |
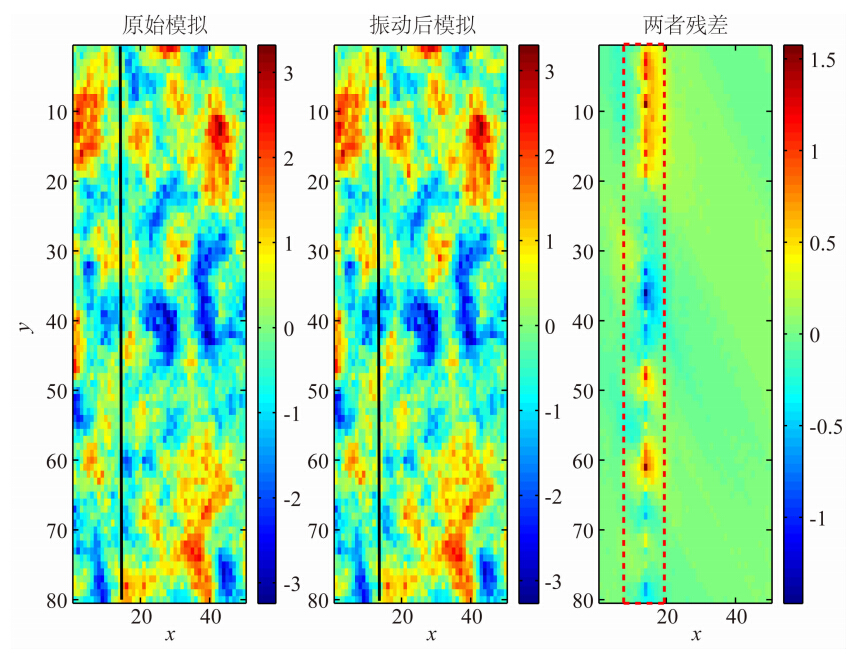 | 图 6 线(第11列)扰动前后模拟结果对比图Fig. 6 Comparison of simulation results before and after line(Line 11)disturbance |
根据以上所述的方法原理，本文建立了基于FFT-MA谱模拟的快速随机反演方法，其基本步骤为：在进行地质统计模拟时，首先通过地质统计方法计算测井曲线的变差函数和协方差，以确定测井数据的空间结构特征，然后利用方程(1)和(2)重构出满足指定空间结构的条件化的谱模拟结果，最后采用逐步变形算法不断更新模拟结果，确保模拟结果与实际地震数据的匹配.图 7表示其具体反演流程.
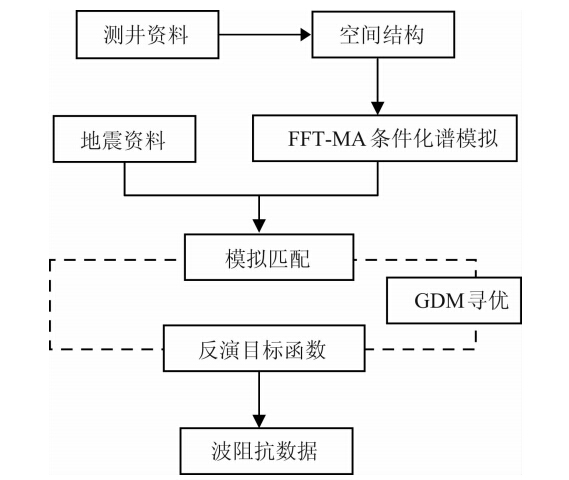 | 图 7 基于FFT-MA谱模拟的快速随机反演流程图Fig. 7 Flow chart of the Fast Stochastic Inversion based on FFT-MA spectrum simulation |
为使随机模拟的地震波阻抗与实际地震数据达到最佳匹配，本文将目标函数定义为：
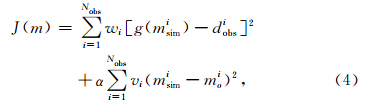
一般地震波阻抗反演的目标函数是N维的，本文通过引入逐步变形算法，将反问题的求解转变为对最佳参数t的搜索，从而变成了一维问题，简化了问题的求解，提高了运算效率.因此，即使采用迭代的思想也可达到目标函数的快速求解.
4.2 目标函数的求解假设一次新的znew的产生即一个新链，每个链上有m个t值，如果在状态tn下得到的目标函数J的数值相对状态tn－1下降了，即J(tn)<J(tn－1)，则跳出最优t的搜索，然后将下一个链的zcurrent更新为当前状态tn下所得的zpropose(公式3)，如果目标函数不降低，则保持该链的zcurrent不变，带入下一个链的计算，如此反复迭代直至目标函数满足收敛条件.
具体步骤可描述为：
①：生成新的znew，与上一步产生的zcurrent组合产生一条新的链；
②：搜索链上的t值，如果存在tn，停止搜索t，将下个链的zcurrent更新为该链上tn时的zpropose，转到①；
③：搜索该链上的t值，如果目标函数一直不下降，zcurrent保持不变，转到①；
④：重复①—③直到目标函数满足收敛条件.
5 模型试算及结果分析 5.1 模型试算为验证算法的有效性，本文首先采用8000个链(即8000次迭代)对单道数据进行了数值试算，t的取值范围为0到π/2，间隔为π/20，所得单道反演结果如图 8所示，从图中可看出，模型波阻抗与反演波阻抗吻合比较好.图 9是其合成地震记录和实际地震记录的对比图，可以看出，模型波阻抗与反演波阻抗吻合非常好.图 10是归一化目标函数的单道收敛效果，可以看出，达到迭代次数时，归一化后的目标函数值为0.0379，即下降了96.3%，在实际计算时，迭代次数为1000多次时即能够使目标函数达到很好的收敛，从而使运算时间大大缩短.
 | 图 8 单道波阻抗反演结果与模型对比图Fig. 8 Comparison of impedance inversion result with model data |
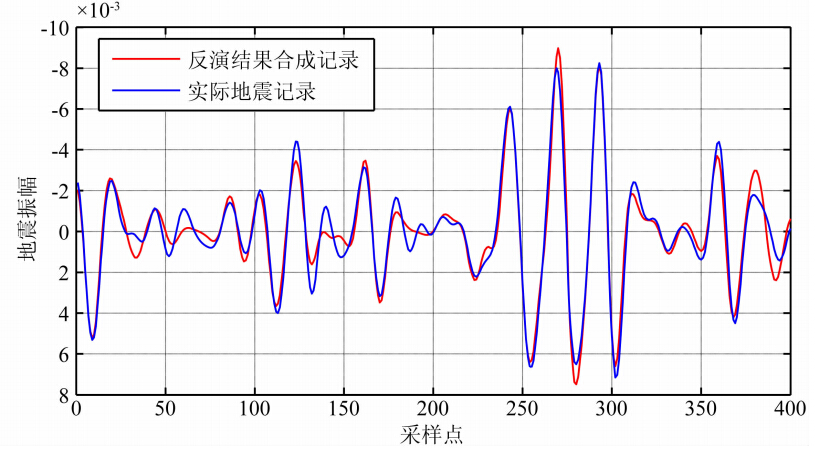 | 图 9 反演结果合成记录与实际地震记录的对比图Fig. 9 Comparison of Synthetic seismic data of inverted impedance and model data |
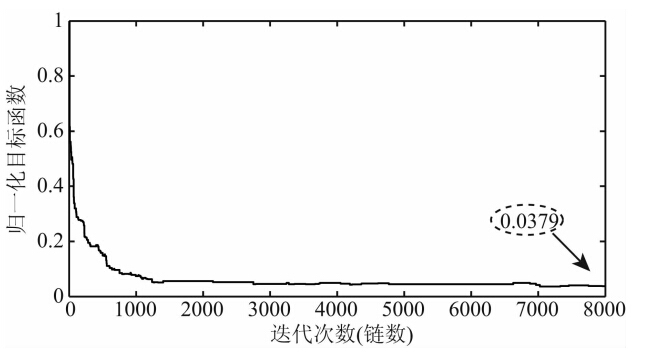 | 图 10 归一化目标函数的收敛效果图Fig. 10 Convergence effect of normalized objective function |
本文还对图 11所示的二维模型进行了测试分析，该模型在第250个采样点位置处有两个薄层.具体反演时，从该模型中抽取5道作为伪井，将模型波阻抗的合成地震记录作为实际地震记录.图 12为反演结果，其中图 12a为稀疏脉冲反演方法所得剖面，图 12b为本文方法所得剖面.与确定性稀疏脉冲方法相比，本文方法能够得到与初始波阻抗(图 11)更加相似的结果，薄层的可辨识性得到提高，尤其在黑色椭圆标出区域，基于FFT-MA谱模拟的快速随机反演可以明显识别出两个薄层，而稀疏脉冲反演只能识别出一个层.因此，利用本文提出的基于FFT-MA谱模拟的快速随机反演方法，能够有效融合测井资料的高频信息，提高地震反演分辨率，识别薄层，为复杂薄互储层的识别提供技术支持.从模型合成地震记录与由反演结果所得合成记录的相关系数对比图(图 13)可以看出，大部分相关系数都大于0.95，体现出二者良好的相关性.
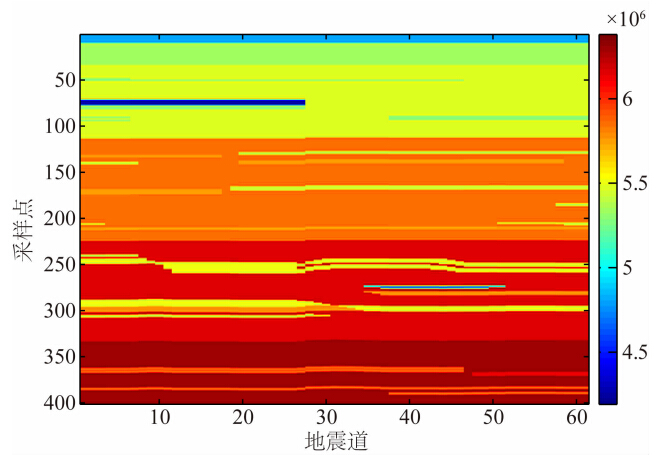 | 图 11 波阻抗模型Fig. 11 Impedance model n |
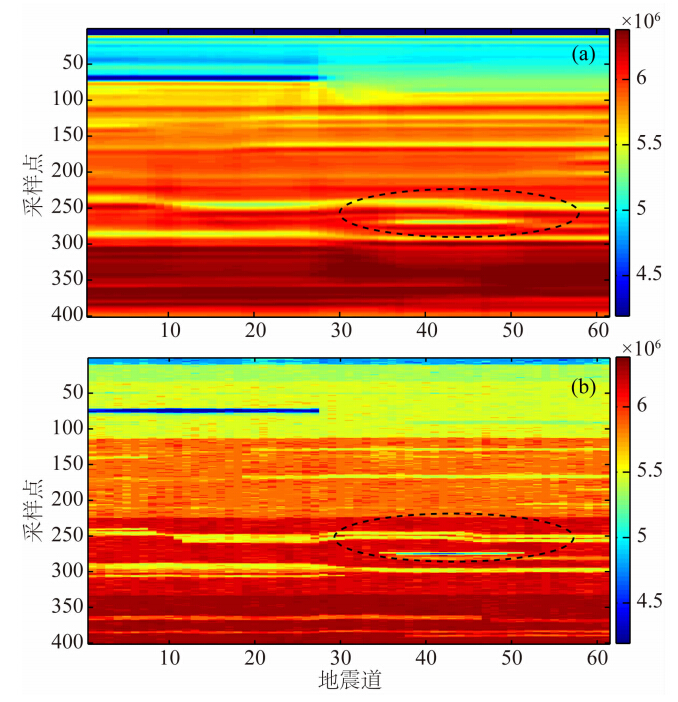 | 图 12 波阻抗反演结果(a)稀疏脉冲反演，(b)基于FFT-MA谱模拟的快速随机反演方法 Fig. 12 Impedance inversion results of(a)Sparse Impulse Inversion and (b)Fast Stochastic Inversion based on FFT-MA spectrum simulation |
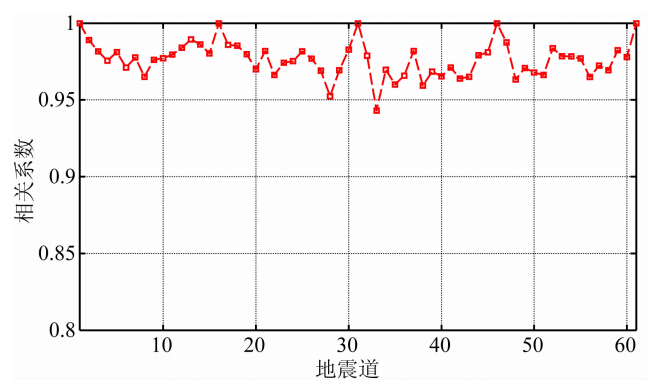 | 图 13 模型合成记录与反演合成记录的相关系数对比图Fig. 13 Correlation coefficient comparison ofmodel synthetic with inversion synthetic |
实际资料来自国内某老油田，该工区目的层段为河流相沉积，河道发育，储集层砂岩纵横向变化大、连通性差、油水关系复杂.工区目的层段砂体发育，纵向上砂岩与泥岩呈互层分布.
本次试算使用的地震资料共有157道，如图 14所示，纵向上采样率2 ms，从1.1 s到1.3 s，提取的子波主频为30 Hz，采用了三口井，分别位于10、88、142地震道位置处.
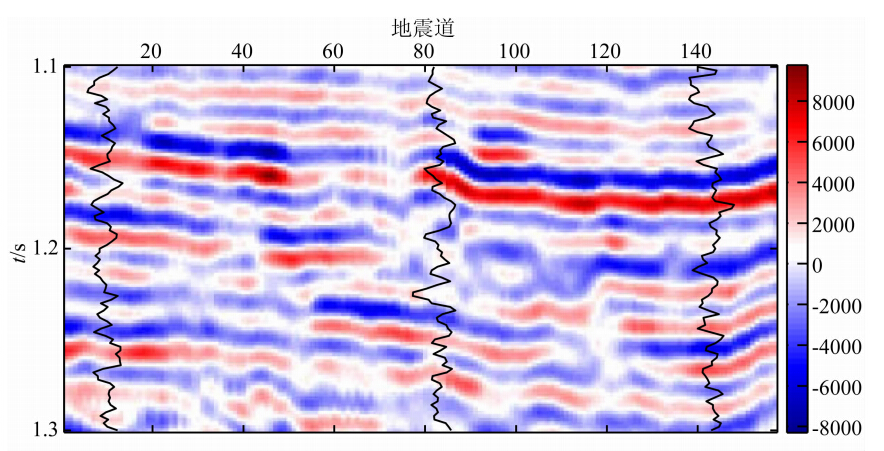 | 图 14 实际地震资料Fig. 14 Real Seismic data |
图 15显示了实际资料的反演结果，其中图 15a为稀疏脉冲反演方法所得结果，图 15b为本文方法所得结果，通过对比可以看出，虽然图 15a所示反演结果基本满足反演要求，但纵向分辨率低，对薄互储层展示效果不好，不能真实反映地下地质情况，因此难以满足油田生产需求.图 15b所示反演结果的纵向分辨率明显提高，砂泥岩互层得到很好的区分，砂体横向连续性也比较合理.从图中黑色椭圆标出的 位置可以看出，在1.25 s目的层附近的两个薄层得到了很好的区分，1.2 s附近的薄单砂体也能够清晰 地分辨，验证了本文提出的基于谱模拟的快速随机 反演方法在薄储层识别中的优势以及本文研究方法的有效性.
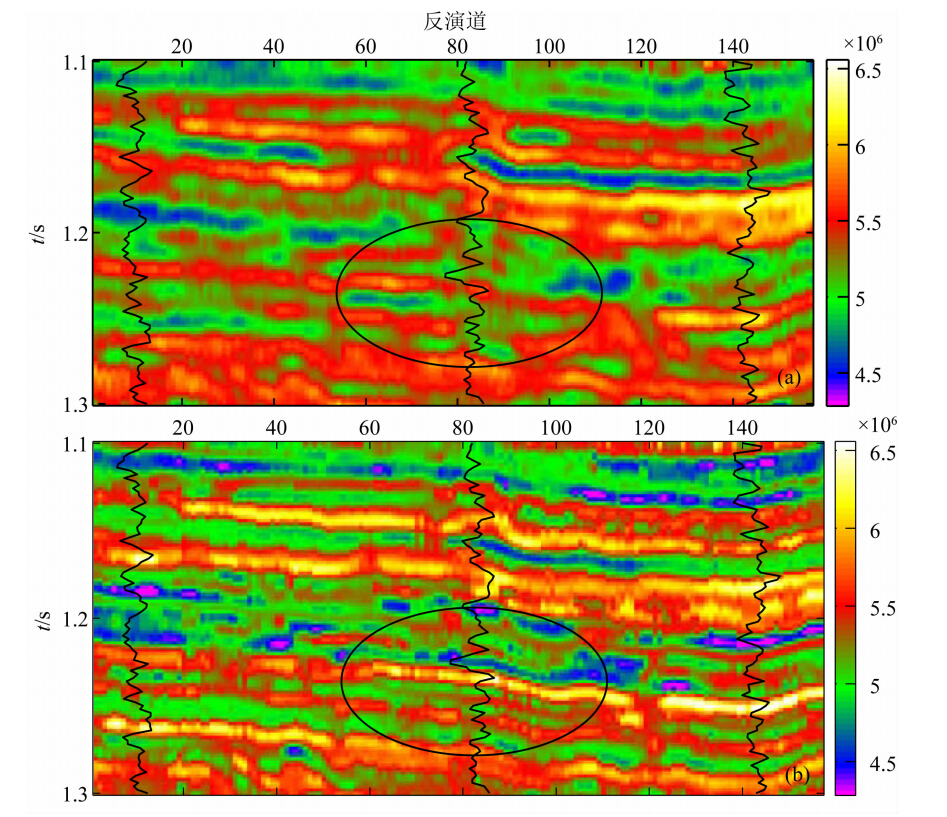 | 图 15 波阻抗反演结果(a)稀疏脉冲反演；(b)基于FFT-MA谱模拟的快速随机反演方法Fig. 15 Impedance inversion results of(a)Sparse Impulse Inversion and (b)Fast Stochastic Inversion based on FFT-MA spectrum simulation |
地震随机反演是一种可有效提高反演分辨率的方法，但存在计算效率低的问题，本文构建的基于FFT-MA谱模拟快速随机反演方法，不仅能够有效融合测井资料的高频信息，获得高分辨率反演结果，而且能够借助FFT-MA在频率域的快速模拟和GDM算法的快速优化更新，一方面加快随机反演的速度，有效提高反演的运算效率，另一方面使反演解得到快速收敛.模型试算和实例分析表明，快速随机反演方法不但可以提高计算效率，而且能够得到与模型吻合的反演结果，比稀疏脉冲反演方法更有效的识别出薄层.另外，由于新方法不受序贯因素的影响，因此，可以在今后的研究中对该方法进行并行运算，将储层分为多个部分同时进行反演，进一步提高计算效率.
| [1] | Bortoli L J, Alabert F, Haas A, et al.1992. Constraining stochastic images to seismic data. // Soares A ed. Geostatistics Tróia '92. Netherlands: Springer, 325-337. |
| [2] | Bosch M, Mukerji T, Gonzalez F E. 2010. Seismic inversion for reservoir properties combining statistical rock physics and geostatistics: A review. Geophysics, 75(5): 75A165-75A176. |
| [3] | Contreras A, Torres-Verdin C, Kvien K, et al. 2005. AVA stochastic inversion of pre-stack seismic data and well logs for 3D reservoir modeling. //EAGE 67th Conference and Exhibition. |
| [4] | Debeye H W, Sabbah E, Made P M. 1996. Stochastic inversion. //66 Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 1212-1215. |
| [5] | Doyen P M. 2007. Seismic Reservoir Characterization: An Earth Modeling Perspective. Houten, The Netherlands: European Association of Geoscientists and Engineers, Publications. |
| [6] | Francis A. 2005. Limitations of deterministic and advantages of stochastic seismic inversion. Canadian Soc. Expi Geophys. Recorder, 30(2): 5-11. |
| [7] | Francis A M. 2006a. Understanding stochastic inversion: Part 1. First Break, 24(11): 69-77. |
| [8] | Francis A M. 2006b. Understanding stochastic inversion: Part 2. First Break, 24(12): 79-84. |
| [9] | Haas A, Dubrule O.1994. Geostatistical inversion—a sequential method of stochastic reservoir modeling constrained by seismic data. First Break,12(11): 561-569. |
| [10] | Helgesen J, Magnus I, Prosser S, et al. 2000. Comparison of constrained sparse spike and stochastic inversion for porosity prediction at Kristin field. The Leading Edge, 19(4): 400-407. |
| [11] | Hu L Y. 2000. Gradual deformation and iterative calibration of Gaussian-related stochastic models. Math. Geology, 32(1): 87-108. |
| [12] | Hu L Y, Ravalec-Dupin M L. 2004. An improved gradual deformation method for reconciling random and gradient searches in stochastic optimizations. Math.Geol., 36(6): 703-719. |
| [13] | Huang H D, Zhang R W, Wei S P. 2009. Research on application of seismic nonlinear random inversion to reservoir prediction in the thin sandstone of continental deposits. Acta Petrolei Sinica (in Chinese), 30(3): 386-390. |
| [14] | Huang Z Y, Gan L D, Dai X F, et al. 2012. Key parameter optimization and analysis of stochastic seismic inversion. Applied Geophysics, 9(1):49-56. |
| [15] | Moyen R, Doyen P M. 2009. Reservoir connectivity uncertainty from stochastic seismic inversion.// 79th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2378-2381. |
| [16] | Oliver D S. 1995. Moving averages for Gaussian simulation in two and three dimensions. Math. Geol., 27(8): 939-960. |
| [17] | Pardo-Igúzquiza E, Chica-Olmo M. 1993. The Fourier integral method: An efficient spectral method for simulation of random fields. Math.Geol., 25(2): 177-217. |
| [18] | Ravalec M L, Noetinger B, Hu L Y. 2000. The FFT moving average (FFT-MA) generator: An efficient numerical method for generating and conditioning Gaussian simulations. Math.Geol., 32(6): 701-723. |
| [19] | Ravalec-Dupin M L, Noetinger B. 2002. Optimization with the gradual deformation method. Math. Geol., 34(2): 125-142. |
| [20] | Sams M, Saussus D. 2008. Comparison of uncertainty estimates from deterministic and geostatistical inversion.// 78th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1486-1490. |
| [21] | Sams M S, Atkins D, Siad N, et al. 1999. Stochastic inversion for high resolution reservoir characterisation in the central Sumatra basin.// Society of Petroleum Engineers Asia Pacific Improved Oil Recovery Conference, 257-260. |
| [22] | Sams M S, Saussus D. 2010. Comparison of lithology and net pay uncertainty between deterministic and geostatistical inversion workflows. First Break, 28(2): 35-44. |
| [23] | Sancevero S S, Remacre A Z, Portugal R S, et al. 2005. Comparing deterministic and stochastic seismic inversion for thin-bed reservoir characterization in a turbidite synthetic reference model of Campos basin, Brazil. The Leading Edge, 24(11): 1168-1172. |
| [24] | Srivastava R P, Sen M K. 2010. Stochastic inversion of prestack seismic data using fractal-based initial models. Geophysics, 75(3): R47-R59. |
| [25] | Yang K, Ai D F, Geng J H. 2012. A new geostatistical inversion and reservoir modeling technique constrained by well-log, crosshole and surface seismic data. Chinese J. Geophys. (in Chinese), 55(8):2695-2704, doi: 10.6038/j.issn.0001-5733.2012.08.022. |
| [26] | Yang X C, Li X F, Zhang M G. 2001. Process and Mathematical basis of investigations of seismic inversion. Process in Geophysics (in Chinese), 16(4): 96-109, doi: 10.3969/j.issn.1004-2903.2001.04.013. |
| [27] | Zhang S X, Zhang F C, Li S P, et al. 2010. Detailed prediction of thin reservoir in Andian area of Biyang Depression. Geophysical Prospecting for Petroleum (in Chinese), 49(1): 34-41. |
| [28] | 黄捍东, 张如伟, 魏世平. 2009. 地震非线性随机反演方法在陆相薄砂岩储层预测中的应用. 石油学报, 30(3): 386-390. |
| [29] | 杨锴, 艾迪飞, 耿建华. 2012.测井、井间地震与地面地震数据联合约束下的地质统计学随机建模方法研究.地球物理学报,55(8):2695-2704, doi: 10.6038/j.issn.0001-5733.2012.08.022. |
| [30] | 杨晓春, 李小凡, 张美根. 2001. 地震波反演方法研究的某些进展及其数学基础. 地球物理学进展, 16(4): 96-109, doi: 10.3969/j.issn.1004-2903.2001.04.013. |
| [31] | 张世鑫, 张繁昌, 李少鹏等. 2010. 泌阳凹陷安店区块薄储层精细预测. 石油物探, 49(1): 34-41. |