2015, Vol. 58
2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
From the results of the numerical simulations, there are three stages in the process of the plume-lithosphere interactions. At the first stage, the plume ascends with the velocity of 2.75 m·a-1 during the first 0.2 Ma, and the surface topography on the top of plume begins to uplift; at the second stage, the plume ascends with the velocity of 0.83 m·a-1 during 0.2 Ma to 0.26 Ma, and the surface topography reaches the peak value; At last stage, after 0.26 Ma the plume begins to move horizontally with the velocity of 0.47 m·a-1 and the bottom of lithosphere begins shear deformation, and when shear deformation reaches a certain degree, the bottom of lithosphere begins to perform delamination. The rheological strength of the crust deeply influences the process of plume-lithosphere interactions. When the rheological strength of the lower crust is weaker, the upper crust's rheological structure controls the degree of the uplift of surface topography. Otherwise, the rheological strength of the lower crust controls the degree of the subsidence of the both sides of the plume. In addition, the simulated results of Emeishan Large Igneous Province (ELIP) are in accordance with the previous results. The simulation results in this paper reflect the process of plume-lithosphere interactions and the effects of the crust's rheological structure on this process better and more clearly. Because of the faults are widely distributed in Emeishan Large Igneous Province (ELIP), which are not considered in this paper, the further research looks forward to take the faults in to account.
1 引言
在Wilson(1963)对夏威夷岛链年龄的递增现象进行探索研究和Morgan(1971)提出了地幔柱的概念后，经过近几十年的发展，地幔柱逐渐成为一种新的大地构造学说，并得到国内外大量地质与地球物理学者的认同.地幔柱被认为是热点轨迹，以及大火成岩省(LIPs)形成的最有可能的解释(Morgan，1981; Richards et al., 1989; Campbell and Griffiths， 1990). 目前地幔柱的研究主要集中在地幔柱形成的条件、机制以及它与岩石圈的相互作用(李建康和王登红，2005)，包括岩石圈的热溶蚀、地壳的上隆、沉陷和断裂等地质条件.常规方法，如地质学、地球化学和地球物理等(卢记仁，1996；张本仁，2001；徐义刚，2002)，均偏重于地幔柱与岩石圈相互作用后在 地球表面上的静态信息.而实验(Griffiths and Campbell， 1990)、数值模拟方法(d′Acremont et al., 2003; Burov and Guillou-Frottier， 2005)则能够显示地幔柱与岩石圈相互作用过程中的动态信息.因此，数值模拟对地 幔柱与岩石圈相互作用的研究起着非常重要的作用.
Griffiths和Campbell(1990)根据表面场观察，给出了与溢流玄武岩和热点轨迹相关的第一个地幔 柱物理模型.早期的实验研究(Griffiths，1986; Olson，1990)认为，地幔柱是由于热边界层上的Rayleigh-Taylor不稳定引起的，形成了一个类似球状的头部和一个很窄的小尾巴.当地幔柱的头部到达岩石圈时，便开始水平运动.发生水平运动的原因可能有：(1)接近表面的浮力比较小；(2)比较邻近自由表面；(3)地幔柱和岩石圈的界面具有比较大的流变差异；(4)岩石圈的下表面层具有抵抗力.
对地幔柱与岩石圈相互作用过程的数值模拟，国内外学者做了大量的研究工作，使得地幔柱研究在数值模拟方面有了很大的发展.Christensen和Harder(1991)提出地幔的三维对流模型，但并未考 虑不同圈层中物质组分的差异；Farnetani和Richards(1994)数值模拟了大陆溢流玄武岩和海底高原与地幔柱活动的关系，并建立了地球圈层中流体黏度随深度的变化结构；Manglik和Christensen(1997)利用数值模拟解释了在地幔柱上升过程中，岩石圈中岩石熔融速率的变化规律；d′Acremont等(2003)数值模拟了海洋大火成岩省的地幔柱与岩石圈相互作用的过程.国内学者(李建康和王登红，2004；Leng and Gurnis， 2012)主要数值模拟了起源于幔核边界处的地幔柱演化过程.
本文将集中模拟地幔柱与岩石圈的相互作用过程.在非牛顿流体近似的基础上，采用温度-压力-应变率相关的黏度模型对其进行二维的数值模拟.通过数值模拟计算，展示了地幔柱与岩石圈相互作用过程中的时空分布图，分析并讨论了地壳流变结构对此过程的影响.最后，展示了其在峨眉山大火成岩省的应用. 2 物理模型 2.1 控制方程
本文利用Ellipsis3D(O′Neill et al., 2006)来求解质量守恒方程、动量守恒方程和能量守恒方程，其中流变关系采用非牛顿流体近似.Ellipsis3D是在Ellipsis(Moresi et al., 2003)的基础上作了部分修改得来的，是一种采用Langrange积分点的有限元程序，其特点是采用欧拉网格，利用粒子追踪岩石的流变历史，并以粒子作为有限单元的积分点，非常适合模拟岩石圈的动力学行为.在Ellipsis3D中，应力张量分成两部分，压力p和偏应力τ：
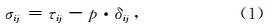
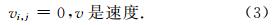
地壳和地幔岩石的流变定律关系式可以表示为(Ranalli，1995)
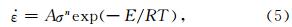
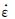为应变率，σ=σ1-σ3为差应力，E为活化能，R=8.314 J·mol-1·K-1为普适气体常数，T为绝对温度，A、n、E为岩石的物性参数.可以将(5)式重写为应力的表达式：
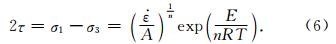
除了上述流变定律以外，岩石在受力条件下的屈服机制及强度弱化机制也是岩石的流变性质非常重要的一个方面，数值模拟中一般采用如下屈服机制(O′Neill et al., 2006)：
地幔柱定量化的地质模型是根据地幔柱起源、发展和演化的背景和条件设计的.由于地幔柱与大陆岩石圈的相互作用发生在上地幔以上，所以地幔 柱的起源一般不需要太深，比如400 km(d′Acremont et al., 2003)，670 km(Burov and Guillou-Frottier， 2005)等.本文参考Burov和Guillou-Frottier(2005)的设置，选取计算深度为670 km.模型采用笛卡尔二维直角坐标系，计算区域为1340 km×670 km.同时，在计算区域的底部设置一个低黏度、高温度(+300 ℃)、半径为70 km的圆形地幔柱初始形态.
根据我国境内四川盆地的平均地壳厚度(黄汲清等，1977)，初步设置莫霍面的深度为45 km，其中包括20 km的上地壳和25 km的下地壳.详细参数见表 1和表 2.表 1是数值计算过程中所使用的共同的物性参数(Burov and Guillou-Frottier， 2005)，表 2是数值模拟过程中不同圈层物质的物性参数.
|
表 1 数值模拟过程中共同的物性参数 Table 1 The common parameters in the numerical modeling |
|
|
表 2 数值模拟过程中不同圈层的物性参数 Table 2 The physical parameters of different layers in the numerical modeling |
假定岩石圈内部热是以传导的形式来进行传播的，从而确定岩石圈的温度剖面.对于地幔，则是在近似绝热温度梯度条件下，确定其初始温度场.本文采用与d′Acremont等(2003)相近似的初始温度条件，岩石圈底部的温度为1330 ℃，岩石圈之下至 670 km深度处，温度从1330 ℃缓慢增长到1600 ℃. 同时，图 1给出了当应变率为1×10-15 s-1时，相应 初始温度下岩石圈的不同流变结构强度剖面，其中(A)采用上地壳和下地壳的代表性岩石分别为花岗岩和长英质麻粒岩，(B)为花岗岩和镁铁质麻粒岩，(C)为花岗岩(湿)和长英质麻粒岩，(D)为花岗岩(湿)和镁铁质麻粒岩.从图 1可以看出，花岗岩和镁铁质麻粒岩的流变强度相对较强.另外，边界条件设置如下：左右两侧，水平速度vxx=0，底部为岩石静压力，上表面为自由表面条件.
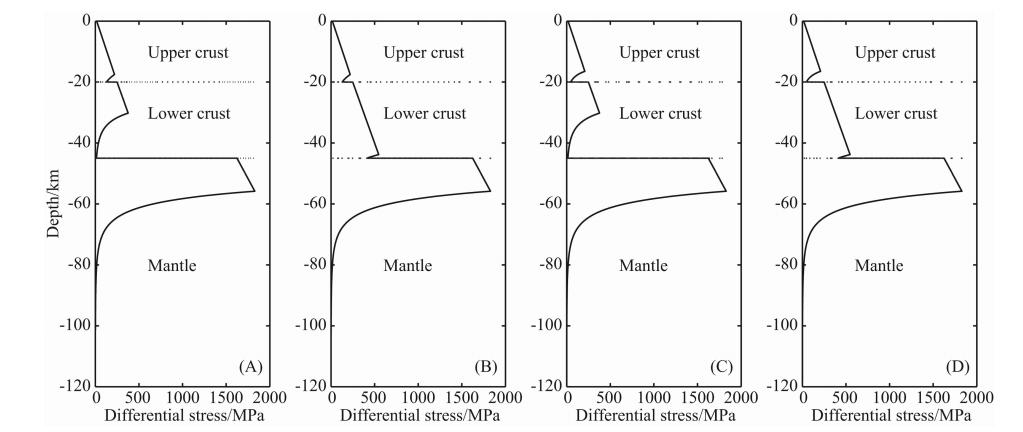 | 图 1 岩石圈流变强度剖面 Fig. 1 Rheology strength profiles for lithosphere |
图 2a—2d显示的是模型B地幔柱与岩石圈相互作用过程中的温度和速度场、相图场、有效黏度图以及地表地形的演化过程.模拟结果显示，该过程大致可以分为三个阶段：
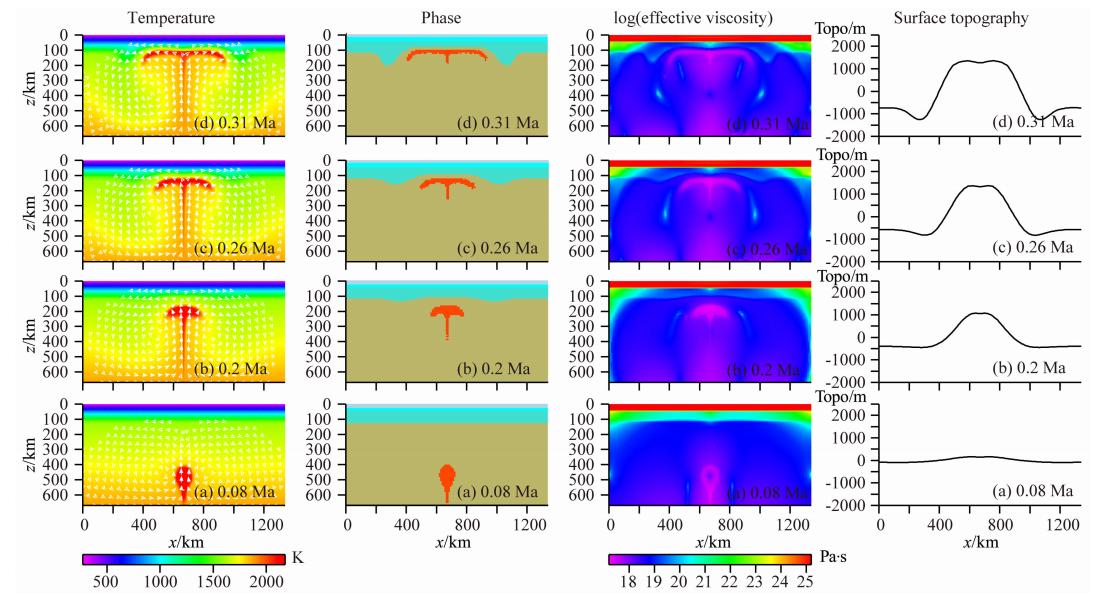 | 图 2 模型B地幔柱与岩石圈相互作用图 第一列：温度和速度场图；第二列：相图—青色代表岩石圈(地壳厚度为45 km)，灰绿色代表上地幔，红色代表地幔柱； 第三列：有效黏度图；第四列：地表地形图. 由下至上(a—d)：地幔柱与岩石圈相互作用过程随时间变化图. Fig. 2 The interaction of plume and lithosphere for model B The first column: temperature and velocity fields; the second column: phase fields—cyan represents lithosphere including 45 km thick crust，grayish-green represents upper mantle，red represents plume; the third column: effective viscosity; the fourth column: surface topography. Bottom to up(a—d): the interaction variation of plume and lithosphere over time. |
第一阶段：如图 2a—2b，温度、密度差异引起地幔柱的重力不稳定，导致地幔柱异常体向上快速上升.从670 km初始异常处，穿越上地幔物质，经大概0.2 Ma到达岩石圈底部.伴随着地幔柱的上升过程，地幔柱顶部的地表地形不断向上隆起.
第二阶段：如图 2b—2c，地幔柱到达岩石圈底部，并不断纵向侵蚀岩石圈的底部，此过程发生在0.2~0.26 Ma之间，总共可达0.06 Ma.我们从相图可以看出，地幔柱在此过程中对岩石圈的底部进行了纵向侵蚀，造成整个岩石圈的明显减薄.同时，在此过程中，地表地形隆起比较剧烈，达到整个相互作用过程的最高高度.
第三阶段：如图 2c—2d，地幔柱以水平运动为主，并不断横向侵蚀岩石圈的底部.从0.26 Ma以后，地幔柱上升速率急剧下降，运动主要以水平运动为主.从相图可以看出，由于岩石圈受到地幔柱的不 断侵蚀，到达一定程度后，可引起岩石圈的拆沉作用.同时，从地表地形图可以看出，地表隆起地形也随之不断缓慢下降，最终将会达到一个稳定的地形高度. 3.2 相互作用过程的岩石圈响应 3.2.1 地表地形
通过数值模拟计算，我们得到不同流变模型下地幔柱与岩石圈相互作用过程中所引起的地表地形的变化，如图 3所示.图 3中，我们分别挑选了比较具有代表性的六个时间点的地表地形图，从a—f为地表地形随时间的演化图.我们可以看出，地幔柱从上升开始，就伴随着顶部地表地形的不断隆升；地幔柱与岩石圈相互纵向作用的0.06 Ma时间里，地幔柱顶部的地表地形进一步隆升达到地表地形隆升的最高值.而地幔柱的两侧距离地幔柱270 km以外的区域先出现对称性的下沉，最后阶段再出现缓慢向上抬升，最终趋向于水平.比较模型A、C，A模型的最高隆升高度可达900 m，而C为2300 m，可以看出，当下地壳流变强度比较小时，上地壳流变强度越大，地表地形隆升幅度越小.上地壳的流变差异导致隆升幅度差异可达两倍之多，可见此情况下上地壳的流变结构对地幔柱顶部地形隆升起着绝对的控制作用.比较模型B、D，B模型的最高隆升高度可达1400 m，而D为1600 m，可以看出，当下地壳流变强 度比较大时，地幔柱顶部隆起差异明显变小，达200 m 左右.比较模型A、B(或者C、D)，可以看出，下地壳的流变结构控制着地幔柱两侧地表地形的下沉幅度，下地壳流变强度越小，下沉幅度越大.
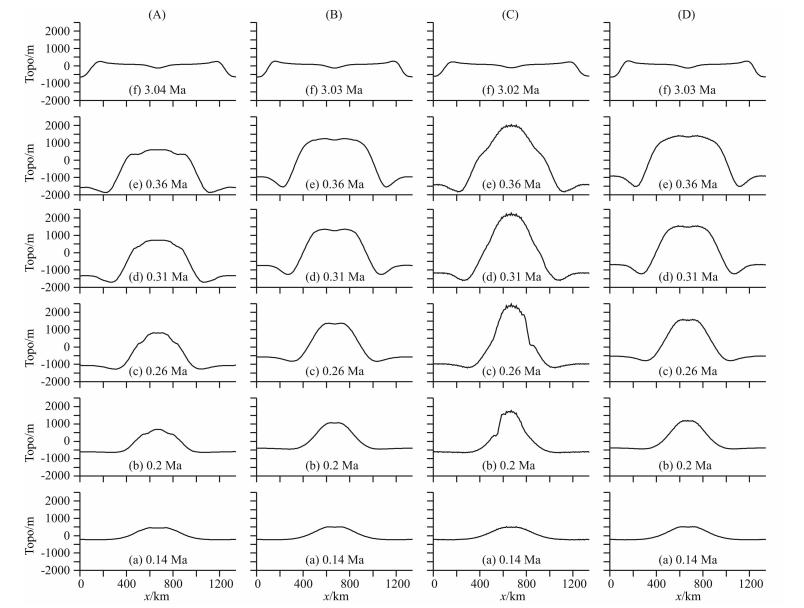 | 图 3 地表地形图 Fig. 3 Surface topography |
另外，从图 3中可以看出，所有模型在距离地幔柱70~470 km两侧地表地形变化差异非常大，靠近地幔柱方向地表表现为向上隆起，而远离地幔柱方向，地表表现为向下沉陷，初步判断在此区域范围内出现伸展型断裂的可能性非常大. 3.2.2 岩石圈底部拆沉作用
地幔柱与岩石圈相互横向作用以后，由于地幔柱对岩石圈的不断侵蚀，最终可引起岩石圈底部的拆沉作用，以模型B为例，如图 4所示.从图 4中的相图可以清楚看到，岩石圈(青色)底部不断受到来自地幔柱的侵蚀，最终发生拆沉作用.由于地幔柱物质到达岩石圈底部，温度较岩石圈大的多，所以对岩石圈底部产生了热溶蚀，由于此时的重力异常不足以驱动其继续向上运移，地幔柱则引起岩石圈底部 剪切变形，对其进行了侧向侵蚀，即横向相互作用.
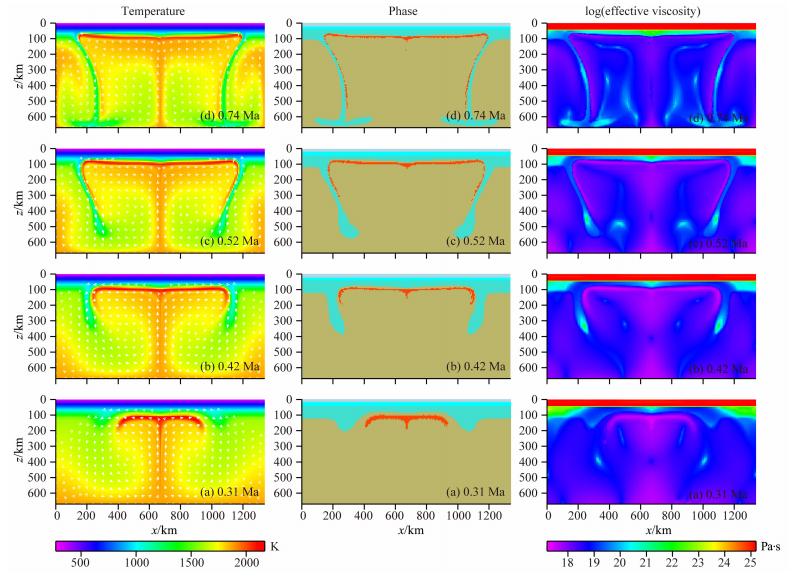 | 图 4 模型B岩石圈拆沉图 第一列：温度和速度场图；第二列：相图—青色代表岩石圈(地壳厚度为45 km)，灰绿色代表上地幔， 红色代表地幔柱；第三列：有效黏度图. 由下至上(a—d)：拆沉作用随时间变化. Fig. 4 The delamination of the lithosphere for model B The first column: temperature and velocity fields; the second column: phase fields—cyan represents lithosphere including 45 km thick crust，grayish-green represents upper mantle，red represents plume; the third column: effective viscosity. Bottom to up(a—d): the delamination variation over time. |
从图 4a—4b，我们可以看出，岩石圈不断受到横向 侵蚀减薄，从最初120 km的厚度，最大减薄到了70 km 的厚度，并且侵蚀出来的岩石圈物质由于对流的作用不断向下拆沉.由此可以说，地幔柱的存在可能会引起岩石圈底部的拆沉作用.
通过上述数值模拟结果可知，地幔柱与岩石圈相互作用过程中，可引起岩石圈底部的热溶蚀、地表地形的上隆、沉陷，以及断裂的产生.下面将综合讨论一下本次数值模拟对地幔柱与岩石圈相互作用过程的认识，下节将给出其在我国峨眉山大火成岩省的应用.
(1)根据上述模拟结果可知，在黏度与温度、应变率有关的流变条件下，地幔柱由670 km相变面上升到岩石圈底部大概需要0.2 Ma的时间.在此 期间地幔柱物质流动的平均速度可达到2.75 m·a-1. 地幔柱与岩石圈相互纵向作用0.2~0.26 Ma，其地幔柱向上的平均速度为0.83 m·a-1. 0.26 Ma以后，地幔柱与岩石圈发生横向相互作用，岩石圈底部剪切变形，最终导致岩石圈底部的拆沉作用，此过程地幔柱侧向平均速度为0.47 m·a-1.由此可以看出，地幔柱与岩石圈相互作用过程中，由于热损耗、浮力降低等原因，速度在不断减小.
(2)从相图随时间的变化可以明显看出，地幔柱上升到岩石圈底部时，其冠部会热溶蚀岩圈的底部，如图 2.当地幔柱冠部与岩石圈底部接触后，岩石圈经加热软化，部分物质被地幔柱扩张所产生的剪应力带出，导致岩石圈的热溶蚀减薄，从120 km的厚度减薄成70 km的厚度.
(3)地幔柱和岩石圈的相互作用还会引起地表的隆升和沉陷，如图 3.从地幔柱向上运动开始，地表地形就开始发生变化，地幔柱顶部地形不断向上隆起，在地幔柱与岩石圈相互纵向作用过程中，地表地形的隆升达到了最高值，随后又慢慢下沉；而地幔柱的两侧距离地幔柱270 km以外的区域则开始先向下沉陷，横向作用过程中，又慢慢向上抬升，直至 趋于水平位置.同时，在距离地幔柱中心70~470 km 的两侧区域，有可能出现伸展型断裂.
(4)通过对四种不同模型的比较发现，当下地壳流变强度比较小时，上地壳的流变强度对地幔柱顶部地表地形的隆升程度起着决定性的作用，流变强度越大，隆升高度越小；而下地壳的流变结构控制着地幔柱两侧地表地形的下沉幅度，下地壳流变强度越小，下沉幅度越大.
(5)地幔柱与岩石圈相互横向作用以后，由于地幔柱对岩石圈底部的不断侵蚀，岩石圈底部不断剪切变形，最终可引起岩石圈底部的拆沉作用，如图 4.从相图可以明显看出，由于地幔柱对岩石圈的横向侵蚀，侵蚀出来的岩石圈物质由于对流的作用不断向下拆沉.由此推断，地幔柱与岩石圈的相互作用可能会引起岩石圈底部的拆沉作用. 4 对峨眉山大火成岩省的应用
地幔柱研究是判断大火成岩省非常重要的一个方法，通过研究地幔柱与岩石圈相互作用过程中所引起的岩石圈变化、地表地形变化等，可以更清楚地认识大火成岩省的形成过程.峨眉山大火成岩省(ELIP)是我国唯一获得国际地学界认可的溢流玄武岩省，主要以喷发中二叠世时期的峨眉山玄武岩为主体，广泛分布于我国西南地区(扬子克拉通西缘)，空间范围南北超过1000 km，东西超过900 km(宋谢炎等，2002).动力学机制也一直是研究的热点.大量学者对其进行了研究，何斌等(2003)通过地球化学、地层学研究发现，峨眉山地幔柱的轴部位于米易—永仁一带，同时，峨眉山地幔柱达到上地幔时轴部直径大约为65~105 km.综合比较，以本文的模型B来代表峨眉山地幔柱模型，即上下地壳分别以花岗岩和镁铁质麻粒岩来表示.
何斌等(2005)根据峨眉山大火成岩省中冲积扇沉积记录，估算出峨眉山玄武岩大规模喷发前穹状隆起轴部地壳抬升高度应大于1300 m，而李宏博(2012)根据地层学等研究，利用实验模型推导出ELIP的最大隆升幅度为1500 m，与本文数值模拟得到的最高隆升高度1400 m基本一致.另外，由于峨眉山地幔柱现已喷发结束，区域构造背景也比较复杂，常规方法对于地幔柱引起的拆沉作用难以进行验证，期待将来能有更新、更有效的方法对其进行检验.
本数值模拟可以用来展现峨眉山地幔柱在无喷发情况下与岩石圈相互作用的过程，但由于峨眉山大火成岩省处在青藏高原的边缘地带，区域构造比较复杂，深大断裂带分布比较多，控制着溢流玄武岩的喷发与展布(李宏博，2012)，而断裂带不在本文的讨论范围之内，有待进一步的讨论研究.总之，通过地幔柱与岩石圈相互作用的数值模拟，有利于更好地解释峨眉山大火成岩省(ELIP)的地质事件. 5 结论
数值模拟结果表明，计算机数值模拟能够较好地反映地幔柱和岩石圈的相互作用过程.通过模拟计算、结果分析以及综合讨论，可以得出以下几点结论：
(1)地幔柱与岩石圈相互作用可以分为三个阶段：地幔柱上升期，时间持续到0.2 Ma，平均速度为 2.75 m·a-1；地幔柱与岩石圈纵向作用，时间从0.2到0.26 Ma，其地幔柱向上的平均速度为0.83 m·a-1；地幔柱与岩石圈横向作用，0.26 Ma以后，岩石圈开始剪切变形，地幔柱水平运动速度为0.47 m·a-1.
(2)地幔柱和岩石圈的相互作用会引起地表的隆升和沉陷.从地幔柱向上运动开始，地表地形就开始发生变化，地幔柱顶部地形不断向上隆起，在地幔柱与岩石圈相互纵向作用过程中，地表地形的隆升达到了最高值，随后又慢慢下沉；而地幔柱的两侧区域则开始先向下沉陷，然后又慢慢向上抬升，直至趋于水平位置.
(3)当下地壳流变强度比较小时，上地壳的流变结构控制着地幔柱顶部地表地形隆起程度，流变强度越大，隆升高度越小；而下地壳的流变结构控制着地幔柱两侧地表地形的下沉幅度，下地壳流变强度越小，下沉幅度越大.
(4)地幔柱上升到岩石圈底部时，其冠部会热溶蚀岩圈的底部.当地幔柱冠部与岩石圈底部接触后，岩石圈经加热软化，部分物质被地幔柱扩张所产生 的剪应力带出，导致岩石圈的热溶蚀减薄，从120 km 厚度变为70 km.随着时间的推移，岩石圈底部剪切变形越剧烈，最终可导致岩石圈底部的拆沉作用.
(5)模拟得到峨眉山大火成岩省的隆升最高高度可达1400 m，但常规方法对于地幔柱引起的拆沉作用难以进行验证，期待更新的方法对其进行验证.同时此地区深大断裂带的分布控制着溢流玄武岩的喷发与展布，但这不在本文的讨论范围之内，有待进一步研究.
致谢 本文使用了科学计算网格ScGrid、CIG提供的开源有限元程序Ellipsis3D进行计算机数值模拟.同时，感谢中国科学院地球深部研究重点实验室提供计算模拟平台，感谢中国科学院超级计算中心提供科学计算网格服务.| [1] | Burov E, Guillou-Frottier L. 2005. The plume head-continental lithosphere interaction using a tectonically realistic formulation for the lithosphere. Geophysical Journal International, 161(2): 469-490. |
| [2] | Campbell I H, Griffiths R W. 1990. Implications of mantle plume structure for the evolution of flood basalts. Earth and Planetary Science Letters, 99(1): 79-93. |
| [3] | Christensen U, Harder H. 1991. 3-D convection with variable viscosity. Geophysical Journal International, 104(1): 213-226. |
| [4] | d'Acremont E, Leroy S, Burov E B. 2003. Numerical modelling of a mantle plume: the plume head-lithosphere interaction in the formation of an oceanic large igneous province. Earth and Planetary Science Letters, 206(3-4): 379-396. |
| [5] | Farnetani C G, Richards M A. 1994. Numerical investigations of the mantle plume initiation model for flood basalt events. Journal of Geophysical Research: Solid Earth (1978—2012), 99(B7): 13813-13833. |
| [6] | Griffiths R W. 1986. Particle motions induced by spherical convective elements in Stokes flow. Journal of Fluid Mechanics, 166: 139-159. |
| [7] | Griffiths R W, Campbell I H. 1990. Stirring and structure in mantle starting plumes. Earth and Planetary Science Letters, 99(1-2): 66-78. |
| [8] | He B, Xu Y G, Xiao L, et al. 2003. Generation and spatial distribution of the Emeishan Large Igneous Province: New evidence from Stratigraphic records. Acta Geologica Sinica (in Chinese), 77(2): 194-202. |
| [9] | He B, Xu Y G, Wang Y M. 2005. The magnitude of Crustal Uplift Prior to the Eruption of the Emeishan Basalt: Inferred from Sedimentary records. Geotectonica et Metallogenia (in Chinese), 29(3): 316-320. |
| [10] | Huang T K, Jen C S, Jiang C F, et al. 1977. An outline of the tectonic characteristics of China. Acta Geologica Sinca (in Chinese), (2): 117-135. |
| [11] | Kirby S H. 1983. Rheology of the lithosphere. Reviews of Geophysics, 21(6): 1458-1487. |
| [12] | Leng W, Gurnis M. 2012. Shape of thermal plumes in a compressible mantle with depth-dependent viscosity. Geophysical Research Letters, 39(5): L05310. |
| [13] | Li H B. 2012. Mantle plume geodynamic significances of the Emeishan Large Igneous Province: Evidence from Mafic Dykes, Geochemistry and Stratigraphic records (in Chinese). Beijing: China University of Geosciences (Beijing). |
| [14] | Li J K, Wang D H. 2004. A preliminary research on the numerical simulation of the Emei Mantle Plume. Acta Geosicientia Sinica (in Chinese), 25(5): 509-514. |
| [15] | Li J K, Wang D H. 2005. Advances in the numerical simulation of the mantle plume. Geological Science and Technology Information (in Chinese), 24(4): 13-20. |
| [16] | Lu J R. 1996. Dynamical characteristics of the Emei Mantle Plume. Acta Geosicientia Sinica (in Chinese), 17(4): 424-438. |
| [17] | Manglik A, Christensen U R. 1997. Effect of mantle depletion buoyancy on plume flow and melting beneath a stationary plate. Journal of Geophysical Research: Solid Earth (1978-2012), 102(B3): 5019-5028. |
| [18] | Moresi L, Dufour F, Mühlhaus H B. 2003. A Lagrangian integration point finite element method for large deformation modeling of viscoelastic geomaterials. Journal of Computational Physics, 184(2): 476-497. |
| [19] | Morgan W J. 1971. Convection plumes in the lower mantle. Nature, 230(5288): 42-43. |
| [20] | Morgan W J. 1981. Hotspot tracks and the opening of the Atlantic and Indian Oceans. //Emiliani C ed. The Sea, ideas and observations on progress in the study of the seas. New York: Wiley Interscience, 7: 443-487. |
| [21] | Olson P. 1990. Hot spots, swells and mantle plumes. // Ryan M P ed. Magma Transport and Storage. New York: John Wiley, 33-51. |
| [22] | O'Neill C, Moresi L, Müller D, et al. 2006. Ellipsis 3D: A particle-in-cell finite-element hybrid code for modelling mantle convection and lithospheric deformation. Computers & Geosciences, 32(10): 1769-1779. |
| [23] | Ranalli G. 1995. Rheology of the Earth. 2nd ed. London: Chapman and Hall. |
| [24] | Richards M A, Duncan R A, Courtillot V E. 1989. Flood basalts and hot-spot tracks: plume heads and tails. Science, 246(4926): 103-107. |
| [25] | Song X Y, Hou Z Q, Wang Y L, et al. 2002. The mantle plume features of Emeishan basalts. Journal of Mineralogy and Petrology (in Chinese), 22(4): 27-32. |
| [26] | Wang H L, Bai W M, Wang Q P. 2011. Numerical simulation of lithosphere delamination at the continental orogenic belts. Chinese J. Geophys. (in Chinese), 54(11): 2851-2863, doi:10.3969/j.issn.0001-5733.2011.11.015. |
| [27] | Wilks K R, Carter N L. 1990. Rheology of some continental lower crustal rocks. Tectonophysics, 182(1-2): 57-77. |
| [28] | Wilson J T. 1963. A possible origin of the Hawaiian Islands. Canadian Journal of Physics, 41(6): 863-870. |
| [29] | Xu Y G. 2002. Mantle plumes, Large Igneous Provinces and their geologic consequences. Earth Science Frontiers (in Chinese), 9(4): 341-353. |
| [30] | Zhang B R. 2001. Magmatic activities from plume-source in the Qinling Orogenic Belt and its dynamic significance. Earth Science Frontiers (in Chinese), 8(3): 57-66. |
| [31] | 何斌, 徐义刚, 肖龙等. 2003. 峨眉山大火成岩省的形成机制及空间展布: 来自沉积地层学的新证据. 地质学报, 77(2): 194-202. |
| [32] | 何斌, 徐义刚, 王雅玫等. 2005. 用沉积记录来估计峨眉山玄武岩喷发前的地壳抬升幅度. 大地构造与成矿学, 29(3): 316-320. |
| [33] | 李宏博. 2012. 峨眉山大火成岩省地幔柱动力学: 基性岩墙群、地球化学及沉积地层学证据［博士论文］. 北京: 中国地质大学(北京). |
| [34] | 李建康, 王登红. 2004. 峨眉地幔柱动力学数值模拟的初步研究. 地球学报, 25(5): 509-514. |
| [35] | 李建康, 王登红. 2005. 地幔柱数值模拟研究进展. 地质科技情报, 24(4): 13-20. |
| [36] | 卢记仁. 1996. 峨眉地幔柱的动力学特征. 地球学报, 17(4): 424-438. |
| [37] | 宋谢炎, 侯增谦, 汪云亮等. 2002. 峨眉山玄武岩的地幔热柱成因. 矿物岩石, 22(4): 27-32. |
| [38] | 黄汲清, 任纪舜, 姜春发等. 1977. 中国大地构造的基本轮廓. 地质学报, (2): 117-135. |
| [39] | 徐义刚. 2002. 地幔柱构造、大火成岩省及其地质效应. 地学前缘, 9(4): 341-353. |
| [40] | 张本仁. 2001. 秦岭地幔柱源岩浆活动及其动力学意义. 地学前缘, 8(3): 57-66. |