2. 江苏省地质勘查技术院, 南京 210000
2. Geological Exploration Technology Institute of Jiangsu Province, Nanjing 210000, China
近年来,随着地球物理各种方法的正反演技术日趋成熟,利用多种地球物理参数对同一地质体进行综合解释已经得到了广泛的应用(Aric et al.,1997;姜枚等,2012a,2012b;高德章等,2004;胡平等,2010).但由于受制于单方法本身的多解性,利用单方法单参数反演结果进行综合解释往往很难获得较为统一的地质-地球物理模型.为了解决这一问题,国内外学者对多方法多参数联合反演方法进行了深入研究(Moorkamp et al.,2007;彭淼等,2012;Colombo and De Stefano,2007;于鹏等,2009).其中,采用模型结构耦合的联合反演已经成为国际上的趋势(Haber and Oldenburg,1997),由Gallardo和Meju(2003)提出的交叉梯度(cross-gradient)耦合方法是比较有代表性的成果.Gallardo和Meju(2007)进行了大地电磁和折射地震二维联合反演算法的研究,通过在反演的目标函数中引入交叉梯度函数来约束不同的模型参数,比传统的直接关系耦合更具有普遍适用性.国内学者也有相关的研究成果,如彭淼等(2013)实现了大地电磁和天然地震的三维联合反演算法.
地球物理反演方法很多,主要包括最小二乘法、共轭梯度法、OCCAM法以及基于现代优化算法技术的组合最优化算法等.其中OCCAM法反演得到的模型综合了数据拟合差和光滑度两项要素(Constable et al.,1987),数据空间法(data-space inversion)是在OCCAM法基础上发展起来的一种反 演方法(Siripunvaraporn and Egbert,2000; Siripunvaraporn et al.,2005).
TDIP是以岩、矿石的激电效应差异为物质基础,通过观测和研究大地激电效应,来探查地下地质情况的一种电法分支方法.该方法在寻找金属矿、能源和工程地质等不同领域均有着广泛的应用,尤其在寻找浸染状矿产资源方面效果显著(傅良魁,1982).国内外学者对TDIP二维反演算法进行了大量研究,但是都是采用分步反演,即先反演出电阻率之后,在所反演出的电阻率模型基础之上再反演极 化率参数(Douglas and Li,1994,1999),这样就存在着极化率反演结果严重依赖于电阻率反演结果等问题.
为了解决上述问题,本文在反演算法中引入了交叉梯度约束,提出了TDIP电阻率和极化率二维同步反演策略,通过设计电阻率和极化率物性结构一致模型和不一致的模型进行测试,讨论该同步反演算法的可靠性和适用性.
2 TDIP二维正反演算法 2.1 TDIP二维正演算法本文采用等效电阻率法(Douglas and Li,1994)进行TDIP正演数值模拟.等效电阻率法以电阻率法的正演计算为基础,该方法大体可以分成三步完成:首先根据各个模型节点上的电阻率和极化率数值,计算出节点上的等效电阻率;然后进行等效电阻率的正演模拟(把电阻率法正演过程略微修改即可),计算出等效视电阻率;最后根据电阻率正演和等效电阻率正演得到的视电阻率和等效视电阻率,即可计算出视极化率,这样就完成了极化率数据数值模拟的整个过程.本文采用的电阻率法正演算法为有限单元法.
2.2 TDIP二维分步反演算法Siripunvaraporn等人在OCCAM的基础上进行了改进,通过一系列数学变换,将M(模型参数个数)行M列的模型空间的叉积矩阵转换为N(观测数据个数)行N列的数据空间叉积矩阵,演变成了数据空间反演法.对于二维和三维反演算法来说,N往往比M小得多,并且该方法不需要求取模型协方差矩阵的逆矩阵,因而大大减少了所需的计算时间和计算机内存,提高了反演效率,是一种实用的反演算法.因此,本文采用的电阻率法反演方法即为数据空间反演(Siripunvaraporn and Egbert,2000; Siripunvaraporn et al.,2005).
本文所采用的TDIP反演方法也是数据空间反演法,其基本过程与电阻率法反演一致,只需要完成TDIP反演的雅可比矩阵求取即可.在电阻率法反演的雅可比矩阵基础上,可以计算得到TDIP反演的雅可比矩阵(Douglas and Li,1994,1999).
3 引入交叉梯度约束的TDIP二维同步反演 3.1 同步反演目标函数本文的同步反演核心思想是,每次迭代中同步更新电阻率和极化率参数,因此只定义一个目标函数,同时反演电阻率和极化率,并加入交叉梯度约束项.目标函数具体形式如下所示:
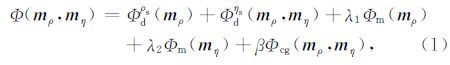
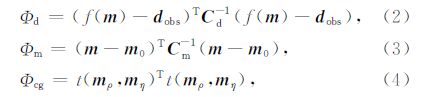
其中,Φd是数据拟合项,Φm是模型光滑项,Φcg是交叉梯度项;λ1和λ2是正则化参数,β是交叉梯度的加权因子,本文选取的加权因子和正则化参数在分步反演和同步反演的所有算例中是一致的; m ρ和m η分别为电阻率和极化率模型向量, m 0为初始模型, C (m)为模型协方差矩阵, C (d)为数据协方差矩阵,起到利用数据误差给观测数据加权的作用; d obs为实测数据向量,f(·)为正演算子;t(·)为交叉梯度算子(Gallardo and Meju,2003,2007) ,在同步反演中引入交叉梯度函数可以实现电阻率参数和极化率参数的相互约束.
电阻率和极化率交叉梯度定义如下:
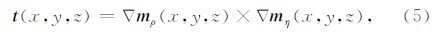
式中, Δ m ρ和Δ m η分别代表电阻率参数和极化率参数的梯度.
对于二维问题,设地质体的走向为y轴方向,则交叉梯度的z分量和x分量是零,y分量表达式如下:
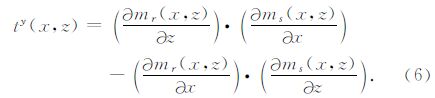
采用五点中心差分格式,离散式(6),得到:
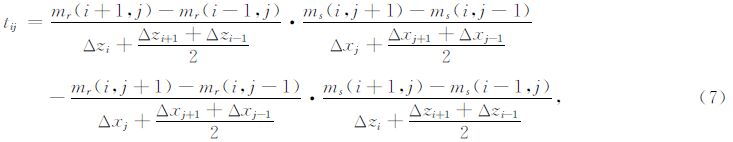
其中,i和j分别表示网格z方向下标和x方向下标.
对目标函数式(1)求其关于模型参数的偏导数令其等于0,并且考虑到公式(Gallardo and Meju,2007)

其中 B 为交叉梯度函数相对模型参数的偏导数矩阵, m ρ0和m η0分别是电阻率参数和极化率参数的初始模型矩阵,参照数据空间反演的数学变换式,得到模型迭代更新的公式:
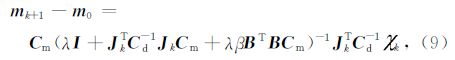
式中 J k是第k次反演迭代过程中的雅可比矩阵, k= d obs-f[ m k]+ J k m k,m k是第k次反演得到的模型向量.
式(9)即为TDIP同步反演第k+1次迭代模型公式.
本文中各参数的取值具体如下:λ=1.0,0.5(即正则化因子初始值为1.0,对数比率上的步长为0.5,在每次迭代中,计算三个不同的正则化因子所对应的反演结果的拟合差,选取拟合差最小的正则化因子,以该正则化因子所对应的结果为该次迭代的反演结果);β的选取至关重要,若取得值过小,则无法体现出交叉梯度项的作用,若取得值过大,会使得模型结果较差,本文中β的选取过程是先计算每次迭代中的λ B T BC (m)和J Tk C -1d J k C (m)项的最大值,取二者的比值的二分之一为β的数值,故而每次迭代β的数值都是变化的,其范围在104~107之间.
由此可见,与分步反演不同,同步反演目标函数中包含了电阻率项和极化率项,并且加入了交叉梯度函数,这样每迭代一次都同步更新电阻率模型和极化率模型参数,并且计算交叉梯度耦合.
3.2 同步反演流程本文所实现的TDIP同步反演算法的流程大体如下:
(1)设置初始模型,输入初始电阻率模型和初始极化率模型;
(2)计算交叉梯度函数,并同时实现电阻率和极化率的模型更新;
(3)计算视电阻率和视极化率数据拟合差之和;
(4)判断拟合差之和是否满足目标函数设置的收敛条件(收敛条件为两次的拟合差之差小于10-6),不设置最大迭代次数,本文所列出的所有分步反演和同步反演算例的收敛条件都是一致的.拟合差的计算公式为
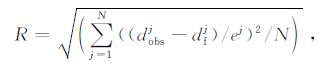
其中,dobs为含有高斯误差的观测数据,d(f)为正演计算数据,e为数据误差项.当模型能够完全拟合不含误差的观测数据时拟合差为1,如果不满足,迭代继续,返回步骤(2)重新计算;如果满足收敛条件,则完成同步反演,跳出迭代,输出反演结果.
4 算例分析基于以上理论部分,本文实现了TDIP二维同步反演算法.为了检验算法的正确性和可靠性,同时对比同步反演结果与分步反演结果的差别,本文进行了理论模型合成数据的反演,分别设计了电阻率和极化率结构一致和不一致的二维模型,下面依次作分析讨论.
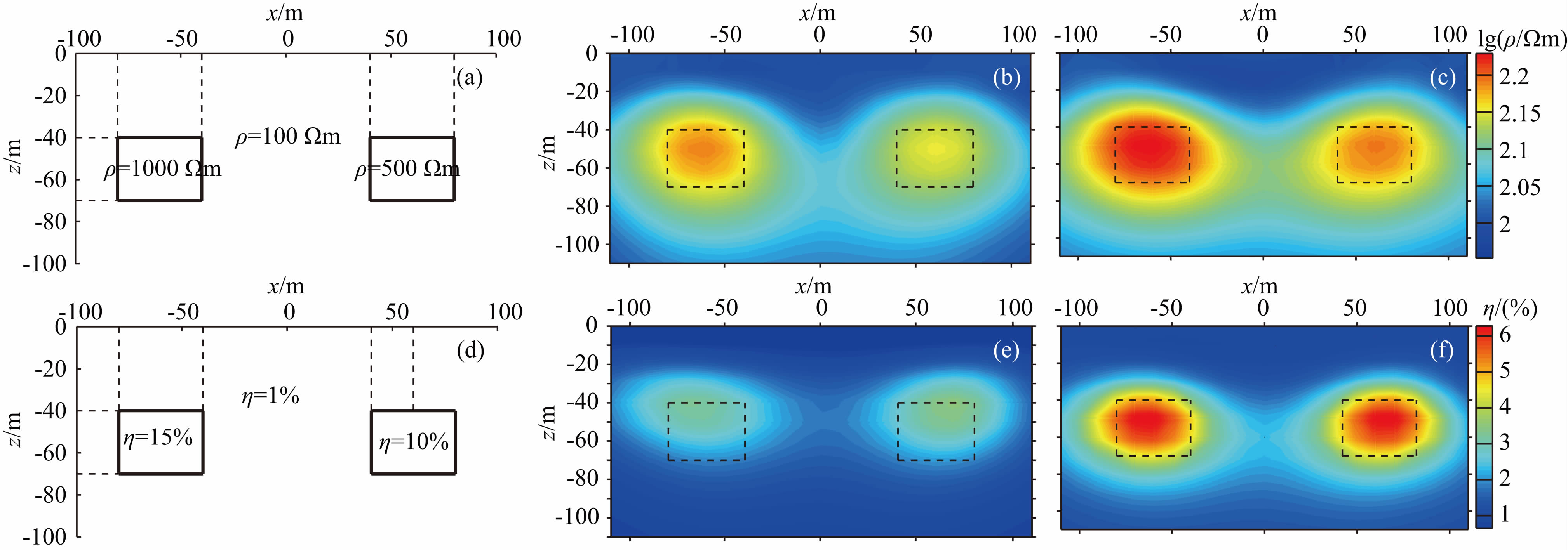
4.1 电阻率和极化率结构一致模型本文设计了双棱柱高阻极化体的物性结构一致模型.左侧模型异常体电阻率为1000 Ωm,极化率为15%,右侧模型异常体电阻率为500 Ωm,极化率为 10%,二者尺寸均为40 m×30 m,顶面埋深均为40 m,二者间距为80 m;异常体埋藏于电阻率为100 Ωm,极化率为2%的均匀半空间中,具体可见图 1a和图 1d所示.观测系统与前文一致,在正演数据中加入2.0%的高斯随机误差.对模型合成数据分别进行分 步反演和同步反演,初始模型采用电阻率为100 Ωm,极化率为1%的均匀半空间,分步反演的结果见图 1b和图 1e,同步反演的结果见图 1c和图 1f.
|
图 1 物性结构一致模型分步反演和同步反演结果对比图 (a)电阻率理论模型;(b)电阻率分步反演结果;(c)电阻率同步反演结果;(d)极化率理论模型;(e)极化率分步反演结果;(f)极化率同步反演结果.图(b)、(c)、(e)、(f)中黑色虚线为棱柱体边界范围. Fig. 1 The comparison of separate inversion and synchronous inversion by a model with the same physical structure (a)Theoretical resistivity model;(b)Resistivity model from separate inversion;(c)Resistivity model from synchronous inversion;(d)Theoretical polarizability model;(e)Polarizability model from separate inversion;(f)Polarizability model from synchronous inversion.In the figure(b),(c),(e),(f),the black dashed lines show the prism margins. |
对反演结果进行分析,结果显示:电阻率的分步反演结果对棱柱体的空间形态有一定的恢复,但是左侧棱柱体电阻率恢复到150 Ωm左右,与电阻率真值(1000 Ωm)有着明显的差距,右侧棱柱体电阻率恢复到130 Ωm左右,与电阻率真值(500 Ωm)差距明显;极化率的分步反演结果能恢复出异常体的大致空间形态,但是对左棱柱体极化率的真实数值(15%)最高只能恢复到3%左右,对右棱柱体极化率的真实数值(10%)最高只能恢复到3%左右.相比于分步反演,二者的埋深均比实际埋深偏浅.图 1c和图 1f中的同步反演结果对棱柱体的空间形态 有更好的恢复,左棱柱体的反演电阻率可达到 200 Ωm左右,右棱柱体的反演电阻率可达到180 Ωm 左右,均比分步反演的结果更加接近于真实电阻率数值;而极化率的同步反演结果可以恢复出两个异常体的埋深,并且两个异常体的极化率均恢复到6.5%左右,相比于分步反演的结果改善显著.
电阻率法分步反演迭代8次,拟合差从8.95下 降到1.45,TDIP分步反演迭代8次,拟合差从26.96 下降到1.81,同步反演迭代了10次,最后收敛时视电阻率的数据拟合差为1.37,视极化率的数据拟合 差为1.54,二者均小于分步反演结果的数据拟合差.
得到分步反演和同步反演的结果之后,计算电阻率模型和极化率模型交叉梯度数值,对于该组模 型而言,分步反演结果的交叉梯度数值为9.87×10-5,同步反演结果的交叉梯度数值为2.12×10-7,可见交叉梯度项的引入,使得同步反演结果的交叉梯度项数值更小.
对于电阻率和极化率结构一致的模型来说,电阻率和极化率的同步反演结果无论从模型逼近程度还是从拟合差大小角度而言都优于分步反演结果.
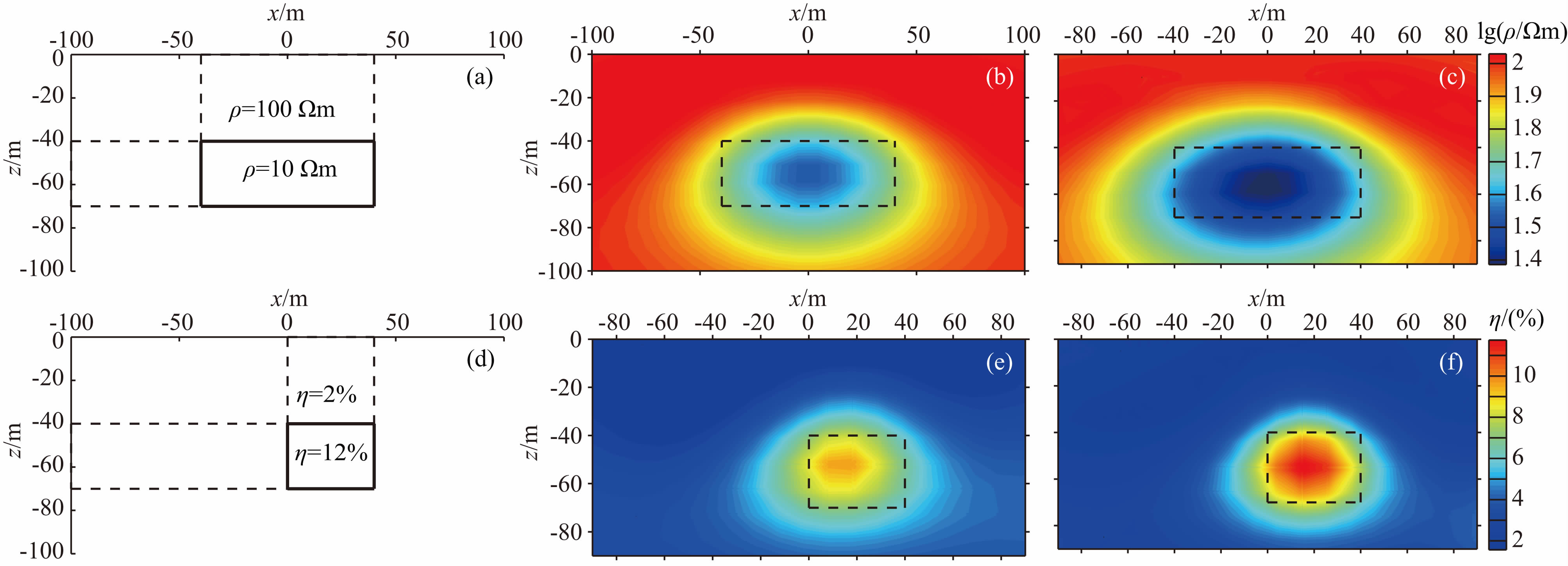
4.2 电阻率和极化率结构不一致模型算例1为了更好地讨论同步反演相对于分步反演的优越性,建立电阻率和极化率结构不一致的模型,即电阻率异常体和极化体异常体的边界并不完全一致.首先设计大尺寸低阻和小尺寸高极化的棱柱异常体模型,其中异常体电阻率为10 Ωm,尺寸为80 m×30 m,异常体极化率为12%,尺寸为40 m×30 m,二者顶面埋深均为40 m,埋藏于电阻率为100 Ωm,极化率为2%的均匀半空间中,具体可见图 2a和图 2d所示.观测系统与前文一致,在正演数据中加入2%的高斯随机误差.对模型合成数据分别进行分步反演和同步反演,初始模型采用电阻率为100 Ωm,极化率为2%的均匀半空间,图 2b和图 2e是分步 反演的结果,图 2c和图 2f是同步反演的结果.
|
图 2 物性结构不一致模型分步反演和同步反演结果对比图 (a)电阻率理论模型;(b)电阻率分步反演结果;(c)电阻率同步反演结果;(d)极化率理论模型; (e)极化率分步反演结果;(f)极化率同步反演结果.图(b)、(c)、(e)、(f)中黑色虚线为棱柱体边界范围. Fig. 2 The comparison of separate inversion and synchronous inversion by a model with different physical structure (a)Theoretical resistivity model;(b)Resistivity model from separate inversion;(c)Resistivity model from synchronous inversion;(d)Theoretical polarizability model;(e)Polarizability model from separate inversion;(f)Polarizability model from synchronous inversion. In the figure(b),(c),(e),(f),the black dashed lines show the prism margins. |
对反演结果进行分析,结果显示:电阻率的分步 反演结果对棱柱体的空间形态有较好的恢复,异常体的埋深和几何位置都较准确,但是棱柱体电阻率只能恢复到30 Ωm左右,与其电阻率真值(10 Ωm)有着一定的差距;极化率的分步反演结果能恢复出异常体的大致空间形态,异常体埋深较为准确,然而 位置比真实情况偏左侧,对棱柱体极化率真值(12%)最高只能恢复到9%,异常体两侧也存在着高极化假异常.相比分步反演,图 2c和图 2f的同步反演结果对棱柱体的空间形态有更好的恢复,棱柱体的电阻率反演结果更接近于电阻率真值,可达到18 Ωm,有一定程度的改善,并且电阻率异常体的尺寸也更接近于真实情况;而极化率的同步反演结果可达到11.5%左右,十分接近极化率真实数值,两侧高极化假异常得到一定程度的压制,异常体的空间分布位置也更加准确,改善显著.电阻率法分步反演迭代9次,数据拟合差从24.91下降到1.66,TDIP分步反演迭代10次,拟合差从17.11下降到2.13;同步反演迭代10次,视电阻率数据拟合差最终为1.55,视极化率数据拟合差为1.79,均略小于分步反演结果的数据拟合差.
得到分步反演和同步反演的结果之后,分别计算二者电阻率模型和极化率模型交叉梯度数值,对于该组模型而言,分步反演结果的交叉梯度数值为 2.04×10-4,同步反演结果的交叉梯度数值为2.47×10-5,可见交叉梯度项的引入,使得同步反演结果的交叉梯度项数值更小.
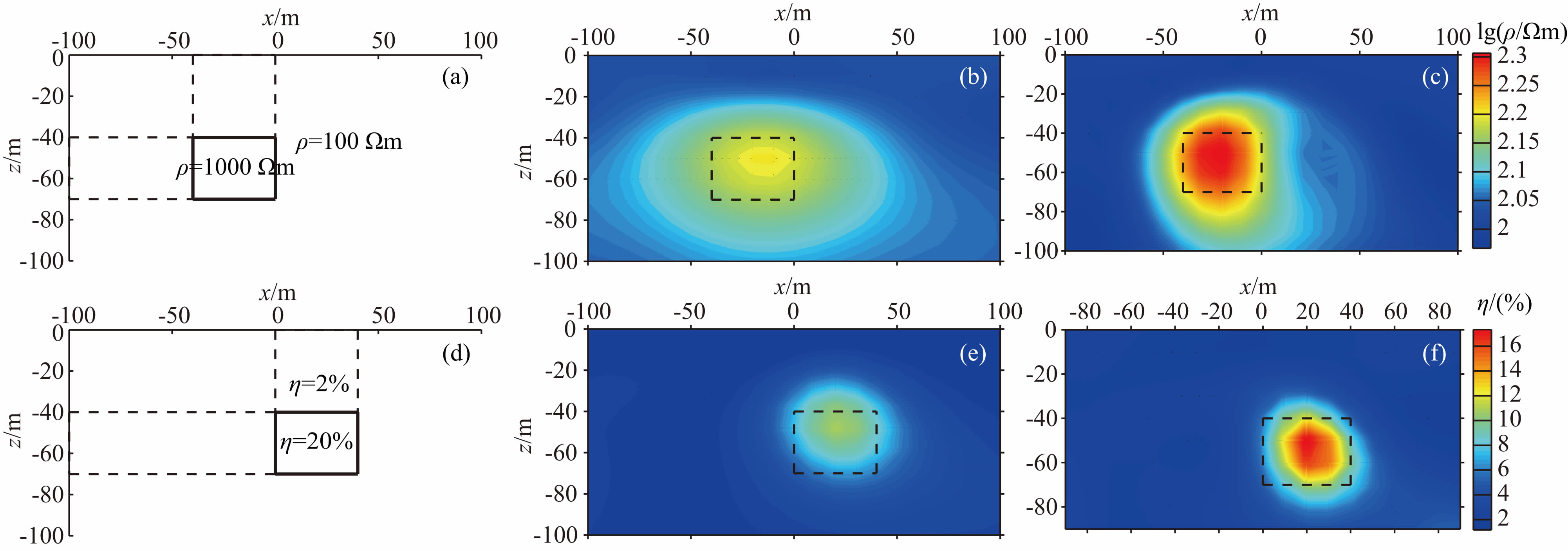
4.3 电阻率和极化率结构不一致模型算例2本文进一步设计了小尺寸高阻体和小尺寸高极化体的物性结构不一致模型.模型异常体电阻率为1000 Ωm,分布在左侧,极化率异常体的极化率为20%,分布在右侧,二者尺寸均为40 m×30 m,顶面埋深均为40 m;异常体埋藏于电阻率为100 Ωm,极化率为2%的均匀半空间中,具体可见图 3a和图 3d所示.观测系统与前文一致,在正演数据中加入2%的高斯随机误差.对模型合成数据分别进行分步反演和同步反演,初始模型采用电阻率为100 Ωm,极化率为2%的均匀半空间,分步反演的结果见图 3b和图 3e,同步反演的结果见图 3c和图 3f.
|
图 3 物性结构不一致模型分步反演和同步反演结果对比图 (a)电阻率理论模型;(b)电阻率分步反演结果;(c)同步反演电阻率结果;(d)极化率理论模型; (e)极化率分步反演结果;(f)极化率同步反演结果.图(b)、(c)、(e)、(f)中黑色虚线为棱柱体边界范围. Fig. 3 The comparison of separate inversion and synchronous inversion by a model with different physical structure (a)Theoretical resistivity model;(b)Resistivity model from separate inversion;(c)Resistivity model from synchronous inversion;(d)Theoretical polarizability model;(e)Polarizability model from separate inversion;(f)Polarizability model from synchronous inversion. In the figure(b),(c),(e),(f),the black dashed lines show the prism margins. |
对反演结果进行分析,结果显示:电阻率的分步反演结果对棱柱体的空间形态有较好的恢复,但是左侧棱柱体电阻率最高恢复到160 Ωm左右,与电阻率真值(1000 Ωm)有着明显差距,并且异常体的分布在左右两侧超出了实际范围,尤其是右侧明显地超出实际边界;极化率的分步反演结果能恢复出异常体的大致空间形态,但是反演结果埋深偏浅,对棱柱体极化率的真实数值(20%)最高只能恢复到10%左右.相比于分步反演,图 3c和图 3f中的同步反演结果对棱柱体的空间形态有更好的恢复,左侧高阻棱柱体的反演电阻率可达到220 Ωm左右,数值上有较显著的改善,并且高阻异常体反演结果的分布范围更加准确,左右两侧偏出异常体实际分布范围的情况得到了明显改善,尤其是右侧边界基本与实际情况吻合,更接近于真实情况;而极化率的同步反演结果可以恢复到14.3%左右,相比于分步反演的结果改善显著,并且反演结果埋深也更加准确,分步反演结果埋深偏浅的情况得到改善.电阻率法分步反演迭代8次,拟合差从6.47下降到1.74,TDIP分步反演迭代7次,拟合差从25.66下降到2.06,同步反演迭代了9次,最后收敛时视电阻率拟合差为1.43,视极化率数据拟合差为1.55,均小于分步反演结果的数据拟合差.
得到分步反演和同步反演的结果之后,计算电阻率模型和极化率模型交叉梯度数值,对于该组模型而言,分步反演结果的交叉梯度数值为1.27×10-4,同步反演结果的交叉梯度数值为1.19×10-6,可见交叉梯度项的引入,使得同步反演结果的交叉梯度项数值更小.
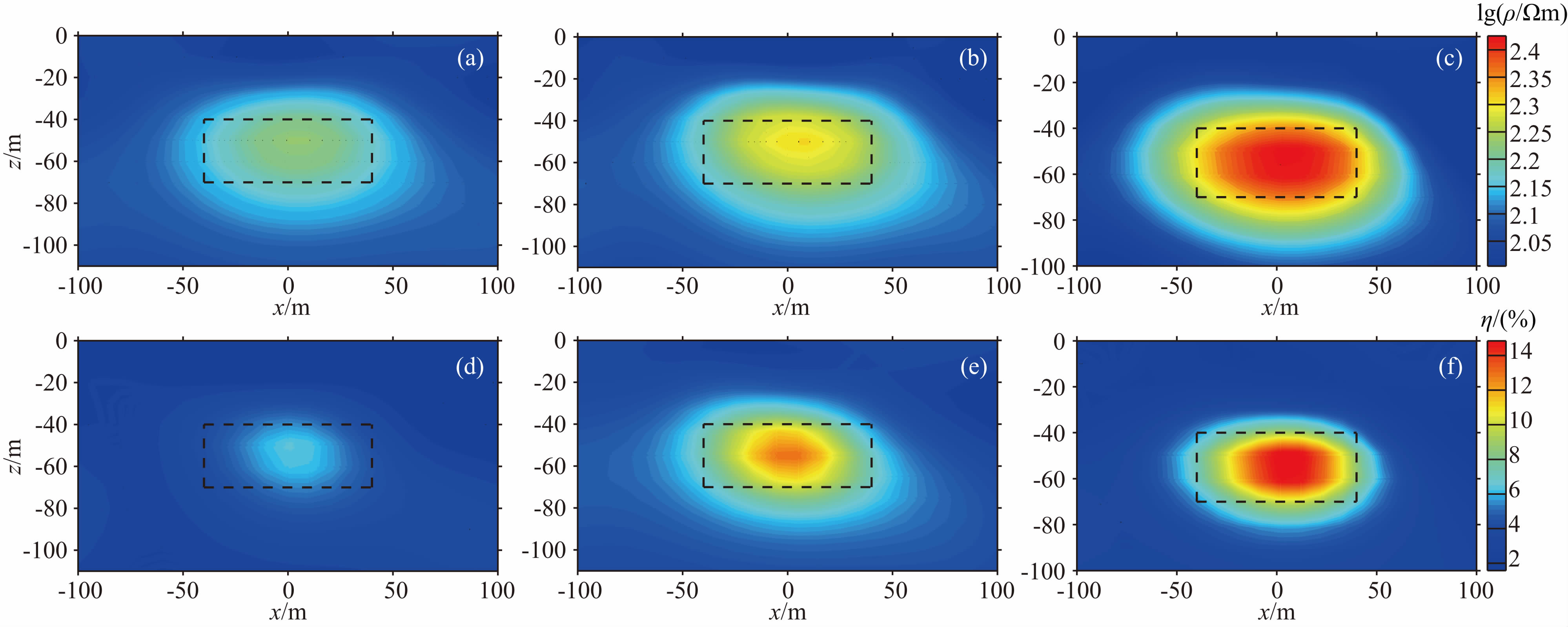
4.4 加入交叉梯度项与未加入交叉梯度项对比模型为了更好地突出目标函数中的交叉梯度项在反演中所起到的作用,本文设计了一组加入交叉梯度项和未加入交叉梯度项的对比模型.模型异常体电阻率为1000 Ωm,极化率异常体的极化率为20%,异常体尺寸为80 m×30 m,顶面埋深为40 m;异常体埋藏于电阻率为100 Ωm,极化率为2%的均匀半空间中.观测系统与前文一致,在正演数据中加入1.5%的高斯随机误差.对模型合成数据分别进行分步反演、未加入交叉梯度项的同步反演和含交叉梯 度项的同步反演,初始模型均采用电阻率为100 Ωm,极化率为2%的均匀半空间,分步反演的结果见图 4a和图 4d,不含交叉梯度项同步反演的结果见图 4b和图 4e,含交叉梯度项同步反演结果如图 4c和图 4f所示.
|
图 4 无交叉梯度项和含有交叉梯度项同步反演结果对比图 (a)电阻率分步反演结果;(b)不含交叉梯度项电阻率同步反演结果;(c)含交叉梯度项电阻率同步反演结果;(d)极化率分步反演结果; (e)不含交叉梯度项极化率同步反演结果;(f)含交叉梯度项极化率同步反演结果.图(b)、(c)、(e)、(f)中黑色虚线为棱柱体边界范围. Fig. 4 The comparison of synchronous inversion without cross-gradient and synchronous inversion with cross-gradient (a)Resistivity model from separate inversion;(b)Resistivity model from synchronous inversion without cross-gradient;(c)Resistivity model from synchronous inversion with cross-gradient;(d)Polarizability model from separate inversion;(e)Polarizability model from synchronous inversion without cross-gradient;(f)Polarizability model from synchronous inversion with cross-gradient. In the figure(b),(c),(e),(f),the black dashed lines show the prism margins. |
对反演结果进行分析,结果显示:电阻率的分步反演结果对棱柱体的空间形态有一定程度的恢复,电阻率最高恢复到180 Ωm左右,与棱柱体电阻率真值(1000 Ωm)有着明显差距,并且异常体左右两侧存在一定程度的假异常;极化率的分步反演结果能恢复出异常体的大致空间形态,但是反演结果对棱柱体极化率的真实数值(20%)最高只能恢复到8%左右.相比于分步反演,图 4b和图 4e中的未加入交叉梯度项同步反演结果对棱柱体的空间形态有更好的恢复,高阻棱柱体的电阻率可达到240 Ωm左右,数值上有较显著的改善,但是异常体还是存在一定程度的假异常;而极化率未加入交叉梯度项同步反演结果可以恢复到12%左右,相比于分步反演的结果改善显著,但是反演结果分布与实际有一定的差距,左右两侧存在较大范围的高极化假异常.图 4c和图 4f是含交叉梯度项同步反演结果,其中反演得到的电阻率模型更加接近于真实情况,可将电阻率数值恢复到280 Ωm左右,并且异常体两侧的假异常明显减少;而极化率结果也得到了改善,数值可以达到14.5%,两侧的假异常也明显减少,因为加入了交叉梯度项,极化率和电阻率模型的相似性得以提高,因此异常体的极化率分布更加准确.电阻率法分步反演迭代7次,拟合差从7.42下降到1.84,TDIP分步反演迭代7次,拟合差从21.81下降到1.96,未加入交叉梯度项的同步反演迭代了9次,最后收敛时视电阻率拟合差为1.63,视极化率数据拟合差为1.75,加入了交叉梯度项的同步反演迭代了11次,最后收敛时视电阻率拟合差为1.55,视极化率数据拟合差为1.45,是三种反演方法中拟合差最小的.
得到不含交叉梯度项反演和含交叉梯度项反演的结果之后,计算电阻率模型和极化率模型交叉梯度数值,对于该组模型而言,前者的交叉梯度数值为2.37×10-5,后者的交叉梯度数值为1.84×10-7,可见交叉梯度项的引入,使得同步反演结果的交叉梯度项数值更小.
总之,加入交叉梯度项的电阻率和极化率的同步反演结果在模型逼近程度和数据拟合差大小方面均优于分步反演和不含交叉梯度项的同步反演结果.
5 结论本文实现了基于交叉梯度耦合的TDIP二维同步反演算法,并设计了电阻率和极化率结构一致和不一致的模型对反演算法进行了理论模型测试.通过对比合成数据的同步反演和分步反演结果,可以得出以下结论:
(1)无论是电阻率和极化率结构一致还是不一致的模型,电阻率的同步反演结果比分步反演对异常体的空间形态都有更好的恢复,尤其是高阻异常体改善效果更加明显.对于低阻异常体而言,电阻率的同步反演结果更接近于电阻率真值,并且异常体分布范围更加准确,而高阻体电阻率的同步反演结果不仅更加接近于电阻率的实际数值,其埋深和空间分布也更加准确.
(2)对于极化率模型而言,同步反演能改善极化率反演结果,使其更接近甚至完全达到极化率真值,并且极化率分步反演结果埋深和空间分布不准确的问题也得到改善.
(3)两组电阻率和极化率结构不一致的模型算例表明,同步反演在电阻率和极化率模型边界不完全一致的时候也能改善反演结果,尤其是电阻率和极化率模型的空间分布准确性改善显著.
(4)对于不同模型而言,同步反演结果不但在模型逼近程度上优于分步反演的结果,同步反演结果的数据拟合差也要小于分步反演的数据拟合差.
(5)加入了交叉梯度约束,使得同步反演算法结果交叉梯度项数值更小,更加符合真实情况,因而该算法具有更普遍的适用性.
致谢 两位匿名评审专家为本文修改提出了细致而宝贵的意见,使得文章增色不菲,在此表示感谢.
| [1] | Aric K, Adam A, Smythe D K. 1997. Combined seismic and magnetotelluric imaging of upper crystalline crust in the Southern Bohemian Massif. First Break, 15(8): 265-271. |
| [2] | Colombo D, De Stefano M. 2007. Geophysical modeling via simultaneous joint inversion of seismic, gravity, and electromagnetic data: Application to prestack depth imaging. The Leading Edge, 26(3): 326-331. |
| [3] | Constable S C, Parker R L, Constable C C. 1987. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics, 52(3): 289-300. |
| [4] | Douglas W O, Li Y G. 1994. Inversion of induced polarization data. Geophysics, 59(9): 1327-1341. |
| [5] | Douglas W O, Li Y G. 1999. Estimating depth of investigation in DC resistivity and IP surveys. Geophysics, 64(2): 403-416. |
| [6] | Fu L K. 1982. Induced Polarization Method (in Chinese). Beijing: Geological Publishing House. |
| [7] | Gallardo L A, Meju M A. 2003. Characterization of heterogeneous near-surface materials by joint 2D inversion of DC resistivity and seismic data. Geophys. Res. Lett., 30(13): 1658. |
| [8] | Gallardo L A, Meju M A. 2007. Joint two-dimensional cross-gradient imaging of magnetotelluric and seismic traveltime data for structural and lithological classification. Geophys. J. Int., 169(3): 1261-1272. |
| [9] | Gao D Z, Zhao J H, Bo Y L, et al. 2004. A profile study of gravitative-magnetic and seismic comprehensive survey in the East China Sea. Chinese J. Geophys. (in Chinese), 47(5): 853-861, doi: 10.3321/j.issn:0001-5733.2004.05.017. |
| [10] | Haber E, Oldenburg D. 1997. Joint inversion: A structural approach. Inverse Problems, 13(1): 63-77. |
| [11] | Hu P, Liu B J, Bai L X, et al. 2010. Synthetic exploration of the buried faults in Olympic park area. Chinese J. Geophys. (in Chinese), 53(6): 1486-1494, doi: 10.3969/j.issn.0001-5733.2010.06.026. |
| [12] | Jiang M, Peng M, Wang Y X, et al. 2012a. Geophysical evidence for deep subduction of Indian lithospheric plate beneath Eastern Himalayan Syntaxis. Acta Petrologica Sinica (in Chinese), 28(6): 1755-1764. |
| [13] | Jiang M, Tan H D, Qian H, et al. 2012b. Geophysical deep structure and genetic model of Jinchuan copper-nickel deposit. Mineral Deposits (in Chinese), 31(2): 207-215. |
| [14] | Moorkamp M, Jones A G, Eaton D W. 2007. Joint inversion of teleseismic receiver functions and magnetotelluric data using a genetic algorithm: Are seismic velocities and electrical conductivities compatible? Geophys. Res. Lett., 34(16): L16311. |
| [15] | Peng M, Tan H D, Jiang M, et al. 2012. Joint inversion of receiver functions and magnetotelluric data: Application to crustal and mantle structure beneath central Namche Barwa, eastern Himalayan syntaxis. Chinese J. Geophys. (in Chinese), 55(7): 2281-2291, doi: 10.6038/j.issn.0001-5733.2012.07.014. |
| [16] | Peng M, Tan H D, Jiang M, et al. 2013. Three-dimensional joint inversion of magnetotelluric and seismic travel time data with cross-gradient constraints. Chinese J. Geophys. (in Chinese), 56(8): 2728-2738, doi: 10.6038/cjg20130821. |
| [17] | Siripunvaraporn W, Egbert G. 2000. An efficient data subspace inversion method for 2-D magnetotelluric data. Geophysics, 65(3): 791-803. |
| [18] | Siripunvaraporn W, Egbert G, Lenbury Y, et al. 2005. Three-dimensional magnetotelluric inversion: data-space method. Phys. Earth Planet. Interiors, 150(1-3): 3-14. |
| [19] | Yu P, Dai M G, Wang J L, et al. 2009. Joint inversion of magnetotelluric and seismic data based on random resistivity and velocity distributions. Chinese J. Geophys. (in Chinese), 52(4): 1089-1097, doi: 10.3969/j.issn.0001-5733.2009.04.026. |
| [20] | 傅良魁. 1982. 激发极化法. 北京: 地质出版社. |
| [21] | 高德章, 赵金海, 薄玉玲等. 2004. 东海重磁地震综合探测剖面研究. 地球物理学报, 47(5): 853-861, doi: 10.3321/j.issn:0001-5733.2004.05.017. |
| [22] | 胡平, 刘保金, 白立新等. 2010. 奥林匹克公园地区隐伏断裂综合 探测. 地球物理学报, 53(6): 1486-1494, doi: 10.3969/j.issn.0001-5733.2010.06.026. |
| [23] | 姜枚, 彭淼, 王有学等. 2012a. 喜马拉雅东构造结岩石圈板片深俯冲的地球物理证据. 岩石学报, 28(6): 1755-1764. |
| [24] | 姜枚, 谭捍东, 钱辉等. 2012b. 金川铜镍矿床的地球物理深部结构与成因模式. 矿床地质, 31(2): 207-215. |
| [25] | 彭淼, 谭捍东, 姜枚等. 2012. 利用接收函数和大地电磁数据联合反演南迦巴瓦构造结中部地区壳幔结构. 地球物理学报, 55(7): 2281-2291, doi: 10.6038/j.issn.0001-5733.2012.07.014. |
| [26] | 彭淼, 谭捍东, 姜枚等. 2013. 基于交叉梯度耦合的大地电磁与地震走时资料三维联合反演. 地球物理学报, 56(8): 2728-2738, doi: 10.6038/cjg20130821. |
| [27] | 于鹏, 戴明刚, 王家林等. 2009. 电阻率和速度随机分布的MT与地震联合反演. 地球物理学报, 52(4): 1089-1097, doi: 10.3969/j.issn.0001-5733.2009.04.026. |
 2015, Vol. 58
2015, Vol. 58


