2. 核工业北京地质研究院, 北京 100029
2. Nuclear Industry Geological Research Institute in Beijing, Beijing 100029, China
随着找矿难度的加大以及电磁法仪器和计算机技术的快速发展,人们对电磁法解决地质问题的期待已越来越高,传统的一维、二维解释模型已不能满足对复杂地质模型的刻画,三维电磁法正、反演技术已提到日程,对此,国内外研究学者作了大量研究工 作(如Eaton,1989; Madden and Mackie,1989; Smith and Booker,1991;Lee and Xie,1993; Oristaglio et al.,1993 ;Pellerin et al.,1993; Nekut,1994; Torres-Verdin and Habashy,1995; Xie and Lee,1995; Newman and Alumbaugh,1996; Oldenburg et al.,2013; 张辉,2006; 徐凯军,2007; 李建平,2008; 翁爱华等,2012等).但是,三维电磁法内存消耗大、计算速度慢,目前还很难投入到实际生产应用当中.Zhdanov和Fang(1996a,1996b)提出拟线性(QL)近似法,通过对比积分方程法、QL近似方法和Born近似方法对不同模型的计算结果,验证了QL近似方法的计算精度,有效解决了积分方程计算速度慢、占用内存多的缺陷.Zhdanov等(2000)实现了三维拟线性反演,对日本Minamikayabe地区7个不同频率(96、48、24、12、6、3和1.5)161个观测点的MT数据进行反演,其结果与Takasugi等(1992)的二维反演结果相近,但是该三维反演结果提供了更为详细的地质结构,为解释该地区高导有利含水区提供了依据.
Zhdanov和Tartaras(2002)提出的局部拟线性(LQL)近似方法,能够在不失计算精度的前提下,为多源电磁正、反演模拟及应用节省大量时间.在此基础上Zhdanov实现了三维电磁反演,该反演能够准确地反演出呈阶梯状逐渐变深的异常体.利用该反演对加拿大某海湾含镍-钴-铬硫矿区的HEM数据进行了反演,从反演结果来看,该区存在两种不同的岩性,研究区中心存在低阻异常体并向南东、北西向延伸,该结果与Oldenburg等(1998)在该区的三维重力反演结果有很好的对应关系.
Yoshioka和Zhdanov(2005)在LQL近似方法的基础上实现了基于Cole-Cole模型的三维频谱激电(SIP)非线性共轭梯度反演,对理论模型进行了反演试算,但只在零频电阻率上取得了良好的反演效果,其他参数反演效果不佳.
与其他电磁法不同,SIP方法的发射和观测方式比较特殊,需要不断更换发射与接收的位置,通过变换收发距离来达到测深的目的.由于换源频繁,QL近似方法用于三维SIP正演需要不断重复计算反射系数,并且每次换源都需要重新计算单元一次场,正演的速度受到了严重的制约.
本文首先利用并矢格林函数和一次场的空间对称性,提出了一种适用于多源电磁法正演的快速QL近似方法,该方法只需在发射源第一次发射时计算并存储单元之间的并矢格林函数和一次场,在之后的每次换源正演计算中不必重新计算.另外,算法将并矢格林函数系数存储成Toeplitz矩阵,利用Toeplitz矩阵的性质减少不必要的计算.然后,基于文中提出的快速QL正演方法,实现了Cole-Cole模型参数范围约束下的三维SIP反演;最后,通过模型试算,验证了正演算法的正确性和反演算法的有效性.
2 正演 2.1 快速QL近似理论在非均匀介质内部电磁场总场 E等于一次场与二次场之和:

E n为发射电流在背景区域内部产生的一次场, E a是由不均匀电导率的分布导致电流产生的二次场.一次场为接地导线发射源在均匀半空间产生的一次场.二次场由Zhdanov和Fang(1996a,1996b)提出的拟线性近似方法求得:
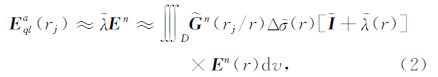
其中,D为异常区域,rj为当前单元,j为当前单元 编号,r为任意单元, E 为拟线性近似解, n为格 林系数,Δ 为异常电导率, 为单位张量矩阵, E n(rj)为单元一次场, 为电反射系数, 可以通过求解下式极小值问题得到:
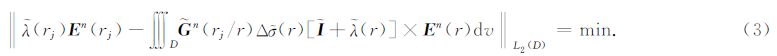
为了数值计算方便,用张量标记,重新将(2)式写成
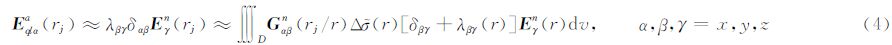
(4)式中δ为delta函数, E (rj)和E (rj)为电场矢量的笛卡尔坐标系分量, G (rj/r)为电场格林张量的笛卡尔坐标系分量.这里用爱因斯坦求和约定(王伯年等,2003):当每项中二个量的角标(上标或下标)重复出现一次时,意味着该角标遍及所有的坐标,并对之求和(例如β=x,y,z).
在异常区域内反射系数是缓慢变化的(Zhdanov和Fang,1996a),因此近似地,可以把(4)式写为
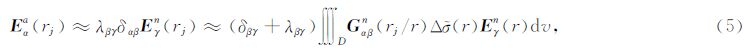
然后可以得到
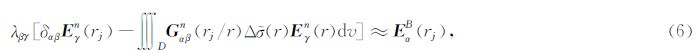
其中, E αB(rj)为Born近似解(Born,1933),(6)式与(2)式一样作了近似处理,通过最小二乘方法可确定满足(6)式的λ:
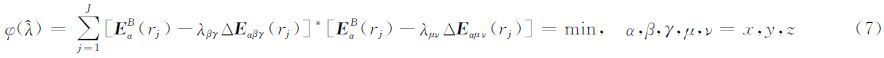

*代表复数的共轭,Δ E αμν为Δ E αβγ的共轭.
求解(7)式,可得反射系数求解公式:
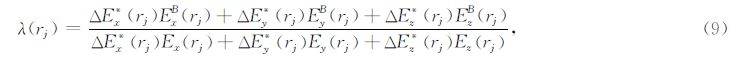
其中
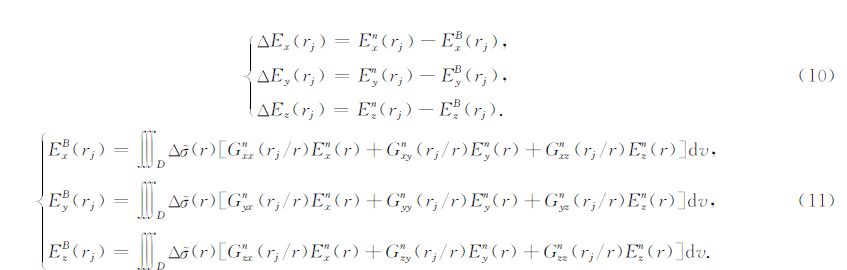
其中,EB为Born近似解,En为一次场,Gn为格林系数.
任意一单元的反射系数,可以由所有单元的异常电导率、一次场以及所有单元对当前单元的格林系数进行简单的线性运算求得,其中格林系数的计算量庞大,耗费时间较多.当对异常体在x、y、z三个方向上均匀地进行剖分,分别为nx,ny,nz,则对x方向,其格林系数矩阵可以写为

其中 Γ (i,j)所代表的物理意义是第j个单元作为源项在第i个单元中心处产生的场,即第j个单元对第i个单元的格林系数.如果第i个单元和第j个单元的相对位置不变,那么 Γ (i,j)的值是相同的,例如 Γ (1,2)= Γ (2,3),因此该矩阵满足Toeplitz矩阵的结构.对于该矩阵,只需要存储第一行和第一列的元素就可以表示出整个矩阵.
并矢格林函数代表的是源在接收点处产生的场,并且满足互换定理(de Lugao,1996),例如
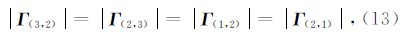
因为场具有方向性,因此上式两端加上绝对值才成立.
y方向和x方向的格林系数矩阵具有相同的结构,但z方向不满足这样的结构,因此格林系数矩阵整体是一个二重Toeplitz矩阵.
格林系数Γ(i,j)有九个分量,分别为G(i,j)xx、G(i,j)xy、G(i,j)xz、G(i,j)yx、G(i,j)yy、G(i,j)yz、G(i,j)zx、G(i,j)zy、G(i,j)zz,根据研究结果,对x方向,各个分量的对称性质为
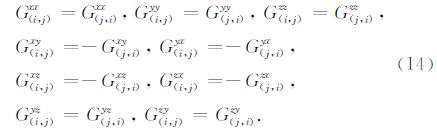
对y方向,各个分量的对称性质为
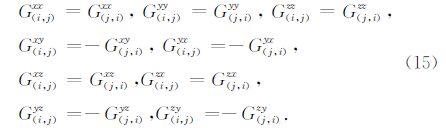
因此快速QL近似方法只计算、存储(12)式矩阵中第一行的元素,尽管比QL近似方法多占用一些内存,但其计算量却是QL近似方法的1/(nxny).
虽然换源需要重新计算反射系数,但每次换源计算反射系数所需要的格林系数矩阵是相同的,因此只需要一次计算格林系数矩阵并将其存储就可以完成所有换源反射系数的计算.
单元一次场关于发射源中心点空间对称,并且只要发射源与接收点的相对位置相同,其场值是相等的,因此利用快速QL近似方法模拟多源电磁法时,单元一次场的计算及存储方式与格林函数相同,这里不再重述.
根据Pelton等(1978)的结论,岩矿石的复电阻率可由Cole-Cole模型描述:
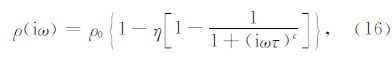
式中,ρ(iω)为复电阻率,ρ0、η、c、τ分别为零频电阻率、极化率、频率相关系数、时间常数,ω=2πf,f为发射频率.
将(16)式的复电阻率形式代入(2)式中,就可以实现考虑激电效应的三维复电阻率正演.
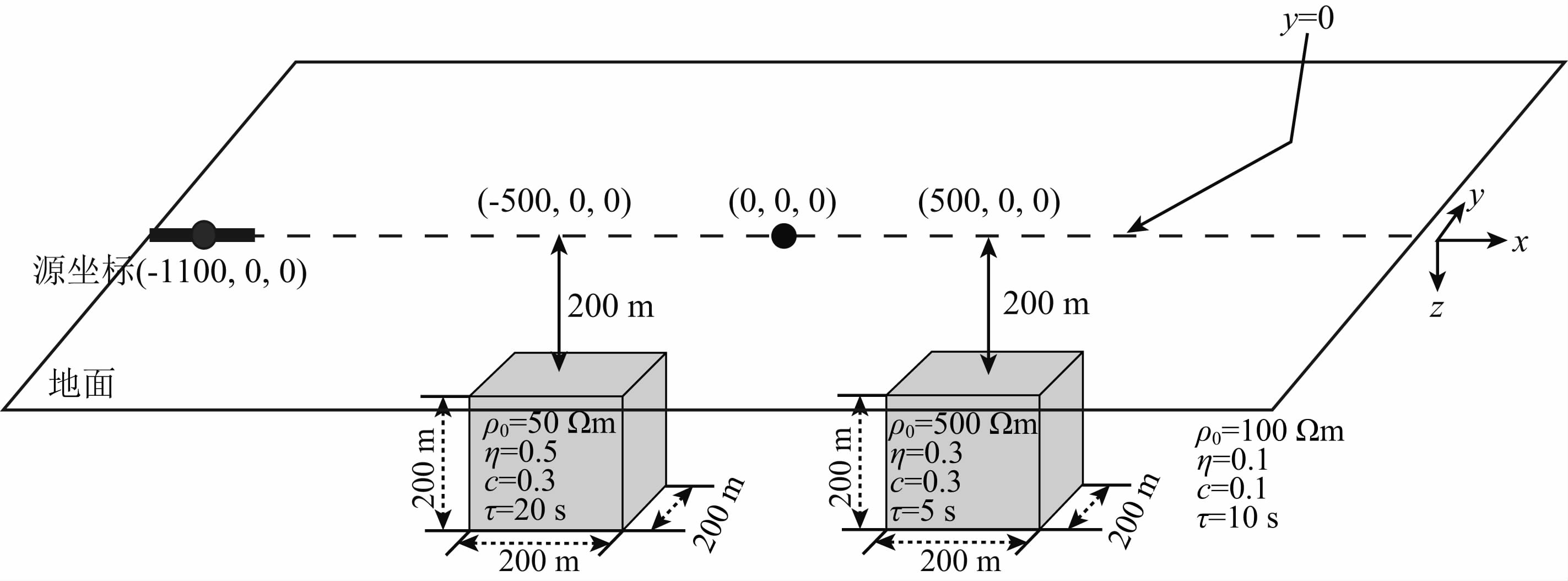
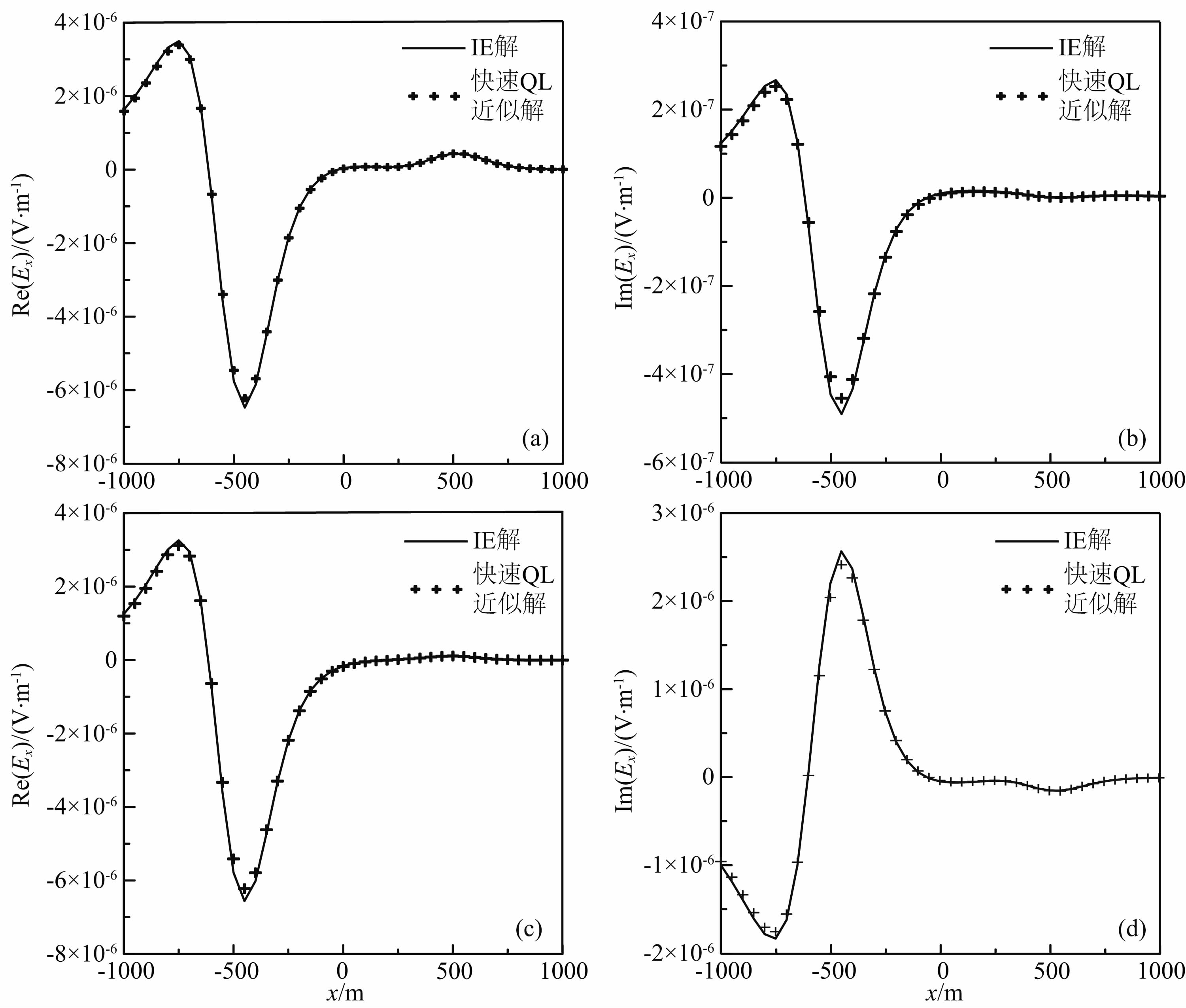
2.2 正演模拟为验证快速QL近似方法的准确性,给出三维正演模型如图 1所示,通过偶极-偶极观测方式进行观测,虚线y=0为测线,发射电流为10A,通过两个频率0.1 Hz和64 Hz进行计算.图 2给出积分方程法(李建平,2008)、快速QL近似方法计算的二次场曲线对比结果.从图中可以看出快速QL近似方法计算精度较高.
|
图 1 三维模型 Fig. 1 3-D model |
|
图 2 积分方程法和快速拟线性近似法的三维SIP正演二次场结果对比, (a、b)发射频率为0.1 Hz;(c、d)发射频率为64 Hz Fig. 2 Comparison the result of secondary field of 3-D SIP modeling between integral equation and the fast quasi-linear approximation.(a) and (b)are transmission frequency of 0.1 Hz.(c) and (d)are transmission frequency of 64 Hz |
表 1给出积分方程法、QL近似方法及快速QL近似方法计算时间及占用内存对比结果,可以看到快速QL近似方法的计算速度较快,而且随着剖分块数增加、接收点数和换源次数增多,快速QL近似方法在计算速度上的优势越加明显.
|
|
表 1 积分方程法、QL近似法和快速QL近似法计算时间和占用内存对比表 Table 1 3-D SIP based on integral equation,the QL approximate and fast QL approximation forward modeling computation time and memory contrast |
通过以上验证及对比,快速QL近似方法计算准确,其精度和占用内存情况完全适用于反演,并且在模拟多源电磁正演时,计算速度较QL近似有了很大提高.
3 参数范围约束下的三维频谱激电反演 3.1 反演理论该反演分为两步,第一步反演物质性质系数m(Zhdanov and Tartaras,2002),第二步反演Cole-Cole模型的四个参数.
3.1.1 反演物质性质系数m假设我们通过拟线性近似方法已经得到了偶极-偶极装置下的二次场,重写(2)式:

其中m为反映地下物质性质的参数,有
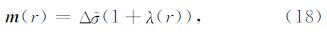
其中,d 为观测数据, E aq为理论数据, G E为格林线性算子, E n为单元一次场,Δ 为异常电导率,λ为反射系数.
由于三维反演的多解性尤为严重,在这里我们采用光滑约束反演方法.建立的目标函数如下:
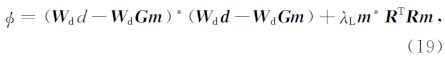
这里*表示复数的共轭, W d为数据方差向量,λL为拉格朗日因子,R 为光滑度矩阵, G =GE(En(r)).上式对 m 求导取极小得到反演方程:
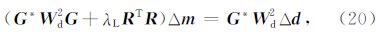
其中Δ d 为观测数据与正演理论数据的残差向量,Δ m 为模型修正量.
拟合精度定义为

RMS为拟合精度,k为数据个数.
求解上述反演问题,本文采用了共轭梯度法,反演流程如下:
(1)给定初始模型m0及拉格朗日因子λL;
(2)计算右端项tdi,tdi= G * W 2dΔ d,令ri=tdi;
(3)计算p= G * W 2d G +λL R T R,保存待用;
(4)hpi=p·tdi;
(5)计算步长tpi,tpi=(r*i·ri)/(td*i·hpi);
(6)更新模型,mi=mi+tpi·tdi,计算拟合差,达到给定精度则跳出循环,否则继续;
(7)ri+1=ri+tpi·hpi;
(8)βi=(r*i+1·ri+1)/(r*i·ri);
(9)tdi+1=ri+1+βi·tdi;
(10)令i=i+1,然后跳到(4).
在反演过程中拉格朗日因子λL可以采取自适应方式进行选择(刘云鹤和殷长春,2013),具体如下:开始给定一个相对较大的λL值进行反演迭代,当反演步长小到一定程度时,将λL值变为原来的十分之一,当λL值或拟合差小于阀值时终止迭代.
3.1.2 Cole-Cole模型参数的确定在反演Cole-Cole模型参数时,本文进行逐块反演.根据拟线性近似理论:
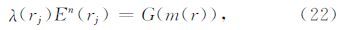
由此可以近似计算出反射系数λ,然后通过(18)式计算每个单元的异常复电导率Δσ(ω).
任意单元的Cole-Cole模型参数可以由下式确定:

这里σ(ω)=σn+Δσ(ω),σn为背景电导率.
对于(23)式,通过四个频率列出非线性方程组,利用共轭梯度迭代求解出Cole-Cole模型参数.考虑到Cole-Cole模型参数均为正实数,且在一定范围内 变化,在这里引入Kim等(1999)、Commer和Newman(2008)给出的约束函数:
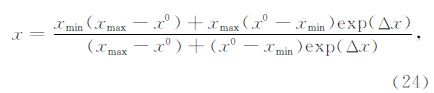
其中x代表Cole-Cole模型参数,Δx为反演参数修正量,x0为初始模型.这样就将模型x限定在(xmin,xmax)范围内,能够有效改善反演的多解性.
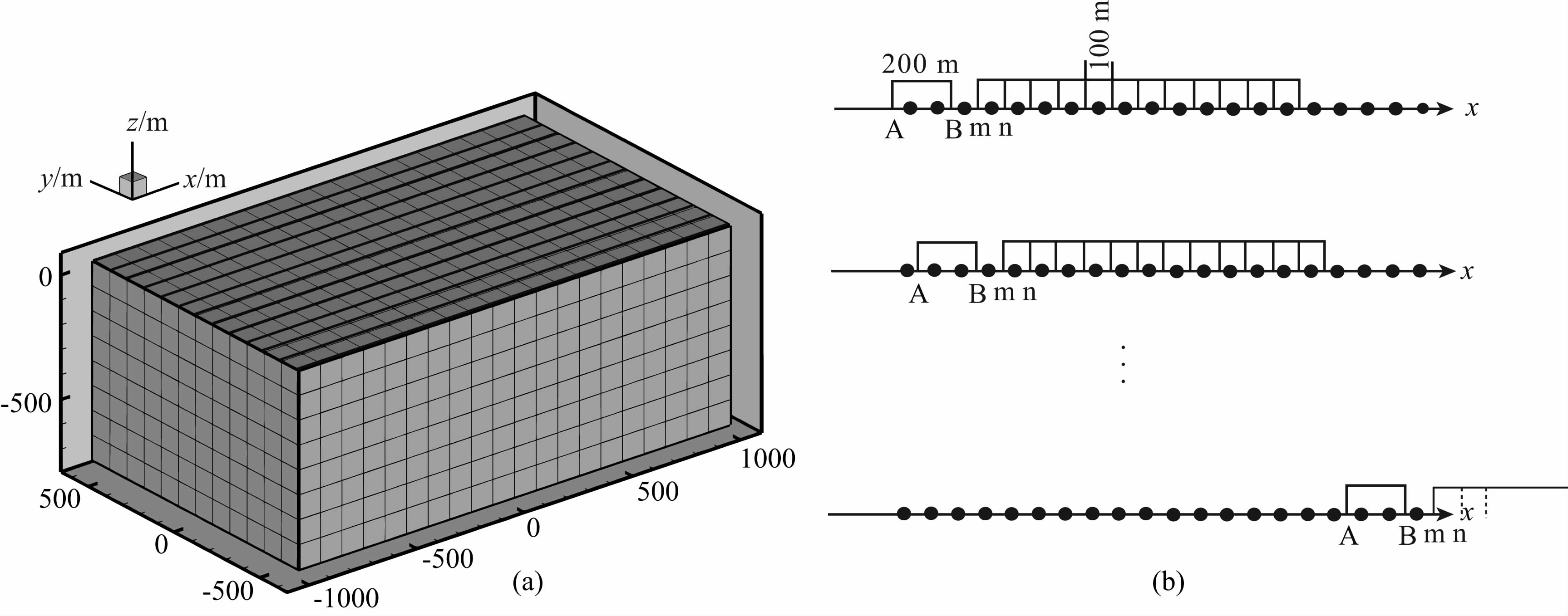
3.2 理论模型反演反演模型如图 1所示,反演区域如图 3所示,地面设置260个观测点,将反演区域均匀剖分成1920块,采用偶极-偶极观测方式如图 3所示,在13条线上进行观测,每次发射的接收点数为12个,每条线换源22次.对该模型通过0.1 Hz、1 Hz、4 Hz及16 Hz四个频率进行正演模拟,得到的地面观测总场作为观测数据,加入1%的高斯噪声进行反演.通 过反演试算,测试该反演的速度、占用内存大小、稳定性及对高阻体和低阻体的反演效果.
|
图 3 三维反演区域(a)及数据观测方式(b) Fig. 3 3-D inversion of target zone(a) and data observation way(b) |
反演物质性质系数m时,给定的初始模型为均匀半空间模型,m(r)=0,r=1,2,…,n;反演Cole-Cole模型参数时,给定初始模型为ρ0=100 Ωm、η=10-5、c=0.1、τ=10 s.由于Cole-Cole模型各参数变化 范围大致为η=0~0.98、τ=10-3~5×103 s、c=0.1~0.6、 ρ0=10-4~105 Ωm,因此给定各参数范围约束的最大(max)值分别为ρ0max=105 Ωm、ηmax=0.98、cmax=0.6、τmax=5×103 s;最小(min)值分别为ρ0min=10-4 Ωm、ηmin=0、cmin=0.1、τmin=10-3s.
给定初始拉格朗日因子值为λL=10-2,随着反演的进行,λL随着迭代步长变小而逐渐减小,当达到给定精度或步长低于阀值时终止迭代.设定的精度为10-5,步长阀值设定为10-4.
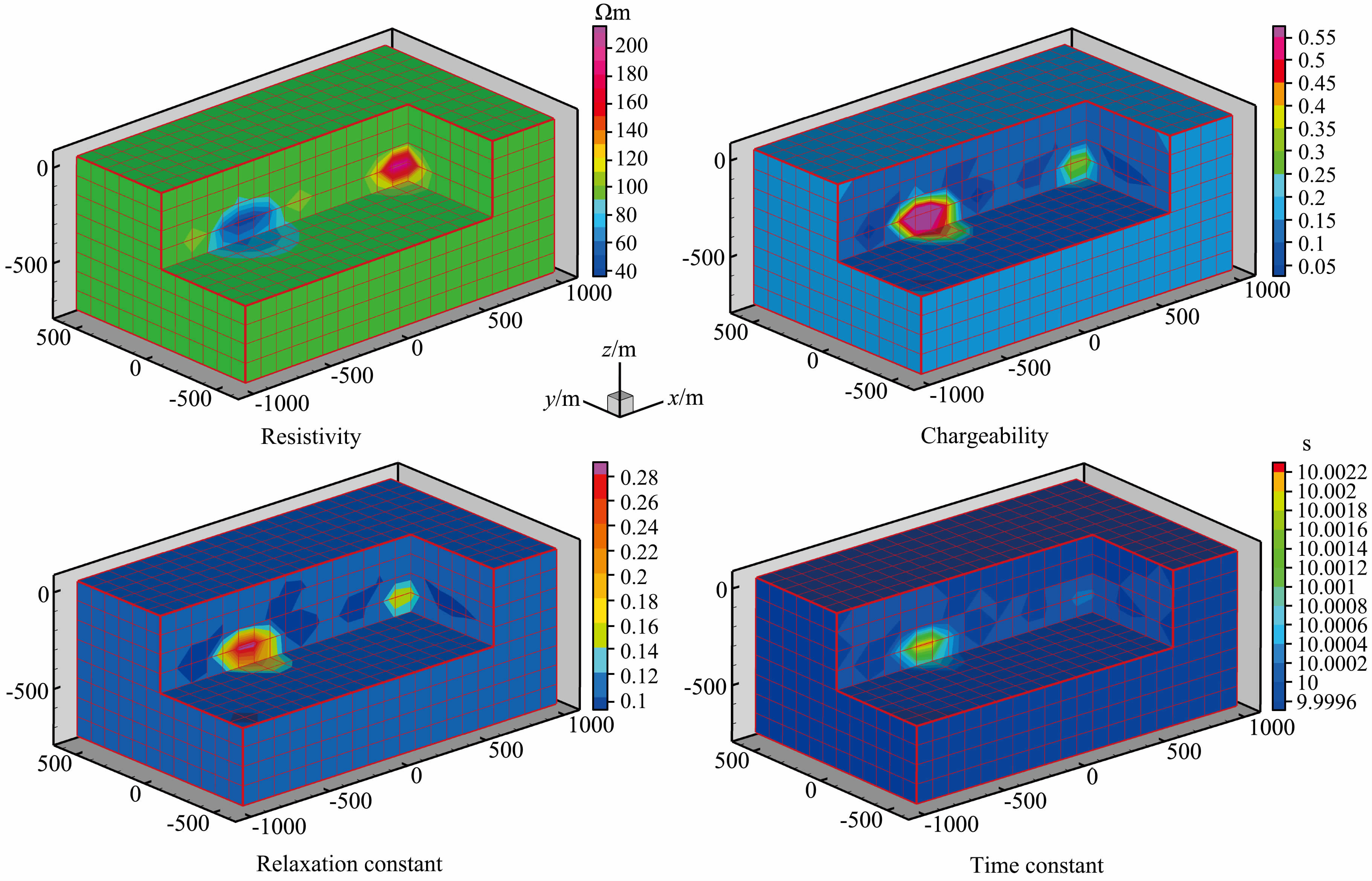
从图 4反演结果来看,该反演能够在零频电阻率、极化率及频率相关系数上有较高的分辨率,时间常数的分辨率差;低阻异常体的反演效果优于高阻异常体的反演效果;所有Cole-Cole模型参数的反演结果都在自身合理的变化范围内,因为范围约束函数强行剔除了不合理的解,是改善反演多解性的重要手段.
|
图 4 反演结果 Fig. 4 The inversion results |
从灵敏性角度分析:零频电阻率的灵敏度高于 其他三个参数;极化率、频率相关系数和时间常数的灵敏度受频率影响,频率越高,极化率的灵敏度越高,而频率相关系数和时间常数的灵敏度越低;Cole-Cole参数反演灵敏性的失衡造成了时间常数的反演结果较差,无法准确反演出异常体的时间常数.
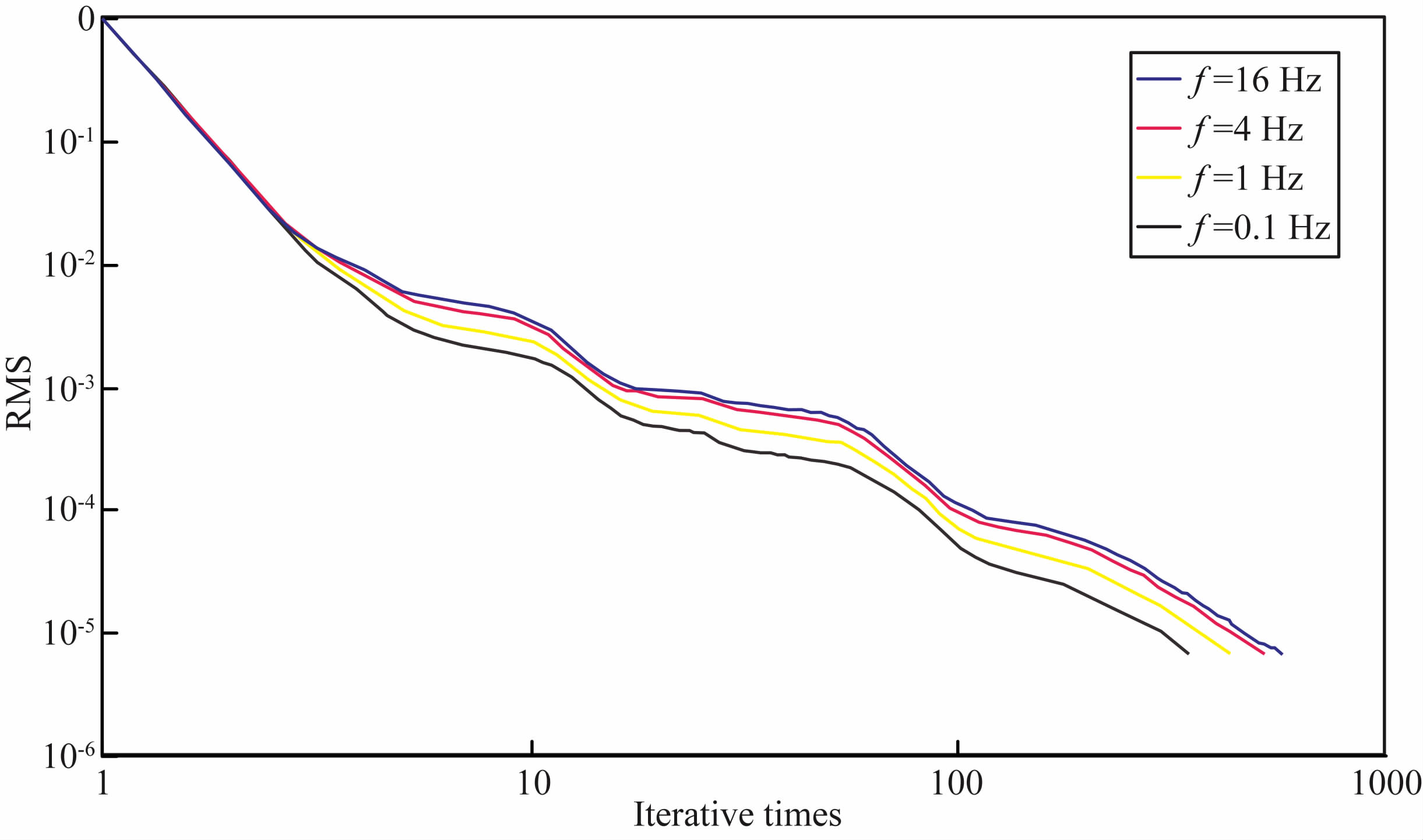
从图 5的收敛曲线中可以看出反演稳定,只是共轭梯度迭代次数较多.表 2给出反演m的时间及占用内存情况;在反演Cole-Cole模型参数时,反演迅速,一般需要几十秒至几分钟的时间.虽然共轭梯度法的迭代次数较多,但总体反演时间短,在三维反演领域内,该反演在速度上具有较大优势,而且占用的内存小,有利于实际生产应用.
|
|
表 2 反演m的时间及占用的内存 Table 2 The time and memory of inversion m |
|
图 5 迭代拟合曲线 Fig. 5 The iterative fitting curve |
本文所有正反演计算均在PC机上进行,计算 机内核为AMD Athlon(tm)II 631 Quad-Core Processor 2.60 GHz,2.99 GB 内存.
4 结论本文提出了快速拟线性近似方法,为多源电磁法正、反演的深入研究奠定了良好的基础;实现了Cole-Cole模型参数范围约束的三维频谱激电反演.取得以下几条结论:
(1)利用并矢格林函数及一次场的空间性质可以有效减少拟线性近似方法的计算量,缩短正演的计算时间.掌握格林函数的物理实质,挖掘格林函数更多的性质并灵活运用,有利于进一步加快拟线性近似方法的计算速度.
(2)频谱激电方法的参数种类较多,各个参数变化范围不一,这增加了三维频谱激电反演的复杂性和多解性.Cole-Cole参数范围约束函数能剔除不合实际的解,有效改善反演的多解性.Cole-Cole模型各参数的灵敏度有高有低,其中时间常数的灵敏度最低,因此该参数的反演结果不佳,但其他参数的反演效果较好.
(3)Cole-Cole参数范围约束的三维频谱激电反演方法对理论模型的反演效果良好,计算速度快、稳定性高、占用内存小,完全能够在普通计算机上处理实际数据.
致谢 感谢贲放、伍亮、孙博、李鹤、苏晓波以及关振玮、张镕哲、陈帅在作者编写论文过程中的帮助.
| [1] | Born M. 1933. Optic. New York: Springer. |
| [2] | Commer M, Newman G A. 2008. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int., 172(2): 513-535. |
| [3] | de Lugao P P, Wannamaker P E. 1996. Calculating the two-dimensional magnetotelluric Jacobian in finite elements using reciprocity. Geophys. J. Int., 127(3):806-810 |
| [4] | Eaton P A. 1989. 3D electromagnetic inversion using integral equations. Geophys. Prosp., 37(4): 407-426. |
| [5] | Kim H J, Song Y, Lee K H. 1999. Inequality constraint in least-squares inversion of geophysical data. Earth, Planets and Space, 51(4): 255-259. |
| [6] | Lee K H, Xie G Q. 1993. A new approach to imaging with low-frequency electromagnetic fields. Geophysics, 58(6): 780-796. |
| [7] | Li J P. 2008. Research on electromagnetic modeling of 3D complex resistivity with topography [Ph. D. thesis] (in Chinese). Changchun: Jilin University. |
| [8] | Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data. Chinese J. Geophys. (in Chinese), 56(12): 4278-4287. |
| [9] | Madden T M, Mackie R L. 1989. Three-dimensional magnetotelluric modelling and inversion. Proc. IEEE, 77(2): 318-332. |
| [10] | Nekut A G. 1994. Electromagnetic ray-trace tomography. Geophysics, 59(3): 371-377. |
| [11] | Newman G A, Alumbaugh D L. 1996. Three-dimensional electromagnetic modeling and inversion on massively parallel computers. Sandia Report SAND, 96-0852. |
| [12] | Oldenburg D W, Li Y, Farquharson C G, et al. 1998. Applications of geophysical inversions in mineral exploration. The Leading Edge, 17:461-465. |
| [13] | Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics, 78(1): E47-E57. |
| [14] | Oristaglio M L, Wang T, Hohmann G, et al. 1993. Resistivity imaging of transient EM data by conjugate-gradient method.// 63rd Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 347-350. |
| [15] | Pellerin L, Johnston J, Hohmann G. 1993. 3-D inversion of EM data.// 63rd Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 360-363. |
| [16] | Pelton W, Ward S, Hallof P, et al. 1978. Mineral discrimination and removal of inductive coupling with multrfrequency IP. Geophysics, 43(3):588-609. |
| [17] | Smith J T, Booker J R. 1991. Rapid inversion of two- and three-dimensional magnetotelluric data. J. Geophys. Res., 96(B3): 3905-3922. |
| [18] | Takasugi S, Keisaku T, Noriaki K, Shigeki M. 1992. High spatial resolution of the resistivity structure revealed by a dense network MT measurement—A case study in the Minamikayabe area, Hokkaido, Japan: J. Geomag. Geoelectr., 44, 289-308. |
| [19] | Torres-Verdin C, Habashy T M. 1995. An overview of the extended Born approximation as a nonlinear scattering approach, and its application to cross-well resistivity imaging.// Progress in Electromagnetic Research Symposium Proc., 323. |
| [20] | Wang B N, Li G F, Cao W W. 2003. On the extension of Einstein's summation convention. Journal of University of Shanghai for Science and Technology (in Chinese), 25(1): 5-7. |
| [21] | Weng A H, Liu Y H, Jia D Y, et al. 2012. Three-dimensional controlled source electromagnetic inversion using non-linear conjugate gradients. Chinese J. Geophys. (in Chinese), 55(10): 3506-3515, doi: 10.6038/j.issn.0001-5733.2012.10.034. |
| [22] | Xie G, Lee K H. 1995. Nonlinear inversion of 3-D electromagnetic data.// Progress in Electromagnetic Research Symposium Proc., 323. |
| [23] | Xu K J. 2007. Study on 2. 5-D complex resistivity electromagnetic forward and inversion [Ph. D. thesis] (in Chinese). Changchun: Jilin University. |
| [24] | Yoshioka K, Zhdanov M S. 2005. Three-dimensional nonlinear regularized inversion of the induced polarization data based on the Cole-Cole model. Physics of the Earth and Planetary Interiors, 150(1-3): 29-43. |
| [25] | Zhang H. 2006. Research of complex resistivity 3-D electromagnetic forward and inversion [Ph. D. thesis] (in Chinese). Changchun: Jilin University. |
| [26] | Zhdanov M S, Fang S. 1996a. Quasi-linear approximation in 3-D electromagnetic modeling. Geophysics, 61(3): 646-665. |
| [27] | Zhdanov M S, Fang S. 1996b. Three-dimensional quasi-linear electromagnetic inversion. Radio Sci., 31(4): 741-754. |
| [28] | Zhdanov M S, Fang S, Hursan G. 2000. Electromagnetic inversion using quasi-linear approximation. Geophysics, 65(5): 1501-1513. |
| [29] | Zhdanov M S, Tartaras E. 2002. Three-dimensional inversion of multitransmitter electromagnetic data based on the localized quasi-linear approximation. Geophys. J. Int., 148(3): 506-519. |
| [30] | 李建平. 2008. 带地形的三维复电阻率电磁场正反演研究[博士论文]. 长春: 吉林大学. |
| [31] | 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究. 地球物理学报, 56(12): 4278-4287. |
| [32] | 王伯年, 李过房, 曹伟武. 2003. 爱因斯坦求和约定的推广. 上海理工大学学报, 25(1): 5-7. |
| [33] | 翁爱华, 刘云鹤, 贾定宇等. 2012. 地面可控源频率测深三维非线性共轭梯度反演. 地球物理学报, 55(10): 3506-3515, doi: 10.6038/j.issn.0001-5733.2012.10.034. |
| [34] | 徐凯军. 2007. 2. 5维复电阻率电磁场正反演研究[博士论文]. 长春: 吉林大学. |
| [35] | 张辉. 2006. 复电阻率三维电磁场正反演研究[博士论文]. 长春: 吉林大学. |
 2015, Vol. 58
2015, Vol. 58


