2015, Vol. 58
2. 中国地质大学地球物理与空间信息学院, 地球内部多尺度成像湖北省重点实验室, 武汉 430074
2. Hubei Subsurface Multi-scale Imaging Key Laboratory, Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China
We present a 2-D MT modeling approach for anisotropic media with topography. The solution is based on a finite-difference (FD) discretization of the second-order Maxwell's equation in terms of electric fields parallel to strike for TE mode and magnetic fields parallel to strike for TM mode. The topography effect is accounted by changing the way in which the sampling electromagnetic fields are arranged, i.e. the sampling fields are in a staggered-order to make sure that the maximum bandwidth of the FD coefficient matrix can be assigned moderate memory spaces. The Weaver's approach is used to deal with the problem that the conductivity of some area on the air-earth interface may vary in the direction perpendicular to strike. Once the primary field is solved, the dual field can be obtained very easily by applying a discrete differential operator to the primary field.
Two synthetic models for modeling the horst structure and graben structure, respectively, are used to evaluate the effects of topography. The responses of models with topography are compared with that of models without topography. It is found that most significant differences occur in the regions with sharp topography boundaries, such as the boundary between the foot of a mountain and the mountainslope and the boundary between the mountain slope and the mountaintop, while the minor differences appear in flat regions. The topography has much greater impact on the TM responses than TE responses, either for the horst model or the graben model. The graben structure can have more effects than the horst structure. The sharper the slope, the greater the influence is.
We demonstrate the validity of the algorithm for 2-D MT anisotropic forward modeling with topography by numerical tests on both synthetic models and real datasets. The effects of topography are assessed by analyzing the modeling results of the horst model and the graben model. Finally, the impacts of the topography on MT responses for both large scale models and sharp slope models are evaluated by fitting the observed MT data through forward modeling.
20世纪50年代初Tikhonov(1950)和Cagnird(1953)分别提出利用天然电磁场进行勘探的方法，从70年代开始大地电磁法进入飞速发展时期，到目前已经成为国内外学者(Weiss and Newman，2002； 赵国泽等，2004；Wannamaker et al，2005；魏文博等，2006，2010；胡祥云等，2013)研究地球内部电性 结构最常用的方法之一.Ku等(1973)发现地形对大地电磁场的影响，20世纪80年代开始，不断有学者将地形因素引入大地电磁数值模拟中，Wannamaker等(1986)用有限元法对起伏地形下二 维大地电磁响应进行数值模拟.Chouteau和Bouehard(1988)研究了二维大地电磁响应的地形校正问题.徐世浙等(1985，1992，1997)用有限元和边界元法计算起伏地形下水平层状介质的大地电磁响应，并对畸变后的大地电磁响应做地形改正，这些研究成果均是基于电性各向同性理论.
20世纪60年代末，Parkhomenko(1967)，Keller(1968)和Hill(1972)分别讨论了岩石中的微各向异性问题，与此同时，电性各向异性现象的理论研究也逐渐发展起来.O′Brienh和Morrison(1967)研究层状各向异性介质中电磁场的递推公式；Reddy和Rankin(1971)研究倾斜各向异性对大地电磁场的影响.Reddy和Rankin(1975)用有限元法对偏微分方程做数值计算，较早对二维电性各向异性问题进行了理论研究.虽然在其后的20多年间(直到2000之后才有学者将其理论改进后用于大地电磁实测资料处理)未能广泛运用在大地电磁实测资料处理中，但其所做研究在理论意义上的影响却尤为深远，不仅让世人重视电性各向异性现象，更为今后的二维电性各向异性研究奠定了理论基础.Pek和Toh(2000)在Reddy和Rankin(1975)研究的基础上，并将前人(Haak，1972；Brewitt-Taylor and Wearver，1976；Cerv et al.，1978)在二维电性各向同性介质中使用的有限差分法引入求解二维电性各向异性问题中，用有限差分法对偏微分方程做数值模拟计算，是正演计算二维电性各向异性介质大地电磁响应方法中影响最为深远和广泛的一种求解方法. Li(2002，2008)细述用有限元法计算二维电性各向异性结构感应电磁场，并于2008年用自适应网格剖分法代替以往的网格剖分法，是一次成功的改进，取得显著的效果.霍光谱等(2012)通过引入权因子成功改进马奎特反演理论，将基于电性各向同性理论的反演方法扩展应用到电性各向异性理论.
基于电性各向异性理论带地形的大地电磁数值模拟在最近20年间才逐渐发展起来，用于实际资料处理的更为少见.Pek和Toh(2000)将公式扩展 应用在大地含地形和海洋测深中.Key和Ovall(2011)使用有限元法采用自适应非结构性网格剖分方式，系统研究二维大地电磁及海洋可控源电磁法，是最近较为系统而完善的方法.
2 带地形的大地电磁电性各向异性二维正演理论本文采用有限差分法参照Pek等(1997，2000，2002)的方法研究带地形的大地电磁二维电性各向异性正演问题.
假设在笛卡尔坐标系中，有一个二维电性结构，它的构造走向平行于x轴，y垂直于x轴，z轴垂直于xy平面，且正向向下.模型由一个有限区域组成，在其中的电性各向异性区域是二维有限结构.假设地表为水平，对应z=0.在地表上空(z<0)为绝缘空气层.来自z→-∞的平面波垂直向下传播，ω=2π/T，T为周期，单位为秒(s).
谐变电磁场的麦克斯韦方程组为
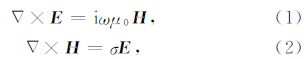
上式为描述电磁场分布的微分方程.e－iωt为时谐因子，σ 为张量电导率.
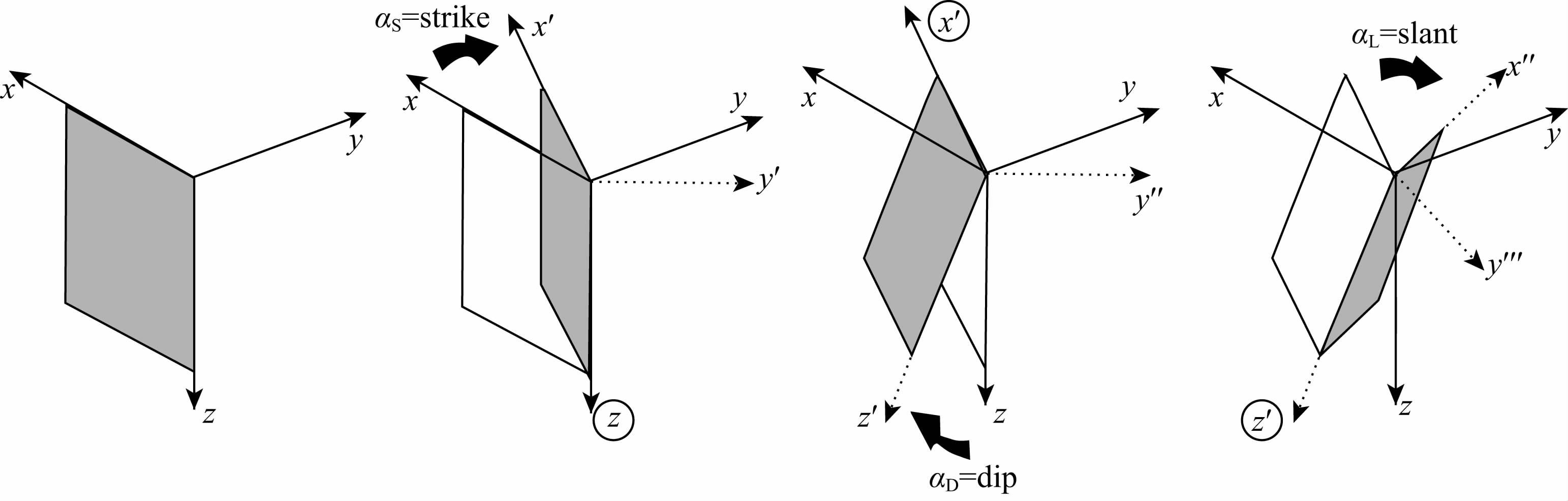
张量电导率 σ 为三阶对称矩阵，可分解为由3个电导率σ1，σ2，σ3和一个旋转矩阵，旋转矩阵又可通过3个Euler′s空间旋转元素依次旋转角度为αL，αD，αS求得，角度αS，αD，αL分别定义为各向异性介质的走向，倾角，倾向(图 1所示).
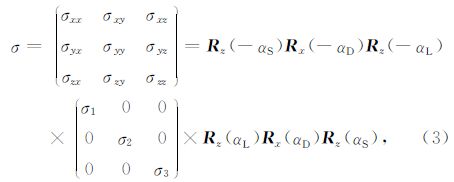
其中 R 为旋转矩阵元素：
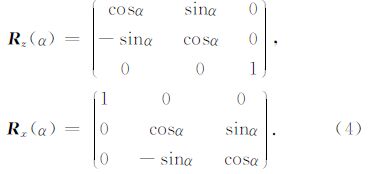
通过公式(3)可以表示空间中任何位置的电性各向异性结构.
由2-D性质∂/∂x=0，将公式简化为只含Ex和Hx的一组二阶偏微分方程(胡祥云等，2013).
电场沿走向时(即TE模式)：
|
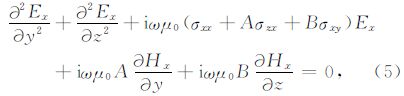
图 1 各向异性基本参数示意图(依次运用三个Euler′s旋转元素αS，αD，αL可将导电面变化到空间任何位置) Fig. 1 Illustration of basic anisotropy parameters(Transformation of conductive dike into general position by successively applying three elementary Euler′s rotation αS，αD and αL) |
磁场沿走向时(即TM模式)：
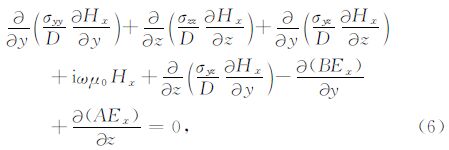
公式(5)—(6)中，
用有限差分法求解公式(5)—(6)，求得网格节点(j，k)上TE模式的近似差分方程，这个近似差分方程代表公式(5)的有限差分形式：
公式(7)中，
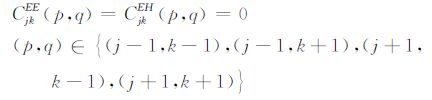
同样可以求得在网格节点(j，k)上TM模式下的线性差分方程：
在公式(8)中，
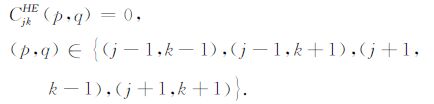
用有限差分法对公式(5)—(6)做数值近似后，须将线性代数公式(7)—(8)安排在一个系统，以便进一步处理.因为包含Ex和Hx两个变量，且这两个变量多数时候并不同时出现在同一个网格节点，TE模式的方程需要在全部网格节点做近似计算，而TM模式的方程只需在导电底层内部做近似计算.
引入地形因素时，对应的有限差分网格可通过起伏地形对应的阶梯函数来近似.并不影响用有限体积法在中心网格节点的任何位置对公式(5)—(6)做近似计算.将变量排入一个系统有两种方式：顺序排列和交错排列.本文选取交错排列方法.
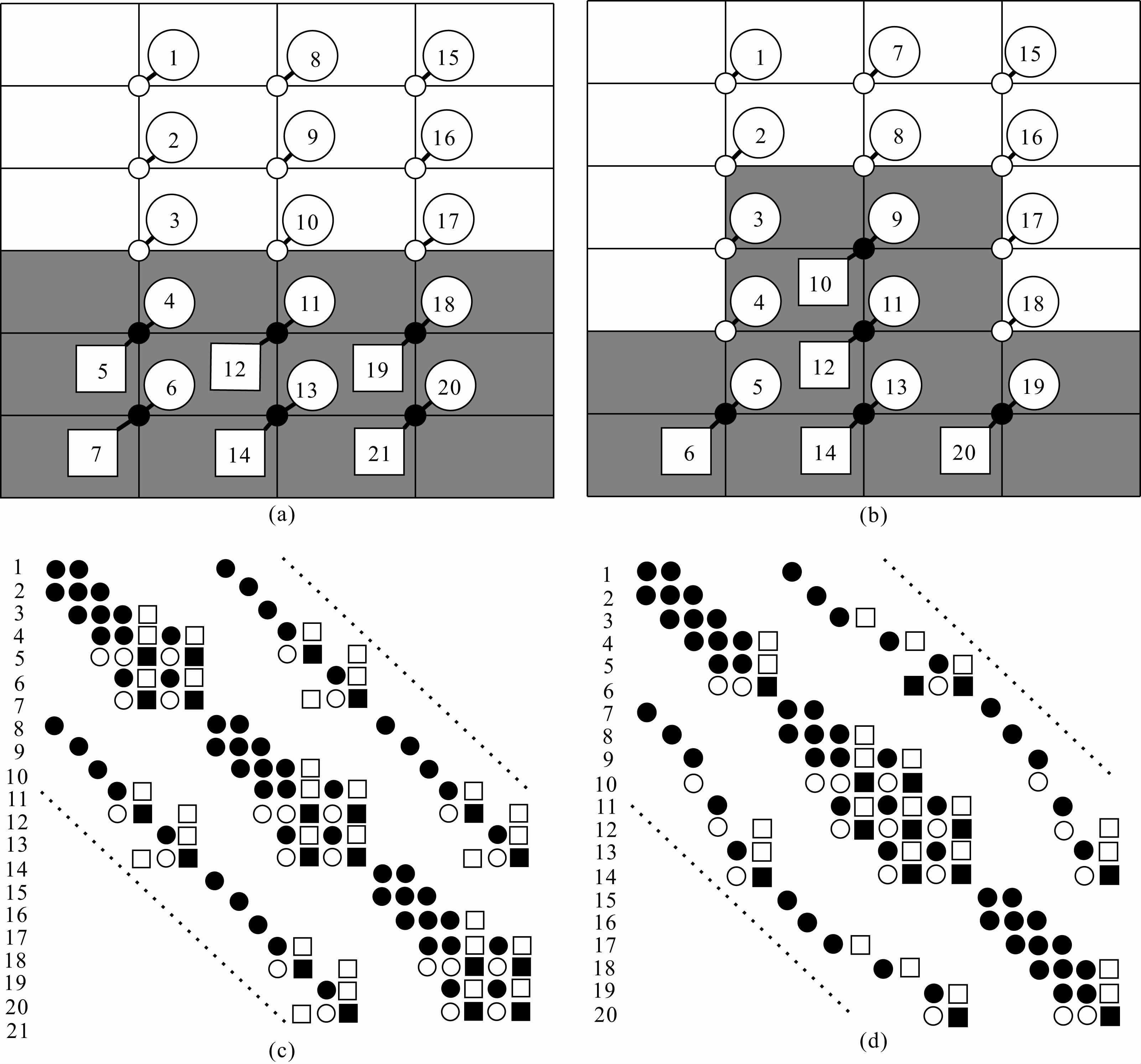
图 2a是水平地形，对应的存储矩阵是2c；2b是起伏地形，对应的存储矩阵是2d.由图 2b可以看到，在网格中，不同的列，Hx的个数是可变的，所以图 2d中有限差分系数矩阵的带宽是可变的：带宽的最宽部分由地形的海拔高度决定；带宽的最窄部分由地形的盆地深度决定.这也是起伏地形相对于水平地形不同的地方，带地形情况下，就必须考虑对公式做相应的有效修改，即：在用高斯消元法对有限差分方程组求解时，须为有限差分系数矩阵的最大带宽分配相应的存储空间.
|
图 2 变量在网格节点中的交错排列方式 符号表示了有限差分线性代数方程组系数矩阵在各个节点的存在情况((a，c)水平地形；(b，d)起伏地形).(a)(b)图中空心圆表示只有电场分量，实心圆表示有电场和磁场分量；(c)(d)图中实心圆代表电场分量，实心方块代表磁场分量，空心符号表示在矩阵模式中由电性各向异性存造成的系数. Fig. 2 The staggered manner of variables in grid nodes((a)(c)the flat earth;(b)(d)topography) The symbols indicate the presence of each node of coefficient matrix of finite difference linear algebraic equations.(a)(b)hollowcircle nodes indicate only the electric field component，solid circle nodes indicate both the electric and magnetic field components;(c)(d)solid circles and solid squares indicate electric and magnetic field components，respectively，hollow symbols indicate the coefficients due to the presence of electricity anisotropy in the matrix mode. |
与水平地表相比，含起伏地形时，TM模式在地-空分界面(y方向上)存在一些不同电导率的区域，如：σj，kσj+1，k+1≠σj+1，kσj，k+1.在这些区域的节点上，没有连续的电流和连续的切向电流.为解决这个问题，须将Weaver等(1985，1986)的光滑方法应用在这些网格节点的局部导电区域.
Weaver等(1985，1986)认识到用矩形网格剖分模型时，有时网格节点四周的4个单元格会存在不同的电导率，并给出解决此问题的方法：
1)对选定的网格节点周围的局部电导率重新塑造为光滑的电导率分布，这并不影响用有限差分法近似求解偏微分方程.
2)使用同样的近似方法(有限差分法)求原始偏微分方程的近似值.
在用有限差分方法对二阶偏微分方程(5)—(6)做近似计算后，可以得到有限差分线性方程组，并求出整个模型中各个节点上的Ex和Hx的近似值.进而可以求出磁场分量Hy和Hz.
求解过程为：
1)将场分量Ex在中心节点的两个负方向上，分别在各自的网格步长中用泰勒公式展开到二阶.
2)用二阶导数替换这些展开项，它们等于原来的二阶方程.
3)在中心节点的两边求出合适的电导率平均值.
4)通过从先前步骤中减去适当比例方程，消除Ex剩下的二阶导数.
在电性各向异性情况中，磁场分量Hx的影响也同样必须重新考虑.它会从本质上影响计算电导率平均值的过程.
在积分单元上对电导率或电阻率求平均值是可以重复多次进行的，但之间的差别很微小，在电性各向异性结构中，电流密度的各个分量不是对应的电场分量乘以标量电导率，而是所有电场分量乘以一个电导率张量.在分界面的边界条件，须对各个区域的不同电导率张量进行合适的修改.
下面将表明通过使用有限体积近似法，Weaver等(1986)的求导公式可用于电性各向异性情况.例 如：Ex在z方向上的导数∂Ex(yj，zk)/∂z.对公式(5)用体积积分法分别计算积分单元Gj，k的两个子单元，即：积分区域的上半部分(z>zk)和下半部分(z
将(z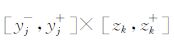
，积分为如下形式：
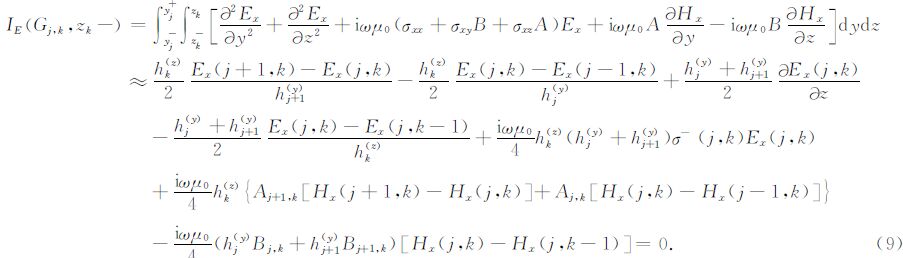
式中，
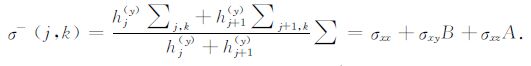
同样可对(z>zk)区域，即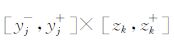： 积分.
为了消去近似方程中水平方向(y方向)的导数，并得到垂直方向上∂Ex(j，k)/∂z的值，将 2hk+1(z)IE(Gj，k，zk－)－2hk(z)IE(Gj，k，zk+)，可得:
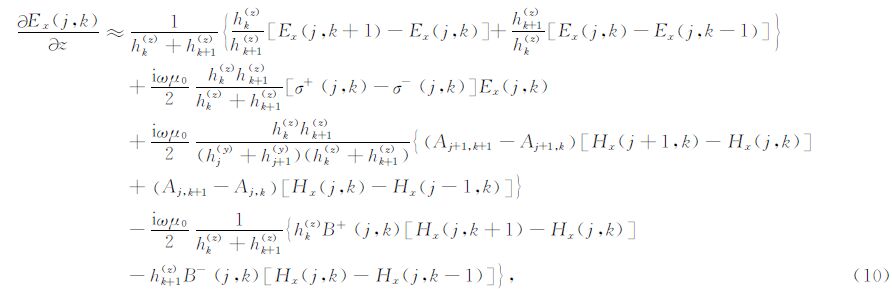
式中，
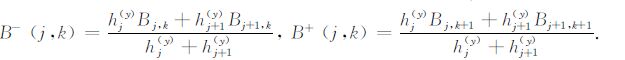
公式(10)前两项只包含电场分量Ex，这与 Weaver等(1986)用于计算电性各向同性情况下改进的求导公式一致.公式(10)中的第一项代表一个导数值，它由网格节点(j，k-1)，(j，k)，(j，k+1)对Ex 做抛物差值计算求出.第二项是一个修改量，它是原始偏微分方程的结果，代表了二阶偏导数∂2Ex/∂z2的值.这个修改量与中心节点上下平均电导率的差成正比.对于存在较大电导率差值时，忽视这个修改量会造成导出的场值精度 快速下降，即使场分量Ex非常准确并有着很高的精度.
公式(10)的后两项包含了磁场分量Hx，表示了在电性各向异性情况下，H极化模式的影响.这些项由电导率张量的非对角元素由集合参数A和B及它们的平均值B-和B+所决定.
同样的，重复以上过程，可以容易求得积分区域Gj，k 的左右积分子区域IE(Gj，k，yj-)和IE(Gj，k，yj+)，并得到∂Ex(j，k)/∂y的近似值.
随后可以计算由麦克斯韦方程组导出的电场分量Ey和Ez，将有限体积积分用于公式(6)中，求出∂Hx/∂y和∂Hx/∂z.
在H极化情况下，求电导率平均值包含一个更重要的性质：在剖分单元Gj，k内，通常情况下不可能找到电场分量Ey和Ez和电流密度jy和jz的一致形式.所以，不得不重新塑造网格节点(j，k)四周的局部电导率分布：消除在积分单元Gj，k内，在局部边界条件中会造成不一致性的那些急剧变化的边界条 件.通过消去适当比例的积分，可以得到关于积分区域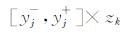 
电场切向分量的一个平均值 
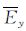(j，k)，如下公式所示：
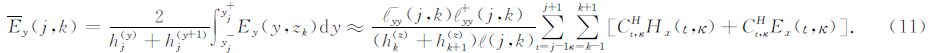
式中，
是电阻率在上、下积分子单元的平均值，
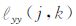是积分单元的电阻率平均值.同样可求出
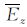(j，k).ι，κ表示网格中的节点位置.
在数据采集过程中，数据质量是基础是关键，大地电磁方法应用成功的与否在很大程度上取决于数
据采集质量.我国地域辽阔，地形复杂多变，工业生产、人文因素引起的强干扰区较为普遍.
大地电磁法多数是研究大尺度构造，虽然在多数情况下，地形的起伏相对于测线长度变化较小，但也存在一些情况，例如在构造带附近，地形会有较为剧烈的变化，此时就要求依据实际情况建立含有起伏
地形的地电模型用于处理解释.对含地形因素的二维电性各向异性地电模型做正演研究，可以为分析研究存在二维电性各向异性介质情况下，地形因素对大地电磁场产生的影响提供理论支撑.
为说明地形的影响，首先对均匀半空间包含地垒和地堑两种地形的情况分别做正演计算.均匀半空间ρ=100 Ωm(图 3所示).
|
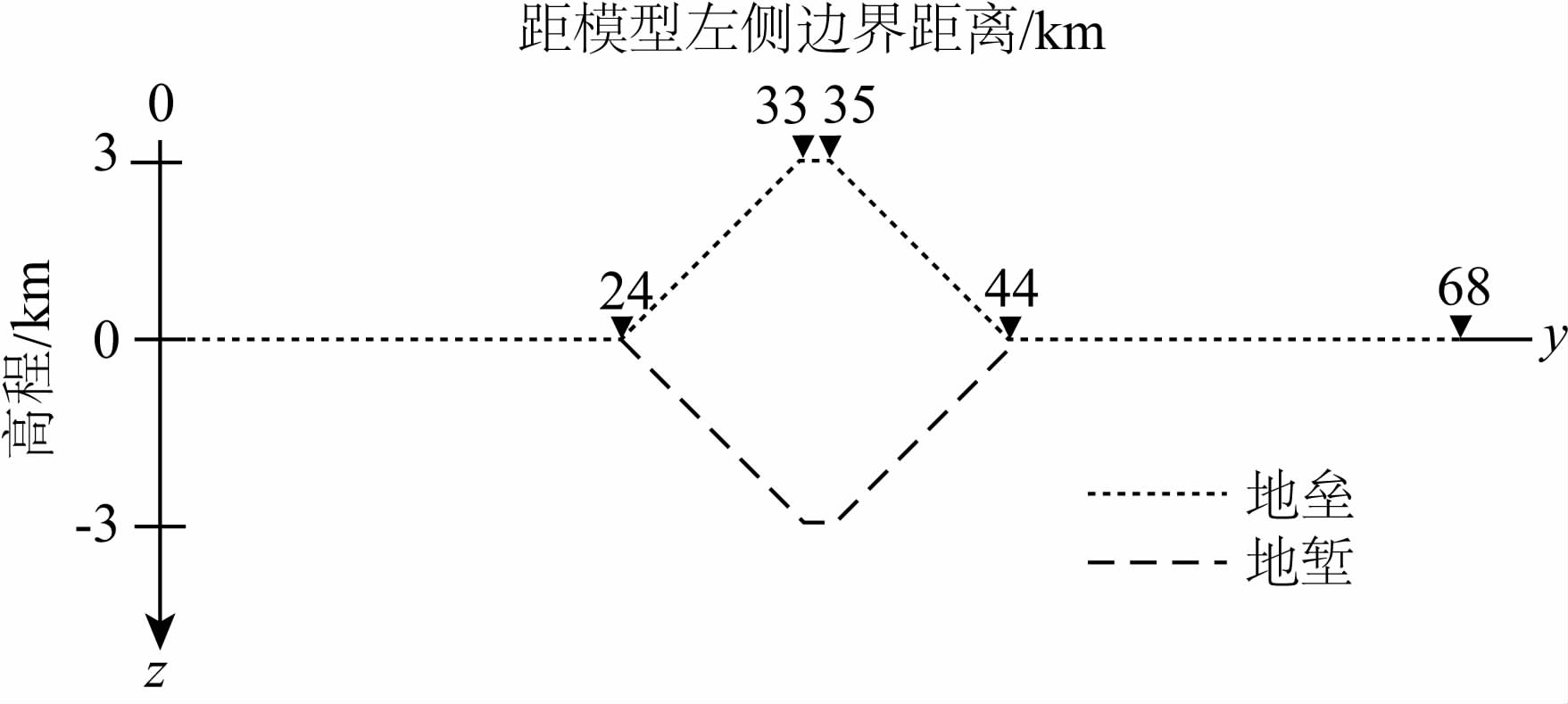
图 3 含地形的均匀半空间 Fig. 3 The homogeneous half-space with topography |
正演计算时将模型剖分为69×47的剖分单元(垂向47个剖分单元)，测点数为69个(即在地表的 网格节点处)，采用21个周期点(0.1，0.3，0.5，0.7，1，3，5，7，10，30，50，70，100，300，500，700，1000，1300，1500，1700，2000).计算结果如图 4、图 5所示.
|
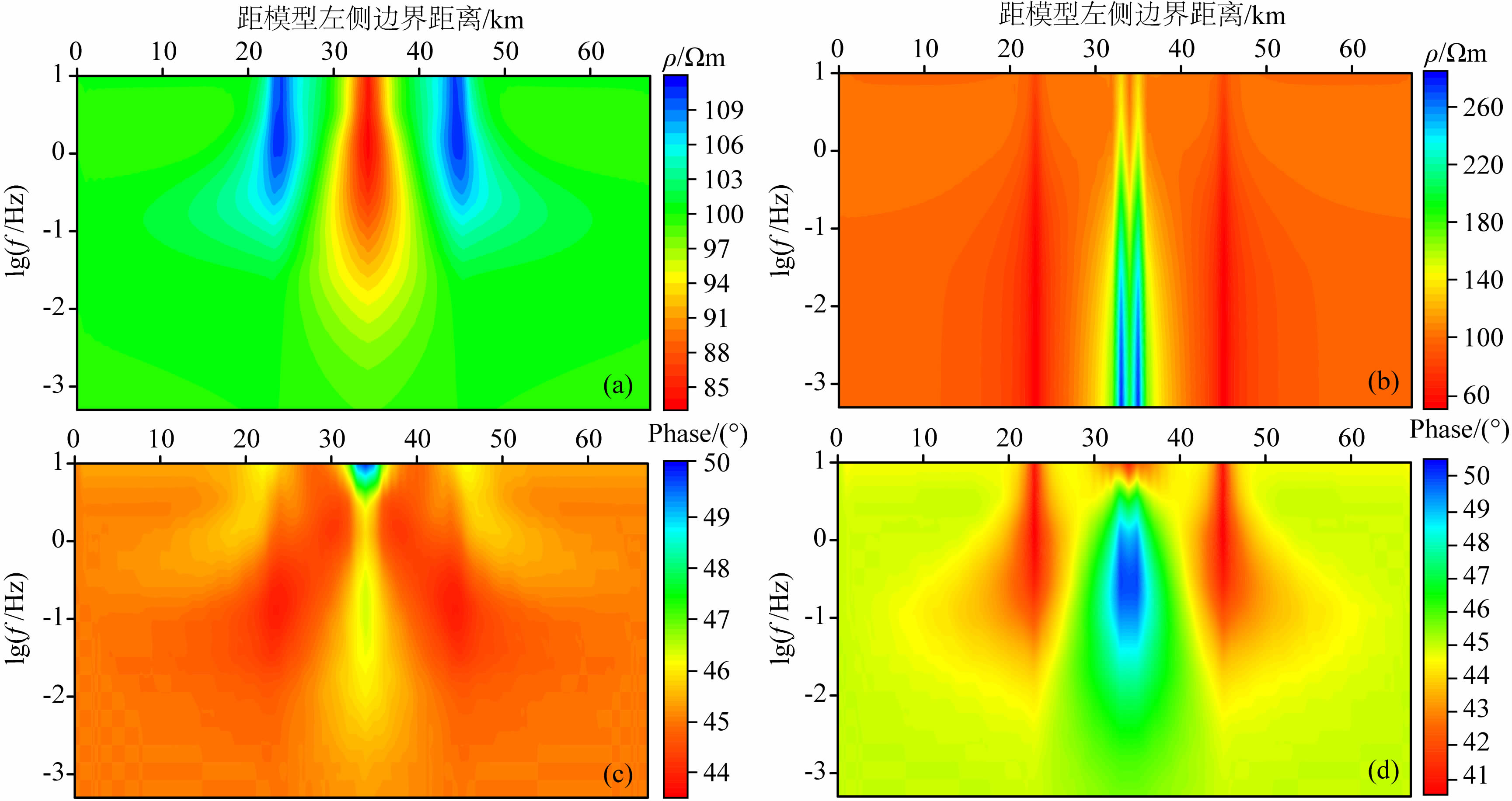
图 4 含地垒地形的均匀半空间的大地电磁响应拟断面图 (a)TE模式视电阻率拟断面图;(b)TM模式视电阻率拟断面图;(c)TE模式阻抗相位拟断面图;(d)TM模式阻抗相位拟断面图. Fig. 4 The pseudo-section of magnetotelluric response of the homogeneous half-space with topography (a)The pseudo-section of apparent resistivity in TE mode;(b)The pseudo-section of apparent resistivity in TM mode;(c)The pseudo-section of impedance phase in TE mode;(d)The pseudo-section of impedance phase in TM mode. |
|
图 5 含地堑地形的均匀半空间的大地电磁响应拟断面图 (a)TE模式视电阻率拟断面图;(b)TM模式视电阻率拟断面图;(c)TE模式阻抗相位拟断面图;(d)TM模式阻抗相位拟断面图. Fig. 5 The pseudo-section of magnetotelluric response of the homogeneous half-space with topography (a)The pseudo-section of apparent resistivity in TE mode;(b)The pseudo-section of apparent resistivity in TM mode;(c)The pseudo-section of impedance phase in TE mode;(d)The pseudo-section of impedance phase in TM mode. |
图 4、图 5分别是均匀半空间中地垒地形和地堑地形的大地电磁响应结果.可以直观看出：无论是 地垒还是地堑，地形的影响主要表现在地形起伏区 域，突出的畸变出现在地形剧烈变化的交汇处(平地与山坡交界及山坡与山顶交界处).在地垒地形的起伏区域，TE模式的视电阻率值和阻抗相位值呈现出小-大-小的变化，TM模式的视电阻率值和阻抗相位值呈现出大-小-大的变化.而在地堑地形的起伏区域，TE模式和TM模式中视电阻率值和阻抗相位值的变化正好与地垒情况相反.此外，无论是地垒还是地堑，地形的影响对于视电阻率值来说主要集中在TE模式的中高频段和TM模式的低频段，而对于阻抗相位来说影响几乎都是在中高频段.最后，地形的影响程度和地形倾角有关.倾角越大，影响就越大；反之，则越小.
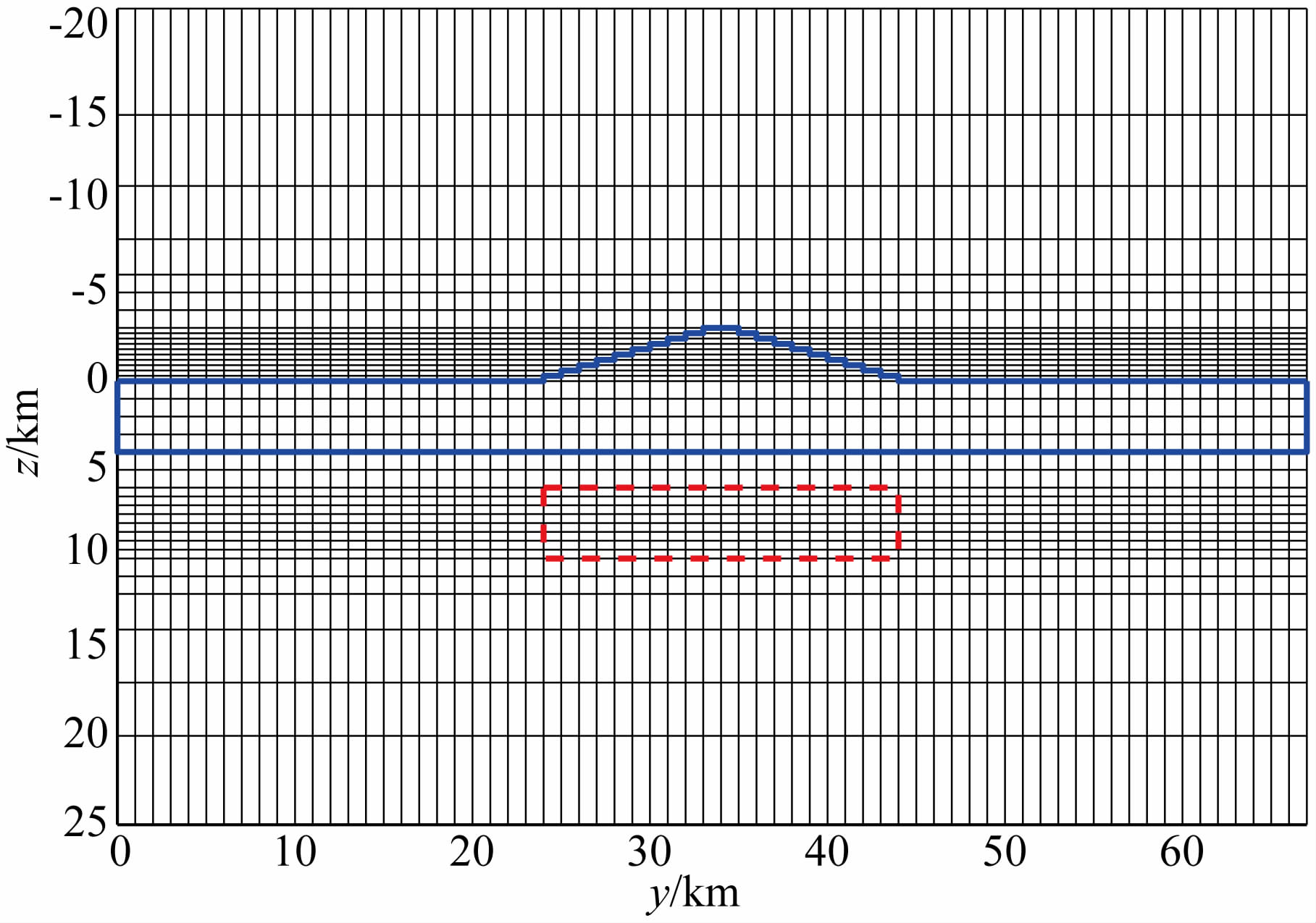
随后在含地垒地形的层状介质中放置一个二维电性各向异性介质，对地电模型做正演计算，并与之前(胡祥云等，2013)未含地形的正演结果作对比，分 析研究大地电磁场的形态特征和分布情况的差异. 模型参数为：介质1：ρ1=300 Ωm；介质2：ρ21=10 Ωm，ρ22=100 Ωm，ρ23=100 Ωm，α=30°；介质3：ρ3=1000 Ωm. 介质1为电性各向同性覆盖层，深度方向上延伸 7 km，从3～-4 km；介质2的大小为20 km×4 km，在水平方向上的位置为24～44 km之间、深度方向上的位置为-6～-10 km之间.地垒的顶部宽度为 2 km，底部为20 km(从24～44 km)，海拔高度3 km(图 6所示).
|
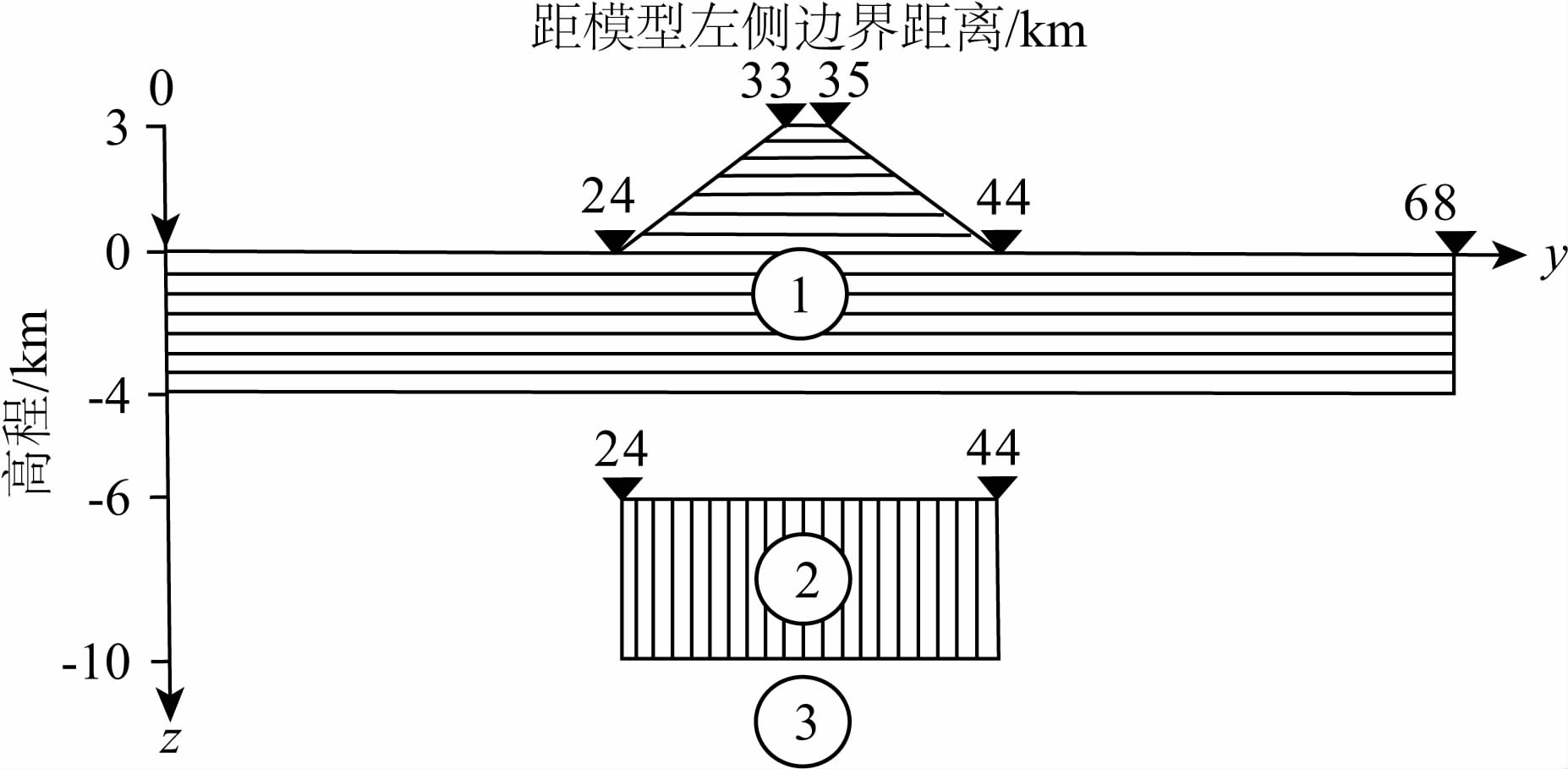
图 6 含地垒地形的层状电性各向异性地电模型 Fig. 6 Electrical anisotropic medium geoelectric model in the layered isotropic medium with topography |
网格剖分情况(图 7)及周期点与均匀半空间地垒相同，计算结果如图 8所示.
|
图 7 网格剖分图 Fig. 7 Meshes of the model |
|
图 8 含地垒地形的层状电性各向异性地电模型的大地电磁响应拟断面图 (a)TE模式视电阻率拟断面图;(b)TM模式视电阻率拟断面图;(c)TE模式阻抗相位拟断面图;(d)TM模式阻抗相位拟断面图. Fig. 8 The pseudo-section of magnetotelluric response of electrical anisotropic medium geoelectric model in the layered isotropic medium with topography (a)The pseudo-section of apparent resistivity in TE mode;(b)The pseudo-section of apparent resistivity in TM mode; (c)The pseudo-section of impedance phase in TE mode;(d)The pseudo-section of impedance phase in TM mode. |
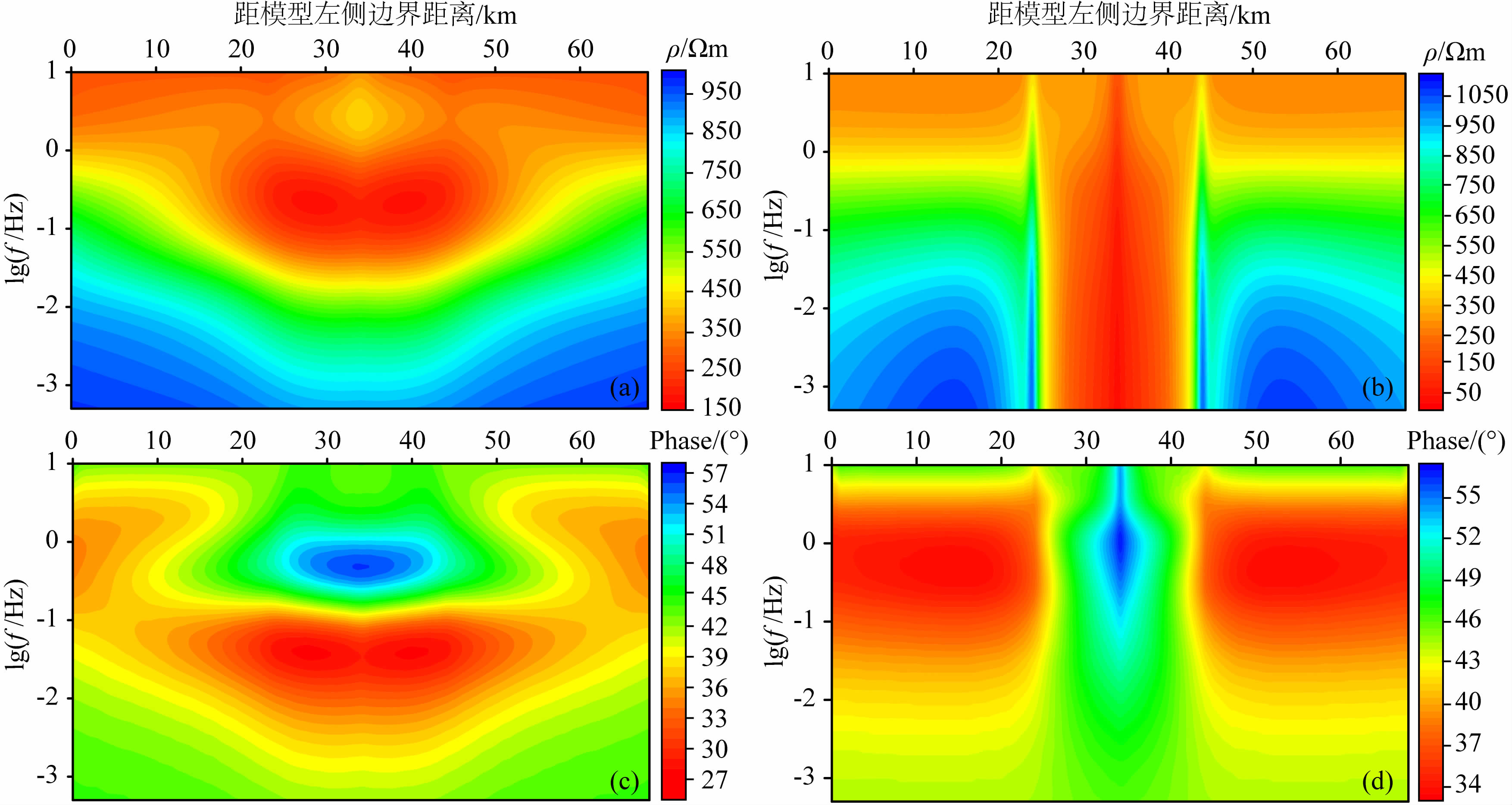
将图 8的结果同之前(胡祥云等，2013)未含地形的正演结果对比可知：含地垒情况下TE模式的视电阻率拟断面图中低阻异常区域在水平方向上的延展有所扩大，图 8a中低阻区域展示了二维电性各向异性介质的存在范围，受地形影响在33～35 km，lg(f)=0的低阻区域有明显凹陷；阻抗相位拟断面图的形态基本一致，细微区别在于含地垒情况下阻抗相位值最大值和最小值区域水平方向上的延伸稍有增加，在33～35 km，lg(f)=-1.5的阻抗相位值有所增大；受地形影响TE模式下的视电阻率最小值有所增大，阻抗相位值几乎无变化.TM模式的视电阻率值和阻抗相位值受地形的影响较为明显，在山脚处(24 km和44 km处)视电阻率值和阻抗相位值均发生了畸变，表现为视电阻率值跳跃增大，阻抗相位值跳跃降低；在山顶处(33～35 km)视电阻率值有明显降低，阻抗相位值有明显增大；受地形影响TM模式下的视电阻率最小值有所降低，阻抗相位最大值有所增大.
在含地堑地形的层状介质中放置一个二维电性各向异性介质，对地电模型做正演计算，并与之前(胡祥云等，2013)未含地形的正演结果做对比分析，介质1、2、3参数同地垒地电模型.地堑的顶部宽度为20 km(从24 km到44 km)，底部为2 km，海拔高度-3 km.如图 9所示.
|
图 9 含地堑地形的层状电性各向异性地电模型 Fig. 9 Electrical anisotropic medium geoelectric model in the layered isotropic medium with topography |
将图 10的结果同之前未含地形的正演结果(胡祥云等，2013)对比可知：含地堑情况下TE模式的视电阻率拟断面图中低阻异常区域在水平方向上的延展有所扩大，图 1a中低阻区域展示了二维电性各向异性介质的存在范围，受地形影响在33～35 km，lg(f)=0的低阻区域有明显凸起；阻抗相位拟断面图的形态基本一致，细微区别在于含地堑情况下阻抗相位值最大值和最小值区域水平方向上的延伸稍有增加，在33～35 km，lg(f)=-1位置阻抗相位值有所减小.TM模式的视电阻率值和阻抗相位值受地形的影响较为明显，在山脚处(24 km和44 km处)视电阻率值和阻抗相位值均发生了畸变，表现为视电阻率值跳跃减小，阻抗相位值跳跃增大；在山顶处(33～35 km)视电阻率值表现为增大-减小-增大的跳跃式畸变，阻抗相位值表现为减小-增大-减小的跳跃式畸变.
|
图 10 含地堑地形的层状电性各向异性地电模型的大地电磁响应拟断面图 (a)TE模式视电阻率拟断面图;(b)TM模式视电阻率拟断面图;(c)TE模式阻抗相位拟断面图;(d)TM模式阻抗相位拟断面图. Fig. 10 The pseudo-section of magnetotelluric response of electrical anisotropic medium geoelectric model in the layered isotropic medium with topography (a)The pseudo-section of apparent resistivity in TE mode;(b)The pseudo-section of apparent resistivity in TM mode; (c)The pseudo-section of impedance phase in TE mode;(d)The pseudo-section of impedance phase in TM mode. |
总体来说，地形因素对于大地电磁响应的影响主要存在于地形的突变位置(平地与山脚交汇处及山坡与山顶交汇处)，而在平稳过渡位置(山坡)对于大地电磁响应的影响较为平缓.其次，不论是地垒地形还是地堑地形，对于TE模式下的视电阻率值和阻抗相位值影响都较小；对于TM模式的影响则较大.此外，地堑地形的影响要强于地垒地形的影响，最后，地形的影响程度和地形倾角有直接关系，地形倾角越大，影响越强烈；反之则越小.
4 大地电磁实测资料解释及电性结构对比分析选取的大地电磁测线位于贵州某地，测线位于贵州山区，地形起伏较大，加入地形的正演拟合结果展示了地形对大地电磁响应的影响.
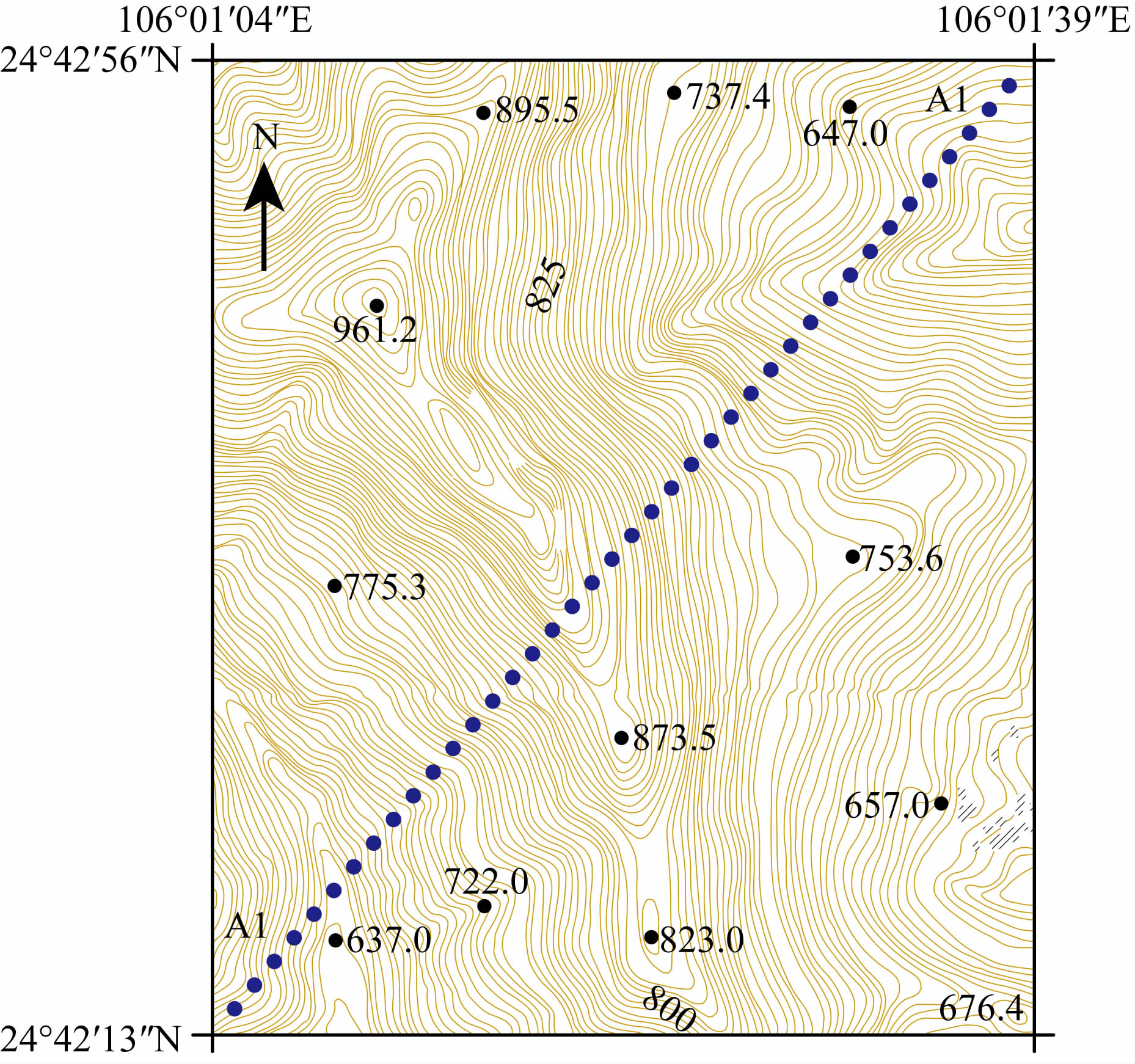
图 11是测线位置图，测线由西南向东北首先穿 过山谷，随后翻过山脊进入山坡平缓区域.测线长1400 m，地形起伏高差240 m，测点距40 m.测线的 视电阻率拟断面图和阻抗相位拟断面图如图 12所示.
|
图 11 测线位置图 Fig. 11 The location of the survey line |
|
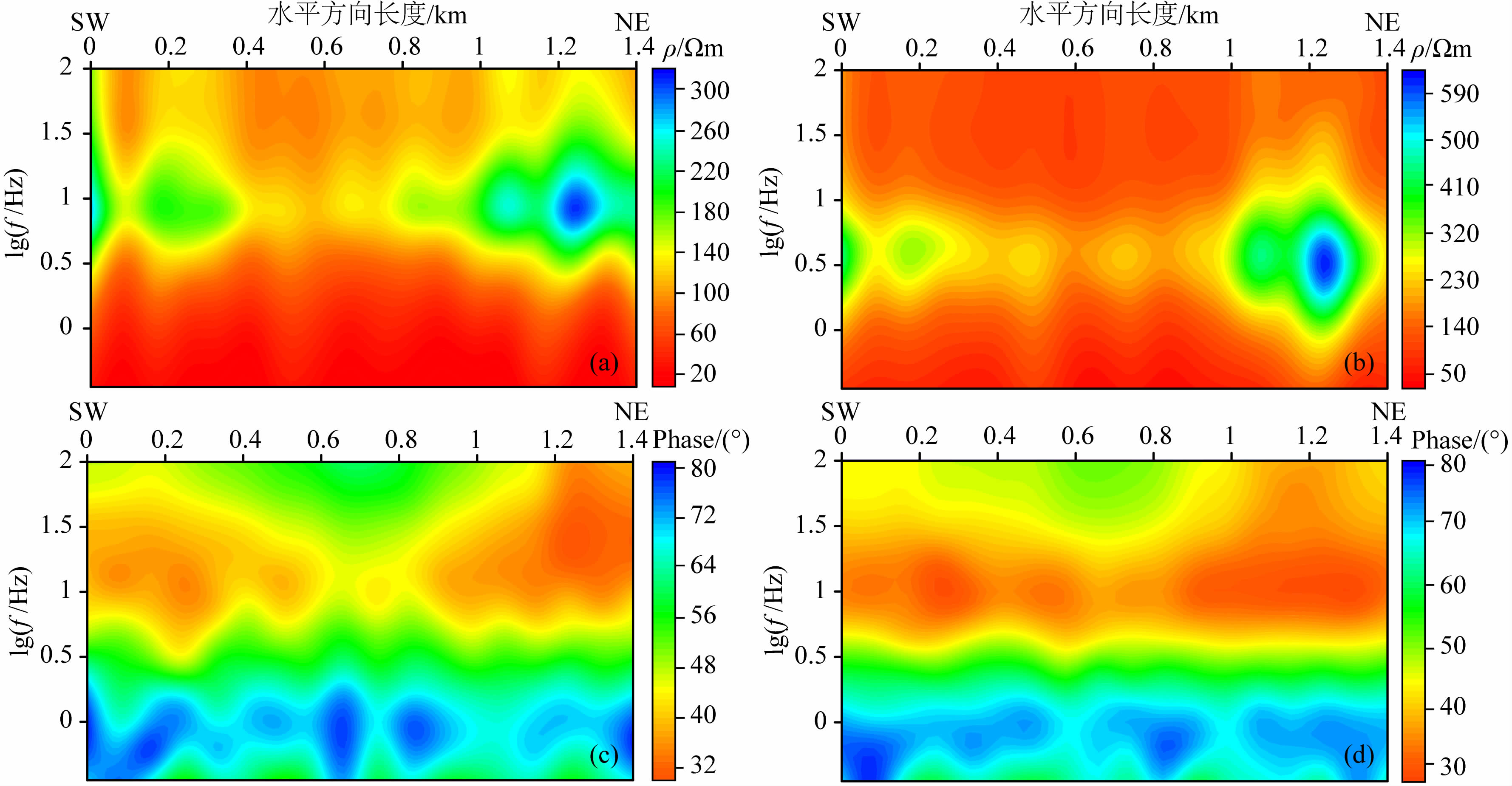
图 12 带地形的二维大地电磁响应拟断面图 (a)TE模式视电阻率拟断面图;(b)TM模式视电阻率拟断面图;(c)TE模式阻抗相位拟断面图;(d)TM模式阻抗相位拟断面图. Fig. 12 The pseudo-section of two-dimension magnetotelluric response with topography (a)The pseudo-section of apparent resistivity in TE mode;(b)The pseudo-section of apparent resistivity in TM mode; (c)The pseudo-section of impedance phase in TE mode;(d)The pseudo-section of impedance phase in TM mode. |
测线的测点距为40 m，对于长度为1400 m的测线来说，数据量是十分充足的.图 12中的4幅拟断面图都不同程度的出现了许多闭合圆圈，即使通过数据插值成图，也不能使这些区域的高/低值平滑.说明实测资料中在同一周期点，水平方向上的数据值跳动十分剧烈.本文通过构建一个含地形的二维电性各向异性地电模型，并对其做正演计算，根据正演拟合的结果分析该区域的电性结构并研究地形对大地电磁响应的影响.
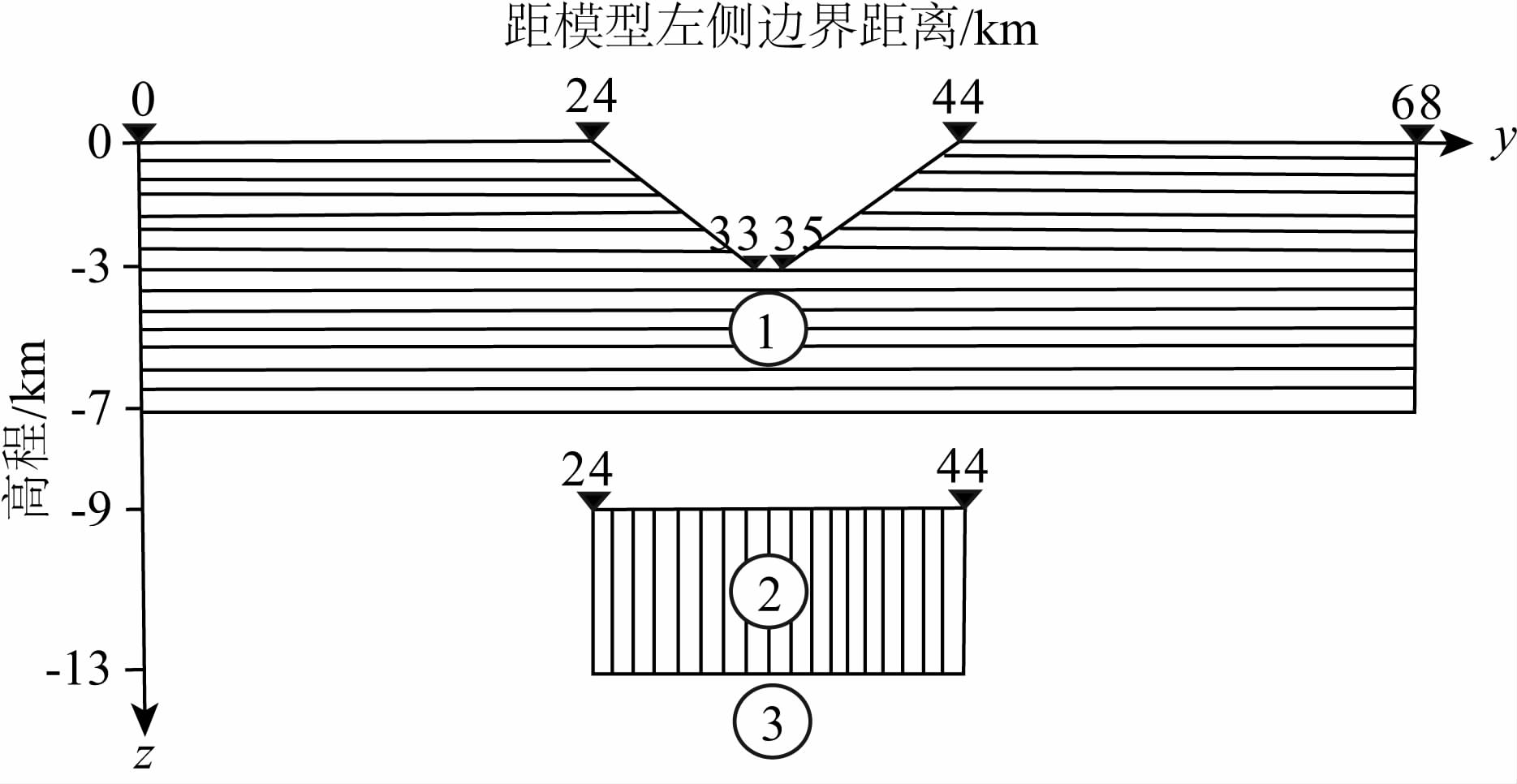
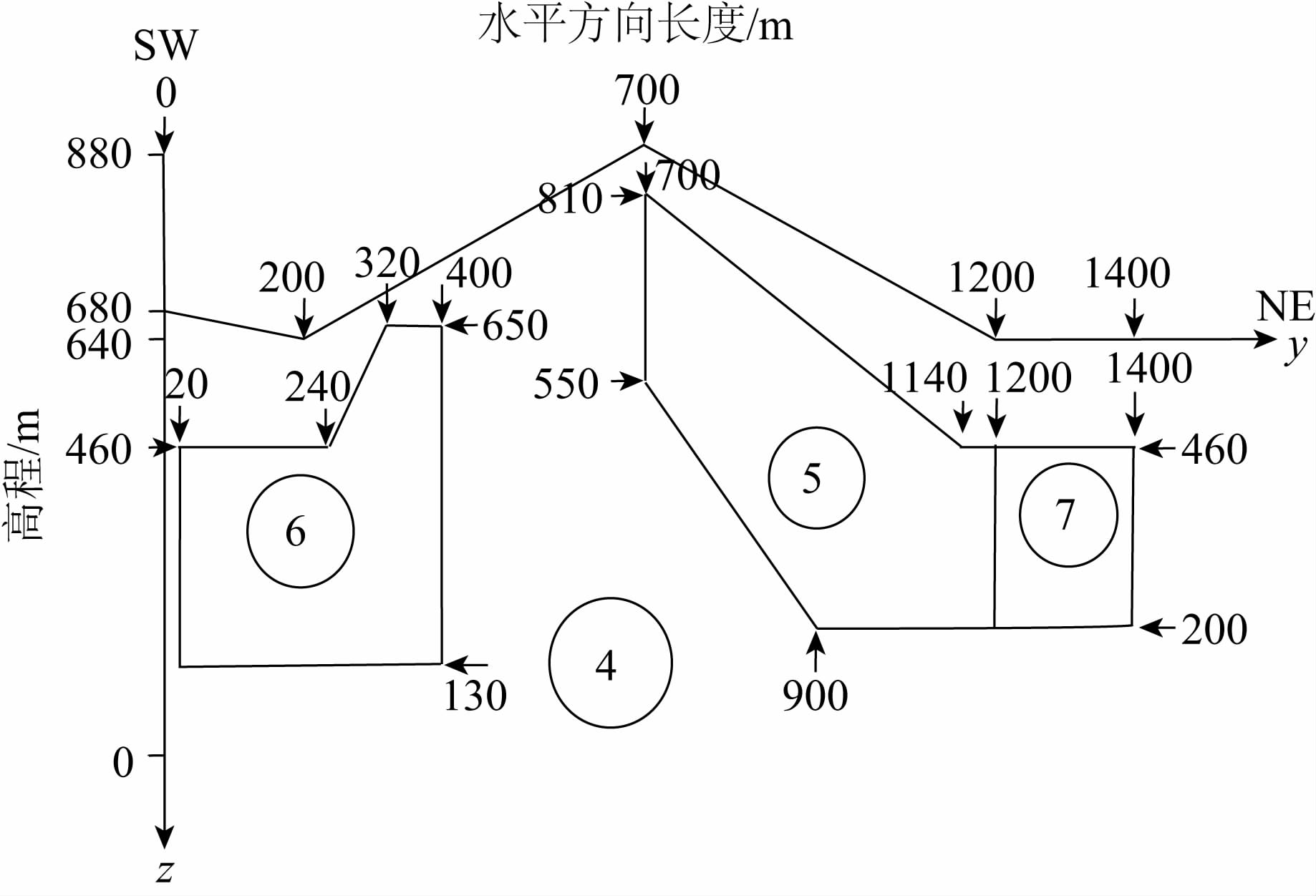
图 13是构建的带地形的二维电性各向异性地电模型，该地电模型包含4个区域(分别由圆圈中的数字所指示)，其中4号区域包含了地形变化，5、6、7号区域为电性各向异性区域(3个区域的α=0°).模型参数如下所示：介质4：ρ4=100 Ωm；介质5：ρ51=1000 Ωm，ρ52=500 Ωm，ρ53=500 Ωm；介质6：ρ61=30000 Ωm，ρ62=300 Ωm，ρ63=300 Ωm；介质7：ρ71=2200 Ωm，ρ72=400 Ωm，ρ73=400 Ωm.各个介质的区域范围如图 13所示.正演计算时将模型剖分为75×80的剖分单元(垂向80个剖分单元)，测点数为75个(即在地表的网格节点处)，采用30个周期点(0.01，0.02，0.03，0.04，0.05，0.06，0.07，0.08，0.09，0.1，0.13，0.15，0.17，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1，2，3，5，7，10，20，30，50).计算结果如图 14所示.
|
图 13 带地形的二维电性各向异性地电模型 Fig. 13 The two-dimensional electrical anisotropic geoelectric model with topography |
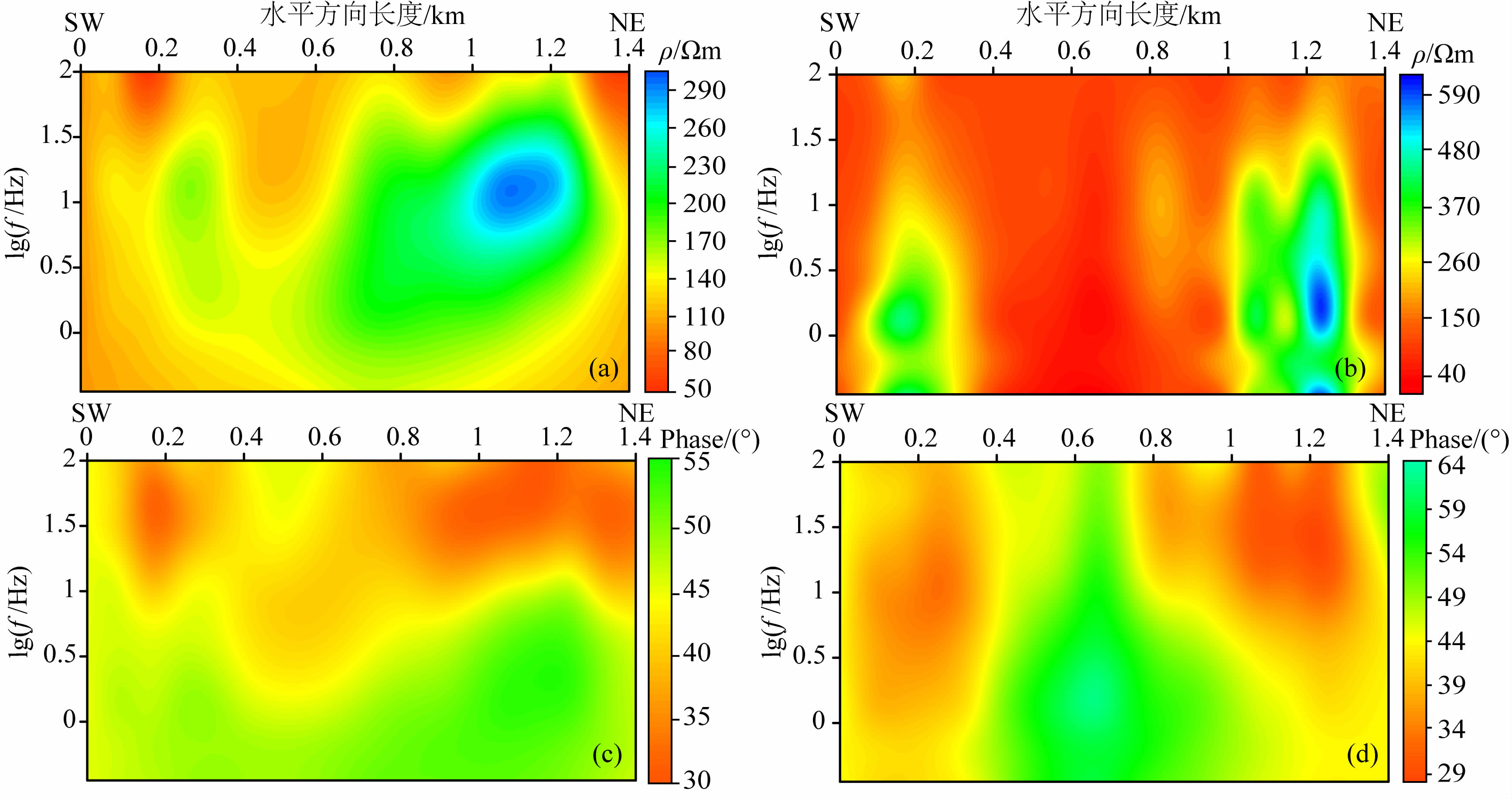
图 14中TE和TM模式的正演结果受地形的影响都较大.正演计算的结果和实测数据有很好的拟合.图 14a中，在lg(f)=1 Hz，水平方向的200～ 400 m，800～1400 m区域出现了对应的高阻区，在X=1000 m和1200 m出现的高阻闭合圆圈也有很好的对应，并且高阻最大值也保持一致.图 14c和图 12c的形态基本保持一致，在阻抗相位的低值区域(lg(f)=2-1 Hz，X=100～300 m及800~1400 m)都表现出高阻介质(5、6、7)在深度方向上的延展范围.图 14b中，在lg(f)=0.5 Hz，水平方向的100~300 m，1000~1200 m区域，出现高阻闭合圆圈，与图 12b中的情况一致，高阻最大值也保持一致.图 14d和图 12d形态稍有差异，主要表现在水平方向600～800 m范围内.图 14d的低值区域在水平方向上很好的呈现出5、6、7三个电性各向异性介质的延展范围.根据正演拟合的结果，推断地形的突变点(X=200、700、1200 m)及5、6、7三个介质的变化点(X=240、320、700、900、1140)是造成数据在同一周期点呈锯齿状起伏的主要原因.总体来说，正演拟合的结果基本上与实测数据一致，不但在位置上一一对应出高阻闭合圈的范围，而且在高阻区域的最大值也能够保持一致.
|
图 14 带地形的二维电性各向异性地电模型的大地电磁响应拟断面图 (a)TE模式视电阻率拟断面图;(b)TM模式视电阻率拟断面图;(c)TE模式阻抗相位拟断面图;(d)TM模式阻抗相位拟断面图. Fig. 14 The pseudo-section of magnetotelluric response of two-dimension electrical anisotropic geoelectric model ith topography (a)The pseudo-section of apparent resistivity in TE mode;(b)The pseudo-section of apparent resistivity in TM mode;(c)The pseudo-section of impedance phase in TE mode;(d)The pseudo-section of impedance phase in TM mode. |
实测资料的正演拟合结果表明：在大尺度下地形起伏较缓时可以忽略地形因素对大地电磁响应造成的影响，而在地形起伏较大区域(如山区和构造带区域)，地形变化会对大地电磁响应造成显著的影响，使得视电阻率值及阻抗相位值在地形突变位置产生畸变，此时就必须重视地形变化带来的影响，必要时需对地形造成的畸变进行校正.
5 结论本文基于Pek(1997，2000)的研究理论，系统而详实的阐述了含地形的二维电性各向异性正演理论；并通过理论研究说明地形因素对大地电磁响应的影响，实测资料的对比研究说明地形因素对大地电磁响应的影响程度.
基于水平地形二维大地电磁各向异性研究成果，引入地形因素，改变变量在网格节点中的排列方 式，选择交错排列方式从而给有限差分系数矩阵的最大带宽分配合理的存储空间，随后，使用Weaver等(1985，1986)的方法解决TM模式下，在地-空分界面Y方向上的一些区域存在不同电导率的问题，对带地形的二维大地电磁电性各向异性正演问题进行系统研究.正演计算地垒及地堑情况下的地电模型，研究地形对大地电磁响应的影响.
以本文的研究成果为基础，将带地形的二维大地电磁电性各向异性理论引入对实测大地电磁资料的处理解释中，说明电性各向异性现象的普遍存在，同时验证理论的正确性及程序的实用性，并且对山区地形起伏剧烈情况下地形变化对大地电磁响应的影响程度深入分析，为今后处理解释大地电磁资料中包含地形因素的电性各向异性现象提供理论依据和技术指导，并开拓了对大地电磁实测资料处理的思路和方法.
致谢 感谢捷克科学院地球物理研究所Josef Pek教授对本文的帮助.
| [1] | Brewitt-Taylor C R, Weaver J T. 1976. On the finite difference solution of two-dimensional induction problems. Geophys. J. Int., 47(2): 375-396. |
| [2] | Cagniard L. 1953. Basic theory of the magneto-telluric method of geophysical prospecting. Geophysics, 18(3): 605-635. |
| [3] | Cerv V, Praus O, Hvodara R M. 1978. Numerical modelling in laterally inhomogeneous geoelectrical structures. Studia Geopyhs. Et Geodaet., 22(1): 74-81. |
| [4] | Chouteau M, Bouehard K. 1988. Two-dimensional terrain correction in magnetotelluric surveys. Geophysics, 53(6): 854-862. |
| [5] | Haak V. 1972. Magnetotellurics: Determination of the transfer functions in regions with lateral changes of the electrical conductivity. Z. Geophys. (in German), 38: 85-102. |
| [6] | Hill D G. 1972. A laboratory investigation of electrical anisotropy in Precambrian rocks. Geophysics, 37(6): 1022-1038. |
| [7] | Hu X Y, Huo G P, Gao R, et al. 2013. The magnetotelluric anisotropic two-dimensional simulation and case analysis. Chinese J. Geophys. (in Chinese), 56(12): 4268-4277, doi: 10.6038/cjg20131229. |
| [8] | Huo G P, Hu X Y, Fang H, et al. 2012. Magnetotelluric joint inversion for anisotropic conductivities in layered media. Acta Phys. Sin. (in Chinese), 62(12): 129101. |
| [9] | Huo G P, Hu X Y, Liu M. 2011. Review of the forward modeling of magnetotelluric in the anisotropy medium research. Progress in Geophys. (in Chinese), 26(6): 1976-1982, doi: 10.3969/j.issn.1004-2903.2011.06.011. |
| [10] | Jin G W, Zhao G Z, Xu C F, et al. 1998. The affection and correction on magnetotelluric response data for inclination two-dimension terrain. Seismology and Geology (in Chinese), 20(4): 454-458. |
| [11] | Keller G V. 1968. Electrical prospecting for oil.// Quarterly of the Colorado School of Mines, v. 63, no. 2. Golden: Colorado School of Mines. |
| [12] | Key K, Ovall J. 2011. A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modelling. Geophys. J. Int., 186(1): 137-154. |
| [13] | Ku C C, Hsieh M S, Lim S H. 1973. The topographic effect in electromagnetic fields. Canadian J. Earth Sci., 10(5): 645-656. |
| [14] | Li Y G. 2002. A finite-element algorithm for electromagnetic induction in two-dimensional anisotropic conductivity structures. Geophys. J. Int., 148(3): 389-401. |
| [15] | Li Y G, Pek J. 2008. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media. Geophys. J. Int., 175(3): 942-954. |
| [16] | O'Brien D P, Morrison H F. 1967. Electromagnetic fields in an N-layer anisotropic half-space. Geophysics, 32(4): 668-677. |
| [17] | Parkhomenko E I. 1967. Electrical Properties of Rocks. US: Springer. |
| [18] | Pek J, Verner T. 1997. Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media. Geophys. J. Int., 128(3): 505-521. |
| [19] | Pek J, Toh H. 2000. Numerical modeling of MT fields in 2-D anisotropic structures with topography and bathymetry considered.// Protokolluber das 18, Kolloquium "Electromagnetische Tiefenforschung". Altenberg, Germany, Hordt, A., and J. Stoll, eds., DGG, 190-199. |
| [20] | Pek J, Santos F A M. 2002. Magnetotelluric impedances and parametric sensitivities for 1-D anisotropic layered media. Computers and Geosciences, 28(8): 939-950. |
| [21] | Reddy I K, Rankin D. 1971. Magnetotelluric effect of dipping anisotropies. Geophysical Prospecting, 19(1): 84-97. |
| [22] | Reddy I K, Rankin D. 1975. Magnetotelluric response of laterally inhomogeneous and anisotropic media. Geophysics, 40(6): 1035-1045. |
| [23] | Tikhonov A N. 1950. On determining electrical characteristics of the deep layers of the earth's crust. Deki. Akud. Nuck., 73: 295-297. |
| [24] | Wang X B, Li Y N, Gao Y C. 1999. Two dimensional topographic responses in magneto telluric sounding and it's correction methods. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 21(4): 327-332. |
| [25] | Wannamaker P E, Stodt J A, Rijo L. 1986. Two-dimensional topographic responses in magnetotellurics modeled using finite elements. Geophysics, 51(11): 2131-2144. |
| [26] | Wannamaker P E. 2005. Anisotropy versus heterogeneity in continental solid Earth electromagnetic studies: fundamental response characteristics and implications for physicochemical state. Surv. Geophys., 26(6): 733-765. |
| [27] | Weaver J T, Le Quang B V, Fischer G. 1985. A comparison of analytic and numerical results for a two-dimensional control model in electromagnetic induction-I. B-polarization calculations. Gephys. J. Int., 82(2): 263-277. |
| [28] | Weaver J T, Le Quang B V, Fischer G. 1986. A comparison of analytical and numerical results for a 2-D control model in electromagnetic induction-I. E-polarization calculations. Geophys. J. Int., 87(3): 917-948. |
| [29] | Wei W B, Jin S, Ye G F, et al. 2006. Conductivity structure of crust and upper mantle beneath the northern Tibetan Plateau: Results of super-wide band magnetotelluric sounding. Chinese J. Geophys. (in Chinese), 49(4): 1215-1225. |
| [30] | Wei W B, Jin S, Ye G F, et al. 2010. On the conductive structure of Chinese continental lithosphere-experiment on "standard monitoring network" of continental EM parameters (SinoProbe-01). Acta Geologica Sinica (in Chinese), 84(6): 788-800. |
| [31] | Weiss C J, Newman G A. 2002. Electromagnetic induction in a fully 3-D anisotropic earth. Geophysics, 67(4): 1104-1114. |
| [32] | Xu S Z, Zhao S K. 1985. The topographic effects on magnetotelluric response. Northwestern Seismological Journal (in Chinese), 7(4): 69-78. |
| [33] | Xu S Z, Wang Q Y, Wang J. 1992. Modeling 2-D terrain effect on MT by the boundary element method. Acta Geophysica Sinica (in Chinese), 35(3): 380-388. |
| [34] | Xu S Z, Li Y G, Liu B. 1997. The method and efficiency of 2-D terrain correction for Hx-polarization of MT. Chinese J. Geophys. (in Chinese), 40(6): 842-846. |
| [35] | Zhao G Z, Tang J, Zhan Y, et al. 2004. Study on the crustal electrical structure and block deformation in Northeast margin of Tibetan Plateau. Science in China (Ser. D) (in Chinese), 34(10): 908-918. |
| [36] | 胡祥云, 霍光谱, 高锐等. 2013. 大地电磁各向异性二维模拟及实例分析. 地球物理学报, 56(12): 4268-4277, doi: 10.6038/cjg20131229. |
| [37] | 霍光谱, 胡祥云, 方慧等. 2012. 层状各向异性介质大地电磁联合反演研究. 物理学报, 61(12): 129101. |
| [38] | 霍光谱, 胡祥云, 刘敏. 2011. 各向异性介质中大地电磁正演研究综述. 地球物理学进展, 26(6): 1976-1982, doi: 10.3969/j.issn.1004-2903.2011.06.011. |
| [39] | 魏文博, 金胜, 叶高峰等. 2006. 藏北高原地壳及上地幔导电性结构-超宽频带大地电磁测深研究结果. 地球物理学报, 49(4): 1215-1225. |
| [40] | 魏文博, 金胜, 叶高峰等. 2010. 中国大陆岩石圈导电性结构研究-大陆电磁参数"标准网"试验(SinoProbe-01). 地质学报, 84(6): 788-800. |
| [41] | 徐世浙, 赵生凯. 1985. 地形对大地电磁勘探的影响. 西北地震学报, 7(4): 69-78. |
| [42] | 徐世浙, 王庆乙, 王军. 1992. 用边界单元法模拟二维地形对大地电磁场的影响. 地球物理学报, 35(3): 380-388. |
| [43] | 徐世浙, 李予国, 刘斌. 1997. 大地电磁Hx型波二维地形改正的方法与效果. 地球物理学报, 40(6): 842-846. |
| [44] | 赵国泽, 汤吉, 詹艳等. 2004. 青藏高原东北缘地壳电性结构和地块变形关系的研究. 中国科学(D辑), 34(10): 908-918. |