就叠后地震数据体而言,利用同相轴的不连续性或者其几何形态是多年来用作断裂刻画的两种主流方法,其代表性的分别为地震相干体计算(Bahorich and Farmer,1995; Marfurt et al.,1998; Gersztenkorn and Marfurt.,1999; Marfurt et al.,1999; Cohen and Coifman,2002; Lu et al.,2005; 谢春临等,2011; 杨涛涛等,2013)与地震曲率属性(Lisle,1994; Roberts,2001; Sigismondi and Soldo,2003; Al-Dossary and Marfurt,2006; Blumentritt et al.,2006; Chopra and Marfurt,2007,2010;王雷等,2010;杨威等,2011;印兴耀等,2014).可以说两种方法各有其优缺点.相干体利用波形的相似性,找出界面的不连续性.理论上,有断裂的地方,无论其断距大小,地震反射界面经过断点时,都会产生地震波振幅及相位的变化,从而引起较低的相干值.对于实际叠后地震资料,受数据处理过程的影响,例如叠加、滤波处理,特别是背景噪声较大,在提高信噪比过程中的平滑滤波,往往会增大断裂处的相干值,从而影响到相干体刻画断裂的精度,因此常常需要在提高信噪比与断裂刻画精度之间做出权衡.而曲率属性则直接通过断裂面的几何形状刻画断裂,它在一定程度上弥补了平滑滤波的影响.但是曲率属性基于二次曲面的考虑,因此常遇到一些具二次曲面特征的地质界面,例如谷地、褶皱转折端等在断裂刻画时造成混淆的情况.另外,当断距比较小时,曲率属性也表现出刻画精度的不足(Yu,2014).针对以上问题,Yu(2014)依断裂面的几何性质,考虑到对断开的界面 及断裂面进行拟合后的曲面是一个具有拐点的三次或更高次的曲面,因此提出了曲率变化率的方法,本次研究在之前工作的基础上,进一步发展了以柱面拟合为基础的断裂刻画方法,在保持原有刻画精度的基础上,显著地提高了计算结果的信噪比.
2 断裂模型分析如图 1a所示,通常断裂面表现为一个曲面,如果用两个相互平行的竖直平面切割这个断裂模型,则当两平面逐渐靠近时,将产生一个次级“阶梯状”模型,如图 1b所示.此时,断裂面将趋于一个平面,而断裂面同两侧地层界面的组合(图 1b中阴影部分)则表现为一个柱面,该柱面具有分段函数表达式.为了表征的方便,我们可以用另一个与之近似的可用连续函数表达的柱面(图 1c)对该模型进行拟合,进而提取所需属性来刻画断裂.令 r 表示图 1c中曲面,则有
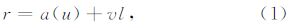
|
图 1 断裂模型分析(修改自Yu,2014) (a)一般断裂模型;(b)断裂子模型;(c)拟合曲面. Fig. 1 Analysis of a fault model(modified from Yu,2014) (a)Fault model;(b)Sub-fault model;(c)Fitting surface of the faulted horizon. |
Yu(2014)根据准线 a(u)存在拐点,具有至少三阶连续可导的特点,用三次函数对其进行拟合,并求拟合曲线的曲率变化率.计算结果表明,相对于曲率属性,曲率变化率在刻画断裂的精度上得到了提高.对于一般三阶以上连续可导的函数 z(x),其曲率变化率 $\overset{\centerdot }{\mathop{\kappa }}\,$计算公式如下:

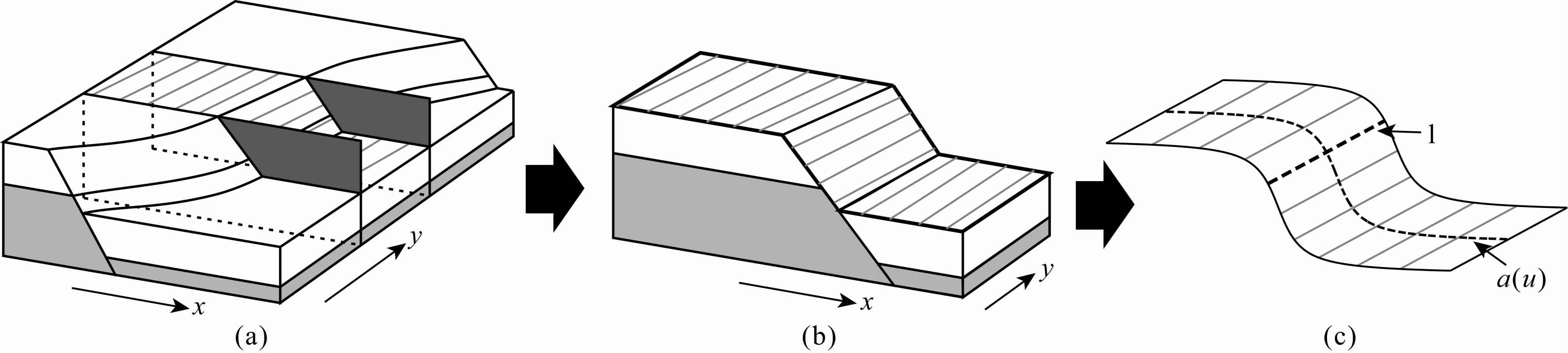
进一步的分析可知,对于三次曲线 z(x),其两端延伸方向同z轴(拟合时地震记录的垂向轴)夹角小于45°,但实际地层界面倾角多介于0°~45°,较少介于45°~90°,即界面延伸方向更趋于水平方向,而非竖直方向.特别是地震所能记录到的资料更是如此,如图 1c中准线两端延伸方向通常与x轴或y轴(横向)的夹角小于45°,而同z轴(垂向)夹角大于45°,这种同三次曲线的延伸方向的不一致就导致了拟合时时常产生“噪声”.如图 2a所示,为了对图中断裂模型较好地拟合,在选用三次曲线时,必须要加大三次函数中一次项的权重,如选 z=0.3x3-1.5x(其函数图形见图 2a中拟合曲线),可以对其中的断裂模型进行较为合适地拟合.该三次曲线的曲率及曲率变化率如图 2a所示,可见,同曲率相比,曲率变化率对断裂的敏感性更强,但是一个断裂对应了4个曲率变化率极值,这将会影响到计算结果的断裂分辨能力.本次研究,充分考虑了实际断裂模型的这一特点,选用反正切函数 z=-arctanx 来拟合断裂模型,如图 2b所示,反正切函数同断裂模型吻合很好,同时基于此函数的曲率变化率克服了三次曲线曲率变化率的不足,即只有一个极大值,这在利用该属性提取断裂信息时,能够有效地提高了计算结果的分辨率.
|
图 2 曲率及曲率变化率的对比 (a)曲率;(b)曲率变化率. Fig. 2 Comparison of curvature and curvature change rate (a)Curvature;(b)Curvature change rate. |
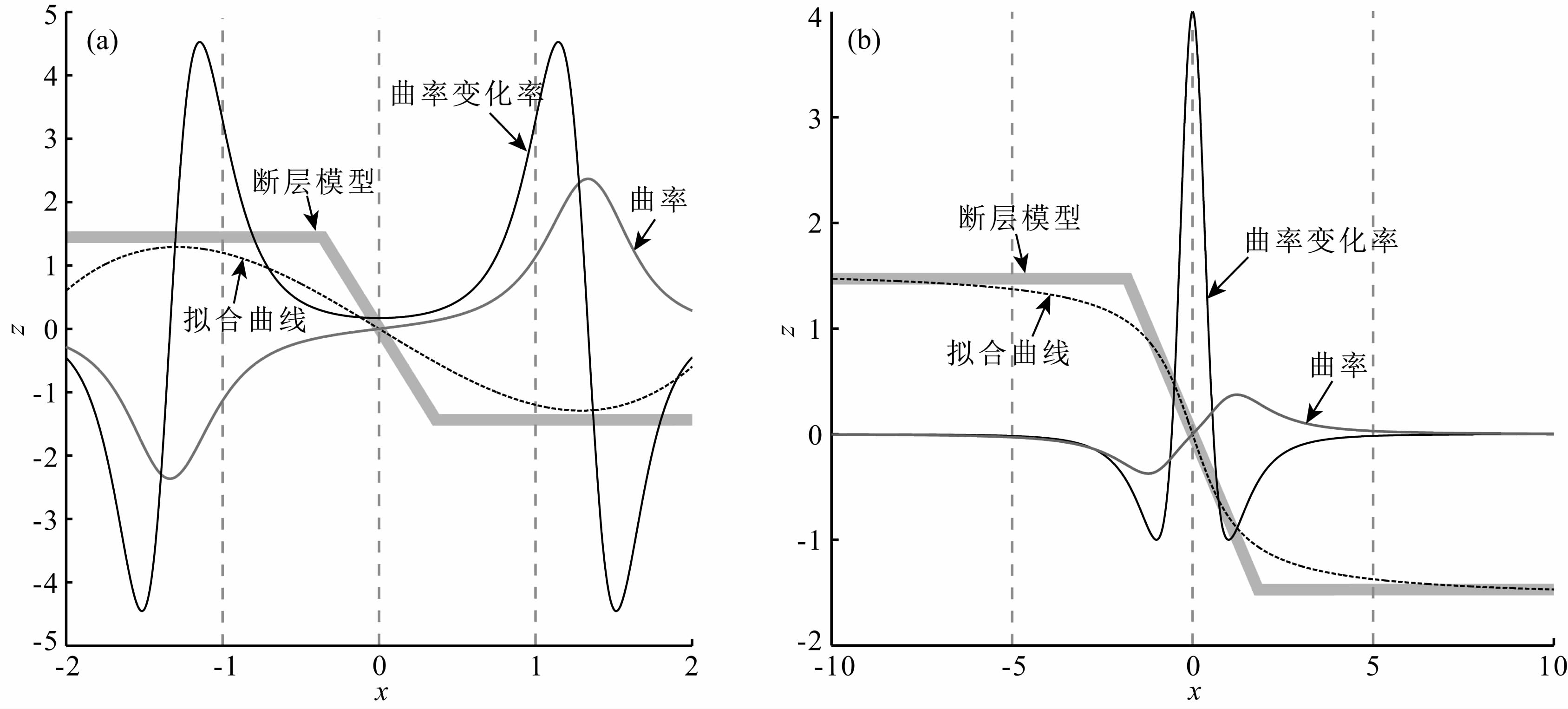
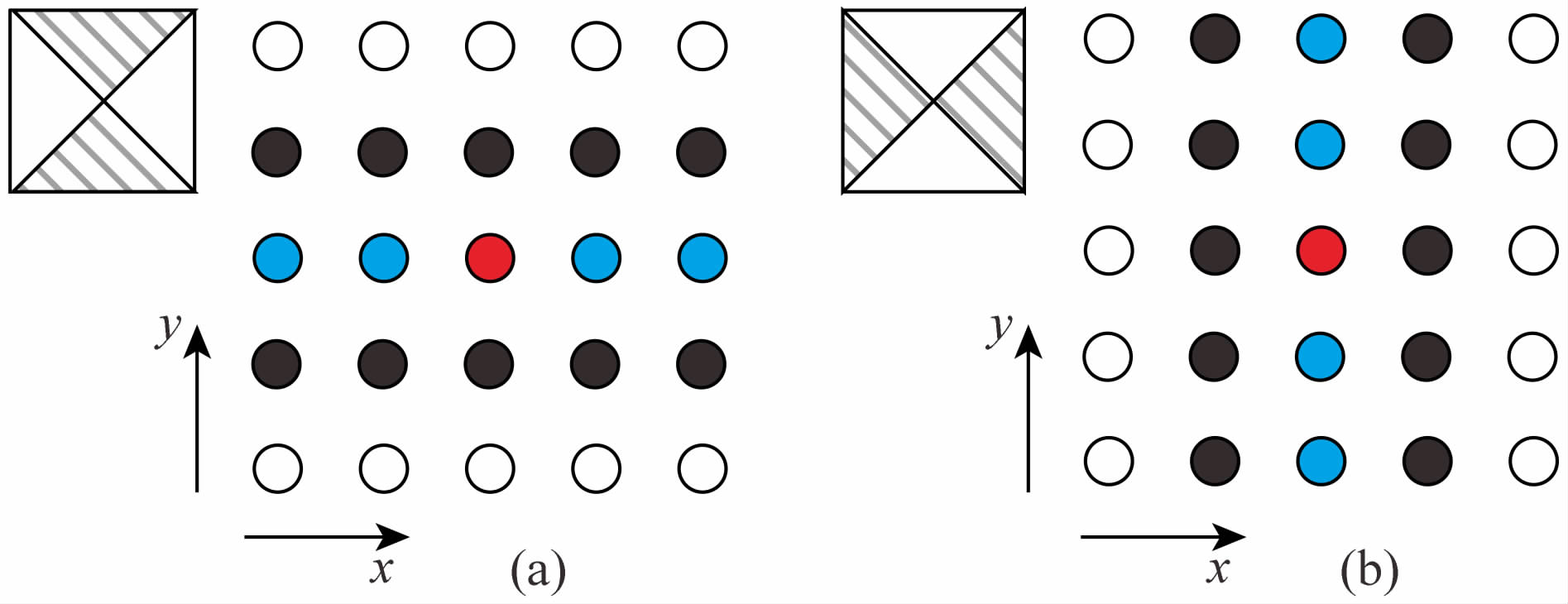
如前文所述,我们可以利用以反正切函数为准线的柱面对断裂面及两侧地层界面的组合进行拟合,然后计算柱面准线的曲率变化率,以此来刻画断裂.该方法包括对断裂模型的拟合及曲率变化率的求取两个方面,其中对断裂模型的拟合分为柱面直母线拟合与准线拟合两个步骤.为了完整表达柱面,我们在水平方向(xy平面)选择5×3个样点(以图 3中彩色及黑色实心圆表示),5个样点方向即为柱面准线延伸方向,3组5个样点是为了确定柱面直母线的延伸方向.
|
图 3 计算所需的样点组合 (a)、(b)沿不同方向选取样点组. Fig. 3 Plan viewof sample sets involved in the computations in this study (a)、(b)Sample sets along different directions. |
对于直母线 l 延伸方向(即断裂的走向),由于涉及到不同样点组的选择,我们首先限定其所在区间.如图 3(a、b)中左上角插图阴影部分所示,图a中代表断裂走向与y轴夹角呈-45°到45°,而图b中代表断裂走向与x轴夹角呈-45°到45°.这两种情况代表了断裂所有可能的走向.对于每种情况,分别拟合其中5个彩色样点,进而求拟合曲线的曲率变化率,受断裂模型自身特点的制约,曲率变化率大者更加接近断裂面倾向的方向,也即确定了断裂走向区间.具体包括两个步骤,分别为:
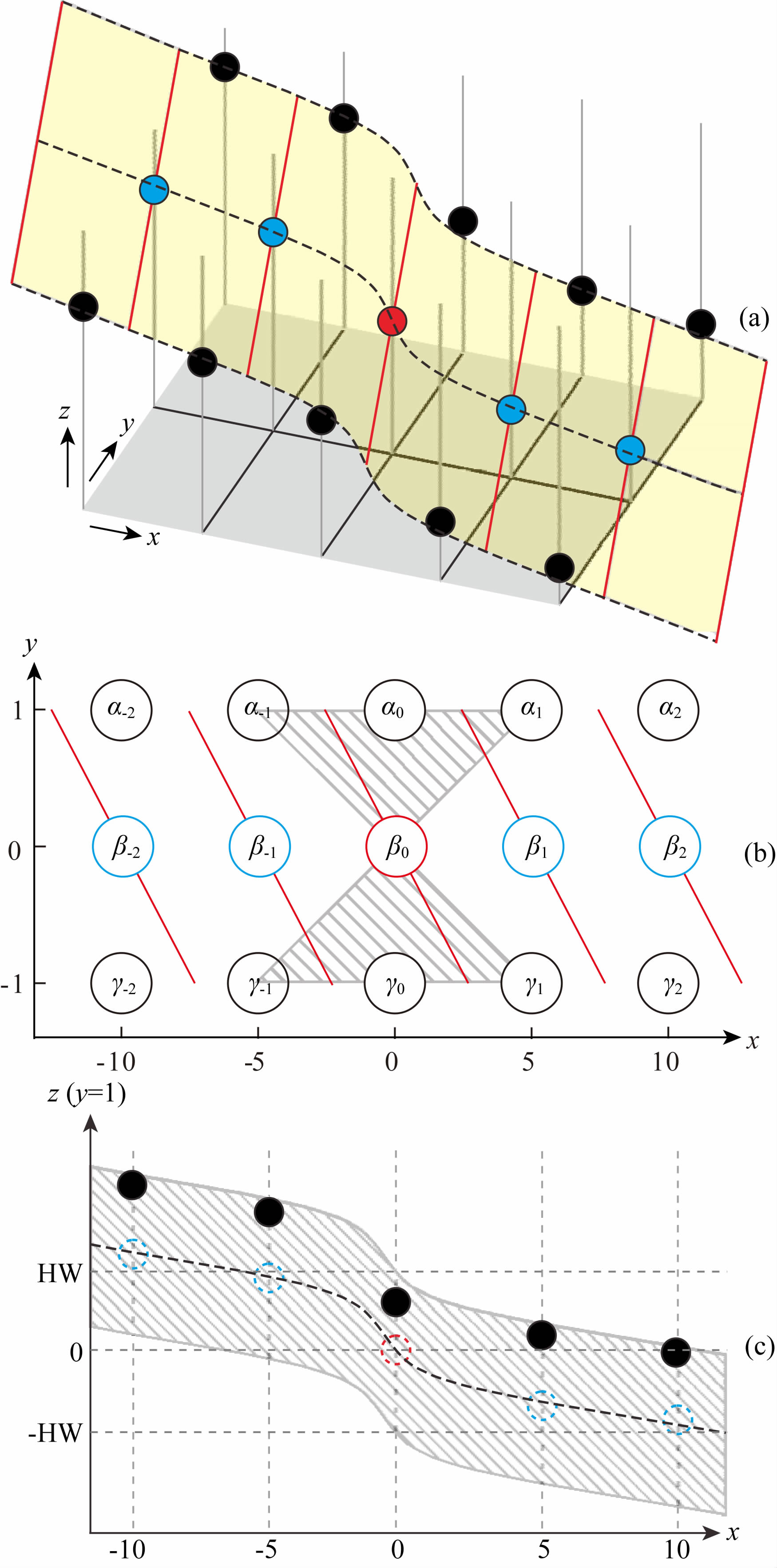
1)样点的拟合.基于前文断裂模型的分析,我们可以用反正切函数对断裂及两侧被断开的界面组合进行很好的拟合.以图 3a样点为例,其样点的空间分布如图 4a所示,各样点的编号如图 4b所示.令坐标原点位于分析点(红色实心圆表示).为了便于拟合,令x轴方向各相邻样点水平间距为5,这样样点分布范围为-10到10.如图 2b中拟合曲线所示,当以闭区间[-10,10]截取反正切函数时,其符合所期望的函数图形.另外,为了便于讨论,令y轴方向各相邻样点水平间距为1.在y=0平面,用以下一般的反正切函数
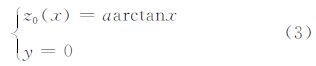
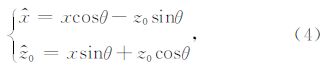
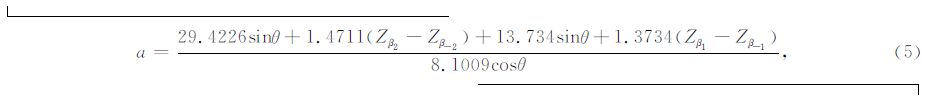
|
图 4 柱面拟合示意图 (a)样点空间分布及柱面拟合示意;(b)、(c)样点编号及扫描范围示意. Fig. 4 Schematic diagram of cylindrical surface fitting (a)Perspective view of the samples involved in the calculation;(b)、(c)Sample number and scanning scope. |
2)在上一步反正切函数拟合的基础上,计算拟合曲线的曲率变化率.我们只需求(3)式中反正切函数的一、二、三阶导数并代入(2)式即得其曲率变化率,推导过程从略,结果为

比较图 3(a、b)中两种情况下曲率变化率在分析点处的值,其中较大者即指明了柱面直母线方向 所在的区间.这里不妨假设图 3a中5个彩色样点的拟合曲线在 分析点处具有较大的曲率变化率,那么我们用图 3a中15个样点来进一步确定柱面直母线方向.假设通过原点的直母线与平面y=1的交点为(p,q),柱面与平面y=1相交于z1,那么根据柱面 性质,z1在形状上与z0完全相同,只是产生了一定的位移,水平位移为p,垂向位移为q,即在平面y=1,有

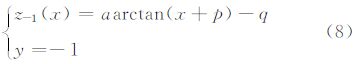
接下来,我们有两种方法确定p、q值.一种是解析法,通过z1、z-1分别同平面y=1、y=-1内的样点进行拟合来确定,另一种是利用逐点扫描法,令p、q在一定范围内逐点取值,求得 z1、z-1 后,再求其与平面y=1、y=-1内各样点的差值,当差值绝对值的和取到最小时,所对应的p、q即为所求.由于第一种方法求解过程中涉及到反三角函数同幂函数乘积的混合求解问题,难以获得解析表达式,因此本次研究采用后者.
如图 4b、c所示,图中阴影部分代表了p、q的取值范围,即p∈[-5,5],q∈[-HW,HW],其中HW为半时窗.通过逐点将(p,q)代入(7)、(8)式,并比较曲线与样点的差值大小,最终确定p、q值.
3.2 柱面准线拟合及曲率变化率的求取在上一步骤中,我们实际上已经对柱面准线在一定程度上进行了拟合,只是仅用到了5个采样点(即图 3中的5个彩色样点),而没有使所有样点参与计算,这样会影响结果的精度及稳定性.如图 4b,对各样点进行编号,利用上一步确定的p、q值,基于最小二乘法,通过(3)、(7)、(8)式的反正切函数对图 4中15个样点进行拟合,确定a值.略去繁琐的推导过程,其结果如下:

最后计算分析点处的曲率变化率,由于坐标原 点设在分析点处,因此(6)式中x=0,于是计算简化为

该方法以同相轴所代表的地质界面形态为基础.当界面发生断裂时,沿断裂面倾向,曲率变化率具有极大值.由于首先对断开的界面进行柱面拟合,柱面准线的延伸方向与断裂面倾向一致,这样通过计算柱面准线的曲率变化率,能够保证计算结果取得极大值,因此能够反映出断裂存在.理论上,在合理拟合断裂的前提下,只要存在垂向上的断距,无论大小,都可以得到曲率变化率的相对高值,但是实际资料,即使滤波处理后,仍存在不少噪声干扰、同相轴横向强弱变化等,均能对结果产生干扰作用.受实际资料的约束,计算结果定性地反映了小断距断裂的平面分布情况.
曲率变化率对界面的变化较为敏感,对地震资料的品质有一定的要求.一般情况下,当信噪比较低时,往往难以从曲率变化率计算结果中,有效分辨出单条断裂,此时,需要对同相轴做平滑处理(如中值滤波、构造约束滤波等).在同相轴平滑处理过程中,界面的形态通常能够保持,特别是断裂引起的界面弯曲形态不会因为平滑而消失.因此,当地震资料品质不高时,只需对其进行平滑滤波,再进行曲率变化率的计算,这样不但能提高结果的信噪比,亦能有效地保留断裂信息.
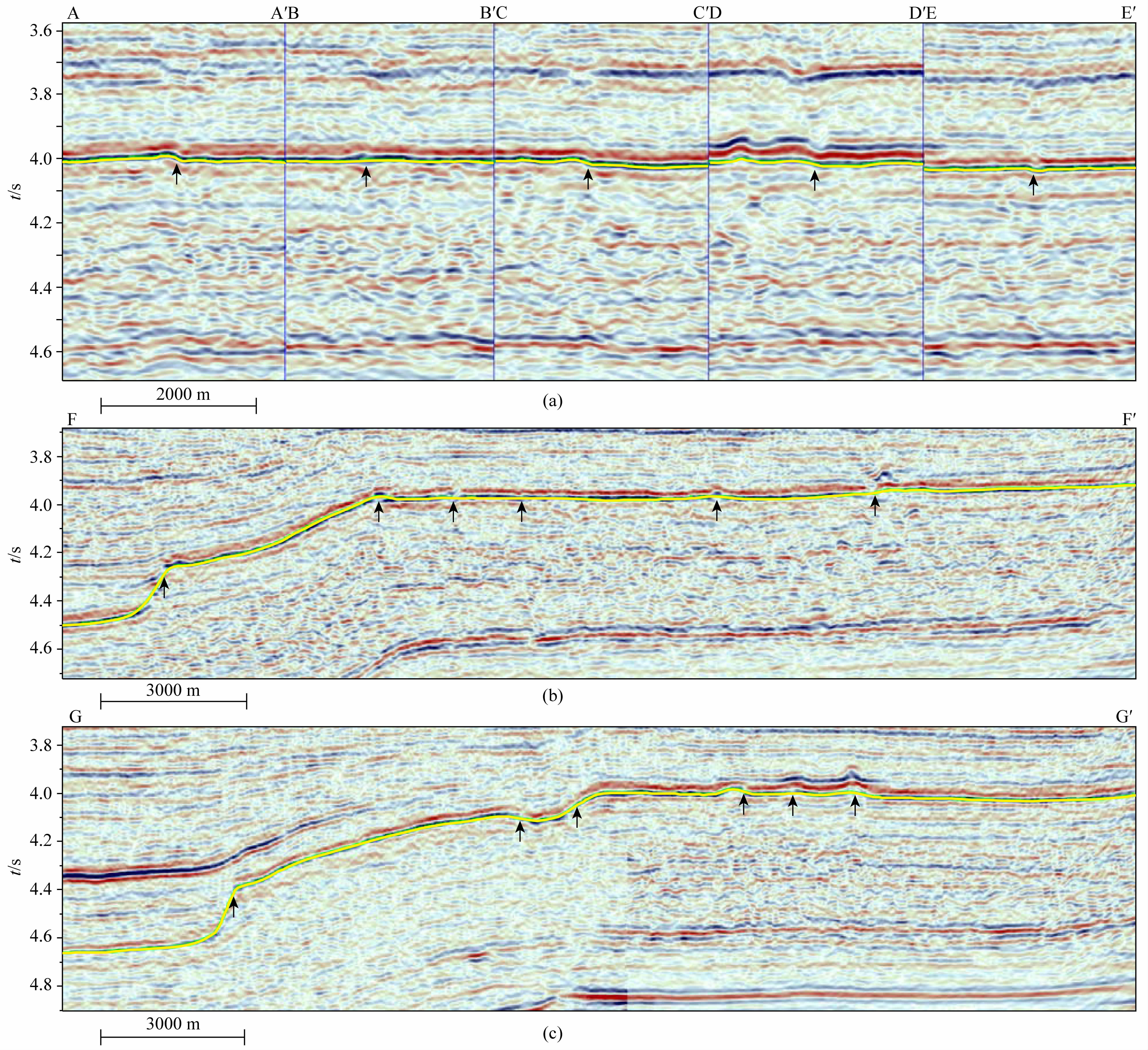
4 应用实例及效果对比下面用一个实例来考察本文方法的优越性.实际叠后地震资料来源于塔中北斜坡的西部平台区,2 ms采样率,面元为25×25 m.该地区,如图中黄线标出的地层界面之上为桑塔木组海相碎屑岩沉积,界面之下为良里塔格组碳酸盐岩沉积,二者之间较大的波阻抗差,使得良里塔格组顶界面在地震资料中被清晰地记录.这也为我们对断裂刻画结果的验证提供了良好的基础.如图 5a中AA′-EE′为同一条 断裂不同段的横切剖面,(b、c)中FF′、GG′为横跨不同断裂的剖面.图中黑色箭头指明了断裂位置.这些剖面中大多数断裂的断距都比较小,另外同一条断裂,不同段断距也不尽相同,如图 5a中BB′、EE′两处断距明显小于AA′、CC′、DD′,甚至在地震剖面上,不经过反复对比,难以识别.这些地震剖面的位置如图 6所示.
|
图 5 横跨断裂的地震剖面 (a)同一断裂不同部分;(b)、(c)横跨不同断裂. Fig. 5 Vertical cross sections across faults and fractures (a)Sections AA′-EE′ across different portions of a fault;(b)、(c)Sections FF′ and GG′ across different faults and fractures. |

|
图 6 不同地震属性断裂刻画效果对比 (a)相干技术;(b)曲率;(c)三次曲线的曲率变化率;(d)反正切曲线的曲率变化率. Fig. 6 Comparison of slices through different seismic attribute volumes (a)Coherence;(b)Curvature;(c)Curvature change rate of cubic curve;(d)Curvature change rate of arctan curve. |
图 6为由不同方法计算的属性体,沿良里塔格组顶面提取的属性切片.(a—d)为分别用地震相干技术、曲率及两种不同柱面拟合下的曲率变化率计算的结果.显然传统的相干技术及曲率属性,在刻画断裂时损失了不少细节,特别是断距较小时.如BB′、EE′在曲率切片上没能显示,EE′在相干体切片上也没能得到显示.相比之下,两种曲率变化率切片刻画出了许多断裂细节,如上述断距较小的BB′、EE′都得到了清晰显示.但是与图 6d相比,图 6c的信噪比较低,这是解释中所不希望出现的结果,因此本次研究在之前研究的基础上,既保留了断裂刻画的细节,又有效地提高了刻画结果的信噪比.如图 2a所示,如果利用三次曲线作为柱面拟合时的准线,则当地层界面倾角较小时,可能会出现同一条断裂对应多个曲率变化率极值,这势必引起许多干扰,特别是断裂密集处,对单条断裂的识别带来一定的困难(图 6c).而使用反正切函数作为柱面准线时(图 2b),有效避免了同一条断裂出现多个极值的问题.对应于本例中的图 6d,可见干扰信号明显得到了抑制,有效改善了个别断裂的拾取.
柱面拟合下的曲率变化率断裂刻画方法是对相干体技术、地震曲率属性的补充,由于其对界面变化的敏感性高于曲率,因此,其优势在于能够刻画更低级别的小断距断裂.实际地质情况,存在诸如河道、带状隆起等局部具有类似断裂的界面组合,会导致该方法存在多解性.因此,在实际地震解释中,应该视其为辅助方法,同时结合剖面的观察,才能既高效地表征断裂,又可避免错误的解释.
5 结论本次研究依断裂模型自身特点,提出了以反正切函数为准线的柱面对断裂模型进行拟合,进而求取准线的曲率变化率达到刻画断裂的目的.曲率变化率本质上具三阶导数特征,对断裂发生处的界面变化较曲率更加敏感,实践表明,同传统的曲率及相干技术相比,曲率变化率能有效地提高断裂刻画的精度,特别是对断距较小,地震剖面上不易直观识别的断裂亦能有效揭示.本方法是对柱面拟合法刻画断裂的进一步发展,考虑到了实际地层倾斜情况,以反正切函数代替三次曲线作为柱面的准线,其计算结果在信噪比方面有了显著的改善.
| [1] | Al-Dossary S, Marfurt K J. 2006. 3D volumetric multispectral estimates of reflector curvature and rotation. Geophysics, 71(5): P41-P51. |
| [2] | Bahorich M, Farmer S. 1995. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube. The Leading Edge, 14(10): 1053-1058. |
| [3] | Blumentritt C H, Marfurt K J, Sullivan E C. 2006. Volume-based curvature computations illuminate fracture orientations—Early to mid-Paleozoic, Central Basin Platform, west Texas. Geophysics, 71(5): B159-B166. |
| [4] | Chopra S, Marfurt K J. 2007. Volumetric curvature attributes for fault/fracture characterization. First Break, 25(7): 35-46. |
| [5] | Chopra S, Marfurt K J. 2010. Integration of coherence and volumetric curvature images. The Leading Edge, 29(9): 1092-1107. |
| [6] | Cohen I, Coifman R R. 2002. Local discontinuity measures for 3-D seismic data. Geophysics, 67(6): 1933-1945. |
| [7] | Gersztenkorn A, Marfurt K J. 1999. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping. Geophysics, 64(5): 1468-1479. |
| [8] | Lisle R J. 1994. Detection of zones of abnormal strains in structures using Gaussian curvature analysis. AAPG Bulletin, 78(12): 1811-1819. |
| [9] | Lu W K, Li Y D, Zhang S W, et al. 2005. Higher-order-statistics and supertrace-based coherence-estimation algorithm. Geophysics, 70(3): P13-P18. |
| [10] | Marfurt K J, Kirlinz R L, Farmer S L, et al. 1998. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics, 63(4): 1150-1165. |
| [11] | Marfurt K J, Sudhakerz V, Gersztenkorn A, et al. 1999. Coherency calculations in the presence of structural dip. Geophysics, 64(1): 104-111. |
| [12] | Roberts A. 2001. Curvature attributes and their application to 3D interpreted horizons. First Break, 19(2): 85-100. |
| [13] | Sigismondi M E, Soldo J C. 2003. Curvature attributes and seismic interpretation: Case studies from Argentina basins. The Leading Edge, 22(11): 1122-1126. |
| [14] | Wang L, Chen H Q, Chen G W, et al. 2010. Application of curvature attributes in predicting fracture-developed zone and its orientation. Oil Geophysical Prospecting (in Chinese), 45(6): 885-889. |
| [15] | Xie C L, Chen S M, Jiang C J, et al. 2011. Application of a method combining trend surface analysis and coherence cube technology to volcanic prediction. Chinese J. Geophys. (in Chinese), 54(2): 368-373, doi: 10.3969/j.issn.0001-5733.2011.02.013. |
| [16] | Yang T T, Wang B, Lü F L, et al. 2013. The application of seismic coherence technology for petroleum exploration. Progress in Geophysics (in Chinese), 28(3): 1531-1540, doi: 10.6038/pg20130349. |
| [17] | Yang W, He Z H, Chen X H. 2011. Application of three-dimensional volumetric curvature attributes to fault identification. Progress in Geophysics (in Chinese), 26(1): 110-115, doi: 10.3969/j.issn.1004-2903.2011.01.011. |
| [18] | Yin X Y, Gao J H, Zong Z Y. 2014. Curvature attribute based on dip scan with eccentric window. Chinese J. Geophys. (in Chinese), 57(10): 3411-3421, doi: 10.6038/cjg20141027. |
| [19] | Yu J B. 2014. Using cylindrical surface-based curvature change rate to detect faults and fractures. Geophysics, 79(5): O1-O9. |
| [20] | 王雷, 陈海清, 陈国文等. 2010. 应用曲率属性预测裂缝发育带及其产状. 石油地球物理勘探, 45(6): 885-889. |
| [21] | 谢春临, 陈树民, 姜传金等. 2011. 趋势面分析与相干体技术在火山岩预测中的应用. 地球物理学报, 54(2): 368-373, doi: 10.3969/j.issn.0001-5733.2011.02.013. |
| [22] | 杨涛涛, 王彬, 吕福亮等. 2013. 相干技术在油气勘探中的应用. 地球物理学进展, 28(3): 1531-1540, doi: 10.6038/pg20130349. |
| [23] | 杨威, 贺振华, 陈学华. 2011. 三维体曲率属性在断层识别中的应用. 地球物理学进展, 26(1): 110-115, doi: 10.3969/j.issn.1004-2903.2011.01.011. |
| [24] | 印兴耀, 高京华, 宗兆云. 2014. 基于离心窗倾角扫描的曲率属性提取. 地球物理学报, 57(10): 3411-3421, doi: 10.6038/cjg20141027. |
 2015, Vol. 58
2015, Vol. 58

